The effect of foreign currency hedging on the probability of financial distress
I thank Don Adams, Phil Dolan, Robert Faff (the Editor), Doug Foster, Elizabeth Sheedy, Tom Smith, Garry Twite, an anonymous referee, and seminar participants at the Australian National University, Macquarie University and the 2008 Accounting and Finance Association of Australia and New Zealand Conference for their helpful comments and suggestions. Financial support from the Macquarie University Applied Finance Centre is gratefully acknowledged. All remaining errors are mine.
Abstract
This paper investigates the effect of foreign currency hedging with derivatives on the probability of financial distress. I use Merton’s (1974) structural default model to compute firms’ distance to default as a proxy for their probability of financial distress. Using an instrumental variables approach to control for endogenous hedging and leverage, I find that the extent of foreign currency hedging is associated with a lower probability of financial distress. Whereas previous research finds that the probability of financial distress is a determinant of a firm’s hedging policy, this paper provides direct evidence supporting the hypothesis that the extent of hedging reduces a firm’s probability of financial distress.
1. Introduction
Theories of hedging based on capital market imperfections argue that firms have incentives to reduce the probability of financial distress by hedging with derivatives. In this paper, I analyse the effect of foreign currency hedging with derivatives on the probability of financial distress.
The estimation of the effect of foreign currency hedging on the probability of financial distress is not straightforward, as it requires both a consideration of the potential endogeneity of hedging and leverage with respect to the probability of financial distress, and an accurate measure of the probability of financial distress. Ignoring the endogeneity of hedging and leverage with respect to the probability of financial distress can underestimate the direct effect of foreign currency hedging on the probability of financial distress. For example, Smith and Stulz (1985) argue that by decreasing volatility, hedging reduces the probability of financial distress, and hence, the expected costs of financial distress. However, Stulz (1996) and Leland (1998) argue that by reducing the probability of financial distress, hedging increases debt capacity. Consequently, an increase in leverage in response to greater debt capacity can offset the aforementioned reduction in the firm’s probability of financial distress. To estimate the direct effect of foreign currency hedging on the probability of financial distress, I use an instrumental variables approach to control for the potential endogeneity of hedging and leverage with respect to the probability of financial distress.
My proxy for a firm’s probability of financial distress is its 1-year distance to default, which is estimated using Merton’s (1974) structural default model. The distance to default measures the difference between the asset value of a firm and the face value of its debt, scaled by the standard deviation of the firm’s asset value. A higher distance to default is associated with a lower probability of financial distress. The distance to default has been adopted in industry by Moody’s KMV and has recently been applied in academic research to estimate a firm’s probability of financial distress.1
I examine whether the extent of foreign currency hedging with derivatives is associated with a higher distance to default. If hedging and leverage are assumed to be exogenous, the extent of foreign currency hedging is positively related to the distance to default, but statistically insignificant. However, after controlling for the endogeneity of hedging and leverage with respect to the distance to default, I find that the extent of foreign currency hedging is associated with a greater distance to default, and hence, a lower probability of financial distress. These results highlight the importance of controlling for endogeneity. I also examine whether the decision to hedge foreign currency risk with derivatives affects the distance to default. I find no evidence that the decision to hedge foreign currency risk is associated with a greater distance to default. This implies that it is not merely the decision to hedge foreign currency risk, but rather the extent of foreign currency hedging that affects the probability of financial distress.
The main contribution of this paper is to provide direct evidence supporting the hypothesis that the extent of foreign currency hedging with derivatives reduces a firm’s probability of financial distress. Previous studies use leverage as a proxy for the probability of financial distress and find that firms with greater leverage hedge more with derivatives.2 The results from these studies are consistent with the hypothesis that the larger the probability of financial distress, the greater the amount of hedging with derivatives. However, unlike this paper, these studies do not examine whether hedging with derivatives is associated with a lower probability of financial distress. This paper also contributes to the literature that investigates the effect of hedging on leverage and the cost of debt financing. Graham and Rogers (2002) find evidence that the extent of hedging increases leverage with the associated tax benefits averaging 1.1 per cent of firm value. Graham and Rogers (2002) argue that the increase in leverage is in response to a reduction in the probability of financial distress induced by hedging. Additionally, Campello et al. (2011) find that firms pay lower interest spreads after hedging programmes are put in place. Campello et al. (2011) argue that this reduction in the cost of debt financing results from a reduction in the probability of financial distress caused by hedging. My paper compliments Graham and Rogers (2002) and Campello et al. (2011) by providing evidence that the extent of hedging is associated with a lower probability of financial distress. Finally, this paper also contributes to the literature that investigates whether firms use derivatives to reduce or increase risk. For example, Guay (1999) finds that firm risk decreases after the initiation of a derivatives programme, while Hentschel and Kothari (2001) find that the use of derivatives neither reduces nor increases firm risk. My findings are consistent with the notion that derivatives are used to reduce rather than to increase risk.
The remainder of this paper is organised as follows. Section 2 reviews prior research on hedging and the probability of financial distress. Section 3 describes the data. Section 4 describes the empirical framework and the construction of the variables used in the analysis. Section 5 presents the results on the relation between foreign currency hedging and the distance to default. Section 6 concludes.
2. Prior research
The relationship between hedging and the probability of financial distress can be grouped into two theoretical explanations. First, Smith and Stulz (1985) argue that by reducing the volatility of firm value, hedging decreases the probability of financial distress, and hence, the expected costs of financial distress. These costs include direct bankruptcy costs, higher contracting costs, the loss of tax shields and the loss of valuable investment opportunities. Bessembinder (1991) extends the Smith and Stulz (1985) financial distress argument by showing that hedging can reduce the incentives for shareholders to underinvest. Second, Stulz (1996) and Leland (1998) argue that by reducing the probability of financial distress, hedging increases a firm’s debt capacity. An increase in leverage in response to greater debt capacity increases firm value because of the tax deductibility of interest payments. Leland (1998) argues that the primary gain from a lower probability of financial distress induced by hedging comes from the tax benefits associated with increased leverage. Leland (1998) notes that this result can be contrasted with Smith and Stulz (1985) who emphasise lower expected financial distress costs given fixed leverage. However, Leland (1998) also argues that some benefits come from lower expected financial distress costs because a portion of the increased debt capacity remains unused.
The above-mentioned theories lead to several empirical predictions. First, if financial distress is costly, the probability of financial distress should be a determinant of a firm’s hedging policy. Second, with fixed leverage, hedging should reduce the probability of financial distress. Finally, hedging should lead to greater debt capacity. Several studies have examined whether the probability of financial distress is a determinant of a firm’s hedging policy. For example, Tufano (1996), Berkman and Bradbury (1996), Gay and Nam (1998), Howton and Perfect (1998), Haushalter (2000), Graham and Rogers (2002), and Knopf et al. (2002) use leverage as a proxy for the probability of financial distress and find that hedging is positively related to leverage. These studies interpret a positive leverage coefficient as evidence that the greater the probability of financial distress the greater the likelihood and extent of hedging. Additionally, Graham and Rogers (2002) find that the extent of hedging is associated with an increase in leverage. This paper extends the literature by directly investigating the relationship between hedging and the probability of financial distress. Specifically, I explore whether hedging with foreign currency derivatives directly reduces the probability of financial distress.
3. Sample
I construct a sample of 401 large US nonfinancial firms over the period 1996 to 2000, based on the screening criteria in Allayannis and Weston (2001). The sample consists of nonfinancial firms listed in COMPUSTAT’s Industrial Annual Files with total assets of more than $500 million in each fiscal year between 1996 and 2000. I retain observations that meet the following criteria: the firm has no missing data on sales and market value; the firm is not financial (SIC codes 6000–6900); the firm is not a regulated utility (SIC codes 4900–4999); the firm’s 10-K reports are available from EDGAR; the firm’s daily stock return is available from the Center for Research in Security Prices (CRSP); the firm has short-term or long-term debt outstanding at fiscal year end; and the firm discloses the notional value of its foreign currency derivative holdings, if any. I further restrict the sample to those firms that face ex-ante foreign currency risk. This is important because it allows us to interpret the absence of foreign currency derivatives as a decision not to hedge rather than a lack of foreign currency risk. I follow Allayannis and Ofek (2001) and Allayannis and Weston (2001) and define firms to have ex-ante foreign currency risk if they disclose foreign sales from operations abroad in the COMPUSTAT Geographic Segment files in the fiscal year of derivative usage. One concern with selecting firms based on their foreign sales from operations abroad is that a firm might not face ex-ante foreign currency risk because of its foreign sales being denominated in US dollars. I therefore exclude from the sample firms that state in their 10-K report that they do not have any foreign currency risk because the majority of their foreign sales are denominated in US dollars. The final sample consists of 401 firms from 1996 to 2000, or 1824 firm year observations, with 324 firms present in all 5 years.3
During the sample period, Statement of Financial Accounting Standard (SFAS) 119 required firms to disclose the notional value, nature and terms of their derivative contracts. SFAS 119 also required firms to disclose whether they use derivatives for trading or nontrading purposes. I only examine foreign currency derivatives held for nontrading purposes. The Financial Accounting Standards Board issued SFAS 133 in June 1998 to supersede SFAS 119. SFAS 133, which is effective for fiscal years beginning July 15, 2000, requires firms to disclose the fair market value of their derivative contracts but does not require the disclosure of notional values. Consequently, the last year of my sample is 2000 because the data are not sufficiently detailed after that time.
4. Empirical framework and variable construction
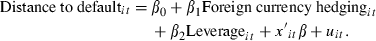()Included in xit are control variables that are discussed in Section 4.2.3. I also include year dummies to control for common shocks to the distance to default of all firms and industry fixed effects at the two-digit SIC level. I do not include firm fixed effects because the main variable of interest in this paper, the extent of foreign currency hedging, has a within firm standard deviation of only 3 per cent and hence varies little over time for a given firm. All standard errors are adjusted for heteroskedasticity (White, 1980) and firm clustering, which accounts for correlation across observations of a given firm. Because a higher distance to default is associated with a lower probability of financial distress, I expect β1, the coefficient on the extent of foreign currency hedging, to be positive.
I use an instrumental variables approach to disentangle the simultaneity of the distance to default, foreign currency hedging and leverage. Identifying the effect of foreign currency hedging on the distance to default requires instrumental variables that affect foreign currency hedging and leverage but do not directly impact the distance to default. The instrumental variables used in the analysis are discussed in Section 4.3. I initially estimate equation (1) with two-stage least squares (2SLS). As 2SLS is suboptimal in the presence of heteroskedasticity, I also estimate equation (1) with a generalised method of moments instrumental variables approach (GMM IV).
4.1. Dependent variable: distance to default
My proxy for the probability of financial distress is a firm’s 1-year distance to default, which is estimated using Merton’s (1974) structural default model. The distance to default measures the number of standard deviations of asset value by which a firm’s assets exceeds the face value of its debt. The estimation of the distance to default follows Crosbie and Bohn (2003), Bharath and Shumway (2008), Hillegeist et al. (2004), and Vassalou and Xing (2004). I use the distance to default as the dependent variable in the analysis rather than the implied probability of default from Merton’s (1974) model because there is much greater variation in the distance to default than the implied probability of default. The details of the calculation of the distance to default are described in the Appendix I.
Alternative proxies for the probability of financial distress include Altman’s (1968)Z-score and Ohlson’s (1980) O-score. These accounting models, however, use information derived from financial statements. Such information is backward looking, because financial statements are designed to measure a firm’s past performance and may not be very informative about the future prospects of a firm. In contrast, Merton’s (1974) model uses the market value of a firm’s equity when calculating its distance to default. As market prices reflect investors’ expectations about a firm’s future prospects, they contain forward looking information, which is thought to be better suited to estimating the likelihood that a firm might default in the future. Moreover, accounting models do not incorporate a firm’s asset volatility when estimating its probability of financial distress. As Hillegeist et al. (2004) suggest asset volatility is important in estimating a firm’s probability of financial distress because it captures the likelihood that the market value of a firm’s assets will fall below the face value its debt. Furthermore, Hillegeist et al. (2004) assess the performance of Merton’s (1974) model with Altman’s (1968)Z-score and Ohlson’s (1980) O-score and find that the theoretical probability of financial distress implied by Merton’s (1974) model, based on the distance to default, provides significantly more information than Altman’s (1968)Z-score and Ohlson’s (1980) O-score. Additionally, Duffie et al. (2007) find that the term structure of conditional default probabilities estimated from bankruptcy data significantly depends on a firm’s distance to default. These findings lend support to the use of the distance to default as a proxy for the probability of financial distress.
4.2. Explanatory variables
4.2.1. Foreign currency hedging
Following previous research, I assume that firms conduct their hedging through the use of derivatives. Consequently, this study investigates the effect of hedging with foreign currency derivatives on the probability of financial distress beyond any hedging firms can achieve with operating and financing decisions. I obtain data on each firm’s foreign currency derivative holdings from 10-K filings available from EDGAR. I search each 10-K filing for text strings such as ‘derivative’, ‘financial instrument’, ‘forward’, ‘hedg’ and ‘market risk’. If a reference is made to any of these key words, I read the surrounding text to obtain data on the year end total notional value of foreign currency forward, and option contracts. Following Allayannis and Ofek (2001), these values do not include currency swaps because these financial instruments are mainly used by firms to either convert foreign debt into domestic debt or to convert domestic debt into foreign debt.
I use two definitions of foreign currency hedging. The first is a continuous variable that captures the extent of foreign currency hedging. The continuous variable is measured by the fiscal year end total notional value of foreign currency forward and option contracts divided by total assets for foreign currency derivative users, or zero for nonusers.4 The second is a dummy variable that is based on the firm’s decision to hedge with foreign currency derivatives.5 This variable is equal to one if a firm reports the use of foreign currency forward or option contracts during the fiscal year, and zero otherwise. I use the continuous variable for most of the analysis. Unlike the dummy variable, this variable captures the extent of a firm’s total foreign currency derivatives ownership.6 The dummy variable is only used in robustness tests.
4.2.2. Leverage
Following Shumway (2001) and Campbell et al. (2008), I measure leverage with the ratio of total liabilities to total assets.7Shumway (2001) finds a significant positive relationship between this variable and the probability of financial distress. Because firms with greater leverage are more likely to have a lower distance to default, I expect a negative coefficient on this variable.
4.2.3. Control variables
I include the following control variables following Shumway (2001) and Campbell et al. (2008).
- 1
Profitability: Profitable firms are more likely to have a greater distance to default than less profitable firms. I control for profitability with the ratio of net income to total assets. I expect a positive coefficient on this variable.
- 2
Excess return: If the equity market discounts firms that are close to financial distress, then a firm’s past excess returns should also predict financial distress as well as its market capitalisation. I measure a firm’s excess return as its annual stock return minus the value weighted CRSP NYSE/AMEX index annual return. Each firm’s annual return is calculated by cumulating its monthly returns. I expect a positive coefficient on this variable.
- 3
Stock return volatility: Firms with greater volatility should have a lower distance to default. I control for volatility with the standard deviation of each firm’s daily stock return over the entire fiscal year. I expect a negative coefficient on this variable. One concern with this variable is that it is an input into the distance to default calculation, which creates a mechanical relationship between the distance to default and the standard deviation of a firm’s daily stock returns in the regressions. In robustness tests, I use the lagged value of the standard deviation of firm’s daily stock return and find that the variable choice does not materially alter the conclusions regarding the effect of foreign currency hedging on the distance to default.
- 4
Firm size: Shumway (2001) finds that smaller firms have a greater likelihood of bankruptcy. I control for firm size by using the natural logarithm of total assets. I expect a firm’s size to be positively related to its distance to default.
- 5
Cash holdings: Campbell et al. (2008) find that firms with greater cash holdings experience lower bankruptcy risk. I control for cash holdings with the ratio of cash and short-term investments to total assets. I expect a positive coefficient on this variable.
4.3. Instrumental variables
In this section, I discuss the instrumental variables used for foreign currency hedging and leverage. A valid instrumental variable is one that affects the distance to default only through its impact on foreign currency hedging and leverage and not directly by itself. That is, a valid instrumental variable must be correlated with foreign currency hedging and leverage but uncorrelated with the error term, uit, in equation (1). Instrumental variables for foreign currency hedging and leverage are difficult to find as it could be argued that any variable that determines foreign currency hedging or leverage might also affect the distance to default. Consequently, I use prior empirical evidence to construct the instrumental variables and test their validity.
4.3.1. Instruments for foreign currency hedging
I follow Geczy et al. (1997), Allayannis and Ofek (2001) and Graham and Rogers (2002) in selecting the instrumental variables for foreign currency hedging. The first instrumental variable is the ratio of research and development expenditure to sales. Geczy et al. (1997) and Allayannis and Ofek (2001) find a positive and significant relation between this variable and foreign currency hedging, consistent with firms hedging to reduce underinvestment costs (Froot et al., 1993). The second instrumental variable is the ratio of foreign sales to total sales. As this variable measures the firm’s risk to foreign currency risk, it is expected to be highly correlated to foreign currency hedging. Allayannis and Ofek (2001) find a positive and significant relation between this variable and foreign currency hedging. The third instrumental variable is a dummy variable set equal to one if the firm reports the use of interest rate or commodity derivatives and zero otherwise.8 This variable is a measure of economies of scale in hedging. Geczy et al. (1997) suggest that firms that use other derivatives are likely to have greater expertise and lower transactions costs in hedging. Geczy et al. (1997) find a positive and significant relation between this variable and foreign currency hedging and use it as an instrument for foreign currency hedging when analysing the effect of hedging on leverage. Finally, I also adopt the Core and Guay (2002) method to estimate the delta of a CEO’s stock and stock option portfolio to control for theories relating to managerial risk aversion (Stulz, 1984; Smith and Stulz, 1985). Delta is the dollar change in value of the CEO’s stock and stock option portfolio with respect to a one per cent change in the firm’s stock price. Graham and Rogers (2002) find a positive and significant relation between this variable and the extent of hedging, suggesting that managerial risk aversion is an important determinant of derivatives use. I follow Chava and Purnanandam (2007) and remove the skewness in delta by using ln(1+delta).9 I also estimate the vega of a CEO’s options portfolio. However, I do not use this variable in the analysis because it is insignificant in the first stage regression.
4.3.2. Instruments for leverage
I follow Titman and Wessels (1988), Rajan and Zingales (1995) and Faulkender and Petersen (2006) in selecting the instrumental variables for leverage. First, I use the ratio of research and development expenditure to total sales and the ratio of advertising expenditure to total sales to measure a firm’s intangible assets. Faulkender and Petersen (2006) find a negative and significant relation between these variables and leverage. Second, I use the natural logarithm of total sales as a measure of firm size. Rajan and Zingales (1995) find a positive and significant relation between this variable and leverage while Titman and Wessels (1988) find a negative and significant relationship. Graham and Rogers (2002) use this variable as an instrument for leverage when analysing the relation between leverage and hedging. Finally, I follow Titman and Wessels (1988) and use the ratio of depreciation and amortisation to total assets to measure nondebt tax shields. I also consider using the ratios of property, plant and equipment to total assets and selling, general and administrative expenses to total sales. However, these variables are insignificant in first stage regressions.
4.4. Summary statistics
Table 1 presents summary statistics on firm characteristics and the variables used in the analysis. The sample includes 1824 firm year observations with a mean (median) value of assets of $8755 ($2566) million and a mean (median) value of sales of $7619 ($2467) million. The mean (median) foreign sales to total sales ratio is 33.2 per cent (31.7 per cent). 67.3 per cent of firms in the sample report the use of foreign currency derivatives and the mean (median) total notional value of foreign currency derivatives, as a percentage of total assets, is 4.8 per cent (1.6 per cent). The average (median) 1-year distance to default is 7.338 (6.468). This implies that for the average (median) firm, it would take a 7.338 (6.468) standard deviation move in the market value of its assets before it will default. The average 1-year probability of default is 0.4 per cent, which is comparable to the 1 year average cumulative default rate for BBB rated firms.10 For the average (median) firm, the total liabilities to assets ratio is 60.7 per cent (60.5 per cent), the net income to assets ratio is 5.7 per cent (5.8 per cent), the excess return is −0.8 per cent (−2.1 per cent), the stock return volatility is 41.7 per cent (37.8 per cent), and the cash holdings ratio is 7.5 per cent (3.5 per cent).
| Variable | N | Mean | Median | Std. Dev. | Min. | Max. |
|---|---|---|---|---|---|---|
| Firm characteristics | ||||||
| Total assets (millions) | 1824 | 8755 | 2566 | 28,858 | 503 | 437,006 |
| Total sales (millions) | 1824 | 7619 | 2467 | 18,199 | 224 | 206,083 |
| Probability of financial distress information | ||||||
| Distance to default | 1824 | 7.338 | 6.468 | 4.410 | −0.550 | 63.142 |
| Probability of default | 1824 | 0.004 | 0.000 | 0.028 | 0.000 | 0.709 |
| Firm hedging information | ||||||
| Total FX derivatives to assets | 1824 | 0.048 | 0.016 | 0.081 | 0.000 | 0.656 |
| FX derivatives dummy | 1824 | 0.673 | 1.000 | 0.469 | 0.000 | 1.000 |
| Control variables | ||||||
| Total liabilities to assets | 1824 | 0.607 | 0.605 | 0.200 | 0.000 | 2.004 |
| Net income to assets | 1824 | 0.057 | 0.058 | 0.084 | −1.149 | 0.578 |
| Excess return | 1824 | −0.008 | −0.021 | 0.421 | −1.723 | 2.281 |
| Stock return volatility | 1824 | 0.417 | 0.378 | 0.169 | 0.073 | 1.771 |
| Firm size | 1824 | 8.057 | 7.850 | 1.197 | 6.221 | 12.988 |
| Cash holdings | 1821 | 0.075 | 0.035 | 0.099 | 0.000 | 0.659 |
| Instrumental variables | ||||||
| R&D to sales | 1824 | 0.033 | 0.012 | 0.052 | 0.000 | 0.513 |
| Foreign sales | 1824 | 0.332 | 0.317 | 0.196 | 0.000 | 1.000 |
| Other derivatives dummy | 1824 | 0.655 | 1.000 | 0.476 | 0.000 | 1.000 |
| ln(1+delta) | 1645 | 6.014 | 5.887 | 1.619 | 0.000 | 13.147 |
| Advertising to sales | 1824 | 0.011 | 0.000 | 0.033 | 0.000 | 0.332 |
| ln(sales) | 1824 | 8.034 | 7.811 | 1.208 | 5.414 | 12.236 |
| Depreciation to assets | 1824 | 0.047 | 0.044 | 0.024 | 0.000 | 0.229 |
- This table presents summary statistics for the variables used in the analysis. The sample includes nonfinancial COMPUSTAT firms with assets greater than $500 million and foreign sales for 1996 to 2000. Distance to default is the number of standard deviations of annual asset growth by which the expected market value of assets exceeds the face value of the firm’s debt estimated from the Merton (1974) model. Probability of default is the implied 1 year probability of default estimated from the Merton (1974) model. Total FX derivatives to assets is the total notional value of foreign currency forward and option contracts divided by total assets. FX derivatives dummy is a dummy variable set equal to one if the firm reports the use of foreign currency forwards or options, and zero otherwise. Total liabilities to assets is the ratio of total liabilities to total assets. Net income to assets is the ratio of net income to total assets. Excess return is the annual return on the firm minus the value weighted CRSP NYSE/AMEX index annual return over the entire fiscal year. Stock return volatility is the standard deviation of the firm’s daily stock return over the entire fiscal year. Firm size is the natural logarithm of total assets. Cash holdings is the ratio of cash and short-term investments to total assets. R&D to sales is the ratio of research and development expenditure to total sales. Foreign sales is the ratio of foreign sales to total sales. Other derivatives dummy is a dummy variable set equal to one if the firm reports the use of interest rate or commodity derivatives and zero otherwise. Delta is the dollar change in value of the CEO’s stock and stock option portfolio with respect to a one per cent change in the firm’s stock price. Advertising to sales is the ratio of advertising expenditure to total sales. ln(sales) is the natural logarithm of total sales. Depreciation to assets is the ratio of depreciation and amortisation expense to total assets.
5. Results
In this section, I discuss the univariate and multivariate results with respect to the effect of foreign currency hedging with derivatives on the probability of financial distress.
5.1. Univariate analysis
Table 2 shows the correlation between the distance to default and the explanatory variables. The largest correlations are those between the distance to default and stock return volatility and the distance to default and the total liabilities to assets ratio. Both of these correlation coefficients are negative, suggesting that firms with greater stock return volatility and leverage have a lower distance to default, which is consistent with the intuition of Merton’s (1974) model. Larger, more liquid and profitable firms with high past returns have a greater distance to default. Finally, the extent of foreign currency hedging is positively correlated with the distance to default, suggesting that the more a firm hedges with foreign currency derivatives, the greater its distance to default.
| Distance to default | Total FX derivatives to assets | Total liabilities to assets | Net income to assets | Excess return | Stock return volatility | Firm size | Cash holdings | |
|---|---|---|---|---|---|---|---|---|
| Distance to default | 1.000 | |||||||
| Total FX derivatives to assets | 0.070* | 1.000 | ||||||
| Total liabilities to assets | −0.380* | 0.049 | 1.000 | |||||
| Net income to assets | 0.371* | 0.073* | −0.387* | 1.000 | ||||
| Excess return | 0.146* | 0.025 | −0.154* | 0.261* | 1.000 | |||
| Stock return volatility | −0.554* | −0.015 | −0.052 | −0.234* | 0.032 | 1.000 | ||
| Firm size | 0.024 | 0.188* | 0.183* | 0.072* | 0.059 | −0.118* | 1.000 | |
| Cash holdings | 0.165* | 0.128* | −0.372* | 0.189* | 0.247* | 0.335* | −0.067* | 1.000 |
- This table presents correlation coefficients for the variables used in the analysis. The sample includes nonfinancial COMPUSTAT firms with assets greater than $500 million and foreign sales for 1996 to 2000. Distance to default is the number of standard deviations of annual asset growth by which the expected market value of assets exceeds the face value of the firm’s debt estimated from the Merton (1974) model. Total FX derivatives to assets is the total notional value of foreign currency forward and option contracts divided by total assets. Total liabilities to assets is the ratio of total liabilities to total assets. Net income to assets is the ratio of net income to total assets. Excess return is the annual return on the firm minus the value weighted CRSP NYSE/AMEX index annual return over the entire fiscal year. Stock return volatility is the standard deviation of the firm’s daily stock return over the entire fiscal year. Firm size is the natural logarithm of total assets. Cash holdings is the ratio of cash and short-term investments to total assets. Coefficients with an asterisk (*) are significantly different from zero at the 1 per cent level.
5.2. Multivariate analysis
Table 3, Column 1, presents the OLS regression results. The estimated coefficient on total FX derivatives to assets is positive but insignificant, suggesting that the extent of a firm’s foreign currency hedging does not affect its distance to default. This is not surprising because the simultaneity between foreign currency hedging, leverage and the distance to default makes it difficult to observe a significant relation between the distance to default and the extent of foreign currency hedging. The estimated coefficients on the total liabilities to assets ratio and control variables all have the predicted sign and are all significant except for the ratio of net income to assets. For example, firm size, excess returns and cash holdings are positively related to the distance to default, while the total liabilities to assets ratio and stock return volatility are negatively related to its distance to default. These results are consistent with Shumway (2001) and Campbell et al. (2008).
| OLS | 2SLS | GMM IV | |
|---|---|---|---|
| Dependent variable: distance to default | (1) | (2) | (3) |
| Total FX derivatives to assets | 0.610 (0.658) | 11.977 (0.048) | 10.691 (0.067) |
| Total liabilities to assets | −6.818 (0.000) | −22.563 (0.000) | −19.970 (0.000) |
| Net income to assets | 1.255 (0.656) | −9.940 (0.127) | −5.294 (0.238) |
| Excess return | 0.525 (0.008) | 0.318 (0.351) | 0.419 (0.097) |
| Stock return volatility | −14.490 (0.000) | −16.838 (0.000) | −16.610 (0.000) |
| Firm size | 0.191 (0.038) | 0.476 (0.043) | 0.413 (0.027) |
| Cash holdings | 9.538 (0.001) | 2.877 (0.207) | 2.674 (0.222) |
| Hausman test | 23.896 (0.000) | 23.896 (0.000) | |
| F statistic from first stage regression | |||
| Total FX derivatives to assets | 7.980 (0.000) | 7.980 (0.000) | |
| Total liabilities to assets | 7.170 (0.000) | 7.170 (0.000) | |
| Hansen’s J statistic | 4.735 (0.449) | 4.735 (0.449) | |
| Number of observations | 1821 | 1642 | 1642 |
| Adjusted R2 | 0.582 | 0.338 | 0.338 |
- This table presents the results of OLS, 2SLS and GMM IV (second stage only) regressions of the distance to default on the extent of foreign currency hedging. The sample includes nonfinancial COMPUSTAT firms with assets greater than $500 million and foreign sales for 1996 to 2000. Distance to default is the firm’s 1-year distance to default estimated from the Merton (1974) model. Total FX derivatives to assets is the total notional value of foreign currency forward and option contracts divided by total assets. Total liabilities to assets is the ratio of total liabilities to total assets. Net income to assets is the ratio of net income to total assets. Excess return is the annual return on the firm minus the value weighted CRSP NYSE/AMEX index annual return over the entire fiscal year. Stock return volatility is the standard deviation of the firm’s daily stock return over the entire fiscal year. Firm size is the natural logarithm of total assets. Cash holdings is the ratio of cash and short-term investments to total assets. In parentheses are p-values based on standard errors adjusted for heteroskedasticity (White, 1980) and firm clustering. The regressions include year dummies and industry fixed effects at the two-digit SIC level, whose coefficient estimates are suppressed. The coefficient of the intercept is also suppressed. Variables significant at the 5 per cent level or less are in bold.
Before estimating equation (1) with 2SLS and GMM IV, I perform a Hausman (1978) test to determine whether the ratios of total FX derivatives to assets and total liabilities to assets are jointly endogenous. Hausman’s test is based on the difference between the OLS estimator (which is consistent and efficient under the null hypothesis of no endogeneity and inconsistent under the alternative) and the instrumental variables estimator (which is consistent under both the null and alternative hypotheses but inefficient under the null). I reject the null hypothesis of no endogeneity at the 1 per cent level. Consequently, OLS regressions that ignore the endogeneity of hedging and leverage with respect to the distance to default can be potentially misleading because they generate inconsistent estimates.
Table 3, Columns 2 and 3, presents the 2SLS and GMM IV results. For the 2SLS regression, the ratio of total FX derivatives to assets is significantly positively related to the distance to default at the 5 per cent level (the p-value is 0.048). For the GMM IV regression, the estimated coefficient on the ratio of total FX derivatives to assets is positive, but it is weakly related to the distance to default with a p-value of 0.067. The higher p-value is expected because GMM IV is more efficient than 2SLS. These results suggest that after controlling for endogenous hedging and leverage, the extent of foreign currency hedging is associated with a greater distance to default, and hence, a lower probability of financial distress.
I now discuss the validity of the instrumental variables. Table 3 reports the F statistics from the first stage regressions.11 The F statistics for both of the first stage regressions are significant at the 1 per cent level. Consequently, I reject the null hypothesis that the instrumental variables are uncorrelated with the endogenous variables. Table 3 also reports Hansen’s (1982)J statistic, which is a test of overidentifying restrictions. Under the null hypothesis, the instrumental variables are uncorrelated with the error term. The J statistic is small with a p-value of 0.449. Consequently, I cannot reject the null hypothesis that the instrumental variables are uncorrelated with the error term.
To emphasise the economic significance of my results, Table 4 presents the change in the distance to default in response to a one standard deviation increase in the explanatory variables. The estimates in Table 4 are based on the estimated coefficients in Regression 3 from Table 3 and the sample standard deviations presented in Table 1. Table 4 shows that the total liabilities to assets ratio and stock return volatility are the most important determinants of the distance to default. A one standard deviation increase in the total liabilities to assets ratio decreases the distance to default by 3.991, while a one standard deviation increase in stock return volatility decreases the distance to default by 2.799. The third most important determinant of the distance to default is the ratio of total FX derivatives to assets. A one standard deviation increase in the ratio of total FX derivatives to assets increases the distance to default by 0.870. That is, a firm that increases its ratio of total FX derivatives to assets by 8.10 per cent12 will increase its distance to default by 0.870 standard deviations. We can use this change in the distance to default to estimate the effect of a one standard deviation increase in the ratio of total FX derivatives to assets on the probability of default. Using the distance to default that is implied from the mean probability of default of 0.4 per cent in Table 1, a one standard deviation in the ratio of total FX derivatives to assets decreases the 1-year probability of default from 0.4 per cent to 0.02 per cent.13 Currency hedging therefore has a strong effect on the probability of default.
| One standard deviation increase in | Change in distance to default |
|---|---|
| Total FX derivatives to assets | 0.870 |
| Total liabilities to assets | −3.991 |
| Net income to assets | −0.443 |
| Excess return | 0.176 |
| Stock return volatility | −2.799 |
| Firm size | 0.495 |
| Cash holdings | 0.264 |
- This table presents the change in the distance to default in response to a one standard deviation increase in the explanatory variables. The sample includes nonfinancial COMPUSTAT firms with assets greater than $500 million and foreign sales for 1996–2000. Distance to default is the firm’s 1-year distance to default estimated from the Merton (1974) model. Total FX derivatives to assets is the total notional value of foreign currency forward and option contracts divided by total assets. Total liabilities to assets is the ratio of total liabilities to total assets. Net income to assets is the ratio of net income to total assets. Excess return is the annual return on the firm minus the value weighted CRSP NYSE/AMEX index annual return over the entire fiscal year. Stock return volatility is the standard deviation of the firm’s daily stock return over the entire fiscal year. Firm size is the natural logarithm of total assets. Cash holdings is the ratio of cash and short-term investments to total assets.
5.3. Robustness
In this section, I test the robustness of the results to alternative probability of financial distress measures and estimation methods. First, I use a modified version of Altman’s (1968)Z-score as used in MacKie-Mason (1990) and Graham (1996) as an alternative measure of the probability of financial distress.14 The modified Z-score excludes the effect of leverage from Altman’s (1968) original Z-score to avoid the mechanical relation between leverage and this variable. Higher values of the modified Z-score are associated with a lower probability of financial distress. Table 5, Panel A, presents summary statistics on this alternative measure of the probability of financial distress. Column 1 presents the correlation between the 1-year distance to default and the modified Z-score. The 1-year distance to default has a 0.330 correlation with the modified Z-score. This low correlation can be explained by the fact that the modified Z-score does not include the market value of a firm’s assets nor its asset volatility. The mean (median) Z-score is 2.090 (2.083).
| Panel A: Summary statistics | |||||||
|---|---|---|---|---|---|---|---|
| Alternative measure of the probability of financial distress | Correlation with distance to default | N | Mean | Median | Std. Dev. | Min. | Max. |
| Altman’s Z-score | 0.330 | 1730 | 2.090 | 2.083 | 0.938 | −4.758 | 5.910 |
| Panel B: GMM IV regressions – second stage | |||
|---|---|---|---|
| Alternative measure of the probability of financial distress | Coefficient on total FX derivatives to assets | Number of observations | Adjusted R squared |
| Altman’s Z-score | 5.445 (0.001) | 1560 | 0.252 |
- This table presents summary statistics of Altman’s Z-score (panel A), and an estimation of the effect of foreign currency hedging on Altman’s Z-score (panel B). The regression include control variables for leverage, net income to assets, firm size, excess returns, stock return volatility, cash holdings, year dummies and industry fixed effects at the two-digit SIC level. In parentheses are p-values based on standard errors adjusted for heteroskedasticity (White, 1980) and firm clustering.
Table 5, Panel B, presents the second stage GMM IV regressions for the modified Z-score. I report the GMM IV regressions because GMM IV is more efficient than 2SLS in the presence of heteroskedasticity. The estimated coefficient on the ratio of total FX derivatives to assets is 5.445 when using the modified Z-score as the dependent variable. This estimated coefficient is significant at the 1 per cent level (the p-value is 0.001). Consequently, the use of the modified Z-score provides further evidence that the extent of foreign currency hedging is associated with a lower probability of financial distress.
Second, I experiment with the amount of long-term debt included in the 1-year distance to default calculation. Following Crosbie and Bohn (2003) and Vassalou and Xing (2004), the face value of debt in the calculation of the 1-year distance to default that is used throughout the analysis includes all debt maturing in 1 year plus one half of long-term debt. I recalculate the 1-year distance to default with zero long-term debt and then with 100 per cent of long-term debt. In unreported regressions, I find that the conclusion that the extent of foreign currency hedging is associated with a greater distance to default is robust to the amount of long-term debt included in the calculation of the 1-year distance to default.
Third, I address the concern that the number of observations in the 2SLS and GMM IV regressions is reduced from 1821 to 1642 because of missing data on the delta of a CEO’s stock and stock option portfolio. To maintain sample size and reduce the risk of sample selection bias, I set missing observations of delta equal to zero and create a dummy variable set equal to 1 if delta is missing and zero otherwise. In unreported regressions, I find that the estimated coefficient on the ratio of total FX derivatives to assets is positive and significant at the 5 per cent level for the 2SLS regression and at the 10 per cent level for the GMM IV regression.
Finally, many studies use a dummy variable to indicate the decision to hedge with derivatives.15 In contrast, I use a continuous hedging variable because this variable captures the extent of a firm’s total foreign currency derivatives ownership. Notwithstanding this, I repeat the analysis using a dummy variable that is set equal to one if a firm reports the use of foreign currency forward or option contracts during the fiscal year, and zero otherwise. In unreported regressions, I estimate equation (1) using the dummy variable with both 2SLS and GMM IV and find no evidence that the decision to hedge foreign currency risk with derivatives is associated with a greater distance to default. This implies that it is not merely the decision to hedge foreign currency risk with derivatives, but rather the extent of foreign currency hedging with derivatives that affects the probability of financial distress.
6. Conclusion
This paper examines the relationship between foreign currency hedging with derivatives and the probability of financial distress for a sample of 401 large nonfinancial firms that are exposed to foreign currency risk. I examine whether foreign currency hedging with derivatives reduces a firm’s probability of financial distress.
Using a firm’s distance to default as a proxy for its probability of financial distress, I find that the extent of foreign currency hedging and leverage are endogenous with respect to the distance to default and that ignoring this endogeneity underestimates the effect of the extent of foreign currency hedging on the distance to default. After controlling for endogeneity with instrumental variable techniques, I find that the extent of foreign currency hedging is associated with a greater distance to default, and hence, a lower probability of financial distress. Whereas previous research finds evidence that firms with a greater probability of financial distress hedge more, this paper provides direct evidence supporting the Smith and Stulz (1985) hypothesis that hedging with derivatives reduces the probability of financial distress.
This paper also adds to our understanding of the effect of hedging on debt capacity and the cost of debt financing. Research on corporate hedging indicates that the extent of hedging is associated with an increase in leverage and lower costs of debt financing. This stream of literature argues that the documented increase in leverage and reduction in the costs of debt financing is in response to a lower probability of financial distress induced by hedging. My paper compliments this literature by providing evidence that the extent of hedging is associated with a lower probability of financial distress.
Footnotes
Appendix
Appendix I
Construction of the distance to default
This appendix describes how I construct the distance to default using Merton’s (1974) structural default model. The construction of the distance to default follows Crosbie and Bohn (2003), Bharath and Shumway (2008), Hillegeist et al. (2004), and Vassalou and Xing (2004).
()
()
()
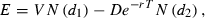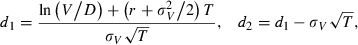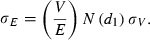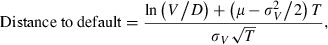()where μ is an estimate of the continuously compounded expected return on the firm’s assets. I set μ equal to the risk free rate, which results in a common expected return on assets. This is consistent with Crosbie and Bohn (2003), who suggest that the expected return on assets should have little default discriminating power. The main advantage of this approach is avoiding estimation errors related to estimating the mean return of a firm’s assets. For example, Vassalou and Xing (2004) estimate μ by calculating the continuously compounded return on V over the past 12 months, which will frequently result in negative expected asset returns. This problem is avoided by choosing a common expected return on assets for all firms rather than a noisily estimated firm specific expected return.
To estimate the distance to default from equation (A4), I must first estimate V and σV because these values are not directly observable. I follow Hillegeist et al. (2004) and estimate V and σV by simultaneously solving equations (A1) and (A3).16 The inputs into the Merton model are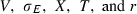 
. E is set equal to the market value of equity at the end of the each fiscal year. σE is estimated by using daily stock return data from CRSP over the entire fiscal year. Following Crosbie and Bohn (2003) and Vassalou and Xing (2004), T is set to 1 year and D is set equal to debt maturing in 1 year plus one half of long-term debt. For r, I use the 1 year treasury constant maturity rate obtained from the Board of Governors of the Federal Reserve System.17 I then simultaneously solve equations (A1) and (A3) numerically for V and σA.
()
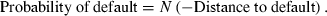