The usefulness of operating cash flow and accrual components in improving the predictive ability of earnings: a re-examination and extension
Abstract
We examine whether the components of accruals and operating cash flows improve the predictive ability of earnings for forecasting future cash flows. Unlike most previous studies, we avoid data estimation errors and sample self-selection bias because we exploit data from Australia where reporting of actual cash flow components had been mandatory since 1992. We show that accrual components and operating cash flow components together are more useful than (i) earnings, (ii) operating cash flows and total accruals and (iii) the combination of operating cash flows with accrual components in forecasting future cash flows. These results are robust to several contextual factors, including the length of the operating cash cycle, industry membership, firm profitability and firm size.
1. Introduction
We investigate whether accrual components and cash flow components of earnings improve the predictive ability of earnings for forecasting future cash flows. To date, research investigating the relevance of accounting data in forecasting future cash flows has concentrated on the relative predicative ability of aggregate cash flow from operations (hereafter, CF) and earnings (e.g., Bowen et al., 1986; Dechow et al., 1998; Subramanyam and Venkatachalam, 2007). However, the role of earnings components (i.e., CF and accruals) in forecasting future cash flows is not fully understood. Barth et al. (2001) provide the first evidence on the role of earnings components, particularly accrual components, in the forecast of future cash flows. Cheng and Hollie (2008) document that incorporating CF components instead of aggregate CF in Barth et al.’s model significantly improves the forecast of future cash flows. Their results, however, do not provide clear insight into the relative importance of CF and accrual components of earnings in predicting future cash flows for two reasons.
Firstly, Cheng and Hollie (2008) analyse estimated rather than actual CF components. This is because their study is premised on the US setting where actual CF components are mostly unavailable because of the predominance of the indirect method of cash flow reporting,1 and thus need to be estimated.2 A focus on actual CF components is important because prior studies (e.g., Krishnan and Largay, 2000; Orpurt and Zang, 2009) provide evidence of material measurement errors when estimating CF components. In particular, Orpurt and Zang (2009) document that estimated CF components are subject to more errors that are significant when they are estimated with balance sheet and income statement information, as done by Cheng and Hollie (2008), rather than with indirect CF information. More importantly, Orpurt and Zang (2009) find that the association of estimated CF components and future cash flows are affected by the degree of these measurement errors.
Secondly, Cheng and Hollie (2008) categorize CF into core and noncore CF based on their relation to operating and non-operating earnings.3 This classification is not entirely consistent with the recommended scheme in the direct method cash flow statement that is widely supported by investors and other groups (see Jones et al., 1995; McEnroe, 1996; Jones and Ratnatunga, 1997; Jones and Widjaja, 1998; Chartered Financial Analyst (CFA) Institute, 2009). Therefore, it is still an open question as to whether direct method CF components convey incremental information to investors and other user groups about the ability of earnings to forecast future cash flows.
In this study, we focus on Australian rather than US firms. Our study has a unique advantage in that Australian firms were required to report actual CF components under the direct method, as per Australian Accounting Standards Board (AASB) 1026: Statement of Cash Flows (AASB, 1991, revised AASB (1997).4 Thus, the direct method CF information available for Australian firms permits us to investigate unequivocally whether disaggregated CF data, as reported under the direct method, are useful in improving the predictive ability of earnings. Our study also goes one step further. It explores the impact of various contextual factors, including the length of the operating cash cycle, industry membership, firm profitability and firm size, on the ability of accrual and CF components of earnings for predicting future cash flows. Accordingly, we address the following research question: do accrual and cash flow components improve the predictive ability of earnings to forecast future cash flows?
To address our research question, we analyse a sample of 348 Australian firms over 1992–2004. To evaluate the forecasting performance of our regression models, we use both within-sample and out-of-sample forecasting tests. We first compare the explanatory power of the models via the adjusted R2 for the within-sample period of 1992–2001. We then examine the forecast accuracy of our models by estimating Theil’s U-statistic and its proportions for the out-of-sample period 2002–2004. Our results suggest that actual CF components enhance the predictive ability of earnings for future cash flows. In particular, we find that reported direct CF components and accrual components together improve cash flow prediction incremental to aggregate CF and accrual components, and aggregate CF and total accruals. Various categorizations of our sample confirm that our findings are not conditional on selected control factors.
Our contribution to the literature is twofold. Firstly, we provide the first evidence using actual cash flow components for the role of disaggregated CF in the predictive ability of earnings for future cash flows. Secondly, we extend the literature by explicitly incorporating certain corporate characteristics (i.e. the length of the operating cash cycle, industry membership, profitability and size) which may be relevant for understanding the predictive ability of aggregate earnings and disaggregated earnings. Our results provide new insights into the characteristics of accruals- and cash-based accounting data relating to future cash flows. For example we find that disaggregating earnings into CF components enhances the predictive ability of earnings when (i) the operating cash cycle is long, (ii) the firm size is small and (iii) the firm makes a loss. We also find that the level of predictive ability of both accruals- and cash-based accounting variables varies across industries.
The remainder of the study is organized as follows. Section 2 reviews the prior literature. Section 3 presents the research design. Section 4 describes the sample. Section 5 reports the main results. Section 6 discusses results from various sensitivity analyses. Section 7 concludes the study.
2. Prior research
Most studies in cash flow prediction examine the relative usefulness of aggregate earnings and CF in forecasting future cash flows. Although the results of earlier studies using estimated CF are mixed (e.g., Bowen et al., 1986; Greenberg et al., 1986), more recent studies using CF as reported in the cash flow statement (e.g., Barth et al., 2001; Subramanyam and Venkatachalam, 2007) indicate that CF is a better predictor of future cash flows than earnings.5Dechow et al. (1998) proposed the first theoretical model using CF and working capital accruals to argue that earnings have higher predictive ability than CF for future cash flows. Building on Dechow et al. (1998), Barth et al. (2001) demonstrated that disaggregating earnings into aggregate CF and major accrual components (i.e. changes in accounts receivable, accounts payable, inventory and the amounts of depreciation expense; amortization expense and the net of other accruals) significantly enhances the predictive ability of aggregate earnings compared to aggregate CF and earnings disaggregated into CF and total accruals.6Cheng and Hollie (2008) then decomposed the CF component of earnings into cash flows from sales, cash flow from cost of goods sold, cash flow from operating expenses and cash flows related to other revenue/expense items. They showed that estimated CF components provide incremental information over and above accrual components. That is, CF and accrual components together outperform Barth et al.’s model which comprises aggregate CF and accrual components only.
The predictive ability of CF components for future cash flows has also been examined by two other US studies: Krishnan and Largay (2000) and Orpurt and Zang (2009). Both studies provide evidence for the higher predictive ability of direct cash flow components for future cash flows compared to aggregate CF. However, they do not directly examine whether CF components improve the predictive ability of earnings for future cash flows beyond accruals.7
Our research design for examining the usefulness of the CF components in improving the predictive ability of earnings differs from previous studies in two important ways. Firstly, the above studies are based on the US companies and required researchers to estimate cash flow components (e.g. Krishnan and Largay, 2000; Orpurt and Zang, 2009). In contrast, we consider Australian data for the period of 1992–2004, when Australian firms were required to report actual cash flow components. Thus, as discussed in Section 1, our sample does not suffer from either self-selection bias or measurement errors as suffered by the US studies.
Secondly, we comprehensively assess the extent to which industry-specific characteristics and three important firm-specific characteristics (namely firm size, profitability and operating cash cycle) influence the usefulness of the CF and accrual components in enhancing the predictive ability of earnings. We are motivated by the conjecture in prior literature that the predictive ability of earnings and earnings components for future cash flows may be influenced by contextual factors (e.g. Dechow et al., 1998; Barth et al., 2001; Cheng and Hollie, 2008).
Our research is related to two Australian studies: Clinch et al. (2002) and Arthur et al. (2010). They provide evidence for the importance of the direct method cash flow disclosures in explaining stock returns and future earnings, respectively. Our study complements these two studies by directly focusing on future cash flows to evaluate the usefulness of CF and accrual components. We believe this focus is important because estimates of future cash flows are fundamental to a firm’s valuation (e.g. Barth et al., 2001), and a primary objective of financial reporting is to provide information to help users evaluate the prospects for future cash flows of a company.8 In addition, Sloan (1996), Xie (2001) and others have documented that the differential persistence of the accruals and CF components of earnings is not accurately priced by the market. Richardson et al. (2005) and Bandyopadhyay et al. (2010) also argue that the ability of accounting measures to predict future earnings reflects their ‘reliability’ rather than their ‘relevance’.9 This line of argument questions the use of share prices and earnings in assessing the relevance of cash flow and accruals, which is the main objective of this research.
3. Research design
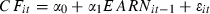 ()
() ()
()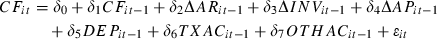 ()
()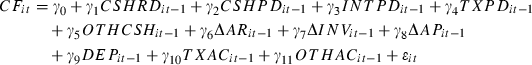 ()
()here, i and t denote firm and year, respectively. Cash flow from operations. CSHRD is cash received from customers. CSHPD is cash paid to suppliers and employees. INTPD is net interest paid, i.e. the difference between interest paid and interest received. TXPD is taxes paid. OTHCSH is other cash flows from operations, i.e. OTHCSH = CF − (CSHRD − CSHPD − INTPD −TXPD). The definitions of other variables are as in model (3).
We follow Clinch et al. (2002) in the selection of cash flow components.11,12 The set of accrual components is mainly consistent with that employed in Barth et al. (2001). The exception is TXAC, which we add to provide comparability with TXPD, as in Clinch et al. (2002). Furthermore, Cheung et al. (1997) find that inter-period tax allocation enhances the prediction of future cash flows.
We use ordinary least squares (OLS) regression models on a pooled time series of cross-sectional data. White’s (1980) heteroscedasticity-corrected variances and standard errors are applied to correct standard errors in the presence of heteroscedasticity. To address the issue of whether the 1-year lagged components of CF and accruals capture different information about current year operating cash flows, we test for the equality of coefficients across the selected CF and accrual components using the chi-square test (hereafter, χ2 test) as employed by Clinch et al. (2002) and Orpurt and Zang (2009). To assess the forecasting ability of the models, we first estimate the adjusted R2 for 1992–2001. Vuong’s (1989) likelihood ratio test for model selection is then applied to test whether the explanatory powers of two competing models significantly differ (Dechow, 1994, Appendix 2).
We use out-of-sample in addition to within-sample forecasting tests because a higher adjusted R2 does not necessarily represent a superior predictive ability (Watts and Leftwich, 1977). Accordingly, we employ Theil’s U-statistic as a forecast error measure, as per Kim and Kross (2005) and Bandyopadhyay et al. (2010). In particular, we compare the forecast accuracy of aggregate and disaggregated earnings (models (1) through (4)) during the period 2002–2004. Theil’s U-statistic is decomposed into bias, variance and covariance proportions. In a good prediction, the covariance proportion, which represents unsystematic errors, is greater than the bias and variance proportions. The bias proportion captures the systematic error, and the variance proportion measures the extent to which the fluctuations in the fitted series follow those in the actual series. Theil’s U-statistic falls between zero and one, with values closer to zero signifying higher forecasting accuracy (Pindyck and Rubinfeld, 1998).
4. Data
Our sample is selected from companies listed on the Australian Stock Exchange (ASX) for the years 1992–2004. We obtain the related data from the Aspect Financial Analysis database. The sample period begins in 1992, the first year, Australian firms were required to report cash flow statements under AASB 1026. As a result of Australia’s adoption of the International Financial Reporting Standards (IFRS) with effect from 1 January 2005, our sample ends in 2004 to avoid any structural change in the data. In our data, CF is the annual amount of net cash flows from operating activities, as reported in the cash flow statement. Earnings are measured at net income before extraordinary items and discontinued operations, as reported in the income statement. The CF components are collected from the cash flow statement. The accrual components are measured from balance sheet information. Following Krishnan and Largay (2000), we deflate all the variables by the number of outstanding ordinary shares.13
Our sample excludes firms in the Financial sector14 because the components of financial statements and accounting regulations in this sector are different from that of other sectors. We require each firm to have data available for all the variables over the sample period, to control for potential changes in sample characteristics. However, this requirement likely introduces a survivorship bias as a result of the inclusion of larger and more successful firms in the sample. To address this concern, unlike the previous related studies, we did not restrict the sample to any company size or specific year-end.15,16 Based on these criteria, the initial sample contains 4537 firm-years representing 349 firms. We diagnosed and removed the outliers (17 observations) using Cook’s distance. Hence, the final sample is 4520 firm-year observations representing 348 firms.17,18
Panel A, Table 1 reports the descriptive statistics for the sample. The mean (median) value of $0.18 ($0.00) per share for CF is larger than the mean (median) for earnings (EARN) which is $0.08 ($−0.00) per share.19 This is mainly because of non-cash expenses (e.g., depreciation expense) included in the variable. Furthermore, the standard deviation of CF is 0.47, higher than that of EARN (0.38). This implies that the accrual process mitigates a substantial portion of CF fluctuations. The mean and median for TAC are negative, indicating that total accruals have an income-decreasing effect. The larger mean and median of DEP than the mean and median of ΔAP, ΔAR and ΔINV suggest higher variability of the current accrual components. The mean (median and standard deviation) values of CSHRD and CSHRD are $2.57 ($0.15, $6.53) and $2.34 ($0.14, $6.23) respectively, all of which are larger than those of INTPD, TXPD and OTHCSH. Thus, the predictive ability of CF would be considerably affected by CSHRD and CSHPD.
| STATS | CF | CSHRD | CSHPD | INTPD | TXPD | OTHCSH | EARN | TAC | ΔAP | ΔAR | ΔINV | DEP | TXAC | OTHAC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Descriptive statistics | ||||||||||||||
| Mean | 0.18 | 2.57 | 2.34 | 0.02 | 0.04 | 0.01 | 0.08 | −0.10 | 0.02 | 0.03 | 0.02 | 0.09 | −0.00 | −0.21 |
| Median | 0.00 | 0.15 | 0.14 | 0.00 | 0.00 | 0.00 | −0.00 | −0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | −0.04 |
| SD | 0.47 | 6.53 | 6.23 | 0.12 | 0.12 | 0.35 | 0.38 | 0.41 | 0.26 | 0.24 | 0.21 | 0.20 | 0.09 | 0.58 |
| CF | CSHRD | CSHPD | INTPD | TXPD | OTHCSH | EARN | TAC | ΔAP | ΔAR | ΔINV | DEP | TXAC | OTHAC | |
| Panel B: Pearson correlation matrix | ||||||||||||||
| CF | 1.00 | |||||||||||||
| CSHRD | 0.44† | 1.00 | ||||||||||||
| CSHPD | 0.40† | 0.99† | 1.00 | |||||||||||
| INTPD | 0.11† | 0.19† | 0.18† | 100 | ||||||||||
| TXPD | 0.58† | 0.50† | 0.48† | −0.07† | 1.00 | |||||||||
| OTHCSH | 0.37† | −0.04** | −0.02 | 0.03** | −0.18† | 1.00 | ||||||||
| EARN | 0.54† | 0.33† | −0.35† | 0.02 | −0.49† | 0.20 | 1.00 | |||||||
| TAC | −0.64† | −0.19† | 0.16† | 0.14† | 0.21† | −0.31† | 0.28† | 1.00 | ||||||
| ΔAP | 0.19† | 0.26† | 0.26† | 0.06† | 0.14† | 0.08† | 0.10† | −0.13† | 1.00 | |||||
| ΔAR | 0.16† | 0.29† | 0.29† | 0.08† | 0.16† | 0.10† | 0.18† | 0.02 | 0.62† | 1.00 | ||||
| ΔINV | 0.07† | 0.21† | 0.22† | 0.12† | 0.11† | 0.09† | 0.11† | 0.03** | 0.37† | 0.39† | 1.00 | |||
| DEP | 0.65† | 0.14† | 0.13† | 0.09† | 0.16† | 0.08† | 0.44† | −0.46† | 0.12† | 0.16† | 0.10† | 1.00 | ||
| TXAC | −0.26† | −0.00 | 0.00 | −0.09† | 0.34† | −0.16† | −0.23† | 0.11† | −0.14† | −0.15† | −0.09† | −0.12† | 1.00 | |
| OTHAC | −0.46† | −0.25† | −0.23† | −0.17† | −0.33† | −0.23† | −0.21† | 0.54† | −0.04† | −0.23† | −0.24† | −0.69† | 0.18† | 1.00 |
- Variable definitions: CF is net cash flow from operating activities under the cash flow statement. EARN is earnings before extraordinary and discontinuing items. TAC is total accruals calculated as the difference between EARN and CF. ΔAP is the change in accounts payable during the year. ΔAR is the change in accounts receivable during the year. ΔINV is the change in inventory during the year. DEP is depreciation and amortization expense. TXAC is accruals in relation to income tax expense. OTHAC is other accruals. CSHRD is cash received from customers. CSHPD is cash paid to suppliers and employees. INTPD is net interest paid. TXPD is taxes paid. OTHCSH is other cash flows from operations. All variables are scaled by the number of ordinary shares outstanding.
- **Indicates significance at the 0.05 level. †Indicates significance at the 0.01 level.
Panel B of Table 1 presents the Pearson correlation coefficients among the accounting variables. The correlations of EARN with CF (r = 0.54) and TAC (r = 0.28) are positive and significant at the 0.01 level. CF has negative correlation with TAC (r = −0.64), TXAC (r = −0.26) and OTHAC (r = −0.46), and positive correlation with ΔAP (r = 0.19), ΔAR (r = 0.16), ΔINV (r = 0.07) and DEP (r = 0.65); all coefficients are significant at the 0.01 level. Regarding CF components, CF is significantly positively associated with CSHRD (r = 0.44), OTHCSH (r = 0.37), CSHPD (r = 0.40), INTPD (r = 0.11) and TXPD (r = 0.58) at the 0.01 level. CF components are significantly related to each other, with the exception of OTHCSH and CSHPD, which are not significantly correlated at conventional levels. The coefficients of correlation among accrual and CF components are mostly significant but lower than 0.50. The correlation between CSHRD and CSHPD is 0.99 and significant at the 0.01 level. This strong correlation is expected given that a firm’s ability to pay its suppliers and employees depends on its cash collection from customers. However, the finding also suggests possible severe multicollinearity. We discuss this concern in our sensitivity analyses in Section 6.
5. Results
5.1. Predictive ability of aggregate earnings, earnings disaggregated into cash flow and total accruals, and cash flow and accrual components
In Table 2, we report the results of regressing current CF on (i) 1-year lagged earnings (model (1)), (ii) 1-year lagged CF and total accruals (model (2)) and (iii) 1-year lagged CF and accrual components (model (3)). Furthermore, a summary of within- and out-of-sample forecasting statistics for models (1), (2) and (3) is presented. As Panel A shows, the coefficient of 0.90 on 1-year lagged earnings (EARN) in model (1) is positive and significant (t-statistic = 7.28) at the 0.01 level. The adjusted R2 of model (1) is 31 per cent. The coefficients on CF (0.85) and TAC (0.25) in model (2) are positive and significant (t-statistic = 11.14, 2.34) at the 0.01 and 0.05 levels, respectively. These results provide evidence that TAC has incremental information content over CF. CF is also more persistent than TAC in predicting future cash flows. In model (3), the coefficient on TXAC is significant at the 0.05 level; the coefficients on CF and the other five accrual components are significant at the 0.01 level. As in Barth et al. (2001), the signs of CF, ΔAR, ΔINV and DEP are all positive, and that of ΔAP is negative. The coefficient on DEP (1.25) is the largest, followed by that on TXAC (0.39), indicating that past long-term accruals have an important role in explaining the variation in current CF.
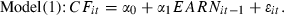
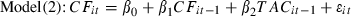
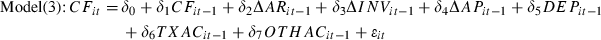
| Variable | Model (1) | Model (2) | Model (3) | |||
|---|---|---|---|---|---|---|
| Coefficient | t-statistic | Coefficient | t-statistic | Coefficient | t-statistic | |
| Panel A: Summary of results for within-sample forecasting tests (3127 firm-years, 1992–2001) | ||||||
| Intercept | 0.10 | 8.53† | 0.05 | 5.77† | 0.01 | 1.47 |
| EARN | 0.90 | 7.28† | ||||
| CF | 0.85 | 11.14† | 0.52 | 7.17† | ||
| TAC | 0.25 | 2.34** | ||||
| ΔAR | 0.21 | 3.61† | ||||
| ΔINV | 0.35 | 2.89† | ||||
| ΔAP | −0.24 | −3.31† | ||||
| DEP | 1.25 | 5.41† | ||||
| TXAC | 0.39 | 2.22** | ||||
| OTHAC | 0.19 | 2.39† | ||||
| Adjusted R2 | 31% | 50% | 58% | |||
| Vuong’s Z-statistic | ||||||
| Model (1) vs. Model (2) | 7.56† | |||||
| Model (2) vs. Model (3) | 2.81† | |||||
| Forecast performance measures | Model (1) | Model (2) | Model (3) | |||
| Panel B: Summary of results for out-of-sample forecasting tests (1042 firm-years, 2002–2004) | ||||||
| Theil’s U-statistic | 0.51 | 0.37 | 0.31 | |||
| Bias proportion | 0.00 | 0.00 | 0.00 | |||
| Variance proportion | 0.00 | 0.12 | 0.04 | |||
| Covariance proportion | 0.99 | 0.88 | 0.96 | |||
- i and t denote firm and year, respectively. CF is net cash flow from operating activities under the cash flow statement. EARN is earnings before extraordinary and discontinuing items. TAC is total accruals calculated as the difference between EARN and CF. ΔAR is the change in accounts receivable during the year. ΔINV is the change in inventory during the year. ΔAP is the change in accounts payable during the year. DEP is depreciation and amortization expense. TXAC is accruals in relation to income tax expense. OTHAC is other accruals. The t-statistic is based on White’s (1980) robust standard errors. Vuong’s Z-statistic relates to Vuong’s (1989) likelihood ratio test for model selection. A significant positive Z-statistic shows that the first model is rejected in favour of the second model. Theil’s U-statistic is a forecast error statistic that lies between zero and one, where one shows the worst fit. In a good prediction, the bias and variance proportions of Theil’s U-statistic are smaller than its covariance proportion.
- **Indicates significance at the 0.05 level. †Indicates significance at the 0.01 level.
A comparison between the adjusted R2 of model (2) (50 per cent) and model (1) (31 per cent) reveals that disaggregating EARN into CF and TAC produces significantly higher explanatory power for future cash flows than aggregate EARN does at the 0.01 level (Vuong’s Z-statistic = 7.56). Nevertheless, decomposing TAC into the six individual accrual components improves the forecast of future cash flows even further. This is evidenced by the higher adjusted R2 of 58 per cent in model (3) compared with that of 50 per cent in model (2), as well as Vuong’s Z-statistic (=2.81) which is significant at the 0.01 level. The results from adjusted R2s and χ2 tests consistently suggest that CF and accrual components together are more useful than aggregate earnings (EARN) in forecasting future cash flows; accrual components individually contribute to the predictive ability of future cash flows, whereas TAC conceals their information content; and accrual components have incremental explanatory power for future cash flows over aggregate CF.
Similar results are obtained from out-of-sample forecasting tests as reported in Panel B of Table 2. The covariance proportions are notably higher than the variance and bias proportions for models (1), (2) and (3), indicating that the three forecasting models predict future cash flows well. Theil’s U-statistic for model (3) is 0.31, which is lower than that of model (1) (0.51) and model (2) (0.37). Therefore, disaggregating earnings into aggregate CF and accrual components is more useful in predicting future cash flows than earnings alone, and CF and TAC together. The above conclusions are consistent with the results in Barth et al. (2001).
5.2. Incremental predictive ability of disaggregated cash flow components
Panel A of Table 3 reports the within-sample forecasting statistics for the regression of current CF on 1-year lagged CF and accrual components (model (4)). Cash flow components are significant at the 0.01 level, with the exception of TXPD, which is statistically insignificant. The coefficient on CSHRD is positive and those on CSHPD and INTPD are negative, which is expected as the former is a cash inflow variable and the latter are cash outflow variables. A comparison of the slope coefficients suggests that CSHRD and CSHPD are more persistent than INTPD and TXPD in the forecast of future cash flows. This is because CSHRD and CSHPD are more closely linked to a firm’s core operations (Cheng and Hollie, 2008). TAXPD shows the lowest persistence. This may be because the item contains both operating and non-operating cash outflows, or because it is related to taxable income in various financial years (AASB, 1997, para. 7.2.1; IASC, 1992, para. 36). These properties can have a negative effect on the ability of TAXPD to predict future cash flows.
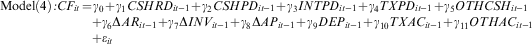
| Variable | Model (4) | |
|---|---|---|
| Coefficient | t-statistic | |
| Panel A: Summary of results for within-sample forecasting tests (3127 firm-years, 1992–2001) | ||
| Intercept | 0.01 | 3.97† |
| CSHRD | 0.40 | 4.91† |
| CSHPD | −0.39 | −7.72† |
| INTPD | −0.77 | −4.05† |
| TXPD | 0.27 | 0.83 |
| OTHCSH | 0.49 | 10.18† |
| ΔAR | 0.14 | 2.01** |
| ΔINV | 0.31 | 2.36** |
| ΔAP | −0.19 | −3.47† |
| DEP | 1.31 | 4.08† |
| TXAC | 0.28 | 0.79 |
| OTHAC | 0.15 | 2.06** |
| Adjusted R2 | 60% | |
| Adjusted R2– Model (1) | 31% | |
| Adjusted R2– Model (2) | 50% | |
| Adjusted R2– Model (3) | 58% | |
| Vuong’s Z-statistic | ||
| Model (3) vs. Model (4) | 1.97** | |
| Tests of coefficient restrictions: | ||
| Null hypothesis | χ2 statistic | p-value |
| H0–1: γ1 = γ2 = γ3 = γ4 = γ5 = 0 | 430.88 | 0.00 |
| H0–2: γ6 = γ7 = γ8 = γ9 = γ10 = γ11 = 0 | 139.77 | 0.00 |
| H0–3: γ1 = γ2 = γ3 = γ4 = γ5 | 97.20 | 0.00 |
| H0–4: γ6 = γ7 = γ8 = γ9 = γ10 = γ11 | 631.50 | 0.00 |
| Forecast performance measures | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| Panel B: Summary of results for out-of-sample forecasting tests (1042 firm-years, 2002–2004) | ||||
| Theil’s U-statistic | 0.51 | 0.37 | 0.31 | 0.30 |
| Bias proportion | 0.00 | 0.00 | 0.00 | 0.00 |
| Variance proportion | 0.00 | 0.12 | 0.04 | 0.04 |
| Covariance proportion | 0.99 | 0.88 | 0.96 | 0.96 |
- i and t denote firm and year, respectively. CF is net cash flow from operating activities under the cash flow statement. ΔAR is the change in accounts receivable during the year. ΔINV is the change in inventory during the year. ΔAP is the change in accounts payable during the year. DEP is depreciation and amortization expense. TXAC is accruals in relation to income tax expense. OTHAC is other accruals. CSHRD is cash received from customers. CSHPD is cash paid to suppliers and employees. INTPD is net interest paid. TXPD is taxes paid. OTHCSH is other cash flows from operations. See text for full description of models (1) to (3). The t-statistics is based on White’s (1980) robust standard errors. Vuong’s Z-statistic relates to Vuong’s (1989) likelihood ratio test for model selection. A significant positive Z-statistic shows that the first model is rejected in favour of the second model. Theil’s U-statistic is a forecast error statistic that lies between zero and one, when one shows the worst fit. In a good prediction, the bias and variance proportions of Theil’s U-statistic are smaller than its covariance proportion.
- **Indicates significance at the 0.05 level. †Indicates significance at the 0.01 level.
In Table 3, Panel A, all the accrual components except TXAC are significant at either the 0.05 or 0.01 level. TXAC is not significant at conventional levels. The coefficients for the accrual components have the signs reported by Barth et al. (2001): that is, CF, ΔAR, ΔINV, DEP and OTHAC are all positive and ΔAP is negative. The χ2 statistics for the null hypotheses that all the cash flow components are equal to each other and they are all equal to zero are rejected at the level of 0.01. This signifies that CF components capture information about future cash flows that aggregate CF conceals. The results from the tests of coefficient restrictions also show that accrual components significantly differ from each other, and differ from zero at the 0.01 level. The adjusted R2 of 60 per cent of model (4) is higher than that of model (3), with Vuong’s Z-statistic (=1.97) being significant at the 0.05 level. Therefore, both cash flow components and accrual components have significant roles in explaining variations in the current CF.
The results of out-of-sample forecasting are consistent with the within-sample forecasting results. In Panel B of Table 3, a covariance proportion that is significantly higher than the bias and variance proportions reveals that model (4) reliably predicts future cash flows. Furthermore, Theil’s U-statistic of model (4) is 0.30, which is lower than that of models (1), (2) and (3) (0.51, 0.37 and 0.31 respectively). These outcomes, along with the findings of within-sample forecasting statistics, consistently support the notion that a model that includes CF components and accrual components outperforms a model based only on the aggregate CF and accrual components in predicting future cash flows. This result extends that of Barth et al. (2001) and provides corroborating evidence to Cheng and Hollie (2008), as it indicates that the components of CF and accruals provide incremental information and convey useful information to accounting users in the prediction of a firm’s future cash flow.
6. Additional analyses
6.1. Industry membership
The relative importance of accruals- and cash-based accounting data is likely to differ across industries. This is so because macro-economic conditions and accounting policy choices are likely to vary across industries. Furthermore, the variations in the mix, types and persistence of accruals are likely to be industry specific (Barth et al., 2001, 2005). Clinch et al. (2002) also maintain that differences in operating environments between Australian mining and non-mining industries may affect the informational role of cash flow-related disclosure. In the spirit of these studies, we re-estimate our cash flow prediction models after grouping firms into industry sectors based on a two-digit global industry classification standard (GICS) code. For industry-level analysis, we require each industry sector to have at least ten firms per year.20,21 Therefore, Telecommunication Services and Utilities sectors, with six and three firms respectively, are excluded from our industry analysis.
Panel A of Table 4 shows that, based on the number of firms, the sample composition by industry sector follows the industry composition of the Australian capital market. Panel B in Table 4 reports coefficient estimations of both CF and accrual components in model (4) and results from the within-sample tests. Panel C reports the out-of-sample forecasting tests for models (1) through (4). The industry analysis supports our main results. However, it is notable that the predictive power of all the regression models is lowest in the Information Technology subsample. In particular, there is no gain in decomposing CF into its components for firms in this industry. Furthermore, judging from the out-of-sample forecasting results in the Health Care subsample, it appears that only model (4) (i.e., accrual and CF components together) provides reliable predictions for future cash flows. These results are consistent with the results of Amir and Lev (1996) and Francis and Schipper (1999). They argue that key accounting variables in high-tech firms, particularly earnings, are often greatly depressed and irrelevant to future cash flows because of the high investment in intangibles, which are either directly expensed or arbitrarily amortized.
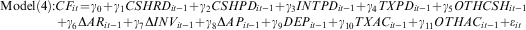
| Industry sector | Number of firms | Sample composition by industry sector, % | Market composition by industry sector, % |
|---|---|---|---|
| Panel A: Sample composition by industry sector | |||
| Energy | 33 | 9.46 | 11.36 |
| Materials | 141 | 40.40 | 36.41 |
| Industrials | 54 | 15.47 | 13.49 |
| Consumer discretionary | 54 | 15.47 | 11.43 |
| Consumer staples | 24 | 6.88 | 3.99 |
| Health care | 18 | 5.16 | 10.43 |
| Information technology | 16 | 4.58 | 8.57 |
| Telecommunication | 6 | 1.72 | 1.68 |
| Utilities | 3 | 0.86 | 2.64 |
| Total sample | 349 | 100.00 | 100.00 |
| Variable | Energy | Materials | Industrials | Consumer discretion | Consumer staples | Health care | Information technology |
|---|---|---|---|---|---|---|---|
| Panel B: Summary of results for within-sample forecasting tests (1992–2001) | |||||||
| Intercept | 0.01 | −0.01 | −0.00 | 0.01† | −0.01 | −0.01† | −0.01† |
| CSHRD | 0.49† | 0.46† | 0.08† | 0.38† | 0.52† | 0.27† | 0.17† |
| CSHPD | −0.51† | −0.44† | −0.06† | −0.37† | −0.51† | −0.28† | −0.16* |
| INTPD | 0.52 | −0.67† | −0.22 | 0.34 | −0.43† | 0.78** | 0.05 |
| TXPD | −0.13 | −0.63† | 0.58† | −0.16 | −0.05 | 1.05† | −0.30 |
| OTHCSH | 0.54† | 0.39** | −0.34** | 0.58† | 0.34† | 0.44† | 0.31 |
| ΔAR | 0.84† | 0.37** | 0.10 | 0.26† | 0.17† | −0.13 | 0.07 |
| ΔINV | 0.46* | 0.09† | 0.15 | 0.21† | 0.28† | 0.01 | 0.01 |
| ΔAP | −1.01† | −0.11† | −0.06 | −0.28† | −0.29 | −0.05 | −0.01 |
| DEP | 0.76* | 0.66† | 0.87† | 0.57† | 0.46† | 0.30† | 0.44 |
| TXAC | −0.31 | 0.11 | 0.00 | −0.60** | −0.42 | 0.25* | 0.23* |
| OTHAC | 0.17† | 0.02 | −0.25† | 0.22† | 0.16 | −0.30† | 0.08 |
| Adj R2 | 81% | 71% | 66% | 63% | 76% | 71% | 12% |
| Adj R2– (1) | 22% | 23% | 31% | 40% | 40% | 9% | 3% |
| Adj R2– (2) | 69% | 63% | 51% | 55% | 66% | 50% | 8% |
| Adj R2– (3) | 73% | 70% | 64% | 61% | 72% | 60% | 12% |
| Vuong’s Z-statistic | |||||||
| (1) vs. (2) | 9.21† | 8.45† | 6.50† | 7.44† | 7.43† | 5.95† | 2.92† |
| (2) vs. (3) | 5.80† | 3.14† | 6.39† | 7.14† | 5.02† | 3.34† | 1.80* |
| (3) vs. (4) | 7.02† | 2.63† | 4.92† | 5.41† | 4.05† | 3.98† | 1.01 |
| Tests of coefficients restrictions: | |||||||
| Null hypothesis | χ2 stat. | χ2 stat. | χ2 stat. | χ2 stat. | χ2 stat. | χ2 stat. | χ2 stat. |
| H0–1 | 161.96† | 149.83† | 102.16† | 105.71† | 247.54† | 78.07† | 38.12† |
| H0–2 | 122.16† | 184.46† | 852.26† | 656.42† | 46.75† | 136.47† | 11.62* |
| H0–3 | 21.88† | 11.77** | 58.57† | 58.11† | 36.78† | 100.56† | 2.62 |
| H0–4 | 107.30† | 147.19† | 781.83† | 370.46† | 46.29† | 141.72† | 11.18** |
| N | 285 | 1214 | 469 | 465 | 200 | 157 | 119 |
| Industry sector | Model 1 | Model 2 | Model 3 | Model 4 | N |
|---|---|---|---|---|---|
| Panel C: Summary of results for out-of-sample forecasting tests (2002–2004) – Theil’s U-statistic | |||||
| Energy | 0.50 | 0.34‡ | 0.29‡ | 0.28‡ | 87 |
| Materials | 0.61 | 0.40‡ | 0.36‡ | 0.34‡ | 407 |
| Industrials | 0.43‡ | 0.30‡ | 0.31‡ | 0.25‡ | 155 |
| Consumer discretionary | 0.35‡ | 0.32‡ | 0.26‡ | 0.28‡ | 152 |
| Consumer staples | 0.41‡ | 0.29‡ | 0.29‡ | 0.27‡ | 68 |
| Health care | 0.71 | 0.39 | 0.24 | 0.26‡ | 53 |
| Information technology | 0.86 | 0.85 | 0.82 | 0.75 | 41 |
- Industry sectors are defined by two-digit Global Industry Classification Standard codes as follows: Energy (10) Materials (15), Industrials (20), Consumer Discretionary (25), Consumer Staples (30), Health Care (35), Information Technology (45), Utilities (55) and Telecommunication (50). Market composition is estimated based on the number of the listed firms on the Australian Stock Exchange capital market in 1992 by industry sectors, excluding firms in Financials sector (40). The data are extracted from Aspect Financial Analysis database. The sample composition by industry sectors (Panel a) is based on the initial sample containing 349 firms. i and t denote firm and year, respectively. CF is net cash flow from operating activities under the cash flow statement. ΔAR is the change in accounts receivable during the year. ΔINV is the change in inventory during the year. ΔAP is the change in accounts payable during the year. DEP is depreciation and amortization expense. TXAC is accruals in relation to income tax expense. OTHAC is other accruals. CSHRD is cash received from customers. CSHPD is cash paid to suppliers and employees. INTPD is net interest paid. TXPD is taxes paid. OTHCSH is other cash flows from operations. See text for full description of models (1) to (3). H0–1 refers to the null hypothesis that cash flow components coefficients are equal to zero. H0–2 refers to the null hypothesis that accrual components coefficients are equal to zero. H0–3 refers to the null hypothesis that cash flow components coefficients are equal. H0–4 refers to the null hypothesis that cash flow components coefficients are equal. Vuong’s Z-statistic relates to Vuong’s (1989) likelihood ratio test for model selection. A significant positive Z-statistic shows that the first model is rejected in favour of the second model. Theil’s U-statistic is a forecast error statistic that lies between zero and one, where one shows the worst fit. In a good prediction, the bias and variance proportions of Theil’s U-statistic are smaller than its covariance proportion. N is the number of observations for analysing within-sample (Panel a) or out-of-sample (Panel b) forecasting tests for model (4) only.
- *Indicates significance at the 0.10 level. **Indicates significance at the 0.05 level. †Indicates significance at the 0.01 level. ‡The covariance proportion is higher than the bias and variance proportions of Theil’s U-statistic.
6.2. Further robustness checks
Robustness tests (un-tabulated) indicate that our main inferences remain the same after partitioning the sample into ‘short’ and ‘long’ operating cash cycles22, ‘small’ and ‘large’ firms23 and loss and profit firms.24 We summarize here the main findings from these tests. Firstly, when the operating cash cycle is long, earnings have greater predictive ability and accrual components are more persistent in forecasting future cash flows. In contrast, the predictive ability of CF components, in particular cash received from the customers (CSHRD) and cash paid to suppliers (CSHPD), is higher when the operating cash cycle is short. Secondly, in relation to firm size, earnings are not a reliable predictor of future cash flows for small firms. Our results also suggest that CF components are more persistent than accruals in predicting future cash flows of small firms. In large firms, both CF and accrual components are highly persistent in predicting future cash flows. Thirdly, regarding loss firms, we find that earnings are a poor predictor of future cash flows. We also find that the predictive ability of our regression models in the loss firms subsample is significantly lower than that of profit firms subsample. In profit firms, both CF and accrual components are important in the predicting future cash flows.
In un-tabulated tests, we also re-estimate our regression models using a random effects approach. This is to overcome, at least partially, the significant limitation of the OLS method, where both intercepts and coefficients are constant. The results from these tests support our inferences from the OLS regressions. Our main findings are also robust to four other sensitivity tests (un-tabulated) as follows: (i) grouping firms into negative and positive CF; (ii) re-estimating our regression models after deflating variables based on average total assets, as per Barth et al. (2001), and market capitalization; (iii) re-estimating regression models across years to control for possible autocorrelations in the residuals, as per Barth et al. (2001); and (iv) using 2-year lagged accounting variables to predict current cash flows.
The Pearson correlation coefficients reported in Table 1 for the full sample indicated that CSHRD is highly correlated (r = 0.99) with CSHPD. To mitigate potential multicollinearity problems arising from this issue, we re-examine our regression models after combining CSHRD and CSHPD into a single variable (see Gujarati, 2003). Our results remain unaltered.
7. Summary and conclusions
We investigate whether the predictive ability of earnings is enhanced by accruals and CF components in forecasting future cash flows. In particular, we compare the predictive ability of earnings against (i) CF and total accruals, (ii) CF and accrual components and (iii) CF components and accrual components. We are motivated by our access to actual direct method CF data reported by Australian listed firms since 1992. We are also motivated by the paucity of research on this important topic. To date, most of the studies in this topic have been premised on the US setting where cash flow components are unavailable and need to be estimated. Such estimation is subject to significant measure errors (Krishnan and Largay, 2000; Orpurt and Zang, 2009). Moreover, the US results may not be generalizable to other contexts because of the self-selection bias of the US samples in terms of cash flow reporting choice (Clinch et al., 2002).
We analyse a sample of 4520 firm-years representing 348 Australian listed companies over 1992–2004. We conduct within-sample tests over 1992–2001 and out-of-sample tests over 2002–2004. We compare the adjusted R2 of the OLS regression estimates with White’s (1980) correction for heteroscedasticity during the within-sample period. We use Theil’s U-static with its three components (bias, variance and covariance proportion) to compare out-of-sample forecasting accuracy. Our study provides evidence that CF components and accrual components together are more useful than (i) aggregate earnings, (ii) earnings disaggregated into aggregate CF and accruals and (iii) earnings disaggregated into aggregate CF and accrual components in forecasting future cash flow. The results also indicate that the components of CF and accruals individually contribute to the predictive ability of earnings, whereas aggregate CF and accruals mask their information content. We also investigate whether our results are sensitive to industry membership, length of the operating cash cycle, reporting of loss and firm size. In relation to industry membership, although the predictive ability of cash flow components is subject to some variability across industries, our main results are unaffected by industry categories. We also find that CF components enhance the predictive ability of earnings relatively more than accrual components when a firm’s operating cash cycle is short and the firm is small. For loss firms, earnings are a poor predictor of future cash flows.
We make two important contributions to the literature on cash flow forecasting. Firstly, we provide the first evidence on the role of disaggregated cash flows in the predictive ability of earnings for future cash flows using actual cash flow components. Secondly, we provide additional evidence on the role of firm characteristics such as size, profitability, industry membership and the length of the cash operating cycle for forecasting future cash flows. Our results are also relevant to the joint FASB/IASB project ‘Financial Statement Presentation’ on whether direct method cash flow statements should be mandated (IFRS Foundation, 2010a; FASB, 2010). In their proposal, the two standard-setters asserted that one of the main reasons why they tentatively decided to mandate the direct method is that the direct-method cash flow components can improve the forecast of future cash flows (see IASC Foundation, 2008; IFRS Foundation, 2010b). Our findings are consistent with this assertion in that the direct-method cash flow statements provide useful incremental information about the predictive ability of earnings beyond that of the indirect-method accrual components.




