The flight-to-quality effect: a copula-based analysis
The authors thank participants at the conference ‘Probability, Financial Derivatives, and Asset Pricing’, Charlottesville, USA, 2005, for helpful comments; we have particularly benefited from advice given by, and discussions with, David Bates, Paul Embrechts, Wake Epps, Dilip Madan, Ross Maller, Sid Resnick, Len Scott and Kent Zumwalt. We also thank participants at seminars at the Australian National University for their thoughts on the paper. Thanks are also due to Mark Moore for assistance with the data.
Abstract
We derive and estimate a copula combining the features of the Frank and Gumbel copulas to analyse the relationship between equity and long-term bond returns. Our analysis of quarterly returns from 1952 to 2003 finds that, in general, there is a positive relationship between equity returns and bond returns. In extreme situations, however, there is approximately a one-in-seven chance of a flight-to-quality effect where large negative equity returns are associated with large positive bond returns.
1. Introduction
The relationship between return and risk is fundamental to our understanding of financial markets. That returns should be higher when risk is higher is a mantra for both finance academics and practitioners. If investors were to expect a systematic increase in the risk of assets in an economy, the expected returns of all assets should increase (and, if risk was expected to fall, vice versa). Asset classes might therefore be expected to have broadly positive correlations and, if this is the case, investors would not be acting unreasonably if they allocated their assets, or devised their hedging strategies, on the basis of these expectations. This paper presents a thoroughgoing analysis of two important asset classes – stocks and long-term bonds – and finds that investors’ expectations of positive covariance between these asset classes can be wrong in extreme events where flights-to-quality occur.
Our analysis finds evidence of a prevailing positive relationship between stock and bond returns although, in extreme circumstances, the ‘normal’ relationship is reversed as investors fly to quality. Our analysis provides the first empirical evidence that flights-to-quality are present in the bond and stock markets.
In order to conduct a methodologically rigorous analysis of the inter-relationship between stocks and bonds, we adapt and extend a copula model. The dependence structure introduced and used in this study is new to both statistics and finance.1 As we have foreshadowed, and will discuss in more detail in the following paragraphs, there are theoretical and empirical arguments pointing to both positive and negative relationships between these assets. Our dependence function, or copula, combines the features of the Frank copula – allowing us to examine any homogenous relationship between stock and bond returns – and the Gumbel copula – allowing us to analyse any dependence structure at the tails of the distribution of the assets’ returns.
Stock and bond returns should have a positive covariance. That is, higher interest rates – and lower bond returns – should be associated with lower equity returns (and vice versa). There are two important reasons why this should be the case. First, if the values of equities are simply the net present value of future cash flows generated for shareholders, higher discount rates reduce the present values of expected cash flows. Second, dampening of expected economic conditions associated with higher interest rates may result in lower expected cash flows, before discounting, to shareholders. Evidence in support of such a relationship between stocks and interest rates may be found in Jensen et al. (1997), Thorbecke (1997), Patelis (1997) and Bernanke and Kuttner (2005).
Analysis has pointed to the existence of ‘flights to quality’. When investors fly to quality they move out of assets with higher expected risk, such as equities, and increase demand for less risky assets such as bonds. Hence, if flights to quality exist, lower equity returns will be associated with higher bond returns. Barsky (1989) and Abel (1988) present models in which relatively risk averse agents, perceiving an increase in the risk of equities, increase demand for bonds as a vehicle for their ‘precautionary saving’ (Barsky, 1989, p. 1134).2 In contrast to work treating monetary policy and interest rates as exogenous to equity returns, Barsky argues for the joint endogeneity of equity and bond returns.
Testing the competing views of the relationship between stock and bond returns is problematic. It may be the case that the two ‘stories’– the discounting story and the flight-to-quality effect story – are competing and that support for one entails rejection of the other. On the other hand, it may be the case that the stories are complementary; that is, there is a ‘normal’ state of affairs that is, on rare occasions, reversed. Methodologies such as regression or cointegration (Engle and Granger, 1987) may predispose analyses to type II errors about events such as flights-to-quality; we may reject the existence of flights-to-quality when, in fact, they are a regular but rare feature in the equity and bond markets. The linear dependence structures estimated using regression, and the linear combination of integrated variables estimated using cointegration analysis, will treat rare events, as we believe flights-to-quality to be, as anomalies. Such prima facie anomalous observations, for example, may be excluded from any empirical analysis on the basis of their appearing to be ‘outliers’. On the other hand, if such prima facie anomalous observations are included, the power of the analysis may be reduced.
Our initial analysis of stock and bond returns suggested that the data are compatible with the two competing stories and that we could not analyse the relationship between stock and bond returns using tools which presuppose linear dependence or linear combinations of variables. Our visual inspection of the data also suggested that utilization of a regime switching model (Hamilton, 1989, 1990; Engle and Hamilton, 1990; Lam, 1990) would also be ill suited for our analysis: the conditional distribution of flights-to-quality could not be estimated for such rare and isolated events. Assuming the flight-to-quality effect constitutes a regular but rare feature in the equity–bond relationship, modelling this effect requires a flexible specification of the bivariate dependence structure of stock and bond returns which further takes into account the presence of rare or extreme events.
Our analysis utilizes a copula model that can capture both ‘normal’ and ‘rare’ states in the relationship of stock and bond returns. Dependence functions, or copulas, allow the separate statistical treatment of the dependence and marginal behaviour of data. Dependence has many different characteristics. Broad symmetric dependence can be measured by correlation or rank correlation (i.e. Spearman’s ρ) and this form of dependence can be modelled using copula families such as the Gaussian copula, the t-copula and the Frank copula (see, for example, Ané and Kharoubi, 2003). Joint coincidence of extreme observations can be characterized by tail dependence. This kind of dependence can be captured by the Gumbel copula, the Clayton copula, and also the t-copula (see, for example, Breymann et al., 2003; Junker et al., 2006; Hatherley and Alcock, 2007). Other approaches, such as non-parametric copulas and conditional copulas, are explored by Scaillet (2002) and Granger et al. (2006).
We derive a copula function that is parsimonious – as it depends on only two parameters – and which can also accommodate broad homogenous and extremal dependence with opposite tendencies. The model is tailor-made for our application and therefore termed the flight-to-quality copula. The frequently used t-copula and the Clayton copula are both related to the flight-to-quality copula, but neither of these commonly used copulas is adequate to study the competing theories of the relationship of bond and stock returns examined in this paper: neither the t-copula nor the Clayton copula can incorporate opposite tendencies of broad and extremal dependence. The working paper of Gonzalo and Olmo (2005) is perhaps the paper most closely related to our study; it also combines ‘normal’ and ‘rare’ states in the dependence relationship within a parsimonious framework.3
In Section 2 we derive the flight-to-quality copula and discuss its properties. We estimate the copula model and present diagnostics in Section 3. Section 4 concludes our analysis.
2. Dependence modelling
The two competing stories outlined in the previous section suggest dependencies of opposite character. Broad positive homogenous dependence conforms with the discounting story. By contrast, the flight-to-quality story can be described by extremal dependence of large negative equity returns with large positive bond returns. Established methodologies of formulating dependence (such as normal, t, any other elliptical distribution, Gumbel or Clayton) cannot cater for the contrary dependence. We therefore derive our dependence structure by specifying the flight-to-quality copula Cftq.
2.1. Copula functions and dependence measures
Copula functions allow us to treat general versions of dependence in a multi-dimensional model. For the present application, we give a brief overview of the topic (Hatherley and Alcock, 2007 also provide a useful overview). A comprehensive treatment of copulas is given by Joe (1997) and Nelsen (1999).
with cumulative distribution function F and marginal cumulative distribution functions F1 and F2, the associated copula is a function C: [0, 1] × [0, 1]→[0, 1] that satisfies
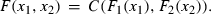()Equation (1) is known as Sklar’s theorem, and states broadly that copulas allow for the separate treatment of dependence and marginal behaviour.
Our study is focused on the dependence of equity and bond returns. Thereby, different kinds of dependencies are of interest. In most cases we expect equity and bond returns to be positively correlated. More robust measures of broad homogenous dependence than correlation are Spearman’s ρs and Kendall’s τ which are both invariant under monotone scaling of the coordinates. Accordingly, both measures are completely determined by the copula function. It is worth noting that the correlation is in general not scale invariant.
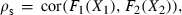
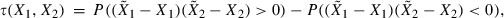
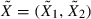is an independent copy of X.We now turn to a dependence measure that captures the behaviour of joint extremes. The flight-to-quality effect we examine might be understood as the simultaneous occurrence of large negative returns in the stock market and large positive returns in the bond market. Therefore, we identify flight-to-quality episodes with tail dependence and denote it using λ. Loosely speaking, tail dependence can be understood as an extremal correlation.
The following approach, adopted from Joe (1997), represents one of many possible definitions of tail dependence.
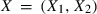is
()
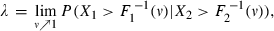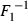and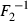 
are the inverse distribution functions of X1 and X2.The tail dependence coefficient as in Equation (2) is usually referred to as upper tail dependence; it quantifies the likelihood of large positive observations in the first coordinate coinciding with large positive observations in the second coordinate. The upper tail dependence is characterized by the upper right-hand corner of the joint distribution function. In general, tail dependence can be applied to measure the probability of joint extreme events in different coordinates.
For modelling and estimating dependence we prefer a parsimonious model. We present two copula functions relevant to our study that belong to the family of Archimedean copulas and are each described by one parameter.
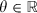is given by
()
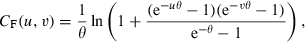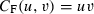for θ = 0. The Frank copula behaves in a fashion similar to the copula induced by the bivariate normal distribution with correlation coefficient ρ. Positive values of θ are associated with positive dependence and negative values of θ with negative dependence. If 
follows a Frank copula with parameter θ, then, by switching the coordinates to (X2, X1), we also obtain a Frank copula with the same parameter θ (invariant under permutation). If we invert one coordinate to (–X1, X2) then we again obtain a Frank copula but with the ‘inverted’ parameter −θ. These are familiar symmetries when measuring dependence with the correlation coefficient and are best known from the bivariate normal distribution. Further, as is the case for the normal copula, the Frank copula does not have tail dependence.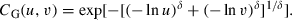
()The Gumbel copula is upper tail dependent with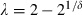 
, has no other form of tail dependence, and is symmetric 
(invariant under permutation).
The independence copula is given by Cπ(u, v) = uv. Both Archimedean copulas have independence as a special case. For the Gumbel copula, independence applies when δ = 1; for the Frank copula, independence applies when θ = 0.
2.2. The flight-to-quality copula
The flight-to-quality copula Cftq combines the Frank copula (see Equation (3)), which allows us to focus on the ‘usual’ positive dependence of stock and bond returns, and the Gumbel copula, allowing us to analyse the tail dependence λftq (see Equation (4)). The copula we propose is a parsimonious model with just two parameters. This set-up facilitates both its estimation and subsequent testing.
()
()The transformed Frank copula CtF inherits all the properties from its parent copulas, Frank and Gumbel. For the flight-to-quality copula Cftq, these properties are then mirrored at the (0, 0.5) plane:
- 1
the parameter θftq=−θ quantifies the extent and direction of broad dependence pattern (the sign changes because of the mirroring); and
- 2
the parameter δftq = δ, or equivalently
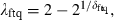measures the tail dependence in the fourth quadrant (negative first and positive second coordinates).
We provide guidance on the interpretation of the flight-to-quality copula Cftq in Figure 1. We have plotted contour lines of densities of the bivariate distributions with copula Cftq under different parameterizations (and standard normal margins).
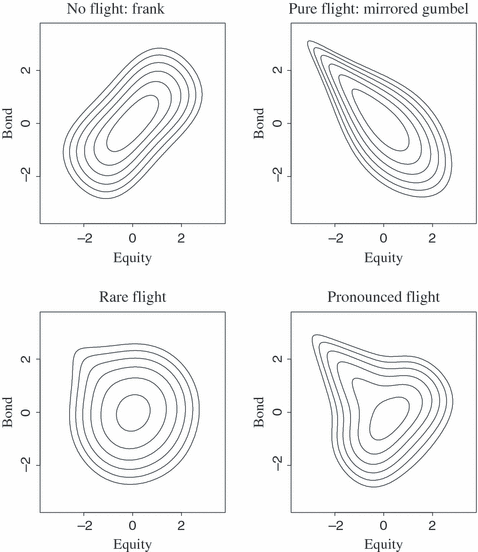
Contour lines of densities of different Cftq model parameterizations with standard normal margins.
If stock and bond positively covary (i.e. if the ‘discounting story’ holds), the copula plotted in the upper left-hand corner of Figure 1 should be sufficient to model the relationship between the returns of stocks and bonds. Here, we have chosen δftq = 1 and θftq = 5, reducing the model to the Frank copula. If the flight-to-quality effect prevails in the data, the copula depicted in the upper right-hand corner of Figure 1 will capture the relationship between the two asset classes. The copula results from δftq = 2 and θftq = 0, giving a mirrored Gumbel density with strong tail dependence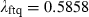 
.
If flight-to-quality effects are rare and relatively undramatic, and if stocks and bonds ‘normally’ exhibit positive covariance, the copula presented in the bottom left-hand corner of Figure 1 will model the relationship between the asset classes (δftq = 1.1 and θftq = 0.95;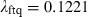 
). If flight-to-quality episodes are stronger and more common, the copula depicted in the bottom right-hand corner will capture the complexity of the relationship between the two asset classes (δftq = 1.5 and θftq = 5.75; 
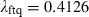).4
The transformed Frank copula CtF spans a nested copula family enabling likelihood ratio tests for comparing different specifications. The family contains Frank CF, Gumbel CG, and the independence copula C, and is specified by the parameter vector (δ, θ) ∈ [1, ∞) × 
. The characteristics of CtF can be readily summarized. For δ ↘ 1, the transformed Frank copula CtF tends to the Frank copula CF. The ‘Frank parameter’θ remains and governs the dependence structure in the centre of the distribution. For | θ | ↘ 0, the transformed Frank copula reduces to the Gumbel. The Gumbel copula CG is symmetric under permutation but is not symmetric under inversion of a coordinate. Finally, for λ ↘ 1 and | θ | ↘ 0, the transformed Frank copula tends to independence given by Cπ.
2.3. Estimation methodology and model diagnostics
The previous section specified the flight-to-quality copula, Cftq, which admits both dependencies as observed in the data. In this section, the estimation of the dependence structure is presented. Measures for comparing different model specifications will also be discussed.
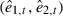(t = 1,…,T). To avoid misidentification, the margins F1 and F2 are estimated non-parametrically by their empirical distribution functions and the uniform standardized residuals 
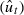(t = 1,…, T) are obtained 
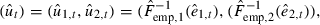for (t = 1,…, T) where 
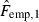and 
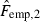denote the empirical margins and ‘−1’ their inverse. In a second step, the copula parameter vector (θftq, δftq) is estimated from 
using maximum likelihood. As shown, for example, by Genest et al. (1995), the resulting estimator is consistent and asymptotically normally distributed
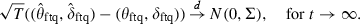
We report the standard errors and resulting t-values as derived by Genest et al. (1995). Alternative estimation methodologies to the semi-parametric approach of Genest et al. (1995) are, for example, the inference functions for margins (IFM) method and maximum likelihood estimation (MLE). Compared with the single-step MLE, IFM is a two-step procedure where in the first step the parameters of the margins are estimated and in the second step the dependence parameters are estimated; both steps use MLE (see Joe (1997, Ch. 10). IFM is often preferable to MLE for computational reasons. In our setting, we focus on avoiding misspecification of the margins as this potentially invalidates the subsequent copula analysis, and therefore we follow Genest et al. (1995).5
In addition to evaluating t-statistics, other measures for comparing different model specifications are explored. When investigating the significance of the flight-to-quality parameter δftq the results have to be interpreted with care. Whereas θftq is a broad dependence parameter that is essentially estimated from ‘normal’ observations, the parameter δftq is of an asymptotic nature and requires a sufficient number of ‘extreme’ observations for a reliable estimation. This situation is well known from extreme value theory and often results in rather large standard errors for ‘extreme’ (asymptotic) parameters.
Likelihood ratio (LR) tests are used to compare the full model to its nested alternatives of homogeneous dependence (no flight-to-quality), solely extremal dependence (pure flight-to-quality) and independence. The first two specifications are illustrated in Figure 1. In the upper left-hand corner no extremal dependence is permitted 
(or δftq = 0 sending this parameter to its boundary value). In the upper right-hand corner, the flight-to-quality copula reduces to the pure flight-to-quality copula (θftq = 0). Here, the LR test is performed as usual. The last reduced model is the independence model (δftq = 1, θftq = 0).
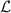and specified as
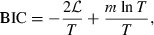
Formally, the entropy EN is the expected value of the negative logarithm of the maximized density function cftq; EN = E[−ln cftq]. In this paper, the expectation is approximated by Monte Carlo simulation. Under independence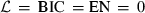 
, as the density of the independence copula cπ is constant 1.
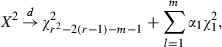()3. Empirical analysis
The model developed for analysing the dependence structure of equity and long-term bond returns is the flight-to-quality copula Cftq (see Section 2.2). A necessary prerequisite for this analysis is that the copula function must be estimated using series of bivariate data that are conditionally independent and identically distributed (i.i.d.) over time. To ensure that this assumption is satisfied, we analyse our data and find a predictable component in real bond returns as well as the effects of heteroscedasticity; consequentially, we orthogonalize and standardize our data to these effects. Following this procedure, the flight-to-quality copula Cftq is estimated. Based on these estimates, their t-values and additional diagnostics, we test the equity and bond data for evidence of the competing stories, i.e. the monetary story and the flight-to-quality story.
3.1. Data and time-series model
We begin our analysis from 1952 following the Federal Reserve Bank’s final lifting of market controls after World War II. We utilize real quarterly returns of the CRSP value-weighted index of US stocks and the CRSP 30 year bond index from 1952 to 2003.6 That is, we have followed seminal asset pricing papers such as Hansen and Singleton (1983) and Mehra and Prescott (1985)7 and adjusted the returns for inflation using the consumer price index (sourced from the US Department of Labor). The period we study is one where inflation varied considerably and removing the effect of inflation removes any confounding effect of this variable on our study.8
We considered higher frequency observations, but our initial analyses revealed that correlations in the data precluded the rigorous application of the copula methodology we believe is required for a thoroughgoing analysis of the relationship between stock and bond returns.9 Using quarterly data facilitates our analysis of the relationship by minimizing noise in the data set.
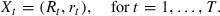()Our sample size of 52 years of quarterly data results in T = 208 bivariate observations. A preliminary analysis suggested the possibility of weak conditional heteroscedasticity in the equity returns, heteroscedasticity in the bond returns, some autocorrelation in bond returns and lagged cross-correlation of bond and equity returns. We utilized these findings to specify different mean and variance equations. The building blocks included lagged variables in the mean equation, structural break analysis for the bond data affecting its mean and variance, and potential GARCH effects.
()
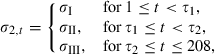()The estimation results for the model in Equations (9) and (10) are given in Table 1. The selection of this particular model indicates that the past real bond returns explain the present evolution of the real equity returns. Such a relationship is perhaps unsurprising given the history of papers modelling equity returns using lagged bond market variables.11 Also note that we incorporated rt−5 in the light of our finding in the preliminary analysis. We have little economic interpretation as to why such an effect may be present in the model. However, the presence of this factor does not affect the outcome of the subsequent dependence analysis.
| Parameter | Estimate | SE | t-value | p-value |
|---|---|---|---|---|
| μ 1 | 0.017359 | 0.006308 | 2.75 | 0.0059 |
| μ 2 | 0.001983 | 0.003319 | 0.60 | 0.5502 |
| κ 1,1 | 0.236266 | 0.093835 | 2.52 | 0.0118 |
| κ 1,2 | 0.201683 | 0.105839 | 1.91 | 0.0567 |
| κ 2,1 | −0.206355 | 0.077206 | −2.67 | 0.0075 |
 |
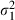0.006885 | 0.000645 | 10.67 | 0.0000 |
 |
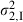0.001204 | 0.000160 | 7.53 | 0.0000 |
 |
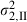0.010158 | 0.003199 | 3.18 | 0.0015 |
 |
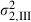0.002844 | 0.000548 | 5.19 | 0.0000 |
| ρ | 0.174877 | 0.070553 | 2.48 | 0.0132 |
 |
557.50 | BIC | −5.2309 |
-
Pseudo-maximum likelihood parameter estimates for the model specified in Equations (9) and (10), including standard errors, t-values and p-values, and maximized likelihood functions
and BIC are reported. Note the correlation coefficient ρ results from the pseudo-maximum likelihood method assuming bivariate normality of innovations.
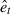serve as input data for the copula-based dependence analysis
()The standardized residuals 
were investigated for independence using the BDS test (see Brock et al., 1987). Setting the trimming parameter ε to 1 standard deviation, the BDS test for the equity and bond series results in p-values of 0.5158 and 0.6661, respectively. This indicates that the null hypothesis of independent data for each coordinate cannot be rejected at any usual confidence level.
Finally, we stress once more that a copula-based dependence analysis as performed subsequently requires a sample that is conditionally i.i.d.
On the basis of our careful preliminary analysis we selected and fitted a time-series model that generated residuals satisfying this requirement. The results of the copula analysis are, however, robust when varying the specification of the time-series model, although, in our case, the results (especially the flight-to-quality parameter) become more distinct for a more appropriate choice of the time series model.
3.2. Estimation results and diagnostics
The dependence structure of the equity and bond returns is analysed using the flight-to-quality copula Cftq which we derived in Section 2. The copula parameters θftq and δftq are estimated by maximum likelihood. The estimates are then used to investigate the data for the presence of the flight-to-quality effect (driven by δftq) and the homogeneous dependence (driven by θftq). The significance of the parameter estimates are assessed by their t-values. This analysis is supported by respective likelihood ratio (LR) tests for nested submodels. Further, the three goodness-of-fit measures BIC, entropy EN, and χ2-statistics are reported.
The maximum likelihood estimation results are reported in Table 2. The parameter for homogenous dependence takes the value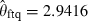 
and is significant at any usual level with a t-value of 3.74. Spearman’s ρs and Kendall’s τ are scale-invariant dependence measures for homogenous dependence, and their estimates are 
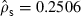and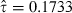 
. This supports the relationship between equity and bond returns as suggested by the discounting story: lower (higher) interest rates appear to increase (reduce) the present values of cash flows and, or, make investors optimistic (pessimistic) about future economic conditions affecting firms’ profitability. The parameter estimate δftq takes the value 1.1147, and is significant at the 95 per cent level.
| θ ftq | δ ftq | ρ s | τ |  |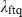
|
|---|---|---|---|---|---|
| ML estimate | 2.9416** | 1.1147* | 0.2506** | 0.1733** | 0.1377* |
| SE | 0.7845 | 0.0574 | (0.0667) | (0.0464) | (0.0596) |
| t-value | 3.74 | 2.00 | (3.76) | (3.74) | (2.31) |
- Maximum likelihood estimates of copula parameters (θftq, δftq) given in Equations (5) and (6), based on uniform standardized residuals of the model in Equations (9) and (10) are reported. The parameters ρs, τ and δftq are functions of the parameter vector (θftq, δftq), and their estimates are given as the function of the point estimate of the underlying parameter vector. The standard errors are computed using the delta method and are reported in brackets. Significance at the **99 per cent; *95 per cent and •90 per cent levels.
The tail dependence estimate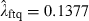 
is derived from 
and implies that we have a one-in-seven chance of observing the flight-to-quality phenomenon given a dramatic drop in the stock market. In extreme conditions, investors fly from stocks and seek the relatively safe haven of bonds.
Figure 2 displays the estimated contour lines of the flight-to-quality copula Cftq based on the maximum likelihood estimates 
and 
.12Figure 2 is comparable with the figure depicted in the bottom left-hand corner of Figure 1, which depicts the rare flight-to-quality effect. The flight-to-quality effect is driven by few data points but constitutes a significant part of the observed dependence pattern. At the 20 per cent level, the flight-to-quality dates ordered by their magnitude are 2002:3, 1998:3, 1987:3, 2000:4, 2001:3, 1960:1, 1957:4.13 The dates include distinct events like the burst of the tech bubble, the Russian bond/LTCM crisis, the 1987 crash, and the terrorist attack on the World Trade Center in New York on 11 September 2001.
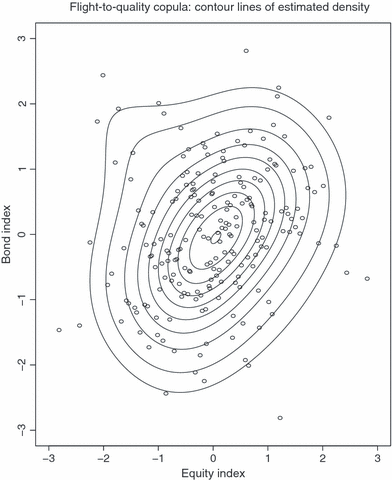
Contour lines of density of estimated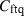 
; given by 
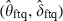in Table 2. The margins are standard normal.
Further support for the analysis reported in Table 2 may be found in the alternative measures to the t-values that we examine. The results of the LR test are in Table 3. The LR statistics confirm the conclusions we draw using the t-values. The null hypothesis that the full model reduces to the submodel with no flight-to-quality parameter (δ = 1) is rejected at any usual confidence level. The homogenous positive dependence is captured by θ. According to the LR statistics, this parameter is highly significant and should be included. If θ is not included in the specification, then the independence specification (0, 1) cannot be rejected against the alternative of pure flight-to-quality (0, δ).
| Null model | Alternative model | |||
|---|---|---|---|---|
| (θftq, δftq) | (θftq,1) | (0, δftq) | (0, 1) | |
| (θftq, δftq) | — | — | — | — |
| (θftq, 1) | 8.31** | — | — | — |
| (0, δftq) | 21.63** | — | — | — |
| (0, 1) | 21.63** | 13.31** | 0.00 | — |
- The full model has parameter (θftq,1, δftq); submodels are indicated by their specific restrictions. Significance at the **99 per cent; *95 per cent and •90 per cent levels.
Bayesian information criterion, entropy and the traditional chi-squared test are alternative criteria for comparing the full copula model with its nested submodels. These criteria allow for the comparison of the two non-nested submodels of no flight-to-quality (θftq, 1) and no homogenous dependence (0, δftq). Table 4 contains BIC, entropy and the intervals of p-values of the chi-squared tests (rather than the test statistics).14
| BIC | Entropy | χ 2, p-value | |
|---|---|---|---|
| (θftq, δftq) | −0.05418 | −0.0508 | 0.3672, 0.3956 |
| (θftq, 1) | −0.03940 | −0.0343 | 0.0742, 0.0907 |
| (0, δftq) | 0.0257 | 0.0000 | 0.0000, 0.0000 |
| (0, 1) | 0.0000 | 0.0000 | 0.0000, 0.0000 |
- The full model has parameter (θftq,1, δftq); submodels are indicated by their specific restrictions.
The full copula model is confirmed by all the three criteria. The full flight-to-quality copula produces the lowest BIC and lowest entropy EN. Furthermore, it has the highest p-values of the χ2 goodness-of-fit test. The reduced model, catering for homogenous dependence but not for the flight-to-quality effect (θftq, 1), comes second in all categories (although it is far from the full model). Using only the χ2-statistic, we see that the reduced model cannot be rejected at the 95 per cent and 99 per cent confidence levels.15 The pure flight-to-quality copula and the independence copula both produce χ2-statistics which reject the null hypothesis of an adequate model fit at the 99 per cent level. The BIC indicates that the extra parameter for the tail dependence is not favourable. Flights-to-quality are clearly rare events: the flight-to-quality effect cannot explain the main part of the dependence structure between equity and bond returns.
4. Summary and conclusion
Our analysis has utilized a transformed Frank copula to analyse the relationship between stock and bond returns. We find evidence that two potentially competing stories – the discounting story and the flight-to-quality story – capture aspects of the data. In the normal course of events, the discounting story describes the relationship between returns of bonds and the value-weighted index. Higher bond returns (i.e. falling interest rates) are associated with higher stock returns and vice versa (as indicated by the statistically significant value of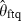 
of 2.9416 and accordingly the values of ρs of 0.2506 and τ of 0.1733). In rare, but dramatic, instances, falling equity prices are associated with increasing bond prices as predicted by the flight-to-quality story. The statistically significant value 
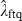of 0.1377 indicates that such a flight-to-quality will be observed in around one in seven large negative equity market movements.
In addition, our analysis has reminded us of the usefulness of copula analysis in finance and economics. We believe our analysis has enabled us to capture the rich inter-relationship between stock and bond returns. Using a more ‘traditional’ form of analysis (such as regression or cointegration) would, we believe, have obscured, if not totally lost, the complexity of the relationship between stock and bond returns.
