Interaction of size, book-to-market and momentum effects in Australia
The authors gratefully acknowledge financial assistance provided by Dimensional Fund Advisors (DFA) Australia and the Australian Research Council through ARC Linkage Grant (LP0453913). The paper forms part of a larger project undertaken collaboratively with Monash University. This paper has been adapted from research presented in Michael O’Brien’s doctoral thesis. The authors thank Joey Low and Daniel Chai for assistance with the database, Phil Gray for discussions on statistical techniques, and Rob Durand and an anonymous referee for comments on the paper.
Abstract
This study seeks to disentangle the effects of size, book-to-market and momentum on returns. Initial results show that each characteristic has a role in explaining returns, but that there is interaction between size and momentum, as well as between size and book-to-market. Three key findings emerge. First, the size premium is the strongest, particularly in the loser portfolios. Second, the value premium is generally limited to the smallest portfolios. Third, the momentum premium is evident for the large- and middle-sized portfolios, but loser stocks significantly outperform winner stocks in the smallest size portfolio. When these interactions are controlled with multivariate regression, we find a significant negative average relation between size and returns, a significant positive average relation between book-to-market and returns, and a significant positive average relation between momentum and returns.
1. Introduction
Prior research, primarily based on US data, has demonstrated a relationship between stock returns and three characteristics: size, book-to-market and momentum (see Fama and French, 1992, 1993). Stocks that are small, and/or that possess high book-to-market (value stocks), and/or have produced strong positive returns over the prior 6 months (winners) tend, on average, to produce high raw returns and abnormal positive returns when adjusted for systematic risk. The opposite is true for large, low book-to-market (growth), loser stocks.
The behaviour of Australian stock returns is less well documented and far more ambiguous. While there is reasonably clear evidence of a small firm premium in the Australian market (Beedles et al., 1988), there is less evidence and less agreement amongst that evidence concerning the existence of the value and momentum premiums. With regard to the value premium, the problem is largely one of lack of evidence owing to the limited availability of Australian data over time and in cross-section. There are several Australian studies which examine momentum (e.g. Brailsford and O’Brien, 2008), but they have yielded inconsistent results. Moreover, few studies in the Australian market have considered how these three characteristics interact in explaining stock returns. Indeed, there is no Australian research that we are aware of which attempts to isolate the contribution of each of the characteristics while holding the other two constant.
The present study has two main aims. First, the paper documents the relationship between returns and the three characteristics using a new accounting data set that is far more comprehensive over time and in cross-section than that employed in prior research. Second, the paper examines the relationship between the characteristics, using an approach that controls for the interaction in order to measure the independent role of each characteristic in explaining returns.
The remainder of this study proceeds as follows. Section 2 outlines relevant prior research with a focus on studies of the Australian market and highlights various limitations with the small number of previous studies. Section 3 details the methodology employed and Section 4 describes the various sources of data. Section 5 presents and discusses the results, while the final section offers a summary and conclusion.
2. Prior research
2.1. Size effect
The size effect, or small firm premium, is the best documented and least ambiguous of the three characteristics. Brown et al. (1983a,b) provide some of the earliest Australian evidence using data from March 1958 to June 1981, where a size effect is clearly evident across decile portfolios formed on the basis of ranked market capitalization. This result has been subsequently corroborated by Beedles et al. (1988) using monthly data from 1974 to 1984. More recent evidence has come from Gaunt et al. (2000), Halliwell et al. (1999), Gaunt (2004), Durand et al. (2007), Kassimatis (2008), Brailsford and O’Brien (2008) and Gharghori et al. (2009), who all confirm the existence of a size premium. Of note, the returns across size portfolios are not monotonic, but rather concentrated peaks occur in the two smallest deciles.
Halliwell et al. (1999), Gaunt (2004), Kassimatis (2008) and Gharghori et al. (2009) examine the size effect as part of a broader study of the application of the Fama–French multi-factor model to Australian stock returns. Halliwell et al. draw on data covering the period 1981–1991, Gaunt et al. use data from 1991 to 2000, while both Kassimatis and Gharghori et al. use data from 1992 to 2005. With the exception of Gharghori et al., these prior studies break their observations into quintile portfolios. All three studies report a clear size premium to the smallest quintile of stocks when reporting raw returns, but little difference across the four remaining size quintiles. A similar result is found when reporting the intercept from the one-factor capital asset pricing model (CAPM) and three-factor Fama–French model, in the case of Halliwell et al. and Gaunt et al., and for a four-factor model in the case of Kassimatis (2008).
Brailsford and O’Brien (2008) endeavour to separate out the role of size and momentum in Australian stock returns. With respect to the size effect, their results are similar to those of Halliwell et al. and Gaunt (2004); for both raw and risk-adjusted returns, the smallest size quintile consistently exhibits the highest returns and little difference in returns across the remaining four size quintiles.
2.2. Momentum
The widely cited US study of momentum is Jegadeesh and Titman (1993) who report clear evidence of return momentum across decile portfolios created on prior returns. That is, extreme portfolios formed on the basis of ranked previous return continue their return path such that prior winners significantly out-perform prior losers over the next 12 months.
Research into momentum in the Australian market is more recent. Hurn and Pavlov (2003) limit their study to the largest 200 companies using Centre for Research in Finance (CRIF) monthly returns from 1973 to 1998, and examine momentum behaviour across all 200 companies, as well as in two sub-groups comprising the largest 50 stocks then the next sized 150 stocks. The performance of a momentum strategy is assessed by assuming a long position in the winner portfolio and a short position in the loser portfolio. The strategy produces significant positive returns for all three groups of stocks and for periods up to 12 months after portfolio formation for both raw and risk-adjusted returns. The momentum effect is stronger for the largest 50 stocks than for the remaining 150 stocks.
Gaunt and Gray (2003) examine autocorrelation in Australian returns over the same time period as Hurn et al. They find positive autocorrelation based on 1 month prior returns that are robust to risk adjustment, but further investigation shows that stocks outside the top 200 drive this result.
Demir et al. (2004) utilize daily returns, across the period 1990–2001, and restrict their sample to stocks on the Australian Stock Exchange (ASX) Approved Securities list or constituents of the All Ordinaries Index. The effect of this restriction is to exclude small, illiquid stocks from the sample and include stocks that are most capable of being short-sold. The authors report highly significant market-adjusted returns over a variety of portfolio formation and holding periods (30–180 days). By comparison with other studies over the commonly investigated 6 month formation and 6 month holding period this strategy produces on average 1.76 per cent per month market-adjusted return to buying the winner decile and selling the loser decile. Further tests reveal that the momentum profits are the highest amongst the smallest quintile stocks (and the lowest volume quintile stocks) and that profits within the size quintiles are driven mainly by the loser stocks.
Durand et al. (2006) create decile portfolios based on periods ranging from 3 to 12 months using CRIF monthly returns from 1980 to 2001. Unlike Hurn et al. and Demir et al., all listed stocks are eligible for inclusion in the ranked portfolios. Contrary to those prior studies, Durand et al. find that the loser portfolio outperforms the winner portfolio with the bulk of this superior performance occurring in July.
Brailsford and O’Brien (2008) provide evidence that reconciles the inconsistent results of prior momentum research by examining the interaction between size and momentum. Specifically, the study finds that when all listed stocks are eligible for inclusion, as in Durand et al., the loser portfolio tends to be comprised of very small companies which exhibit strong positive returns. This is particularly the case when equal-weighted portfolio returns are calculated. Thus, those studies that report the loser portfolio outperforming the winner portfolio, such as Durand et al. (2006), appear to be picking up a small firm effect rather than a true momentum effect. Brailsford and O’Brien also allocate stocks to one of five size portfolios and one of five momentum portfolios, and find that momentum profits are earned only within the largest three size quintiles, with the bulk of those risk-adjusted profits arising from the short side of the momentum strategy.
2.3. Value effect
Australian evidence on the book-to-market effect (or value effect) is limited, due primarily to the lack of a comprehensive database with the necessary data required to calculate book value (see Faff 2001). Fama and French (1998) offer the first analysis of Australian data in their examination of value and growth across 13 countries. Their study covers the period 1975–1995 using data from the Morgan Stanley Capital International (MSCI) database and, as a result, comprises a relatively small number of large stocks with an average of just 80 stocks per year, or less than 10 per cent of listed stocks. Surprisingly, despite the limited range of stocks, Australia produces the highest difference of all countries between the annual return on the extreme book-to-market portfolios of 12.32 per cent, with the highest book-to-market portfolio returning 17.62 per cent and the lowest book-to-market portfolio producing 5.30 per cent.
Halliwell et al. (1999) are able to obtain book values for around 50 per cent of listed stocks over the period 1979–1990. Stocks are allocated to size quintiles and to book-to-market quintiles. A positive relationship is evident between book-to-market and excess return, although this is restricted mainly to within the largest three size quintiles. This relationship is still evident after using the Fama–French three-factor model to generate expected returns, in which the HML factor shows very little explanatory power.
Gaunt (2004) undertakes a similar study to Halliwell et al. but covers a different period, 1991–2000, and has wider cross-sectional coverage of stocks due to better access to data on book value. Gaunt finds that the highest book-to-market portfolio produces a higher raw return than the lowest book-to-market portfolio across all size quintiles but is statistically significant in only the largest three quintiles. When the Fama–French three-factor model is used to generate expected returns, the value premium is maintained in the second and third largest size quintiles but is no longer evident in the largest size quintile.
Kassimatis (2008) also undertakes a Fama–French-type examination over the period 1992–2005 using date from Datastream, which is a database that is generally skewed to the larger listed companies. Kassimatis finds that raw returns are greater in the high book-to-market portfolio compared with the low book-to-market portfolio for the largest four size quintiles but not in the smallest size quintile. These findings remain when a four-factor model (Fama–French three-factor model plus a momentum variable) is used to generate expected returns.
Gharghori et al. (2007) examine data covering 1993–2004 and find a significant positive relationship between book-to-market and returns. They also report a relationship between size and book-to-market in that the two highest book-to-market deciles have an average market capitalization that is significantly smaller than the other deciles.
Most recently, Gharghori et al. (2009) using data from 1993 to 2005 find some evidence of a book-to-market effect with a significant difference between the raw return on the lowest book-to-market and highest book-to-market portfolios. However, there is not a monotonic increase in returns across the six portfolios. In addition, the intercept terms in the three-factor Fama–French model are significant for the four largest book-to-market portfolios, and there is no statistically significant difference between the intercept on the lowest and highest book-to-market portfolios. So, to maximize portfolio sizes, Gharghori et al. do not, unlike other research, dual sort stocks on book-to-market and size, and thus they are not able to comment on any interaction between value and size.
Overall, the above studies suggest a value effect in the Australian market which may be related to size. The evidence points to a value effect at the large end of the market, which is exacerbated when one considers that the research has been conducted using data drawn from only larger stocks. Further, evidence of the magnitude of the value effect is variable.
2.4. Summary of Australian evidence
The prior Australian research suggests a relationship between size and returns, but this appears limited to a premium to the smallest (micro1) firms with little difference in returns across remaining companies in the top 80–90 per cent of stocks. With regard to momentum, the evidence has been mixed, although Brailsford and O’Brien (2008) have uncovered a relationship between momentum and size, and when this relationship is taken into account, momentum is evident only in the larger listed stocks. From the limited research, a value premium also appears to exist, but again there is a relationship with size such that it is limited to the larger stocks.
The documented interaction between size and momentum, and the apparent interaction between size and book-to-market, suggest that we need a better understanding of how all three variables interact when explaining stock returns. This study aims to add to that understanding, and to do so with a new data set, which covers a much longer period and provides a far greater coverage of stocks.
3. Method
The objective of the study was to assess how size, book-to-market and momentum influence Australian equity returns. To control and isolate the effects of these three characteristics, portfolios are created, by triple sorting on each characteristic. As discussed below, the data set provides a comprehensive coverage of listed Australian stocks over the last 25 years and it has not previously been the subject of empirical tests.
The formation of portfolios involves the following. For each month, we first rank all stocks in the sample by market capitalization at the end of each month, where each stock is assigned to one of three size-based portfolios. The first 30 per cent of stocks are assigned to portfolio 1 (large), i.e. this portfolio contains the 30 per cent of listed stocks with the largest market capitalization. The next 40 per cent of stocks are assigned to portfolio 2, while the last 30 per cent of stocks are assigned to portfolio 3 (micro).
Independently, all stocks are ranked by their book-to-market ratio, and assigned to one of three book-to-market portfolios. Portfolio 1 (growth) contains the 30 per cent of stocks with the lowest book-to-market ratio, portfolio 2 contains the next 40 per cent of stocks, while portfolio 3 (value) contains the final 30 per cent of stocks with the highest book-to-market ratios. Thus, procedure follows the well-established route initiated by Fama and French (1993).
Finally, all stocks are independently ranked by their past 6 month price momentum (largest first) and assigned to one of three portfolios with the first 30 per cent of stocks assigned to portfolio 1 (winner), the next 40 per cent of stocks entering portfolio 2 and the final 30 per cent entering portfolio 3 (loser).2
After these three independent sorts, each stock has been assigned to one size portfolio, one book-to-market portfolio and one momentum portfolio. The intersection of these three sorts gives a total of 27 size, book-to-market and momentum portfolios. These portfolios are held constant between annual formation periods. For each month we calculate equal and value-weighted returns resulting in a series of 300 monthly returns covering the period January 1982 to December 2006.
In applying our models, we utilize these triple-sorted size, book-to-market and momentum portfolios. These portfolios control for the three effects of interest and the procedure allows a test for how the different characteristics influence returns.
In the first instance, we report raw returns for each of the 27 portfolios and investigate whether these returns differ systematically across the three characteristics. Note that the size, book-to-market and 6 month price momentum characteristics are calculated each month. Next, a more robust multivariate regression analysis is performed in order to disentangle the relationships. Point estimates are calculated and the statistical significance of these relationships is tested.
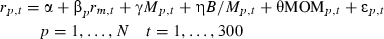()Taking logarithmic values of the variables of interest provides consistency with previous studies and reduces the impact of outliers. α, γ, η, θ, βp are regression estimates. γ, η and θ measure the effect on returns of log market capitalization, book-to-market ratios and price momentum, respectively.
The econometric technique allows for common γ, η and θ to be estimated which measures the average relationship across all portfolios. This is accomplished by stacking each equation in the system to form the following matrices:
()
()
()
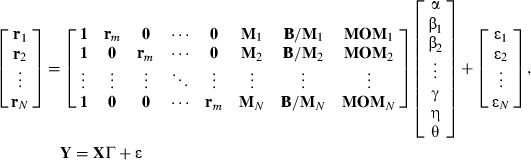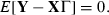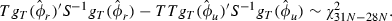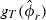and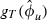 
are the empirical moment condition vectors for the restricted and unrestricted model, respectively; S−1 is the optimal weighting matrix; and T is the number of observations.It is important to stress that the method tests for the average relation of the characteristics and returns. The primary purpose of our paper is to disentangle the separate influences of size, book-to-market and momentum influences on returns. The regression constraints are placed on the size, book-to-market and momentum slope coefficients to be identical across portfolios, while allowing β to vary across portfolios. We have selected β to be the unconstrained factor in the regression as we are less interested in β as a factor. Our focus is on the size, book-to-market and momentum characteristics. The resultant interpretation is that we measure the average relation across all portfolios. In later analysis we also allow all coefficients to vary across each portfolio.
4. Data
As noted above, the challenge in conducting this study in Australia is the limited availability of accounting data required to calculate book value. The coverage of stocks declines with the passage of time and even obtaining wide cross-sectional coverage over the 1990s can be problematic. To conduct this study we construct a new database.
First, accounting data are hand collected from annual reports for the period 1981–2005. Company annual reports were catalogued and stored by the ASX and its forebears until the late 1990s. These reports were collected by the Company Reporting Service (CRS) which was a service previously provided by the ASX. We rely upon the CRS as the initial source of annual reports for the period 1981–1997. These source files constitute the documents made available to the market at the time.
To extend the collection beyond 1997 and supplement the earlier period for some companies whose reports could not be located on the CRS, original copies of annual reports have also been collected. This has been accomplished through a variety of methods including accessing reports either through company websites or directly requesting a copy. Over the time period studied, data are collected from at least 98 per cent of all companies that produced an annual report.4
Following Fama and French (1992, 1993) we define book value as the total value of equity plus deferred tax5 minus outside equity interests and the value of preference shares capital. Consistent with previous studies, companies with negative book values6 and all property trusts7 and investment funds are dropped from the sample. To form book-to-market ratios we match the book values to market capitalization information from the CRIF database. To be consistent with previous literature and to avoid any look-ahead bias because the release of accounting information is later than the balance date on the annual report, only accounting information that is at least 6 months old is used. For example, book values are calculated for 31 December 1982 using accounting information released prior to and including 30 June 1982.
The returns data are sourced from the CRIF price relative file, which contains monthly returns for stocks listed on the ASX. The match between the accounting data and returns data was on the basis of several identifiers as the ASX code alone does not provide an accurate match due to the re-issue of ASX codes and company name changes.
Table 1 provides summary information on the 27 size, book-to-market and momentum portfolios. Panels A–D report the mean number of companies, market capitalization, book-to-market ratios and price momentum, respectively, for each of the 27 portfolios.
| Winner | 2 | Loser | ||
|---|---|---|---|---|
| Panel A: Number of companies | ||||
| Large | Growth | 36 | 50 | 19 |
| 2 | 39 | 64 | 18 | |
| Value | 15 | 20 | 5 | |
| 2 | Growth | 29 | 36 | 38 |
| 2 | 46 | 61 | 40 | |
| Value | 39 | 44 | 24 | |
| Micro | Growth | 10 | 14 | 34 |
| 2 | 18 | 27 | 43 | |
| Value | 33 | 40 | 47 | |
| Panel B: Mean market capitalization ($million) | ||||
| Large | Growth | 1140.3 | 1656.4 | 848.0 |
| 2 | 1173.9 | 1418.0 | 747.0 | |
| Value | 665.1 | 690.3 | 585.3 | |
| 2 | Growth | 28.8 | 28.2 | 23.7 |
| 2 | 26.7 | 27.5 | 22.9 | |
| Value | 23.4 | 24.2 | 21.2 | |
| Micro | Growth | 4.7 | 4.3 | 4.0 |
| 2 | 4.7 | 4.4 | 3.9 | |
| Value | 4.2 | 3.9 | 3.4 | |
| Panel C: Mean book-to-market ratios | ||||
| Large | Growth | 0.34 | 0.36 | 0.32 |
| 2 | 0.82 | 0.81 | 0.82 | |
| Value | 2.15 | 1.85 | 2.01 | |
| 2 | Growth | 0.33 | 0.34 | 0.31 |
| 2 | 0.86 | 0.85 | 0.84 | |
| Value | 2.44 | 2.80 | 3.23 | |
| Micro | Growth | 0.32 | 0.32 | 0.31 |
| 2 | 0.88 | 0.88 | 0.87 | |
| Value | 3.57 | 3.64 | 2.73 | |
| Panel D: Mean 6 month price momentum (%) | ||||
| Large | Growth | 44.09 | 3.14 | −35.01 |
| 2 | 40.85 | 3.53 | −28.81 | |
| Value | 48.02 | 3.73 | −33.21 | |
| 2 | Growth | 60.50 | 1.54 | −41.62 |
| 2 | 55.78 | 2.21 | −36.95 | |
| Value | 60.97 | 2.68 | −37.62 | |
| Micro | Growth | 59.25 | 0.63 | −61.69 |
| 2 | 53.75 | 0.80 | −48.33 | |
| Value | 56.44 | 1.60 | −47.22 | |
- Mean number of companies, market capitalization, book-to-market ratios and 6 month price momentum of the 27 size–book-to-market–momentum portfolios during the period 1982–2006 are presented. The portfolios are formed by first ranking each stock on the basis of market capitalization, then independently by book-to-market ratio and finally an independent sort on 6 month price momentum each month. The 27 portfolios are formed by the intersection of the three independent sorts.
The general trends in the portfolios conform with results from previous studies. First, growth stocks tend to be larger, on average, than value stocks. This is demonstrated in panel A, where the proportion of number of companies classified as growth and large is approximately 40 per cent compared with approximately 15 per cent of stocks classified as value and large. Further, panel B indicates that the mean market capitalization of large growth portfolios are approximately double that of the large-value portfolios. This pattern continues for all three size breaks where the mean market capitalization of each growth portfolio is always higher than its value portfolio counterpart.
Second, winner stocks tend to be larger than loser stocks. Panel A suggests that the proportion of stocks classified as large and winner is 32 per cent, while large loser stocks make up approximately 17 per cent. Over 42 per cent of stocks classified as winners reside in the middle-sized tertile, while over 44 per cent of stocks classified as losers are classified as micro. The mean market capitalization figures indicate that, in general, each winner portfolio has a larger market capitalization than its loser portfolio counterpart.
Third, there is some evidence that stocks classified as value are more likely to be classified as winners, while growth stocks are more likely to be classified as losers. Across the size classifications, on average, 87 value stocks fall into the winner portfolios compared with 76 of value stocks in the loser portfolios; only 75 growth stocks make it into the winner portfolios compared with 91 growth stocks in the loser portfolios.
5. Results
5.1. Raw returns
We first examine the returns on the various portfolios formed on the basis of size, book-to-market ratios and momentum. Table 2, columns 1–5 report the equal-weighted portfolio returns, standard deviation and t-statistic results.
| Equal-weighted Portfolio Return | Value-weighted Portfolio Return | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Winner | 2 | Loser | Winner | 2 | Loser | ||||
| Panel A: Mean monthly returns (%) | |||||||||
| Large | Growth | 1.84 | 0.53 | −1.46 | Large | Growth | 1.21 | 0.69 | −1.03 |
| 2 | 1.40 | 1.07 | −0.45 | 2 | 1.24 | 1.17 | −0.18 | ||
| Value | 1.62 | 1.21 | −0.47 | Value | 1.61 | 0.97 | −0.10 | ||
| 2 | Growth | 1.21 | 0.35 | −0.98 | 2 | Growth | 1.31 | 0.51 | −1.23 |
| 2 | 1.42 | 0.78 | −0.22 | 2 | 1.56 | 0.67 | −0.43 | ||
| Value | 1.11 | 0.93 | 0.52 | Value | 1.28 | 0.79 | 0.20 | ||
| Micro | Growth | 0.53 | 1.42 | 4.03 | Micro | Growth | −0.07 | 0.63 | 1.97 |
| 2 | 1.45 | 2.04 | 4.44 | 2 | 1.09 | 1.34 | 2.85 | ||
| Value | 1.65 | 2.53 | 6.48 | Value | 1.04 | 1.92 | 4.11 | ||
| Panel B: Standard deviation (%) | |||||||||
| Large | Growth | 7.18 | 5.83 | 8.79 | Large | Growth | 7.08 | 6.98 | 8.60 |
| 2 | 5.65 | 4.37 | 8.62 | 2 | 6.00 | 4.96 | 8.99 | ||
| Value | 5.74 | 5.39 | 10.66 | Value | 6.72 | 6.83 | 11.45 | ||
| 2 | Growth | 9.51 | 6.78 | 8.80 | 2 | Growth | 9.19 | 6.44 | 8.66 |
| 2 | 7.88 | 4.76 | 6.78 | 2 | 7.63 | 4.43 | 6.70 | ||
| Value | 7.10 | 4.93 | 7.95 | Value | 6.96 | 4.94 | 8.22 | ||
| Micro | Growth | 13.42 | 12.60 | 11.05 | Micro | Growth | 12.83 | 11.48 | 10.58 |
| 2 | 10.82 | 8.09 | 9.68 | 2 | 10.75 | 7.69 | 9.37 | ||
| Value | 9.46 | 7.41 | 9.74 | Value | 9.52 | 7.04 | 8.83 | ||
- Mean monthly portfolio returns, standard deviation of monthly returns and t-statistic of portfolio returns of each of the 27 size–book-to-market–momentum portfolios during the period 1982–2006 are presented. Panels A and B report the equal- and value-weighted return results, respectively. The portfolios are formed by first ranking each stock based on market capitalization, then independently by book-to-market ratio and finally 6 month price momentum each month. The 27 portfolios are formed by the intersection of the three independent sorts.
One of the immediate observations from Table 2 is that value portfolios outperform growth portfolios but more so for the small portfolios. That is, the value effect tends to be more pronounced at the small end of the market. Recall that prior Australian evidence has generally found a value effect in data sets comprising relatively large stocks, although Gharghori et al. (2007) report that value stocks tend to be smaller in size. Within the smaller portfolios, the value effect is quite large, measuring over 1 per cent per month. In the larger portfolios, value stocks still tend to outperform growth stocks, but the evidence presented in Table 2 shows that the value effect is more complicated, with momentum interacting with the value effect.
A second observation concerns the relationship between size and momentum. As the average size of the portfolio decreases, the mean monthly return increases for the loser portfolio, but the effect is much less evident for stocks classified as winners (or the middle momentum portfolio).
Third, consistent with previous evidence, portfolios classified as winners outperform loser portfolios in the two largest size tertiles, but the reverse is true for stocks that are classified in the smallest size tertile. In the smallest portfolios, losers outperform winners, and by a considerable margin. That is, the traditional momentum effect is only evident in the larger size portfolios. These results are consistent with Brailsford and O’Brien (2008) who found a momentum effect only among larger stocks and that loser portfolios outperform winner portfolios within the smallest size quintiles. The ‘perverse’ momentum effect among the smaller stocks may be a result of low share prices (see Smith and Durand, 2007). Supportive evidence is found in panel B wherein the standard deviation is generally the highest among the smallest size portfolios.
The value-weighted return results reported in Table 2, columns 6–10, are consistent with the observations drawn from equal-weighted portfolio returns. Generally, the value-weighted returns reduce the magnitude of returns across all portfolios, which is not surprising given that equal-weighted returns over-weight the returns on small stocks.
To further examine the observed relationships in Table 2, we report in Table 3 mean monthly portfolio returns for each of the nine difference portfolios. For example, panel A shows the mean monthly return on the micro minus large portfolio (MML) while holding value and momentum constant.
| Equal-weighted portfolio return (%) | Value-weighted portfolio return (%) | ||||||
|---|---|---|---|---|---|---|---|
| Winner | 2 | Loser | Winner | 2 | Loser | ||
| Panel A: MML | |||||||
| Growth | −1.33 | 0.89 | 5.49 | Growth | −1.27 | −0.06 | 3.01 |
| (−2.01*) | (1.42) | (9.71**) | (−1.94) | (−0.09) | (5.11**) | ||
| 2 | 0.05 | 0.97 | 4.90 | 2 | −0.15 | 0.17 | 3.02 |
| (0.11) | (2.35*) | (8.87**) | (−0.27) | (0.40) | (5.28**) | ||
| Value | 0.03 | 1.33 | 6.96 | Value | −0.57 | 0.95 | 4.22 |
| (0.07) | (3.30**) | (10.19**) | (−1.05) | (2.13*) | (6.18**) | ||
| Panel B: VMG | |||||||
| Large | −0.22 | 0.68 | 0.97 | Large | 0.40 | 0.28 | 0.92 |
| (−0.72) | (2.55*) | (1.76) | (1.09) | (0.72) | (1.42) | ||
| 2 | −0.11 | 0.58 | 1.50 | 2 | −0.04 | 0.29 | 1.43 |
| (−0.30) | (2.13*) | (4.42**) | (−0.10) | (1.04) | (3.82**) | ||
| Micro | 1.14 | 1.12 | 2.45 | Micro | 1.14 | 1.29 | 2.13 |
| (1.89) | (2.03*) | (5.53**) | (2.01*) | (2.53*) | (5.02**) | ||
| Panel C: WML | |||||||
| Growth | 2 | Value | Growth | 2 | Value | ||
| Large | 3.31 | 1.85 | 2.13 | Large | 2.25 | 1.42 | 1.75 |
| (7.53**) | (4.16**) | (3.76**) | (4.37**) | (2.99**) | (2.69**) | ||
| 2 | 2.19 | 1.65 | 0.58 | 2 | 2.54 | 1.99 | 1.08 |
| (5.10**) | (4.11**) | (1.35) | (5.87**) | (4.96**) | (2.36*) | ||
| Micro | −3.58 | −2.99 | −4.83 | Micro | −2.13 | −1.76 | −3.07 |
| (−4.99**) | (−5.82**) | (−9.82**) | (−3.24**) | (−3.44**) | (−6.35**) | ||
- Mean monthly portfolio returns and t-statistic (in parentheses) of portfolio returns of each of the nine difference portfolios during the period 1982–2006 are presented. The micro minus large (MML) difference portfolios are formed by subtracting the return of the large portfolio from the return of the micro portfolio while holding the book-to-market and momentum tertile constant. The value minus growth (VMG) and winner minus loser (WML) difference portfolios are formed in a similar way. Significance at the **1 per cent and *5 per cent levels.
In panel A we are able to focus on the size premium. For equal-weighted portfolio returns, the differences are positive in all cases except for the winner-growth portfolio, and statistically significant for five of the eight positive differences. The statistically strongest size effect is evident in the loser portfolios; so, there is some suggestion of interaction between size and momentum. This broad conclusion carries into the value-weighted return portfolios.
Panel B reports the mean monthly return on the value minus growth portfolios (VMG) while holding size and momentum constant. For both equal- and value-weighted portfolio returns, all but one or two differences are positive, although strong statistical significance is limited to the smallest size portfolios, and strongest among small losers. Hence, we confirm the earlier finding that a strong value effect appears present in the smaller portfolios.
Panel C reports the mean monthly return on the winner minus loser portfolios (WML) while controlling for book-to-market and size. The main finding is the positive difference for the large- and middle-sized portfolios and the negative difference for the micro-sized portfolio. These differences are statistically significant at 1 per cent in nearly all cases.
In summary, Tables 2 and 3 reveal three key findings. First, the size premium is the strongest, and by a significant amount, in the loser portfolios. Second, the value premium is generally limited to the smallest portfolios. Third, the momentum premium is evident for the large- and middle-sized portfolios, but loser stocks significantly outperform winner stocks in the smallest size portfolio.
Our results are generally consistent with the findings of Liew and Vassalou (2000) which indicate that size, book-to-market ratios and momentum all have differing effects on returns. However, the effects of one characteristic appear to be related to the remaining two characteristics. In particular, both the size and value effects are the strongest in the loser portfolios.
Using sorts based on various characteristics allows us to gain an understanding as to how these characteristics influence returns. However, such differences may be related to different levels of risk within each portfolio. In the next section, we more rigorously test whether size, book-to-market ratios and price momentum effects are present once risk is taken into account by using multivariate regression analysis.
5.2. Multivariate regression analysis
First, we estimate β and report these results in Table 4. Panel A reports estimates derived from equal-weighted returns, while panel B reports estimates derived from value-weighted returns. There is not a substantial difference in estimates between panels A and B.
| β estimate | t-statistic | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Winner | 2 | Loser | Winner | 2 | Loser | ||||
| Panel A: Equal-weighted returns | |||||||||
| Large | Growth | 1.17 | 0.87 | 1.13 | Large | Growth | 12.42** | 15.46** | 9.45** |
| 2 | 0.95 | 0.78 | 0.98 | 2 | 14.39** | 17.38** | 7.06** | ||
| Value | 0.85 | 0.78 | 0.98 | Value | 9.13** | 16.90** | 9.81** | ||
| 2 | Growth | 1.18 | 0.82 | 1.01 | 2 | Growth | 14.93** | 15.32** | 4.80** |
| 2 | 0.98 | 0.58 | 0.75 | 2 | 11.36** | 13.89** | 4.20** | ||
| Value | 0.89 | 0.71 | 0.78 | Value | 10.03** | 17.07** | 6.10** | ||
| Micro | Growth | 1.21 | 0.79 | 0.99 | Micro | Growth | 10.01** | 4.03** | 4.38** |
| 2 | 0.99 | 0.70 | 0.81 | 2 | 6.20** | 6.37** | 3.92** | ||
| Value | 0.97 | 0.62 | 0.83 | Value | 11.47** | 6.95** | 4.87** | ||
| Panel B: Value-weighted returns | |||||||||
| Large | Growth | 1.07 | 1.01 | 1.30 | Large | Growth | 13.42** | 36.56** | 15.33** |
| 2 | 0.93 | 1.01 | 1.06 | 2 | 20.34** | 23.77** | 6.88** | ||
| Value | 0.83 | 0.90 | 1.29 | Value | 17.78** | 14.10** | 8.31** | ||
| 2 | Growth | 1.13 | 0.73 | 1.02 | 2 | Growth | 14.81** | 14.16** | 4.76** |
| 2 | 0.99 | 0.56 | 0.78 | 2 | 9.04** | 12.25** | 4.45** | ||
| Value | 0.93 | 0.70 | 0.83 | Value | 9.04** | 18.57** | 5.07** | ||
| Micro | Growth | 1.18 | 0.78 | 1.02 | Micro | Growth | 9.26** | 4.46** | 4.25** |
| 2 | 1.02 | 0.71 | 0.83 | 2 | 7.26** | 6.10** | 3.72** | ||
| Value | 1.00 | 0.66 | 0.82 | Value | 11.24** | 8.78** | 5.02** | ||
| Panel C: Differences between βs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Micro minus large | Value minus growth | Winner minus loser | |||||||||
| Winner | 2 | Loser | Winner | 2 | Loser | Growth | 2 | Value | |||
| Growth | 0.11 | −0.23 | −0.28 | Large | −0.24 | −0.11 | −0.01 | Large | −0.23 | −0.13 | −0.46 |
| 2 | 0.09 | −0.30 | −0.23 | 2 | −0.20 | −0.03 | −0.19 | 2 | 0.11 | 0.21 | 0.10 |
| Value | 0.17 | −0.24 | −0.47 | Micro | −0.18 | −0.12 | −0.20 | Micro | 0.16 | 0.19 | 0.18 |
-
Regression results of estimating the equation:
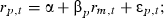
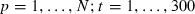where rp,t and rm,t are month t returns on portfolio p less the 13 week treasury note and the AGSM-CRIF value-weighted market index in month t less the 13 week treasury note are presented. α and βp are regression estimates. The equations are estimated using GMM on the triple-sorted size–book-to-market–momentum equal- and value-weighted portfolio returns. Significance at the **1 per cent and *5 per cent levels.
Differences between βs for MML, VMG and WML are presented in panel C and it is this set of results that are of most interest. For the size portfolios, the loser portfolios display consistently lower βs compared with the larger portfolios. Second, the value portfolios exhibit consistently lower βs than their corresponding growth portfolios. Third, the winner portfolios exhibit lower βs than loser portfolios only for the large-sized portfolios, whereas the losers exhibit smaller βs than winners for the small-sized portfolios. Hence, across all three characteristics, the largest returns tend to be associated with lower βs. This can be seen by a comparison between panels C in Tables 3 and 4.
These findings cast doubt on the ability of β to explain the size, book-to-market and momentum effects in Australia. Moreover, the findings suggest that the CAPM cannot explain excess returns because portfolios with higher average returns demonstrate lower market risk.
We now turn to the multivariate model as specified in equation (1). Regression estimates of α, γ, η and θ for the 27 equal-weighted and value-weighted portfolio returns from equation (1) are reported in panel A of Table 5, while panel B reports the estimates of β for each portfolio. These estimates provide insight into whether the various characteristics are significant explanators in a multivariate setting. Recall that the method tests for the average relation between returns and the characteristics of size, book-to-market and momentum while β is allowed to vary across portfolios.
| Panel A: Main effects | |||
|---|---|---|---|
| Intercept | Market capitalization | Book-to-market ratio | Price momentum |
| α, (t-value) | γ (t-value) | η (t-value) | Θ (t-value) |
| Equal-weighted Returns | |||
| 0.0138 | −0.0029 | 0.0047 | 0.0078 |
| (5.58)** | (−5.95)** | (3.60)** | (3.11)** |
| D-test, γ=η =θ=0 | 71.62** | ||
| Value-weighted Returns | |||
| 0.0039 | −0.0012 | 0.0044 | 0.0112 |
| (1.87) | (−2.85)** | (3.69)** | (4.75)** |
| D-test, γ = η = θ = 0 | 55.69** | ||
| Panel B: β estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| β estimate | t-statistic | ||||||||
| Winner | 2 | Loser | Winner | 2 | Loser | ||||
| Equal-weighted returns | |||||||||
| Large | Growth | 1.15 | 1.08 | 1.29 | Large | Growth | 22.00** | 15.25** | 18.97** |
| 2 | 0.91 | 0.82 | 1.05 | 2 | 25.79** | 19.27** | 9.70** | ||
| Value | 0.82 | 0.73 | 1.04 | Value | 15.94** | 11.48** | 9.07** | ||
| 2 | Growth | 1.27 | 0.90 | 1.17 | 2 | Growth | 17.14** | 12.89** | 13.28** |
| 2 | 0.97 | 0.64 | 0.81 | 2 | 15.51** | 15.74** | 9.60** | ||
| Value | 0.77 | 0.62 | 0.88 | Value | 9.62** | 16.21** | 8.09** | ||
| Micro | Growth | 0.90 | 1.16 | 1.16 | Micro | Growth | 4.98** | 9.88** | 7.93** |
| 2 | 0.97 | 0.69 | 0.89 | 2 | 5.58** | 6.22** | 4.76** | ||
| Value | 0.79 | 0.54 | 0.85 | Value | 6.58** | 4.23** | 3.50** | ||
| Value-weighted returns | |||||||||
| Large | Growth | 1.18 | 1.28 | 0.98 | Large | Growth | 21.41** | 7.80** | 4.91** |
| 2 | 1.02 | 0.93 | 1.11 | 2 | 20.97** | 14.40** | 11.09** | ||
| Value | 0.92 | 0.86 | 1.12 | Value | 13.44** | 8.42** | 9.61** | ||
| 2 | Growth | 1.26 | 0.88 | 1.17 | 2 | Growth | 18.16** | 15.76** | 14.31** |
| 2 | 0.97 | 0.62 | 0.83 | 2 | 14.59** | 15.51** | 9.18** | ||
| Value | 0.79 | 0.64 | 0.88 | Value | 10.10** | 17.58** | 7.30** | ||
| Micro | Growth | 0.95 | 1.08 | 1.18 | Micro | Growth | 6.06** | 11.63** | 8.90** |
| 2 | 0.97 | 0.69 | 0.95 | 2 | 5.43** | 7.02** | 5.94** | ||
| Value | 0.84 | 0.57 | 0.79 | Value | 7.19** | 4.72** | 3.78** | ||
-
Regression results of estimating the equation:
; 
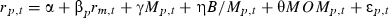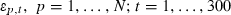where rp,t and rm,t are month t returns on portfolio p less the 13 week treasury note and the AGSM-CRIF value-weighted market index in month t less the 13 week treasury note. Mp,t and B/Mp,t are the natural logarithm of average market capitalization and book-to-market ratios of portfolio p at the start of month t. MOMp,t is the natural logarithm of average price momentum of portfolio p over the previous 6 months. α, γ, η, θ, βp are regression estimates. γ, η and θ measures the effect on returns of log market capitalization, book-to-market ratios and price momentum, respectively. The equations are estimated using GMM on the triple-sorted size–book-to-market–momentum equal- and value-weighted portfolio returns. Significance at the **1 per cent and *5 per cent levels.
Note that when moving to the multivariate analysis, we do not analyse individual portfolios. Rather, the test employed involves a cross-sectional approach because the relationship between size, book-to-market and momentum is by definition a cross-sectional relationship (e.g. Brown et al. (1983a, p. 41)): ‘since the relation between excess returns and S (size) is cross-sectional, it is not possible to estimate a separate [α] and [γ]’.
The results in Table 5 indicate that size, book-to-market ratio and momentum have significant estimated coefficients. The negative sign on size is consistent with an inverse relationship between market capitalization and size. The positive signs on the book-to-market and momentum variables are also consistent with expectations in that previous evidence has found a positive premium. These results are consistent with international studies that have found that market capitalization, book-to-market ratios and momentum help explain the cross-sectional variation in stocks returns beyond β. We formally test whether the size, book-to-market and momentum estimates are jointly equal to zero by using the D-statistic. The results of this test indicate a strong rejection of the null hypothesis.
In more detail, it is interesting to compare our estimate for the size effect to Gaunt et al. (2000) who utilize a similar technique to measure size and share price effects. The sample period in that study covered 1974–1997 and employed equal-weighted portfolio returns. The point estimate for their sample period was −0.0029 (t = −9.12) which matches our estimate of −0.0029 (t = −5.95) for our equal-weighted portfolio returns. Recall that our sample period covers 1982–2006. This would indicate that the size effect has persisted in Australia and has been relatively constant over time.
While some prior Australian studies have found evidence of a positive relationship between returns and book-to-market ratios, the positive and significant parameter estimate on the book-to-market ratio is the strongest evidence of the impact of book-to-market on returns in Australia.
Finally, there has been mixed evidence on momentum in Australia and the results in the prior section confirmed these conflicting results. Table 5 demonstrates that past price momentum is significantly positively related to returns. Recall that the results in Table 2 indicate that for the largest 70 per cent of the market there is a positive relationship between price momentum and portfolio returns, while for the smallest 30 per cent this effect is reversed. The regression results allow these conflicting outcomes to be disentangled and suggest that on average past price momentum is positively related to returns.
The functional form of the regression (i.e. the independent variables are logarithmic transformations) means that the γ, η and θ coefficients indicate how portfolio returns will change given a percentage change in the portfolio’s market capitalization, book-to-market ratio and price momentum. For example, a one percentage change in book-to-market ratio would lead to an increase in portfolio returns of 0.47 per cent for equal-weighted returns and 0.44 per cent for value-weighted returns. The results indicate that a percentage change in price momentum has the largest impact on returns followed by book-to-market ratios and market capitalization.
Panel B of Table 5 reports the β estimates on the portfolios. All estimates are positive and significant. As expected, the β estimates vary across the portfolios.
Despite the significant estimates on all variables in Table 5, the intercept remains significant in the equal-weighted analysis. This finding indicates that after taking into account market risk, size, book-to-market ratios and price momentum there is evidence that a significant proportion of the cross-section of returns is left unexplained. However, the intercept from the value-weighted regression is insignificant suggesting that the model is potentially quite powerful.
In unreported work, we also investigate the potential influence of seasonal effects. To incorporate potential seasonalities, January, June and July dummy variables are augmented to equation (1). To capture any seasonal variation in the size, book-to-market and momentum effects, interaction variables are included. That is, the January, June and July monthly dummy variables are interacted with the market capitalization, book-to-market and price momentum variable. The resultant estimates for the ‘other months’ on the size variable (γ), book-to-market ratio (η) and price momentum (θ) are generally consistent with the results reported in Table 5.8 Again, we employ the D-statistic to test whether the coefficient estimates are jointly equal to zero. The results of this test reject the null hypothesis. In summary, these results imply that during the majority of the year the size, book-to-market and price momentum effects are relatively stable.
As a final note, Lo and MacKinlay (1990) among others suggest that empirical results such as these may be sensitive to choices in research design. A relatively large proportion of Australian stocks are thinly traded which can yield biased β estimates. Hence, we repeated the analysis using thin-trading corrected βs. We note that there is an argument to adjust all parameters, but we follow tradition and adjust only the β estimate. The results reveal that correcting the βs for thin trading does not substantially change the magnitude or significance of the regression estimates, and our prior conclusions still hold. For example, the estimate on the book-to-market variable is 0.0046 (t = 3.93) compared with 0.0044 (t = 3.69) in Table 5. Similar findings apply to other parameter estimates.
5.3. Individual portfolio effects
The multivariate analysis employed tests for average relations. Recall that the method involves forming portfolios cross-sorted on the characteristics, then running the regressions. The regression constraints are placed on the size, book-to-market and momentum slope coefficients to be identical across portfolios. However, an alternative test involves allowing the slope coefficients on the characteristics to vary across portfolios. That is, we can run regressions on each of the 27 portfolios.9
As expected, the results in Table 6 reveal varying effects across the 27 portfolios. The most consistent results are found on the momentum parameter which is generally significant and positive particularly for the middle-ranked and loser portfolios. However, we do not place a deal of weight on these results as the number of stocks in some portfolios is quite small (refer to Table 1), and it is inevitable that the nature of any systemic influence will be diminished and quite variable across portfolios that are subject to the triple-sorting procedure that has been employed. Nonetheless, the results are of some interest for future work.
| Winner | 2 | Loser | t-statistic | ||||
|---|---|---|---|---|---|---|---|
| Winner | 2 | Loser | |||||
| α Estimate | |||||||
| Large | Growth | 0.48 | −1.32 | −4.85 | 0.22 | −1.10 | −1.60 |
| 2 | 3.10 | 1.28 | −0.26 | 1.82 | 0.96 | −0.06 | |
| Value | 0.01 | −2.06 | −4.65 | 0.01 | −0.64 | −1.60 | |
| Middle | Growth | −5.30 | −2.68 | 3.44 | −2.07 | −1.27 | 1.43 |
| 2 | −4.25 | −5.04 | −0.16 | −0.96 | −2.26* | −0.05 | |
| Value | −5.97 | −1.91 | 0.54 | −2.30* | −1.02 | 0.15 | |
| Micro | Growth | −2.08 | −0.27 | 6.63 | −0.74 | −0.15 | 3.77** |
| 2 | −5.82 | 1.66 | 5.66 | −2.20* | 0.85 | 1.79 | |
| Value | −1.78 | 3.96 | 4.48 | −0.77 | 2.66** | 1.23 | |
| β Estimate | |||||||
| Large | Growth | 1.17 | 1.27 | 1.00 | 19.68** | 7.58** | 4.72** |
| 2 | 1.02 | 0.92 | 1.12 | 20.27** | 17.11** | 10.98** | |
| Value | 0.92 | 0.85 | 1.12 | 13.66** | 8.34** | 9.14** | |
| Middle | Growth | 1.25 | 0.87 | 1.19 | 17.60** | 16.67** | 13.01** |
| 2 | 0.97 | 0.61 | 0.84 | 14.42** | 14.99** | 8.14** | |
| Value | 0.79 | 0.65 | 0.88 | 9.97** | 17.35** | 7.21** | |
| Micro | Growth | 0.98 | 1.08 | 1.15 | 5.74** | 12.59** | 9.09** |
| 2 | 0.97 | 0.68 | 0.91 | 5.45** | 7.43** | 6.31** | |
| Value | 0.86 | 0.56 | 0.75 | 6.73** | 4.87** | 3.94** | |
| γ Estimate | |||||||
| Large | Growth | −0.07 | 0.25 | 0.56 | −0.24 | 1.30 | 1.41 |
| 2 | −0.32 | −0.22 | −0.10 | −1.28 | −0.99 | −0.15 | |
| Value | 0.09 | 0.28 | 0.90 | 0.33 | 0.67 | 2.03* | |
| Middle | Growth | 2.43 | 1.35 | −1.34 | 2.19* | 1.43 | −1.16 |
| 2 | 1.53 | 1.66 | 0.21 | 0.92 | 2.16* | 0.21 | |
| Value | 1.83 | 0.53 | −0.08 | 2.57* | 0.94 | −0.08 | |
| Micro | Growth | 1.53 | −0.23 | −1.40 | 1.06 | −0.12 | −0.84 |
| 2 | 2.22 | −1.09 | −1.05 | 1.02 | −0.62 | −0.43 | |
| Value | −0.79 | −1.72 | −1.79 | −0.62 | −2.25* | −1.20 | |
| η Estimate | |||||||
| Large | Growth | −0.13 | 0.75 | 0.17 | −0.23 | 1.61 | 0.12 |
| 2 | −0.53 | −1.15 | −1.75 | −0.68 | −1.64 | −1.13 | |
| Value | 0.73 | 0.37 | −0.17 | 0.99 | 0.20 | −0.13 | |
| Middle | Growth | 3.43 | 1.91 | −0.20 | 2.60** | 1.79 | −0.11 |
| 2 | 2.51 | 2.67 | 1.57 | 1.05 | 2.07* | 1.13 | |
| Value | −0.16 | 0.03 | −0.19 | −0.14 | 0.09 | −0.26 | |
| Micro | Growth | 1.16 | −0.19 | 2.41 | 0.55 | −0.08 | 1.01 |
| 2 | 2.00 | −1.43 | 3.28 | 0.56 | −0.51 | 0.91 | |
| Value | −0.96 | −0.90 | 2.15 | −1.00 | −1.19 | 0.89 | |
| θ Estimate | |||||||
| Large | Growth | −0.30 | −2.92 | 1.28 | −0.17 | −2.28* | 1.04 |
| 2 | −2.47 | 1.45 | 2.86 | −1.45 | 1.37 | 1.63 | |
| Value | −1.07 | 3.35 | 3.86 | −0.93 | 1.29 | 3.77** | |
| Middle | Growth | 2.91 | 8.42 | 4.51 | 1.24 | 5.12** | 3.21** |
| 2 | 0.82 | 6.75 | 3.91 | 0.33 | 4.01** | 2.14* | |
| Value | 1.49 | 8.12 | 2.37 | 0.85 | 4.65** | 1.19 | |
| Micro | Growth | 0.44 | 17.16 | 1.45 | 0.20 | 4.55** | 1.80 |
| 2 | 6.21 | 13.84 | 3.68 | 3.42** | 4.22** | 1.60 | |
| Value | 7.00 | 11.14 | 2.58 | 3.31** | 5.04** | 2.34** | |
-
Regression results of estimating the equation:
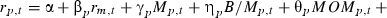
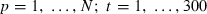where rp,t and rm,t are month t returns on portfolio p less the 13 week treasury note and the AGSM-CRIF value-weighted market index in month t less the 13 week treasury note. Mp,t and B/Mp,t are the natural logarithm of average market capitalization and book-to-market ratios of portfolio p at the start of month t. MOMp,t is the natural logarithm of average price momentum of portfolio p over the previous 6 months. α, γ, η, θ, βp are regression estimates. γ, η and θ measures the effect on returns of log market capitalization, book-to-market ratios and price momentum, respectively. The regression is estimated on the triple-sorted size–book-to-market–momentum equal- and value-weighted portfolio returns. Significance at the **1 per cent and *5 per cent levels.
6. Conclusion
In this study we have analysed whether market capitalization, book-to-market ratios and price momentum have separate effects in explaining portfolio returns. Previous Australian studies have generally looked at these effects either individually or two at a time, and have used limited data sets. This is the first Australian study that considers how the three variables interact with each other in explaining returns. Forming portfolios using a triple sort allows the three variables of interest to be individually controlled for, permitting a better understanding on how each characteristic influences returns and how each effect influences each other.
The use of a new data set that covers all listed stocks over the last 25 years represents a significant improvement over previous studies in both cross-sectional and time-series coverage, especially in relation to the book-to-market effect.
The results demonstrate variations in returns related to size, book-to-market ratios and price momentum. Specifically, we confirm the well-known size effect. Further, we document a value effect. That is, portfolios formed with stocks that possess high book-to-market ratios have higher returns than portfolios with low book-to-market ratios. Finally, we find that portfolios of past winners outperform past losers, except that this effect is reversed for the smallest size portfolios. These results generally conform with previous evidence, although the enhanced data set provide greater confidence in the findings.
The main contribution of the study involves the analysis of the interaction between the three characteristics. Our initial evidence points to three key findings. First, the size premium is the strongest, and by a significant amount, in the loser portfolios. Second, the value premium is generally limited to the smallest portfolios. Third, the momentum premium is evident for the large- and middle-sized portfolios, but loser stocks significantly outperform winner stocks in the smallest size portfolio.
To control for these interactions, a multivariate framework is used to test whether each of the characteristics influences excess returns once market risk is taken into account. The multivariate tests reveal a number of interesting findings. First, market capitalization is significantly negatively related to returns. Second, the book-to-market effect is significantly positively related to returns. Third, price momentum is significantly positively related to returns. These effects are not explained by β risk. Fourth, there is evidence that there are strong positive returns in the month of January and July, which are not fully captured by market risk, market capitalization, book-to-market ratios or price momentum. These findings are robust to using a thin trading corrected β.
In an academic sense, this paper adds to our understanding of how various characteristics impact on returns. Further, the study presents evidence as to how the characteristics relate to each other. In a practical sense, the findings point to where the apparent return anomalies can be found in the market. One dominant observation is that the small loser portfolio is where much of the abnormal return behaviour is located. However, stocks in this portfolio have an average capitalization of only around $5m which is too small to be of general interest to most investors.
