Persistence and the four-factor model in the Australian funds market: a note
The views expressed in this paper are the authors’ and do not necessarily reflect the views of Schroders Investment Management. The authors thank Karen Benson, Philip Gray and seminar participants at RMIT and the Asian Finance Association conference 2009 for helpful comments.
Abstract
We investigate whether Australian fund managers are able to deliver persistent performance using Carhart’s (1997) four-factor model. Short- and long-term persistence is examined and the sample is also divided into unit trusts and superannuation funds. We do not find evidence of persistence in any sample of funds. We find that winner (loser) funds tend to hold past winner (loser) stocks. Winner and loser unit trusts both appear to have positive exposure to small stocks.
1. Introduction
Performance persistence is the ability of funds to maintain their performance ranking, relative to either a benchmark or other funds, over a number of years. Studies have shown that investors rely heavily on past fund performance as a source of information when deciding in which funds to invest (Capon et al., 1996; Johnson, 2006). This means that investors want a fund which is performing well when they buy into it to continue to do well in the future. If fund performance persists, buying funds that have performed well in the past is a profitable (and rational) investment strategy.
In this paper, we examine whether there is persistence in the performance of Australian funds and, specifically, whether there is evidence of persistence after the funds’ exposures to the size, book-to-market and momentum factors are removed. Our second aim is to determine whether performance persistence depends upon the type of fund. There is evidence from the US market that funds designed for different purposes have differing characteristics (Del Guercio and Tkac, 2002; James and Karceski, 2006). In Australia, it has been compulsory for employees to contribute a percentage of their salary for retirement savings since the introduction of the ‘superannuation guarantee’ in 1992. By contrast, investors who own unit trusts have chosen to do so – unit trusts are discretionary investments. Superannuation funds and unit trusts can therefore be thought of as two different products. Consequently, there could be differences in the ability of superannuation funds and unit trusts to deliver persistent performance; so we also analyse the two groups separately. Finally, we explore long- and short-term persistence because the literature to date has not found conclusive evidence on how long, if at all, fund performance is able to persist.
Previous literature on whether fund performance does, in fact, persist does not provide conclusive answers. One of the earlier studies of persistence is Grinblatt and Titman (1992), who find evidence of performance persistence. By contrast, Hendricks et al. (1993) find short-term (1 year) persistence but no evidence of longer term persistence. Brown and Goetzmann (1995) find significant persistence in performance in just over half of the 12 years they study but also find reversal in some years. The authors find it is solely the poor performers who persistently underperform. Berk and Tonks (2007) document that it is the funds which perform poorly in both the current year and the previous year that exhibit persistent underperformance. By contrast, Gruber (1996) and Elton et al. (1996) find persistence in the performance of both outperforming and underperforming funds. Bollen (2005) finds evidence of short-term persistence in top-performing funds’ returns, but the result disappears over the longer term.
If good fund performance persists, the question arises as to how managers are able to deliver this performance. Grinblatt et al. (1995) test whether funds follow momentum strategies, i.e. whether they buy past ‘winning’ stocks and sell past ‘losers’. They find a strong relationship between fund performance and momentum. Interestingly, they find managers are more likely to buy past winners than sell past losers.
Carhart (1997) explicitly tests whether persistence in performance can be explained by common factors in stock returns. He finds a strong positive (negative) relation between the 1 year momentum factor and the returns on the best (worst) performing decile of funds. This indicates that the portfolios of the best funds are tilted towards previously winning stocks and consequently capture the premium earned on past winning stocks. Similarly, the top decile of funds seems to tilt their portfolios to capture the premium on small stocks.
There has been little published research into persistence in performance in the Australian funds market. An early study by Bird et al. (1983) does not find persistence in the performance of a sample of superannuation funds, while Sawicki and Ong (2000) do not find evidence of long-term (3 year) persistence. By contrast, Bilson et al. (2005) find some evidence of superannuation fund performance persistence over a 3 year time period using raw returns but no evidence of persistence using models that allow for risk. Hallahan (1999) finds persistence in the performance of fixed interest funds but not other styles of funds.
One potentially confounding factor in persistence studies is survivorship bias. Brown et al. (1992) argue that survivorship bias will lead to spurious findings of persistence, but Grinblatt and Titman (1992) argue that it leads to spurious reversal. In the Australian context, Hallahan and Faff (2001) conclude that survivorship bias results in spurious findings of performance reversal, although Bilson et al. (2005) find that survivorship bias does not affect their results. The fact that many of the Australian studies use survivorship-biased samples may explain why most studies have not found evidence of persistence in the performance of Australian funds.
To date, there has been little research in Australia that has been able to disentangle persistence from common factors that explain stock returns as defined by Carhart (1997). In the US market, Fama and French’s (1993) and Carhart’s (1997) size, book-to-market and momentum factors are widely used to explain stock returns. In Australia, there is also evidence to suggest that the size, value and momentum premiums exist, but the location and extent of these premiums in the underlying stock market may be different from those of the US market. In particular, the small premium appears predominately located in micro-stocks (Durand et al., 2007). There is evidence that the value premium is larger and more consistent across all size categories than in the USA (Halliwell et al., 1999; Gaunt, 2004; Durand et al., 2006a). Finally, the Australian evidence suggests momentum is the strongest using a 6 month strategy rather than an annual strategy, and it is possibly found only in the larger firms (Demir et al., 2004; Durand et al., 2006b; Brailsford and O’Brien, 2008). These results indicate that although still present and potentially exploitable, the size, value and momentum effects in Australia are different from those of the US market. This suggests that if we are to detect performance persistence, we need to control for these effects with factors constructed using Australian data.
Our results show no evidence of performance persistence for any type of fund over any length of time once size, value and momentum factor loadings are taken into account. We find evidence suggesting that winner (loser) funds tend to hold past winning (losing) stocks. In addition, we also find that in the short term, both winning and losing unit trusts are positively exposed to the SMB factor. This suggests that both winning and losing unit trusts tilt their holdings towards smaller stocks. We do not find evidence of funds loading on the HML factor. In the long term, the clear differences in the characteristics of winning and losing funds’ portfolios disappear.
The rest of this paper proceeds as follows. The data are described in Section 2 and methodology in Section 3. Section 4 presents the results and robustness tests and Section 5 concludes the paper.
2. Data
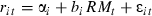 ()
()We delete all funds which have β < 0.5 or β > 1.5.1 In total there are 779 unit trusts and 1485 superannuation funds. We use the 13 week treasury note from the Australian Graduate School of Management Centre for Research in Finance (AGSM-CRIF) database as our proxy for the risk-free asset.2 Market return is the AGSM-CRIF value-weighted market return.
SMB, HML and UMD factors for the Australian market are formed following Fama and French (1993) and Carhart (1997). Book values are hand collected from annual reports produced by each company listed on the Australian stock market during our sample period.3 Market capitalization information is from the AGSM-CRIF database.
We rank all stocks on the ASX by market capitalization and assign stocks with a market capitalization higher than the median market capitalization to the big portfolio. All other stocks are assigned to the small portfolio. We then independently rank stocks by their book-to-market ratios. The first 30 per cent of stocks with the lowest book-to-market ratios are assigned to the low portfolio, the next 40 per cent of stocks are assigned to the neutral portfolio and the 30 per cent of stocks with the highest book-to-market ratios are assigned to the high portfolio. This leads to all stocks being assigned to one of two size portfolios and one of three book-to-market portfolios, giving a total of six portfolios. These portfolio assignments are held fixed for 12 months and value-weighted returns are calculated. After 12 months we repeat the process and re-assign all portfolios. The SMB factor is then calculated as the difference between the average value-weighted return across the three small portfolios (small-low, small-neutral and small-high) and the average value-weighted return across the three big portfolios (big-low, big-neutral and big-high). Similarly, we calculate the HML factor as the difference between the average value-weighted return across the two high book-to-market portfolios (big-high and small-high) and the average value-weighted return across the two low book-to-market portfolios (big-low and small-low).
We use a similar method to form UMD. First, each stock is assigned to one of two size portfolios as described above. Independently, we rank all stocks by their past momentum over the previous 6 months.4, 5 We assign all stocks with returns higher than the 30th percentile as up, and those stocks in the lowest 70th percentile as down. We form the UMD factor by calculating the average value-weighted return of the up portfolios less the average value-weighted return of the down portfolios.
3. Methodology
We follow the methodology of Hendricks et al. (1993) and Carhart (1997) to test for performance persistence. Funds are placed into one of 10 portfolios based on their previous period’s return (ranking period return). We then calculate the portfolio’s equally weighted monthly return over the subsequent period (holding period). Ranking periods and holding periods are equal lengths of time. This procedure is repeated and new portfolio assignments made each period. We form a portfolio constructed by the difference between the best (winner) portfolio and worst (loser) portfolio. Where a fund dies during the holding period, its returns are included up until the fund dies and then the portfolio weights are adjusted. For robustness, we also form value-weighted portfolios and divide fund returns into five portfolios instead of 10.
Three-, 6-, 12- and 36-month ranking and holding periods are used in order to establish whether there is short-term or long-term persistence in fund performance.6 Additionally, we investigate whether there are differences across superannuation funds and unit trusts. Consequently, the portfolios are initially formed for the full sample of funds, and then portfolios of unit trusts and superannuation funds are formed separately.
 ()
()A significantly positive α indicates performance persistence and a significantly negative α, reversal. A significantly negative α could also be interpreted as supporting overreaction – if investors systematically overreact to information we should observe performance reversal, i.e. past losers (winners) becoming future winners (losers) (DeBondt and Thaler, 1985).7 If funds predominantly hold small stocks, value stocks or past winning stocks, we should observe significantly positive coefficients on SMB, HML and UMD, respectively.
4. Results
Descriptive statistics on RM (the excess return on the market), SMB, HML and UMD are in panel A of Table 1. The mean and median of each of the four factors are positive as expected, indicating a premium on the market, small stocks, stocks with high book-to-market ratios and past winners. However, for each series the minimum is negative, indicating that the premiums did not occur in every single month of the sample. Panels B and C display descriptive statistics on the funds. Panel B of Table 1 shows the number of funds in each of the three samples. From the minimum and maximum figures, it is clear that there is a large dispersion in the number of funds, particularly for superannuation funds. The number of funds in each sample increases over time, with the minimum number of funds occurring in the early part of the sample, and the maximum in the later. Panel C shows the annualized ranking period returns. By construction, the returns decline monotonically from the winner to the loser portfolios. Interestingly, the average unit trust performance is better than the average superannuation fund performance over our sample period, although the difference in the performance of the winner and loser funds is lower for superannuation funds than for unit trusts. Finally, the range of past returns between the loser and winner portfolios declines as the number of months increases. This may indicate that the longer the time period under analysis, the more fund returns tend towards the mean return.
| Panel A: Factor characteristics | ||||
|---|---|---|---|---|
| RM | SMB | HML | UMD | |
| Mean | 0.0061 | 0.0046 | 0.0085 | 0.0114 |
| Median | 0.0104 | 0.0012 | 0.0096 | 0.0125 |
| Maximum | 0.0761 | 0.2079 | 0.1078 | 0.1203 |
| Minimum | −0.1010 | −0.1815 | −0.0995 | −0.1478 |
| Std. deviation | 0.0310 | 0.0560 | 0.0279 | 0.0423 |
| Panel B: Number of funds | ||||||||||||
| Full sample | Superannuation funds | Unit trusts | ||||||||||
| 3 months | 6 months | 12 months | 36 months | 3 months | 6 months | 12 months | 36 months | 3 months | 6 months | 12 months | 36 months | |
| Mean | 583 | 556 | 496 | 350 | 337 | 319 | 279 | 177 | 247 | 237 | 217 | 173 |
| Median | 443 | 431 | 387 | 328 | 229 | 219 | 196 | 168 | 214 | 212 | 191 | 160 |
| Minimum | 111 | 110 | 111 | 126 | 25 | 26 | 27 | 34 | 85 | 84 | 84 | 92 |
| Maximum | 1706 | 1671 | 1511 | 617 | 1110 | 1085 | 981 | 338 | 596 | 586 | 530 | 279 |
| SD | 472 | 455 | 407 | 216 | 318 | 307 | 273 | 134 | 154 | 149 | 134 | 83 |
| Winner | 0.3963 | 0.3346 | 0.3017 | 0.2360 | 0.3226 | 0.2607 | 0.2330 | 0.1958 | 0.4504 | 0.3805 | 0.3342 | 0.2572 |
| 9 | 0.2217 | 0.1961 | 0.1864 | 0.1737 | 0.1918 | 0.1700 | 0.1609 | 0.1529 | 0.2486 | 0.2239 | 0.2113 | 0.1884 |
| 8 | 0.1683 | 0.1591 | 0.1540 | 0.1503 | 0.1480 | 0.1427 | 0.1403 | 0.1399 | 0.1835 | 0.1740 | 0.1670 | 0.1633 |
| 7 | 0.1360 | 0.1365 | 0.1361 | 0.1377 | 0.1243 | 0.1271 | 0.1274 | 0.1312 | 0.1469 | 0.1471 | 0.1445 | 0.1441 |
| 6 | 0.1138 | 0.1208 | 0.1227 | 0.1291 | 0.1039 | 0.1141 | 0.1171 | 0.1252 | 0.1218 | 0.1264 | 0.1285 | 0.1341 |
| 5 | 0.0900 | 0.1042 | 0.1112 | 0.1219 | 0.0863 | 0.0992 | 0.1077 | 0.1196 | 0.0963 | 0.1100 | 0.1152 | 0.1258 |
| 4 | 0.0699 | 0.0894 | 0.0987 | 0.1151 | 0.0670 | 0.0862 | 0.0964 | 0.1130 | 0.0725 | 0.0910 | 0.1008 | 0.1180 |
| 3 | 0.0426 | 0.0705 | 0.0847 | 0.1076 | 0.0451 | 0.0716 | 0.0844 | 0.1072 | 0.0416 | 0.0697 | 0.0850 | 0.1103 |
| 2 | 0.0023 | 0.0411 | 0.0637 | 0.0980 | 0.0138 | 0.0479 | 0.0703 | 0.0988 | −0.0078 | 0.0337 | 0.0576 | 0.0973 |
| Loser | −0.1231 | −0.0547 | −0.0098 | 0.0507 | −0.0853 | −0.0198 | 0.0182 | 0.0647 | −0.1495 | −0.0787 | −0.0257 | 0.0435 |
| Average | 0.1118 | 0.1198 | 0.1249 | 0.1320 | 0.1018 | 0.1100 | 0.1156 | 0.1248 | 0.1204 | 0.1278 | 0.1318 | 0.1382 |
- Panel A shows descriptive statistics on the Australian factors formed following Carhart (1997). RM is the monthly AGSM-CRIF value-weighted market return less the 13 week treasury note return. SMB, HML and UMD are monthly size, book-to-market and momentum mimicking portfolios. Panel B shows descriptive statistics on the number of funds in each of the three samples of funds over each of the ranking and holding periods. Panel C shows the average annualized ranking period return of each portfolio in the three samples of funds.
Table 2 shows the results for the full sample – the sample comprising both unit trusts and superannuation funds.8 We find no evidence of persistence across any portfolio for any time period; the αs are all insignificant.9 This result also suggests that, in line with previous Australian studies using stock returns (see, for example, Brailsford, 1992; Gaunt, 2000), the overreaction hypothesis described by DeBondt and Thaler (1985) is not supported in the Australian market.
| Portfolio | α | RM | SMB | HML | UMD | Adj. R2 |
|---|---|---|---|---|---|---|
| Three-month ranking and holding periods | ||||||
| Winner | 0.0007 (0.57) | 1.0130** (25.71) | 0.1206** (4.36) | 0.0118 (0.27) | 0.0965** (4.56) | 0.83 |
| Loser | 0.0007 (0.49) | 0.9116** (23.11) | 0.0339 (1.36) | −0.0297 (−0.59) | −0.1521** (−4.92) | 0.80 |
| Winner–loser | 0.0000 (0.00) | 0.1014 (1.91) | 0.0867** (2.71) | 0.0415 (0.62) | 0.2486** (6.69) | 0.20 |
| Six-month ranking and holding periods | ||||||
| Winner | 0.0012 (0.95) | 1.0273** (25.93) | 0.1190** (3.72) | 0.0294 (0.60) | 0.1065** (3.98) | 0.85 |
| Loser | −0.0010 (−0.69) | 0.9171** (21.36) | 0.0664** (2.76) | 0.0364 (0.69) | −0.1586** (−5.80) | 0.79 |
| Winner–loser | 0.0022 (1.20) | 0.1102 (1.87) | 0.0526 (1.51) | −0.0070 (−0.09) | 0.2651** (7.50) | 0.22 |
| Twelve-month ranking and holding periods | ||||||
| Winner | 0.0003 (0.23) | 1.0030** (25.95) | 0.1077** (3.88) | 0.0769 (1.50) | 0.0288 (1.18) | 0.84 |
| Loser | −0.0006 (−0.38) | 0.9312** (21.73) | 0.0768** (2.24) | 0.0259 (0.45) | −0.1375** (−3.78) | 0.77 |
| Winner–loser | 0.0009 (0.47) | 0.0718 (1.30) | 0.0309 (0.75) | 0.0510 (0.62) | 0.1664** (3.67) | 0.10 |
| Thirty-six-month ranking and holding periods | ||||||
| Winner | −0.0012 (−0.64) | 0.8977** (14.55) | 0.0462 (1.47) | −0.0006 (−0.01) | −0.1280** (−3.12) | 0.72 |
| Loser | −0.0008 (−0.67) | 1.0373** (26.19) | 0.0614** (2.76) | 0.0917 (1.52) | −0.0238 (−0.83) | 0.84 |
| Winner–loser | −0.0004 (−0.19) | −0.1396** (−1.97) | −0.0152 (−0.41) | −0.0922 (−1.14) | −0.1042 (−1.86) | 0.04 |
- Results from estimating equation (2): rpt = αp + bpRMt + spSMBt + hpHMLt + upUMDt + ɛpt for the full sample of funds are shown. Funds are ranked over 3, 6, 12 or 36 months, placed into deciles and monthly returns calculated with new portfolio assignments occurring every 3, 6, 12 or 36 months, respectively. Winner and loser represent portfolios of funds in the best and worst deciles, respectively, and winner–loser is a portfolio constructed as the difference between the winner portfolio and loser portfolio. RM is the AGSM-CRIF value-weighted market return less the 13 week treasury note return. SMB, HML and UMD are size, book-to-market and momentum mimicking portfolios. Newey–West HAC t-statistics are in parentheses. The sample period is January 1992 to December 2006. Significance at the **5 per cent level.
The coefficients on RM are significantly positive across all winner and loser portfolios. This is to be expected, as our sample comprises only equity funds. A number of interesting patterns emerge from a closer examination of how funds load onto the three factors. Winner funds have a significantly positive loading on the SMB factor at the 3, 6 and 12 month periods, suggesting winner funds tend to hold smaller stocks. Interestingly, loser funds also appear to have a bias towards smaller stocks for the periods longer than 3 months. The difference portfolio (winner–loser) has a significantly positive coefficient on the SMB factor at 3 month periods. Given that the coefficient on SMB for the winner portfolio is larger than that of the loser portfolio, the result suggests winner funds may hold smaller stocks than loser funds. However, at 36 months coefficients on SMB for the winner and difference portfolios are insignificant. Interestingly, none of the portfolios have significant loadings on the HML factor.
The winner portfolios have significantly positive coefficients on the UMD factor for 3 and 6 month periods, and the loser portfolios have significant negative coefficients on this factor for 3, 6 and 12 month periods. Additionally, the coefficients on the difference portfolios are significantly positive for up to 12 months. These results are in line with Carhart (1997) and indicate that winner funds tend to hold past winning stocks, whereas loser funds tend to hold past losing stocks. There are two alternative explanations for this finding. Either winner funds actively trade on momentum and loser funds are contrarian, or winner (loser) funds just happen to be holding past winning (losing) stocks in their portfolios. Recall that Grinblatt et al. (1995) found fund managers tended to buy past winning stocks but not sell past loser stocks. This would suggest that winner funds actively pursue momentum strategies, but loser funds do not divest themselves of past losing stocks. We are not able to distinguish between these two alternatives because data on fund holdings and turnover are not available. At 36 months, these patterns disappear.
We conclude that funds’ performance does not persist. In terms of portfolio holdings, in the short term (less than 12 months), winner funds appear to have slightly higher market exposure, hold smaller stocks and past winning stocks. Loser funds also tend to hold smaller stocks but have significant exposure to past losing stocks.
Results for the sample of superannuation funds are found in Table 3. Again we see significantly positive coefficients on RM for all winner and loser portfolios. None of the αs are significant, suggesting that superannuation fund performance does not persist.10 Recent evidence suggests that investors are very unlikely to change their superannuation fund when given the opportunity to do so (Fear and Pace, 2008). Fewer than 10 per cent of investors switched funds after the introduction of the Choice of Fund Policy in July 2005, with about half of those who did switch doing so because they changed jobs or because their employer changed their default fund. Our findings suggest that this outcome is not surprising. As superannuation performance does not persist, it will be difficult for investors to determine whether a different superannuation fund is a better investment than the fund they currently hold.
| Portfolio | α | RM | SMB | HML | UMD | Adj. R2 |
|---|---|---|---|---|---|---|
| Three-month ranking and holding periods | ||||||
| Winner | −0.0003 (−0.27) | 0.9481** (30.77) | 0.0526** (2.09) | −0.0414 (−1.01) | 0.0873** (3.74) | 0.85 |
| Loser | 0.0016 (1.25) | 0.9239** (20.30) | 0.0365 (1.34) | −0.0426 (−0.72) | −0.1042** (−3.17) | 0.80 |
| Winner–loser | −0.0019 (−1.08) | 0.0242 (0.52) | 0.0161 (0.56) | 0.0012 (0.02) | 0.1915** (5.90) | 0.13 |
| Six-month ranking and holding periods | ||||||
| Winner | 0.0008 (0.61) | 0.9447** (31.18) | 0.0446 (1.28) | −0.0756 (−1.53) | 0.0877** (2.42) | 0.84 |
| Loser | 0.0004 (0.41) | 0.8907** (25.81) | 0.0310 (1.70) | 0.0356 (0.83) | −0.1415** (−7.04) | 0.85 |
| Winner–loser | 0.0004 (0.24) | 0.0540 (1.22) | 0.0136 (0.32) | −0.1111 (−1.53) | 0.2292** (5.39) | 0.24 |
| Twelve-month ranking and holding periods | ||||||
| Winner | 0.0010 (0.91) | 0.8986** (27.49) | 0.0334 (1.40) | 0.0021 (0.04) | −0.0050 (−0.24) | 0.84 |
| Loser | 0.0007 (0.41) | 0.9718** (23.91) | 0.0772** (2.14) | −0.0624 (−0.80) | −0.0391 (−0.75) | 0.78 |
| Winner–loser | 0.0003 (0.17) | −0.0732 (−1.37) | −0.0438 (−1.19) | 0.0645 (0.56) | 0.0342 (0.58) | 0.04 |
| Thirty-six-month ranking and holding periods | ||||||
| Winner | 0.0005 (0.27) | 0.9251** (22.61) | 0.0191 (1.01) | −0.0982 (−1.36) | −0.0535 (−1.87) | 0.80 |
| Loser | −0.0006 (−0.49) | 1.0311** (35.30) | 0.0299 (1.40) | 0.0833 (1.32) | −0.0410 (−1.33) | 0.85 |
| Winner–loser | 0.0010 (0.50) | −0.1060** (−2.10) | −0.0109 (−0.48) | −0.1815 (−1.87) | −0.0125 (−0.26) | 0.03 |
- Results from estimating equation (2): rpt = αp + bpRMt + spSMBt + hpHMLt + upUMDt + ɛpt for superannuation funds are shown. Funds are ranked over 3, 6, 12 or 36 months, placed into deciles and monthly returns are calculated, with new portfolio assignments occurring every 3, 6, 12 or 36 months, respectively. Winner and loser represent portfolios of funds in the best and worst deciles, respectively, and winner–loser is a portfolio constructed as the difference between the winner portfolio and loser portfolio. RM is the AGSM-CRIF value-weighted market return less the 13 week treasury note return. SMB, HML and UMD are size, book-to-market and momentum mimicking portfolios. Newey–West HAC t-statistics are in parentheses. The sample period is January 1992 to December 2006. Significance at the **5 per cent level.
However, there are still some interesting features to be seen in the results. There is little evidence of these funds tilting their portfolios towards small stocks, and coefficients on SMB are not significant for any of the difference portfolios. Superannuation funds’ returns do not load onto the HML factor. However, they do load onto the UMD factor. For the 3 and 6 month periods, the coefficients on the winner (loser) portfolios are significantly positive (negative), and the coefficients on the difference portfolios are significantly positive. These results indicate that, similar to the full sample of funds, winner superannuation funds hold past winning stocks, but loser superannuation funds tend to hold past losing stocks. However, the 12 and 36 month results are different, with none of the coefficients significant.
Table 4 displays results for unit trusts. In general, the results are in line with the other samples, with no evidence of performance persistence.11 Results on the SMB, HML and UMD factors are similar to those of the full sample of funds. Winner and loser funds both appear to hold smaller stocks and winning (losing) unit trusts tend to hold past winning (losing) stocks. Unit trust exposure to the UMD factor seems to be stronger at the 3 and 6 month periods than full-sample exposure. Again, any patterns in loadings are no longer evident at 36 month periods.
| Portfolio | α | RM | SMB | HML | UMD | Adj. R2 |
|---|---|---|---|---|---|---|
| Three-month ranking and holding periods | ||||||
| Winner | 0.0009 (0.61) | 1.0408** (21.89) | 0.1497** (5.26) | 0.0377 (0.69) | 0.1130** (3.85) | 0.79 |
| Loser | 0.0000 (0.03) | 0.9225** (18.38) | 0.0404 (1.59) | −0.0040 (−0.07) | −0.1818** (−5.30) | 0.75 |
| Winner–loser | 0.0008 (0.38) | 0.1183 (1.85) | 0.1094** (2.91) | 0.0417 (0.48) | 0.2948** (6.22) | 0.20 |
| Six-month ranking and holding periods | ||||||
| Winner | 0.0014 (0.86) | 1.0591** (20.05) | 0.1684** (5.36) | 0.0672 (1.07) | 0.1360** (4.06) | 0.82 |
| Loser | −0.0013 (−0.80) | 0.9221** (15.93) | 0.0772** (2.61) | 0.0334 (0.50) | −0.1810** (−5.08) | 0.71 |
| Winner–loser | 0.0027 (1.13) | 0.1370 (1.75) | 0.0912** (2.42) | 0.0338 (0.33) | 0.3170** (6.42) | 0.20 |
| Twelve-month ranking and holding periods | ||||||
| Winner | −0.0002 (−0.12) | 1.0484** (21.37) | 0.1521** (4.90) | 0.1356 (2.28) | 0.0290 (0.88) | 0.81 |
| Loser | −0.0010 (−0.54) | 0.9127** (15.59) | 0.0964** (2.34) | 0.0179 (0.27) | −0.1709** (−3.68) | 0.68 |
| Winner–loser | 0.0008 (0.35) | 0.1357 (1.88) | 0.0556 (1.05) | 0.1178 (1.24) | 0.1999** (3.25) | 0.10 |
| Thirty-six-month ranking and holding periods | ||||||
| Winner | −0.0005 (−0.23) | 0.8664** (12.60) | 0.0709 (1.79) | −0.0021 (−0.03) | −0.1195** (−2.83) | 0.67 |
| Loser | −0.0011 (−0.66) | 1.0447** (19.84) | 0.0310 (0.92) | 0.0541 (0.68) | −0.0571 (−1.44) | 0.76 |
| Winner–loser | 0.0007 (0.23) | −0.1783** (−2.00) | 0.0400 (0.88) | −0.0563 (−0.50) | −0.0624 (−0.97) | 0.02 |
- Results from estimating equation (2): rpt = αp + bpRMt + spSMBt + hpHMLt + upUMDt + ɛpt for unit trusts are shown. Funds are ranked over 3, 6, 12 or 36 months, placed into deciles and monthly returns calculated, with new portfolio assignments occurring every 3, 6, 12 or 36 months, respectively. Winner and loser represent portfolios of funds in the best and worst deciles, respectively, and winner–loser is a portfolio constructed as the difference between the winner portfolio and loser portfolio. RM is the AGSM-CRIF value-weighted market return less the 13 week treasury note return. SMB, HML and UMD are size, book-to-market and momentum mimicking portfolios. Newey–West HAC t-statistics are in parentheses. The sample period is January 1992 to December 2006. Significance at the **5 per cent level.
4.1.Robustness tests12
Our study is the first in Australia to investigate persistence in fund performance using Carhart’s (1997) factor formations. The method used to form these factors, described above, is in line with Fama and French (1993) and Carhart (1997). However, Fama and French (1993) and Carhart (1997) developed their factors for the US market, but the underlying characteristics of the Australian stock market are different from those of the USA. In particular, the Australian market is dominated by a small number of large market capitalization stocks. Using equal numbers of stocks in the size portfolios means that the big portfolio is dominated by these large stocks but also contains a large number of smaller stocks. By contrast, the small portfolio only contains very small stocks that could be difficult to invest in and may be outside the investible universe of our funds. As a robustness test, we therefore re-form the factors using the proportion of total market capitalization to determine the size break points. Stocks in the top 90 per cent are classified as big, while all other stocks are classified as small. This formation aligns the big portfolio with the large capitalization investible universe in Australia, while small more accurately reflects the investible small capitalization universe. Results are very similar: there is still no evidence of persistence in performance. There are a few minor differences in terms of factor loadings. We now find the winner and loser portfolios of all three groups of funds have positive loadings on the SMB factor for all time periods. Additionally, the loser portfolios load positively on HML in the time periods longer than 3 months.
In our initial analysis, we divided funds into deciles of performance, following Carhart (1997). However, there are far fewer funds in our sample than in Carhart’s. This means that in some cases the number of funds in each portfolio is quite small. This is particularly true for the superannuation funds, where the minimum number of funds in a portfolio is two (see panel B of Table 1). For robustness, then, we also perform our analysis using five portfolios of performance instead of 10. Results are almost identical.
In line with Carhart (1997), we equally weighted fund returns to form the portfolios. For robustness, we value weight fund returns. Results are not substantially different. Funds are placed into the performance deciles depending upon their ranking period return. This results in the first few observations in each series being lost because they are used to calculate this return. Essentially this means that our sample time periods across the four ranking/holding periods are different. The worst affected are the 36 month results whose sample period becomes January 1995 to December 2006. We therefore rerun all the analysis using January 1995 to December 2006 as our sample period. Results are very similar to those from the longer sample period. Overall, our robustness tests uphold our initial findings – we find no evidence of performance persistence for any sample of funds.
5. Conclusion
In this paper we investigate persistence in the performance of Australian funds using Carhart’s (1997) four-factor model. We do not find evidence of persistence in fund performance for any of the three samples of funds under investigation: all funds, superannuation funds or unit trusts.
In the short term, we find both winning and losing funds have significant positive exposure to the SMB factor for unit trusts and our sample comprising all funds. This result suggests that these funds tend to hold smaller capitalization stocks. In addition, in the short term, all winning (losing) portfolios tend to load positively (negatively) onto the UMD factor, implying that winning (losing) funds tend to hold past winning (losing) stocks. Interestingly, funds do not appear to load onto the HML factor.
Our results suggest that, in line with research from other markets, selecting funds that have performed well in the past is not a good investment strategy, and could explain why few investors have changed their superannuation fund since the introduction of the Choice of Fund Policy in July 2005. However, our results do show that investing in winning funds may be a convenient way for investors to gain exposure to small capitalization stocks as well as the short-term momentum in the underlying Australian stock market.




