Transitional credit modelling and its relationship to market value at risk: an Australian sectoral perspective
We thank the editor, Robert Faff, and two anonymous referees for their very helpful comments.
Abstract
Internal credit risk modelling is important for banks for the calculation of capital adequacy in terms of the Basel Accords, and for the management of sectoral exposure. We examine Credit Value at Risk (VaR), Conditional Credit Value at Risk (Credit CVaR) and the relationship between market and credit risk. Significant association is found between different Credit CVaR methods, and between market and credit risk. Simpler Credit CVaR methods are found to be viable alternatives to more complex methodology. The relationship between market and credit risk is used to develop a new model that allows banks to incorporate industry risk into transition modelling, without macroeconomic analysis.
1. Introduction and context
A huge focus has been placed on credit risk modelling in the banking industry with the advent of Basel II and the significant benefits to banks who are able to demonstrate a reduced capital requirement. Previous studies have examined market and credit risk from a sectoral perspective (Allen and Powell, 2007a, 2007b), and, importantly, have established a significant positive relationship between those industries that are risky from a market perspective and those that are risky from a credit perspective. As this relationship is an important component of this article, and to ensure that this article is self-contained, the key findings and methodology of these previous studies are summarized in Appendix I. The importance of sectoral risk was examined, with overconcentration of credit risk being a key contributor to bank failure (refer to Jackson, 1996). Also examined in these studies was the importance of Credit CVaR as a measure of credit risk due to its ability to measure extreme credit risk, and to address shortcomings with VaR, such as lack of sub-additivity (for CVaR studies, see Artzner et al., 1999, 1997; Bucay and Rosen, 1999; Huang et al., 2008; Trindade et al., 2007; Uryasev et al., 2000).
The present study focuses on transition matrix modelling of credit risk, based on the methodology of CreditMetrics (Gupton et al., 1997) and CreditPortfolioView (Wilson, 1998). We examine Credit VaR and Credit CVaR, and introduce new Credit CVaR techniques. For clarity, where VaR relates specifically to credit risk or specifically to market risk, it has been stated as ‘Credit VaR’ or ‘Market VaR’. The same applies to CVaR. A naked VaR or CVaR applies to both credit risk and market risk.
The CreditMetrics approach calculates Credit VaR based on probabilities of portfolio assets moving from one asset rating class to another. Transition matrix modelling studies are not nearly as abundant as studies on market risk models or other credit risk models, such as the structural approach. The key reason for this is the lack of publicly available data. Therefore, a benefit of this study is that it provides some insights into an area not often explored in other studies. There is particularly a lack of study in this area in an Australian context. Some examples of other studies touching on ratings-based modelling or transition matrices that can be referred to include bond pricing aspects (Jarrow et al., 1997; Lando, 2004; Thomas et al., 1999), time or business cycle sensitivity (Altman and Kao, 1992; Cowan, 2001), discussion of the transition modelling approach (Crouhy et al., 2000; Saunders and Allen, 2002), and fixed interest credit spreads in Australia (Carrett, 2004).
CreditPortfolioView incorporates industry risk, based on macroeconomic factors, into transition matrix modelling. We have already mentioned the importance of industry risk measurement in managing sectoral concentration and reducing bank failure and, therefore, the incorporation of industry factors into credit modelling is intuitively appealing. However, macroeconomic approaches to measurement of industry risk are not popular in Australia, as noted by the Australian Prudential Regulation Authority (1999, p. 4) in their statement: ‘Currently none of the Australian banks favours a credit risk modelling approach conditioned on the state of the economy. Apart from the additional modelling complexity involved, the banks express concern that errors in forecasting economic turning points could lead, in particular, to a shortfall in desired capital coverage just as the economy turns sharply downwards.’
Based on the premise that all risks inherent in an industry should already be captured in market prices and Market VaR, together with the positive relationship we have previously established between market and credit risk, we develop credit industry risk factors based on Market VaR that can be used by banks to manage risks, such as sectoral concentration. These factors are also incorporated into a new transition model (which we call iTransition) without the need for macroeconomic analysis.
As our study examines and incorporates existing CreditMetrics, CreditPortfolioView and Credit CVaR approaches, these are discussed in Sections 3, 4 and 5. Our modelling methodology is provided in Section 6, with results discussed in Section 7. Industry risk factors and our iTransition model are presented in Section 8 and conclusions in Section 9.
2. Summary of key contributions
This study is anticipated to provide a number of benefits. It addresses a need for additional research on Credit VaR, Credit CVaR and industry risk in Australia. The approaches discussed in the study can assist banks in several facets of risk management, such as capital allocation and managing sector risk concentration. New insights are provided into Credit VaR and Credit CVaR, and the association between credit and market risk. The study develops a new model combining market and credit approaches. Unique Credit VaR and Credit CVaR modelling methodologies are formulated. Although we use Australian data, these techniques have universal application.
3. Credit metrics
3.1. Transition table
This approach incorporates a transition matrix that shows the probability (ρ) of a borrower moving from one credit grade to another, based on historical data. This is shown as follows for a BBB rated asset:
| BBB | ρAAA | ρAA | ρA | ρBBB | ρBB | ρB | ρCCC/C | ρD |
In order to capture all states of probability, the sum of probabilities in each row must equal 1. CreditMetrics illustrate their model (Gupton et al. 1997, p. 20) using a Standard and Poor's (S&P) transition matrix that includes a ‘not rated’ category per Table 1, which CreditMetrics remove, and adjust all remaining ratings on a pro-rata basis.
| AAA (%) | AA (%) | A (%) | BBB (%) | BB (%) | B (%) | CCC/C (%) | D (%) | NR (%) | |
|---|---|---|---|---|---|---|---|---|---|
| AAA | 87.44 | 7.37 | 0.46 | 0.09 | 0.06 | 0.00 | 0.00 | 0.00 | 4.59 |
| AA | 0.60 | 86.65 | 7.78 | 0.58 | 0.06 | 0.11 | 0.02 | 0.01 | 4.21 |
| A | 0.05 | 2.05 | 86.96 | 5.50 | 0.43 | 0.16 | 0.03 | 0.04 | 4.79 |
| BBB | 0.02 | 0.21 | 3.85 | 84.13 | 4.39 | 0.77 | 0.19 | 0.29 | 6.14 |
| BB | 0.04 | 0.08 | 0.33 | 5.27 | 75.73 | 7.36 | 0.94 | 1.20 | 9.06 |
| B | 0.00 | 0.07 | 0.20 | 0.28 | 5.21 | 72.95 | 4.23 | 5.71 | 11.36 |
| CCC/C | 0.08 | 0.00 | 0.31 | 0.39 | 1.31 | 9.74 | 46.83 | 28.83 | 12.52 |
| D | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
- Source: Standard & Poor's, 2005b, p. 12.
The CreditMetrics model obtains forward zero curves for each category (based on risk-free rates) expected to exist in a year's time. Using the zero curves, the model calculates the market value (V) of the loan, including the coupon, at the 1 year risk horizon. Probabilities in the table are multiplied by V to obtain a weighted probability. Based on the revised probability table, Credit VaR can be obtained by calculating the probability weighted portfolio variance and standard deviation (σ), and then calculating Credit VaR using a normal distribution (e.g. 1.645σ for a 95 per cent confidence level).
3.2. Joint probabilities
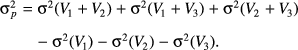 (1)
(1)3.3. Transition asset thresholds and Monte Carlo modelling
CreditMetrics maintains that there is a series of asset values that determine a company's rating (Gupton et al., 1997). If a company's asset value falls or increases to a certain level, at the end of that period, its new asset value will determine the new rating at that point in time. These bands of asset values are referred to by CreditMetrics as asset thresholds. The percentage of changes in assets (or ‘asset returns’) are assumed to be normally distributed and, using the probabilities from the transition matrix table, probabilities (Pr) of asset thresholds ZDef, ZCCC and so on, can be calculated as follows:
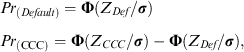 (2)
(2)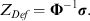 (3)
(3)CreditMetrics apply the asset thresholds to Monte Carlo modelling using three steps. First, asset return thresholds, as discussed above, need to be generated for each rating category. Second, scenarios of asset returns need to be generated using a normal distribution. The third step is to map the asset returns in Step 2 with the credit scenarios in Step 1. A return falling below a rating corresponds to the rating above it.
Thousands of scenarios are normally generated from which a portfolio distribution and Credit VaR are calculated.
4. Credit portfolio view
This section provides a summary of the model as presented by various sources, including Wilson (1998), Saunders and Allen (2002), Pesaran et al. (2003) and Crouhy et al. (2000).
CreditPortfolioView uses a transition matrix approach, but is based on the premise that there is not equal transition probability among borrowers of the same grade, as is assumed by CreditMetrics. CreditPortfolioView links macroeconomic factors to migration probability, such as gross domestic product growth, unemployment rates and interest rates.
The model groups firms into countries and industries. The probability of default is determined by an industry and country variable, which is common to all firms in that industry or country. The model shows the probability that a firm in a given country and given industry, rated at a given grade at the start of the period, will move to another grade by the end of the period.
A migration adjustment ratio is calculated as the conditional probability divided by the unconditional probability.
Assuming that a migration adjustment is applied to a probability, each of the cells in the row must be recalibrated, as each row must equal 1. CreditPortfolioView provides standard values that can be chosen should the user not want to calculate all of the individual shifts. This can be used along with CreditMetrics to calculate an adjusted Credit VAR figure.
5. CVaR
CVaR measures extreme risk, and is used primarily in the insurance industry. It has been gaining popularity as a credit measure with the recognition that credit portfolios are characterized by a small number of large losses. CVaR is conditional upon losses exceeding VaR. If VaR is measured at a confidence level of 95 per cent, then CVaR represents the 5 per cent of worst losses. Per Appendix I, we have applied CVaR to market and structural credit models using both parametric and non-parametric measures (Allen and Powell, 2007a, 2007b). The parametric methods measure the tail 5 per cent of the portfolio based on a normal distribution, whereas the non-parametric methods measure the actual 5 per cent worst losses.
Some parallels can be drawn here between these CVaR methodologies and downside risk (semivariance) versus multivariance arguments applying to beta measurements under the Capital Asset Pricing Model (CAPM). Estrada (2007) states that semivariance of returns is a more useful risk measure than variance of returns for equities. This is because investors do not dislike upside volatility, they only dislike downside volatility; variance assumes symmetric returns (not always noted in practice) whereas semivariance is equally useful in measuring symmetric and asymmetric returns; and semivariance combines skewness and variance into one measure. Estrada finds evidence supporting downside beta using a sample of country index data on developed and emerging nations, including Australia. Using multivariate testing on Australian equity data, Faff (2001), in contrast, finds support for the dual beta CAPM under bull and bear market conditions.
Our parametric Credit CVaR assumes symmetrical returns (similar to variance beta measurements) as it comprises the 5 per cent of returns beyond parametric Credit VaR. Our non-parametric CVaR method (analytical model) is based on the actual 5 per cent worst returns (those applying to the worst credit ratings) and, therefore, has parallels to the downside risk framework.
Uryasev et al. (2000) use the S&P transition matrix for calculating CVaR contribution to a portfolio. They base CVaR on the worst 5 per cent using Monte Carlo simulation techniques. The portfolio they used was the same portfolio used by Bucay and Rosen (1999) in a case study applying CreditMetrics Credit VaR methodology. The portfolio consisted of 197 bonds issued by 86 obligors in 29 countries. Credit CVaR is measured on a portfolio contribution basis (i.e. Credit CVaR for each country in their study is calculated as a percentage of total Credit CVaR), and the study looks to optimize portfolios by minimizing Credit CVaR. More recently, Huang et al. (2008) use CVaR to deal with uncertain exit times in portfolio selection, and Trindade et al. (2007) introduce an asymmetric control approach to portfolios using CVaR, which shapes residual distributions by constraining one of the tail means not to exceed prescribed values.
6. Methodology
6.1. Credit VaR methodology
We follow the CreditMetrics methodology as described in Section 3.1 of this document with joint probabilities calculated per Section 3.2. For probabilities, we use the S&P Global Average 1 Year Transition Rates in Table 1.
Our portfolio consists of 241 companies, across 14 industries, representing all the rated entities in Australia for which sufficient data are available. Data are not as readily available for transition modelling in an Australian context in comparison to our structural and market modelling where all companies in the dataset are listed with share and balance sheet data easy to obtain. Transitional modelling requires ratings and debt data. To obtain as complete a picture as possible, we obtained data from a variety of sources. This includes DataStream et al. (2005, 2006), S&P (2005a, 2006) and Moody's (2005, 2006). As our data contain a mix of Moody's and S&P ratings, we map Moody's to S&P using the mapping in Table 2.
| S&P | Moody's | Fitch | KMV EDF value (%) |
|---|---|---|---|
| AAA | Aaa | AAA | (0.00, 0.02) |
| AA+ | Aa1 | AA+ | (0.02, 0.03) |
| AA | Aa2 | AA | (0.03, 0.04) |
| AA− | Aa3 | AA− | (0.04, 0.05) |
| A+ | A1 | A+ | (0.05, 0.07) |
| A | A2 | A | (0.07, 0.09) |
| A− | A3 | A− | (0.09, 0.14) |
| BBB+ | Baa1 | BBB+ | (0.14, 0.21) |
| BBB | Baa2 | BBB | (0.21, 0.31) |
| BBB− | Baa3 | BBB− | (0.31, 0.52) |
| BB+ | Ba1 | BB+ | (0.52, 0.86) |
| BB | Ba2 | BB | (0.86, 1.43) |
| BB− | Ba3 | BB− | (1.43, 2.03) |
| B+ | B1 | B+ | (2.03, 2.88) |
| B | B3 | B | (2.88, 4.09) |
| B− | Caa1 | B- | (4.09, 6.94) |
| CCC+ | Caa2 | CCC+ | (6.94, 11.78) |
| CCC | Caa3 | CCC | (11.78, 14) |
| CCC− | Ca | CCC− | (14, 16.70) |
| CC | C | CC | (16.7, 17.00) |
| C | (17.00, 18.25) | ||
| D | (18.25, 20) |
- This table provides a calibration between the well-known rating agencies. This calibration is important when modelling data, which contains loans from different ratings services. The final column shows ratings calibrated to KMV Estimated Default Frequency (EDF) values, which are a component of our prior structural credit risk modelling as discussed in Appendix I. Source of Rating Agency Calibrations: Bank for International Settlements (as cited in Saunders & Allen, 2002, p. 43). Source of EDF Calibrations: KMV Credit Monitor as cited in Lopez (2002, p. 25).
6.2. Credit CVaR methodology
In order to present a comprehensive picture of Credit CVaR, we model four different methods. This includes Parametric, Analytical, Monte Carlo simulation and Portfolio Contribution (also using Monte Carlo methodology). For all the Credit CVaR methods, we use the same probability matrix as for Credit VaR, per Section 6.1.
6.2.1. Parametric method
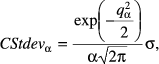 (4)
(4)This method will result in the same industry rankings as Credit VaR, given that it is the tail end of the normal distribution and does not alter relative risk positions of industries.
6.2.2. Analytical method
This method has been developed by this study, based on the actual riskiest return (as opposed to simulated forward debt used by Monte Carlo).
We begin in the same manner as we do for calculating Credit VaR, by using the same probability matrix and values to generate probability weighted asset returns. We then extract the worst 5 per cent of these returns for each industry to form a Credit CVaR portfolio, and then continue using CreditMetrics methodology to calculate portfolio returns for each industry (except we are now using the lowest 5 per cent of returns instead of all returns).
6.2.3. Monte Carlo method
We compile an asset threshold table using the methodology described in Section 3.3. We then generate 20 000 scenarios of asset returns (the same number as Uryasev et al., 2000) using a normal distribution. Scenarios are then mapped to the asset threshold table to obtain a rating for each scenario. We select the lowest 5 per cent of simulated returns for each industry to compile a conditional portfolio, and then use CreditMetrics methodology to calculate portfolio returns for each industry, in the same manner as for our analytical model above.
6.2.4. Portfolio contribution method
We commence by using the same methodology as described above, but then calculate Credit CVaR contribution to the total portfolio, per the method used by Uryasev et al. (2000) described in Section 5. The difference between our Monte Carlo method described in Section 6.2.3 and the Portfolio Contribution method is illustrated in the following example. Assume a two industry portfolio consisting of industry x and industry y with each industry having an identical risk spread of extreme values (e.g. both have 95 per cent of debt rated as B and 5 per cent as C). Also assume that the $A value of the debt in x (say $A20m) was double that of y ($A10m). For our Monte Carlo method, they have the same relative risk (and same Credit CVaR), as they have the same risk spread. However, when calculating contribution to portfolio, Credit CVaR of x is double that of y (Credit CVaRx = 5 per cent of $A20m, whereas Credit CVaRy = 5 per cent of $A10m). Therefore, although the Portfolio contribution method has relevance to the portfolio optimization study, it would only be useful to comparison of industry Credit CVaR if banks lend to all industries in proportion to their market share. As this is not the case, we hold that our Analytical and Monte Carlo methods discussed above are more relevant in the context of our industry ranking comparisons.
7. Results
The Credit VaR model ranks Healthcare, Food, Beverage and Tobacco, and Other Consumer Discretionary as being the highest risk. The financial sector (Banks, Insurance, Diversified Financials) and Telecommunications have a low Credit VaR. An industry will achieve a low VaR ranking if it has companies with higher average credit ratings than the high Credit VaR industries.
Although most of the industries follow a similar Credit CVaR ranking spread to Credit VaR, there are some noticeable differences such as with Diversified Financials. This is because Credit CVaR is only looking at the 5 per cent tail, and Diversified Financials has a higher percentage of low ranked assets in the tail than most of the other industries (i.e. the tail does not follow a normal distribution).
The table shows undiversified rankings, but we have also calculated diversified rankings per Section 3.2. Applying a non-parametric Spearman rank correlation test (95 per cent confidence level), we find no significant difference in industry rankings between any of the Credit VaR and Credit CVaR methods presented in Table 3, or between diversified and undiversified Credit VaR rankings. This shows that the analytical Credit CVaR method is a viable alternative to the Monte Carlo method, and is a much simpler, less time consuming and less modelling intensive method. However, in making this claim, we stress that this relates only to long-term data. The S&P probability matrix used for our analytical approach is generated over more than 20 years. The 20 000 simulations generated by Monte Carlo equate to 80 years. These long time-frames smooth the data, yielding accurate long-term probabilities, resulting in a close match between the Monte Carlo outcomes and the Analytical approach. Appendix I shows that for both credit and market modelling, longer time-frames yield more consistent data, but there can be significant variations from year to year. Within the S&P matrix, there will be year-on-year differences, and the Monte Carlo modelling also has different outcomes for each of the 80 year periods. We maintain that it is important to consider long-term data for establishing accurate probabilities, but shorter time-frames should also be analysed by banks to gain an understanding of variations that can occur from year to year.
| Industry | VaR | CVaR parametric | CVaR analytical | CVaR Monte Carlo |
|---|---|---|---|---|
| Banks | 1 | 1 | 1 | 1 |
| Diversified Financials | 5 | 5 | 8 | 8 |
| Energy | 8 | 8 | 7 | 7 |
| Food, Beverage and Tobacco | 13 | 13 | 14 | 14 |
| Healthcare | 14 | 14 | 13 | 13 |
| Insurance | 3 | 3 | 4 | 4 |
| Media | 10 | 10 | 9 | 10 |
| Metals and Mining | 4 | 4 | 2 | 2 |
| Other Consumer Discretionary | 12 | 12 | 12 | 12 |
| Other Materials | 11 | 11 | 10 | 9 |
| Real Estate | 6 | 6 | 6 | 5 |
| Telecommunication Services | 2 | 2 | 3 | 3 |
| Transportation | 9 | 9 | 11 | 11 |
| Utilities | 7 | 7 | 5 | 6 |
- This table presents undiversified industry ranking outputs from our Credit VaR and Credit CVaR modelling, with 1 being the lowest risk and 14 being the highest risk. Credit VaR is based on CreditMetrics methodology as presented in Section 2.1. Parametric Credit CVaR is the 5 per cent tail end of the normal distribution, using expression (4). The analytical method is based the actual worst 5 per cent for each industry as described in Section 6.2.2. The Credit CVaR Monte Carlo method is based on 20 000 simulations for each industry as described in Section 6.2.3.
In discussing the differences between their Monte Carlo and standard (based on current ratings) Credit VaR approaches, CreditMetrics state that the standard or ‘analytical’ (estimates computed directly from formulas) approach has the advantages of speed and precision (no random noise introduced) (Gupton et al., 1997). They state that the disadvantages are for larger portfolios where speed is no longer true and that it limits the availability of statistics that can be estimated. These same observations will hold true for Credit CVaR. Therefore, a modeller's preference to use an analytical Credit CVaR approach like ours or a Monte Carlo approach will depend on aspects such as the modeller's requirements for speed and the size of the portfolio.
Using the Portfolio Contribution method (see Table 4), we achieve the following results:
| Industry | CVaR |
|---|---|
| Banks | 0.0569 |
| Diversified Financials | 0.1738 |
| Energy | 0.0273 |
| Food, Beverage and Tobacco | 0.1848 |
| Healthcare | 0.0328 |
| Insurance | 0.0057 |
| Media | 0.1308 |
| Metals and Mining | 0.0114 |
| Other Consumer Discretionary | 0.0210 |
| Other Materials | 0.0593 |
| Real Estate | 0.0280 |
| Telecommunication Services | 0.0149 |
| Transportation | 0.1402 |
| Utilities | 0.1133 |
- This table shows CVaR calculated as each industry's contribution to the worst 5 per cent of 20 000 Monte Carlo simulations, as described in Section 6.2.4.
Food, Beverage and Tobacco, and Diversified Financials have the highest contribution to the worst 5 per cent of the portfolio. The difference between our Monte Carlo method and the Portfolio Contribution method (and the limitations of the latter) is illustrated when comparing Diversified Financials and Other Consumer Discretionary. Other Consumer Discretionary has a much higher Credit CVaR ranking than Diversified Financials using our non-parametric Credit CVaR approaches. However, as Diversified Financials has a much higher portion in dollar values of our total portfolio debt than Consumer Discretionary, Diversified Financials has a much higher percentage than Other Consumer Discretionary using the Portfolio Contribution approach (the same principle accounting for the high percentage attributed to Food, Beverage and Tobacco).
8. Industry risk factors and iTransition
From a market perspective, all risks inherent in an industry should already be captured in market prices of equities and Market VaR. As discussed in Appendix I, we have found that there is a positive relationship among industries between market risk (equities) and credit risk (using structural modelling); that is, the same industries that are risky from a market perspective are also risky from a credit perspective. Structural modelling shows that the primary determinants of credit risk (Probability of Default (PD)) are the distance to default (a factor of equity and debt) and asset volatility (influenced primarily by equity movements). Therefore, if we know equity Market VaR, and we know the size of the relationship between equity Market VaR and Credit PD for each industry, then we are able to use these to measure credit risk. Based on this premise, we develop industry risk factors (i), without macroeconomic analysis, and which can be used by a bank to formulate policies such sector concentration or incorporation into a transition matrix (iTransition).
Similar to the CreditPortfolioView framework, we incorporate industry factors into a transition matrix, but using our equity and structural modelling as described in Appendix I to derive industry factors, rather than using macroeconomic factors. The probability of a loan (in this example a B rated loan) moving to another rating category is modified by an industry factor i, as follows:
| B | ρAAAi | ρAAi | ρAi | ρBBBi | ρBBi | ρBi | ρCCC/Ci | ρDi |
The sum of all ρ's in the row is 100 per cent; hence, capturing all states of probability.
This approach benefits banks by allowing the incorporation of industry factors, but without the intensive economic modelling and forecasting they do not favour. In doing this, the model follows the premise that not all borrowers of the same grade have an equal transition. It makes the assumption that it is not necessary to incorporate macroeconomic factors into the model, as relative industry risk and susceptibility to economic factors will be reflected in historical share price movements as measured by our market VaR indices. However, we cannot base the industry factors on share price movements alone, as this is not the only component of credit risk. Therefore, we need to calculate the relationship between market and credit risk. Our equity market model described in Appendix I measures market risk (Market VaR) and our structural model measures credit risk (credit PD). iTransition measures relative industry risk as the relative impact on PD if the equity Market VaR were to materialize for each industry (i.e. losses equal to Market VaR). For example, if an industry had an equity VaR of 30 per cent and that VaR was realized, what would be the impact on Credit PD?
The model requires four key steps. First, obtain transition probabilities (ρ). We use the transition matrix approach described in this study, based on the S&P Global Average 1 Year Transition Rates from 1981 to 2004 (2005b). Second, calculate an industry adjustment factor i for each industry using the relationship between Market VaR and Credit PD for each industry. Third, modify each transition probability using the factors calculated in Step 2. Lastly, calculate Credit VaR based on the revised transition probabilities, using the CreditMetrics methodology described in Sections 3.1 and 3.2. Industry adjustment factors have been calculated for each of our industries and are shown in Table 5.
| Industry | Equity VaR | Equity weighted standard deviation | Structural weighted asset standard deviation | i |
|---|---|---|---|---|
| Banks | 0.3030 | 0.1842 | 0.0278 | 0.5237 |
| Diversified Financials | 0.4145 | 0.2520 | 0.0828 | 1.6070 |
| Energy | 0.5904 | 0.3589 | 0.2811 | 1.4380 |
| Food, Beverage and Tobacco | 0.3987 | 0.2424 | 0.1503 | 0.7945 |
| Healthcare | 0.6008 | 0.3652 | 0.2813 | 1.1641 |
| Insurance | 0.5366 | 0.3262 | 0.0938 | 0.3548 |
| Media | 0.4561 | 0.2773 | 0.1898 | 1.0662 |
| Metals and Mining | 0.5595 | 0.3401 | 0.2570 | 1.0038 |
| Other Consumer Discretionary | 0.5154 | 0.3133 | 0.2377 | 0.9578 |
| Other Materials | 0.4662 | 0.2834 | 0.2093 | 0.8263 |
| Real Estate | 0.3931 | 0.2390 | 0.1520 | 1.1948 |
| Telecommunication Services | 0.3640 | 0.2213 | 0.1565 | 0.7675 |
| Transportation | 0.4732 | 0.2877 | 0.1643 | 0.7176 |
| Utilities | 0.3777 | 0.2296 | 0.1201 | 1.5839 |
- This table shows key components of industry adjustments. The first column shows the equity Market VaR for each industry as calculated by our equity model described in Appendix I. The second column shows the associated standard deviation (Market VaR/1.645 at 95 per cent confidence level from standard statistical tables). The third column shows the asset standard deviation as calculated by our structural model as described in Appendix I. Column 4 shows the industry adjustment factor i, the calculation of which is described immediately following the table.
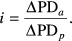 (5)
(5)Let us consider Banks and Diversified Financials as another example. Both industries have low equity and, therefore, have a very short distance to default in terms of our structural model. Therefore, movements in equity affect these industries more than most other industries. However, Banks have a very low asset volatility (standard deviation of 2.8 per cent) compared to Diversified Financials (standard deviation of 8.3 per cent). In practice, neither of these two industries have a significant impact on Credit VaR under the iTransition model as compared to an unconditional approach. This is because the bulk of assets for both industries are in the AA and above categories which have a PD very close to 0 per the S&P probability matrix. Therefore, any additional weighting has little overall impact (i.e. even a 100 per cent change in a PD close to 0 results in a PD that is still close to 0). Industries having a larger percentage of assets in lower ratings have a greater impact. An example is Healthcare, where the bulk of assets are rated BB and i is 1.16. Under the iTransition model, Healthcare PD would increase from 1.32 to 1.53 per cent. Although this increase of 0.2 per cent may not seem overly significant at first, it should be noted that all the Big Four Australian Banks have loan assets of around $A300bn plus, meaning each shift in PD of 0.1 per cent in the loan portfolio equates to around $A300m.
Therefore, for our model, all you need to know to calculate i is the Market VaR and the relationship between Market VaR and Credit PD for each industry, as opposed to undertaking a macroeconomic analysis.
Using the industry factors in Table 5, we recalculate the original probability matrix for each rating category (see Table 6). For example, by applying the adjustments to all AAA assets, we can obtain a weighted average i for all AAA assets – with a weighting > 1 showing that AAA assets have an industry risk > 1, and so on, for all the rating categories. We then apply the industry factor weighting to the PD factor in column D of the matrix for each rating category, and then re-calibrate the remainder of the categories so each row = 1.
| AAA (%) | AA (%) | A (%) | BBB (%) | BB (%) | B (%) | CCC/C (%) | D (%) | |
|---|---|---|---|---|---|---|---|---|
| AAA | 91.64 | 7.72 | 0.48 | 0.09 | 0.06 | 0.00 | 0.00 | 0.00 |
| AA | 0.63 | 90.44 | 8.12 | 0.61 | 0.06 | 0.11 | 0.02 | 0.01 |
| A | 0.05 | 2.15 | 91.32 | 5.78 | 0.45 | 0.17 | 0.03 | 0.04 |
| BBB | 0.02 | 0.22 | 4.10 | 89.62 | 4.68 | 0.82 | 0.20 | 0.33 |
| BB | 0.04 | 0.09 | 0.36 | 5.78 | 83.01 | 8.07 | 1.03 | 1.63 |
| B | 0.00 | 0.08 | 0.22 | 0.31 | 5.84 | 81.75 | 4.74 | 7.05 |
| CCC/C | 0.09 | 0.00 | 0.35 | 0.45 | 1.50 | 11.13 | 53.53 | 32.95 |
- Using the weightings in Table 5, we recalculate the original probability matrix in Table 1 as per the methodology in Section 4. Essentially, we recalculate the PD factor in column D of the matrix, and then using reverse linear regression we re-calibrate the remainder of the categories so each row = 1.
After adjusting for non-rated assets as per Section 3.1, our iTransition table showed little change for Rating Categories A and above. BBB showed an increase of 0.2 per cent, BB an increase of 0.3 per cent, and B an increase of 6.1 per cent. As previously mentioned, these levels can constitute highly significant movements in dollar terms when considering the large value of bank loan assets. Because our portfolio has a high weighting of large A and above assets, and a range of industries (some with i > 1 and some with i < 1), we expect that our overall portfolio changes resulting from iTransition are small. Based on the revised transition matrix, our results in Table 7 show that the Australian portfolio Credit VaR reduced slightly, mainly due to the high weighting of Banks in the portfolio, which have i < 1, per Table 5. Credit CVaR increased slightly. This is to be expected, due to the high representation of assets with i > 1 in the tail end of the portfolio such as Diversified Financials and Healthcare per Table 5.
| Undiversified 95% Credit VaR | Diversified Portfolio 95% Credit VaR | Credit CVaR Analytical | |
|---|---|---|---|
| Original | 0.0242 | 0.0124 | 0.0342 |
| iTransition | 0.0239 | 0.0121 | 0.0354 |
- This table compares key results using the original probability matrix in Table 1 to results using the iTransition Probability Matrix in Table 6. Undiversified Credit VaR ignores correlation, while Diversified Credit VaR is based on joint probabilities as discussed in Section 3.2.
A bank with a greater spread of ratings is likely to experience more movement when iTransition is applied, depending on their spread of industries. Annual reports of the major Australian banks show a high propensity towards Real Estate, which has a high i of 1.19, meaning application of the iTransition model as opposed to a Standard Transition model will have a significant impact on PD.
As listed companies represent the bulk, by value, of all companies in Australia, calculating i from listed companies gives a good reflection of overall risk for each industry. Listed company data are readily available, and industry risk (i) can be easily calculated by banks from listed data on an annual basis (to tie in with balance sheet data being available annually), and updated as required by banks to reflect movements in equity. This could be used by banks to manage their credit policies such as sector concentration limits, or to incorporate into their transition matrix modelling which they could apply across their entire loan portfolio. Although public access to data, other than data required for calculation of i, is not easily accessible for transition modelling, this does not affect banks as they will be calculating Credit VaR and Credit CVaR from their own database.
9. Conclusions
Understanding industry risk is critical to banks in managing their sector concentration, as overconcentration is a key contributor to bank failure. The study examines and introduces a range of transitional matrix techniques for modelling and including industry risk. There is found to be significant association in industry rankings between diversified and undiversified Credit VaR, and a range of Credit CVaR methodologies. This provides a wide range of industry metrics for banks to use to determine relative industry risk. The association between the metrics shows simpler methods, such as the analytical approach to be a viable alternative to more complex methods such as Monte Carlo simulation. Selection of the most appropriate methodology will depend on factors, such as the length of historical data available, the bank's requirement for speed and the size of their portfolio.
This study has also developed new methodology for calculating industry risk and for incorporating industry factors into transition matrix modelling. This can benefit banks as the method does not require macroeconomic analysis which is not favoured by banks. Modelling requires Market VaR and a market-credit factor for each industry which banks could either model themselves or use the factors we have calculated.
Appendix
Appendix I
Prior studies on VaR and CVaR in Australia
As this paper builds on our previous work (Allen and Powell, 2007a, 2007b), this appendix summarizes key components of these prior studies.
Market VaR and Market CVaR
We use companies in the Australian All Ordinaries Index and obtain a Market VaR measurement for equities for each industry based on the universal GICS industry codes. Consistent with RiskMetrics (J. P. Morgan & Reuters, 1996) who introduced Market VaR, and the approach commonly used by banks, a parametric approach is used for calculating Market VaR at the 95 per cent level. Market VaR is obtained by calculating the annualized standard deviation (σ) of correlated daily returns, and then calculating Market VaR using a normal distribution (1.645σ for a 95 per cent confidence level). Market CVaR is calculated as the average of those returns beyond VaR (in our case, the extreme 5 per cent of returns). Fifteen years of historical data are analysed using a 7 year rolling window approach to calculate Market VaR. Seven years is the period required by the advanced Basel approach for modelling credit losses, and is the period used by the authors in their structural credit modelling below. Using the same period for credit and market modelling allows comparison of market and credit modelling outcomes. Market VaR and Market CVaR rankings for the industries are compared, using a range of parametric, non-parametric, diversified and undiversified metrics. Comparisons are also made between different time periods. There is found to be significant association in industry rankings across all these metrics (using a Spearman rank correlation coefficient at the 95 per cent level) when using the 7 year rolling window approach, as well as association between rankings over time. For comparison, we also use 1 year data frames, which find no association between metrics or between historical time periods.
Structural Credit PD and Credit CPD
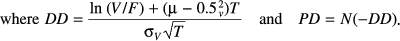
DD (at time period T) is a function of the distance between the market value of assets V (as measured by liabilities and equity) and debt F, and the volatility of those assets σ (impacted primarily by equity movements). µ is the annual return (drift) of the firm's assets. KMV find the PD values obtained by these formulae to be too small, and calibrate PD's to an Estimated Default Frequency (EDF), using their vast historical database of defaults. As we are interested in rankings rather than absolute values, we are able to use either the PD, EDF or DD values as they all yield the same ranking. We calculate the Conditional Probability of Default (CPD) by using the worst 5 per cent of asset returns as the σ-value in the DD formula. Similar to the market modelling, a range of Credit VaR and Credit CVaR metrics were used to rank industries, including parametric, non-parametric, diversified and undiversified methods. Again, significant industry association was demonstrated between metrics and over time using 7 year rolling windows, but not when using 1 year time frames.
Comparisons between Market and Credit Modelling
Rankings for Market VaR, Market CVaR, Credit PD and Credit CPD values are shown in Table A1. A Spearman ranking correlation coefficient applied to the rankings shows significant association at the 95 per cent confidence level between Market VaR and Credit PD, and between Market CVaR and Credit CPD, using 7 year rolling windows.
| Market model | Credit model | |||||||
|---|---|---|---|---|---|---|---|---|
| Annual undiversified 95% VaR | Diversified portfolio 95% VaR | Parametric CVaR | Non-parametric CVaR | Undiversified PD | Diversified PD | CPD | Non-parametric CPD | |
| Automobiles and Components | 19 | 14 | 19 | 19 | 21 | 22 | 21 | 23 |
| Banks | 1 | 5 | 1 | 1 | 17 | 19 | 17 | 11 |
| Capital Goods | 11 | 8 | 11 | 11 | 15 | 9 | 15 | 17 |
| Chemicals | 8 | 15 | 8 | 9 | 13 | 18 | 13 | 14 |
| Commercial Services and Supplies | 18 | 9 | 18 | 18 | 18 | 8 | 18 | 18 |
| Construction Materials | 9 | 17 | 9 | 7 | 4 | 13 | 4 | 3 |
| Consumer Durables and Apparel | 16 | 23 | 16 | 16 | 11 | 17 | 11 | 13 |
| Diversified Financials | 7 | 2 | 7 | 8 | 2 | 3 | 2 | 4 |
| Energy | 21 | 13 | 21 | 20 | 7 | 5 | 7 | 7 |
| Food and Staples Retailing | 3 | 11 | 3 | 2 | 5 | 12 | 5 | 5 |
| Food, Beverage and Tobacco | 6 | 3 | 6 | 5 | 8 | 7 | 8 | 9 |
| Healthcare Equipment and Services | 15 | 6 | 15 | 15 | 12 | 4 | 12 | 16 |
| Hotels, Restaurants and Leisure | 14 | 16 | 14 | 17 | 10 | 11 | 10 | 10 |
| Insurance | 17 | 18 | 17 | 21 | 25 | 25 | 25 | 25 |
| Media | 10 | 7 | 10 | 10 | 6 | 6 | 6 | 6 |
| Metals and Mining | 20 | 19 | 20 | 14 | 14 | 14 | 14 | 8 |
| Paper and Forest Products | 22 | 21 | 22 | 22 | 22 | 21 | 22 | 21 |
| Pharmaceuticals and Biotechnology | 23 | 22 | 23 | 23 | 19 | 15 | 19 | 20 |
| Real Estate | 5 | 1 | 5 | 6 | 3 | 2 | 3 | 2 |
| Retailing | 13 | 12 | 13 | 13 | 20 | 16 | 20 | 19 |
| Software and Services | 24 | 24 | 24 | 24 | 23 | 20 | 23 | 22 |
| Technology Hardware and Equipment | 25 | 25 | 25 | 25 | 24 | 24 | 24 | 24 |
| Telecommunication Services | 2 | 20 | 2 | 3 | 9 | 23 | 9 | 12 |
| Transportation | 12 | 10 | 12 | 12 | 16 | 10 | 16 | 15 |
| Utilities | 4 | 4 | 4 | 4 | 1 | 1 | 1 | 1 |
- This table ranks the outcomes for each column, with 1 being the lowest risk and 25 the highest risk. Market VaR is calculated using a parametric approach to equity returns at the 95 per cent confidence level. Undiversified Market VaR is based on uncorrelated the returns for companies within the industry. Diversified Market VaR shows correlated outcomes. Parametric Market CVaR is based on returns exceeding parametric Market VaR per equation 4. Non-parametric Market VaR is based on the actual worst 5 per cent of returns. Calculation of Credit PD and Credit CPD is described earlier in this appendix. Parametric Credit CPD is based on asset returns exceeding parametric asset returns per formula 4. Non-parametric Credit CPD is based on the actual worst 5 per cent of asset returns.




