Constructing Asset Pricing Models With Specific Factor Loadings
We acknowledge the very helpful criticisms (and encouragement) of the referees on previous drafts of the paper.
Abstract
We demonstrate how one can build pricing formulae in which factors other than beta may be viewed as determinants of asset returns. This is important conceptually as it demonstrates how the additional factors can compensate for a market portfolio proxy that is mis-specified, and also shows how such a pricing model can be specified ex ante. The procedure is implemented by first selecting an ‘orthogonal’ portfolio which falls on the mean-variance efficient frontier computed from the empirical average returns, variances and covariances on the equity securities of a large sample of firms. One then determines the inefficient index portfolio which leads to a vector of betas that when multiplied by the average return on the orthogonal portfolio, and which when subtracted from the vector of average returns for the firms comprising the sample, yields an error vector that is equal to the vector of numerical values for the variables that are to form the basis of the asset pricing formula. There will then be a perfect linear relationship between the vector of average returns for the firms comprising the sample, the vector of betas based on the inefficient index portfolio and such other factors that are deemed to be important in the asset pricing process. We illustrate computational procedures using a numerical example based on the quality of information contained in published corporate financial statements.
An important question in the field of asset pricing and its applications is how to interpret significantly weighted variables and/or factors other than the index portfolio, which is taken as a proxy for the market portfolio, in empirical tests of the capital asset pricing model (CAPM). Given that these ‘extended’ empirical specifications of the CAPM are widely used in areas of the accounting literature such as financial statement analysis and empirical investigations of the relation between the quality of information summarized in corporate financial statements and the cost of capital, this is an important issue (Botosan, 1997; Botosan and Plumlee, 2002; Francis et al., 2005; Core et al., 2008). A popular explanation is that the CAPM is either mis-specified, or is incomplete as a model of market returns (Fama, 1996; Fama and French, 1992, 1993, 1995, 1996). An alternative, and equally plausible explanation, however, is that the index portfolio used in empirical estimation is a mis-specified or an incomplete proxy for the market portfolio.1 In the same way that the efficiency of the market portfolio and the validity of the CAPM are joint hypotheses (Roll, 1977), there are theoretical limits to disentangling the elements of the question posed above. However, by deriving a formal connection between non-zero loadings on factors additional to the equity risk premium and the extent to which the market portfolio proxy is inefficient, we argue that this provides a more likely explanation of the significance in equity valuation of factors such as the book-to-market ratio for equity and firm size, none of which has been justified in the literature on a priori grounds.
The purpose of this paper then is to look at this issue from a different viewpoint and to pose the following question, which will be analysed from an analytical perspective using the mathematics of the efficient set and standard linear algebra. Suppose that the CAPM is correct. How would one choose an inefficient index portfolio (not the true market portfolio) to generate chosen factor loadings on a pre-specified set of additional variables, and having done this, how would this inefficient index portfolio look in relation to the true market portfolio? We respond to this question by introducing a procedure by which an empirical researcher can determine the inefficient index portfolio that yields a set of betas which when taken in conjunction with such other factors as the researcher stipulates are to be important in the asset pricing process (e.g., firm size, market-to-book ratios, quality of information summarized in corporate financial statements, etc.) will be perfectly correlated with the ex post average returns earned by the firms on which the empirical analysis is based. This places the largely ad hoc nature of the asset pricing formulae which characterize the empirical research of the area onto a similar footing as the CAPM in the sense that asset average returns have a perfect linear relationship with the selected risk factors deemed to be important in the asset pricing process.
FUNDAMENTAL RESULTS
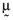 be the n × 1 vector whose elements are the empirical average returns and Ω be the n × n matrix whose elements are the empirical variances and covariances of the returns on these risky assets. Furthermore, one can determine the set of mean-variance efficient portfolios implied by
be the n × 1 vector whose elements are the empirical average returns and Ω be the n × n matrix whose elements are the empirical variances and covariances of the returns on these risky assets. Furthermore, one can determine the set of mean-variance efficient portfolios implied by 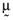 and Ω, in which case it follows (Roll, 1977):
and Ω, in which case it follows (Roll, 1977):
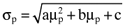 ()
()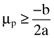 defines the expected return on the global minimum variance portfolio. Figure 1 provides a graphic summary of the relationship between the standard deviation, σp, and the expected return, µp, on any given efficient portfolio. Moreover, one can draw a chord from the origin which is just tangential to the locus of mean-variance efficient portfolios.2 The point of tangency defines an ‘orthogonal’ portfolio with an average return of
defines the expected return on the global minimum variance portfolio. Figure 1 provides a graphic summary of the relationship between the standard deviation, σp, and the expected return, µp, on any given efficient portfolio. Moreover, one can draw a chord from the origin which is just tangential to the locus of mean-variance efficient portfolios.2 The point of tangency defines an ‘orthogonal’ portfolio with an average return of 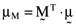 where
where 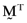 is the transpose of the vector
is the transpose of the vector 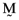 whose elements are the proportionate investments in each of the n risky assets comprising the orthogonal portfolio. One can then compute the vector of asset betas,
whose elements are the proportionate investments in each of the n risky assets comprising the orthogonal portfolio. One can then compute the vector of asset betas, 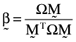 , relative to the orthogonal portfolio in which case it follows
, relative to the orthogonal portfolio in which case it follows 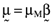 —that is, there is a perfect linear relationship between the vector of asset average returns,
—that is, there is a perfect linear relationship between the vector of asset average returns, 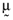 , and the betas,
, and the betas, 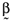 , computed relative to the chosen orthogonal portfolio.
, computed relative to the chosen orthogonal portfolio.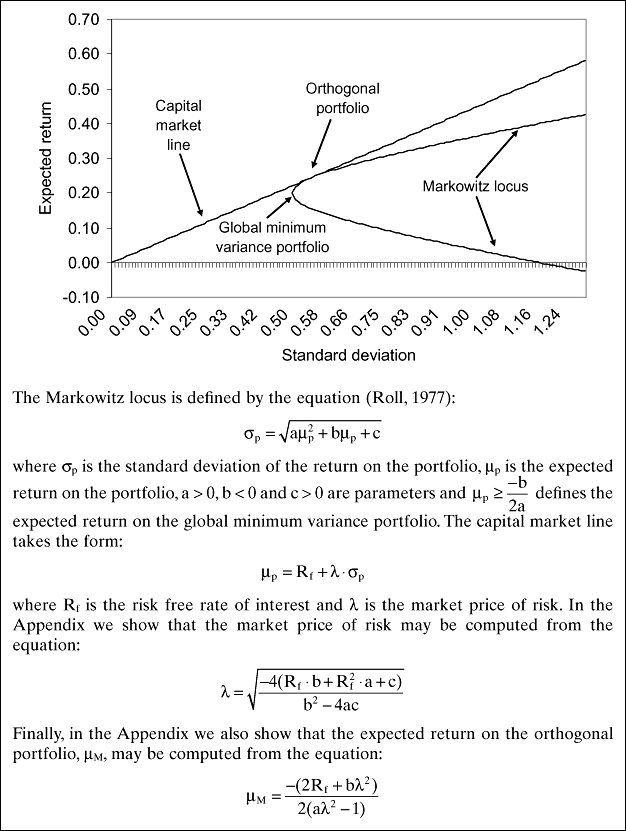
MARKOWITZ LOCUS
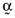 , that have the same average return as the orthogonal portfolio considered earlier, or
, that have the same average return as the orthogonal portfolio considered earlier, or 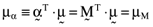 . Ashton and Tippett (1998, p. 1329) show that the proportionate investment vectors for these inefficient index portfolios,
. Ashton and Tippett (1998, p. 1329) show that the proportionate investment vectors for these inefficient index portfolios, 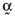 , are related to the proportionate investment vector for the orthogonal portfolio,
, are related to the proportionate investment vector for the orthogonal portfolio, 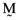 , through the formula:
, through the formula:
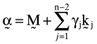 ()
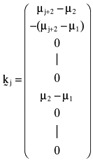
()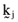 are self financing ‘kernel’ or ‘arbitrage’ portfolios and the γj are parameters that vary over the set of real numbers. Moreover, the arbitrage portfolios,
are self financing ‘kernel’ or ‘arbitrage’ portfolios and the γj are parameters that vary over the set of real numbers. Moreover, the arbitrage portfolios, 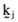 , can be determined by solving the system of equations:
, can be determined by solving the system of equations:
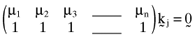 ()
()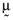 , and
, and 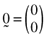 is the null vector. One can solve the above system of equations and thereby show that the arbitrage portfolios take the form:
is the null vector. One can solve the above system of equations and thereby show that the arbitrage portfolios take the form:
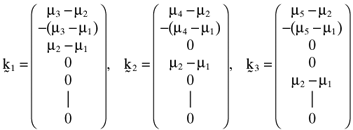
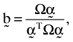 based on these inefficient index portfolios in which case it follows:
based on these inefficient index portfolios in which case it follows:
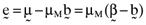 ()
()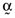 . Now, if one pre-multiplies this latter expression by
. Now, if one pre-multiplies this latter expression by 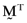 it follows from results summarized in Ashton and Tippett (1998, pp. 1330–31) that the average error from basing the calculation of betas on the inefficient index portfolio will be
it follows from results summarized in Ashton and Tippett (1998, pp. 1330–31) that the average error from basing the calculation of betas on the inefficient index portfolio will be 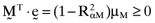 , where
, where 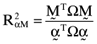 is the coefficient of determination between the return on the orthogonal portfolio,
is the coefficient of determination between the return on the orthogonal portfolio, 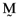 , and the inefficient index portfolio,
, and the inefficient index portfolio, 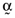 . Not unsurprisingly, the average error is inversely related to the coefficient of determination between the return on the inefficient index portfolio and the return on the orthogonal portfolio and will always be positive. If, however, one weights the error vector,
. Not unsurprisingly, the average error is inversely related to the coefficient of determination between the return on the inefficient index portfolio and the return on the orthogonal portfolio and will always be positive. If, however, one weights the error vector, 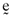 , by the proportionate investments comprising the inefficient index portfolio,
, by the proportionate investments comprising the inefficient index portfolio, 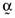 , then the average error will be identically equal to zero; that is,
, then the average error will be identically equal to zero; that is, 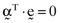 .
.Here it is important to note that one can use the above analysis to specify a particular error vector and then determine the inefficient index portfolio from which a set of betas may be computed that, when taken in conjunction with the error vector, will have a perfect linear relationship with the average returns vector. This in turn means that one can employ the analysis summarized here to determine the inefficient index portfolio that leads to a pricing formula in which asset average returns are perfectly correlated with the size of the affected firm, the market-to-book ratio for its equity, the quality of the information summarized in a firm's financial statements or any other set of variables which the empirical researcher wishes to argue are important determinants of asset prices. We have previously observed that this is of considerable importance in empirical research where it is often necessary to build pricing formulae in which factors other than beta are seen as instrumental determinants of asset returns.
NUMERICAL EXAMPLE
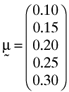

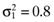 while the covariance of the return between the first and second asset is σ12= 0.1 =σ21. The remaining entries in Ω are to be similarly interpreted. Now, it is not hard to show that the set of mean-variance efficient portfolios implied by the average returns vector,
while the covariance of the return between the first and second asset is σ12= 0.1 =σ21. The remaining entries in Ω are to be similarly interpreted. Now, it is not hard to show that the set of mean-variance efficient portfolios implied by the average returns vector, 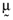 , and variance-covariance matrix, Ω, given above is as follows:
, and variance-covariance matrix, Ω, given above is as follows:
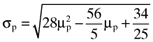 ()
()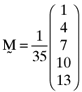 ()
()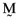 , is comprised of an
, is comprised of an 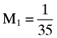 proportionate investment in the first asset, an
proportionate investment in the first asset, an 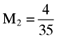 proportionate investment in the second asset, an
proportionate investment in the second asset, an 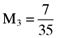 proportionate investment in the third asset and so on. This in turn means that the orthogonal portfolio has an average return and variance of
proportionate investment in the third asset and so on. This in turn means that the orthogonal portfolio has an average return and variance of 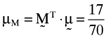 and
and 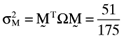 , respectively. One can then compute the vector of betas based on the orthogonal portfolio; namely:
, respectively. One can then compute the vector of betas based on the orthogonal portfolio; namely:
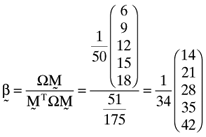 ()
()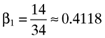 , the beta for the second asset is
, the beta for the second asset is 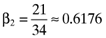 , and so on. Moreover, the reader will be able to confirm that there is a perfect linear relationship between the vector of average returns and the vector of betas on which the example is based, or:
, and so on. Moreover, the reader will be able to confirm that there is a perfect linear relationship between the vector of average returns and the vector of betas on which the example is based, or:
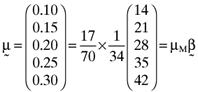
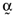 , which have the same average return,
, which have the same average return, 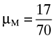 , as the orthogonal portfolio,
, as the orthogonal portfolio, 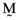 , defined above, namely:
, defined above, namely:
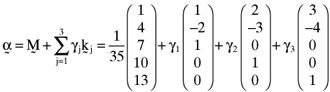 ()
()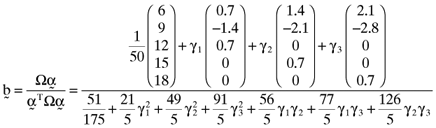 ()
() , and there will be a perfect linear relationship between the betas and the average returns.6 When, however, any of γ1, γ2 and γ3 assume values other than zero there is no longer a perfect relationship between asset betas and their average returns. Moreover, prior analysis shows that the relationship between the error vector,
, and there will be a perfect linear relationship between the betas and the average returns.6 When, however, any of γ1, γ2 and γ3 assume values other than zero there is no longer a perfect relationship between asset betas and their average returns. Moreover, prior analysis shows that the relationship between the error vector,  , and betas based on the orthogonal,
, and betas based on the orthogonal, 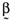 , and inefficient index portfolios,
, and inefficient index portfolios, 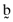 , will be as follows:
, will be as follows:
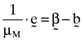 ()
()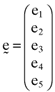 , will be:
, will be:
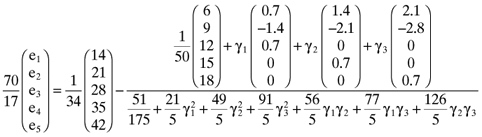 ()
()It is important to note that the error expression given here is based on five equations but that there are eight unknowns—namely, the components of the errorvector, e1, e2, e3, e4, e5, and the three parameters γ1, γ2 and γ3, which characterize the inefficient index portfolio. Hence, three of these eight variables can be specified so as to satisfy exogenously specified criteria. More generally, if the analysis is based on n assets then n − 2 elements of the error vector,  , can be exogenously specified before the inefficient index portfolio on which the asset pricing formula is to be based is determined. If, for example, the researcher determines that firm size, the market-to-book ratio and the quality of the information summarized in a firm's financial statements are to be important factors in the asset pricing process, then he can specify numerical values for any n − 2 elements of the error vector so that they accommodate this hypothesis perfectly. There will then be a perfect linear relationship between the average returns for the n − 2 firms for which the elements of the error vector have been specified and the factors (beta, firm size, market-to-book ratio, quality of accounting information, etc.) the researcher stipulates are to be important in the asset pricing process. Moreover, since large samples typify the empirical research of the area (Fama and French, 1992, 1993, 1995, 1996), the two firms for which there will be an inexact relationship can have only a minor impact on the analysis and can safely be excluded from any subsequent work based on the sample.
, can be exogenously specified before the inefficient index portfolio on which the asset pricing formula is to be based is determined. If, for example, the researcher determines that firm size, the market-to-book ratio and the quality of the information summarized in a firm's financial statements are to be important factors in the asset pricing process, then he can specify numerical values for any n − 2 elements of the error vector so that they accommodate this hypothesis perfectly. There will then be a perfect linear relationship between the average returns for the n − 2 firms for which the elements of the error vector have been specified and the factors (beta, firm size, market-to-book ratio, quality of accounting information, etc.) the researcher stipulates are to be important in the asset pricing process. Moreover, since large samples typify the empirical research of the area (Fama and French, 1992, 1993, 1995, 1996), the two firms for which there will be an inexact relationship can have only a minor impact on the analysis and can safely be excluded from any subsequent work based on the sample.
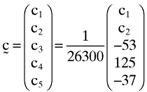 ()
()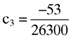 ,
, 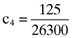 and
and 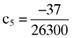 , respectively. Now here it will be recalled that the researcher wants a coefficient of five (5) to be associated with the accruals quality measures in an empirically determined asset pricing formula which relates betas and the accruals quality measures to asset average returns. Given this, the researcher will need to determine the inefficient index portfolio which leads to the following error vector:
, respectively. Now here it will be recalled that the researcher wants a coefficient of five (5) to be associated with the accruals quality measures in an empirically determined asset pricing formula which relates betas and the accruals quality measures to asset average returns. Given this, the researcher will need to determine the inefficient index portfolio which leads to the following error vector:
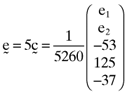 ()
()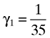 ,
, 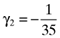 ,
, 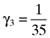 ,
, 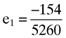 and
and 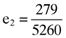 , that will lead to betas which return an error vector with the desired elements. Substituting the computed values for γ1, γ2 and γ3 into equation (8) shows that the inefficient index portfolio which will lead to betas that are compatible with the error vector (13) will be:
, that will lead to betas which return an error vector with the desired elements. Substituting the computed values for γ1, γ2 and γ3 into equation (8) shows that the inefficient index portfolio which will lead to betas that are compatible with the error vector (13) will be:
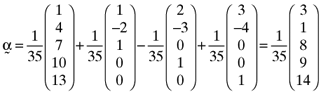 ()
()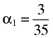 proportionate investment in the first asset, an
proportionate investment in the first asset, an 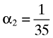 proportionate investment in the second asset, an
proportionate investment in the second asset, an  proportionate investment in the third asset and so on. This will also mean that the betas for this inefficient index portfolio will be:
proportionate investment in the third asset and so on. This will also mean that the betas for this inefficient index portfolio will be:
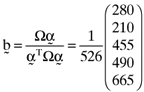 ()
()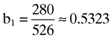 , the beta for the second asset is
, the beta for the second asset is 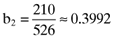 and so on. As expected, the linear relationship between the average returns and betas predicted by the CAPM breaks down when betas are based on the inefficient index portfolio detailed here. Indeed, the vector of errors in the average returns that arise from basing the calculation of betas on the inefficient index portfolio turns out to be:
and so on. As expected, the linear relationship between the average returns and betas predicted by the CAPM breaks down when betas are based on the inefficient index portfolio detailed here. Indeed, the vector of errors in the average returns that arise from basing the calculation of betas on the inefficient index portfolio turns out to be:
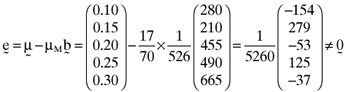 ()
()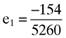 while the error in the average return for the second asset is
while the error in the average return for the second asset is 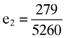 . More important, however, is that the errors associated with the average returns for the third (
. More important, however, is that the errors associated with the average returns for the third (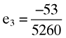 ), fourth (
), fourth (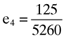 ) and fifth (
) and fifth (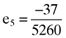 ) firms are exactly five times the accruals quality measures as summarized in the vector (13). Here it will be recalled that this is no coincidence as the index portfolio on which the calculation of betas is based was deliberately designed to return a perfect linear relationship between the average return, beta and the accruals quality measures for all but the first two firms on which the example is based. Thus, one can use the third, fourth and fifth elements of the vector of betas (15) and the vector of accruals quality measures (12) to confirm that there is a perfect linear relationship between the average return, beta and the accruals quality measure for the affected firms, namely9:
) firms are exactly five times the accruals quality measures as summarized in the vector (13). Here it will be recalled that this is no coincidence as the index portfolio on which the calculation of betas is based was deliberately designed to return a perfect linear relationship between the average return, beta and the accruals quality measures for all but the first two firms on which the example is based. Thus, one can use the third, fourth and fifth elements of the vector of betas (15) and the vector of accruals quality measures (12) to confirm that there is a perfect linear relationship between the average return, beta and the accruals quality measure for the affected firms, namely9:
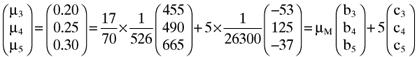
There is of course nothing unique about the asset pricing formula determined here. If, for whatever reason, the empirical researcher needs the accruals quality measure to play an even more important role in the returns generating process then he could increase the coefficient associated with the accruals quality measure in the error vector (13) and then determine the inefficient index portfolio which returns betas which are compatible with the existence of a perfect linear relationship between the average returns, betas and the revised and more prominent accruals quality measures. Alternatively, if the researcher wants to show that other variables, such as firm size and/or the market-to-book ratio for equity are important in the asset pricing process then he can fix the coefficients associated with the vectors summarizing these two variables at the desired levels and thereby determine the error vector which needs to be substituted into equation (11). The researcher can then solve equation (11) and in so doing determine the inefficient index portfolio that leads to a set of betas which, when taken in conjunction with the vectors summarizing firm size and the market-to-book ratio, will have a perfect linear relationship with the average returns vector.
SUMMARY CONCLUSIONS
Davis et al. (1997, p. 390) have observed that ‘the acid test of a multifactor [asset pricing] model is whether it explains differences in average returns’. Given this, our purpose here is to demonstrate how one can build pricing formulae in which factors other than beta are viewed as instrumental determinants of asset returns. The procedure is implemented by first determining the mean-variance efficient frontier corresponding to the empirical average returns, variances and covariances on the equity securities of a large sample of firms. If one then wishes to ‘prove’ that beta is a ‘sufficient statistic’ for the determination of the average returns, all one need do is to compute the vector of betas corresponding to an appropriately chosen orthogonal portfolio on the mean-variance efficient frontier. It then follows that a simple least squares regression will show that there is a perfect linear relationship between the average returns and betas based on the chosen orthogonal portfolio. Other factors, such as firm size, the market-to-book ratio and the quality of the information summarized in a firm's financial statements can add nothing to a regression based on these two variables.
The conventional requirement, however, is to build a pricing formula in which firm size, the market-to-book ratio and/or some other combination of variables (such as the quality of the information summarized in a firm's financial statements) can be viewed as instrumental determinants of asset prices. To do this one must first determine an ‘error vector’ by choosing the coefficients to be associated with the variables that are to be important in the asset pricing process. Thus, for each firm in the sample one could multiply a firm size variable by its chosen coefficient and also, the market-to-book ratio and information quality variables can be multiplied by their chosen coefficients. The error vector is then comprised of the sum of these three variables for each firm in the sample. It is then necessary to determine the inefficient index portfolio which leads to a vector of betas that when multiplied by the average return on the orthogonal portfolio and which, when subtracted from the vector of average returns for the firms comprising the sample, yields the error vector based on the firm size, market-to-book ratios and information quality variables determined earlier. There will then be a perfect linear relationship between the vector of average returns for the firms comprising the sample and the vector of betas based on the inefficient index portfolio, the vector comprised of the firm size variables, the vector made up of the market-to-book ratios and the vector comprised of the information quality measures for each of the firms in the sample.
The fundamental theorem on which our analysis is based is that an inefficient index portfolio will always exist that is compatible with a pre-specified pricing formula in which factors other than beta appear to have a significant impact on asset prices. Here, however, Dittmar (2002, p. 370) notes that while asset pricing formulae determined using procedures similar to this often ‘perform well empirically [they] require ad hoc specifications of . . . the set of priced factors . . . Since the sets of potential factors . . . are large, the researcher has considerable discretion over the model to be investigated.’ This in turn will mean that ‘tests based on [such]ad hoc assumptions [will] lack power and . . . the possibility exists for overfitting the data and factor dredging’. The analysis conducted and the examples given in this paper show just how easy it can be to construct asset pricing formulae that fit the data well, even though ‘they ignore’ and often infringe ‘the theoretical restrictions that arise from a [properly developed] structural model’ of the asset pricing process (Dittmar, 2002, p. 370; Lally, 2004).
Appendix
APPENDIX. ORTHOGONAL PORTFOLIO AND THE MARKET PRICE OF RISK
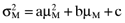
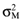 is the variance of the return on the orthogonal portfolio, and, a > 0, b < 0 and c > 0 are parameters. Likewise, from the capital market line we have:
is the variance of the return on the orthogonal portfolio, and, a > 0, b < 0 and c > 0 are parameters. Likewise, from the capital market line we have:
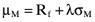
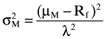
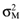 as given by the Markowitz locus and the capital market line:
as given by the Markowitz locus and the capital market line:
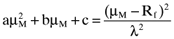
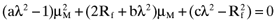
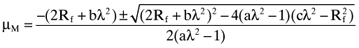
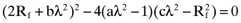
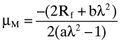
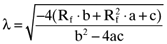
references
Footnotes
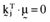 or that all the arbitrage portfolios have an average return of zero.
or that all the arbitrage portfolios have an average return of zero.
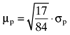 , where as previously, µp is the average return on the portfolio and σp is the standard deviation of the return on the portfolio. The equation for the capital market line is determined using the formula summarized in the Appendix and the notes which accompany Figure 1.
, where as previously, µp is the average return on the portfolio and σp is the standard deviation of the return on the portfolio. The equation for the capital market line is determined using the formula summarized in the Appendix and the notes which accompany Figure 1.
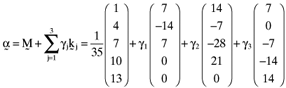
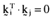 for integral i and j and provided i ≠ j. Stating inefficient index portfolios in terms of orthogonal arbitrage portfolios has distinct computational advantages over the expression for the inefficient index portfolios summarized in the text.
for integral i and j and provided i ≠ j. Stating inefficient index portfolios in terms of orthogonal arbitrage portfolios has distinct computational advantages over the expression for the inefficient index portfolios summarized in the text.

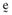 happen ‘by chance’ (that is, on a set of measure zero) to be equal to the exogenous values for these variables.
happen ‘by chance’ (that is, on a set of measure zero) to be equal to the exogenous values for these variables.




