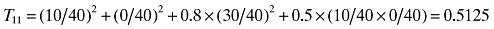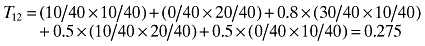The Measurement of Comparability in Accounting Research
The author acknowledges helpful feedback provided by participants at the European Accounting Association Conference 2009 in Finland, the Sino-Australia Conference 2008 in China, and the editor and two anonymous reviewers.
Abstract
Indices of harmony such as the H, C, I and T indices have been developed and used in the accounting literature to quantify the level of comparability of company accounts. This has led to advances in definitions of comparability as well as empirically quantifying the extent of comparability between actual company accounts. These are important because the general concept of comparability is considered desirable, as highlighted by its inclusion as one of four qualitative characteristics in the framework of the International Accounting Standard Board (IASB).
This paper rebuts criticisms of harmony indices in the accounting literature by arguing these criticisms either: (a) apply to old indices but not to newer ones, (b) apply to most empirical accounting research, (c) are based on incorrect or irrelevant assertions, or (d) relate to alternative definitions of harmony. This assists the use and interpretation of harmony indices and advances our understanding of what comparability means. New indices within the T index framework are also proposed by directly comparing company accounts and therefore avoiding the previous requirement to define ‘accounting methods’. A new index R is also proposed to capture international harmony between countries when within-country uniformity is absent.
Indices of harmony are used to quantify the degree to which the accounts of companies are comparable. For example, the accounts of two companies may not be considered comparable if one company uses fair value while the other uses historical cost (Cairns et al., 2011). It is possible to debate the merits of forcing all companies to prepare accounts that are comparable with each other, and this debate will depend on many factors such as the types of companies being compared (their country, industry, etc.) and the policy choice under consideration. Nevertheless, it is hard to argue that no one should be interested in the extent to which the accounts of different companies are comparable. For example, comparability of company accounts is one of four qualitative characteristics in the International Accounting Standard Board (IASB) framework. This does not imply that other features, including the other qualitative characteristics of understandability, relevance and reliability, are not important. In practice, compromises between conflicting desirable features may need to be made. Nevertheless, measuring the extent to which the accounts of companies are comparable is an important topic that deserves the attention of researchers, standard setters and practitioners. Practical definitions of comparability are crucial in this regard and this makes indices of harmony, both theoretical discussions of what constitutes comparability as well as practical measurements of comparability between actual accounts of companies, significant contributions in accounting research.
Nobes (2006) examines motives and opportunities that suggest differences in IFRS practice will persevere and hence users will, for several reasons he proposes, encounter non-comparability between company accounts. Harmony indices should be an integral part of implementing his research agenda precisely because they are specifically designed to summarize the level of comparability.
An index of harmony produces a value between 0 when no two companies have accounts that are comparable with each other (full disharmony) and 1 when the accounts of all companies are comparable with each other (full harmony). Thus an index of harmony can, when used appropriately and based on empirical evidence from the actual accounts of companies, be one source of information concerning which aspects of the accounts are less comparable than others. Furthermore, changes in index values over time can indicate areas where harmony is increasing (harmonization) or decreasing. Cairns et al. (2011), for example, uses harmony indices to provide insights into changes in comparability pre- and post-IFRS, for both companies within and between the U.K. and Australia. For example, they show comparability has significantly decreased with the adoption of IFRS for some policy choices.
Van der Tas (1988) introduced the H, C and I indices of harmony. Since then the literature has considered the relative merits of these indices, their properties and extensions of them. The definition of harmony has also been debated. The literature that considers these issues includes van der Tas (1988, 1992), Tay and Parker (1990), Archer and McLeay (1995), Archer et al. (1995, 1996), Christiansen (1995), Herrmann and Thomas (1995), Morris and Parker (1998), McLeay et al. (1999), Pierce and Weetman (2000), Aisbitt (2001), Taplin (2004), Ali (2005), Ali et al. (2006), Astami et al. (2006) and Jaafar and McLeay (2007).
Throughout this paper we use the term ‘policy choice’ to mean the accounting method used to deal with particular transactions. Examples include the treatment of goodwill and the depreciation of fixed assets. We use the term ‘accounting method’ for the various options to account for this policy choice. For example, FIFO and LIFO are accounting methods for inventory. For convenience, ‘not-disclosed’ is also referred to as an accounting method for those companies that do not disclose their treatment of the policy choice.
There are many definitions of harmony in the accounting literature (see Tay and Parker, 1990). For example, McLeay et al. (1999) consider full harmony to exist when the distribution of accounting methods used is the same for all countries, Aisbitt (2001) and Rahman et al. (2002) also consider whether different companies disclose the same items, and Jaafar and McLeay (2007) consider full harmony to occur when similar companies are comparable. This paper uses harmony to mean comparability of company accounts, as defined above, to maintain consistency with the original concept in van der Tas (1988) and most of the past literature cited in this paper. Most of the arguments in this paper, however, apply to indices summarizing these other definitions of harmony. An important contribution of this paper for standard setters and users is to advance a common understanding of what comparability of company accounts can mean. This is essential if statements that comparability is desirable (IASB framework) are to have credibility.
This paper is motivated by criticisms of harmony indices in the accounting literature, most notably Aisbitt (2001) who is cited by other authors criticizing indices of harmony. These criticisms are: inability to make causal conclusions; problems when accounting methods are not disclosed; definitions of the accounting methods; a lack of benchmarks for index values; a lack of theoretical work; distinctions between policy choices and disclosure; statistical significance and sample sizes; and comparisons of within- and between-country indices. In the defence of Aisbitt, there has been significant progress in index methodology since 2001, including the flexible framework of indices called the T index (Taplin, 2004), making some of her criticisms redundant. Furthermore, criticisms of any method are always welcomed, especially when they lead to flawed methods being abandoned or motivate improved methods. More recently, however, the review paper on international harmonization and compliance research (Ali, 2005), reiterated most of these criticisms of harmony indices. Although Ali cites these recent developments, they were not fully represented, perhaps because they were too recent in 2005, ‘no study has so far been carried out based on the T index’ (pp. 26–7),1 or because, as an anonymous reviewer of the T index pointed out, the versatility of the T index is both an advantage and a disadvantage because its formula is cumbersome and difficult to grasp. This suggests a need to provide further descriptions of how to use the full versatility of the T index to refine definitions of, and measure, comparability.
This paper aims to correct any imbalance in the literature by providing a defence for harmony indices. This will provide a more balanced perspective of the value and limitations of modern harmony indices. In particular, it shows how criticisms made of harmony indices in the accounting literature either
- 1
no longer apply because they have been addressed by methodological improvements since the criticisms were originally made,
- 2
apply to most research methodology in accounting and not to indices alone,
- 3
are based on incorrect or irrelevant assertions, or
- 4
relate to alternative definitions of harmony.
Furthermore, this paper attempts to rectify some misconceptions concerning the properties of harmony indices and to illustrate novel ways to define and measure comparability. In particular, this paper shows how harmony indices can be defined directly from the comparability between the accounts of a pair of companies without reference to definitions of ‘accounting methods’. This conceptual advancement provides access to new indices and enables refined notions of comparability to be explored. A new index R consistent with suggestions in the literature that international harmony occurs when the statistical distribution of accounting methods is the same across countries is also introduced. Previous research has relied on doing so with statistical significance tests, such as the simple chi-squared tests in Parker & Morris (2001), which as a statistical test summarize the strength of evidence against a null hypothesis rather than a level of harmony. In this regard it is hoped that international accounting studies on harmony will be encouraged and improved. Debates on the concept or meaning of comparability between company accounts will be enhanced with formal definitions of comparability, which harmony indices demand.
1: THE FLEXIBLE FRAMEWORK OF HARMONY INDICES REFERRED TO AS THE T INDEX
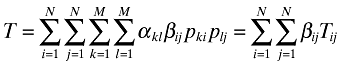 ()
()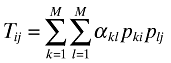 ()
()-
αkl is the coefficient of comparability between accounting methods k and l,
-
βij is the weighting for the comparison between companies in countries i and j,
-
pki is the proportion of companies in country i that use accounting method k,
-
plj is the proportion of companies in country j that use accounting method l,
-
Tij is the level of harmony between country i and country j (for i≠j),
-
Tii is the level of harmony within country i (called the national harmony of country i), and
-
the αkl and βij are between 0 and 1 (inclusive), the βij sum to 1, and there are N countries (labelled 1 to N) and M accounting methods (labelled 1 to M).
Table 1 contains hypothetical data for three accounting methods and three countries that will be used to illustrate the T index. In this data, for example, 10, 0 and 30 companies from country 1 use methods 1, 2 and 3 respectively.
| Method k | Country i | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 1 | 10 | 10 | 0 |
| 2 | 0 | 20 | 0 |
| 3 | 30 | 10 | 10 |
| Total | 40 | 40 | 10 |
- Each entry Xki is the number of companies using the accounting method k in country i, for each of three accounting methods in three countries.
An understanding of the T index is enhanced by first examining equation (2). When i=j, Tii equals the comparability within country i and when i≠j, Tij equals the comparability between countries i and j. In the simplest case where two companies using the same method are completely comparable (αkk= 1 for all k) and two companies using different methods are completely non-comparable (αkl= 0 for all k≠ 1) it follows that Tii equals the Herfindal index (van der Tas, 1988) for country i, 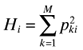 and Tij (i≠j) equals the two country I index
and Tij (i≠j) equals the two country I index 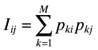 . There are N within-country i indices Tii and N (N− 1) between two country indices Tij (i≠j), although by definition Tij=Tji so there are only N (N− 1)/2 unique indices. Table 2 summarizes these values for the data in Table 1.
. There are N within-country i indices Tii and N (N− 1) between two country indices Tij (i≠j), although by definition Tij=Tji so there are only N (N− 1)/2 unique indices. Table 2 summarizes these values for the data in Table 1.
| Country i | Country j | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 1 | 0.63 | 0.25 | 0.75 |
| 2 | 0.25 | 0.38 | 0.25 |
| 3 | 0.75 | 0.25 | 1.00 |
More sophisticated indices allow one or more of the following possibilities:
- 1
αkl= 1 when k≠l, so two accounting methods are completely comparable to each other,
- 2
αkk= 0, so two companies using the same accounting method are completely non-comparable (e.g., because they both do not disclose their accounting method),
- 3
αkl is strictly between 0 and 1 when k≠l because a company using accounting method k is partially comparable to a company using accounting method l, and/or
- 4
αkk is strictly between 0 and 1 because two companies using the same accounting method are partially comparable (e.g., due to partial disclosure such as straight line depreciation is used but the period of depreciation is not disclosed).
For example, suppose methods 1 and 2 in Table 1 are partially comparable, so a company using method 1 is only half as comparable to a company using method 2 as it is to a company using method 1. Suppose method 3 is completely non-comparable to methods 1 and 2 but due to partial disclosure two companies using method 3 are only 80% comparable. Table 3 contains the corresponding αkl and Table 4 contains the values of the Tij when these αkl are applied to the data in Table 1.
| Method k | Method l | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 1 | 1 | 0.5 | 0 |
| 2 | 0.5 | 1 | 0 |
| 3 | 0 | 0 | 0.8 |
| Country i | Country j | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 1 | 0.51 | 0.28 | 0.60 |
| 2 | 0.28 | 0.49 | 0.20 |
| 3 | 0.60 | 0.20 | 0.80 |
The Tij are easily interpreted as follows. When each αkl equals either 0 or 1, Tij (for i≠j) equals the probability that a randomly selected company from country i has accounts that are comparable to a randomly selected company from country j. When some αkl are between 0 and 1 this interpretation no longer holds but Tij can still be interpreted as the average comparability between pairs of companies when one company from the pair is from country i and the other is from country j. Similar interpretations hold for Tii except both companies are from country i and the same company can be selected in the pair (sampling with replacement).
The T index equals a weighted average of these within and between two country indices, with the βij specifying the weights in this weighted average. For example, when summarizing the level of comparability between companies in different countries (between-country index) we may specify βij= 0 and take an unweighted average of the Tij (i≠j) using βij= 1/[N (N− 1)]. Such an average based on Table 2 is T= 0.42 and based on Table 4 is T= 0.36.
Thus the T index is the average comparability of pairs of companies. If each αkl equals either 0 or 1 it is also the probability that two randomly selected companies have accounts that are comparable.
Taplin (2004) provided the four criteria below to illuminate similarities and differences between previous indices and to assist researchers choose sensible values for the αkl and βij. The first two of these criteria below determine the βij and the last two characterize the αkl. Simple indices are special cases; for example, the H index is obtained by using options 1a2a3a4a and the between-country C index with options 1a2c3a4a, but the T index is far more flexible than this.
Company/Country Weightings
| 1a. | Companies are weighted equally, bi=ni/n, where ni is the number of companies from country i in the sample and n is the total number of companies in the sample, so bi is the proportion of companies in the sample from country i. This means a country receives weight proportional to the number of companies sampled from that country. |
| 1b. | Countries are weighted equally, bi= 1/N, where N is the number of countries, |
| 1c. | Countries are weighted according to the total population number of companies in each country, 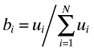 where µi is the total number of companies in country i (e.g., the total number of companies listed on the stock exchange rather than the number of companies in the sample). where µi is the total number of companies in country i (e.g., the total number of companies listed on the stock exchange rather than the number of companies in the sample). |
International Focus
| 2a. | Overall, βij=bibj, |
| 2b. | Within country, βij= 0 if i≠j and when i=j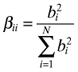 , , |
| 2c. | Between country, 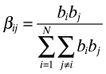 if i≠j and when i=j βij= 0. if i≠j and when i=j βij= 0. |
Multiple Accounting Policies
| 3a. | Multiple accounting policies are not allowed, αkl= 0 if k≠l, |
| 3b. | Multiple accounting policies are allowed if completely comparable, αkl= 1 when methods k and l are completely comparable and αkl= 0 when they are completely incomparable, |
| 3c. | Multiple accounting policies are allowable with fractional comparability, αkl takes a value on the continuum from 0 (completely incomparable) to 1 (completely comparable). |
Non-Disclosure
Here it is assumed non-disclosure is the last accounting method M.
| 4a. | Not applicable, companies who do not disclose a method are removed from the sample, |
| 4b. | Comparable to everything, αkM=αMl=αMM= 1 for all accounting methods k and l, |
| 4c. | Comparable to nothing, αkM=αMl=αMM= 0 for all accounting methods k and l, |
| 4d. | Comparable to the standard (or default) method s,αks=αkM, αsl=αMl for all k and l. |
Taplin (2004, 2006) discussed in detail the justification and implications of choosing specific options for these four criteria. This presented a useful ‘next step’ in sophistication from the simple H, C and I indices, and modifications of these indices, in the past literature. This was beneficial because it showed how previous indices possessed specific properties which may or may not be ideal for a specific problem. For example, the I index weights countries equally but the H and C indices weight countries based on sample sizes. Furthermore, it assisted researchers learning to apply the relatively complicated T index.
Unfortunately, it is possible that this concentration on options from the four criteria has resulted in the full versatility of the T index remaining obscured. In particular, all previous indices do not allow partial comparability and options 3b and 3c do not specify precise values for the αkl. This makes implementation of the T index using its full flexibility less routine, but specifying values for the αkl is where significant progress both in the measurement and definition of comparability lies. Sections 2 to 9 address this issue by responding to the criticisms of harmony indices and expanding on the versatility of the T index through refined choices for the αkl.
2: CASUAL INFERENCE
Aisbitt (2001, pp. 60–1) discusses problems with making causal conclusions (such as whether changes in legislation cause harmonization) from empirical associations (such as values of harmony indices tend to be higher after changes in legislation). Ali (2005, p. 29) reiterated this concern. Causal conclusions are plausible with randomized experiments (more typically found in the experimental sciences than accounting) than observational studies (including most accounting research). In a randomized experiment, causal conclusions are possible because the randomization ensures that any statistically significant differences, if not due to the relationship under examination, are due to chance (through the random assignment of individuals to treatment groups).
An observational study involves no intervention in the form of the randomization described above.2 For example, since some companies are not randomly selected to have legislation changes applied to them (treatment group) while the others do not (placebo group) it is problematic to conclude legislation causes harmonization even if harmonization is significantly higher in the treatment group. High economic growth could cause both changes in legislation and harmonization, without legislation having any direct impact on harmony.
Although most accounting research, both qualitative and quantitative, is observational in nature this does not imply this research has no value. Furthermore, there are techniques that can be employed to strengthen the case for causation rather than only association. For example, Ali (2005, p. 30) acknowledges Murphy (2000) and Peill (2000) who ‘attempted to address some of these shortcomings by using a longitudinal design and using a control sample to provide benchmarks of the harmonization values obtained’. The inclusion of a control group is important because if harmony does not increase in the control group (where no effort of harmonization has been applied) but harmony does improve in the study group (where effort has been applied) then we have stronger evidence this effort improved harmony.
In summary, we agree that causal conclusions should be made with caution; however, this comes from the observational nature of the data (not from the use of indices of harmony), applies to most accounting research, and quantifying the extent to which company accounts are comparable with an index is valuable even if we do not know what caused this level of comparability.
3: NON-DISCLOSURE
When a company is silent on the method used for a policy choice interpretation can be more difficult, especially if it is unknown whether the policy choice is not applicable or whether an accounting method was applied but not disclosed. This is an important distinction when it comes to an assessment of whether the accounts of a company are comparable with the accounts of another company. When the policy choice is not applicable to a company, we may consider its accounts comparable with the accounts of all other companies. When the policy choice is applicable but we do not know which accounting method was applied, comparability is low.
This issue has been discussed by numerous authors, including Archer et al. (1995), Archer and McLeay (1995), Christiansen (1995), Morris and Parker (1998), Pierce and Weetman (2000) and Taplin (2004), usually in the context of improving simple indices to appropriately summarize the level of harmony in the presence of non-disclosure. Generally, these improvements consist of breaking the property of the simpler indices that non-disclosing companies (defined to be using the same accounting method) have accounts that are completely comparable with each other. In particular, Pierce and Weetman (2000) and Taplin (2004) highlight maximal effects on the index value by presenting ranges of values depending on whether non-disclosing companies are considered comparable to other companies.
Researchers should not have the unrealistic expectation that a harmony index will be presented as a single value rather than a range. In practice, all index values should be presented as a range because the level of harmony, as with most statistics, is estimated imperfectly. The width of this range can be more important than a single estimate of the level of harmony. Furthermore, values for harmony indices, as with most statistics, are estimated imperfectly. The situation is similar to ranges of index values arising from sampling variation (see Section 8). Hence modern indices, when used correctly, can quantify the level of harmony in the presence of non-disclosure.
4: DEFINITIONS OF THE ACCOUNTING METHODS
Several related criticisms concern determination or definition of accounting methods and how researchers assign firms to accounting methods. These problems are the extent to which accounting methods are mutually exclusive, the number of possible accounting methods, the minimal value of an index and the classification of a company to one of the accounting methods. These are briefly summarized below before explaining how these criticisms can be avoided using the T index.
Mutually Exclusive Accounting Methods
In the discussion of non-disclosure, Aisbitt (2001, p. 63) raised the issue of whether the accounting methods are mutually exclusive. She gives an example for depreciation, where companies use either A: straight line, B: reducing balance, or C: maximum permitted for tax purposes. It is possible methods A and C, for example, are identical in some circumstances.
Number of Accounting Methods
Aisbitt (2001, pp. 63–5) demonstrates with an artificial example how the value for an index can be higher when there are fewer accounting methods. In her example, this results from taking five possible accounting methods (A, B, C, D and E) and collapsing them into two accounting methods (A and B* where B* includes any of the methods B, C, D or E). Doing so results in a higher value for the index because two companies using different methods from B, C, D or E are considered to be not comparable under the original five methods but completely comparable under the two methods. Aisbitt suggests this makes comparison of index values for policy choices with different numbers of accounting methods difficult, and points out this problem exists in the studies of van der Tas (1988), Emenyonu and Gray (1992), Herrmann and Thomas (1995), Archer et al. (1995), and Emenyonu and Adhikari (1998).
Minimum Values of Indices
Archer et al. (1995, p. 70) calculate minimum values the C index can take when there are J accounting methods, and state that this is approximately equal to 1/J when the number of sampled companies is large.3 This occurs when each accounting method is used with equal frequency. They also discuss the minimum value for within-country and between-country C indices. Aisbitt (2001, p55) also provides minimal values for each of her C indices and advocates the necessity of this in order for harmony indices to be correctly compared either between or within studies since in practice the lower bound is non-zero but depends on the number of accounting methods.
Classification of Companies to an Accounting Method
Aisbitt (2001, p. 65) points out that it ‘is not always easy to classify the practices of particular companies’. For example, one company may amortize goodwill for one acquisition over five years and another acquisition over twenty years. She allocated the company to the accounting method using the longest period and criticized harmony indices because she believed this resulted in a harmony value too small. For depreciation, she classified companies according to the method used by the domestic company even though different methods were sometimes used by foreign subsidiaries.
Modern Approaches to Defining Accounting Methods
The above criticisms are overcome by using a more sophisticated index or a finer distinction between many accounting methods. In many situations this could be considered an unnecessary complication if the objective is to obtain an approximate estimate of the level of harmony. In particular, statistical inference techniques (see Section 8) are important because often the gain in precision is negligible compared to the large statistical uncertainty. For example, the above combination of methods B, C, D and E into a single method B* has the advantage of simplicity (we now only need to consider two methods instead of five) but is less precise if methods B, C, D and E are in fact not equivalent when it comes to comparability of accounts. If nearly all companies using method B* actually use method B then this could be a satisfactory approximation. If not, then the simpler approach using methods A and B* is inappropriate, but this is not a criticism of harmony indices but a criticism of using indices inappropriately.
We suggest there are two ways of approaching the definition of the accounting methods depending on whether one is fixated on the concept of there being a small number of fixed accounting methods or whether one applies a more abstract notion of comparability between accounts. We now discuss these two conceptual approaches.
Most people find it useful to classify all of the possible accounting methods for a particular policy choice into a small number of methods. This has the benefit of simplicity and exposition because people can process the information involved with a few accounting methods in much the same way they can obtain at least approximate information from knowing whether a company is deemed to operate in the manufacturing sector. The disadvantage is that this generally results in a loss of information. Firstly, some companies may be difficult to classify into one of the groups. Secondly, while at a superficial level we may treat companies within the same group as the same this is only an approximation.
For an index of harmony it is therefore important to consider the consequences of classifying two companies as using the same accounting method. One immediate consequence for most indices is that the accounts of these two companies will be deemed to be equally comparable to any other company for this policy choice. For example, two companies classified as using the amortization method for goodwill (even though they use different periods) will be considered to have the same comparability with a company using the write-off method. More significantly, most indices4 will deem the accounts of these two companies to be completely comparable to each other if they are classified to be using the same accounting method. This may result in an index value that is too high.
These broad issues of comparability were solved by options 3b and 3c of the T index, developed in Taplin (2004). For example, the higher index value introduced by assuming the accounts of all companies using amortization for goodwill are completely comparable can be addressed by assuming companies using the amortization method are 90% comparable with each other. Although the decision to use a comparability coefficient such as 0.9 may be somewhat arbitrary, any subjective value is likely to be superior to the extreme value of 100% comparability. Furthermore, it should be possible to justify an approximate value based on knowledge of the practices employed by the companies (e.g., by examination of the sampled accounts).
For example, Astami et al. (2006) in their analysis of fixed assets valuations identified not only cost and revaluation but three other accounting methods where a proportion of assets between zero and one were revalued (Mix 1: up to one-third, Mix 2: between one-third and two-thirds, and Mix3: over two-thirds revalued). Table 5 contains the partial comparability between different accounting methods used by Astami et al. (2006). For example, since companies in Mix 2 use approximately half cost and half revaluation, the comparability of two companies using this mix is approximated as 1/2. If one company uses cost and another uses Mix 1, then the comparability is approximated to be 5/6 (since Mix 1 is between zero and one-third, or about one-sixth, revaluation).
| Cost | Mix 1 | Mix 2 | Mix 3 | Mix 4 | Revaluation | |
|---|---|---|---|---|---|---|
| Cost | 1 | 5/6 | 1/2 | 1/6 | 1/2 | 0 |
| Mix 1 | 5/6 | 26/36 | 1/2 | 10/36 | 1/2 | 1/6 |
| Mix 2 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 |
| Mix 3 | 1/6 | 10/36 | 1/2 | 26/36 | 1/2 | 5/6 |
| Mix 4 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 |
| Revaluation | 0 | 1/6 | 1/2 | 5/6 | 1/2 | 1 |
For anyone who rejects these broad groups as insufficient to capture the variation in accounts we suggest more accounting methods could be entertained. This could include more groups depending on the exact fraction of assets revalued, or depending on which assets are revalued. In this case the partial comparability options of the T index will be essential since with a large number of accounting methods it is likely there will be a continuum of comparability between two methods ranging from zero to one (as in the fixed assets valuation example above). Alternatively, our second conceptual approach that follows could be considered.
Our second conceptual approach abandons the requirement for accounting methods and considers the comparability between pairs of company accounts directly. To do so, all we require is a rule specifying the level of comparability between the accounts of two companies. Although accountants have traditionally found it useful to think of there being a finite number of ‘accounting methods’, this is unnecessary to quantify the level of comparability using the T index.
For the Astami et al. (2006) example for fixed assets valuations, the comparability between two companies i and j could be defined as 1 −|ri−rj|, where ri and rj are the fractions of the assets revalued for companies i and j respectively. Thus, unlike simple indices comparing discrete categories called accounting methods, this measure of comparability is defined on a continuous characteristic of companies with an infinite number of possible values.
In practice, since there will be a finite number of companies the second conceptual approach can be implemented by defining each company as using its own unique accounting method (so the number of accounting methods equals the number of sampled companies). This is not an intuitive use of the term ‘accounting method’ and so the term should not be viewed in the traditional way, but a computational trick to see how the second conceptual approach is within the T index framework of indices. Prior to the T index this would be inconceivable because different accounting methods were considered completely non-comparable with each other, resulting in inappropriately low index values.
We illustrate this computational trick with a simple example containing four companies, denoted A, B, C and D, that use methods A, B, C and D respectively. Methods A and B are actually the same accounting method, so it is sensible (but not necessary) to classify both companies A and B to be using the combined method denoted AB. Companies C and D use methods that are slightly different to each other (80% comparable, so could crudely be considered to be using the same method, denoted CD). Companies C and D use methods that are very different (i.e., non-comparable) to the method used by companies A and B.
In Panel A of Table 6 we have the alpha matrix when each company is allocated its own accounting method. Since companies A and B use the same method, the first two rows are identical (as are the first two columns). Since companies C and D are similar we have assigned a partial comparability of α34= 0.8. This illustrates the second conceptual approach described above. We now examine Panels B and C of Table 6, which apply the first conceptual approach, and explain how this can be viewed as an approximation to the second conceptual approach.
|
Panel A: Four methods |
||||
|---|---|---|---|---|
| A | B | C | D | |
| A | 1 | 1 | 0 | 0 |
| B | 1 | 1 | 0 | 0 |
| C | 0 | 0 | 1 | 0.8 |
| D | 0 | 0 | 0.8 | 1 |
|
Panel B: Three methods |
|||
|---|---|---|---|
| AB | C | D | |
| AB | 1 | 0 | 0 |
| C | 0 | 1 | 0.8 |
| D | 0 | 0.8 | 1 |
|
Panel C: Two methods |
||
|---|---|---|
| AB | CD | |
| AB | 1 | 0 |
| CD | 0 | 0.9 |
- Companies A to D use methods A to D respectively. Methods A and B are the same method, also referred to as method AB. Methods C and D are slightly different to each other but as an approximation could be classified into the combined group CD.
In Table 6, Panel B, methods A and B have been combined into the method AB. The combination of methods A and B results in no loss of information: Panels A and B imply the same comparability between any pair of companies and hence the same level of harmony. In Panel C of Table 6 methods C and D have similarly been combined into the method CD. This is less natural because these accounting methods are distinct even if they do result in similar accounts. We have assigned a partial comparability of 0.9 between two companies using method CD (an average of the four comparabilities in the lower right of Panels A and B) as an approximation.
Simple indices that do not allow for partial comparability such as the H, C and I indices use the value of 1 in place of 0.9 for the bottom right entry of Table 6, Panel C, and will therefore result in a value too high. Alternatively, if, as in Panel B, methods C and D are not combined, then the partial comparability between methods C and D would be considered 0 instead of 0.8. This would result in a value too low. In practice, the inaccuracy resulting from these approximations may be small. If not, or if any potential inaccuracy is to be avoided, the second conceptual approach (Table 6, Panel A) can be used. Researchers should document and justify any approximation used.
Astami et al. (2006) implicitly apply an approximation by using the first conceptual approach and defining mixture accounting methods for fixed assets valuations. For example, all companies using a mixture of revalue and cost but revalued at most one-third of their fixed assets were classified as using the accounting method Mix 1. The comparability between a company classified into this accounting method and a company revaluing all its fixed assets could be anywhere from 2/3 to 1, but this is approximated with the midpoint, 5/6 (see Table 5). In general, Astami et al. (2006) make an approximation that the fraction of assets revalued are evenly spread within each range defined by the accounting method.
To understand how the second conceptual approach can be implemented in practice we consider depreciation of a fixed asset. Suppose our first selected company depreciates using the straight line method over five years. This company is abbreviated with SL5 within the thick ellipse of panel (a) of Notes: Values on lines indicate the level of comparability between companies at either end of the line and Panels (a) to (d) progressively add one additional company. Figure 1. The line joining this company to itself has an assigned value of 1 indicating the accounts of two companies who both use SL5 are considered completely comparable to each other. In panel (b) of Figure 1, we introduce our second company that uses the reducing balance method over five years (RB5). Values on lines in this graph indicate two companies both using this reducing balance method are completely comparable but a company using SL5 is completely non-comparable with a company using RB5, as is typically assumed in simple indices. In panel (c) of Figure 1 we introduce a third company using straight line depreciation over three years (SL3). While SL3 is completely non-comparable to RB5, a company using SL5 and a company using SL3 are considered 70% comparable.5 If our next company used one of the previous methods (SL5, RB5 or SL3) it would be equivalent and more efficient to note this accounting method has two companies rather than create another thick ellipse representing another company. Finally, our last company that uses straight line but does not disclose the period of depreciation (SL) is added in panel (d) of Figure 1. Due to the partial disclosure this company is only considered 50% comparable with another company using the same method (SL) or straight line depreciation with a disclosed period (SL3 or SL5). Thus we assume companies disclosing the period of depreciation (SL5 and SL3) are more comparable with each other (70%) than with a company that does not disclose the period (50%).6Table 7 contains the alpha matrix corresponding to the graphical display in panel (d) of Figure 1.
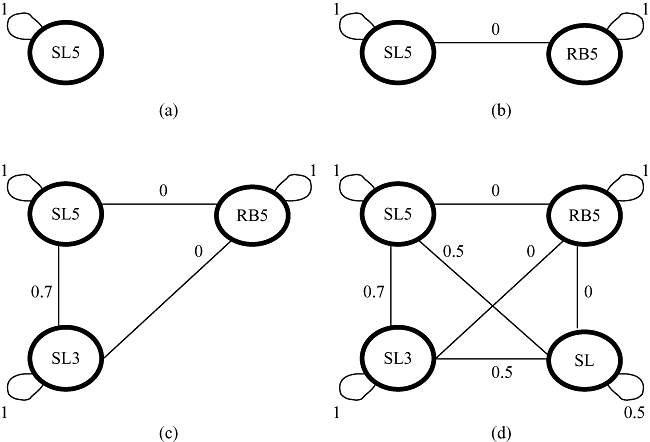
GRAPHICAL DISPLAY CONSTRUCTING COMPARABILITY BETWEEN COMPANIES USING STRAIGHT LINE DEPRECIATION OVER FIVE YEARS (SL5), THREE YEARS (SL3), UNDISCLOSED PERIOD (SL) AND FOR A COMPANY USING REDUCING BALANCE OVER FIVE YEARS (RB5)
| SL5 | RB5 | SL3 | SL | |
|---|---|---|---|---|
| SL5 | 1 | 0 | 0.7 | 0.5 |
| RB5 | 0 | 1 | 0 | 0 |
| SL3 | 0.7 | 0 | 1 | 0.5 |
| SL | 0.5 | 0 | 0.5 | 0.5 |
The alpha matrix requires a number of entries equal to the number of methods squared under the first conceptual approach or the square of the number of companies under the second conceptual approach. Since in practice many companies use accounting methods that are the same or differ in a way that is deemed to be negligible, the first conceptual approach is recommended for implementation in practice but the second conceptual approach recommended conceptually.
The above discussion illustrates how it is the approximation employed (if any) that needs to be documented rather than the number of possible accounting methods. In particular, minimum values of an index based on the number of accounting methods are irrelevant. This is because the number of possible accounting methods is theoretically infinite in the population of all companies and how small it is in the sample depends on the properties of the sample (particularly the number of methods observed in the sample) and the conceptual approach implemented. If we are told there are only two different accounting methods rather than five then we a priori expect a higher level of harmony. The number of observed accounting methods is important information itself that should not be ignored, factored out, or held constant in order for a legitimate comparison. Instead of focusing on the definition of accounting methods we suggest attention should focus on an accurate assessment of the level of comparability between pairs of companies, as demanded explicitly by the second conceptual approach.
5: LACK OF BENCHMARKS
Ali (2005, p. 29) suggests indices of harmony are difficult to interpret because there is a lack of benchmarks describing whether a particular value represents a high or low level of harmony. Ali et al. (2006) suggested greater than 0.8 represents high, between 0.8 and 0.6 moderate, and less than 0.6 low levels of harmony. Earlier, Parker and Morris (2001) suggested similar benchmarks for the H index of greater than 0.9 representing ‘considerable’, between 0.75 and 0.9 ‘some’, and less than 0.75 as ‘little’ harmony.
This criticism holds for almost any index or summary statistic currently used. For example, there are no benchmarks for correlation coefficients other than similar judgemental approaches such as ‘correlations greater than 0.8 are high’. Coefficients of determination (or R-squared values) are commonly quoted in regression but they similarly have no absolute benchmarks. In different disciplines and in different contexts useful benchmarks have evolved through repeated application to data even though there are no theoretical justifications for benchmarks. Even the traditional benchmark of 0.05 for a statistical p-value is by convention, and not universally accepted as the appropriate benchmark in all disciplines. Thus this criticism is not specific to indices of harmony but could be applied to almost all indices or statistics that are successfully used to convey useful information. Useful benchmarks for harmony indices will evolve as more index values are reported in the literature and useful benchmarks are proposed and debated. In this regard Ali et al. (2006) is to be applauded.
Benchmarks and interpretation of index values are enhanced when indices have simple scales on which they can be easily interpreted. For example, the T index equals the probability that two randomly selected companies (or an average over pairs of companies) have accounts that are comparable. This is a useful definition because in practice it is common for the accounts of two companies to be compared, but in any case it is easier to conceptualize the comparability of two companies. The I index for N countries, on the other hand, is the Nth root of the probability that N randomly selected companies, one from each country, have accounts that are all comparable with each other. Conceptually, this is more difficult firstly because few people have a sufficient understanding of Nth roots and secondly because the idea of N companies having accounts that are all simultaneously comparable with each other is more difficult. This difficulty of interpreting the scale on which the I index is based does not make this index wrong, only that practitioners must learn to appreciate its relatively complex and less intuitive scale.
Once the scale of the index is understood there should be no barriers to comparing index values based on different samples. For example, comparing index values based on different countries is legitimate and indeed an important research question, although it is preferable that the same index is used in all countries, or at least an index that uses the same scale (such as the probability that two randomly selected companies have accounts that are comparable).
6: LACK OF THEORETICAL WORK
Gernon and Wallace (1995, pp. 79–80) and Ali (2005, p. 29) argue that harmonization studies are not motivated by theory and this limits their value. Rahman et al. (2002) also discuss this issue, and while they acknowledge the work done in this area by Doupnik and Salter (1995) and Nobes (1998) they argue there are many factors, including firm specific as well as regulatory and cultural, that impact on the level of harmony. That is, the situation is complex and any simple theory is likely to be crude and not reflect reality well. This could be interpreted as a characteristic of an area that requires future research rather than a conclusion to reject studies using harmony indices.
We argue that quantifying the extent to which company accounts are comparable is valuable even without a formal theoretical framework. This is because it is important to know how comparable the accounts of different companies are. We claim this is the case even if companies are given complete freedom to choose any accounting method for a particular policy choice and regulators are not attempting harmonization. If policy makers desire harmonization then it is valuable to quantify the extent to which harmonization has occurred (even if any harmonization cannot be attributed to the specific actions of the policy makers).
Gernon and Wallace (1995, p. 79) make the valid point that investors, policy makers and other users of annual reports may not compare annual reports based on individual items but compare values at a more aggregate level such as before tax earnings and earnings per share. This is an important point; however, these aggregate values depend on more micro level decisions such as the accounting methods used. If everyone was only interested in aggregate figures then annual reports would only include these aggregate figures. Canibano and Mora (2000, p. 356) provided an alternative perspective: ‘Measuring separately gives more refined results because one is able to measure the degree of material measurement harmony for each sort of transaction or event accounted for in the financial report, whereas measuring harmony of the aggregate of all sorts of transactions or events gives only aggregate results, making it difficult to draw policy conclusions on the basis of these measurements’.
7: POLICY CHOICE OR DISCLOSURE
Van der Tas (1992, pp. 212–13) stressed the important distinction between measurement harmony and disclosure harmony but authors such as Aisbitt (2001) are applying the same harmony indices to both. We briefly summarize this distinction here because failure to recognize the distinction can lead to either inappropriate applications of harmony indices or different definitions of harmony. Measurement harmony refers to the extent to which different companies use the same accounting method. For example, perfect measurement harmony would exist if every company used historical cost to value assets. Disclosure harmony refers to the extent to which all companies disclose the same information (such as segmental turnover). Perfect disclosure harmony exists when all companies disclose the same items.
As van der Tas (1992, p. 213) pointed out, if a standard harmony index was used for disclosure harmony then ‘harmony would increase when, instead of 60 per cent, 80 per cent of the companies do not disclose information concerning a particular item’. Furthermore, full harmony would be achieved if all company accounts contain no information. Great care should therefore be taken when using and interpreting harmony indices in this context.
8: STATISTICAL SIGNIFICANCE AND SAMPLE SIZES
The lack of statistical methods associated with harmony indices has severely hampered rigorous research using these indices. For example, most studies on harmony fail to explicitly recognize the difference between the level of harmony in the whole population (which is of interest) and the level of harmony in the sample (which is calculated). This was identified early, for example by Tay and Parker (1990, p. 83). Archer et al. (1996) and Canibano and Mora (2000) examined statistical significance for harmony but only Taplin (2003, 2010) provided standard errors for a harmony index value. Standard errors are important because they provide an assessment of the accuracy with which sample data have estimated the level of harmony in the population. They are also important in the calculation of confidence intervals and p-values, and for determining required sample sizes for a study. Taplin (2010) shows how all these can be performed for any index within the T index framework.
Prior to this work, researchers were forced to make ad hoc and subjective judgments concerning not only what could be concluded from index values but also how many companies to include in a study. For example, the justification Aisbitt (2001) provided for her sample size of twelve companies from each of four countries was: ‘The sample size chosen was intended to be large enough to have some expectation of being representative but small enough to allow intimate knowledge of the annual reports.’ (p. 53). This is commendable because other studies generally provide worse, or no, justification.
Aisbitt (2001, p. 53) claimed ‘the number of observations affects the indices’ and Ali (2005, pp. 29–30) criticizes harmony indices on the basis that ‘The measurement indexes used are very sensitive to the sample size’. We refute this claim except to reiterate that index values calculated from very small samples will, in the usual statistical sense, be very imprecise estimates of the true level of harmony in the population.
In particular, the attempt by Aisbitt (2001, p. 53) to ensure the sample sizes for each country were equal by increasing the available data ‘with “dummy” observations exhibiting characteristics mirroring those of the actual observations’ was unnecessary even for the C indices used in her study. This may have been an attempt to ensure all countries receive equal weight in the calculation of the index (since C indices weight countries according to sample size); however, this can be achieved more satisfactorily using option 1b of the T index.
9: WITHIN- VERSUS BETWEEN-COUNTRY INDICES
With the introduction of the within-country and between-country C indices of Archer et al. (1995) research can focus on different aspects of international harmony. The unified framework of Taplin (2004) included this aspect with the international focus option of the T index (2a: overall, 2b: within country, 2c: between country) but generalized to other possible foci such as comparing one country with other countries, Taplin (2004, p. 69).
Rather than viewing these foci as measuring different aspects of international harmony useful for different research objectives, some authors have made comparisons between these different indices without consideration of the properties of the indices. For example, Aisbitt (2001, p. 56): ‘Perhaps unsurprisingly, given the different regulations in each country, the level of harmony within countries was higher than the level of harmony between countries and hence the total level of harmony’. This result that the level of harmony within countries is higher than the level of harmony between countries is indeed unsurprising. For the indices calculated in Aisbitt (2001) it is a mathematical fact that has nothing to do with different regulations in each country, highlighting the importance of research into the properties of indices so their values can be interpreted correctly. The following result, expressed in terms of the T index and proved in the Appendix, gives necessary but not sufficient conditions to ensure the between-country index cannot exceed the corresponding within-country index.
International Comparability Theorem
The within-country T index (option 2b) is always greater than or equal to the between-country T index (option 2c) if the same αkl are used for both indices and the following two conditions hold:
- 1
αkl= 0 when k≠l, and
- 2
countries are weighted equally.
The first of these conditions is satisfied by simple indices. For example, the H, I and C indices typically require accounting methods to be completely comparable with themselves and completely non-comparable with each other: αkk= 1 and αkl= 0 for all k≠l.
The second of these conditions typically holds because international accounting research often concentrates on comparisons between countries and each country is considered equally important. It is satisfied using option 1b of the T index. Option 1a where companies receive equal weight will achieve the same result if the sample sizes for each country are equal. This is often considered a desirable characteristic of the research design since the decision to employ a smaller sample size from one country begs the question of whether inclusion of that country in the research design was at all warranted.
10: ALTERNATIVE DEFINITIONS OF COMPARABILITY
Despite general agreement that the qualitative feature of comparability is desirable there is less agreement over precise definitions of comparability and perhaps different definitions are appropriate for different situations. Indices play an important role in these discussions because their mathematical definitions demand precision while descriptions in words can leave ambiguity. Thus indices can advance common understandings of different notions of comparability.
Archer et al. (1996) and McLeay et al. (1999) suggest international harmony exists when the statistical distribution of accounting methods used are the same across countries. That is, the proportion of companies in country i using method k, pki, can depend on k but not on i. They argue companies should be free to choose the most appropriate accounting method for their circumstances and since these circumstances vary from company to company (e.g., depending on industry) it is unreasonable to expect all companies to adopt the same accounting method. Thus Archer et al. (1996) suggest the between-country C index does not capture international harmony because it is lowered by variation in accounting methods within countries as well as between countries. Their statistical modelling accounts for this; however, they provide no index corresponding to their notion of comparability. Authors such as Aisbitt (2001) informally try to capture this notion of comparability by comparing within-country and between-country indices, but we now provide a formal way of doing so with a new index R.
We define the international comparability index R as the ratio of the indices (between-country index divided by within-country index). When R equals 0, the between-country index must equal 0 and there is perfect disharmony between countries. When R equals 1 the between-country and within-country indices are equal, so the between-country level of harmony is fully explained by the level of harmony within countries. This occurs when the distribution of accounting methods is the same for each country, as advocated by Archer et al. (1996) and McLeay et al. (1999). From our example in Table 2, the within-country T index is T= (0.63 + 0.38 + 1.00)/3 = 0.67 while the between-country index is T= 0.42 (the average of all off-diagonal Tij values). Hence R= 0.42/0.67 = 0.63, so given the extent to which companies within the same country are comparable, the comparability of company accounts from different countries is only 63% of its maximum possible value.
Jaafar and McLeay (2007, p. 157) interpret harmony by ‘presuming that accounting will be fully harmonized when all firms operating in similar circumstances adopt the same accounting treatment for similar transactions, regardless of their domicile’. We now elaborate on several approaches to make these words rigorous within the T index framework.
First, the comparability between companies k and l can be defined as αkl= 1 when they operate in different circumstances regardless of the accounting treatment used. This is more easily approached by comparing pairs of companies rather than accounting methods. For example, two companies using straight line depreciation at different rates because their assets depreciate at different rates may be considered completely comparable. Alternatively, two companies using straight line depreciation at the same rate may be considered non-comparable if this rate is inappropriate for the assets of one of the companies. This requires a shift away from traditional thinking of accounting methods such as ‘straight line depreciation’, possibly abandoning the notion of accounting methods entirely because we would require several accounting methods using straight line depreciation corresponding to different circumstances. Furthermore, companies using an appropriate method for their circumstances could be considered completely comparable to each other and companies using an inappropriate method for their circumstances non-comparable (αkl= 0) to every other company.
Second, comparisons between companies operating in different circumstances could be ignored in the same way that the within-country C index (or T index, option 2b) ignores comparisons between companies in different countries. For example, a within industry T index can be computed as the proportion of pairs of companies, selected randomly from within the same industry, that are comparable. Such an index can be computed either within or between countries (so the pair of companies compared are not only in the same industry but must also be in the same, or different, countries). Hence a corresponding (international within-industry comparability) R index can be calculated from their ratio. These approaches differ because in the first approach pairs of companies from different industries are considered comparable irrespective of their policy choice while in the second approach they are not considered.
Third, while industry may be a convenient indicator of whether companies operate in similar circumstances this is largely due to the simple categorical groups for industry typically used. The T index allows different weights to be assigned to different pairs of companies in a continuous way, not only weights of zero and one. For example, when calculating the proportion of companies that are comparable pairs of companies could be weighted by their similarity in size. Previously, different weights for pairs of companies were only proposed in the context of weighting companies based on the number of companies per country (option 1 of the T index). Essentially, we only require a numerical formula to define the extent to which companies operate in similar circumstances. Such a formula is necessary to make the definition of comparability in Jaafar and McLeay (2007) precise.
Furthermore, it is important to realize that the T index can be applied to more than a single policy choice. As illustrated with the second conceptual approach in Section 4, all that is required is a value between 0 and 1 to quantify the level of comparability between any pair of companies. For example, when examining several policy choices we may define this comparability between two companies as an average of the comparability over the several policy choices, possibly weighted by the importance of each transaction for these companies. Alternatively, using the minimum of the comparability values for these several policies implies that a lack of comparability for any single policy choice is sufficient to render the two company accounts incomparable. Finally, the T index can be applied to continuous variables, as illustrated by the example from Astami et al. (2006) where the proportions of assets revalued by two companies was converted into a comparability score on a 0 to 1 scale. Research into holistic comparability of company accounts appears to be under-researched.
11: CONCLUSION
This paper has discussed the criticisms of harmony indices in the literature. It has been shown that many of these criticisms have been resolved by recent advancements in harmony indices and many arise from a misunderstanding of the properties of indices. The criticisms of harmony indices that are largely justified apply equally to the vast majority of accounting research. It is hoped the points made in this paper will counteract the criticisms of harmony indices in the literature and provide a more balanced perspective on the valuable part harmony indices can play in accounting research. By formally defining the meaning of comparability through an index, such as the options under the T index or the newly introduced R index, debate on the merits and definition of comparability can be advanced.
Formal definitions of comparability are essential for standard setters and users because measurement of comparability is an essential precursor to understanding or improvement. If no common understanding of how comparability is measured exists then the term comparability becomes meaningless and should not be used, including in the IASB framework. For example, comparability does not have to mean uniformity: company accounts can be considered completely comparable even though different accounting methods are followed. Mathematical definitions of harmony indices remove ambiguity in a way that is difficult for words and hence can enhance discussion on the meaning of comparability (or harmony). If standard setters are to develop policies to improve comparability for the benefit of users, then methods to define and measure comparability are essential. Comparability research is still in its infancy and requires further empirical studies examining company accounts, surveys investigating requirements by users, and theoretical discussions on concepts of comparability.
It should be recognized that, like any other method, harmony indices can be used inappropriately. Criticism directed at inappropriate use of any method is welcome but this does not mean the method should be criticized. There have been substantial improvements in harmony indices in recent years to the point where current techniques are sophisticated and require some expertise to be applied appropriately. This paper aims to improve future harmony research by explaining how modern harmony indices should be used and interpreted correctly.
With recent advances in index methodology, future research using harmony indices should show substantial improvement over previous studies. For example, Murphy (2005) when examining the effect of International Accounting Standards (IASs) during 1994 to 1999 used a control sample in recognition of the causality issue. This led her to the informative, if still qualified, conclusion in her abstract: ‘Based on the data from these samples it appears that the adoption of IASs has influenced companies' choice of accounting methods used.’ Future research using harmony indices will be well placed to provide important accounting insights if it utilizes all recent developments. Furthermore, future advances in the measurement of harmony, including what it means for the accounts of two companies to be comparable, are important contributions to accounting research. This research should not be limited to specific policy choices such as depreciation of fixed assets considered in the past literature but applied to multiple policy choices, disclosure patterns and presentation since presenting accounts in different formats lowers comparability.
Appendix
In this appendix we show the within-country T index (option 2b) is always greater than or equal to the between-country T index (option 2c) if the same αkl are used for both indices and the following two conditions hold:
- 1
αkl= 0 for all k≠l, and
- 2
countries are weighted equally.
Let pki denote the proportion of companies in country i using accounting method k
(k= 1, . . . , M, i= 1, . . . , N).
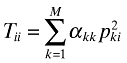
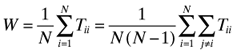 where the summation for j is over all countries 1 to N except for country i. Since
where the summation for j is over all countries 1 to N except for country i. Since 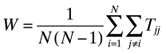 as well it follows that
as well it follows that 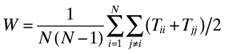
The between-country index for countries i and j is 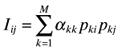 and the between-country index is
and the between-country index is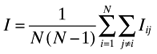 .
.
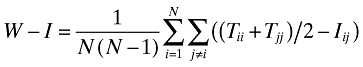
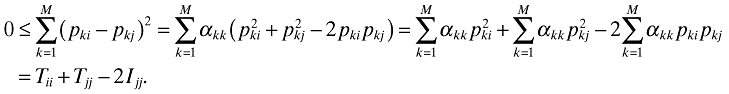
This completes the proof that the within-country index is greater than the between-country index.