Volume 46, Issue 1 pp. 28-59

Full Access

The Value Relevance of Management Forecasts and Their Impact on Analysts' Forecasts: Empirical Evidence From Japan

KOJI OTA,

KOJI OTA

Faculty of Commerce, Kansai University

Search for more papers by this author

KOJI OTA,

KOJI OTA

Faculty of Commerce, Kansai University

Search for more papers by this author

First published: 24 February 2010

https://doi.org/10.1111/j.1467-6281.2009.00299.x

Citations: 45

Koji Ota ([email protected]) is an Associate Professor in the Faculty of Commerce, Kansai University.

The author gratefully acknowledges the helpful comments and suggestions of Richard Heaney, Greg Shailer, Ruttachai Seelajaroen, Ken Pholsena, Atsushi Sasakura, Akinobu Syutou, Hia Hui Ching, Graeme Dean and two anonymous referees. Special thanks are due to Kazuyuki Suda and Yoshiko Oshiro for the provision of forecast data.

Share a link

Email
Wechat
Bluesky

Abstract

A major financial disclosure feature in Japan is that stock exchanges require firms to provide next year's earnings forecasts. This study investigates the value relevance of Japanese management earnings forecasts and their impact on analysts' earnings forecasts. First, the value relevance of management forecasts is investigated using a valuation framework provided by Ohlson (2001), in which firm value is expressed as a function of book value, current earnings and next year's expected earnings. The analysis yields that of the three accounting variables examined, management forecasts have the highest correlation and incremental explanatory power with stock price.

Next, the impact of management forecasts on analysts' forecasts is examined. The results show that more than 90% of changes in analysts' forecasts are explained by management forecasts alone. Further analysis reveals that the heavy dependence of financial analysts on management forecasts in formulating their own forecasts may partially be attributed to the relatively high accuracy of management forecasts. At the same time, financial analysts also somewhat modify management forecasts when certain financial factors indicate that the credibility of management forecasts is in doubt.

Overall, this study presents empirical evidence that Japanese management forecasts provide useful information for the market and have a significant influence on analysts' forecasts.

A major disclosure difference between Japan and other countries is that management of almost all listed firms in Japan provides forecasts of next year's key accounting figures. This practice was initiated in 1974 at the request of Japan's stock exchanges. Although the forecasts are technically voluntary, almost all Japanese firms comply with the request and provide them.¹ As a consequence, management forecasts of the upcoming year's sales, ordinary income, net income, earnings per share and dividends per share are announced simultaneously with the most recently completed year's actual accounting data in annual press releases. This unique practice in Japan makes it possible to conduct a large-scale study on management forecasts over a long period of time.

The motivation is to increase our understanding of the usefulness of management forecast information. The provision of management forecasts is an extra clerical burden on listed firms, because firms are asked to present not only forecast figures but also qualitative explanations and supporting data upon which those figures are based. Therefore, it is of interest to assess whether management forecasts provide useful information for market participants that could offset the extra cost. Since Japan is the only country that effectively mandates the provision of management forecasts, the findings in this study may also have potential policy implications for other countries that are trying to encourage the disclosure of prospective financial information.

While management forecasts are much less common in the U.S., existing evidence shows that they have information content (e.g., Patell, 1976; Waymire, 1984; Ajinkya and Gift, 1984). Pownall and Waymire (1989) find that announcements of management earnings forecasts are associated with larger stock price reactions than annual earnings announcements. Similar results are also reported using Japanese management forecasts. Darrough and Harris (1991) and Conroy et al. (1998) examine the information content of two different types of earnings that are publicized at the same time, namely actual annual earnings and management forecasts of next year's earnings, and find that stock price reactions around the announcement date are more pronounced to forecast earnings than to actual earnings. Thus, the information content of management forecasts has been explored in Japan and other countries.

Information content studies typically use an event study approach and investigate the market reaction to the release of new information. In order to implement an event study design, the researcher must identify the event date and specify the unexpected portion of the accounting variables. This can make an event study impracticable because it is difficult to identify the announcement date and specify expectations for many accounting amounts (Barth 2000).

In contrast to information content studies, a large number of studies in the last decade have adopted a new approach to determine the usefulness of accounting information in the stock market. These studies typically assess the association between market values and accounting numbers of interest and are often referred to as value relevance studies. The value relevance research characterizes market value at a point in time as a function of a set of accounting variables such as assets, liabilities, revenues, expenses and net income (Beaver, 2002). Thus, value relevance studies can address the research question of whether a particular accounting amount is reflected in price incrementally to other conditioning variables.

The first objective of this article is to investigate the value relevance of management forecasts of earnings (hereafter MFE). The most commonly used regression models in value relevance studies are price and return based models whose theoretical foundations are derived from the Ohlson (1995) linear information dynamics (e.g., Collins et al., 1997; Francis and Schipper, 1999; Lev and Zarowin, 1999; Ely and Waymire, 1999). However, other information, ν, in Ohlson's information dynamics is often omitted from the regression models because of the difficulty in its observation. Ohlson (2001) shows analytically that ν can be given concrete empirical content if next year's expected earnings are observable. In this case, firm value can be expressed as a linear function of book value of equity, current earnings and next year's expected earnings. This study utilizes MFE as a proxy for next year's expected earnings, and compares the value relevance of book value, current earnings and MFE using the price and the return models. The price model regresses stock price on book value, current earnings and MFE, and the return model regresses stock returns on earnings, earnings changes and changes in MFE. Yearly cross-sectional regressions for the twenty-one-year period spanning 1979 through 1999 are estimated and the incremental R²s obtained are used as a metric to determine the value relevance of each explanatory variable. The results indicate that MFE (changes in MFE) have the highest correlation and incremental explanatory power with stock price (returns) among the three accounting variables.

Value relevance studies can address questions of not only whether particular accounting amounts are used by investors in valuing firms' equity, but also how they are used. Thus, this article also investigates the role of current earnings in equity valuation. In the Ohlson (2001) framework for equity valuation, current earnings are predicted to serve as an indicator of the implied growth in future earnings (Hand, 2001). In other words, for a given book value of equity and next year's expected earnings, the lower the current earnings, the higher the implied growth in future earnings. Therefore, the coefficients on current earnings are expected to be negative in the regression models. The results show that the estimated coefficients on current earnings in the price model are significantly negative in most years, which is consistent with Ohlson's prediction. The role of current earnings in the presence of management forecasts appears to be an implied growth indicator.

The second objective of this article is to examine the relative usefulness of management forecast information in comparison with other available forecasts such as analysts' forecasts. A number of studies document the large impact that management forecasts have on analysts' forecasts. For example, Hassell et al. (1988) and Baginski and Hassell (1990) examine changes in analysts' forecasts of earnings (hereafter AFE) following the release of management forecasts and find that analysts revise their earnings forecasts toward management forecasts. Moreover, Conroy et al. (1993, 1994) compare the accuracy of AFE in Japan to those in the U.S. and find that AFE for Japanese companies are more accurate than those for U.S. firms. They attribute the better forecast accuracy in Japan, at least partially, to the availability of management forecasts for Japanese companies and the incorporation of management insight into analysts' forecasts. These findings imply that analysts' forecasts may be of limited use in Japan, where management forecasts are widely available.

When the value relevance of management forecasts is compared with that of analysts' forecasts, minimal difference in value relevance is observed. Further analysis reveals that more than 90% of changes in analysts' forecasts are explained by management forecasts alone, and that the estimated coefficients of regressing AFE on MFE are not significantly different from one in eleven of the twenty-one years examined. Management forecasts appear to have a great impact on analysts' forecasts.

The following forecast accuracy tests also reveal that the forecast accuracy of AFE improves significantly after the release of MFE, and that MFE are much more accurate than random-walk earnings forecasts. These findings suggest that the relatively high forecast accuracy of MFE may partially explain the heavy dependence of financial analysts on management forecasts in predicting next year's earnings.

Although the findings hitherto support the limited use of analysts' forecasts in the presence of management forecasts, analysts' earnings forecasts are not entirely identical with management earnings forecasts. As a matter of fact, the forecast accuracy test shows that AFE are significantly more accurate than MFE, though the difference is small. This begs the question of when analysts' forecasts differ from management forecasts. It is quite rational for analysts to search for additional information on their own when they expect the recently publicized management forecasts to have high forecast errors. The subsequent tests show that analysts are to some extent aware of the effects of certain financial factors, such as firm size, the previous year's management forecast accuracy and earnings level, on the forecast accuracy of extant management forecasts.

In summary, the empirical evidence adduced here suggests that management forecasts have a large impact on market pricing of equities and provide useful information for market participants. Managers usually have access to inside information about future performance of firms that is not available to outsiders. The unique disclosure practice in Japan that encourages management to publicize earnings forecasts seems to function to help alleviate the information asymmetry that otherwise exists between managers and outsiders.

The findings in this article also indicate the large influence that management earnings forecasts have on analysts' earnings forecasts. Financial analysts appear to depend greatly on management forecasts in formulating their own forecasts. This may imply that analysts play a rather limited role in forecasting firms' future performance when firms' insiders' views are readily available.

BACKGROUND ON JAPAN'S MANAGEMENT FORECASTS

The timing and extent of corporate disclosure in Japan is affected by legal and stock exchange requirements. The Securities and Exchange Law, which covers companies listed on the security exchanges, requires firms to file annual securities reports (‘Yuka Shoken Hokokusho’) with the Ministry of Finance within three months of fiscal year end. The form and content of the annual securities report is prescribed by the Ministry of Finance Ordinance (‘Kigyounaiyoutouno Kaijinikansuru Naikakufurei’), and the report provides detailed information on business activities and financial condition of an enterprise in a fiscal year. The annual securities report also contains some forecast information. In Section 1, Item 3 of this report (‘Plans for New Installation and/or Retirement of Facilities’), firms provide quantified forecasts of new capital investment and retirement of extant facilities, and how they intend to finance them (Nobes and Parker, 2004). Although the scope and amount of information being disclosed is extensive and comprehensive, there is a three-month time lag between the disclosure of the report and the closing of the firm's fiscal year.

In order to supplement the lack of timeliness in statutory disclosure under the Securities and Exchange Law, Japan's stock exchanges, which are self-regulatory organizations, request that listed firms publicize condensed financial statements (‘Kessan Tanshin’) immediately upon board of director approval of a draft of financial statements.² As a result, earnings figures are public well before the three-month legal deadline. For the vast majority of Japanese companies, earnings announcements take place twenty-five to forty trading days after fiscal year end. This practice of timely disclosure was initiated by the stock exchanges in 1974, at which time a letter was sent to listed firms requesting them to disclose key accounting information. Accordingly, management forecasts of main accounting items, which are net sales, ordinary income, net income, earnings per share and dividends per share, for the upcoming year are provided in the condensed financial statements together with current financial results.³ Thus, technically speaking, the provision of management earnings forecasts is voluntary without any legal backing. In fact, some financial institutions, especially securities firms, do not provide earnings forecasts, citing the difficulty of predicting the future business environment. However, as a whole, compliance has been so high that almost all firms provide earnings forecasts.

At least, the following three factors seem to have contributed to the disclosure of management forecasts taking root in Japan. First, since the inception of the timely disclosure practice in 1974, stock exchanges in Japan have been making continuous efforts to make firms comply with the request to provide forecasts of key accounting information. Second, legal guidelines prescribed by the Ministry of Finance Ordinance regarding revisions of management forecasts are established. Under the guidelines, firms are required to announce revised forecasts immediately when a significant change in previously published forecasts arises (e.g., ±10% of sales, ±30% of ordinary income, ±30% of net income). To the extent firms follow the guidelines, they will not be held liable for missing their initial forecasts. This is in contrast with the safe harbour for forward-looking statements in the U.S. (the Private Securities Litigation Reform Act of 1995). The Reform Act was intended to encourage companies to make good faith projections without fear of a securities lawsuit but has been said to be ineffective due to ambiguity in interpretations (Roake and Davidson, 1996; Rosen, 1998). Third, Japan is not culturally a litigious country and class action securities litigation against companies and management is traditionally less common. These factors seem to have contributed to create a favourable environment in which most firms issue earnings forecasts.

Perhaps, with due caution about different legal systems and cultural backgrounds, Japan's disclosure system could serve as a model case for other countries that are trying to encourage firms to disclose forward-looking information.

RESEARCH DESIGN

Price and Return Models

Investigating the relation between accounting numbers and firm value requires a valuation model. The most pervasive valuation model today draws on Ohlson (1995) (Barth, 2000; Barth et al., 2001; Ota, 2003). The Ohlson linear information dynamics coupled with the residual income valuation model allows a firm value to be expressed as a function of book value and earnings. Based on this valuation formula, the price and the return models are derived and are the most frequently employed regression models in value relevance research. The price model regresses stock price on book value and earnings, and the return model regresses stock returns on earnings and earnings changes.

However, both models ignore an important variable in the Ohlson (1995) linear information dynamics, which is ‘other information’ν. This variable, ν, symbolizes information that is not captured by current financial statements but is value relevant in equity valuation. Further analysis by Ohlson (2001) demonstrates that next year's forecast earnings can be used to estimate ν, and that a firm value can be described as a function of book value, current earnings and next year's forecast earnings. Based on this innovative insight, the price and the return models that incorporate earnings forecasts are developed. The price model regresses stock price on book value, earnings and forecast earnings, and the return model regresses stock returns on earnings, earnings changes and changes in forecast earnings.

This study uses MFE as a proxy for forecast earnings and estimates the following price and return models to investigate the value relevance of accounting numbers.

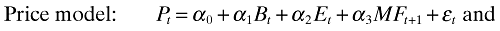
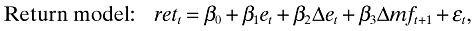
where P_t is share price three months after year-end t, B_t is book value per share at year-end t, E_t is earnings per share for year t, MF_t is MFE per share for year t that are announced simultaneously with E_t₋₁ usually within ten weeks into year t, ret_t is the stock return over the twelve-month period commencing on the third month after year-end t − 1, e_t is earnings per share for year t deflated by P_t₋₁, Δe_t is annual changes in earnings per share deflated by P_t₋₁: (E_t − E_t₋₁) / P_t₋₁, and Δmf_t is annual changes in management forecasts of next year's earnings per share deflated by P_t₋₁: (MF_t − MF_t₋₁) / P_t₋₁.⁴

Although the price model regressions are known to suffer from potentially serious scale problems that are often referred to as ‘scale effects’ (Brown et al., 1999; Easton, 1999; Lo and Lys, 2000; Gu, 2005), Kothari and Zimmerman (1995) and Ota (2003) suggest that using the price model in conjunction with the return model permits more definitive inferences.⁵ Both the price and the return models are thus used in this study.

Decomposition of R²

Yearly regressions are run using the price and the return models and the R²s obtained are decomposed to examine the incremental explanatory power of each explanatory variable. This method, derived theoretically by Theil (1971), is widely used to investigate the relative importance of explanatory variables in the model (e.g., Collins et al., 1997; King and Langli, 1998; Blacconiere et al., 2000).

Let subscripts of R² denote the regressors in the model. The total R² of the price model is then expressed as R²_B·E·MF, because it has three regressors, namely B, E, and MF. R²_B·E·MF can be decomposed into four components:

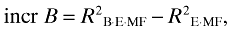
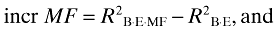
where incr B, incr E, and incr MF represent the incremental explanatory power provided by book value (B), current earnings (E), and MFE (MF) respectively. Common effect denotes the multicollinearity effect, and it is the discrepancy between the total R² and the sum of the incremental explanatory power of all regressors (Theil, 1971, p. 179). The total R² of the return model is likewise decomposed.

Value Relevance of Management Forecasts vs. Analysts' Forecasts

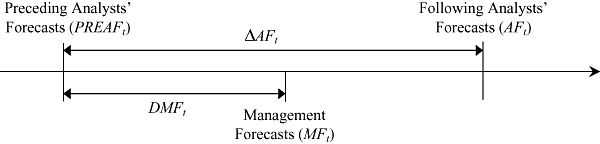
To investigate the usefulness of management forecasts relative to other alternative forecasts in pricing of equities, the value relevance of management and analysts' forecasts is compared. Analysts' forecasts of earnings (hereafter AFE) are collected from the Kaisha Shikihou (1979–1999 June issues, Toyo Keizai Inc.), which is generally accepted by the Japanese securities industry as the standard publication source for analysts' forecasts (Conroy, Harris et al., 1998; Conroy, Eades et al., 2000). The Kaisha Shikihou analysts' forecasts are published on a quarterly base in mid March, June, September and December each year. Since firms' financial condition and future performance are reviewed every quarter, analysts' forecasts do not contain any old forecasts. For March year-end firms, which are most common in Japan, the previous year's actual earnings and this year's earnings forecasts are usually announced at the annual earnings announcements in the last week of May. Therefore, by the time analysts' forecasts in June are published, management forecasts for this year are already announced. The time-series line below depicts the sequence of events.

inline image

To examine the difference in value relevance between MFE and AFE, the following two non-nested models are estimated each year from 1979 to 1999, and the superiority of one model over the other is examined using the Vuong (1989) model selection test.

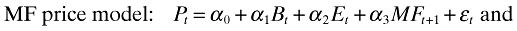
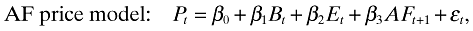
where AF_t is AFE per share for year t that are publicized immediately after MF_t in mid June of year t.

Impact of Management Forecasts on Analysts' Forecasts

Three tests are employed to assess the impact of management forecasts on analysts' forecasts. First, analysts' forecast revisions after the release of management forecast news are examined. This is done by using the following regression model that is employed in many prior studies (e.g., Hassell et al., 1988; Baginski and Hassell, 1990; Williams, 1996).

inline image

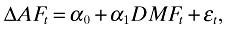(1)

where PREAF_t is AFE per share for year t that are publicized before MF_t in mid March of year t − 1, AF_t is AFE per share for year t that are publicized after MF_t in mid June of year t, ΔAF_t is changes in AFE per share after the release of MF_t deflated by SP_t: (AF_t − PREAF_t)/SP_t, MF_t is MFE per share for year t that are announced in May of year t, DMF_t is the difference between MFE per share and the preceding AFE per share deflated by SP_t: (MF_t − PREAF_t)/SP_t, and SP_t is share price at the beginning of year t (1 April of year t).

It is posited that good (bad) news from management result in upward (downward) analysts' forecast revisions. Therefore, a significantly positive coefficient on DMF is expected.

Second, analysts' earnings forecasts are regressed on management earnings forecasts. If analysts simply mimic earnings forecasts announced by management, the estimated coefficient on management earnings forecasts will be one.⁶

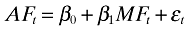(2)

Third, the ex post forecast accuracy of four earnings forecasts, namely preceding AFE (PREAF_t), random-walk forecasts of earnings (E_t₋₁), current MFE (MF_t) and following AFE (AF_t), are examined. Random-walk forecasts of earnings use the recently completed year's actual earnings as expected earnings for the next year. If management forecasts are informative to analysts, the accuracy of analysts' forecasts will improve significantly after the release of management forecasts.⁷

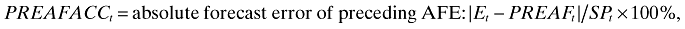
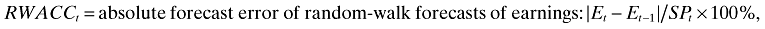
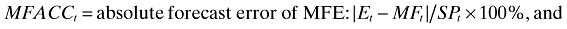
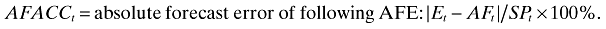
Analysts' Awareness of Bias in Management Forecasts

There is a stream of research that examines the impact of certain financial factors on the systematic bias in management forecasts. The first factor is financial distress. Prior research has documented optimism in financial disclosures released by managers of financially distressed firms. Using a sample of eighty-one U.K. firms that received modified audit reports, Frost (1997) finds that managers of distressed firms make disclosures about expected future performance that are overly optimistic relative to actual financial outcomes. While Frost conducts an univariate analysis, Irani (2000) performs a multivariate analysis and finds a positive linear correlation between optimism in MFE and the degree of financial distress. These results suggest that financially distressed firms are inclined to issue more optimistic earnings forecasts.

The second factor is firm growth. Previous studies have suggested that high-growth firms have more incentives to announce less optimistic forecasts. Matsumoto (2002) and Richardson et al. (1999, 2004) investigate the propensity for firms to avoid negative earnings surprises and find that high-growth firms are more likely to guide analysts' forecasts downward to meet their expectations at the earnings announcement. Choi and Ziebart (2004) also find that high-growth firms tend to release less optimistic management forecasts. One possible explanation for these findings is that the stock market reaction to negative earnings surprises is particularly large for high-growth firms, so that they are inclined to issue less optimistic earnings forecasts in order to avoid earnings disappointments (Skinner and Sloan, 2002).

The third factor is firm size. Several studies have found that firm size is associated with firms' forecast behaviour such as forecast precision and venue (Baginski and Hassell, 1997; Bamber and Cheon, 1998). Choi and Ziebart (2004) also document that MFE are more optimistic for small firms than for large firms. It is often hypothesized that managers of large firms regard publicized earnings forecasts as commitments to the investment community and other interested parties. Their projections, therefore, tend to be conservative in order to avoid missing the forecasts. On the other hand, managers of small firms may consider earnings forecasts as their targets for the upcoming year, so that their projections tend to be optimistic.

The fourth factor is the persistence of prior management forecast errors. Williams (1996) reports that the accuracy of a prior management earnings forecast serves as an indicator to analysts of the believability of a current management forecast. Hirst et al. (1999) conduct an experimental study and find that prior forecast accuracy by management affects investors' earnings predictions when current management forecasts are given to them. Although these results do not provide direct evidence on the persistence of management forecast errors, they indicate that the investment community believes in the persistence.

The last factor is earnings level. Previous studies on analysts' earnings forecasts have shown that forecast error varies with the level of realized earnings (Butler and Saraoglu, 1999; Brown, 2001; Eames et al., 2002; Eames and Glover, 2003). These studies report that forecast optimism intensifies as earnings level becomes lower. Unexpected earnings shocks such as big baths and restructuring costs are one possible explanation for the observed relation between forecast error and earnings level.

Based on these reasonings, the following regression model that explains the forecast accuracy of management forecasts is estimated. The expected signs are shown in parentheses below equation.

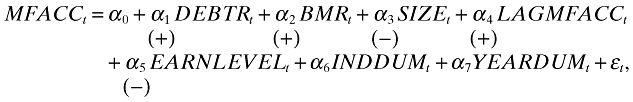((3a))

where DEBTR_t is total liabilities divided by total assets at the beginning of year t, BMR_t is book- to-market ratio at the beginning of year t, SIZE_t is log of inflation-adjusted market value of equity at the beginning of year t,⁸LAGMFACC_t is one-year lagged MFACC_t, EARNLEVEL_t is earnings for year t divided by market value of equity at the beginning of year t, INDDUM is a set of industry dummy variables, and YEARDUM is a set of year dummy variables.

Equation (3a) includes DEBTR to proxy for financial distress, BMR for firm growth, SIZE for firm size, LAGMFACC for the persistence of management forecast errors, and EARNLEVEL for the impact of realized earnings level on forecast errors. INDDUM and YEARDUM are also included to control for possible variation in forecast errors across industry and over the years.

Next, to investigate whether analysts are aware of the bias in management forecasts and make correct adjustments that lead to the higher forecast accuracy in publicizing their own forecasts, the following regression models are estimated. The expected signs are shown in parentheses below the equations.

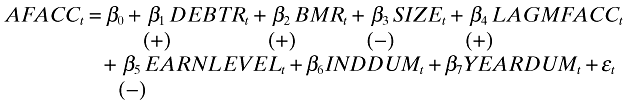((3b))

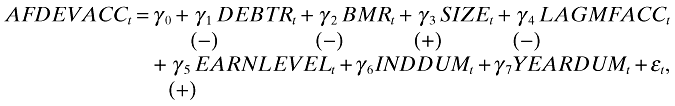((3c))

where AFDEVACC_t is the difference in forecast accuracy between AFE and MFE: AFACC_t − MFACC_t.

The explanatory variables of equations (3b) and (3c) are the same as those of equation (3a). Equation (3b) uses AFACC instead of MFACC as the dependent variable. Since management forecasts are predicted to have a large impact on analysts' forecasts, the expected signs of the estimated coefficients of equation (3b) are the same as those of equation (3a). Equation (3c) focuses on the difference in forecast accuracy between analysts' and management forecasts. If analysts are aware of the contributing factors to the systematic bias in management forecasts, the signs of the estimated coefficients will be reversed to lessen the bias. Therefore, under the hypothesis of analysts' awareness of the bias in management forecasts, the expected signs of the estimated coefficients of equation (3c) are the opposite of those of equation (3a).

DATA AND DESCRIPTIVE STATISTICS

Sample Selection

The sample is selected from the 1979 to 1999 time period using the following criteria⁹:

1
the firms are listed on one of the eight stock exchanges in Japan or traded on the over-the-counter (OTC) market,
2
the fiscal year ends in March (78% of listed firms), and
3
banks, securities firms, and insurance firms are excluded (5% of listed firms).

There are eight stock exchanges in Japan, namely Tokyo, Osaka, Nagoya, Sapporo, Niigata, Kyoto, Hiroshima, and Fukuoka. The Tokyo Stock Exchange (TSE) is by far the largest among them. As of June 1999, 2,433 firms are listed on the stock exchanges in Japan, of which 1,854 firms are listed on the TSE. In terms of volume and value, the TSE accounts for 80%–90% of the nation's trading. The OTC market (generally called the JASDAQ market after the NASDAQ market in the U.S.) consists of small and newly listed firms. As of June 1999, the number of issues listed on the OTC market stands at 853. The OTC market, however, accounts for merely 2%–4% of the trading volume and value in Japan.

Annual accounting data and stock price data are extracted from Nikkei-Zaimu Data and Kabuka CD-ROM 2000. MFE are manually collected from the Nihon Keizai Shinbun (the leading business newspaper in Japan). Other necessary data such as stock splits, capital reduction and changes in par values are collected from Kaisha Shikihou CD-ROM.

The selection process yields 29,587 firm-year observations, which represents approximately 70% of listed firms in Japan. The selected sample firms are fairly representative across firm size and industry sectors except for firms in the retail industry, many of which traditionally have a February year-end and thus are omitted from the sample. To ensure that the results are not sensitive to extreme values, observations in the extreme 1% of both tails of the distribution of all variables are removed.¹⁰ This results in the final sample of 27,993 observations for the price model and 25,491 observations for the return model. The sample for the return model is smaller because it requires the first-differenced data, which are earnings changes and changes in MFE. For the same reason, the analysis period for the return model is one year shorter than that for the price model.

Descriptive Statistics

Panel A of Table 1 presents descriptive statistics and the Pearson correlation coefficients for the price model variables. It reveals that three explanatory variables, which are book value, current earnings and MFE, are all positively correlated with stock price. Above all, MFE have the highest correlation coefficient of 0.701. Panel B of Table 1 contains descriptive statistics and the Pearson correlation coefficients for the return model variables. The correlation coefficients of the three explanatory variables, which are earnings, earnings changes and changes in MFE, are lower than their counterparts in the price model. This finding is consistent with many prior studies that use both the price and the return models (e.g., Harris et al., 1994; Nwaeze, 1998; Francis and Schipper, 1999; Lev and Zarowin, 1999; Ely and Waymire, 1999). As with the price model, changes in MFE exhibit the highest correlation coefficient of 0.320 with stock returns.

Table 1.
DESCRIPTIVE STATISTICS AND CORRELATIONS AMONG VARIABLES IN THE PRICE AND THE RETURN MODELS

Panel A: Price model ^a
Descriptive statistics (in yen)
Variable	Average	S.D.	Min	1Qrt	Median	3Qrt	Max
Stock price (P_t)	962.5	937.6	85.0	401.0	698.0	1160.0	12560.0
Book value (B_t)	449.8	364.7	−19.4	184.0	344.5	603.1	2859.4
Earnings (E_t)	26.3	29.2	−57.8	8.0	18.6	37.5	220.6
MFE (MF_t)	29.4	29.5	−27.4	9.4	20.0	39.4	268.3

Pearson correlation coefficients
Variable	Stock price (P_t)	Book value (B_t)	Earnings (E_t)	MFE (MF_t)
Stock Price (P_t)	1.000
Book value (B_t)	0.539	1.000
Earnings (E_t)	0.626	0.633	1.000
MFE (MF_t)	0.701	0.670	0.939	1.000

Panel B: Return model ^b
Descriptive statistics
Variable	Average	S.D.	Min	1Qrt	Median	3Qrt	Max
Returns (ret_t)	0.0575	0.4295	−0.7749	−0.2464	−0.0009	0.2686	3.3998
Earnings (e_t)	0.0280	0.0324	−0.2641	0.0129	0.0255	0.0420	0.1882
Earnings changes (Δe_t)	−0.0005	0.0232	−0.1788	−0.0074	0.0010	0.0072	0.2066
Changes in MFE (Δmf_t)	0.0006	0.0152	−0.1226	−0.0057	0.0006	0.0064	0.1413

Pearson correlation coefficients
Variable	Returns (ret_t)	Earnings (e_t)	Earnings changes (Δe_t)	Changes in MFE (Δmf_t)
Returns (ret_t)	1.000
Earnings (e_t)	0.193	1.000
Earnings changes (Δe_t)	0.175	0.363	1.000
Changes in MFE (Δmf_t)	0.320	0.202	0.540	1.000

^a The sample consists of 27,993 firm-year observations.
^b The sample consists of 25,491 firm-year observations.
P_t= stock price three months after year-end t,
B_t= book value per share at year-end t,
E_t= earnings per share for year t,
MF_t= MFE per share for year t that are announced simultaneously with E_t₋₁ usually within 10 weeks into year t,
ret_t= stock return over the 12-month period commencing on the third month after year-end t − 1,
e_t= earnings per share for year t deflated by P_t₋₁,
Δe_t= annual change in earnings per share deflated by P_t₋₁: (E_t − E_t₋₁)/P_t₋₁, and
Δmf_t= annual change in management forecasts of next year's earnings per share deflated by P_t₋₁: (MF_t − MF_t₋₁)/P_t₋₁.

High correlations among the explanatory variables are also observed. Particularly, the correlation coefficient between earnings and MFE yields a value of 0.939. This may raise concerns about multicollinearity in the price model in which both variables are included as explanatory variables. However, multicollinearity is not only determined by intercorrelations among the explanatory variables but also by the variance of the explanatory variables (Maddala, 1992, p. 294). Thus, the impact of multicollinearity is not clear given these descriptive statistics. The variance-inflation factor (VIF) and the condition index are calculated to measure the degree of collinearity among the three explanatory variables in the price model (Greene, 2000, p. 40). The results are:

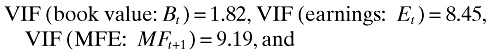
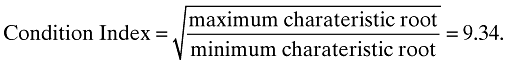
The benchmarks of the VIF and the condition index for collinearity are VIF > 10 and Condition Index > 30 (Kennedy, 1998, p. 190). The values obtained here are below the benchmarks. Thus, multicollinearity is not expected to pose a material problem in the estimation of the model.

EMPIRICAL RESULTS

The Value Relevance of Book Value, Current Earnings, and Management Forecasts of Earnings

Table 2 summarizes the results of yearly cross-sectional regressions of the price and the return models. The number of observations ranges from 712 in 1979 to 2,270 in 1999 for the price model, and from 707 in 1980 to nearly 2,200 in 1999 for the return model. The estimated coefficients on both MF_t₊₁ for the price model and Δmf_t₊₁ for the return model are significantly positive in all years examined at the 0.01 level with the average annual coefficients of 20.12 and 8.30, and the average annual t-statistics of 7.82 and 9.11, respectively. The estimated coefficients on B_t for the price model are significantly positive in all twenty-one years at the 0.01 level, while the estimated coefficients on e_t for the return model are significantly positive in only twelve of the twenty years at the 0.05 level. The average annual coefficients of B_t and e_t are 0.61 and 1.49, and the average annual t-statistics for B_t and e_t are 6.07 and 4.33, respectively.

Table 2.
YEARLY REGRESSIONS OF THE PRICE AND THE RETURN MODELS: YEARS 1979–1999

Year	# obs.	B_t	E_t	MF_t ₊₁	R ²	# obs.	e_t	Δe_t	Δmf_t ₊₁	R ²
	Price model: P_t=α₀+α₁B_t+α₂E_t+α₃MF_t₊₁+ε_t					Return model: ret_t=β₀+β₁e_t+β₂Δe_t+β₃Δmf_t₊₁+ε_t
1979	712	0.72	−2.61	7.79	0.495	n/a	n/a	n/a	n/a	n/a
1979	712	(7.55)**	(−2.63)**	(5.52)**	0.495	n/a	n/a	n/a	n/a	n/a
1980	732	0.66	−3.42	8.32	0.518	707	0.30	0.17	3.51	0.157
1980	732	(5.86)**	(−3.61)**	(7.40)**	0.518	707	(1.42)	(0.56)	(7.13)**	0.157
1981	750	0.41	−3.80	13.07	0.575	720	1.93	−0.71	6.18	0.244
1981	750	(2.84)**	(−3.02)**	(7.64)**	0.575	720	(7.85)**	(–2.62)**	(10.41)**	0.244
1982	760	0.46	−4.43	11.26	0.558	742	0.07	0.06	2.65	0.093
1982	760	(4.38)**	(−4.38)**	(7.59)**	0.558	742	(0.37)	(0.18)	(4.89)**	0.093
1983	772	0.72	−1.55	10.06	0.462	753	0.56	0.44	3.34	0.124
1983	772	(4.99)**	(−0.81)	(3.47)**	0.462	753	(2.80)**	(1.28)	(7.00)**	0.124
1984	807	0.39	−6.18	21.60	0.470	764	0.89	0.50	6.20	0.145
1984	807	(2.31)**	(−2.58)**	(5.96)**	0.470	764	(2.58)*	(0.86)	(6.99)**	0.145
1985	824	0.65	−0.56	11.59	0.423	794	−0.30	2.15	4.71	0.078
1985	824	(3.83)**	(−0.23)	(4.13)**	0.423	794	(–0.77)	(3.34)**	(4.57)**	0.078
1986	847	1.05	−2.45	15.30	0.383	812	1.68	−1.40	12.96	0.151
1986	847	(5.51)**	(−0.98)	(4.89)**	0.383	812	(2.57)*	(–1.06)	(8.00)**	0.151
1987	943	0.90	−11.72	26.52	0.378	844	0.99	0.13	8.06	0.087
1987	943	(5.05)**	(−3.74)**	(7.45)**	0.378	844	(1.94)	(0.14)	(6.56)**	0.087
1988	1,104	0.82	−1.29	15.78	0.356	937	−0.09	6.24	10.46	0.174
1988	1,104	(5.84)**	(−0.54)	(5.67)**	0.356	937	(–0.14)	(4.78)**	(6.42)**	0.174
1989	1,301	0.72	−3.85	16.90	0.467	1,091	−0.36	1.03	10.77	0.118
1989	1,301	(5.99)**	(−1.68)	(7.52)**	0.467	1,091	(–0.65)	(0.88)	(6.92)**	0.118
1990	1,427	0.90	−22.95	50.54	0.616	1,286	8.87	−1.73	23.28	0.265
1990	1,427	(4.66)**	(−4.37)**	(9.70)**	0.616	1,286	(7.54)**	(–0.80)	(7.87)**	0.265
1991	1,546	0.65	−23.12	47.31	0.645	1,423	4.23	−3.31	16.07	0.311
1991	1,546	(4.46)**	(−5.13)**	(9.84)**	0.645	1,423	(10.79)**	(–3.76)**	(14.18)**	0.311
1992	1,628	0.50	−5.29	19.46	0.661	1,525	3.13	−2.93	8.36	0.175
1992	1,628	(8.73)**	(−2.97)**	(10.19)**	0.661	1,525	(10.43)**	(–4.52)**	(11.73)**	0.175
1993	1,663	0.67	−5.39	19.64	0.676	1,605	0.02	−1.09	6.06	0.061
1993	1,663	(13.24)**	(−3.59)**	(10.53)**	0.676	1,605	(0.07)	(–2.03)*	(8.61)**	0.061
1994	1,747	0.82	−10.99	27.60	0.665	1,647	0.53	1.10	8.94	0.176
1994	1,747	(12.22)**	(−7.69)**	(14.14)**	0.665	1,647	(2.27)*	(2.10)*	(11.73)**	0.176
1995	1,854	0.42	−3.71	15.83	0.684	1,734	2.17	0.16	4.36	0.165
1995	1,854	(9.85)**	(−2.61)**	(9.07)**	0.684	1,734	(11.28)**	(0.44)	(8.44)**	0.165
1996	1,994	0.52	−7.20	23.52	0.672	1,845	−1.24	1.27	8.56	0.154
1996	1,994	(8.17)**	(−3.97)**	(11.43)**	0.672	1,845	(–3.97)**	(2.28)*	(11.10)**	0.154
1997	2,106	0.27	−6.54	22.66	0.612	1,976	2.58	−0.80	9.24	0.220
1997	2,106	(4.68)**	(−2.69)**	(8.94)**	0.612	1,976	(11.92)**	(–2.04)*	(14.61)**	0.220
1998	2,206	0.22	4.10	10.22	0.530	2,093	1.67	0.25	4.22	0.171
1998	2,206	(4.32)**	(2.65)**	(5.48)**	0.530	2,093	(10.85)**	(0.99)	(11.77)**	0.171
1999	2,270	0.26	−6.16	27.57	0.554	2,193	2.13	−0.23	8.09	0.236
1999	2,270	(3.03)**	(−1.82)	(7.68)**	0.554	2,193	(7.54)**	(–0.69)	(13.25)**	0.236
Average	1,333.0	0.61	−6.15	20.12	0.543	1,274.6	1.49	0.06	8.30	0.165
Average	1,333.0	(6.07)	(−2.68)	(7.82)	0.543	1,274.6	(4.33)	(0.02)	(9.11)	0.165

* Significant at the 0.05 level (two-tailed).
** Significant at the 0.01 level (two-tailed).
t-statistics based on White's standard errors are provided in parentheses.
P_t= stock price three months after year-end t,
B_t= book value per share at year-end t,
E_t= earnings per share for year t,
MF_t= MFE per share for year t that are announced simultaneously with E_t₋₁ usually within 10 weeks into year t,
ret_t= stock return over the 12-month period commencing on the third month after year-end t − 1,
e_t= earnings per share for year t deflated by P_t₋₁,
Δe_t= annual change in earnings per share deflated by P_t₋₁: (E_t − E_t₋₁)/P_t₋₁, and
Δmf_t= annual change in management forecasts of next year's earnings per share deflated by P_t₋₁: (MF_t − MF_t₋₁)/P_t₋₁.

Value relevance studies provide insights into not only whether particular accounting amounts are used in the market, but also how those accounting amounts are used by investors in valuing firms' equity. Ohlson's (2001) theoretical analysis delineates the role of current earnings in equity valuation. His appendix 1 shows analytically that the coefficient on current earnings is negative in the presence of forecast earnings. Hand (2001, p. 124) comments, '[a]n intuition regarding β₂ (the negative coefficient on current earnings) is that, for a given current book equity and expected next-period earnings, the larger the current income, the lower the implied growth in earnings'. Thus, in Ohlson's framework for equity valuation, the role of current earnings is considered to be a benchmark from which the future growth in earnings can be inferred. Accordingly, the signs of estimated coefficients on current earnings are of particular interest here. The empirical results reported in Table 2 show that the estimated coefficients on E_t for the price model are negative in all years except for year 1998, and they are statistically significant in fourteen of the twenty-one years examined at the 0.01 level. The average annual coefficient on E_t is –6.15, and the corresponding t-statistic is –2.68. On the other hand, the results for the return model are weak. The average annual coefficient on Δe_t is 0.06, and the corresponding t-statistic is merely 0.02. Thus, although the results for the return model are somewhat ambiguous, those for the price model are consistent with Ohlson's theoretical analysis, suggesting the role of current earnings in equity valuation being an indicator of the implied growth in future earnings.

Figure 1(a) and Figure 1(b) illustrate the incremental explanatory power of accounting variables for the price model and the return model respectively. The incremental explanatory power of each regressor and the common effect are stacked on one another so that they collectively add up to the total explanatory power of the model. From inspection of both figures, it appears that MF_t₊₁ for the price model and Δmf_t₊₁ for the return model have the highest incremental explanatory power among the three accounting variables for each model. The differences in incremental explanatory power among explanatory variables in the price model are examined in Panel A of Table 3. The results of the two-way ANOVA reject the null hypothesis of no difference in incremental explanatory power among the three variables.¹¹ Further analysis by Tukey's multiple comparison method indicates that the incremental explanatory power of MF is significantly larger than that of B and E. The nonparametric Friedman test also produces the same results.¹² The results for the return model are presented in Panel B of Table 3 and they are similar to those for the price model. The incremental explanatory power of Δmf is significantly larger than that of e and Δe.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

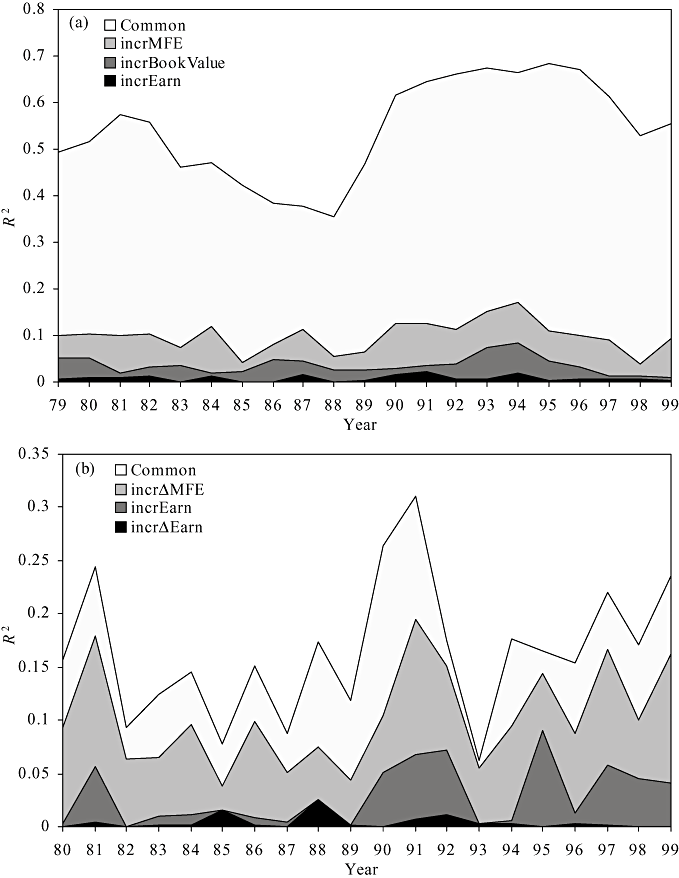
(a) THE INCREMENTAL EXPLANATORY POWER OF BOOK VALUE, EARNINGS, AND MANAGEMENT FORECASTS OF EARNINGS FOR THE PRICE MODEL: YEARS 1979–1999^a;
(b) THE INCREMENTAL EXPLANATORY POWER OF EARNINGS, EARNINGS CHANGES, AND CHANGES IN MANAGEMENT FORECASTS OF EARNINGS FOR THE RETURN MODEL: YEARS 1980–99^b
The incremental explanatory power of each variable and the common effect are stacked on one another so that they collectively add up to the total R² of the model.
^a The price model is estimated: *P_t*=α₀+α₁*B_t*+α₂*E_t*+α₃*MF_t*₊₁+*ε_t*. incr B (incrBookValue) =R²_B·E·MF − R²_E·MF, incr E (incrEarn) =R²_B·E·MF − R²_B·MF, incr MF (incrMFE) =R²_B·E·MF − R²_B·E, and common effect (Common) =R²_B·E·MF − (incr B+ incr E+ incr MF). Subscripts of R² denote the regressors.
^b The return model is estimated: *ret_t*=β₀+β₁*e_t*+β₂*Δe_t*+β₃*Δmf_t*₊₁+*ε_t*. incr e (incrEarn) =R²_e·Δe·Δmf − R²_Δe·Δmf, incr Δe (incrΔEarn) =R²_e·Δe·Δmf − R²_e·Δmf, incr Δmf (incrΔMFE) =R²_e·Δe·Δmf − R²_e·Δe, and common effect (Common) =R²_e·Δe·Δmf − (incr e+ incr Δe+ incr Δmf). Subscripts of R² denote the regressors.
*P_t*= stock price three months after year-end t,
*B_t*= book value per share at year-end t,
*E_t*= earnings per share for year t,
*MF_t*= MFE per share for year t that are announced simultaneously with *E_t*₋₁ usually within 10 weeks into year t,
*ret_t*= stock return over the 12-month period commencing on the third month after year-end t−1,
*e_t*= earnings per share for year t deflated by *P_t*₋₁,
*Δe_t*= annual change in earnings per share deflated by *P_t*₋₁: (*E_t* − *E_t*₋₁)/*P_t*₋₁, and
*Δmf_t*= annual change in management forecasts of next year's earnings per share deflated by *P_t*₋₁: (*MF_t* − *MF_t*₋₁)/*P_t*₋₁.

Table 3.
TWO-WAY ANOVA AND MULTIPLE COMPARISONS OF INCREMENTAL EXPLANATORY POWER BETWEEN BOOK VALUE, EARNINGS, AND MANAGEMENT FORECASTS OF EARNINGS FOR THE PRICE MODEL; AND BETWEEN EARNINGS, EARNINGS CHANGES AND CHANGES IN MANAGEMENT FORECASTS OF EARNINGS FOR THE RETURN MODEL

Panel A: Price model
	Parametric^a	Nonparametric^b
Two-way ANOVA	F _{(2, 40)} 51.9**	χ ² ₍₂₎ 32.7**
Multiple comparisons
incr MF—incr B	0.0347**	20**
incr MF—incr E	0.0546**	37**
incr B—incr E	0.0199**	17*

Panel B: Return model
	Parametric^a	Nonparametric^b
Two-way ANOVA	F _{(2, 38)} 53.3**	χ ² ₍₂₎ 31.3**
Multiple comparisons
incr Δmf—incr e	0.0492**	22**
incr Δmf—incr Δe	0.0701**	35**
incr e—incr Δe	0.0209*	13

^a For parametric tests, the two-way analysis of variance without replication method and Tukey's multiple comparison method are used.
^b For nonparametric tests, the Friedman two-way analysis of variance by ranks and its multiple comparison method are used.
* Significant at the 0.05 level.
** Significant at the 0.01 level.
incr MF=R²_B·E·MF − R²_B·E,
incr B=R²_B·E·MF − R²_E·MF,
incr E=R²_B·E·MF − R²_B·MF,
incr Δmf=R²_e·Δe·Δmf − R²_e·Δe,
incr e=R²_e·Δe·Δmf − R²_Δe·Δmf, and
incr Δe=R²_e·Δe·Δmf − R²_e·Δmf,
where subscripts of R² denote the regressors.
P_t= stock price three months after year-end t,
B_t= book value per share at year-end t,
E_t= earnings per share for year t,
MF_t= MFE per share for year t that are announced simultaneously with E_t₋₁ usually within 10 weeks into year t,
e_t= earnings per share for year t deflated by P_t₋₁,
Δe_t= annual change in earnings per share deflated by P_t₋₁: (E_t − E_t₋₁)/P_t₋₁, and
Δmf_t= annual change in management forecasts of next year's earnings per share deflated by P_t₋₁: (MF_t − MF_t₋₁)/P_t₋₁.

Overall, regardless of the model specification, management forecasts appear to be the most consistently statistically significant accounting variable.

The Comparison of the Value Relevance between Management and Analysts' Forecasts

Panel A of Table 4 summarizes the results of yearly cross-sectional regressions of the MF price model and the AF price model. The averages of the twenty-one estimated coefficients are reported and the corresponding Fama–MacBeth t-statistics are provided in parentheses. The average estimated coefficients on MF_t₊₁ is 20.12 with Fama–MacBeth t-statistic of 8.09, while that on AF_t₊₁ is 20.09 with Fama–MacBeth t-statistic of 7.73. With regard to the explanatory power of the models, the average adj.R² for the MF price model is 0.543, while that for the AF price model is 0.542. There appears to be minimal difference in estimated coefficients and explanatory power between the MF price model and the AF price model.

Table 4.
THE COMPARISON OF THE VALUE RELEVANCE BETWEEN MANAGEMENT AND ANALYSTS' EARNINGS FORECASTS

Panel A: MF and AF price model ^a
MF price model: P_t=α₀+α₁B_t+α₂E_t+α₃MF_t₊₁+ε_t AF price model: P_t=β₀+β₁B_t+β₂E_t+β₃AF_t₊₁+ε_t
	B_t	E_t	MF_t ₊₁/AF_t₊₁	adj.R²
MF price model	0.61	−6.15	20.12	0.543
MF price model	(12.07)**	(−4.29)**	(8.09)**	0.543
AF price model	0.62	−6.39	20.09	0.542
AF price model	(12.23)**	(−4.23)**	(7.73)**	0.542

Panel B: Model selection using the Vuong test ^b
	MFE more value relevant	MFE = AFE	AFE more value relevant
Number of years	1	17	3

^a Panel A reports the average estimated coefficients and the average adjusted R² from the 21 annual cross-sectional regressions. Fama-MacBeth t-statistics are provided in parentheses.
^b Panel B reports the number of years in which MFE (AFE) are statistically significantly more value relevant than AFE (MFE) at the 0.05 level or higher using the Vuong model selection test. The Vuong model selection test is a relative discrimination test based on the standardized LR ratio, and its test statistic has a standard normal distribution.
* Significant at the 0.05 level (two-tailed).
** Significant at the 0.01 level (two-tailed).
P_t= stock price three months after year-end t,
B_t= book value per share at year-end t,
E_t= earnings per share for year t,
MF_t= MFE per share for year t that are announced simultaneously with E_t₋₁ usually within 10 weeks into year t, and
AF_t= AFE per share for year t that are publicized immediately after MF_t.

Panel B of Table 4 reports the results of the Vuong (1989) test for non-nested model selection. Of the twenty-one pairs of yearly regressions, seventeen cannot reject the null hypothesis of no difference between the MF and the AF price models. MFE (AFE) are statistically more value relevant than AFE (MFE) in only one (three) of the twenty-one years. The Vuong (1989) model selection tests for the return specification produce the similar results (not tabulated).

Thus, in terms of value relevance, there is minimal difference between management and analysts' earnings forecasts.

The Results of the Impact of Management Forecasts on Analysts' Forecasts

Panel A of Table 5 presents the results of estimating equation (1). The estimated coefficient on DMF_t is 0.9127 and is highly statistically significant. With regard to the explanatory power of the model, the adj.R² has a value of 0.912, which suggests that more than 90% of changes in analysts' forecasts are explained by management forecasts alone.

Table 5.
THE IMPACT OF MANAGEMENT FORECASTS ON ANALYSTS' FORECASTS

Panel A: Changes in AFE after the release of MFE
ΔAF_t=α₀+α₁DMF_t+ε_t			(1)
	Constant	DMF_t	adj.R²
Estimated coefficient (t-statistic)	−0.0004	0.9127	0.912
Estimated coefficient (t-statistic)	(–10.7)**	(419.0)**	0.912

Panel B: Pooled sample estimation
AF_t=β₀+β₁MF_t+ε_t			(2)
Estimated coefficient	β ₁	The null of β₁ equals one	t-statistic
Estimated coefficient	1.0025	The null of β₁ equals one	5.56**

Panel C: Annual sample estimation ^a
AF_t=β₀+β₁MF_t+ε_t		(2)
	β ₁ equals one is NOT rejected	β ₁ equals one is rejected
Number of years	11	10

^a Panel C reports the number of years in which the estimated coefficient on MF_t, β₁, is statistically significantly different from one at the 0.05 level or higher.
* Significant at the 0.05 level (two-tailed).
** Significant at the 0.01 level (two-tailed).
PREAF_t= AFE per share for year t that are publicized before MF_t in mid March of year t−1,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
ΔAF_t= changes in AFE per share after the release of MF_t deflated by SP_t: (AF_t − PREAF_t)/SP_t,
MF_t= MFE per share for year t that are announced in May of year t,
DMF_t= the difference between MFE per share and the preceding AFE per share deflated by SP_t: (MF_t − PREAF_t)/SP_t, and
SP_t= share price at the beginning of year t (1 April of year t).

Panel B of Table 5 reports the results of estimating equation (2) using a pooled sample, while Panel C of Table 5 provides the results of year-by-year estimation. The pooled regression results in Panel B show that the estimated coefficient on MF_t, β₁, is 1.0025 and the null hypothesis of β₁ equals one is rejected at the 0.01 level. However, the year-by-year estimation results in Panel C indicate that the null hypothesis of β₁ equals one is not rejected in eleven of the twenty-one years at the 0.05 level.

These findings are indicative of the significant influence that management forecasts have on analysts' expectations about future earnings.

Panel A of Table 6 provides the descriptive statistics of the forecast accuracy of four earnings forecasts, namely PREAFACC, RWACC, MFACC and AFACC, and Panel B of Table 6 reports the results of the paired mean difference tests. The average PREAFACC, RWACC, MFACC and AFACC are 1.838%, 1.800%, 1.540% and 1.524% respectively, and the mean differences in forecast accuracy among the four earnings forecasts are all statistically significant. The forecast accuracy of analysts' forecasts improves significantly after the release of management forecasts with the average absolute forecast error decreasing from 1.838% to 1.524%. The improvement in analysts' forecast accuracy after the release of management forecasts is also visually evident in Figure 2, in which the annual average absolute forecast errors of the four forecasts are shown in bar-chart form.

Table 6.
THE COMPARISON OF FORECAST ACCURACY BETWEEN PRECEDING ANALYSTS' FORECASTS, RANDOM-WALK FORECASTS, MANAGEMENT FORECASTS, AND FOLLOWING ANALYSTS' FORECASTS

Panel A: Descriptive statistics (%)
	Average	S.D.	Min	1Qrt	Median	3Qrt	Max
PREAFACC	1.838	0.029	0.000	0.348	0.922	2.119	72.616
RWACC	1.800	0.030	0.000	0.337	0.856	2.027	64.899
MFACC	1.540	0.026	0.000	0.266	0.733	1.720	45.164
AFACC	1.524	0.025	0.000	0.265	0.732	1.709	43.589

Panel B: Difference in forecast accuracy
Pairs	Difference	Paired t-test	Wilcoxon signed-rank test
PREAFACC − RWACC	0.038%	2.61**	14.44**
PREAFACC − MFACC	0.298%	25.30**	39.30**
PREAFACC − AFACC	0.314%	28.17**	41.36**
RWACC − MFACC	0.260%	15.33**	19.06**
RWACC − AFACC	0.276%	17.14**	20.67**
MFACC − AFACC	0.016%	4.62**	9.57**

* Significant at the 0.05 level (two-tailed).
** Significant at the 0.01 level (two-tailed).
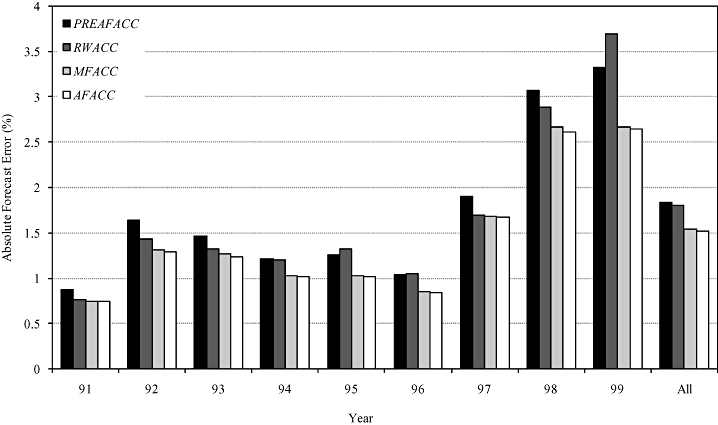
PREAFACC_t= absolute forecast error of preceding AFE: |E_t − PREAF_t|/SP_t × 100%,
RWACC_t= absolute forecast error of random-walk forecasts of earnings: |E_t − E_t₋₁|/SP_t × 100%,
MFACC_t= absolute forecast error of MFE: |E_t − MF_t|/SP_t × 100%,
AFACC_t= absolute forecast error of following AFE: |E_t − AF_t|/SP_t × 100%,
PREAF_t= AFE per share for year t that are publicized before MF_t in mid March of year t − 1,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
MF_t= MFE per share for year t that are announced in May of year t,
E_t= actual earnings per share for year t that are announced in May of year t + 1 (E_t and MF_t_+ 1 are announced simultaneously), and
SP_t= share price at the beginning of year t (1 April of year t).

The difference in forecast accuracy between random-walk forecasts and management forecasts is also noteworthy. Random-walk forecasts use actual earnings, which are announced simultaneously with MFE, as a proxy for next year's expected earnings. Random-walk forecasts have the average absolute forecast error of 1.800%, while management forecasts have that of 1.540%. Thus, using MFE as a proxy for next year's expected earnings leads to much smaller absolute forecast error than using naive time-series forecasts of earnings. This may partially explain why analysts rely largely on management forecasts in formulating their own forecasts.

Overall, MFE appear to have a great impact on AFE, and the relatively high accuracy of MFE may be one of the main reasons why management forecasts are viewed by analysts as an important source of information.

The Results of the Analysts' Awareness of Bias in Management Forecasts

Table 7 presents descriptive statistics and correlations among variables in equations (3a), (3b) and (3c). Panel B of Table 7 shows that DEBTR, BMR and LAGMFACC are positively correlated with MFACC and AFACC, and are negatively correlated with AFDEVACC. On the other hand, SIZE and EARNLEVEL are negatively correlated with MFACC and AFACC, and are positively correlated with AFDEVACC. Thus, the signs of univariate correlations are all consistent with the expected signs in equations (3a), (3b) and (3c).

Table 7.
DESCRIPTIVE STATISTICS AND CORRELATIONS AMONG VARIABLES IN THE FORECAST ACCURACY MODELS

Panel A: Descriptive statistics
	Average	S.D.	Min	1Qrt	Median	3Qrt	Max
MFACC	1.428	2.429	0.000	0.239	0.666	1.611	40.986
AFACC	1.399	2.357	0.000	0.235	0.661	1.582	40.834
AFDEVACC	−0.029	0.421	−12.344	0.000	0.000	0.000	19.524
DEBTR	0.626	0.199	0.010	0.487	0.645	0.785	0.998
BMR	0.613	0.472	0.008	0.312	0.497	0.760	7.063
SIZE	10.429	1.510	6.119	9.340	10.302	11.391	17.563
LAGMFACC	1.253	1.908	0.000	0.226	0.630	1.490	39.040
EARNLEVEL	0.026	0.035	−0.500	0.012	0.024	0.040	0.541

Panel B: Pearson correlation coefficients
	MFACC	AFACC	AFDEVACC	DEBTR	BMR	SIZE	LAG MFACC	EARN LEVEL
MFACC	1.000
AFACC	0.985	1.000
AFDEVACC	−0.256	−0.085	1.000
DEBTR	0.118	0.116	−0.028	1.000
BMR	0.292	0.296	−0.026	−0.276	1.000
SIZE	−0.306	−0.305	0.057	−0.025	−0.374	1.000
LAGMFACC	0.421	0.415	−0.105	0.140	0.208	−0.295	1.000
EARNLEVEL	−0.328	−0.308	0.169	−0.075	0.152	−0.061	−0.092	1.000

MFACC_t= absolute forecast error of MFE: |E_t − MF_t|/SP_t × 100%,
AFACC_t= absolute forecast error of following AFE: |E_t − AF_t|/SP_t × 100%,
AFDEVACC_t= the difference in forecast accuracy between AFE and MFE: AFACC_t − MFACC_t,
DEBTR_t= total liabilities divided by total assets at the beginning of year t,
BMR_t= book-to-market ratio at the beginning of year t,
SIZE_t= log of inflation-adjusted market value of equity at the beginning of year t,
LAGMFACC_t= one-year lagged MFACC_t,
EARNLEVEL_t= earnings for year t divided by market value of equity at the beginning of year t.
MF_t= MFE per share for year t that are announced in May of year t,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
E_t= actual earnings per share for year t that are announced in May of year t + 1 (E_t and MF_t_+ 1 are announced simultaneously), and
SP_t= share price at the beginning of year t (1 April of year t).

Table 8 reports the regression results from estimating equations (3a), (3b) and (3c). With regard to equation (3a), the estimated coefficients on DEBTR, BMR and LAGMFACC are significantly positive, while those on SIZE and EARNLEVEL are significantly negative. The signs of the estimated coefficients are all consistent with the expected signs in the table. The results from the estimation of equation (3a) suggest that firms in financial distress with high debt ratios issue less accurate management forecasts, that growth firms with low book-to-market ratios announce more accurate management forecasts, that small firms publicize less accurate management forecasts, that firms whose previous year's management forecasts were less accurate tend to remain so in their current forecasts, and that firms with low earnings level issue less accurate management forecasts. The control variables, INDDUM and YEARDUM, are also both statistically significant, indicating the need to control for variation in management forecast accuracy across industry and over the years.

Table 8.
ANALYSTS' AWARENESS OF BIAS IN MANAGEMENT FORECASTS

MFACC_t=α₀+α₁DEBTR_t+α₂BMR_t+α₃SIZE_t+α₄LAGMFACC_t+α₅EARNLEVEL_t+α₆INDDUM_t+α₇YEARDUM_t+ε_t (3a) AFACC_t=β₀+β₁DEBTR_t+β₂BMR_t+β₃SIZE_t+β₄LAGMFACC_t+β₅EARNLEVEL_t+β₆INDDUM_t+β₇YEARDUM_t+ε_t (3b) AFDEVACC_t=γ₀+γ₁DEBTR_t+γ₂BMR_t+γ₃SIZE_t+γ₄LAGMFACC_t+γ₅EARNLEVEL_t+γ₆INDDUM_t+γ₇YEARDUM_t+ε_t (3c)
Variables	Expected sign^a	(3a) MFACC	(3b) AFACC	Expected sign^a	(3c) AFDEVACC
CONSTANT	?	3.496	3.321	?	−0.175
CONSTANT	?	(17.02)**	(16.09)**	?	(–4.12)**
DEBTR	+	1.313	1.335	–	0.022
DEBTR	+	(15.92)**	(16.10)**	–	(1.26)
BMR	+	1.052	1.045	–	−0.007
BMR	+	(14.28)**	(14.06)**	–	(–0.53)
SIZE	–	−0.227	−0.220	+	0.007
SIZE	–	(–22.65)**	(–22.48)**	+	(3.27)**
LAGMFACC	+	0.306	0.292	–	−0.014
LAGMFACC	+	(13.58)**	(13.60)**	–	(–2.33)**
EARNLEVEL	–	−26.493	−24.268	+	2.224
EARNLEVEL	–	(–15.57)**	(–14.43)**	+	(8.00)**
INDDUM ^b		642.54**	411.03**		74.70**
YEARDUM ^b		423.84**	580.64**		167.40**
adj.R²		0.393	0.376		0.074
#obs.		25,184	25,184		25,184

^a The expected signs are based on the discussion in subsection ‘Analysts’ Awareness of Bias in Management Forecasts'.
^b For statistical significance testing, Wald statistics based on White's heteroskedastic-consistent covariance matrix are provided.
* Significant at the 0.05 level (one-tailed).
** Significant at the 0.01 level (one-tailed).
t-statistics based on White's standard errors are provided in parentheses.
MFACC_t= absolute forecast error of MFE: |E_t − MF_t|/SP_t × 100%,
AFACC_t= absolute forecast error of following AFE: |E_t − AF_t|/SP_t × 100%,
AFDEVACC_t= the difference in forecast accuracy between AFE and MFE: AFACC_t − MFACC_t,
DEBTR_t= total liabilities divided by total assets at the beginning of year t,
BMR_t= book-to-market ratio at the beginning of year t,
SIZE_t= log of inflation-adjusted market value of equity at the beginning of year t,
LAGMFACC_t= one-year lagged MFACC_t,
EARNLEVEL_t= earnings for year t divided by market value of equity at the beginning of year t.
INDDUM= a set of industry dummy variables,
YEARDUM= a set of year dummy variables,
MF_t= MFE per share for year t that are announced in May of year t,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
E_t= actual earnings per share for year t that are announced in May of year t + 1 (E_t and MF_t_+ 1 are announced simultaneously), and
SP_t= share price at the beginning of year t (1 April of year t).

The estimation results of equation (3b) are much the same as those of equation (3a), which is quite predictable considering the similarity between AFACC and MFACC. However, when we focus on the difference between analysts' forecasts and management forecasts, we can gain meaningful insights into how analysts view management forecasts.

The estimation results of equation (3c) show that the signs of the estimated coefficients on SIZE, LAGMFACC and EARNLEVEL are all consistent with the expected signs in the table, and that they are all statistically significant at the 0.01 level. Note that the estimated coefficients in equation (3c) are the differences between those in equation (3b) and those in equation (3a), because AFDEVACC is defined as the difference between AFACC and MFACC. These results suggest that analysts are aware of the effects that SIZE, LAGMFACC and EARNLEVEL have on the forecast accuracy of management forecasts and make adjustments to them when they publicize their own forecasts. For example, the signs of the estimated coefficients on LAGMFACC in equations (3a) and (3c) are positive, 0.306, and negative, –0.014, respectively, which suggests that analysts are aware of the persistence of the previous year's management forecast errors and somewhat discount current management forecasts. On the other hand, the estimated coefficients on DEBTR and BMR in equation (3c) are not statistically significant. It appears that analysts are not aware of the bias in management forecasts caused by these factors.

To investigate further the effects of SIZE, LAGMFACC and EARNLEVEL on the relative forecast accuracy of management and analysts' forecasts, equally weighted quintile portfolios based on the magnitude of SIZE, LAGMFACC and EARNLEVEL are constructed and the forecast accuracy of management and analysts' forecasts is compared.

For the SIZE portfolios reported in Panel A of Table 9, the differences between AFACC and MFACC get steadily smaller as firm size portfolios become larger from SIZE 1 (smallest firms) to SIZE 5 (largest firms), suggesting analysts' awareness of bias in management forecasts announced by small firms. For the LAGMFACC portfolios reported in Panel B of Table 9, the differences get larger as the previous year's absolute management forecast errors become larger from LAGMFACC 1 (firms with the smallest absolute forecast errors) to LAGMFACC 5 (firms with the largest absolute forecast errors), indicating analysts' awareness of the persistence of the previous year's management forecast errors. For the EARNLEVEL portfolios reported in Panel C of Table 9, the differences become monotonically smaller as firms' earnings levels get higher from EARNLEVEL 1 (firms with the lowest earnings level) to EARNLEVEL 5 (firms with the highest earnings level), suggesting analysts' awareness of low earnings firms having high management forecast errors. The results of the paired mean difference tests using the paired t-test and Wilcoxon signed-rank test generally indicate that analysts' forecasts become more significantly more accurate than management forecasts as the forecast accuracy of management forecasts gets lower.

Table 9.
THE IMPACT OF FIRM SIZE, PREVIOUS YEAR'S MANAGEMENT FORECAST ACCURACY AND EARNINGS LEVEL ON THE RELATIVE ACCURACY BETWEEN MANAGEMENT AND ANALYSTS' FORECASTS

Panel A: Quintile portfolios based on firm size
1 = small 5 = large	AFACC	MFACC	Difference	Paired t-test	Wilcoxon signed-rank test
SIZE 1	2.347%	2.412%	−0.065%	−6.37**	−9.02**
SIZE 2	1.620%	1.653%	−0.034%	−5.31**	−7.17**
SIZE 3	1.255%	1.272%	−0.017%	−5.07**	−5.17**
SIZE 4	1.045%	1.059%	−0.015%	−4.69**	−6.53**
SIZE 5	0.730%	0.743%	−0.013%	−4.21**	−6.61**
Pooled	1.399%	1.428%	−0.029%	−10.81**	−15.59**

Panel B: Quintile portfolios based on previous year's management forecast accuracy
1 = small 5 = large	AFACC	MFACC	Difference	Paired t-test	Wilcoxon signed-rank test
LAGMFACC 1	0.725%	0.728%	−0.003%	−1.95	−0.85
LAGMFACC 2	0.856%	0.858%	−0.002%	−1.21	−2.06*
LAGMFACC 3	1.079%	1.093%	−0.013%	−4.10**	−5.66**
LAGMFACC 4	1.485%	1.515%	−0.029%	−7.08**	−9.13**
LAGMFACC 5	2.849%	2.945%	−0.096%	−8.04**	−11.76**
Pooled	1.399%	1.428%	−0.029%	−10.81**	−15.59**

Panel C: Quintile portfolios based on earnings level
1 = low 5 = high	AFACC	MFACC	Difference	Paired t-test	Wilcoxon signed-rank test
EARNLEVEL 1	2.807%	2.925%	−0.118%	−12.69**	−18.18**
EARNLEVEL 2	0.719%	0.734%	−0.016%	−5.05**	−5.35**
EARNLEVEL 3	0.751%	0.757%	−0.007%	−1.85	−3.98**
EARNLEVEL 4	0.890%	0.896%	−0.006%	−1.75	−3.08**
EARNLEVEL 5	1.829%	1.826%	0.004%	0.50	−1.43
Pooled	1.399%	1.428%	−0.029%	−10.81**	−15.59**

* Significant at the 0.05 level (two-tailed).
** Significant at the 0.01 level (two-tailed).
For each panel, all firms are classified into equally weighted quintile portfolios based on their rankings of SIZE, LAGMFACC and EARNLEVEL. Portfolio 1 comprises firms with the smallest or lowest SIZE, LAGMFACC and EARNLEVEL, while portfolio 5 comprises firms with the largest or highest SIZE, LAGMFACC and EARNLEVEL. The mean values of AFACC and MFACC are reported for each portfolio, and the differences are statistically tested using the paired t-test and Wilcoxon signed-rank test.
MFACC_t= absolute forecast error of MFE: |E_t − MF_t|/SP_t × 100%,
AFACC_t= absolute forecast error of following AFE: |E_t − AF_t|/SP_t × 100%,
SIZE_t= log of inflation-adjusted market value of equity at the beginning of year t,
LAGMFACC_t= one-year lagged MFACC_t,
EARNLEVEL_t= earnings for year t divided by market value of equity at the beginning of year t.
MF_t= MFE per share for year t that are announced in May of year t,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
E_t= actual earnings per share for year t that are announced in May of year t + 1 (E_t and MF_t₊₁ are announced simultaneously), and
SP_t= share price at the beginning of year t (1 April of year t).

Thus, findings suggest that analysts are to some extent aware of the influence of certain financial factors on the forecast accuracy of management forecasts.

The Overall Tests on the Analysts' Awareness of Bias in Management Forecasts

To further corroborate the findings in the previous subsection that analysts are aware of the impact of certain financial factors on the forecast accuracy of management forecasts, the following regression model is estimated. The expected sign is shown in parentheses below the equation.

((3d))

The dependent variable, AFDEVACC (AFACC–MFACC), is the incremental forecast accuracy of analysts' forecasts over management forecasts, while the explanatory variable, MFACC (the absolute forecast error of MFE), is a linear combination of the financial factors in equation (3a). Thus, equation (3d) can be construed as an overall test of the hypothesis of analysts' awareness of predictable bias in management forecasts.

Panel A of Table 10 reports the regression results from estimating equation (3d). The estimated coefficient on MFACC, δ₁, is significantly negative, –0.044, suggesting that analysts' forecasts become more accurate than management forecasts as management forecasts get less accurate.

Table 10.
THE OVERALL TESTS OF ANALYSTS' AWARENESS OF BIAS IN MANAGEMENT FORECASTS

Panel A: The overall regression test
AFDEVACC_t=δ₀+δ₁MFACC_t+ε_t		(3d)
Variables	Expected sign	(3d) AFDEVACC
CONSTANT	?	0.035
CONSTANT	?	(5.47)**
MFACC	–	−0.044
MFACC	–	(–8.20)**
adj.R²		0.065
#obs.		25,184

Panel B: Quintile portfolios based on management forecast accuracy
1 = small 5 = large	AFACC	MFACC	Difference	Paired t-test	Wilcoxon signed-rank test
MFACC 1	0.099%	0.081%	0.018%	8.68**	11.43**
MFACC 2	0.321%	0.311%	0.010%	4.85**	0.61
MFACC 3	0.680%	0.680%	0.000%	0.00	−4.89**
MFACC 4	1.355%	1.371%	−0.016%	−3.98**	−9.30**
MFACC 5	4.540%	4.696%	−0.155%	−13.16**	−19.15**
Pooled	1.399%	1.428%	−0.029%	−10.81**	−15.59**

* Significant at the 0.05 level (one-tailed).
** Significant at the 0.01 level (one-tailed).
t-statistics based on White's standard errors are provided in parentheses.
For Panel B, all firms are classified into equally weighted quintile portfolios based on their rankings of MFACC. MFACC 1 comprises firms with the smallest MFACC (the smallest absolute forecast errors), while MFACC 5 comprises firms with the largest MFACC (the largest absolute forecast errors). The mean values of AFACC and MFACC are reported for each portfolio, and the differences are statistically tested using the paired t-test and Wilcoxon signed-rank test.
MFACC_t= absolute forecast error of MFE: |E_t − MF_t|/SP_t × 100%,
AFACC_t= absolute forecast error of following AFE: |E_t − AF_t|/SP_t × 100%,
AFDEVACC_t= the difference in forecast accuracy between AFE and MFE: AFACC_t − MFACC_t.
MF_t= MFE per share for year t that are announced in May of year t,
AF_t= AFE per share for year t that are publicized after MF_t in mid June of year t,
E_t= actual earnings per share for year t that are announced in May of year t + 1 (E_t and MF_t₊₁ are announced simultaneously), and
SP_t= share price at the beginning of year t (1 April of year t).

Moreover, as with Table 9, the equally weighted quintile portfolios based on the magnitude of MFACC are constructed, and the forecast accuracy of management and analysts' forecasts for each portfolio is compared. The results are presented in Panel B of Table 10 and show that analysts' forecasts become significantly more accurate than management forecasts as the forecast accuracy of management forecasts falls from MFACC 1 (firms with the smallest absolute forecast errors) to MFACC 5 (firms with the largest absolute forecast errors).

These findings imply that analysts are likely to make more adjustments to management forecasts that have higher absolute forecast errors in publicizing their own forecasts, and they provide further evidence for the analysts' awareness of systematic bias in management forecasts.

SUMMARY AND CONCLUSION

A major financial disclosure feature in Japan is that stock exchanges request firms to publicize forecasts of next year's key accounting figures. As a result, management forecasts of the upcoming year's earnings are announced simultaneously with the recently completed year's actual earnings at the annual earnings announcement. This article investigates the value relevance of MFE using the Ohlson (2001) framework that expresses firm value as a function of book value, current earnings and next year's expected earnings. The findings indicate that of the three accounting variables examined, MFE (changes in MFE) have the highest correlation and incremental explanatory power with stock price (returns). They also suggest that, in the presence of forecast earnings, current earnings serve as a benchmark from which future earnings growth can be inferred.

This article also examines the influence of management earnings forecasts on analysts' earnings forecasts. The results show that more than 90% of changes in analysts' forecasts are explained by management forecasts alone, and that the estimated coefficients of regressing AFE on MFE are not significantly different from one in eleven of the twenty-one years examined. Management earnings forecast information appears to have a great impact on analysts' expectations about firms' future earnings prospects. Further analysis reveals that the heavy dependence of analysts on management forecasts may partially be attributed to the relatively high forecast accuracy of management forecasts. Management forecasts appear to incorporate all available information at the time when they are published. Financial analysts, however, also modify management forecasts in publicizing their own forecasts when certain financial factors indicate that the credibility of management forecasts is in doubt.

Overall, the findings in this article suggest that management earnings forecasts provide the market and financial analysts with valuable information, and they present supportive evidence for the usefulness of management forecasts.

references

Ajinkya, B., and M. Gift, ‘Corporate Managers' Earnings Forecasts and Symmetrical Adjustments of Market Expectations’, Journal of Accounting Research, Vol. 22, No. 2, 1984.
10.2307/2490657
Web of Science® Google Scholar
Amir, E., and B. Lev, ‘Value-Relevance of Nonfinancial Information: The Wireless Communications Industry’, Journal of Accounting and Economics, Vol. 22, Nos 1−3, 1996.
Web of Science® Google Scholar
Baginski, S., and J. Hassell, ‘The Market Interpretation of Management Earnings Forecasts as a Predictor of Subsequent Financial Analyst Forecasts Revision’, The Accounting Review, Vol. 65, No. 1, 1990.
Web of Science® Google Scholar
Baginski, S., and J. Hassell, ‘Determinants of Management Forecast Precision’, The Accounting Review, Vol. 72, No. 2, 1997.
Web of Science® Google Scholar
Bamber, L. S., and Y. S. Cheon, ‘Discretionary Management Earnings Forecast Disclosures: Antecedents and Outcomes Associated with Forecast Venue and Forecast Specificity Choices’, Journal of Accounting Research, Vol. 36, No. 2, 1998.
10.2307/2491473
Web of Science® Google Scholar
Barth, M., ‘Valuation-Based Accounting Research: Implications for Financial Reporting and Opportunities for Future Research’, Accounting and Finance Vol. 40, No. 1, 2000.
10.1111/1467-629X.00033
Web of Science® Google Scholar
Barth, M., W. Beaver and W. Landsman, ‘The Relevance of the Value Relevance Literature for Financial Accounting Standard Setting: Another View’, Journal of Accounting and Economics, Vol. 31, Nos 1–3, 2001.
CAS Web of Science® Google Scholar
Beaver, W., ‘Perspectives on Recent Capital Market Research’, The Accounting Review, Vol. 77, No. 2, 2002.
10.2308/accr.2002.77.2.453
Web of Science® Google Scholar
Blacconiere, W., M. Johnson and M. Johnson, ‘Market Valuation and Deregulation of Electric Utilities’, Journal of Accounting and Economics, Vol. 29, No. 2, 2000.
10.1016/S0165-4101(00)00021-5
Web of Science® Google Scholar
Brown, L., ‘A Temporal Analysis of Earnings Surprises: Profits versus Losses’, Journal of Accounting Research, Vol. 39, No. 2, 2001.
10.1111/1475-679X.00010
Web of Science® Google Scholar
Brown, S., K. Lo and T. Lys, ‘Use of R² in Accounting Research: Measuring Changes in Value Relevance Over the Last Four Decades’, Journal of Accounting and Economics, Vol. 28, No. 2, 1999.
10.1016/S0165-4101(99)00023-3
Web of Science® Google Scholar
Butler, K., and H. Saraoglu, ‘Improving Analysts' Negative Earnings Forecasts’, Financial Analysts Journal, Vol. 55, No. 3, 1999.
10.2469/faj.v55.n3.2271
Web of Science® Google Scholar
Choi, J., and D. Ziebart, ‘Management Earnings Forecasts and the Market's Reaction to Predicted Bias in the Forecast’, Asia Pacific Journal of Accounting and Economics, Vol. 11, No. 2, 2004.
10.1080/16081625.2004.10510641
Google Scholar
Collins, D., E. Maydew and I. Weiss, ‘Changes in the Value-Relevance of Earnings and Book Values Over the Past Forty Years’, Journal of Accounting and Economics, Vol. 24, No. 1, 1997.
10.1016/S0165-4101(97)00015-3
CAS Web of Science® Google Scholar
Conroy, R., K. Eades and R. Harris, ‘A Test of the Relative Pricing Effects of Dividends and Earnings: Evidence from Simultaneous Announcements in Japan’, The Journal of Finance, Vol. 55, No. 3, 2000.
10.1111/0022-1082.00245
Web of Science® Google Scholar
Conroy, R., R. Harris and Y. Park, ‘Published Analysts' Earnings Forecasts in Japan: How Accurate are They? Pacific-Basin Finance Journal, Vol. 1, No. 2, 1993.
10.1016/0927-538X(93)90004-2
Google Scholar
Conroy, R., R. Harris and Y. Park, Analysts' Earnings Forecast Accuracy in Japan and the United States, The Research Foundation of the Institute of Chartered Financial Analysts, 1994.
Google Scholar
Conroy, R., R. Harris and Y. Park, ‘Fundamental Information and Share Prices in Japan: Evidence from Earnings Surprises and Management Predictions’, International Journal of Forecasting, Vol. 14, No. 2, 1998.
10.1016/S0169-2070(98)00029-6
CAS PubMed Web of Science® Google Scholar
Darrough, M., and T. Harris, ‘ Do Management Forecasts of Earnings Affect Stock Prices in Japan?’ in W. T. Ziemba, W. Bailey, and Y. Hamao (eds), Japanese Financial Market Research, North Holland, 1991.
Google Scholar
Eames, M., and S. Glover, ‘Earnings Predictability and the Direction of Analysts' Earnings Forecast Errors’, The Accounting Review, Vol. 78, No. 3, 2003.
10.2308/accr.2003.78.3.707
Web of Science® Google Scholar
Eames, M., S. Glover and J. Kennedy, ‘The Association Between Trading Recommendations and Broker-Analysts' Earnings Forecasts’, Journal of Accounting Research, Vol. 40, No. 1, 2002.
10.1111/1475-679X.00040
Web of Science® Google Scholar
Easton, P., ‘Security Returns and the Value Relevance of Accounting Data’, Accounting Horizons, Vol. 13, No. 4, 1999.
10.2308/acch.1999.13.4.399
Google Scholar
Ely, K., and G. Waymire, ‘Accounting Standard-Setting Organizations and Earnings Relevance: Longitudinal Evidence from NYSE Common Stocks, 1927−93’, Journal of Accounting Research, Vol. 37, No. 2, 1999.
10.2307/2491411
CAS Web of Science® Google Scholar
Francis, J., and K. Schipper, ‘Have Financial Statements Lost Their Relevance? Journal of Accounting Research, Vol. 37, No. 2, 1999.
10.2307/2491412
CAS Web of Science® Google Scholar
Frost, C., ‘Disclosure Policy Choices of UK Firms Receiving Modified Audit Reports’, Journal of Accounting and Economics, Vol. 23, No. 2, 1997.
10.1016/S0165-4101(97)00006-2
Web of Science® Google Scholar
Glantz, S., and B. Slinker, Primer of Applied Regression and Analysis of Variance, 2nd ed., McGraw-Hill, 2001.
Google Scholar
Greene, W., Econometric Analysis, 4th ed., Prentice Hall, 2000.
10.1111/0002-9092.00010
Google Scholar
Gu, Z., ‘Scale Factor, R², and the Choice of Levels versus Returns Models’, Journal of Accounting, Auditing and Finance, Vol. 20, No. 1, 2005.
10.1177/0148558X0502000104
Google Scholar
Hand, J., ‘Discussion of “Earnings, Book Values, and Dividends in Equity Valuation: An Empirical Perspective” ’, Contemporary Accounting Research, Vol. 18, No. 1, 2001.
10.1506/6A7C-74ML-TGBD-DYBW
CAS Web of Science® Google Scholar
Harris, T., M. Lang and H. Möller, ‘The Value Relevance of German Accounting Measures: An Empirical Analysis’, Journal of Accounting Research, Vol. 32, No. 2, 1994.
10.2307/2491281
Web of Science® Google Scholar
Hassell, J., R. Jennings and D. Lasser, ‘Management Earnings Forecasts: Their Usefulness as a Source of Firm-Specific Information to Security Analysts’, The Journal of Financial Research, Vol. 11, No. 4, 1988.
10.1111/j.1475-6803.1988.tb00091.x
Web of Science® Google Scholar
Hirst, E., L. Koonce and J. Miller, ‘The Joint Effect of Management's Prior Forecast Accuracy and the Form of its Financial Forecasts on Investor Judgment’, Journal of Accounting Research, Vol. 37 (Supplement), 1999.
10.2307/2491347
Web of Science® Google Scholar
Irani, A., ‘Determinants of Bias in Management Earnings Forecasts’, Accounting Enquiries, Vol. 10, No. 1, 2000.
Web of Science® Google Scholar
Kennedy, P., A Guide to Econometrics, 4th ed., The MIT Press, 1998.
Google Scholar
King, R., and J. Langli, ‘Accounting Diversity and Firm Valuation’, The International Journal of Accounting, Vol. 33, No. 5, 1998.
10.1016/S0020-7063(98)90012-7
CAS Google Scholar
Kothari, S., and J. Zimmerman, ‘Price and Return Models’, Journal of Accounting and Economics, Vol. 20, No. 2, 1995.
10.1016/0165-4101(95)00399-4
Web of Science® Google Scholar
Lev, B., and P. Zarowin, ‘The Boundaries of Financial Reporting and How to Extend Them’, Journal of Accounting Research, Vol. 37, No. 2, 1999.
10.2307/2491413
Web of Science® Google Scholar
Lo, K., and T. Lys, ‘The Ohlson Model: Contribution to Valuation Theory, Limitations, and Empirical Applications’, Journal of Accounting, Auditing and Finance, Vol. 15, No. 3, 2000.
10.1177/0148558X0001500311
Google Scholar
Maddala, G., Introduction to Econometrics, 2nd ed., Prentice Hall, 1992.
Google Scholar
Matsumoto, D., ‘Management's Incentives to Avoid Negative Earnings Surprises’, The Accounting Review, Vol. 77, No. 3, 2002.
10.2308/accr.2002.77.3.483
Web of Science® Google Scholar
Nobes, C., and R. Parker, Comparative International Accountings, 8th ed., Prentice Hall, 2004.
Google Scholar
Nwaeze, E., ‘Regulation and the Valuation Relevance of Book Value and Earnings: Evidence From the United States’, Contemporary Accounting Research, Vol. 15, No. 4, 1998.
10.1111/j.1911-3846.1998.tb00571.x
Google Scholar
Ohlson, J., ‘Earnings, Book Values, and Dividends in Equity Valuation’, Contemporary Accounting Research, Vol. 11, No. 2, 1995.
10.1111/j.1911-3846.1995.tb00461.x
Google Scholar
Ohlson, J., ‘Earnings, Book Values, and Dividends in Equity Valuation: An Empirical Perspective’, Contemporary Accounting Research, Vol. 18, No. 1, 2001.
10.1506/7TPJ-RXQN-TQC7-FFAE
Web of Science® Google Scholar
Ota, K., ‘The Impact of Price and Return Models on Value Relevance Studies: A Review of Theory and Evidence’, Accounting Research Journal, Vol. 16, No. 1, 2003.
Google Scholar
Patell, J., ‘Corporate Forecasts of Earnings per Share and Stock Price Behavior: Empirical Tests’, Journal of Accounting Research, Vol. 14, No. 2, 1976.
10.2307/2490543
Web of Science® Google Scholar
Pownall, G., and G. Waymire, ‘Voluntary Disclosure Credibility and Securities Prices: Evidence From Management Earnings Forecasts, 1969−73’, Journal of Accounting Research, Vol. 27, No. 2, 1989.
10.2307/2491233
Web of Science® Google Scholar
Richardson, S., S. Teoh and P. Wysocki, Tracking Analysts' Forecasts Over the Annual Earnings Horizon: Are Analysts' Forecasts Optimistic or Pessimistic?, Working Paper, University of Michigan, 1999.
Google Scholar
Richardson, S., S. Teoh and P. Wysocki, ‘The Walkdown to Beatable Analyst Forecasts: The Role of Equity Issuance and Insider Trading Incentives’, Contemporary Accounting Research, Vol. 21, No. 4, 2004.
10.1506/KHNW-PJYL-ADUB-0RP6
CAS Web of Science® Google Scholar
Roake, T., and G. Davidson, The Private Securities Litigation Reform Act of 1995, Fenwick & West LLP, 1996.
Google Scholar
Rosen, R., ‘The Statutory Safe Harbor for Forward-Looking Statements after Two and a Half Years: Has it Changed the Law? Has it Achieved What Congress Intended? Washington University Law Quarterly, Vol. 76, No. 2, 1998.
Google Scholar
Siegel, S., and J. Castellan, Nonparametric Statistics for the Behavioral Sciences, 2nd ed., McGraw-Hill, 1988.
Web of Science® Google Scholar
Skinner, D., and R. Sloan, ‘Earnings Surprises, Growth Expectations, and Stock Returns or Don't Let an Earnings Torpedo Sink Your Portfolio’, Review of Accounting Studies, Vol. 7, Nos 2–3, 2002.
10.1023/A:1020294523516
Google Scholar
Theil, H., Principles of Econometrics, John Wiley & Sons, 1971.
Google Scholar
Vuong, Q., ‘Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses’, Econometrica, Vol. 57, No. 2, 1989.
10.2307/1912557
Web of Science® Google Scholar
Waymire, G., ‘Additional Evidence on the Information Content of Management Earnings Forecasts’, Journal of Accounting Research, Vol. 22, No. 2, 1984.
10.2307/2490672
Web of Science® Google Scholar
Williams, P., ‘The Relation Between a Prior Earnings Forecast by Management and Analyst Response to a Current Management Forecast’, The Accounting Review, Vol. 71, No. 1, 1996.
CAS Google Scholar

Footnotes

1 A survey reports that already in 1980, more than 90% of listed firms excluding those in the financial sector provided management forecasts.

2 The condensed financial statements (‘Kessan Tanshin’) are available from the Tokyo Stock Exchange (TSE) website (http://www.tse.or.jp).

3 All forecasts are publicized in the form of point forecasts except for dividends per share that are sometimes provided in the form of range forecasts.

4 Throughout the article, ‘earnings’ means ordinary income, net of tax. However, tax applicable to ordinary income is not reported in the income statement in Japan. Therefore, ordinary income, net of tax, is estimated using the following formula:

where OI_t is ordinary income for year t, CorpTR_t is the corporation tax rate for year t, and ResidentTR_t is the residents' tax rate for year t. The residents' tax is levied by local municipalities and its tax rate differs slightly across regions. The standard tax rate is used in this study. The corporation business tax is ignored until 1998, because it is included in general and administrative expenses until 1998. For the year 1999, the effective tax rate is calculated and used.

5 Amir and Lev (1996, note 9) also use both the price and the return models citing the same reason.

6 I owe this point to an anonymous reviewer.

7 Since preceding AFE are available only after 1991, the sample period for this analysis is reduced to 1991 to 1999.

8 Inflation-adjustment is done by using the consumer price index released from the Statistics Bureau of the Ministry of Internal Affairs and Communications.

9 The sample period is limited to 1979–99 due to the difficulty in collecting forecast data. Management and analysts' earnings forecasts are hand-gathered from the Nihon Keizai Shinbun (the major business newspaper in Japan) and the Kaisha Shikihou (the Japan company quarterly handbook) respectively.

10 The results presented later are qualitatively similar when observations in the extreme 0.5%, 1.5% and 2.0% are removed.

11 The two factors in the two-way ANOVA are accounting variables and time.

12 See Glantz and Slinker (2001) for Tukey's multiple comparison method and Siegel and Castellan (1988) for the Friedman test.

Citing Literature

Volume46, Issue1

March 2010

Pages 28-59

The Value Relevance of Management Forecasts and Their Impact on Analysts' Forecasts: Empirical Evidence From Japan

Abstract

BACKGROUND ON JAPAN'S MANAGEMENT FORECASTS