Discussion of Penman

This quote exemplifies the importance placed on intangibles and their recognition. In simple terms, Penman's retort is that if the intellectual property in the corn is valuable economically, its effect will appear in sales and income. By using this information, a stock analyst will be informed of the firm's large and increasing sales of corn or corn products, and will value it on that basis, excusing the accountant from a difficult if not nonsensical job of attaching a value to the IP in the corn (if indeed it is the IP rather than what was already in the corn, or in its marketing, or in the marketing of the IP, that is driving those healthy sales).

The analyst's job is to value the company or its securities by assimilating all sources of relevant information. Paraphrasing Penman, it is hard to imagine that this will be assisted by identifying all the intangible assets in the company ‘one-by-one’, as if there is some end to them, and then adding their values together, and then to the sum of the tangibles. An accountant may be tempted to do this, particularly given the increased fees on offer and the allure of doing ‘valuation’ rather than just ‘counting’, but it is hard to imagine what the end result would mean, or to think of it as a proxy for the kind of value estimate that an analyst produces by looking at the firm as a whole, rather than as a sum of tangible and intangible assets (more or less arbitrarily defined). In other words, if the accountant's underlying objective is to achieve a book-to-market ratio of one, and thus somehow reconcile or validate his own work against the stock market, then the well known problem of the holistic asset value V(x+y+z) not equalling the sum of its components, V(x) +V(y) +V(z), or even some permutation such as V(x) +V(y+z), suggests that he will be lucky to succeed (unless something like ‘goodwill’ is plugged in as the balancing item).

Extending this argument, Penman maintains that accounting adds value not by mimicry or by justifying itself according to how closely book value matches stock market value or analysts’ consensus value, but as a source of independent and occasionally contrary, if not unwelcome, information. For example, when a dot-com stock is trading at a very high price, it may greatly assist the investment community if its balance sheet appearance remains clearly in keeping with there being few unexpired tangible assets, rapidly dwindling cash in the bank, and no sales contracts yet at all. The fashionable view may be that this sort of ‘facts-based’ accounting misses the point, since the firm's one key asset is its intellectual property or human capital. But if that is the case, there are other ways to get such innately qualitative information into the marketplace, and to demonstrate its veracity more convincingly than can be done with one extra line in the balance sheet. For Penman, the conventional transactions-based historical cost accounting representation of the firm stands as a stark reminder that as yet, at least, the firm's intellectual property has not produced any cash inflow, only losses. This is not an error in the making, even potentially, since as soon as cash flows arise, the accountant reports them and the analyst uses that accounting information (e.g., sales and growth in sales), combined with what is inferred from other sources about the firm's intellectual or other intangible foundations, to make an overall assessment of its economic value.

Penman's view of accounting as a way to ‘test’ market sentiment is consistent with his philosophical positioning of accounting as essentially a forecasting tool (cf. Barth et al., 2001). If we think of accounting numbers as forecasts or as signals on which to condition forecasts,¹ then their essential attributes can be explicated in the terms of information economics or, more specifically, the Bayesian framework for combining signals from different, and possibly dependent, sources. In the remainder of this comment, I propose a theoretical model that amplifies Penman's way of thinking by exhibiting the value of independence in accounting statements, interpreted as signals or forecasts. Pushed further, this model implies that, provided signal accuracy is maintained, accounting information is of greatest value to the user when it is negatively correlated with other competing signals of value. The intellectual roots of models such as this and those employed by O'Hara are in Bayesian statistics, where there is an extensive body of theory by which to combine signals and measure the value of information relative to what is contained already in a combined forecast. See, for example, Winkler (1981), Clemen and Winkler (1986) and Clemen et al. (1995).

The following model is similar to the Bayesian model of market-maker belief revision developed in a series of finance and accounting papers by Easley and O'Hara (e.g., 1987, 1992, 2004, 2008; Easley et al., 2002). The firm or security has two possible future values, V=High or V=Low. There are two sources of relevant information, s₁ and s₂. Signal s₁ represents a consensus of broker advice, reduced to a single recommendation, s₁=Buy or s₁=Hold. The second signal is a measure of accounting ‘income’, taking values s₂=‘+’ (up) or s₂=‘−’ (down), relative to some benchmark or prior expectation.

The likelihoods (or ‘error characteristics’) of these two signals are

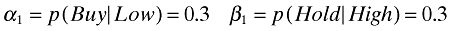
respectively. Note that signals s₁ and s₂ have the same error probabilities. These are all set quite arbitrarily at 0.3, implying that individually the two signals are equally good. This assumption avoids arguments about whether the market or the accountant offers better information, and is not critical to the results of the analysis. Likewise, the constant error rate of 30 per cent could be changed without mattering to the outcome.

By the law of complete probability,

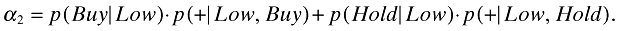
Hence, p(+|Low, Hold) = (α₂−α₁p(+|Low, Buy))/(1 −α₁).

Similarly,

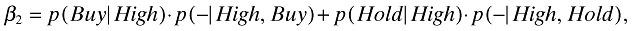
giving, p(−|High, Hold) = (β₂− (1 −β₁)p(−|High, Buy))/β₁.

It follows, therefore, that by setting two of the probabilities that describe the conditional dependence of s₂ on s₁, say p(+|Low, Buy) and p(−|High, Buy), the other six are also determined, as functions of the preset constants α₁, α₂, β₁, β₂.

Given these specifications, the probability of V=High conditional on the combined evidence, s₁ and s₂, p(High|s₁, s₂), is found using Bayes’ theorem

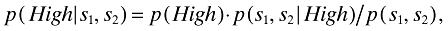
where p(s₁, s₂) =Σ_vp(V)p(s₁|V)p(s₂|V,s₁). In the example calculations below, we assume a uniform prior distribution, p(High) =p(Low) = 0.5, but again this is quite arbitrary and the same results obtain with any prior p(High) not too close to zero or one (certainty).

The expected (average) accuracy of the posterior distribution depends not only on the individual accuracy (‘error characteristics’) of the two signals, but also on their stochastic dependence. To examine the effect of dependence between s₁ and s₂, either positive or negative, the information content of the posterior probability distribution is measured by its entropy or expected negative log score

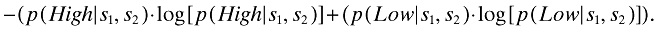
This measure, denoted hereafter by Entropy(s₁, s₂), lies between an ideal of zero and a worst case of −(0.5 log[0.5]+ 0.5 log[0.5]) = 0.693. Note that the highest entropy (least informative) posterior probability distribution is p(High|s₁, s₂) = 0.5. Zero entropy represents certainty and occurs when p(High|s₁, s₂) ∈ {0, 1}. Related explanation is provided by O'Hara (1995, pp. 85–6, 171–2). For theory on the possible economic interpretation of entropy and its relationship to other measures of statistical information or the ‘distance between two probability distributions’, see Daley and Vere-Jones (2004), Roulston and Smith (2002) and Jose et al. (2008).

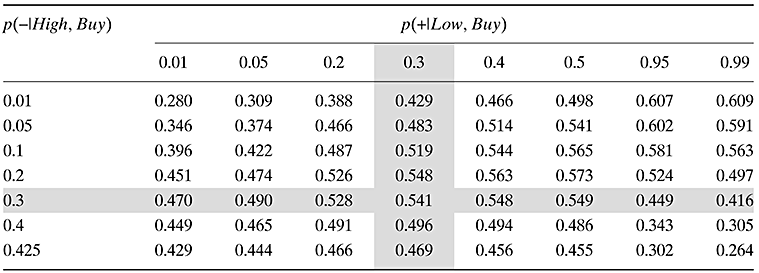
Table 1 shows calculated values of the expected entropy of the posterior probability distribution based on the combination of s₁ and s₂, {s₁, s₂}

Table 1.
EXPECTED ENTROPY OF POSTERIOR PROBABILITY DISTRIBUTION BASED ON THE COMBINATION OF SIGNALS s₁ AND s₂ AS A FUNCTION OF LIKELIHOODS p(+|Low, Buy) AND p(−|High, Buy)

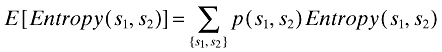(1)

over a feasible range of possible values of p(+|Low, Buy) and p(−|High, Buy). It is important to focus on the conditional error probabilities as they determine whether signal s₂ adds much information (concerning V) to what is already entailed within s₁. If, in the extreme, p(+|Low, Buy) = 1and p(−|High, Buy) = 0 (implying therefore p(+|High, Buy) = 1), the two signals are always ‘the same’ and hence neither adds anything to the other (individually they remain equally informative). From the user's perspective, this is the danger that accounting presents when it ties its measures too rigidly to the signals emanating at the same time from markets or market sentiment (embodied for example in analyst-consensus forecasts).

The expected entropy values (1) set out in Table 1 are presented as functions of p(+|Low, Buy) and p(−|High, Buy). The point at which the two signals s₁ and s₂ are statistically independent is where p(+|Low, Buy) =p(+|Low) =α₂ (= 0.3) and p(−|High, Buy) =p(−|High) =β₂ (= 0.3). This point, highlighted by the shaded intersection in Table 1, has expected entropy of 0.541.

Positive dependence between s₁ and s₂ requires that either p(+|Low, Buy) > 0.3 or p(−|High, Buy) = 1 −p(+|High, Buy) < 0.3. Negative dependence arises the same way, but with the inequality signs reversed. Signal s₂ is thus more positively correlated with s₁ as we move towards the north-east corner of Table 1. The extremity is where signal s₂ has conditional error characteristics p(+|Low, Buy) = 1 and p(−|High, Buy) = 0, as noted above, in which case it is redundant and the expected entropy is 0.611 (which could be achieved with either signal s₁ or s₂ on its own).

The main result shown in Table 1 is that even though the error characteristics α₁, α₂, β₁, β₂ of the two individual signals are held constant, their joint information content, measured by the expected entropy of the resulting posterior distribution, tends to fall noticeably as they become more positively dependent.

An ideal signal is not only accurate of itself, in the sense that it has low error frequencies, it also has a tendency to be accurate when other signals are not. In this way it can protect the decision maker from over-exuberance, rather than confirm existing prejudices and fuel the flames. The theoretical information value of a signal is a trade-off between being accurate and being different. Redundancy or herding is a known tendency of professional forecasters and stock analysts, and accountants may feel the same temptation when producing book values that emulate stock market values, but to be most valuable (informative) an expert opinion should have a contrarian or at least independent basis, while not being so odd or narrowly founded that it becomes inaccurate (in the sense that its error frequencies become too high).

This is essentially Penman's point. To be of greatest use, accounting reports must be ‘accurate’ or informative of themselves—as has always been understood. The much less well understood requirement of informative accounting, underpinning Penman's position on valuing (indeed not valuing) intangibles, is its role as an antidote against information cascades. The idea of an information cascade (e.g., Bikhchandani et al., 1992, 1998) is that when our evidence is scarce, and we see a credible authority reporting in a certain way, we tend to follow even though unbeknown to us that authority's own evidence is just as weak. And when another party sees these two reports both leaning one way, it tends to follow suit, even though its private information may have pointed somewhat in the other direction. From this juncture on, any further opinion provider will naturally feel comforted by what appears to be a unanimous position, and, by falling into line, will only add to the illusion of overwhelming agreement. This is the mechanism that explains what is known sometimes as rational herding.

The possibility of accounting as potentially a contributor, consciously or otherwise, to an information cascade is explained in the following passage from a related paper by Nissim and Penman (2008, pp. 33–4) on the merits of fair value accounting:

CONCLUSION

There is an important cultural issue left unanswered by the call for accounting to exert its own way of looking at things, and adhere not only to a creed of professional or personal independence, but also to methods that say something more than what is evident already in market prices. That is whether accounting should establish itself as a means to systematically prick ‘bubbles’ and perhaps correct for other behavioural phenomena distorting the pool of information and sentiment that drives them. The model presented in this commentary supports not merely the long established ideal of accounting information being ‘independent’. It goes on to show that if possible the signals produced by accounting or any formal information system should ideally be contrarian relative to competing information, albeit not to the extent that their statistical accuracy suffers so much that they are less valuable on the whole. For more on this compromise between being (often) right and being (often) different, see Nau (2002) and Johnstone (2007).

In a companion paper, Penman proposes that it is asking too much of accounting to be the constant naysayer or counterweight to whatever error exists in a consensus of all its competing information sources.

It should be noted, however, that ‘independence’ in the sense that Nissim and Penman use the term means (simplistically perhaps) that accounting signals are based on different measures or different observations than much of the opinion impounded in market prices. This of itself can make accounting measures negatively correlated with the market or with competing signals. More likely, however, since it is so hard in general to be both contrary and correct, and because analysts make use of accounting reports in assessing firm values, there is surely a natural positive correlation between analysts’ values and accounting values, at least over the long run.² Penman's position is that this correspondence should not be seen as defining the accounting objective, contrary to what remains a widely received view: