Trade costs in empirical New Economic Geography
Abstract
Trade costs are a crucial element of New Economic Geography (NEG) models. Without trade costs there is no role for geography. In empirical NEG studies the unavailability of direct trade cost data calls for the need to approximate these trade costs by introducing a trade cost function. In doing so, hardly any attention is paid to the (implicit) assumptions and empirical consequences of the particular trade cost function used. Based on a meta-analysis of NEG market access studies as well as on the results of estimating the NEG wage equation for a uniform sample while using different trade costs functions, we show that the relevance of the key NEG variable, market access, depends nontrivially on the choice of trade cost function. Next, we propose an alternative way to approximate trade costs that does not require the specification of a trade cost function, the so called implied trade costs approach. Overall, our results stress that the specification of trade costs can matter a lot for the conclusions reached in any empirical NEG study. We therefore call for a much more careful treatment of trade costs in future empirical NEG studies.
Resumen
Los costos de comercio son un elemento crucial de los modelos de la Nueva Geografía Económica (NEG, siglas en inglés). Sin los costos de comercio no hay un rol para la geografía. En estudios empíricos de NEG, la falta de disponibilidad de datos de costos directos de comercio directo crea la necesidad de estimar estos costos de comercio mediante la introducción de una función de costos de comercio. Al hacer esto, apenas se presta atención a las suposiciones (implícitas) y consecuencias empíricas de la función de costo utilizada en particular. Basado en un meta análisis de estudios de acceso de mercado de NEG, así como en los resultados de estimar la ecuación salarial de NEG para una muestra uniforme al tiempo que utilizando diferentes funciones de costos de comercio, mostramos que la relevancia de la variable clave para la NEG, acceso a mercados, depende considerablemente de la elección de la función de costos de comercio. A continuación, proponemos una alternativa para estimar costos de comercio que no requiere especificar una función de costos de comercio, el llamado enfoque de costos de comercio implícitos. En resumen, nuestros resultados insisten en que el especificar los costos de comercio puede tener mucha importancia para las conclusiones alcanzadas en cualquier estudio empírico de NEG. Pedimos por tanto un tratamiento mucho más cuidadoso de los costos de comercio en futuros estudios empíricos de NEG.

1 Introduction
Trade costs are a key element of new economic geography models. Without trade costs there is no role for geography (see e.g., Krugman 1991; Venables 1996; Puga 1999). It is therefore not surprising that trade costs are also an important ingredient of empirical studies in NEG. They are, for example, a vital ingredient of a region's or country's (real) market access (Head and Mayer 2004; Redding and Venables 2004).
The empirical specification of trade costs is, however, far from straightforward.1 Problems with the measurement of trade costs arise because trade costs are very hard to quantify. They most likely consist of various subcomponents that potentially interact, overlap and/or supplement each other. Obvious candidates are transport costs, tariffs and non-tariff barriers (NTBs), but also less tangible costs arising from, for example, institutional and language differences have been incorporated in previous studies (Hummels 2001; Anderson and van Wincoop 2004).
Given the unavailability of a direct measurement of bilateral trade costs, all empirical NEG studies turn to the indirect measurement of trade costs. In doing so, they closely follow the empirical trade literature (see Anderson and van Wincoop 2004 for a survey of the latter) and assume a so-called trade cost function. This trade cost function aims to proxy the unobservable trade costs by combining information on observable trade cost proxies such as distance, common language, tariffs, and adjacency with functional form assumptions that specify how the included trade cost proxies combine to provide an approximation of actual trade costs. The assumptions made about this trade cost function, for example, functional form, parameter hetero- or homogeneity, which observable trade cost proxies to include, or how to estimate each proxy's effect, all potentially have a (crucial) effect on the results of any empirical NEG study.
As the measurement of trade costs is only a means to an end in the empirical new economic geography (NEG) literature, the potential impact of the choice of trade cost specification for the alleged (ir)relevance of market access is typically ignored. Virtually all empirical studies in NEG simply use one particular trade cost function and do not (or only marginally) address the sensitivity of their results to their chosen approximation of trade costs.
This paper aims to overcome this lack of attention. We systematically assess whether the conclusions regarding the relevance of market access depend on the choice of trade cost approximation by estimating the NEG wage equation (empirical work on NEG has heavily focused on verifying this relationship). We do this in two different ways. First we perform a meta-analysis of existing empirical NEG wage equation studies to see if the size and significance of the estimated market access coefficient depends on the trade cost function used to approximate trade costs. Second, we estimate the NEG wage equation for a uniform sample of 60 countries using different trade costs functions, and again verify whether this results in nontrivially different estimates of the relevance of market access. Both the results of the meta-analysis and our same-sample-different-trade-costs-approximations results show that the choice of trade cost function can have non-trivial effects when it comes to the empirical relevance of market access in determining its wage levels. Moreover the trade cost function used not only matters in terms of the size or the significance of the market access coefficient, but also in terms of the spatial or geographical reach of income shocks.
Given this sensitivity, we finally suggest an alternative strategy that does not require the specification of a trade cost function. This strategy uses the information contained in bilateral trade flows and calculates so-called implied trade costs based on a ‘trick’ with the trade equation that follows directly from NEG theory. By making two additional assumptions regarding internal trade costs on the one hand and the symmetry of bilateral trade costs on the other hand, Head and Ries (2001) show that one can directly infer trade costs from bilateral trade flows.2 Notwithstanding these two assumptions, the use of implied trade costs avoids many of the arbitrary (and oftentimes un-testable) assumptions made when using a trade cost function to approximate trade costs. Given the problems surrounding the specification of a trade cost function, we argue that the use of implied trade costs constitutes an interesting alternative.
Overall, and although we are unable to unequivocally prove a best way to approximate trade costs, we view our paper as a call for much more attention in empirical research in NEG to the way trade costs are dealt with. Trade costs are one of the most important ingredients of any theoretical contribution in NEG. We hope that future empirical work will do more justice to this important role, and that more attention will be paid to the sensitivity of results with respect to the specific choices with respect to the trade costs approximation.
2 NEG, the wage equation and the importance of trade costs
Before turning to the empirical contribution of our paper, we briefly set out a standard theoretical NEG model. Our exposition is largely based on the seminal paper by Redding and Venables (2004).3 We focus on the crucial role of trade costs in predicting the spatial wage structure that lies at the heart of virtually all empirical NEG studies.
2.1 NEG theory and the wage equation
Assume the world consists of i= 1, . . . , R regions,4 each home to an agricultural and a manufacturing sector. In the manufacturing sector, firms operate under internal increasing returns to scale, represented by a fixed input requirement ciF and a marginal input requirement ci. Each firm produces a different variety of the same good under monopolistic competition using the same Cobb-Douglas technology combining two different inputs. The first is an interregionally immobile factor, with price wi and input share β, the second is an interregionally mobile factor with price vi and input share γ, where γ+β=1.5
Manufacturing firms sell their variety to all regions and this involves shipping the goods to foreign markets. This is where trade costs come in: these are assumed to be of the iceberg-kind and the same for each variety produced: in order to deliver a quantity xij(z) of variety z produced in region i to region j, xij(z)Tij has to be shipped from i. A proportion (Tij − 1) of output is ‘paid’ as trade costs (Tij= 1 if trade is costless).6 Taking these trade costs into account gives the following profit function for each firm in region i,
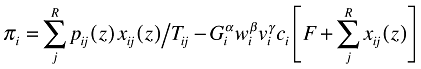 (1)
(1)where pij(z) is the price of a variety produced in region i and Gj is the price index for manufacturing varieties that follows from the assumed CES-structure of both consumer and producer demand for manufacturing varieties (see below).
Turning to the demand side, each firm's product is both a final (consumption) and an intermediate (production) good. It is assumed that these products enter both utility and production in the form of a CES-aggregator with σ the elasticity of substitution between each pair of product varieties. Given this CES-assumption about both consumption and intermediate production, it follows directly that in equilibrium all product varieties produced in region i are demanded by region j in the same quantity (for this reason varieties are no longer explicitly indexed by z). Denoting region j's expenditure on manufacturing goods (coming from both firms and consumers) as Ej, region j's demand for each product variety produced in region i can be shown to be (following utility maximization and cost minimization on behalf of consumers and producers respectively):
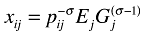 (2)
(2)Maximization of profits (1) combined with demand as specified in (2) gives the well-known result in the NEG literature that price differences between regions in a good produced in region i only arise from differences in trade costs, namely, pij=piTij with pi a constant markup over marginal costs specific to region i independent from the final export destination j:
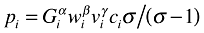 (3)
(3)Next, free entry and exit drive (maximized) profits to zero, which pinpoints equilibrium output per firm at 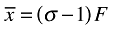 . Finally combining this equilibrium output with equilibrium price (3) and equilibrium demand (2), and noting that in equilibrium the price of the interregionally mobile factor of production will be the same across regions (vi=v for all i), gives the equilibrium wage of the composite factor of immobile production, namely, labour:
. Finally combining this equilibrium output with equilibrium price (3) and equilibrium demand (2), and noting that in equilibrium the price of the interregionally mobile factor of production will be the same across regions (vi=v for all i), gives the equilibrium wage of the composite factor of immobile production, namely, labour:
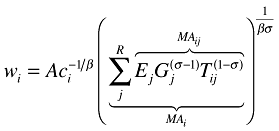 (4)
(4)where A is a constant (that contains among others the substitution elasticity, σ, and the fixed costs of production, F).
Equation (4) is NEG's wage equation. This equation lies at the heart of all empirical studies in NEG that try to establish whether, as equation (4) indicates, there is a spatial wage structure with wages being higher in economic centres (e.g., Mion 2004; Redding and Venables 2004; Hanson 2005; Brakman et al. 2006; Knaap 2006).7 A region's manufacturing wage level is a function of a region's level of technology, ci, that determines marginal costs, and, most importantly for our present purposes, real market access 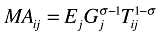 : a trade cost weighted sum of all regions' market capacities. Note that market access stresses an important role of economic geography: the closer (or better connected) a region to other (big) regional markets, the higher its market access. Trade costs play a crucial role in (4). The lower trade costs, the higher a region's market access, the higher the wages that firms can offer their workers to remain profitable. Trade costs are thus of vital importance in determining the spatial distribution of wages.
: a trade cost weighted sum of all regions' market capacities. Note that market access stresses an important role of economic geography: the closer (or better connected) a region to other (big) regional markets, the higher its market access. Trade costs play a crucial role in (4). The lower trade costs, the higher a region's market access, the higher the wages that firms can offer their workers to remain profitable. Trade costs are thus of vital importance in determining the spatial distribution of wages.
2.2 The trade costs function
The relatively simple iceberg specification of trade costs that is used in all theoretical NEG models, does not specify in any way what trade costs are composed of. It is precisely the need to specify Tij more explicitly in empirical research that motivates this paper. Given the unavailability of a direct measurement of bilateral trade costs, empirical NEG studies turn to the indirect measurement of trade costs (see Hummels 2001; Anderson and van Wincoop 2004 for a detailed discussion about the inability of directly observing trade costs).
All NEG papers that estimate wage equation (4) specify a trade cost function: a function that combines observable proxies of trade costs with assumptions regarding the unobservable components of trade costs to approximate actual trade costs. In its most general form a trade cost function is:
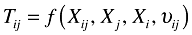 (5)
(5)The trade costs involved in shipping goods from region i to region j are a function f of cost factors that are specific to the importer or the exporter (Xj and Xi respectively), such as infrastructure, institutional setup or geographical features of a region (access to the sea, mountains), bilateral cost factors related to the actual journey from j to i, Xij, such as transport costs, tariffs, sharing a common border, language barriers, membership of a free trade union, etc, and unobservable factors, υij. Given that actual transport cost data is mostly unavailable, these are in turn usually proxied by bilateral distance, but sometimes also actual travel times or population weighted distance measures are used (see Appendix A for an overview of trade cost functions used in several empirical NEG studies).
Following Bosker and Garretsen (2010), who in turn base themselves on Anderson and van Wincoop (2004), the actual trade cost function used involves assumptions regarding: (i) functional form [f in (5)] specifying how the different included observed trade cost proxies together determine trade costs (e.g., multiplicatively vs. additively (Hummels 1999), or an exponential vs. a power distance function?); (ii) variables included (which set of region-specific and bilateral trade costs proxies to include?); (iii) regularity conditions (heterogeneity between regions in the impact of trade costs, for example, the distance penalty may be higher in Africa than in Europe); (iv) modeling internal trade costs; (v) how to deal with the unobservable component of trade costs; and (vi) estimating the trade cost function's parameters (which estimator to use, how to deal with zero trade flows?).
Given all these issues8 that one has to decide upon when using a trade cost function to approximate trade costs, two questions immediately come to mind. First, is the specification of a trade cost function without problems or does the choice for a specific trade cost function nontrivially affect the empirical results when estimating the NEG wage equation? Second, if the trade cost specification is indeed not without its problems, is there perhaps an alternative estimation strategy to approximate trade costs that does not involve the specification of a trade cost function?
The first question will be taken up in the next section and the second question is the topic of Section 4. In Section 3, we first perform a meta-analysis of NEG wage equation studies to assess whether the estimated effect of market access systematically differs when using different trade cost specifications. In the second part of Section 3, we focus on a uniform sample of 60 countries. Similar to the meta-analysis, but now using one and the same sample we verify whether the choice of trade cost function affects the conclusions reached regarding the relevance of market access when estimating the NEG wage equation.
The second question is answered in Section 4 where we propose an alternative way to proxy trade costs. This method, which we call implied trade costs, uses two additional assumptions as well as a relationship between bilateral trade flows and bilateral trade costs from NEG theory that together allow for the calculation of trade costs without having to specify a trade cost function.
3 Market access and its sensitivity to the trade cost function used
Before turning to the estimation results, we first briefly outline the two main empirical strategies (see Head and Mayer 2004) that are used in empirical NEG studies to estimate the wage Equation (4). We discuss these explicitly as they each estimate the trade cost function's parameters in a different way.
3.1 How to estimate the wage equation?
Taking logs on both sides of (4) gives the following non-linear equation that can be estimated:
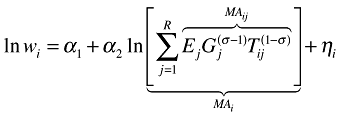 (6)
(6)where ηi captures the technological differences, ci, between regions that typically consists of both variables that are correlated (modelled by including e.g., measures of physical geography or educational quality) and/or variables that are uncorrelated (modelled by an i.i.d. lognormal disturbance term) with market access. The α's are the estimated parameters from which in principle the structural NEG parameters can be inferred (see e.g., Redding and Venables, 2004; Hanson, 2005).
The first empirical strategy to estimate (4) was introduced by Hanson (2005) and involves the direct non-linear estimation of (6). Studies that also use this direct non-linear estimation strategy include Brakman et al. (2004; 2006) and Mion (2004). All these studies use a trade cost function to approximate Tij. The trade cost function used is directly substituted for Tij in (6). Its parameters are jointly estimated along with the parameters of the wage equation.
The second strategy stems from Redding and Venables (2004).9 Instead of directly estimating (6), this estimation strategy first makes use of the trade equation that follows from NEG theory by aggregating (2) the demand from consumers in region j for a good produced in region i over all firms producing in region i:
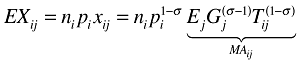 (7)
(7)Exports from region i to region j depend on the ‘supply capacity’, 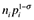 , of region i (the product of the number of firms and their price competitiveness), the ‘market capacity’,
, of region i (the product of the number of firms and their price competitiveness), the ‘market capacity’, 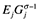 , of region j and the bilateral trade costs Tij between i and j. Estimating (7) one obtains estimates of both market capacity and bilateral trade costs that can be used (see Redding and Venables 2004 for the details) to construct each region's market access (using the MAij term from (7) in (6)). These constructed values of market access are subsequently used to estimate (6). All empirical NEG studies using this two-step procedure also approximate trade costs by specifying a trade cost function. However, and very different from the direct estimation strategy, the parameters of the distance function are not jointly estimated with the parameters of the NEG wage equation. Trade costs enter in the first step, when estimating the trade equation. The parameters of the trade cost function are estimated separately from the parameters of the wage equation. They are, in the first step, jointly estimated with each region's market capacity and subsequently used in the construction of the predicted values of market access. The parameters of the wage equation are then estimated in a second step.
, of region j and the bilateral trade costs Tij between i and j. Estimating (7) one obtains estimates of both market capacity and bilateral trade costs that can be used (see Redding and Venables 2004 for the details) to construct each region's market access (using the MAij term from (7) in (6)). These constructed values of market access are subsequently used to estimate (6). All empirical NEG studies using this two-step procedure also approximate trade costs by specifying a trade cost function. However, and very different from the direct estimation strategy, the parameters of the distance function are not jointly estimated with the parameters of the NEG wage equation. Trade costs enter in the first step, when estimating the trade equation. The parameters of the trade cost function are estimated separately from the parameters of the wage equation. They are, in the first step, jointly estimated with each region's market capacity and subsequently used in the construction of the predicted values of market access. The parameters of the wage equation are then estimated in a second step.
Given the different ways in which these two empirical strategies identify the parameters in the trade cost function we will explicitly focus on each of these two estimation strategies separately in the remainder of the paper.
3.2 Meta-analysis: Does the trade cost specification matter? – part I
The use of meta-analyses has been quite common in the social and medical sciences since the 1970s, but it is only fairly recently that meta analyses are used in economics. A meta-analysis combines results regarding one particular estimate (e.g., the effect of distance on exports – see Disdier and Head 2008) from already existing empirical studies. The goal is to see if the observed variation in certain estimates (here, the size of the market access coefficient in NEG wage equation studies) can be seen as a result of differences in the underlying model specification, the sample used, the time period involved, the estimation technique applied, etc. Meta analyses in economics have been done on topics like economic growth (Abreu et al. 2005), agglomeration effects (de Groot et al. 2007), international trade (Linders 2006; Disdier and Head 2008), currency unions (Rose and Stanley 2005), or labour economics (Card and Krueger 1995). Most closely related to our topic, Disdier and Head (2008), perform a meta-analysis on the distance effect in bilateral trade or gravity studies. To the best of our knowledge, we are the first to use a meta-analysis on the size of the estimated coefficient on market access in NEG wage equation studies.
To carry out a meta-analysis certain requirements have to be met. Most importantly, a sufficient number of studies on the topic of interest have to have been carried out in the past to allow for a meaningful analysis. To conduct our meta-analysis, we have therefore collected 262 estimates of the coefficient on market access in [α2 in (6)] from 22 different papers. Appendix B lists these papers along with the number of estimates of the market access coefficient that they each contain. All these papers approximate trade costs by specifying a trade cost function. Our main interest is to verify whether the estimated market access coefficient is systematically related to how each study specifies its trade cost function. We therefore split the sample according to three different characteristics of the trade cost function.
- 1
An exponential vs. a power distance function to model the transport cost component of trade costs.10
- 2
A multiplicative trade cost function that includes more trade cost proxies that simply distance vs. one that includes only distance.
- 3
If a multiplicative trade cost function is used: region specific trade cost proxies (e.g., quality of region's infrastructure) are included vs. no region specific trade cost proxies (i.e., only bilateral proxies such as distance) are included.
Table 1 shows the distribution of these characteristics across our 262 collected estimates of the coefficient on market access from previous empirical NEG studies.
| Function | Total | Direct | 2-step |
|---|---|---|---|
| Exponential | 64 | 64 | 0 |
| Power | 198 | 25 | 173 |
| Multiplicative | 174 | 1 | 173 |
| Only distance | 88 | 88 | 0 |
| Region specific trade cost proxies | |||
| Yes | 32 | 0 | 33 |
| No | 229 | 89 | 140 |
| Total | 262 | 89 | 173 |
Most studies model trade costs' dependence on distance using a power function. Also, the majority of studies employs a multiplicative trade cost function when estimating the wage equation including more trade cost proxies than simply distance in the trade cost function. Finally, the bulk of studies model trade costs using bilateral trade cost proxies only (e.g., distance or sharing a common language), they do not consider region-specific measures of trade costs such as being landlocked, the quality of a region's infrastructure, etc.
Further distinguishing between the two different estimation strategies employed to estimate the NEG wage equation (see section 3.1), reveals two important differences between the trade cost function used in each of the two strategies. First, studies using the direct estimation method virtually always use a trade cost function containing distance as the only trade cost proxy, whereas studies using the two-step method always use a trade cost function consisting of other trade cost proxies in addition to distance. Second, studies using the two-step method always use a power function to model trade costs' dependency on distance, whereas studies using the direct method much more often opt for an exponential distance function.
There is a priori no reason for these differences in the choice of trade cost function between the two estimation strategies. They are in our view an (unfortunate) by-product of the different way the trade cost function's parameters are estimated. In the direct method these are estimated jointly with the market access coefficient. This amounts to using nonlinear estimation techniques: adding additional variables to the trade costs' function introduces additional nonlinearity, making it increasingly difficult to estimate all parameters of interest, explaining the use of merely distance in the trade cost function. In the two-step method the trade costs function's parameters are estimated in the first step, separately from the market coefficient, using NEG's trade equation (7). This first step amounts to estimating a gravity model (the workhorse model in the empirical trade literature), in which it is common practice to use a trade cost function consisting of (many) more trade cost proxies than only distance and a power function to model trade costs' dependency on distance. Even though this difference between the two estimation strategies may be accidental, we will see that we have to keep this in the back of our mind when interpreting our meta-analysis results.
Turning to our meta-analysis, Figure 1 starts by showing the distribution of all 262 estimated market access coefficients reported in previous studies. Table 2 complements this by showing the corresponding mean, standard deviation and median.
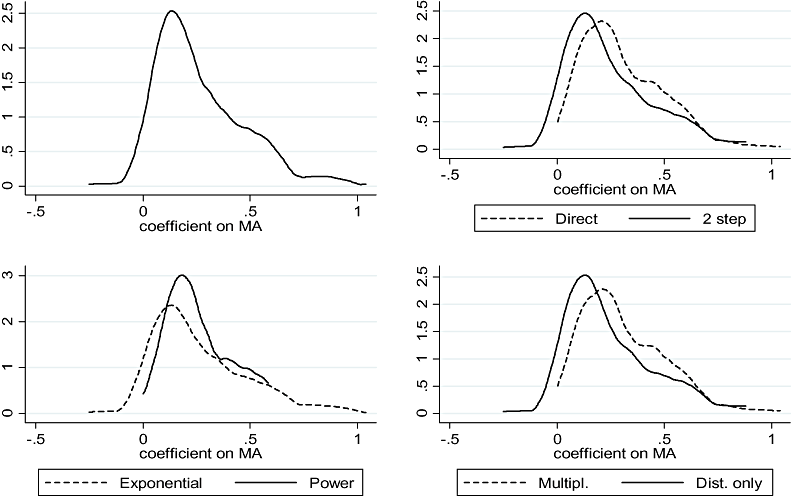
Distribution of estimated market access (MA) coefficients
| Sample | Mean | St. dev. | Median |
|---|---|---|---|
| Total | 0.266 | 0.205 | 0.203 |
| Direct | 0.309 | 0.197 | 0.237 |
| 2 step | 0.244 | 0.206 | 0.170 |
| Exponential | 0.263 | 0.154 | 0.203 |
| Power | 0.267 | 0.220 | 0.210 |
| Multiplicative | 0.243 | 0.206 | 0.169 |
| Distance only | 0.311 | 0.198 | 0.239 |
Besides reporting results for the total sample, Figure 1 and Table 2 also compare results when distinguishing the estimated market access coefficients by the estimation strategy used (upper right panel), whether a multiplicative trade cost function is used or not (lower left panel), and the distance function used (lower right panel).
The distribution of estimated market access coefficients varies across the different trade cost specifications (see the lower panels), but typically the estimated market access coefficient is positive. Moreover, the lower two panels suggest that there may indeed be some variation in the estimated market access coefficient depending on the choice of trade cost function. It is this variation in the estimated market access coefficient across the trade cost function characteristics that we want to exploit more systematically in the meta-analysis.11
In estimating our ‘meta model’, we follow Disdier and Head (2008) and opt for a random effects estimation (allowing for random ‘study’ effects). Table 3 shows the estimation results. The first column of Table 3 focuses on the relevance of the trade cost function variables only. Studies using a multiplicative trade cost function and studies using an exponential distance function report significantly lower market access coefficients. To control for the possibility that the difference in market access coefficient between trade cost specifications is driven by other characteristics of the empirical studies, we add several other variables as explanatory variables in our meta regression in columns 2–4.
| Method: | Random effects | |||
|---|---|---|---|---|
| Dependent variable: | Estimated MA – coefficient | |||
| Only distance | + sample info | + method info | + method and sample info | |
| Published | – | – | −0.109 | −0.044 |
| (0.079) | (0.037) | |||
| GDP per capita for wages | – | −0.049 | – | −0.062 |
| (0.065) | (0.051) | |||
| Additional control variables in the wage equation | – | – | −0.112*** | −0.114*** |
| (0.042) | (0.042) | |||
| Fixed effects | – | – | −0.058 | −0.125*** |
| (0.049) | (0.039) | |||
| First differenced | – | – | 0.018 | −0.023 |
| (0.076) | (0.074) | |||
| Instrumented | – | – | 0.114** | 0.125*** |
| (0.046) | (0.041) | |||
| Direct estimation strategy | – | – | −0.188* | −0.112** |
| (0.104) | (0.054) | |||
| Regions | – | −0.204** | – | −0.244*** |
| (0.08) | (0.056) | |||
| Sectors | – | −0.176*** | – | −0.097** |
| (0.03) | (0.043) | |||
| Firms or individuals | – | −0.238*** | – | −0.236*** |
| (0.089) | (0.049) | |||
| Exponential distance function | −0.135* | −0.157** | 0.002 | −0.021 |
| (0.072) | (0.066) | (0.061) | (0.054) | |
| Multiplicative distance function | −0.181** | −0.224*** | −0.262*** | −0.242*** |
| (0.03) | (0.055) | (0.092) | (0.063) | |
| Region specific trade cost proxies | 0.04 | −0.090* | −0.09 | 0.156 |
| (0.085) | (0.139) | (0.102) | (0.111) | |
| Foreign market access | – | – | 0.047 | 0.042 |
| (0.042) | (0.043) | |||
| First year of the data | – | −0.003** | – | −0.004*** |
| (0.001) | (0.001) | |||
| No. Of observations | 262 | 262 | 262 | 262 |
| R2 | 0.045 | 0.307 | 0.239 | 0.411 |
- Notes: Estimates obtained using a random effects estimator, with individual paper random effects. Standard errors robust to heteroscedasticity and clustered by individual paper in parentheses. ***, **, * denotes significance at the 1%, 5%, 10% levels respectively.
This addition of explanatory variables shows that our findings are robust to controlling for characteristics of the sample used in each of the studies (see column 2). However, when controlling for characteristics of the estimation strategy used in each of the studies, only the use of a multiplicative trade cost function remains of significantly negative influence on the estimated market access coefficient. The negative effect of the use of an exponential distance function is now picked up by the dummy variable indicating the use of the direct estimation strategy. This shows that one can indeed, given in our view the largely accidental correspondence between the choice of trade cost function and the estimation strategy used (see Table 1 and the ensuing discussion), easily ascribe an effect to the choice of distance function that may instead be driven by the choice of estimation strategy.12
The results in Table 3 are a first indication that the choice of trade cost function may indeed nontrivially affect the conclusions reached regarding the relevance of market access in determining wage levels. But, given that the exponential/power distance function distinction as well as the split between multiplicative and ‘only distance’ trade cost functions correlates strongly with a split along the direct versus two-step estimation strategy dimension, we are not totally confident yet that we are able to adequately isolate the effect of the choice of trade cost function from the effect of choice of estimation strategy used to estimate the wage equation's parameters. This is why we now turn to a second way to establish if the trade cost specification matters for the conclusions reached regarding market access: we estimate the NEG wage equation (6) for a single uniform sample using three different trade cost functions. We do this by using both the direct and the two-step estimation strategy which allows us to more clearly distinguish the importance of the trade cost function used from the estimation strategy employed.
3.3 One sample – different trade cost functions: Does the trade cost specification matter? – part II
3.3.1 Data
The results in the remainder of this paper are based on a sample of 60 countries13 in 1996 (see Appendix C for a complete list of these countries). In order to be able to estimate the wage equation, we have collected data on GDP and GDP per capita from the Penn World Tables (as wage data is not available for all countries in our sample, we follow Redding and Venables 2004, and use (real) GDP per capita as a proxy). We capture the differences in marginal costs, ci in (4), by including three education variables in the wage equation, namely, the percentage of the population over 15 years old that completed primary, secondary and tertiary education (taken from Barro and Lee 2001). As our potential trade cost proxies, we have collected data on bilateral distances, contiguity, common language, and indicators of a country being landlocked, an island nation, or a Sub-Saharan African country (see Limao and Venables 2001). Finally, we have collected bilateral trade data from the Trade and Production 1976–1999 database provided by the French institute CEPII,14 that we need when using the two-step estimation strategy (and also when constructing implied trade costs in Section 4). A nice feature of the CEPII data is that it reports both bilateral trade and internal trade data for most of the countries in our sample.
3.3.2 Three trade cost functions and their relevance for market access
Table 4 shows the three different trade cost functions that we use to verify the sensitivity of the estimated market access coefficient with respect to the choice of trade cost approximation.
| Abbreviation | Trade cost function |
|---|---|
| I | 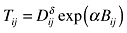 |
| II | Tij= exp(τDij) |
| III | 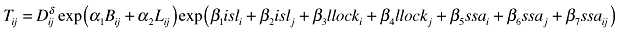 |
- Notes: Dij denotes a measure of distance between regions i and j, usually great-circle distance, but sometimes also other distance measures such as travel times (Brakman et al. 2004) or population weighted great-circle distance (Breinlich 2006) have been used. Bij denotes a border dummy, either capturing the (alleged positive) effect of two regions being adjacent (Redding and Venables 2004; Knaap 2006) or the (possibly country-specific) effect of crossing a national border (Breinlich 2006; Hering and Poncet 2006). The variables isl, llock, ssa refer respectively to whether the country/region is an island, landlocked or located in sub-Saharan Africa (Venables 2010).
The first two trade cost functions (labelled I and II) are chosen as they are the ones used by the two papers (Redding and Venables 2004 and Hanson 2005) that introduced the two-step and direct estimation strategy respectively; the former (I) using a power distance function, the latter (II) an exponential distance function. The multiplicative function (labelled as III) allows trade costs to depend not only on bilateral variables but also on importer/exporter specific trade cost factors, namely, being landlocked (llock), being an island nation (isl) and being a Sub-Saharan African country (ssa). Such a multiplicative function is quite common in the empirical trade literature (see e.g., Limao and Venables, 2001). These three types of trade cost functions are also the ones that have been used most extensively in the NEG studies that underlie our meta-analysis in section 3.2 (see Table 1 and Appendix A).
Using each of the above three trade cost functions, we estimate the NEG wage equation (6) by either employing either the direct or the two-step estimation strategy. In both cases, we follow Redding and Venables (2004) and proxy a country's wage level by its GDP per capita; also in both cases we use real GDP to proxy GiEi– see also Redding and Venables (2004, section 7). Our main focus is the size and significance of the market access coefficient (α2 in (6)). When employing the direct estimation strategy we directly estimate (6) using NLS. When using the two-step estimation method instead, we first construct market access based on the estimation of the NEG trade equation specified in (7) using the recently proposed (Santos Silva and Tenreyro, 2006) Pseudo Poisson Maximum Likelihood (PPML) method (see Appendix D for the results of this first step). Next, in the second step, we use this constructed market access measure to estimate (6) by simple ordinary least squares (OLS).15 Besides market access, we include three education variables to the wage equation. They capture the term ηi in (6) which stands for possible technological differences between countries, ci, in (3) that may also drive the observed cross-country differences in GDP per capita (see e.g., Breinlich 2006).
The estimation results are shown in Tables 5 and 6. Table 5 focuses on total market access and Table 6 on so-called foreign market access (i.e., total market access excluding access to one's own internal market16). Each column gives first the estimation strategy (two-step or direct) and second the trade cost approximation (I, II, or III) that was used.
| Estimation strategy | Two-step | Two-step | Two-step | Direct | Direct | Direct |
|---|---|---|---|---|---|---|
| Trade cost function | I | II | III | I | II | III |
| MA | 0.49*** | 0.19* | 0.40*** | 0.84* | 0.57 | 0.80 |
| [3.57] | [1.90] | [3.60] | [1.86] | [0.20] | [1.57] | |
| Education | ||||||
| Primary | 0.02*** | 0.02*** | 0.02*** | 0.02*** | 0.02*** | 0.01*** |
| [4.98] | [4.88] | [3.48] | [3.11] | [5.40] | [2.64] | |
| Secondary | 0.04*** | 0.04*** | 0.03*** | 0.03*** | 0.04*** | 0.03*** |
| [6.03] | [7.97] | [5.03] | [4.51] | [7.33] | [4.07] | |
| Tertiary | 0.04*** | 0.04*** | 0.03*** | 0.04*** | 0.04*** | 0.05*** |
| [5.62] | [5.50] | [4.54] | [7.49] | [6.25] | [8.26] | |
| No. of obs | 60 | 60 | 60 | 60 | 60 | 60 |
- Notes: Dependent variable is log of GDP per capita. t-values based on robust standard errors in brackets. ***, * denotes significance at the 1% and 10% levels respectively.
| Estimation strategy | Two-step | Two-step | Two-step | Direct | Direct | Direct |
|---|---|---|---|---|---|---|
| Trade cost function | I | II | III | I | II | III |
| FMA | 0.32** | 0.26* | 0.31** | 0.14 | 0.66 | 0.68 |
| [2.11] | [1.90] | [2.05] | [0.70] | [0.21] | [0.60] | |
| Education | ||||||
| Primary | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| [4.82] | [4.89] | [3.72] | [4.67] | [5.34] | [4.34] | |
| Secondary | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| [6.86] | [7.57] | [5.59] | [6.82] | [8.19] | [7.07] | |
| Tertiary | 0.04 | 0.04 | 0.03 | 0.04 | 0.04 | 0.04 |
| [5.76] | [5.56] | [4.90] | [4.13] | [6.13] | [3.79] | |
| No. of obs | 60 | 60 | 60 | 60 | 60 | 60 |
- Notes: Dependent variable is log of GDP per capita. t-values based on robust standard errors in brackets. **, * denotes significance at the 5% and 10% levels respectively.
As in our meta-analysis the size of the coefficient on market access is quite sensitive to the estimation strategy as well as to the chosen trade cost function. Even more importantly, its significance appears to also depend nontrivially on the choice of trade cost function and estimation method. Keeping the estimation strategy the same, we observe that, when using the direct estimation strategy in particular, the market access coefficient is generally insignificant irrespective of the trade cost function used.17 Only when using distance function I, total market access is significant at the 10 percent level. When applying the two-step estimation strategy instead,18 the coefficient of market access (both total and foreign) is generally significant but varies in magnitude across the trade cost functions used. However, when using distance function II, market access (both total and foreign) is only significant at the 10 percent level.
3.4 Three trade cost functions and the spatial reach of GDP shocks
The fact that the size of the market access coefficient differs across estimations in Tables 5 and 6 could obscure that, due to the different trade cost approximation used, market access is not measured uniformly across specifications. It could be the case that an x% increase in a country's GDP increases other countries' market access by z% when using one particular trade cost function and y% when using another, even when the estimated market access coefficient is the same when using either trade cost function. As a result differences in estimated market access coefficients are potentially meaningless.
To verify this we conducted the following thought experiment. Suppose that Belgium experiences a positive 5 percent GDP shock: to what extent does this shock, given our estimation results above, spill over to the other countries in our sample via its impact on each country's market access? The 5 percent increase in Belgian GDP increases Belgian demand for goods from all other countries. The actual magnitude of this increase depends crucially on the strength of the spatial linkages between Belgium and any specific country and thus on the measurement of trade costs: namely, the lower trade costs with Belgium, the larger the impact of the positive Belgian GDP shock on a country's GDP per capita.
Based on the estimation results from Table 5 and depending on the specific trade cost approximation (and estimation strategy) used we have calculated the resulting GDP per capita changes experienced by all other countries in response to the increased demand for their products from Belgium in each of the six different cases that we distinguished.
Figure 2 plots the resulting percentage increase in GDP per capita in all other countries (except Belgium itself) for four of these cases19 (e.g., ‘direct-I’ means estimation of the wage equation using the direct estimation strategy and trade cost function I from Table 4). Figure 2 shows that a more elaborate or heterogeneous trade cost specification increases the variation of the impact of the Belgian GDP shock for countries at a similar distance to Belgium. Moreover this heterogeneity in differences in spatial reach corresponds predictably to the type of trade cost specification used (i.e., to the cost proxies included in the trade cost function in addition to distance).
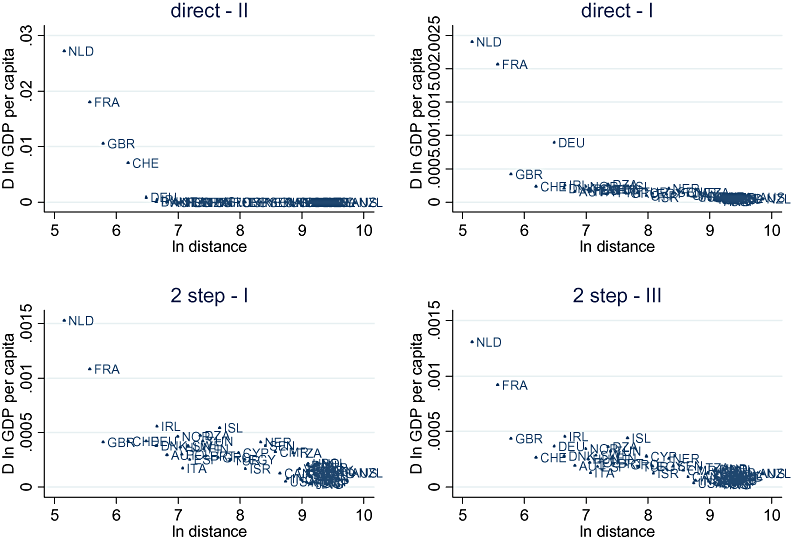
Spatial impact of a 5 percent GDP shock in BelgiumNotes: The correlation between ln distance and the impact of the 5% Belgian GDP shock is, going from upper left to lower right: −0.31, −0.65, −0.78 and −0.77 respectively.
In the case of the direct estimation strategy (compare the two top panels), both the magnitude of the impact of the Belgian GDP shock as well as its spatial reach depend nontrivially on the trade cost function assumed. When using the exponential distance function (II), the impact of the shock is substantially larger for countries closer to Belgium but peters out much quicker compared to using a power distance function and allowing for a border effect (I) − a result of the extremely fast exponential distance decay.20 Also the positive border effect shows up clearly: when using distance function I, Germany which borders Belgium is more affected by the shock than Great Britain or Switzerland, whereas the latter two are more affected than Germany when not allowing for a border effect in the distance function (II).
The differences are much smaller when comparing the lower two panels based on using two different trade cost functions when applying a two-step estimation strategy. However, given the estimated effect of the country-specific trade cost proxies included in III but not in II, a closer look reveals that Sub-Saharan African countries (located on the x-axis between a log distance of 8 and 9) and landlocked countries are relatively less, and island nations (see e.g., Great Britain (GBR)) are relatively more affect by the Belgian GDP shock. However these differences are small given the predominance of distance and the border effect in determining trade costs (see also Appendix D).
3.5 Summing up: The specification of the trade cost function matters!
Combining the evidence obtained from both our meta-analysis (section 3.1) and our one-sample-different-trade-cost-function estimations (sections 3.2 and 3.3), we can only conclude that both the size and significance of the estimated effect of (foreign) market access on GDP per capita can be quite sensitive to the type of trade cost function used to approximate trade costs. Moreover, the spatial reach of GDP shocks is nontrivially (and predictably!) affected by the choice of trade cost function. Given this sensitivity of the results to the trade cost function used, we now turn to an alternative way to approximate trade costs that does not involve the specification of a trade cost function.
4 Implied trade costs
Our proposed alternative way to approximate trade costs is based on Head and Ries (2001). Using the NEG trade Equation (7), they show that trade costs can be directly inferred from bilateral trade data:
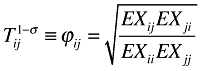 (8)
(8)where EXij denotes imports of region j from region i and EXii denotes the total amount of goods consumed in region i that is also produced in region i. ϕij is introduced for notational convenience as a measure of the so-called ‘free-ness’ of trade (see Baldwin et al. 2003). It ranges from 0 to 1, with 0 meaning prohibitive and 1 meaning completely free trade.
Head and Ries (2001) use Equation (8) to construct implied trade costs (disaggregated at the industry level) between the US and Canada. They show a gradual decline in trade costs over time and use regression methods to decompose it into a tariff and a non-tariff barrier component. Other papers that have already used (8) to construct implied trade costs are Head and Mayer (2004), Brakman et al. (2006), and Novy et al. (2008). We argue that (8) can also be used in the estimation of the wage equation (6). As far as we know our paper is the first to do so. We think that implied trade costs as specified by (8) provide an interesting alternative to approximating trade costs by making use of a trade cost function. Precisely because the calculation of (8) does not require the specification of a trade cost function it avoids the need for some of the (arbitrary) assumption made when using a trade cost function approach. Moreover, the structure of the implied trade costs function is entirely consistent with both theoretical underpinnings and empirical observations of distance cost structures in transport pricing (McCann 2001), logistics shipments (McCann 1993, 1998), as well as the movement of ideas (McCann 2007) and people (McCann et al. 2010), all of which have square root properties characteristic of the Baumol-Tobin transactions-costs principle.
But the use of implied trade costs (unfortunately) also has its drawbacks. First, there is the additional data requirement. As can be readily seen from (8), the construction of implied trade costs requires the availability of bilateral trade flows as well as internal trade flows, EXii, for all countries in the data set. Own-trade data are usually not readily available, but when both total export and production data are available they can be constructed as a country's or region's total own production minus exports (see e.g., Head and Ries 2001; Head and Mayer 2004; Hering and Poncet 2006). In the complete absence of bilateral trade data, implied trade costs cannot be calculated at all. As bilateral trade data are increasingly difficult to come by the lower the spatial scale of the analysis, implied trade costs are simply an unviable alternative to the use of a trade cost function in empirical studies that focus on cities, municipalities or neighborhoods. They are however a viable alternative to studies at the country or regional level. Increasingly bilateral trade data between subnational regions is becoming available (Helliwell and Verdier 2001; Knaap 2006; Hering and Poncet 2006). Also Breinlich (2006) suggests a clever trick (based on some assumptions) to infer intraregional trade data from international trade data, hereby facilitating the use of implied trade costs at the regional level.
Second, two important assumptions are needed in order for the implied trade cost approach to work. Without them bilateral trade flows cannot be used to infer implied trade costs. They follow directly from the way implied trade costs are derived. Substituting (7) for both bilateral and internal trade (i.e., the EXij's in (8)), we arrive at (8) in the following way:
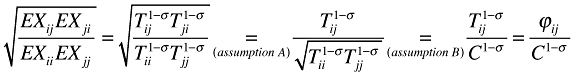 (9)
(9)Where the following two assumptions are made:
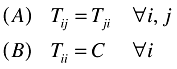 (10)
(10)That is to say, trade costs involved when shipping from region i to region j are the same as shipping from region j to region i (10A), and internal trade costs are a constant and the same for each region21 (10B). How do these two assumptions relate to the six issues that one faces when using a trade costs function instead (see section 2.2 and Table 2 in Bosker and Garretsen 2010)?
Table 7 makes a comparison based on the six issues that were already introduced in section 2.2, with assumptions (10A) and (10B) in bold. The potential advantage of using implied trade costs clearly comes to the fore. It avoids most of the assumptions one has to (implicitly) make when using a trade cost function to approximate trade costs. But this verdict, of course, depends on the alleged innocence of assumptions (10A) and (10B).
| Issue | Trade cost function | Implied trade costs |
|---|---|---|
| Functional form | Assumed | Not an issue |
| Regularity conditions | Ad hoc assumptions are (implicitly) made | Symmetry of bilateral trade costs |
| Variable inclusion | Many candidates, which ones to include? | Not an issue |
| Variable measurement | No consensus, choices need to be made | Not an issue |
| Internal trade cost | Assumed to depend on internal distance | Assumed to be the same for each country |
| Unobservable component | Needs explicit care (additional assumptions) | Implicitly taken into account |
| Estimating the parameters | Choice of estimation method not always straightforward | Not necessary |
Assumption (10A), symmetric bilateral trade costs, is arguably the least problematic of the two. It is also a very common assumption in empirical NEG studies that use a trade cost function. For example, all the papers in Table A1 (except the second, more elaborate, trade cost function used by Redding and Venables, 2004) use a trade cost functions that (implicitly) assumes symmetric bilateral trade costs. In effect, all trade cost functions that include only bilateral trade cost proxies implicitly assume symmetric trade costs. Arguably the most problematic assumption when using implied trade costs is assumption (10B). Many authors (Head and Mayer 2004; Anderson and van Wincoop 2004) have stressed the importance of dropping this assumption when doing empirical work, as it is, for example. hard to believe that internal trade costs are the same in a small country like Luxembourg as in a large country like Canada. However, given the other above-mentioned virtues of using implied trade costs, combined with the fact that in most existing empirical studies these internal trade costs are usually also rather crudely specified (i.e., a (sophisticated) function of each country's area only), we argue that they should be considered as an alternative way to deal with trade costs in empirical NEG studies.
4.1 Implied trade costs vs the three trade cost functions
Before immediately turning to the use of implied trade costs when estimating the NEG wage equation, this subsection verifies to what extent implied trade costs differ from using one of the three trade cost functions employed in section 3.2. To this end, we have calculated implied trade costs for as many bilateral pairs of countries as possible using (8). This leaves us with no less than 3,808 observed bilateral ϕijs. How much of these implied trade costs can be accounted for by the three different trade cost functions from Table 4? Or, to put it differently, does the use of implied trade costs provide a proxy for trade costs that differs from the proxies obtained using one of the trade cost functions in Table 4? And what about the (ir)relevance of the underlying assumptions when calculating implied trade costs, see (10A) and (10B)?
To answer the first question we simply regressed the bilateral22ϕijs on each of the three different trade cost functions in Table 4. Table 8 shows the results that are again obtained using the PPML estimator to take account of the zeros in implied trade costs. Note that because of assumption (10A) we cannot split the country-specific trade cost proxies into an exporter and an importer part, so that each country-specific trade cost proxy enters only once.23
| Trade cost function: | I | II | III |
|---|---|---|---|
| Distance | −0.854*** | −0.0002*** | −0.861*** |
| [0.000] | [0.000] | [0.000] | |
| Contiguity | 0.707 | – | 0.865** |
| [0.139] | – | [0.016] | |
| Common language | – | – | −0.235 |
| – | – | 0.138 | |
| Landlocked | – | – | −1.150*** |
| – | – | [0.000] | |
| Island | – | – | 0.241 |
| – | – | 0.127 | |
| Ssa | – | – | −1.148*** |
| – | – | [0.000] | |
| Ssa both | – | – | 1.222** |
| – | – | [0.011] | |
| (Pseudo) R2 | 0.113 | 0.058 | 0.144 |
| No. of observations | 3,808 | 3,808 | 3,808 |
- Notes: p-values in brackets. ***, ** denotes significance at the 1% and 5% levels respectively. Landlocked takes the value 0 if neither country is landlocked, 1 if one of the two countries is landlocked and 2 if both countries are landlocked; similarity for island and ssa (Sub-Saharan Africa).
When comparing the results in Table 8 to those obtained in Table D1 we observe several differences in the significance of the determinants of trade costs. For example, contiguity is not significant when using trade cost function I in Table 8 whereas it is significant in Table D1. Similarly, island nations face significantly lower trade costs according to column 3 in Table D1, but not so when taking the results in column 3 of Table 8 seriously.24 Also, as can be readily seen from the (pseudo) R2 for each of the three regressions, the trade cost functions capture at most 14.4 percent of the variation in implied trade costs. In case of trade cost function II this is only 5.8 percent! Approximating trade costs through implied trade costs differs quite a bit from obtaining these costs by estimating the parameters of an a priori specified distance function. Note also that the inclusion of country-specific trade cost proxies in column 3 improves the fit.25 The flexibility of the use of implied trade costs compared to the use of trade cost functions provides a useful alternative way to proxy trade costs in our view.
This last conclusion depends, however, on the validity of the two assumptions, (10A) and (10B), underlying the calculation of implied trade costs. To shed some light on the (ir)relevance of assumption (10A) the last three rows of Table D1 are instructive. As we mentioned before, when one believes that only bilateral trade cost proxies such as distance, contiguity and sharing a common official language matter, assumption (10A) is automatically satisfied. But we have been arguing that also country-specific proxies such as being landlocked are important to take into account. Allowing these proxies to have a different effect (i.e., different parameter) when estimating (7) implicitly violates (10A). This is so unless one cannot reject that the coefficients on the importer and exporter variant of a variable are the same. On the basis of Table 8 we cannot perform such tests, but using the results in Table D1 does provide some indication into the relevance of these assumptions. The results of testing whether the effect of a particular country-specific trade cost proxy is similar when considering exports and imports are shown at the bottom of column 3 in Table D1. In case of all three country-specific variables we cannot reject that their impact is the same on both imports and exports. In the case of the specific sample that we use, the assumption of symmetric bilateral trade costs does not appear that stringent.
The other assumption, constant internal trade costs across all regions (10B), is a more problematic one. Substantial differences do exist across regions in the trade costs involved with internal trade. But is this assumption more ‘harmful’ than the assumption made in empirical studies using a trade cost function? The standard practice in current empirical NEG studies is to make internal trade costs dependent on a region's internal distance only, which, given the way internal distance is calculated (Dii= 2/3(areai/π)1/2 ), boils down to saying that internal trade costs are larger the larger a region's surface area. This may improve on assuming them to be equal across regions, but maybe not substantially so.26 To assess this in case of our sample of countries, we estimate the NEG trade equation using only our observations on internal trade.27Table 9 shows the results of doing this using the same three different trade cost functions as before (see again Table 4).
| Trade cost function: | I | II | III |
|---|---|---|---|
| Internal distance | −0.195 | −0.001*** | −0.176 |
| [0.152] | [0.000] | [0.240] | |
| Landlocked | – | – | −0.025 |
| – | – | [0.927] | |
| Island | – | – | −0.070 |
| – | – | [0.836] | |
| Ssa | – | – | −0.256 |
| – | – | [0.350] | |
| GDP importer | 1.404*** | 1.434*** | 1.382*** |
| [0.000] | [0.000] | [0.000] | |
| (Pseudo) R2 | 0.879 | 0.886 | 0.880 |
| No. of observations | 93 | 93 | 93 |
- Notes: p-values in brackets. *** denotes significant at the 10% level.
Except in case of the trade cost function II, none of the three trade cost proxies is found to be significant in explaining the variation in internal trade. In the case of the country-specific variables this may not be that surprising (why should it matter for a country's internal trade costs whether or not it is an island or landlocked?). What is most striking is that also internal distance, the widely used proxy for internal trade costs mostly turns out to be insignificant (again except in case of trade cost function II).
The results in Table 9 illustrate that incorporating internal trade costs by proxying them using internal distance may also not be without problems. Although the assumption of equal internal trade costs across countries when calculating implied costs is clearly unrealistic, adequately incorporating internal trade costs is also far from straightforward when using a standard trade cost function approach. Indeed, approximating internal trade costs by a clever transformation of a region's or a country's area, as is done by virtually all empirical NEG papers, may be just as harmful as assuming them away.
4.2 Implied trade costs and the relevance of market access
With the exception of the strong assumption on internal trade costs (10B), we think that the use of implied trade costs has many advantages over the use of a trade cost function when one's main point of interest is to establish the relevance of one of NEG's main predictions namely that market access matters for the spatial distribution of income.28
In order to assess the impact of the use of our suggested alternative way to approximate trade costs on the conclusions reached regarding the relevance of market access, we again estimate the NEG wage equation (6), but now using implied trade costs in the construction of market access, namely:
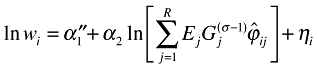 (11)
(11)where 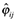 , the calculated implied trade costs replace
, the calculated implied trade costs replace 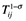 in (6), and we again include the same three education variables to capture differences in ci across countries. Note that since C is assumed to be constant across countries, its exact value has no impact on the estimated coefficient on market access (it ends up in the constant
in (6), and we again include the same three education variables to capture differences in ci across countries. Note that since C is assumed to be constant across countries, its exact value has no impact on the estimated coefficient on market access (it ends up in the constant 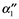 ). Again, we proxy wages by GDP per capita and GiEi by real GDP. We estimate (11) using the direct estimation strategy. Table 10 shows the results for total market access and, in order to in some extent abstract from the thorny issue of internal trade costs, also when including foreign market access instead.
). Again, we proxy wages by GDP per capita and GiEi by real GDP. We estimate (11) using the direct estimation strategy. Table 10 shows the results for total market access and, in order to in some extent abstract from the thorny issue of internal trade costs, also when including foreign market access instead.
| Method | Direct | Direct | |
|---|---|---|---|
| MA | 0.11* | FMA | 0.26*** |
| [1.94] | [3.84] | ||
| Education | |||
| Primary | 0.02*** | 0.02*** | |
| [4.77] | [3.84] | ||
| Secondary | 0.04*** | 0.04*** | |
| [9.22] | [6.08] | ||
| Tertiary | 0.03*** | 0.03*** | |
| [3.46] | [4.58] | ||
| No. Of observations | 60 | 60 |
- Notes: Dependent variable is log of GDP per capita. t-values based on robust standard errors in brackets. ***, * denotes significance at the 1% and 10% levels respectively.
The results show that market access, based on the use of implied trade costs, is a significant determinant of GDP per capita, despite the fact that a direct estimation strategy is used (compare the results of using this estimation strategy in Tables 5 and 6).29 Note that, possibly given the problematic assumption (10B) alluded to before, total market access is less significant (only at the 10% level) than foreign market access. When focusing on foreign market access one abstracts from the thorny issue of internal trade costs by considering a country's access to other countries' markets only.
Similar to Figure 2, Figure 3 further specifies the results in Table 10 by showing the spatial impact of a 5 percent shock to Belgian GDP based on the results in column 1. Moreover, Table 11 depicts the correlation of the GDP per capita changes when using each of the three trade cost function shown in Figure 2 with those obtained using implied trade costs.

Implied trade costs: the spatial impact of a 5 percent shock to Belgian GDPNote: the correlation between ln distance and the effect of the 5 percent Belgian GDP shock is: −0.67.
| Correlation with GDP shock when using ϕ | ||
|---|---|---|
| Trade costs function | Two-step | Direct |
| III | 0.78*** | – |
| II | – | 0.12 |
| I | 0.82*** | 0.68*** |
- Notes: *** denotes significance at the 1% level.
Figure 3 shows that when using implied trade costs, the effect of the 5 percent Belgian GDP shock is generally lower than when using a trade cost function to approximate trade costs. Moreover, and in line with the way these implied trade costs are calculated (9), countries that trade a lot with Belgium relative to their amount of internal trade,30 for example, Tunisia, Sweden, the Netherlands or Portugal, experience a relatively larger impact of the Belgian income shock than countries that do not export/import a substantial amount of their total trade to/from Belgium but to other countries (e.g., France, Germany or Great Britain).
Table 11 adds to this by showing that although the effect of the Belgian GDP shock when using the implied trade costs approximation of trade costs does correlate positively with that when using a trade cost function approach, this correlation is far from perfect, and in one case even insignificant. The use of implied trade costs avoids having to make (oftentimes arbitrary and non-testable) assumptions regarding the exact trade cost specification used: assumptions that can non-trivially affect the conclusions reached regarding both the magnitude and significance of market access' effect on income levels, as well as the implied spatial reach of GDP shocks.
5 Conclusions
Trade costs are a crucial element of new economic geography (NEG) models, without trade costs geography does not matter in NEG. The size of trade costs crucially determines the strength of regions' spatial interdependencies and thereby the relevance of market access. The unavailability of actual trade cost data requires empirical research in NEG to approximate trade costs. Despite the crucial importance of trade costs in NEG models, most empirical NEG studies generally do not pay much attention to the possible implications of their particular trade cost approximation used.
We show in this paper that the way trade costs are approximated matters empirically for the conclusions reached regarding the relevance of market access in determining spatial differences in income levels (one of NEG's main predictions). Based on both the evidence from a meta-analysis of previous empirical NEG studies and the results obtained using a uniform sample but different trade cost approximations, we find that the way trade costs are approximated matters for the conclusions reached regarding the empirical relevance of NEG, namely, the strength and geographical reach of spatial interdependencies.
Finally, and although we are unable to statistically determine the ‘best’ way of approximating trade costs, we suggest an alternative to the current standard practice of approximating trade costs when doing empirical work in NEG. In particular, instead of approximating trade costs by assuming a trade cost function that specifies how several observable proxies of trade costs interact to jointly serve as an approximation of actual trade costs, we propose the use of so-called implied trade costs. The use of implied trade costs constitutes a theory-based alternative that avoids the need to make many of the (arbitrary) assumptions that are made when assuming a trade cost function. Given the sensitivity of the conclusions reached regarding the relevance of NEG to these (arbitrary) assumptions regarding the trade cost function, we argue that the use of implied trade costs is a viable alternative to approximate trade costs when doing empirical work on NEG.
Overall, our main message for future empirical work on NEG is that the choice of trade costs approximation, which any empirical NEG study faces, should be given far more attention. In particular, the robustness of the results with respect to the choice of a trade cost proxy warrants much more scrutiny than is current practice in empirical work on NEG.
Appendices
Appendix A
| Paper | Sample | Trade cost function |
|---|---|---|
| Direct estimation | ||
| Hanson (2005) | US counties | Tij= exp(τDij) |
| Brakman et al. (2004) | German regions | 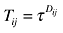 |
| Brakman et al. (2006) | European regions | 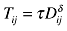 |
| Mion (2004) | Italian regions | Tij= exp(τDij) |
| Two-step estimation | ||
| Redding and Venables (2004) | World countries | 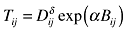 or or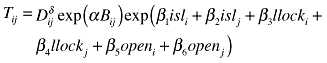 |
| Knaap (2006) | US states | 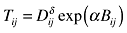 |
| Breinlich (2006) | European regions | 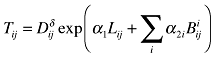 |
| Hering and Poncet (2006) | Chinese cities | 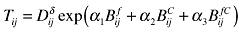 |
- Notes: Dij denotes a measure of distance, usually great-circle distance, but sometimes also other measures such as travel times (e.g., Brakman et al. 2004) or population weighted great-circle distance (e.g., Breinlich 2006) have been used. Bij denotes a border dummy, either capturing the (alleged positive) effect of two countries/regions being adjacent (e.g., Redding and Venables 2004; Knaap 2006) or the (possibly country-specific) effect of crossing a national border (e.g., Breinlich 2006; Hering and Poncet 2006).
Appendix B
| No. of estimates | |
|---|---|
| Amiti and Cameron 2007 | 17 |
| Bosker and Garretsen 2009 | 29 |
| Bosker, Brakman, Garretsen and Schramm 2010 | 1 |
| Boulhol and De Serre 2008 | 4 |
| Brakman, Garretsen, Gorter, vd Horst and Schramm 2005 | 1 |
| Brakman, Garretsen and Schramm 2004 | 5 |
| Brakman, Garretsen and Schramm 2006 | 1 |
| Breinlich 2006 | 17 |
| Fingleton 2005 | 2 |
| Fingleton 2006 | 4 |
| Hanson 2005 | 12 |
| Head and Mayer 2006 | 18 |
| Hering and Poncet 2006 | 16 |
| Kiso 2005 | 15 |
| Knaap 2006 | 10 |
| Mayer 2008 | 28 |
| Mion 2004 | 6 |
| Niebuhr 2006 | 4 |
| Paillacar 2007 | 29 |
| Pires 2006 | 20 |
| Redding and Venables 2004 (& 2000, 2001 versions) | 22 |
| Roos 2005 | 1 |
| Total | 262 |
Appendix C
| Albania | Egypt | Latvia | Portugal |
| Algeria | El Salvador | Lithuania | Romania |
| Argentina | Estonia | Macau | Russia |
| Armenia* | Ethiopia* | Macedonia | Saint Lucia |
| Australia | Finland | Malawi* | Senegal |
| Austria | France | Malaysia | Singapore |
| Bahamas* | Germany | Malta | Slovakia |
| Bangladesh* | Greece | Mauritius | Slovenia |
| Barbados* | Guatemala* | Mexico | South Africa |
| Belgium | Honduras | Moldova* | Spain |
| Bolivia | Hong Kong | Mongolia | Sri Lanka* |
| Brazil | Hungary | Morocco | Sweden |
| Bulgaria | Iceland | Nepal* | Switzerland |
| Cameroon | India | Netherlands | Taiwan |
| Canada | Indonesia | New Zealand | Tanzania |
| Cape Verde* | Ireland | Niger | Thailand |
| Chile | Israel | Nigeria | Trinidad and Tobago* |
| China | Italy | Norway | Tunisia |
| Colombia | Japan | Oman | Turkey |
| Costa Rica | Jordan* | Pakistan* | United Kingdom |
| Côte d'Ivoire | Kenya* | Panama | United States of America |
| Cyprus | Korea | Peru | Uruguay |
| Czech Republic | Kuwait* | Philippines | Venezuela |
| Denmark | Kyrgyzstan | Poland | Zimbabwe* |
| Ecuador |
- Notes: * means the country is excluded in the wage equation estimation.
Appendix D. The first step – estimation of the trade equation
To infer the trade cost function's parameters from bilateral (and internal) trade flows we estimate the trade equation using the PPML estimation strategy. This estimation strategy is able to take account of the zero trade flows in a way that (contrary to NLS) also deals with the heteroscedasticity that is inherently present in trade flow data (see Santos Silva and Tenreyro 2006). It gives the PPML method an advantage over the often used Tobit and/or OLS methods.31
| Trade cost function | I | II | III |
|---|---|---|---|
| Distance | −0.72 | −0.0002 | −0.71 |
| [0.00] | [0.00] | [0.00] | |
| Internal distance | 0.03 | −0.001 | 0.05 |
| [0.75] | [0.00] | [0.67] | |
| Contiguity | 0.75 | – | 0.93 |
| [0.00] | – | [0.00] | |
| Common language | – | – | 0.01 |
| – | – | [0.95] | |
| Landlocked importer | – | – | −0.44 |
| – | – | [0.01] | |
| Landlocked exporter | – | – | −0.25 |
| – | – | [0.05] | |
| Island importer | – | – | 0.28 |
| – | – | [0.00] | |
| Island exporter | – | – | 0.53 |
| – | – | [0.00] | |
| Ssa importer | – | – | −0.77 |
| – | – | [0.00] | |
| Ssa exporter | – | – | −1.01 |
| – | – | [0.00] | |
| Ssa importer and exporter | – | – | 0.35 |
| – | – | [0.15] | |
| GDP importer | 0.75 | 0.74 | 0.74 |
| [0.00] | [0.00] | [0.00] | |
| GDP exporter | 0.85 | 0.84 | 0.84 |
| [0.00] | [0.00] | [0.00] | |
| Own trade dummy | 1.60 | 3.80 | 1.50 |
| [0.01] | [0.00] | [0.02] | |
| (Pseudo) R2 | 0.95 | 0.94 | 0.96 |
| No. of observations | 8,774 | 8,773 | 8,774 |
| Importer = exporter? | |||
| – landlocked | – | – | [0.38] |
| – island | – | – | [0.29] |
| – ssa | – | – | [0.19] |
- Notes: p-values based on robust standard errors in brackets; importer = exporter? shows the p-value of a test of equality of the importer and exporter variant of a certain country specific variable.
To allow for the more elaborate multiplicative trade cost functions (column III), we follow Redding and Venables (2004, p. 76) and replace the importer and exporter dummies by importer and exporter GDP.32 In all specifications the distance coefficient is significant: the larger the distance between countries, the higher their trade costs. Also sharing a common border (contiguity) significantly lowers trade costs, a finding consistent with earlier studies (e.g., Limao and Venables 2001 and Redding and Venables 2004). When estimating the multiplicative specification, the results show the importance of also considering country-specific trade cost proxies. Being landlocked or a Sub-Saharan African country raises trade costs, whereas being an island lowers these costs. These findings are very much in line with the results reported in Limao and Venables (2001) and show that these country-specific trade cost proxies cannot a priori be ignored. Importer and exporter GDP also have the expected (positive) effects on trade.
Appendix E
| Method | Two-step dum | Two-step dum | Two-step dum | Two-step dum | |
|---|---|---|---|---|---|
| distance function | I | II | I | II | |
| MA: | 0.39*** | 0.11** | FMA: | 0.26** | 0.21 |
| [4.35] | [2.23] | [2.11] | [1.45] | ||
| Education | |||||
| Primary | 0.02 | 0.02 | 0.02 | 0.02 | |
| [5.23] | [4.20] | 4.76] | [4.85] | ||
| Secondary | 0.04 | 0.04 | 0.04 | 0.04 | |
| [6.51] | [7.23] | 7.49] | [7.94] | ||
| Tertiary | 0.03 | 0.03 | 0.04 | 0.04 | |
| [4.39] | [3.86] | 5.40] | [3.47] | ||
| No. of observations | 60 | 60 | 60 | 60 |
- Notes: Dependent variable is log of GDP per capita. t-values based on robust standard errors in brackets. ***, **, * denotes significance at the 1%, 5% and 10% respectively.




