Interspecies allometric scaling: prediction of clearance in large animal species: Part II: mathematical considerations
Abstract
Interspecies scaling is a useful tool for the prediction of pharmacokinetic parameters from animals to humans, and it is often used for estimating a first-time in human dose. However, it is important to appreciate the mathematical underpinnings of this scaling procedure when using it to predict pharmacokinetic parameter values across animal species. When cautiously applied, allometry can be a tool for estimating clearance in veterinary species for the purpose of dosage selection. It is particularly valuable during the selection of dosages in large zoo animal species, such as elephants, large cats and camels, for which pharmacokinetic data are scant. In Part I, allometric predictions of clearance in large animal species were found to pose substantially greater risks of inaccuracies when compared with that observed for humans. In this report, we examine the factors influencing the accuracy of our clearance estimates from the perspective of the relationship between prediction error and such variables as the distribution of body weight values used in the regression analysis, the influence of a particular observation on the clearance estimate, and the ‘goodness of fit’ (R2) of the regression line. Ultimately, these considerations are used to generate recommendations regarding the data to be included in the allometric prediction of clearance in large animal species.
Introduction
Within the published literature, there are numerous examples of studies that use published pharmacokinetic data to estimate the allometric relationship between a parameter such as clearance or volume of distribution vs. body weight (W). In this regard, among its uses, it is especially important for estimating an appropriate dose in large animal species for which there does not exist pharmacokinetic or clinical information to support dose estimation (Hunter & Isaza, 2002; Isaza & Hunter, 2004). It is also used to predict a terminal elimination half-life value, which may be applied by extension services such as the FARAD (http://www.farad.org) for estimating withdrawal times when drugs are administered to food-producing animals in an extralabel manner (Craigmill & Cortright, 2002).
Similar to its use for selecting the first time dose in humans (Boxenbaum & DiLea, 1995), interspecies extrapolation serves an important function within the framework of veterinary medicine. While it is now well-established that clearance can be extrapolated from small laboratory animals to man with a fair degree of accuracy, provided the rule of exponents is used (Mahmood & Balian, 1996), it is not known if the clearance from small animals can be extrapolated to large animals with the same degree of accuracy. Despite numerous examples of the successful application of allometric scaling (Mordenti, 1986; Hu & Hayton, 2001), there are also examples of its failure to accurately predict drug pharmacokinetics across species (Riviere et al., 1997).
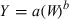 (1)
(1)In Part I, we examined the accuracy of predicting clearance in large animal species. Unlike predictions for human clearance values, the inclusion of correction factors (brain weight and maximum life span potential) failed to improve predictions in large animal species. In addition, the error associated with the clearance predictions for large animal species tended to be substantially diminished when at least one large animal species was included in the regression analysis. Oftentimes, within the veterinary literature, there has been an assumption that if scaling is based upon an allometric equation associated with a high correlation coefficient (R2), there will also be a high degree of accuracy in the predicted pharmacokinetic parameter. However, the validity of this assumption is rarely tested because of the absence of data in the predicted animal species.
In this report, we examine the factors influencing the accuracy of our clearance predictions by addressing the following questions:
- •
How does the distribution of W used in the regression analysis influence our predictions of clearance?
- •
For any species included in the regression analysis, how does its location on the X-axis (i.e. its value of W relative to that of the other observed data points) influence our predictions of Y? Can we anticipate that the impact on prediction error can be forecasted by the ‘goodness of fit’ (R2) of the regression line?
- •
What recommendations can be made regarding the data to be included in the regression analysis to minimize these prediction errors?
Inaccuracies in the allometric equation may lead to the selection of a sub-therapeutic dose if the dose is too low, a toxic dose if the prediction is too high, or withdrawal time predictions that lead to the presence of violative (potentially unsafe) residues in edible tissues. Therefore, it is important that the mathematical underpinnings associated with these regression procedures be appreciated and appropriate caution exercised. With this objective in mind, we manipulated datasets for which there was extensive species-specific information (i.e. organ weights) in an effort to illustrate the potential sources of error that can influence the accuracy of our allometric predictions. It is our hope that through these examples, investigators can be reminded of the basic principles underlying linear regression analysis and, therefore, allometric scaling.
Methods
Prediction errors based upon the degree of extrapolation
Prediction error was estimated as the ratio of observed/predicted values. To examine the errors that can occur due simply to the process of linear regression and data extrapolation, we needed a dataset that contained a large array of species across a wide range of W. We also needed a parameter for which an allometric relationship could be clearly established and for which we anticipate minimal bias due to species-specific metabolic idiosyncrasies. Therefore, we elected to conduct this exercise using data on the relationship between organ weight and W. These data were published in the 1956 Handbook of Biological Data by William Spector (1956). A total of 28 animal species were used to evaluate the relationship between log10W (kg) vs. log10 organ weight (g) for the heart, liver, lung and kidneys.
To explore the relationship between prediction error and the magnitude of the organ weight extrapolation, we used subsets of the original dataset. This reflects the limited datasets usually available for allometry. To address our numerous questions, the following subsets were analyzed (for heart and kidneys weights only):
- •
Organ weight vs. W using four small animal species (mouse, rat, dog and monkey). These animal species were selected because these are the animals most frequently associated with preclinical trials for human pharmaceuticals. This is termed the ‘small species dataset’.
- •
Organ weight vs. W using four large animal species (cattle, buffalo, giraffe and zebra). This is termed the ‘large species dataset’.
- •
Organ weight vs. W using the small species dataset plus the data associated with one large animal species (cattle).
- •
Organ weight vs. W using the large species dataset plus the data associated with one small animal species (mouse).
Using each of the resulting regression equations, we predicted the kidney and heart organ weight for elephants and humans. We compared our predictions to the actual organ weights (the ratio of observed vs. predicted values). We also generated the following additional dataset-specific predictions:
- •
Small animal dataset: predictions were generated for buffalo, zebra, cattle, and giraffe.
- •
Large animal dataset: predictions were generated for mouse, rat, dog, and monkey.
- •
Small animal dataset plus one large animal species: predictions were generated for buffalo, zebra, and giraffe.
- •
Large animal dataset plus one small animal species: predictions were generated for rat, dog, and monkey.
Influence of error in Y variable estimate: relationship to W
The kidney weight of dogs, mice, rats, cattle, and elephants were estimated using the values of ‘a’ and ‘b’ determined from the regression of log10W on log10 kidney weight based on the data from all 28 animal species (log10Y = 0.8482x + 2.004). This was termed the Yno error estimate for these species, and the corresponding equation was termed the ‘no error’ regression equation. Based upon this ‘no error’ equation, we also calculated kidney weights for hypothetical species whose values of W ranged from 0.1 to 10 000 kg. These values (for the real and hypothetical species) were termed the ‘Yno error values’ (i.e. the error free dataset). A 100% error was introduced into the Y value of either the mouse (Ymouse error), dog (Ydog error), or elephant (Yelephant error) data and the allometric equation was recalculated. The Y values for all real and hypothetical animal species were then determined from the allometric equation calculated by using each of the modified datasets separately (i.e. separate equations that incorporated either the with dog error, mouse error or the cattle error).The ratio of Y values (without error/with error) were determined across the hypothetical species with Ws ranging from 0.1 to 10 000 kg. This exercise provided an opportunity to describe the influence of location on the accuracy of the allometric predictions and helped to describe the importance of animal weight on the magnitude of impact that that error will have on either the slope or the intercept of the regression equation.
Real example: difference in pharmacokinetic predictions when using two different equations reported for same drug
We wanted to examine how the allometric equation can vary as a function of the data used in the analysis. Therefore, we found an example of one drug, enrofloxacin, for which there are two published articles that provide interspecies estimates of clearance: Cox et al. (2004) and Bregante et al. (1999). Using the respective equations reported by each set of authors, we predicted enrofloxacin clearance across a range of hypothetical animal weights and examined the ratio of predicted values obtained by these two sets of allometric equations. As the equation reported by Bregante et al. was based upon free drug clearance values while the equation by Cox et al. was based upon total body clearance, we recalculated the allometric equation reported by Bregante et al., using only the uncorrected mean clearance values that were provided in their manuscript.
Results
For completeness, we include Table 1, which contains the organ weight information provided in the Spector book chapter. Thus, the reader can conduct their own manipulation of these data. We also provide the allometric equations associated with the regression of body weight to organ weight across all 28 animal species in 1-5.
| Species | Breed | Number animals | Sex | BW (kg) | Organ weights g/100 g BW) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Brain | Heart | Kidney | Liver | Lung | |||||
| Man | Negro | 7 | m | 47 | 2.73 | 0.81 | 0.51 | 2.81 | |
| White (US) | 7 | m | 67 | 1.96 | 0.42 | 0.41 | 2.3 | 0.73 | |
| White (EU) | 4 | m | 49 | 2.53 | 0.64 | ||||
| Buffalo | African | 4 | m,f | 700 | 0.09 | 0.47 | 0.24 | 0.98 | 0.94 |
| Camel | 1 | m | 450 | 0.12 | |||||
| Caribou | 4 | m,f | 98 | 0.3 | 0.9 | 0.13 | 1.83 | 2.1 | |
| Cat, domestic | Felis catus | 10 | m,f | 3.3 | 0.77 | 0.45 | 1.07 | 3.59 | 1.04 |
| Cattle | Holstein | 5 | m | 900 | 0.05 | 0.37 | 0.2 | 0.92 | 0.69 |
| Cattle | Holstein | 98 | f | 600 | 0.07 | 0.37 | 0.24 | 1.2 | 0.72 |
| Cheetah | 2 | m | 21 | 0.39 | 0.51 | 0.47 | 3.22 | 1.16 | |
| Chimpanzee | 1 | m | 52 | 0.84 | 0.48 | ||||
| Chimpanzee | 1 | f | 44 | 0.74 | 0.5 | 0.48 | 2.75 | 1.3 | |
| Dog | 4 | m,f | 13 | 0.59 | 0.85 | 0.3 | 2.94 | 0.94 | |
| Elephant | Loxodonta africana | 1 | m | 6600 | 0.08 | 0.39 | 0.27 | 1.62 | 2.08 |
| Gazelle | 2 | m,f | 24 | 0.38 | 1 | 0.43 | 2.15 | 1.15 | |
| Giraffe | 1 | m | 1200 | 0.06 | 0.41 | 0.18 | 1.56 | 0.99 | |
| Goat | Capra hircus | 1 | m | 28 | 0.41 | 1.9 | |||
| Guinea pig | Cavia prcellus | 58 | m | 0.26 | 1.33 | 0.53 | 1.17 | 5.14 | 1.18 |
| Guinea pig | Cavia prcellus | 10 | f | 0.43 | 0.92 | 0.39 | 0.86 | 3.86 | 1.07 |
| Hippo | Hippopotams amphibius | 1 | f | 1350 | 0.05 | 0.34 | 0.23 | 1.75 | 0.84 |
| Horse | Equus caballus | 1 | m | 635 | 0.1 | 0.88 | 0.27 | 1.34 | 0.9 |
| Horse | Equus caballus | 1 | f | 770 | 0.08 | 0.61 | 0.23 | 0.87 | 0.7 |
| Lion | Panthera leo | 4 | m | 125 | 0.19 | 0.85 | 2.12 | ||
| Lion | Panthera leo | 3 | f | 97 | 0.2 | 0.54 | 0.53 | 3.24 | 2.06 |
| Monkey blackhowler | 28 | m,f | 6.2 | 0.81 | 0.33 | 0.58 | 3.25 | 0.63 | |
| Monkey rhesus | 4 | m | 3.3 | 2.78 | 0.38 | 2.09 | |||
| Monkey rhesus | 7 | f | 3.6 | 2.57 | 0.34 | 1.89 | |||
| Mouse jumping | Azpus hudsonicus | 4 | m,f | 0.018 | 3.57 | 1.03 | 1.26 | 5.63 | 1.34 |
| Mouse meadow | Microtus drummond | 67 | m,f | 0.023 | 0.29 | 0.68 | 1.53 | 4.56 | 1.7 |
| Rabbit, giant flemmish | 2 | m | 3.7 | 0.29 | 0.29 | 0.61 | 2.66 | ||
| Rabbit, giant flemmish | 22 | f | 2.5 | 0.4 | 0.35 | 0.7 | 3.19 | 0.53 | |
| Rat, Norway | Rattus norvegiucs | 3 | m,f | 0.25 | 1.22 | 0.52 | 1.09 | 3.35 | 0.79 |
| Squirrel, red | Sciurus hudsonicus | 4 | m | 0.18 | 2.57 | 0.86 | 0.62 | 2.18 | 1.45 |
| Squirrel, red | Sciurus hudsonicus | 4 | f | 0.25 | 2.02 | 0.73 | 0.53 | 2.68 | 1.28 |
| Swine | Sus scrofa | 36 | f | 102 | 0.32 | 0.26 | 1.51 | ||
| Tiger | Panthera tigris | 1 | f | 160 | 0.14 | 0.27 | 1.14 | 0.64 | 0.57 |
| Wolf | Canis lupus | 1 | m | 22 | 0.52 | 1.08 | 0.82 | 0.276 | 3.56 |
| Zebra | Equus quagga | 4 | m,f | 280 | 0.2 | 1.42 | 0.35 | 1.67 | 0.8 |
Plot of log kidney weight (g) as a function of log BW (kg). The allometric equation for the regression conducted using all 28 data points included in Table 1 is: log10 Kidney weight = 0.8482(BW) + 0.8703; R2 = 0.9817.
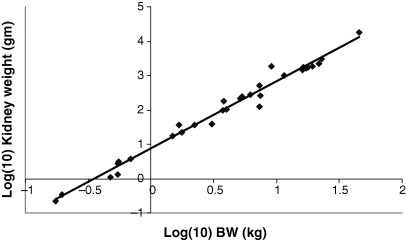
Plot of log heart weight (g) as a function of log BW (kg). The allometric equation for the regression conducted using all 28 data points included in Table 1 is: log10 Heart weight = 0.9783(BW) + 0.7603; R2 = 0.9822.
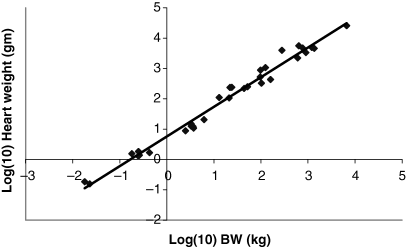
Plot of log liver weight (g) as a function of log BW (kg). The allometric equation for the regression conducted using all 28 data points included in Table 1 is: log10 liver weight = 0.8791(BW) + 1.471; R2 = 0.9733.
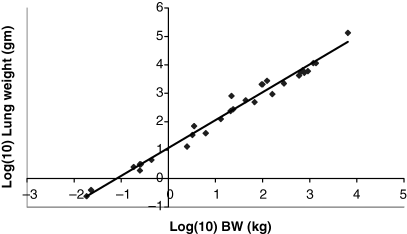
Plot of log lung weight (g) as a function of log BW (kg). The allometric equation for the regression conducted using all 28 data points included in Table 1 is: log10 lung weight = 0.9807(BW) + 1.0721; R2 = 0.9828.
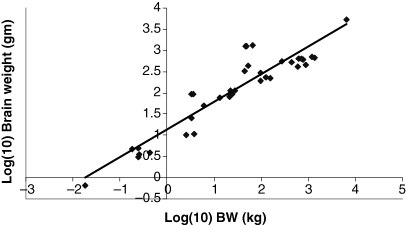
Plot of log brain weight (g) as a function of log BW (kg). The allometric equation for the regression conducted using all 28 data points included in Table 1 is: log10 Brain weight = 0.7033(BW) + 1.027; R2 = 0.8636.
Examining the error structure influencing the accuracy of allometric extrapolations
Prediction errors based upon the degree of extrapolation
The dataset included 28 species whose weights ranged from 0.023 kg (mouse) to 6600 kg (elephant). As seen in 1-5, there is a highly correlated linear relationship between the log weights of the various organs (kidney, heart, lung and liver) and the values of log W of the various animal species (R2 > 0.95). Interestingly, brain weight did not scale as well as did the other organ systems. The changes in slope (b) and intercept (a) for the entire dataset vs. the various data subsets are provided in Table 2. From these results, we see that the slopes and intercepts associated with the regression analysis performed on four large animal species are markedly different than that associated with the other data subsets. Particularly noteworthy is the absurdly large intercept seen both for the kidney and the heart (46.5 and 1805 g for the kidney and heart, respectively).
| All species | Small animal species | Large animal species | Cattle + 4 small species | Mouse + 4 large species | |
|---|---|---|---|---|---|
| Kidney | |||||
| b | 0.85 | 0.77 | 0.54 | 0.82 | 0.83 |
| a | 7.41 | 6.09 | 46.5 | 6.60 | 6.76 |
| Heart | |||||
| b | 0.98 | 0.91 | 0.10 | 0.93 | 0.92 |
| a | 5.76 | 5.62 | 1805* | 5.72 | 8.33 |
- *This very large intercept value reflects the magnitude of error associated with inclusion of species with similar weights in the scaling procedure.
The data subsets were examined for differences in prediction accuracy as compared with that seen when using all 28 available data points (Tables 3 and 4). The largest prediction errors consistently occurred when allometric extrapolations were based upon a dataset containing solely large animal species. In most cases, of the four subsets examined, large animal organ weight prediction were the most accurate when the regression analysis included four small (mouse, rat, dog, and monkey) plus one large animal species (cattle). Inclusion of only one small animal species in a large animal dataset generally did not perform as well as the latter.
| 28 Animal dataset† | Small animal species | Large animal species | 1 large + 4 small species | 1 small + 4 large species | |
|---|---|---|---|---|---|
| Dog | 0.60 | 0.64 | 1.94 | ||
| Rat | 1.19 | 0.12 | 1.08 | ||
| Mouse | 1.16 | 0.06 | |||
| Monkey | 1.03 | 0.28 | 1.04 | ||
| Cattle | 0.85 | 0.46 | |||
| Buffalo | 0.87 | 0.54 | 0.89 | ||
| Zebra | 1.11 | 0.71 | 1.10 | ||
| Giraffe | 0.71 | 0.43 | 0.73 | ||
| Elephant | 1.38 | 0.79 | 3.29 | 1.50 | 1.77 |
| Human | 1.05 | 0.70 | 0.60 | 0.99 | 1.15 |
- *When more than one set of values were available on a particular species (e.g. there were three sets of data available for monkey), one set was selected for estimating prediction error under all conditions.
- †Error based upon interpolated values.
| 28 Animal dataset† | Small animal species | Large animal species | 1 large + 4 small species | 1 small + 4 large species | |
|---|---|---|---|---|---|
| Dog | 1.56 | 0.04 | 1.37 | ||
| Rat | 0.88 | 0.0001 | 0.74 | ||
| Mouse | 1.09 | 0.0005 | |||
| Monkey | 0.60 | 0.01 | 0.52 | ||
| Cattle | 0.74 | 0.76 | |||
| Buffalo | 0.94 | 0.96 | 1.15 | ||
| Zebra | 2.79 | 2.85 | 3.34 | ||
| Giraffe | 0.83 | 0.85 | 1.03 | ||
| Elephant | 0.82 | 0.83 | 5.94 | 1.05 | 0.76 |
| Human | 0.80 | 0.82 | 0.08 | 0.93 | 0.71 |
- *When more than one set of values were available on a particular species (e.g. there were three sets of data available for monkey), one set was selected for estimating prediction error under all conditions.
- †Error based upon interpolated values.
To determine if the large animal species selected for inclusion in the ‘4 small + 1 large’ regression analysis had a substantial influence on the accuracy of the kidney or heart weight predictions, we recalculated the regression line, exchanging either elephant or buffalo for cattle. As seen in Table 5 (kidney) and Table 6 (heart), the results of the regression analysis generated using four small and one large animal species were similar, regardless of the species selected to represent the large animal.
| species | Obs/buffalo | Obs/elephant | Obs/cattle |
|---|---|---|---|
| Dog | |||
| Rat | |||
| Monkey | |||
| Mouse | |||
| Buffalo | 0.81* | 0.62 | 0.89 |
| Zebra | 1.01 | 0.80 | 2.42 |
| Giraffe | 0.66 | 0.50 | 0.73 |
| Elephant | 1.32 | 0.94* | 1.50 |
| Human | 0.93 | 0.77 | 0.99 |
| Cattle | 0.70 | 0.53 | 0.77* |
- *Back extrapolated values.
| Large species | Obs/Pred | ||
|---|---|---|---|
| Buffalo | Elephant | Cattle | |
| Dog | |||
| Rat | |||
| Monkey | |||
| Mouse | |||
| Buffalo | 0.99* | 1.07 | 1.15 |
| Zebra | 2.92 | 3.13 | 3.34 |
| Giraffe | 0.87 | 0.95 | 1.03 |
| Elephant | 0.86 | 0.96* | 1.05 |
| Human | 0.83 | 0.88 | 0.93 |
| Cattle | 0.78 | 0.85 | 0.92* |
- *Back extrapolated values.
Influence of error in Y variable estimate: relationship to W
To ascertain the degree to which one value can influence the regression equations, the kidney weight of the dog, mouse or elephant was sequentially changed (one at a time) by introducing a 100% error (doubling the weight of the kidney). The other species included in the regression analysis (rat and cattle) were not modified. The question being addressed was whether the ratio of kidney weight predicted without error (Yno error) vs. with error varied as a function of where the error was introduced along the Y-axis. The resulting slope and intercept values are provided in Table 7.
| b | a | R 2 | |
|---|---|---|---|
| No error | 0.848 | 5.47 | 1.0 |
| Elephant error | 0.888 | 5.70 | 0.996 |
| Dog error | 0.849 | 6.30 | 0.995 |
| Mouse error | 0.808 | 6.96 | 0.997 |
Introducing error into the mouse data and into the elephant data had equal but opposite effects on the slope of the line. However, the error in the mouse data had a greater impact on the value of the intercept, thereby compensating for the change in slope when predicting kidney weights for the large animal species. Conversely, the impact of mouse error on the kidney weight predictions of small animal species was comparable with the impact of elephant error on the predictions in large animal species (Table 8), Thus, when there is a limited number of species associated with the regression analysis, each datapoint has the greatest impact on the predictions of Y for animals whose values of W are closest to the deviant observation. While this outcome may be intuitively obvious, this basic point is sometimes overlooked by investigators when performing allometric scaling.
| Species with error | Mouse | Dog | Elephant | |
|---|---|---|---|---|
| kg | 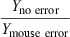 |
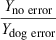 |
 |
|
| Dog | 13 | 0.87 | 0.87* | 0.87 |
| Elephant | 6600 | 1.12 | 0.87 | 0.68* |
| Mouse | 0.023 | 0.68* | 0.87 | 1.12 |
| 0.1 | 0.72 | 0.87 | 1.05 | |
| 10 | 0.86 | 0.87 | 0.88 | |
| 100 | 0.95 | 0.87 | 0.80 | |
| 1000 | 1.04 | 0.87 | 0.73 | |
| 10 000 | 1.14 | 0.87 | 0.67 | |
- *Back extrapolated values.
If we compare the error occurring in predictions for large animal species, the greatest error risk was associated with the dataset containing error in the elephant organ weight (e.g. 27% over-prediction for a 1000 kg animal). In contrast, the introduction of error in the mouse data resulted in only a 4% under-prediction for the 1000 kg animal. When a midpoint species (dog) is the source of the error, the change is primarily in the intercept rather than the slope. Consequently, the resulting magnitude of prediction error (Yno error/Ydog error) is comparable throughout the range of W values examined. It is also of interest to note that the dog predictions were consistently robust to the changes, exhibiting the least fluctuation in predicted values. This is consistent with its location at the central point on the curve. It should be noted that in real life situations, this ‘data error’ can appear both in either W and/or in the pharmacokinetic parameter.
Real example: difference in pharmacokinetic predictions when using two different equations reported for same drug
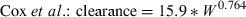 (2)
(2)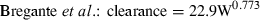 (3)
(3)| Hypothetical W | Bregante et al., prediction of total clearance | Cox et al., prediction of total clearance | Total clearance predictions Bregante/Cox |
|---|---|---|---|
| 1 | 23 | 16 | 1.44 |
| 10 | 136 | 92 | 1.47 |
| 100 | 805 | 536 | 1.50 |
| 1000 | 4769 | 3115 | 1.53 |
Discussion
Despite the potential for extrapolation error, the reality is that allometric predictions are needed across many veterinary practice situations. For this reason, it is important to consider mechanisms for minimizing these errors. In Part I (Mahmood et al., 2006), we reported that when generating allometric predictions of clearance for large veterinary species, the inclusion of at least large animal in the scaling, with or without human data, can improve the accuracy of the predictions. In this current report (Part II), we clearly see that in addition to the physiological issues discussed in Part I, there is a simple mathematical basis for this observation.
Interspecies scaling is conducted across species with values of W that generally vary by several orders of magnitude. Even when the smallest species is the laboratory mouse (0.02 kg) and the largest is the dog (10–12 kg), this amounts to almost a 500- to 600-fold difference in W. When a pharmacokinetic parameter is predicted in humans, the human W is outside the regression line. Although, this practice belies the general notion that the prediction of a given parameter should only be made within the range of the independent (X-axis) parameter, the W of man is only about sevenfold greater than that of the dog. On the other hand, large animals like horse, camel, donkey, and mule are almost 30- to 50-fold heavier than the canine. This wide margin of difference between weights may be one of the reasons that the predicted pharmacokinetic values in large animals are in error.
Looking at the results of the extrapolation exercises using heart and kidney weights, a ‘rule of thumb’ is that slightly better predictions in large animal species are generated when the regression analysis includes several small plus one large animal species. However, as seen in our analysis, it is difficult to obtain an a priori determination of which large animal species will produce the least biased allometric prediction. Nevertheless, we did observe that there are certain factors that can be considered for minimizing the risk of prediction error.
Based upon the conditions examined in this study, we can see that deviation in even one animal species can markedly skew our predictions. In fact, when we selectively added error to the ‘actual’ values of any particular animal species, we found that the greatest bias occurs in predictions for species of similar weight. Therefore, it is important to base extrapolations on as many species of similar weights as is technically feasible.
In the comparison of clearance values estimated on the basis of the equations provided by Bregante et al. vs. Cox et al., we find that despite the similarity in these equations, there was a 50% difference in the clearance values predicted in large animal species. This observation underscores the importance of recognizing the magnification of error that occurs when converting from logarithmic back to a linear scale. Most importantly, even in the presence of a high correlation coefficient, extrapolation error can be substantial and therefore, a high R2 should interpreted as a criterion for assuring a high level of accuracy in our interspecies predictions.
As we attempted to illustrate in this set of exercises, it is important to keep sight of the fundamental principles underlying simple linear regression (Draper & Smith, 1981). When we use log–log transformation to plot the relationship between clearance and W, we are assuming that there is a constant % CV about the values of clearance associated with W being considered. If this is not a correct assumption, the use of linear regression analysis is not appropriate. Simply translated, allometry functions under an assumption that the variability in clearance (expressed relative to a species population mean) is identical across target animal species (becomes linearized by using a log–log plot). This point is rarely addressed in published allometry study reports.
We are also relying upon an assumption that the function describing the relationship between log10 clearance and log10W is best described by a single slope and intercept. This assumption raises one very important stumbling block: the reliance on R2 as an indicator of prediction accuracy. As seen in the organ datasets and in our exercises in Tables 7 and 8, a high R2 value does not necessarily indicate that particular segments within the total range of W values would not have been better fit if we used some nonlinear regression method. A minor deviation in linearity is particularly critical when we recognize that our clearance estimates must ultimately be back-transformed to the linear scale.
Even if the relationship is indeed linear, we need to appreciate the factors that may influence the variance about the slope of the line or about the intercept. As we saw with our organ weight example, a substantial change in the slope of the line can occur by altering the weight range of the animal species (even though R2 values typically remained very high). We also found that the nature of the change in the regression equation resulting from a modification in a single species parameter value depended upon where the animal was located within the range of Ws. The value of the intercept was most greatly influenced by the mouse parameter value. Mouse error also influenced the slope. Introducing error in the midrange value (dog) had little to no effect on slope but some effect on intercept. Elephant values had negligible impact on the value of the intercept but had a substantial effect on slope. These findings are consistent with the simple principle that the prediction error in a regression equation is at its minimum at the midpoint of the line and increases as we move in either direction from that midpoint. Therefore, our best predictions are most likely to occur when we interpolate a parameter value for species that fall within the midpoint of our observed values of W.
In conclusion, the following points need to be considered when predicting doses for large animal species on the basis of allometric equations:
- •
A large value of R2 should not be interpreted to indicate that there will necessarily be a high degree of accuracy in our allometric predictions.
- •
Prediction error is largest at the upper and lower limits of W.
- •
When information on only small laboratory species is available, the impact of extrapolation error, physiological differences, and the assumptions associated with the extrapolations should be considered.
- •
If at all possible, data from at least one large animal species should be included to reduce the potential error in the clearance predictions that could lead to the administration of either toxic or sub-therapeutic dosages to these veterinary patients.




