Using model-data fusion to interpret past trends, and quantify uncertainties in future projections, of terrestrial ecosystem carbon cycling
Abstract
Uncertainties in model projections of carbon cycling in terrestrial ecosystems stem from inaccurate parameterization of incorporated processes (endogenous uncertainties) and processes or drivers that are not accounted for by the model (exogenous uncertainties). Here, we assess endogenous and exogenous uncertainties using a model-data fusion framework benchmarked with an artificial neural network (ANN). We used 18 years of eddy-covariance carbon flux data from the Harvard forest, where ecosystem carbon uptake has doubled over the measurement period, along with 15 ancillary ecological data sets relative to the carbon cycle. We test the ability of combinations of diverse data to constrain projections of a process-based carbon cycle model, both against the measured decadal trend and under future long-term climate change. The use of high-frequency eddy-covariance data alone is shown to be insufficient to constrain model projections at the annual or longer time step. Future projections of carbon cycling under climate change in particular are shown to be highly dependent on the data used to constrain the model. Endogenous uncertainties in long-term model projections of future carbon stocks and fluxes were greatly reduced by the use of aggregated flux budgets in conjunction with ancillary data sets. The data-informed model, however, poorly reproduced interannual variability in net ecosystem carbon exchange and biomass increments and did not reproduce the long-term trend. Furthermore, we use the model-data fusion framework, and the ANN, to show that the long-term doubling of the rate of carbon uptake at Harvard forest cannot be explained by meteorological drivers, and is driven by changes during the growing season. By integrating all available data with the model-data fusion framework, we show that the observed trend can only be reproduced with temporal changes in model parameters. Together, the results show that exogenous uncertainty dominates uncertainty in future projections from a data-informed process-based model.
Introduction
Terrestrial ecosystems mediate a large portion of the CO2 flux between the Earth's surface and the atmosphere, with approximately 120 Pg C yr−1 taken up by gross photosynthesis, and a slightly smaller amount respired back (Prentice et al., 2000; Beer et al., 2010; Pan et al., 2011). The balance of these two numbers, net ecosystem exchange (NEE), drives the terrestrial carbon cycle and is tightly coupled to the growth rate of atmospheric CO2 (Bousquet et al., 2000; Knorr et al., 2007). For policy makers, and many earth-system scientists, a major goal of global change research is therefore to understand the processes responsible for changes in terrestrial carbon cycling and to project future states of ecosystems and climate at decadal, or even longer time scales (Clark et al., 2001; Luo et al., 2011).
Increasingly, many long-term data sets show trends that demand investigation. Inventory data show increased forest growth rates in eastern North America (McMahon et al., 2010), potentially due to recent changes in climate, nutrient deposition, or community structure. Similar increases in tropical (Lewis et al., 2009) and temperate (Urbanski et al., 2007; Salzer et al., 2009; Dragoni et al., 2011; Pilegaard et al., 2011) forest carbon uptake have been reported (but see Fahey et al., 2005), and have been linked to changes in the growing season length, and vegetation dynamics. Open questions remain as to the dominant controls of such long-term changes, and the relative importance of climatic and biotic factors (Richardson et al., 2007). As we move into a data-rich era in ecology (Luo et al., 2008), and an era of advanced data mining (e.g., Abramowitz et al., 2007; Moffat et al., 2010) and model uncertainty analysis techniques (e.g., Braswell et al., 2005; Wang et al., 2009; Williams et al., 2009; Keenan et al., 2011c), we are now in a position to address such long-term questions.
Process-based models are the most commonly used tools for the projection of long-term ecosystem function. For terrestrial vegetation, the term ‘process-based’ incorporates a broad range of methodologies for describing eco-physiological processes, from semi-empirical relationships to mechanistic descriptions based on physical laws. Such models are often shown to reproduce observations ‘reasonably well’ (e.g., Braswell et al., 2005; Williams et al., 2005). However, model intercomparisons and model-data comparison studies show tremendous variations among models for both short- and long-term projections (e.g., Friedlingstein et al., 2006; Siqueira et al., 2006; Sitch et al., 2008; Schwalm et al., 2010; Dietze et al., 2011; Keenan et al., in press).
Model-data fusion (also referred to as ‘data assimilation’, or ‘inverse modeling’) (Wang et al., 2009; Keenan et al., 2011c) is a means by which to use observational data to optimize a model and quantify model uncertainty. The approach identifies combinations of model parameters that give an equivalent model-data agreement. In this way, data from different sources can be synthesized using the model as the interpreter, independent of parameter assumptions. Results are conditional on model structure, and the information content of observational data along with data uncertainties (Raupach et al., 2005; Keenan et al., 2011c). For example, model-data fusion applications of both simple (Braswell et al., 2005) and complex (Medvigy et al., 2009) models at Harvard forest acknowledged the limitation of using only one or two data streams to constrain model parameterization.
Even with an optimized model, results remain contingent on model structure. An optimized model is therefore not necessarily correct or even good. For example, if the model structure is inadequate, or the model parameters are not well constrained, an optimized model can get the right answer for the wrong reason or through a variety of unverified process combinations (equifinality) (Beven, 2006). It is thus important to test the optimized model against data that was not used for training. Another approach to assessing model performance is to test the optimized model using an independent ‘benchmark’. Empirical data-mining tools such as artificial neural networks (ANN) can serve as an excellent means by which to benchmark model performance (Abramowitz et al., 2007). Such data-mining tools have been shown to capture the complex response of ecosystem carbon cycling to climatic drivers (Moffat et al., 2010). They therefore provide an indication of how well a good (though not necessarily best) model should be expected to perform.
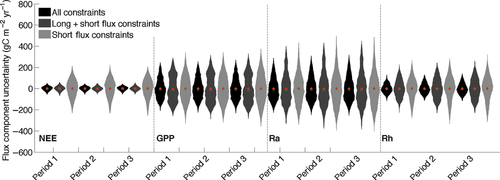
Carbon uptake at Harvard forest has increased from ~200 to ~500 g C m−2 yr−1 during the 18-year period from 1992 to 2009; around this long-term trend, there is also interannual variability on the order of ±117 g C m−2 yr−1 (1 SD). In this paper, we use a parsimonious forest carbon cycle model, embedded in a multiple constraints Markov-chain Monte Carlo optimization framework, to examine trends and variability in uptake. We first assess the impact of using different data constraints on uncertainty in model performance, both in training and test periods. An ANN approach (Moffat et al., 2010) is then used to benchmark the optimized process-based model. By examining how the use of different constraints can reduce uncertainty, we test whether recent changes in uptake are driven by concurrent trends external to the model system (exogenous factors) or model-internal (endogenous) factors. The impact of endogenous uncertainty in ecological forecasting is also assessed and compared with current trends in carbon uptake at the Harvard forest.
Materials and methods
Site
All data used were obtained within the footprint of the eddy-covariance tower at the Harvard Forest Environmental Measurement Site (HFEMS) (http://atmos.seas.harvard.edu/lab/hf/index.html), which is located in the New England region of the northeastern United States (42.53 N 72.17 W, elevation 340 m) (Wofsy et al., 1993; Barford et al., 2001; Urbanski et al., 2007). The forest within the tower footprint is largely deciduous, dominated by red oak (Quercus rubra, 52% basal area), red maple (Acer rubrum, 22% basal area), eastern hemlock (Tsuga canadensis, 17% basal area), and a secondary presence of white pine (Pinus strobus) and red pine (Pinus resinosa) is also found within the tower footprint.
Data
We used 18 complete years (1992–2009) of hourly meteorological and eddy-covariance (Wofsy et al., 1993; Goulden et al., 1996; Barford et al., 2001; Urbanski et al., 2007) measurements of NEE (http://atmos.seas.harvard.edu/lab/data/nigec-data.html). Hourly gap-filled meteorological variables used include incident photosynthetically active radiation (PAR), air temperature above the canopy, soil temperature at a depth of 5 cm, vapor pressure deficit (VPD), and atmospheric CO2 concentration. Quality controlled hourly eddy-covariance observations (without gap-filling) of NEE were used to optimize the ecosystem model and train the ANN. Gap-filled NEE values were only used to provide annual sums for evaluating optimized model performance.
For ancillary data constraints, we used measurements of leaf area index (LAI), soil organic carbon content, carbon in roots, carbon in wood, wood carbon annual increment, observer-based estimates of bud-burst and leaf senescence, leaf litter, woody litter, and continuous and manual measurements of soil respiration (Table 1), downloaded from the Harvard forest data repository (http://harvardforest.fas.harvard.edu/data/archive.html).
| Measurement | Frequency | No. of data points | Reference |
|---|---|---|---|
| Eddy-covariance | Hourly | 73 198 | Urbanski et al. (2007) and a |
| Soil respiration 1 | Hourly | 26 430 | Savage et al. (2009) |
| Soil respiration 2 | Hourly | 19 030 | Phillips et al. (2010) |
| Soil respiration 3 | Weekly | 498 | b |
| Leaf area index | Monthly | 51 | Norman (1993), Urbanski et al. (2007), and a |
| Leaf litter fall | Yearly | 10 | Urbanski et al. (2007) and a |
| Woody biomass | Yearly | 15 | Jenkins et al. (2004), Urbanski et al. (2007), and a |
| Woody litterfall | Yearly | 8 | Urbanski et al. (2007) and a |
| Root biomass | 1 year | 1 | DIRT projecta |
| Forest floor carbon | 1 year | 1 | Gaudinski et al. (2000) |
| Budburst | Yearly | 15 | O'Keefe (2000)a |
| Leaf drop | Yearly | 14 | O'Keefe (2000)a |
| Soil carbon pools | 3 years | 3 | Gaudinski et al. (2000), Magill et al. (2000), Bowden et al. (1993) |
| Soil carbon turnover | One | 1 | Gaudinski et al. (2000) |
| Proportion of heterotrophic respiration in soil | One | 1 | Gaudinski et al. (2000) |
In addition to the ancillary data available from the Harvard forest data repository, we used two other model constraints: (1) annual estimates of the contribution of root respiration to total soil respiration and (2) estimates of turnover times of soil organic matter pools. Radiocarbon and soda-lime (in combination with trenching) based estimates of the contribution of autotrophic respiration (Ra) to total soil respiration (Rsoil) were obtained from Gaudinski et al. (2000), Bowden et al. (1993), and E. Davidson (unpublished results). Bowden et al. (1993) provided a mean annual estimate of belowground autotrophic respiration as roughly 33% of total annual soil respiration. Gaudinski et al. (2000) and E. Davidson (unpublished results) suggested an approximate error of roughly 50% associated with this estimate. Although annual fluxes were constrained to a specific proportion, Ra : Rsoil could vary on shorter timescales. Turnover times of litter and the two soil organic matter pools (slow, passive) were also taken from Gaudinski et al. (2000). Microbial biomass turnover times were estimated as 1.7 ± 1.3 years (E. Davidson unpublished results).
Estimates of uncertainty were used for each data stream in the optimization. Uncertainty estimates for NEE were taken from Richardson et al. (2006), where uncertainties were shown to follow a double-exponential distribution, with the standard deviation of the distribution specified as a linear function of the flux. Estimates of uncertainty due to flux gap-filling (which apply to the annual NEE totals) were taken from Barr et al. (2009). Soil respiration uncertainty estimates were taken from Savage et al. (2009) and Phillips et al. (2010), where measurement uncertainty increased linearly with the magnitude of the flux. LAI sampling uncertainties were estimated as the standard error (n = 34 plots) of the mean LAI. Litterfall sampling errors were calculated as the standard error (n = 34 plots) of the annual total litterfall across all plots. Uncertainty of carbon in wood was calculated from the standard error (n = 34 plots, 635 trees) of the mean plot-level cumulative increment, which averaged ~10% over all years. Two independent measurements (Bowden et al., 1993; Gaudinski et al., 2000) were used to constrain the initial value of total soil C content (CSOM = 8.3 ± 1.4 kg C m−2; mean ± 1 SE), with uncertainties estimated based on the standard deviation between datasets. Root biomass uncertainties were estimated from spatial variation in the samples (n = 21 plots), taken in the control plots of the DIRT project (http://www.lsa.umich.edu/eeb/labs/knute/DIRT/). Uncertainty estimates for the dating of phenological events were based on the between tree standard deviation.
Additionally, three different soil respiration data sets, two automated and one manual, were used (Savage et al., 2009; Phillips et al., 2010). Although seasonal cycles were similar between the data sets, disagreement in the magnitude of the flux was evident between the different soil respiration data sets, reflecting high spatial variability in soil characteristics. We included three additional scaling parameters (data harmonizing parameters) in the optimization process (e.g., van Oijen et al., 2011). These scale different chamber datasets to account for the possibility that a particular dataset is not representative of the mean soil respiration of the tower footprint. This thus harmonizes the magnitude of the different soil respiration data streams to give an estimate of the spatial average soil respiration of the tower footprint, but then leverages the temporal patterns in the data as model constraints.
The FöBAAR model
We developed a forest carbon cycle model that strikes a balance between parsimony and detailed process representation. Working on an hourly timescale, FöBAAR (Forest Biomass, Assimilation, Allocation and Respiration) calculates photosynthesis from two canopy layers, and respiration from eight carbon pools [leaf, wood, roots, soil organic matter (microbial, slow and passive pools), leaf litter and (during phenological events) mobile stored carbon], using as environmental forcings canopy air temperature (Ta), 5 cm soil temperature (Ts), photosynthetic active radiation (PAR), VPD, and atmospheric CO2.
The canopy in FöBAAR is described in two compartments representing sunlit and shaded leaves (Sinclair et al., 1976; Wang & Leuning, 1998). Intercepted radiation by sunlit or shade leaves depends on the position of the sun, and the area of leaf exposed to the sun based on leaf angle and the canopy's ellipsoidal leaf distribution (Campbell, 1986). Here, we assume a spherical leaf angle distribution. Assimilation rates for sunlit and shaded leaves are calculated through the commonly used Farquhar approach (Farquhar et al., 1980; De Pury & Farquhar, 1997), with dependencies on absorbed direct and diffuse radiation, air temperature, VPD, and the concentration of CO2 within the leaf inter-cellular spaces. Stomatal conductance is calculated using the Ball–Berry model (Ball et al., 1987), coupled to photosynthetic rates through the analytical solution of the Farquhar, Ball Berry coupling (Baldocchi, 1994). Rates of photosynthesis are dependent on the minimum between rate of carboxylation and the proportional rate of electron transport. The canopy integrated (over space and time) RuBP (ribulose-1,5-bisphosphate) rate of carboxylation, Vc, and the rate of electron transport, J, are calculated following Farquhar et al. (1980) and De Pury & Farquhar (1997). The CO2 compensation point and the mitochondrial respiration rate are calculated using an Arrhenius-type equation (Bernacchi et al., 2001).
Maintenance respiration is calculated as a fraction of assimilated carbon. The remaining assimilate is allocated to foliar carbon, then to the wood and root carbon pools on a daily time step. Mobile stored carbon relates only to foliage and is respired only during periods of bud-burst and leaf-fall. Carbon allocation and canopy phenology are simulated as in the DALEC model (Williams et al., 2005; Fox et al., 2009).
Root respiration is calculated hourly and coupled to photosynthesis through the direct allocation to roots. Dynamics of soil organic matter is modeled using a three-pool approach (microbial, slow, and passive pools) (Knorr & Kattge, 2005). Decomposition in each pool is calculated hourly, with a pool specific temperature dependency. Litter decomposition is also calculated hourly, but on an air temperature basis. Litter and root carbon are transferred to the microbial pool, then to the slow and finally to the passive pool.
In total, 35 model parameters (including three data harmonization parameters, Table 2; P40, P41, P42) and seven initial pools were optimized, giving a total of 42 free parameters. The inclusion of the initial biomass and soil pools in the optimization process removed the need for a model spin-up.
| Id | Name | Definition | Min | Max | 90% CI |
|---|---|---|---|---|---|
| Initial carbon pools (g C m−2) | |||||
| P1 | R C | Carbon in roots | 20 | 500 | 28, 205 |
| P2 | W C | Carbon in wood | 8 000 | 14 000 | 7 792, 10 931 |
| P3 | LitC | Carbon in litter | 10 | 1 000 | 146, 528 |
| P4 | SOMC slow | Carbon in slow cycling soil organic matter layer | 10 | 1 000 | 95, 278 |
| P5 | SOMC passive | Carbon in passive cycling soil organic matter layer | 1 500 | 12 000 | 1 800, 4 560 |
| P6 | MobC | Mobile carbon | 75 | 200 | 90, 175 |
| Allocation and transfer parameters | |||||
| P7 | Af | Fraction of GPP allocated to foliage | 0.1 | 1 | 0.31, 0.48 |
| P8 | Ar | Fraction of NPP allocated to roots | 0.5 | 1 | 0.57, 0.83 |
| P9 | Lff | Litterfall from foliage (Log10) | −6 | −0.85 | −1.12, −0.88 |
| P10 | Lfw | Litterfall from wood (Log10) | −6 | −1 | −5.14, −4.88 |
| P11 | Lfr | Litterfall from roots (Log10) | −6 | −1 | −2.62, −1.88 |
| P12 | Fc_lf | Fraction of Cf not transferred to mobile carbon | 0.3 | 0.8 | 0.36, 0.52 |
| P13 | Lit2SOM | Litter to slow SOMC transfer rate (Log10) | −6 | −1 | −2.79, −2.09 |
| P14 | Lit2SOM Td | Litter to slow SOMC temperature dependence | 0.01 | 0.5 | 0.01, 0.07 |
| P15 | SOMS2SOMP | Slow SOMC to passive SOMC rate | 0.03 | 0.8 | 0.07, 0.77 |
| P16 | SOMS2SOMP Td | Slow SOMC to passive SOMC temp. dependence | 0.01 | 0.8 | 0.03, 0.55 |
| Canopy parameters | |||||
| P17 | LMA | Leaf mass per area (g C m−2) | 50 | 120 | 81, 120 |
| P18 | MaxFol | Maximum canopy carbon content (g C m−2) | 150 | 600 | 180, 550 |
| P19 | Vcmax | Velocity of carboxylation (umol mol−1) | 60 | 175 | 90, 165 |
| P20 | Ea Vcmax | Activation energy for Vcmax | 58 000 | 75 000 | 58 000, 75 000 |
| P21 | Ed Vcmax | Deactivation energy for Vcmax | 200 000 | 250 000 | 200 000, 250 000 |
| P22 | Ea Jmax | Activation energy for the electron transport rate | 40 000 | 50 000 | 40 000, 50 000 |
| P23 | Ed Jmax | Deactivation energy for the electron transport rate | 180 000 | 230 000 | 180 000, 230 000 |
| P24 | Rd | Rate of dark respiration | 0.01 | 1.1 | 0.01, 1.1 |
| P25 | Q10 Rd | Temperature dependence of Rd | 0.4 | 2.8 | 0.45, 2.75 |
| Phenology parameters | |||||
| P26 | GDD0 | Day of year for growing degree day initiation | 50 | 150 | 91, 117 |
| P27 | GDD1 | Growing degree days for spring onset | 135 | 300 | 135, 277 |
| P28 | Air Ts | Leaf senescence onset mean air temperature (°C) | 0 | 15 | 11, 12.4 |
| P29 | GDD2 | Spring photosynthetic GDD maximum | 500 | 1 000 | 660, 1 000 |
| Respiration parameters | |||||
| P30 | Litd | Litter respiration rate (Log10) | −7 | −1 | −6.6, −3.7 |
| P31 | LitdTd | Litter respiration temperature dependence | 0.001 | 0.1 | 0.01, 0.1 |
| P32 | SOMSd | Slow cycling SOMC respiration rate (Log10) | −6 | −1 | −4.55, 3.11 |
| P33 | SOMSdTd | Slow cycling SOMC temperature dependence | 0.01 | 0.2 | 0.01, 0.19 |
| P34 | SOMPd | Passive cycling SOMC respiration rate (Log10) | −6 | −1 | −6.38, −5.15 |
| P35 | Rrootd | Root respiration rate (Log10) | −6 | −1 | −5.09, −3.77 |
| P36 | RrootdTd | Root respiration rate temperature dependence | 0.01 | 0.2 | 0.07, 0.2 |
| P37 | MobCr | Mobile stored carbon respiration rate (Log10) | −6 | −0.5 | −1.5, 0.5 |
| P38 | MobCTr | Fraction of mobile transfers respired | 0 | 0.1 | 0, 0.1 |
| P39 | Maintr | Fraction of GPP respired for maintenance | 0.1 | 0.5 | 0.1, 0.44 |
| Scaling parameters | |||||
| P40 | Rsoil1 | Soil respiration scaling co-efficient (data set 1) | 0.5 | 2 | 0.96, 1.65 |
| P41 | Rsoil2 | Soil respiration scaling co-efficient (data set 2) | 0.5 | 2 | 0.62, 1.53 |
| P42 | Rsoil3 | Soil respiration scaling co-efficient (data set 3) | 0.5 | 2 | 0.45, 1.65 |
Model-data fusion
An adaptive multiple constraints Markov-chain Monte Carlo (MC3) optimization was used to optimize the process-based model and explore model uncertainty. The algorithm uses the Metropolis–Hastings (M-H) approach (Metropolis & Ulam, 1949; Metropolis et al., 1953; Hastings, 1970) combined with simulated annealing (Press et al., 2007). It is loosely based on that of Braswell et al. (2005), and it is adaptive in the sense that the step size, which is expressed as a fraction of the initial parameter range, is automatically adjusted to obtain a fixed acceptance rate. Preliminary tests with synthetic data indicated an acceptance rate of ~21% gave optimal efficiency (good mixing) for the posterior exploration. Prior distributions for each parameter given in Table 2 were assumed to be uniform (noninformative, in a Bayesian context).
The optimization process uses a two-step approach. In the first stage, the parameter space is explored for 100 000 iterations using the MC3 optimization algorithm. At each iteration, the current step size is used as the standard deviation of random draws from a normal distribution with mean zero, by which parameters are varied around the previous accepted parameter set. Parameters that fall outside the initial parameter range are ‘bounced’ back within their range. This stage identifies the optimum parameter set by minimizing the cost function [see Eqn (2)], and 100 000 model iterations were used to identify the optimum parameter set, as longer runs led to no improvement.
In the second stage, the parameter space is again explored, and a parameter set is accepted if the cost function for each data stream (defined below) passes a χ2 test (at 90% confidence) for acceptance/rejection (after variance normalization based on the minimum cost function obtained (e.g., Franks et al., 1999; Richardson et al., 2010). This approach is preferable to using the aggregate cost function, as it ensures that model predictions are consistent with each of the individual data streams.
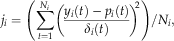 (1)
(1)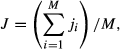 (2)
(2)Thus, each individual cost function is averaged by the number of observations, and the average of the cost functions from all data streams is taken as the total cost function. In this manner, each data stream is given equal importance in the optimization (Franks et al., 1999; Barrett et al., 2005).
Model benchmarking – ANN ensemble
We used an ANN to benchmark the FöBAAR model performance (e.g., Abramowitz et al., 2007) and characterize the climatic sensitivity of ecosystem-atmosphere carbon exchange. An ANN is an inductive modeling approach based on statistical multivariate modeling (Bishop, 1995; Rojas, 1996) by which one can map drivers directly onto observations (e.g., Moffat et al., 2010). The benchmarking framework used in this paper is based on a feed-forward ANN with a sigmoid activation function trained with a back propagation algorithm (Moffat et al., 2010). An ensemble of six ANNs was trained on nongap-filled eddy-covariance carbon fluxes only. It should be noted that the ANN is a benchmark only for short-term environmental controls on hourly NEE, as it does not account for lagged effects on ecosystem state or function, or long-term changes in pool sizes.
The ANN was also used as a gap-filling tool to compare the gap-filled eddy-covariance carbon fluxes. When used as a gap-filling tool (e.g., Moffat et al., 2007), the ANN was trained on each year of eddy-covariance carbon flux data separately. Thus applied, the ANN agreed with the annual carbon flux from the independently gap-filled data with a root mean square error of 32 g C m−2.
Experimental set-up
We divided the 18 years of available data into three distinct 6 year periods (1992–1997; 1998–2003; 2004–2009; Fig. 2) to perform two experiments. In the first experiment, we used the middle period (Period 2, Fig. 1) to quantify the added benefit of using different data streams as constraints. This involved optimizing FöBAAR using as constraints either: (1) only hourly NEE data, (2) hourly, monthly, and yearly NEE data, or (3) all eddy-covariance carbon flux data (hourly, monthly, yearly) and ancillary data (Table 1). We then assessed the optimized model performance for the two periods not used for training. The ANN was trained to the eddy-covariance carbon flux data for the same 6 year period on which the FöBAAR model was trained and compared with the FöBAAR model.
The second experiment was designed to test whether model deficiencies highlighted by the first experiment could be resolved by training the model on each period. In the second experiment, we used all available data to optimize the FöBAAR model on each 6 year period individually. This allowed us to assess changes in model parameters when optimized on different periods.
Finally, for each of the three approaches to constraining the model (1, 2, and 3 above) in the first experiment, we projected carbon stocks and fluxes to 2100, to assess the effect of each constraint approach on the future propagation of uncertainty.
Downscaled future climate projections
For the climate change projection, we used downscaled data (Hayhoe et al., 2007) from the regionalized projection of the GFDL-CM global coupled climate-land model (Delworth et al., 2006) driven with socioeconomic change scenario A1FI (Denham KL et al., 2007). Model projections for Harvard forest under this scenario predict an increase in atmospheric CO2 to 969 ppm by 2100 and an increase in mean annual temperature from 7.1 to 11.9 °C.
Results
Assessing the benefit of additional constraints
We first tested the benefit of using flux and ancillary data for constraining model projections. Here, we use the middle six years of the time series (Period 2, Fig. 2) to optimize the FöBAAR model and the other two periods for testing, assessing three different approaches to constraining the model (see 2 section). When using only hourly NEE as a constraint, uncertainty in annual mean NEE model estimates was large (±200 g C m−2 yr−1 95% CI, Fig. 1). Particularly large uncertainty was evident among the component fluxes of gross primary productivity (±320 g C m−2 yr−1), autotrophic (±410 g C m−2 yr−1) and heterotrophic respiration (±290 g C m−2 yr−1). The use of monthly and annual flux aggregates largely reduced uncertainty in model estimates of annual NEE (to ±60 g C m−2 yr−1) during both the training and test periods, though only slightly reduced equifinality, shown in Fig. 1 as relatively large uncertainties in the component fluxes. Using all available data to constrain the model only slightly reduced uncertainty for annual flux estimates but gave a large reduction in uncertainty in the responsible processes (Fig. 1). Uncertainty in modeled fluxes in the test periods was comparable to that in the training period for each of the constraint approaches.
FöBAAR and ANN evaluation in training and test periods
In the following analysis, we trained both FöBAAR using all constraints and the ANN on Period 2 using only short-term flux constraints (Fig. 2), and tested the models on the other two periods. When trained on Period 2, neither FöBAAR nor the ANN captured the large increase in annual NEE during Period 3 (Fig. 3). The mean annual NEE estimated from the gap-filled tower data for the last 6 years of the time series (Period 3, Fig. 2) was roughly twice that of the previous 6 year period (Period 2, Fig. 2). In contrast, both FöBAAR and the ANN mean annual NEE for Period 3 were comparable with that of Period 2 (Fig. 2). As with all models that do not consider dynamic vegetation, FöBAAR and ANN predictions of NEE outside the training period make the implicit assumption that the climatic sensitivity of ecosystem function does not change between years. Long-term temporal trends in the residuals between the modeled and observed annual NEE can be interpreted as an alteration in the carbon uptake of the ecosystem that is independent of recent changes in the climate variables included in the model. Long-term trends in Harvard forest mean annual uptake [increased by ~300 g C m−2 (~150%) between Period 1 and Period 3] were thus shown to be independent of any recent changes in climate drivers included here.
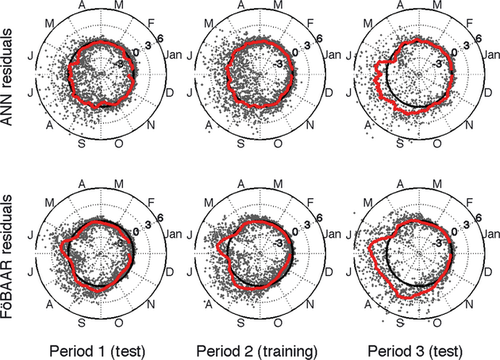
In general, when trained on Period 2, the FöBAAR model reproduced the mean values for the ancillary data streams, but not the interannual variability. FöBAAR-modeled carbon in wood for Period 2 was well simulated with an RMSE of 51 g C yr−1 (Table 3). Mean annual wood increments were also well captured, allowing for the accurate reproduction of biomass accumulation. Outside of the training period, RMSE performance for woody biomass was reduced, most noticeably for mean annual woody increment in Period 3, where the model under-predicted growth. Interannual variability in modeled wood increment did not show a significant correlation with the observations in any period (Table 3). For canopy processes, the seasonal evolution of LAI was well captured during the training period (r2: 0.89, RMSE: 0.49 m2 m−2). Mean bud-burst dates were well simulated (RMSE: 4.17 days), though interannual variability was not (r2: 0.24). Mean leaf senescence was simulated with a similar accuracy (RMSE: 3.4 days) though model correlation with inter-annual variability in senescence was low (r2: 0.35). Outside of the training period, model skill at reproducing observations of LAI and phenology declined (Table 3), most notably in Period 3, and in particular for inter-annual variability in leaf senescence. The magnitude of leaf litterfall was well simulated for the training period (RMSE: 12 g C m−2) but much less so for Period 3 (RMSE: 51 g C m−2), and interannual variability was poorly captured in all three periods.
| Period 1 (test) | Period 2 (trained) | Period 3 (test) | Period 3 (trained) | |||||
|---|---|---|---|---|---|---|---|---|
| r 2 | RMSE | r 2 | RMSE | r 2 | RMSE | r 2 | RMSE | |
| ANN | ||||||||
| NEE day | 0.77 | 0.17 | 0.74 | 0.19 | 0.76 | 0.22 | ||
| NEE night | 0.11 | 0.10 | 0.17 | 0.10 | 0.19 | 0.10 | ||
| NEE annual | ns | 118.18 | ns | 73.40 | ns | 213.80 | ||
| FöBAAR | ||||||||
| NEE day | 0.79 | 0.16 | 0.76 | 0.19 | 0.75 | 0.25 | 0.78 | 0.20 |
| NEE night | 0.09 | 0.11 | 0.15 | 0.11 | 0.10 | 0.11 | 0.14 | 0.11 |
| NEE annual | ns | 63.23 | ns | 90.57 | ns | 298.27 | ns | 87.3 |
| Soil respiration | ns | ns | 0.90 | 0.68 | 0.71 | 1.17 | 0.70 | 1.08 |
| Leaf area index | 0.89 | 0.86 | 0.89 | 0.49 | 0.76 | 0.85 | 0.84 | 0.71 |
| Litter fall | ns | ns | ns | 11.58 | ns | 50.56 | ns | 13.34 |
| Woody biomass | 1.00 | 60.15 | 0.96 | 52.93 | 0.99 | 111.44 | 0.99 | 56.08 |
| Woody increment | ns | 0.01 | ns | 0.06 | ns | 0.15 | ns | 0.02 |
| Bud burst | 0.20 | 4.24 | 0.24 | 4.17 | 0.21 | 3.70 | 0.32 | 0.57 |
| Leaf drop | 0.17 | 5.74 | 0.35 | 3.42 | 0.18 | 3.68 | 0.18 | 3.68 |
| FöBAAR vs. ANN | ||||||||
| NEE day | 0.76 | 0.18 | 0.76 | 0.18 | 0.71 | 0.21 | ||
| NEE night | 0.62 | 0.06 | 0.63 | 0.05 | 0.54 | 0.06 | ||
| NEE annual | ns | 79.18 | ns | 70.58 | ns | 80.70 | ||
For hourly daytime NEE in the training period, FöBAAR and the ANN performed comparably (r2: 0.76, 0.74), with an equivalent RMSE (0.19). The ANN showed better data-model agreement for the night-time fluxes than the FöBAAR model (Table 3). Cumulative annual fluxes show that both models tended to slightly underestimate the total annual NEE. Neither the FöBAAR model nor the ANN captured the high uptake seen in 2001 (data not shown), suggesting that the observed uptake in this year was not driven by the climatic variables included in this study. The ANN residuals showed no seasonal bias during the training period, whereas the optimized FöBAAR was slightly biased toward underestimating uptake during the growing period, and underestimating carbon released by the ecosystem during winter months (Fig. 3).
For the testing periods, both the ANN and the FöBAAR model performed well for hourly NEE fluxes during 1992–1997 (Period 1, Fig. 3), with no systematic temporal biases (Fig. 3). During 2004–2009, FöBAAR and the ANN both showed strong systematic biases, but only during the growing season (Period 3, Fig. 3) in particular during the months of June, July, August, and September. The correlation of measured and ANN/FöBAAR-modeled day-time NEE for the 2004–2009 period was equivalent to that of the other two periods, but a larger bias was evident for hourly predictions which accumulated to a large bias in the annual total (Table 3). This shows that good correlation to short-term fluxes does not eliminate the possibility of large bias at longer time scales.
Model extrapolation in time
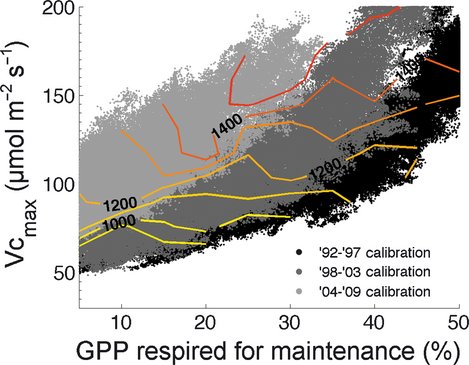
With a perfect understanding of the system, a model trained on one period should be able to predict the fluxes in the other periods. Experiment 1 showed that neither model used here could do so at Harvard forest. In Experiment 2, we calibrated the FöBAAR model to each period individually. When calibrating FöBAAR to all of the available data on the three individual periods, little bias is evident for FöBAAR NEE during that period, but large biases are evident in the other periods (Fig. 4). Calibrating to the whole time series thus over-estimates annual NEE for the first period, gives low bias in annual NEE for the middle period, and under-estimates annual NEE for the last period. Inter-annual variability in NEE was not captured by the model when trained on any period. Long-term changes in estimated modeled canopy photosynthetic potential (here Vcmax, P19) were needed to reproduce the observations. Reproducing the required trend in NEE required an increase in Vcmax of ~50% over the 18 years (Fig. 5). Vcmax co-varied strongly with the proportion of assimilate lost through maintenance respiration (Fig. 5). Such parameter equifinality could explain previous findings that models with very different Vcmax values can give comparable estimates of canopy photosynthesis (e.g., Keenan et al., 2011b). Although the use of multiple constraints allowed for the constraining of 24 of the 42 free model parameters, no other significant changes in parameters could be detected between the different periods.
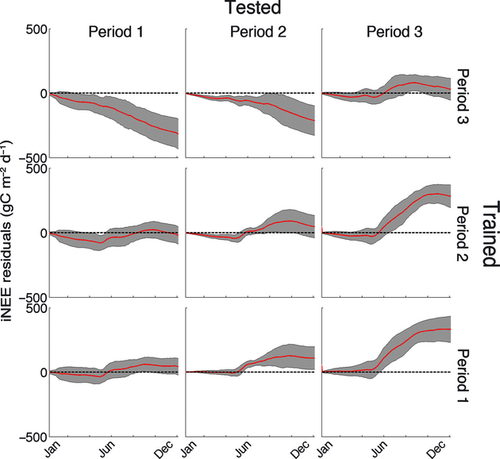
Long-term changes at Harvard forest
From a carbon accounting perspective, changes in the measured annual increment in aboveground biomass over the 18 years (Period 1: ~100 g C m−2; Period 2: 185 g C m−2; Period 3: 220 g C m−2) do not fully account for the observed increase in ecosystem carbon storage (NEE). In Period 2, measured aboveground biomass increment was 72% of all carbon sequestered. In Period 3, biomass increment accounted for 42% of observed carbon sequestered. In our model system, which accurately reproduced the mean biomass increment for each period, the remaining increase in uptake could only accumulate in the litter, root, or soil pools. In the model, any increase in the root, litter, or microbial pools would cause an observable increase in soil respiration, yet no increase in soil respiration was observed between the different periods. As the only viable alternative, the model predicted that the remaining uptake (after discounting for increases in aboveground biomass) accumulated in the slow cycling carbon pool at a rate of 300 g C m−2 yr−1 during Period 3. This contrasted with the accumulation rate of ~70 g C m−2 yr−1 in Periods 1 and 2. This implies that the reported large increase in net ecosystem carbon uptake, if true, should be detectable in the slow cycling carbon pool.
Ecological forecasting
Long-term model projections of future carbon cycling and stocks (using posterior parameter distributions from the FöBAAR model optimized on Period 2) were strongly dependent on the data used to constrain the model (Fig. 6). The use of short-term (hourly) NEE flux data alone, although it gave a good fit to available hourly NEE measurements (Table 3), led to poor constraint of the long-term evolution of the carbon sink-source state of the forest. Future projections of annual NEE were highly uncertain and ranged from ~ 600 to −900 g C m−2 yr−1 (90% CI) in the last decade of the century, compared with an average range of −50 to −520 g C m−2 yr−1 (90% CI) in present day conditions (when using only hourly NEE flux data). Largest uncertainty propagated beyond 2050. Uncertainty in autotrophic respiration increased by ~50% by the end of the century and uncertainty in heterotrophic respiration doubled.
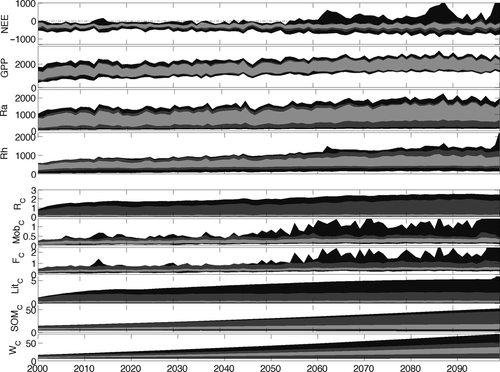
The use of long-term (monthly and annual) flux constraints greatly reduced future flux uncertainty. For example uncertainty in future NEE was reduced to within a range of −50 to −450 g C m−2 yr−1. The largest reduction in uncertainty came from the synchronous use of all data constraints available. The additional use of biometric constraints particularly reduced endogenous uncertainty in future projections of all carbon stocks. With the use of all data constraints, uncertainty in projections of all future stocks and fluxes was within present day uncertainty, with the exception of the slow cycling carbon pools (soil organic matter and carbon in wood). Interestingly, projected future carbon sequestration under climate change is never predicted to increase to the extent observed in the last 18 years at Harvard forest.
Discussion
High-frequency eddy-covariance measurements of forest-atmosphere carbon exchange contain a wealth of information, which can be used to characterize an ecosystems response to climatic drivers, and the evolution of that response over time. When used to constrain a terrestrial carbon cycle model, a large improvement in posterior vs. prior model performance can be achieved for high-frequency fluxes (e.g., Medvigy et al., 2009), along with a reduction in the posterior uncertainty of some model parameters (e.g., Braswell et al., 2005). The annual carbon balance of an ecosystem, however, is not an instantaneous response to a driver, but an accumulation of ecosystem responses to climate variability within the year (le Maire et al., 2010). Here, we show that when using only high-frequency measurements of NEE, small high-frequency model biases can accumulate to give large uncertainty in the total modeled annual carbon balance of the ecosystem over annual and inter-annual time periods. The resulting uncertainty range is of a similar magnitude to the range among models reported from model inter-comparison studies (Heimann et al., 1998; Cramer et al., 2001; Schwalm et al., 2010; Keenan et al., in press). By incorporating information on long-term (monthly, annual) cumulative fluxes into the model optimization, we greatly reduced the uncertainty in model estimates of the annual carbon budget of the forest in both training and test periods.
This reduction was not as pronounced, however, for the components of the carbon budget. When using only eddy-covariance carbon flux data, modeled gross primary productivity and ecosystem respiration compensated for each other to give the observed value for NEE. Such equifinality (Beven, 2006) between quantities allows for large uncertainty in both, but good model performance for the net value of ecosystem carbon exchange. The use of additional constraints in conjunction with eddy-covariance carbon flux data led to a reduction in uncertainty in the component parts of NEE during the test and training periods, if not in NEE itself. In particular, the additional use of biometric and soil flux constraints led to a halving of uncertainty in heterotrophic respiration, and a large reduction in uncertainty regarding the size of the carbon pools.
Synchronously using 15 different data streams as constraints successfully reduced posterior uncertainty in 24 of 42 parameters. The well-constrained nature of the model was evidenced by the accurate simulation of multiple compartments of the ecosystem at various different time scales. Previous model-data fusion efforts have focused on using one or two constraints (with some notable exceptions, e.g., Xu et al., 2006; Medvigy et al., 2009; Richardson et al., 2010; Ricciuto et al., 2011; Weng & Luo, 2011), which invariably led to a low number of constrainable parameters (e.g., ~4 to >6 parameters, Wang et al., 2007; Knorr & Kattge, 2005). Here, constrained parameters were typically associated with processes for which data was available. For instance, the soil organic matter and wood carbon initial pools were well constrained by the measurement data, while the canopy carbon reserve pool was not constrained, as no measurements of mobile canopy carbon were included. Five additional parameters, which were not well constrained, demonstrated strong co-variance with other parameters, thus giving information as to their true distribution. Vcmax and the proportion of recent assimilate used for maintenance respiration serve as a good example in this study – where higher Vcmax was compensated for by higher maintenance respiration (Fig. 5). It should be noted that the absolute values of Vcmax reported here are specific to the model used. Different assumptions regarding the distribution of light and temperature within the canopy affect the value of Vcmax needed to reproduce the observed fluxes (e.g., Keenan et al., 2011b), potentially along with the value assumed for the proportion of assimilate lost to maintenance respiration as shown here. The increased use of multiple data streams in the future will help better constrain models and aid our understanding of long-term processes. However, not all additional data constraints give the same reduction in model uncertainty (Richardson et al., 2010; Ricciuto et al., 2011). In this study, components of ecosystem carbon cycling most uncertain after the integration of all available data were related to gross primary productivity, and the timing and magnitude of aboveground growth and maintenance respiration. Identifying which additional data would better inform model projections should be a focus of future efforts.
By testing the optimized process-based model against the ANN, we have shown that process-based models can reproduce observed NEE measurements as well as data-mining tools. This shows that parsimonious model structures are sufficient to reproduce the observed short-term variability represented in eddy-covariance carbon flux data. It also suggests that although eddy-covariance fluxes undoubtedly contain more information than any other individual data constraint, they are not sufficient to adequately test many aspects of more complex models (e.g., Medvigy et al., 2009; Zaehle & Friend, 2010; Bonan et al., 2011). As in other studies (e.g., Hanson et al., 2004; Braswell et al., 2005; Siqueira et al., 2006; Richardson et al., 2007; Urbanski et al., 2007; Richardson et al., 2010; Keenan et al., in press; but see Desai, 2010), the process-based model failed to accurately reproduce observed inter-annual variability in carbon cycling and biomass increments, even within the training period. As the process-based model here was optimized to the data, parameter error can be discounted, leaving model structural error, biotic effects, or missing drivers (e.g., diffuse radiation: Moffat et al., 2010) as potential culprits for the poor model performance for inter-annual variability. Lagged effects of climate variability on ecosystem state (e.g., Gough et al., 2009) have been shown to affect model performance on interannual timescales (Keenan et al., in press), potentially due to inaccurate model allocation structures (Gough et al., 2009). Though it has been suggested that process-based models may effectively reproduce inter-annual variability (Desai, 2010; but see Keenan et al., in press), both biotic and abiotic factors are known to affect normal between-year variability (Richardson et al., 2007). Further work on model structural error, biotic effects, and the impact of unaccounted for drivers should improve our ability to accurately model interannual variability in terrestrial carbon cycling in the future.
Eddy-covariance measurements at Harvard forest suggest a long-term trend of increasing uptake over the 1992–2009 period, with a particularly pronounced increase in uptake in the last 6 years. Results here suggest that long-term changes evidenced by the eddy-covariance carbon flux data are independent of recent changes in climate variables included in this study. By comparing the temporal distribution of model-data residuals, we found that nonclimate driven change in carbon fluxes is only evident during the growing season. By comparing the posterior parameters for the FöBAAR model optimized on three separate 6 year periods of contrasting uptake, we show that even with increased leaf area, substantial increases in canopy productivity (here Vcmax) are needed to reproduce the observed fluxes.
Although carbon in wood, leaf area and litter-fall all exhibit increases over the past 18 years, a large proportion of the estimated increased uptake is unaccounted for in the measured carbon stocks. Our model results suggest that the rate of accumulation of slow cycling soil organic matter doubled in Period 3 compared with the two earlier periods. Under that working hypothesis, the large influx of carbon in recent years should therefore be detectable with an appropriate sampling intensity (Fernandez et al., 1993) in soil organic matter measurements, with largest increases in the slow cycling soil carbon pool. Without adequate measurements, our model results regarding the fate of the sequestered carbon should not be regarded as strong evidence, and provide but a testable hypothesis. Current efforts to quantify age and residence times of soil carbon with techniques such as isotopic analysis and radiocarbon dating should aid in identifying the ultimate fate of the sequestered carbon.
Inventory data reports an increase in the biomass of Red Oak within the tower footprint (~20% increase over the last 18 years), and a concurrent increase in Red Oak leaf area. Other species in the footprint of the tower do not show a comparable increase, with the exception of a slight increase in understory Hemlock. Changes in community dynamics provide one potential explanation of the changes in ecosystem uptake. Increasing understory activity has been suggested to have the potential to explain trends (Jolly et al., 2004), through enhanced photosynthetic uptake before the overstory canopy has developed in spring, or after it has senesced in autumn. Understory activity, however, is unlikely to explain the consistent higher uptake throughout the season as observed here. The observed increase in forest carbon uptake could also be due to higher atmospheric CO2 levels (Cramer et al., 2001), or the cumulative effect of nitrogen deposition. Farquhar et al. (1980) photosynthesis model used in this study accounts for effects of increased atmospheric carbon, though there is significant uncertainty as to the direct effect of carbon fertilization (e.g., Long et al., 2006). Although nitrogen deposition at Harvard forest is 10–20 times above historic background levels (http://www.chronicn.unh.edu/), it remains only ~12% of annual N mineralization (Munger et al., 1998), and control data from long-term nitrogen fertilization studies do not report a significant increase in foliar nitrogen (data not shown). It should be noted that there is no evidence to suggest that any of the processes discussed above could, in isolation, realistically lead to a ~50% increase in the photosynthetic potential of the canopy.
Future projections from terrestrial models have been reported to diverge greatly under climate change (Friedlingstein et al., 2006; Heimann & Reichstein,2008). Such divergence could be explained by process misparameterization, or misspecification. We show that using short-term high-frequency eddy-covariance carbon flux data alone to inform model parameterization allows for divergent future projections, even with good model performance when tested against current data. Parameter misspecification could therefore potentially explain the different future trajectories reported by different models. We show that using orthogonal constraints can reduce this divergence, leading to a better data-informed model projection. Using long-term flux data in combination with biometric data greatly reduced endogenous (internal to the model system) uncertainty in predictions of how net carbon sequestration at Harvard forest would respond to future climate change. Considerable uncertainty in the components of NEE remained, due to equifinality between gross photosynthesis and autotrophic respiration.
Although process-based models should theoretically be more reliable than empirical models under future climate scenarios (see Keenan et al., 2011a for discussion), not all processes are fully understood (e.g., species adaptation, down-regulation, nitrogen cycling). Such exogenous uncertainty is shown here to be large, with the optimized model incapable of reproducing the observed long-term trend in carbon cycling at Harvard forest without temporal changes in parameters. This suggests that, when the model is sufficiently informed by data, model process representation still represents a large source of uncertainty for making future projections, making the statistical uncertainty in ecological forecasts an underestimate of the true uncertainty.
Models of forest carbon cycling, such as the one used here, have been coupled with earth-system models to project terrestrial carbon sinks and sources (e.g., Sitch et al., 2008) and feedbacks to climate change in the 21st century (Cox et al., 2000; Fung et al., 2005; Friedlingstein et al., 2006). Results have been incorporated into the assessment reports of the Intergovernmental Panel on Climate Change (Denham KL et al.,2007) to guide mitigation efforts by governments and public (Solomon et al., 2007), though models diverge largely when projecting the future responses to climate change (Friedlingstein et al., 2006; Denham KL et al., 2007). None of the terrestrial carbon cycle models used, however, are directly informed by data. Here, we have shown how this can lead to overconfidence in individual model projections. Model intercomparison studies that use data-informed models would be a significant step toward rigorously assessing errors due to model process representation, and improving our ability to provide policy-actionable predictions of future carbon cycle responses to change.
Acknowledgements
Carbon flux and biometric measurements at HFEMS have been supported by the Office of Science (BER), US Department of Energy (DOE) and the National Science Foundation Long-Term Ecological Research Programs. T. F. K. and A. D. R. acknowledge support from the Northeastern States Research Cooperative, and from the US DOE BER, through the Northeastern Regional Center of the National Institute for Climate Change Research. T. F. K., A. D. R., and J. W. M. acknowledge support from NOAA's Climate Program Office, Global Carbon Cycle Program, under award NA11OAR4310054. We thank Y. Ryu, M. Toomey, and S. Klosterman for useful feedback. We especially thank the many participants who have sustained the long-term data collection, and in particular the summer students engaged in collecting field data who were supported by NSF Research Experience for Undergraduates (REU) program, and the Harvard Forest Woods Crew for logistical and maintenance support.




