International Transactions in Operational Research
Volume 31, Issue 3 pp. 1609-1630
Article
Open Access

An efficient method for optimizing nested open pits with operational bottom space

Nelson Morales, 

Corresponding Author

Nelson Morales

Département des génies civil, géologique et des mines, Polytechnique Montréal, Montreal, Canada

Corresponding author.

Search for more papers by this author
Gonzalo Nelis, 

Gonzalo Nelis

Research and Innovation in Mining Group (RIMG), DIMM, Universidad Técnica Federico Santa María, Valparaiso, Chile

Search for more papers by this author
Jorge Amaya, 

Jorge Amaya

Centro de Modelamiento Matemático, Universidad de Chile, Santiago, Chile

Search for more papers by this author
First published: 17 October 2023
https://doi.org/10.1111/itor.13390
Citations: 1

Abstract

Determining a set of nested pits to support the design of an open pit mine that leads to high economic value is crucial for the strategic planning of these operations; thus, practitioners rely on optimization methods for finding high-value solutions. However, current approaches are not sufficient as they lack at least one of the following features: fast computations of optimal solutions, good geometric properties, and nestedness of the pits. In this work, we propose an optimization model to address the problem of determining multiple nested pits by introducing a cost-based penalty for not meeting precedence constraints linked to a minimum bottom width. Using penalties instead of constraints is novel and turns out to have several advantages. First, the constraint matrix is totally unimodular; thus, the problem can be solved efficiently. Second, the model can be parameterized to generate nested pits. Therefore, our model is the first published model that is efficient, can be solved to optimality, preserves the nestedness of the solutions, and produces geometries more amenable for mine design, without the need for heuristics. Finally, we devise an iterative method that profits from the nestedness of the solutions to speed up the resolution and test the model in three different data sets, with different geometrical and cost parameters for a total of 135 different instances. The results show that the geometry of the bottom pits is indeed improved and that we can solve the problems up to optimality up to 80% faster than an off-the-shelf solver.

1 Introduction

Two critical steps in the strategic planning of open-pit mines are determining the ultimate pit problem, “UPIT,” and producing a sequence of nested pits. The ultimate pit determines the economic envelope of the mine; thus, providing a first approximation of the total economic value and tonnage of the ore reserves. The nested pits serve as a basis for defining the mining sequence and the design of mining phases which partition the deposit into operational volumes that include space and access ramps for the mining equipment.

The input of UPIT is given by a discretization of the deposit into a three-dimensional array of blocks, B. Each block i ∈ B $i \in B$ is associated with an economic value p i $p_i$ that depends on its geological attributes (particularly its grade and tonnage) and economic and operational parameters such as ore price, costs, and metallurgical recovery. The set of blocks, together with its relevant attributes (for instance, grades and tonnages), is known as the block model and is constructed from ground samples and the aid of geostatistical methods.

The excavation of the pit must comply with slope angles to ensure the stability of the walls. At the strategic level of the ultimate pit, this is controlled by overall slope angles. These angles are modeled as precedence constraints stating that to extract a certain block, others located above that block must be extracted before. For this, a set P ⊆ B × B $P \subseteq B \times B$ of precedence arcs is used, with ( i , j ) ∈ P $(i,j) \in P$ , indicating that block j must be extracted if i is extracted.

UPIT can be expressed as the binary linear program (1)–(3) below, where variable x i = 1 $x_i=1$ if and only if block i ∈ B $i\in B$ is extracted.
UPIT ( p , B , P ) max ∑ i ∈ B p i x i , $$\begin{align} \textrm {UPIT}(p,B,P) \nobreakspace \max \nobreakspace & \sum _{i\in B} p_i x_i ,\end{align}$$ (1)
x i ≤ x j ∀ ( i , j ) ∈ P , $$\begin{align} & x_i \le x_j & \forall (i,j)\in P ,\end{align}$$ (2)
x i ∈ { 0 , 1 } ∀ i ∈ B . $$\begin{align} & x_i \in \lbrace 0,1\rbrace & \forall i \in B. \end{align}$$ (3)

Vector p is referred to as the value vector because, as indicated before, p i $p_i$ is the net profit obtained from block i ∈ B $i \in B$ . Whenever it is clear, we omit the parameters of UPIT( p , B , P $p,B,P$ ) and write for example UPIT(p) or even UPIT to refer to the problem defined by (1)–(3).

Solving UPIT corresponds to finding a set of blocks such that the addition of their economic values is the highest possible and complies with the precedence constraints (2). Even though the word pit literally means “a large hole in the ground,” it is customary that the term refers to the material that was extracted to create the excavation, or in the case of the ultimate pit, the blocks i ∈ B $i \in B$ such that x i = 1 $x_i=1$ . We adhere to this practice.

It is known that the integrality constraints (3) can be relaxed, and UPIT can be solved up to optimality using the Lerchs and Grossmann algorithm (Lerchs and Grossmann, 1965). Moreover, UPIT can be reduced to a graph closure problem in the directed graph G = ( B , P ) $G =(B,P)$ (Picard, 1976), which in turn corresponds to a minimum cut problem for which pseudoflow algorithms and others apply (Hochbaum and Chen, 2000; Hochbaum, 2008). These results are relevant from the practical point of view, as realistic block models range from several thousand to millions of blocks. Thus, having efficient algorithms to compute the pits is critical.

Another interesting property of UPIT is that it is monotonic with regard to p (Lerchs and Grossmann, 1965). That is, if x , x ′ $x,x^{\prime }$ are the optimal solutions for value vectors p ≤ p ′ $p \le p^{\prime }$ (respectively), then x ≤ x ′ $x \le x^{\prime }$ .

The practical relevance of nested pits is illustrated in Fig. 1, which presents a section of a conceptual two-dimensional (2D) deposit, with the surface represented by a segmented line, waste as white area, and ore (profitable material) in gray. The bold lines represent pit contours, with the ultimate pit being the greatest one and a second, smaller pit on the right side of the figure. Extraction starts at the surface and is done bench by bench (some labeled with letters (a) to (g) in the figure). It follows from the picture that mining the ultimate pit directly (center) requires to mine large amounts of waste (benches (a) and (b)) before reaching profitable (gray area) parts, which has a negative financial impact. Conversely, mining a smaller pit first (right) requires mining less waste at the beginning (benches (d) and (e)) thus advancing the extraction of ore and delaying, for example, the waste in bench (g), all of which improves the net present value. The decision problem to optimize the extraction order is called the production scheduling, but its study is outside the scope of this work. For instance, in this conceptual example, the optimal schedule may involve mining benches (f) and (g) at the same time.

Details are in the caption following the image
Fig. 1
Open in figure viewerPowerPoint
Conceptual design of an ultimate pit and a nested pit. The gray area represents profitable material and the bold lines pit profiles. Left: The ultimate pit. Center: Ultimate pit partitioned into benches. Right: Nested pit and one inner pit partitioned into benches.

In practice, engineers rely on the nestedness property for generating a sequence of many (potentially hundreds) nested pits. This is achieved by considering a sequence of value vectors p k , k = 1 , … , K $p^k, k=1, \ldots , K$ such that p k ≤ p k + 1 , ∀ k = 1 , … , K − 1 $p^k \le p^{k+1}, \forall k=1, \ldots , K-1$ and by solving UPIT ( p k ) $(p^k)$ for each k = 1 , … , K $k=1,\ldots ,K$ ; thus, generating potentially K nested pits.

After the pits are generated, some pits are selected. This stage is named pushback selection as the volume (as blocks) between consecutive selected pits is called pushback. Pushbacks serve as the basis for designing mining phases, which are actual volumes to be mined (Jelvez et al., 2020). Phases are fundamental for the design of an open pit mine as they can be mined with relative independence, and each phase has its own layout in terms of walls and access roads (Read and Stacey, 2009; Thomson et al., 2020). In this paper, we focus on the generation of the nested pits and not later stages like pushback selection, phase design, or production scheduling. For detailed descriptions and methods for these problems, we refer the reader to Jelvez et al. (2020), Morales et al. (2023), and Espinoza et al. (2013), respectively.

Even though nested and ultimate pits are used as a design guide for mining phases, it is apparent from its formulation that UPIT in fact does not consider relevant operational constraints related to the geometry of the resulting pits; thus, some researchers have investigated methods to address this limitation. We discuss some of these geometrical aspects and relevant associated efforts in the following sections.

1.1 Slope angles and precedence arcs

The ultimate pit considers only overall slope angles; however, the design of the pit walls is a much more complex task which must consider several design parameters (Read and Stacey, 2009; Hustrulid et al., 2013). Because of this, some authors have focused on modeling complex slope angles using precedence arcs. For example, Khalokakaie et al. (2000) extend the Lerchs and Grossmann algorithm to consider multiple slope definitions across the mine. They consider one angle for each cardinal direction and use linear interpolation for the angles in between. Shishvan and Sattarvand (2012) and Gilani and Sattarvand (2015) improve the methodology by using nonlinear interpolation, which they show to work better. These works address the modeling of slope angles in terms of precedence arcs, that is, their methods are complementary to other models discussed in this work, including the proposed model.

1.2 Operational space at the bottom of the pit

The removal of material from the mine surface is performed by large pieces of machinery that require space for movement and operation; however, the planning methodology proposed by Lerchs and Grossmann omits this requirement. This limitation of the approach is known both by commercial solutions and the research community. For example, Wharton and Whittle (1997) indicate that the ultimate pit was never meant to produce operational pit shapes and, therefore, the method generates geometries with irregular floors, sharp corners, etc. Because of this, they propose a postprocessing algorithm for improving the geometry after the optimization process has ended. Their approach uses squared “templates” for smoothing the solutions of UPIT. This approach is the one implemented in Whittle, a leading planning software (Whittle, 2018).

Several authors have proposed methods that account for the geometrical limitations of the method and aim to generate volumes that comply with considerations such as minimum space requirements at the bottom of the pit or shapes that are more amenable for designing mining phases afterwards.

Bai et al. (2018) propose a method based on mathematical programming and the iterative application of some operators to generate pits that comply with geometric properties such as minimum space at the bottom, smoothness, and continuity. Using a block-by-block schedule and discount rate, they apply their method in two case studies. Using a simple approximation of the net present value (NPV), they report that the decrease of the NPV between the initial pushbacks and the practicable ones ranges from 0.5% to 7%.

Tabesh et al. (2014) develop a multistep pushback design algorithm based on mathematical programming and clustering for generating pushbacks composed of mining “polygons.” To find solutions for the model, they devise and implement a greedy heuristic approach and local search in such a way that the pushbacks satisfy capacity constraints. Finally, a refinement procedure is provided to improve the geometry.

Nancel-Penard and Morales (2022) introduce a mathematical optimization model that determines one pit subject to geometrical constraints related to connectivity, minimum space and widths at the bottom, and minimum and maximum tonnages. They utilize a preprocessing method for speeding up the computation process, apply their formulation in three publicly available instances from MineLib (Espinoza et al., 2013) to generate several nested pits and use the NPV approximation proposed by Tabesh et al. (2014). Their work shows significant improvements in the geometry of the pits with a decrease in value between 1.5% and 5.6% when compared to traditional nested pits.

Another work that is worth mentioning is Cullenbine et al. (2011). This model is oriented to solve the production scheduling problem, that is, it considers the slope constraints and capacity constraints that are typical for production scheduling. However, it also contains an additional constraint forcing that each extracted block must have at least one of its four adjacent neighbors also extracted. The resulting model is computationally hard to solve; thus, the authors proposed a sliding time window heuristic to solve it.

1.3 Access ramps

Another important element of pit design is the access roads (ramps) needed for the equipment to move between different levels in the mine. The design of ramps transforms the nested pits into a real operational design of the mine. Ramp design relies heavily on computer-aided design and mining software, but it is mostly manual and highly dependent on the user.

Morales et al. (2017) and Nancel-Penard et al. (2019) propose an optimization model for computing a pit with enough space to accommodate the access ramps. The methodology starts with a reference pit (e.g., the ultimate pit) and computes one that is “close” to it but maximizes the economic value and has space for the ramps. The approach is tested on several instances to show that it generates good results, that can be used as a guide for the design of the mining phases by an engineer, and that the final designs are better than those that directly use the ultimate pit as a guide.

Yarmuch et al. (2020) address the problem of finding the best ramp within the pit and optimizing the road network outside. For the in-pit ramp, they propose a binary linear model that aims to minimize construction of the ramp. The model is hard to solve, and, therefore, the authors have to develop a heuristic.

Finally, except for papers that address modeling using precedence arcs, all previous works propose methodologies that take blocks as an input and report blocks in the output; therefore, they require a manual stage to draw the final design. Because of this, Morales et al. (2023) propose an algorithm that automates the latter stage and shows that the fully automated procedure generates designs that are better than those drawn by an engineer on 15 instances based on three block models—two publicly available in MineLib.

1.4 Contribution of this paper

Most of the works presented in previous sections formulate mathematical models in which the pit must satisfy geometrical constraints. In some cases, the resulting formulations are complex and hard to be solved; hence, the authors resort to some heuristic procedures for finding approximate solutions. In other cases, the geometrical constraints are not modeled in the optimization model but addressed by procedural methods in a postprocessing stage. In this case, there is no mathematical formulation for evaluating the quality of the solutions objectively. Another important issue is that several works aim to optimize a single pit; hence, the generation of nested pits must be done iteratively, outside the mathematical model. Unfortunately, in this case, these methods cannot ensure that the pits will be nested or force the property procedurally, which may lead to suboptimal results and that can impact the subsequent phase design stage.

In this paper, we aim to address some of the drawbacks described before. Specifically, we focus on the challenges described in Section 1.2, that is, having enough space at the bottom of the pit. Our motivation comes from two sources. First, the computational complexity of previous efforts that addressed geometrical constraints, which has required developing heuristic approaches for finding good solutions. Second, in reality, even mines that use large loading machines also utilize smaller equipment, for example, for creating the initial space for large shovels. Indeed, shovels may require space between 50 to 100 m for operation (e.g., the Komatsu P&H 4100XPC shovel, measures 15× 15 m and has a cut radius of 24 m (Nancel-Penard and Morales, 2022); thus, smaller equipment which is less productive and more expensive to operate is needed for initial excavation. Therefore, narrow pit bottoms are not infeasible, just more expensive to be mined. In fact, smaller equipment is less productive and has higher operating costs. Therefore, narrow pit bottoms are not unfeasible but more expensive.

The later observation motivates us to incorporate the space requirements not as a constraint of the problem but as a penalty that models the additional cost of using smaller equipment for digging in narrow areas. As it turns out, using this approach results in an optimization model that has a favorable structure and good theoretical properties:
  • 1. We prove that our model can be solved efficiently using continuous linear programming and, as in the case of UPIT. This implies that solutions can be found in polynomial time (Karmarkar, 1984). Indeed, apart from UPIT, our model is the only published one that is proven to be solvable up to optimality using efficient algorithms.
  • 2. We show that, as it happens with the ultimate pit, our model is monotonic with regard to the value vectors of the blocks, that is, it generates nested pits when the value vectors increase. That is, our model extends UPIT by adding considerations related to bottom space but without losing the nestedness property.
  • 3. We devise an iterative approach to take advantage of the nestedness of the solutions to speed up the computation time for solving the optimization model. This method is exact, that is, not a heuristic.

Finally, to validate the results mentioned in the previous list, we apply the proposed model in three block models. The results show that the incremental approach is shown to reduce the computation time by an average of 26% and up to 80% in some cases, from a practical standpoint. Moreover, comparing the economic value and tonnage of solutions of the ultimate pit and our proposed model reveals that the pits obtained using our model are significantly different from the traditional ultimate pit and nested pits, which may imply that, in some cases, the traditional approach may not provide the best guide for designing mining phases.

2 Mathematical modeling and theoretical results

In this section, we introduce the optimization model (which is a binary linear program) and present theoretical results related to its solutions. A summary of the notation can be found in Table 1.

Table 1. Summary of the notation.
Symbol Description
i , j ∈ B $i,j \in B$ Blocks and set of blocks.
( i , j ) ∈ P ⊂ B $(i,j) \in P \subset B$ Arcs and set of strong precedence arcs.
( i , j ) ∈ Q ⊂ B $(i,j) \in Q \subset B$ Weak arcs and a set of weak precedence arcs.
p i , i ∈ B $p_i, i \in B$ Economic value of block i.
c i j , ( i , j ) ∈ $c_{ij}, (i,j) \in$ Reduction in cost of excavating block i if block j has been excavated.
x i $x_i$ Binary variable that is 1 if block i is excavated and 0 otherwise.
y i j $y_{ij}$ Binary variable that is 1 if block i is excavated but its weak predecessor block j has not, and 0 otherwise.

To present the mathematical model, we extend the notation of the ultimate pit; thus, as in that model, we consider that B is the set of blocks, p is the value vector, and P ⊆ B × B $P \subseteq B \times B$ is the set of precedence arcs. In the context of our extension, we will refer to the precedence arcs in P as strong arcs and say that j is a strong predecessor of i if ( i , j ) ∈ P $(i,j) \in P$ . As with UPIT, these arcs model the overall slope angle to ensure the stability of the pit walls and remain part of the model, that is, the pit resulting must comply with the same overall slope angles that UPIT.

To model the penalties, we consider Q ⊆ B × B $Q\subseteq B\times B$ , another set of precedence arcs such that Q ∩ P = ∅ $Q \cap P = \emptyset$ and for ( i , j ) ∈ Q $(i,j) \in Q$ we assume a cost c i j > 0 $c_{ij}>0$ . With these new elements, we introduce the following extension of UPIT:
UPIT + ( p , B , P , Q ) max ∑ i ∈ B p i x i − ∑ ( i , j ) ∈ Q c i j y i j , $$\begin{align} \textrm {UPIT}^+(p,B,P,Q) \nobreakspace \max \nobreakspace &\sum _{i \in B} p_i x_i \ - \ \sum _{(i,j)\in Q} c_{ij} y_{ij},\end{align}$$ (4)
x i ≤ x j ∀ ( i , j ) ∈ P , $$\begin{align} & x_i \le x_j & \forall (i,j) \in P ,\end{align}$$ (5)
x i − x j ≤ y i j ∀ ( i , j ) ∈ Q , $$\begin{align} & x_i - x_j \le y_{ij} & \forall (i,j) \in Q ,\end{align}$$ (6)
x i ∈ { 0 , 1 } ∀ i ∈ B , $$\begin{align} & x_i \in \lbrace 0,1\rbrace & \forall i \in B ,\end{align}$$ (7)
y i j ∈ { 0 , 1 } ∀ ( i , j ) ∈ Q . $$\begin{align} & y_{ij} \in \lbrace 0,1\rbrace & \forall (i,j) \in Q. \end{align}$$ (8)

Because the set Q also defines precedence arcs, but that can be violated if a cost c i j $c_{ij}$ is paid when the precedence constraint associated with arc ( i , j ) $i,j)$ is violated, we refer to these arcs as weak precedence arcs and say that j is a weak predecessor of i if ( i , j ) ∈ Q $(i,j)\in Q$ . As before, whenever possible, we drop input parameters in the notation and write, for example, UPIT+( p , B $p,B$ ) or UPIT+(p) for the optimization problem (4)–(8).

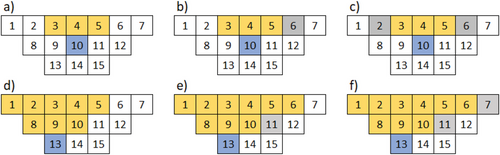
Figure 2 illustrates the concept of strong and weak predecessors in a small 2D example: (a) Arcs ( 10 , 3 ) , ( 10 , 4 ) , ( 10 , 5 ) ∈ P $(10,3),(10,4), (10,5) \in P$ , which means that extracting block 10 requires extracting all three blocks (3, 4, and 5) before mining block 10. (b, c) Arcs ( 10 , 2 ) , ( 10 , 6 ) ∈ Q $(10,2), (10,6) \in Q$ , which means that blocks 2 and 6 are weak predecessors of block 10. Therefore, they are not required to be extracted if block 10 is mined, but doing so decreases the cost of mining block 10. (d) The strong predecessors of block 13 are blocks 1–5 and 8–10. These blocks must be mined if block 13 is extracted. (e) Block 11 is a weak predecessor of 13. If block 11 is mined, then extracting block 13 becomes less expensive by a value of c13, 11. (f) As block 7 is a weak predecessor of block 11, mining it reduces the cost of mining block 11 by c11, 7.

Details are in the caption following the image
Fig. 2
Open in figure viewerPowerPoint
Examples of weak and strong predecessors. Yellow blocks 3–5 are strong predecessors of block 10. Green blocks 2 and 6 are weak predecessors of block 10. Block 13 has strong predecessors 1–5, and 8–10 and weak predecessor 11.

We will now prove two theoretical results related to properties of UPIT+. First, we will show that the constraint matrix is unimodular and, therefore, the integrality constraints (8) can be relaxed. Second, we show that solutions of UPIT+ are nested, that is, the set of extracted blocks grows if the value vector increases.

Proposition 1. (Unimodularity of UPIT+)The constraint matrix of UPIT+( p , B , P , Q $p,B,P,Q$ ) is totally unimodular.

Proof.Let A P $A_P$ be the | P | × | B | $|P| \times |B|$ matrix where for each ( i , j ) ∈ P $(i,j) \in P$ , the corresponding row of A P $A_P$ has a 1 in the ith column and a −1 in the jth column. Similarly, let A Q $A_Q$ be the | Q | × | B | $|Q| \times |B|$ matrix, which is defined analogously for Q, and let I be the identity matrix of size | Q | $|Q|$ . Then, the constraints of ( U P I T + ) $(UPIT^+ )$ can be written as [ A P 0 A Q − I ] [ x y ] ≤ 0 $ [ \def\eqcellsep{&}\begin{array}{cc}A_P & 0 \\ A_Q & -I \end{array} ]\quad [ \def\eqcellsep{&}\begin{array}{c}x \\ y \end{array} ] \le 0$

Now [ A P A Q ] $[ \def\eqcellsep{&}\begin{array}{c}A_P \\ A_Q \end{array} ]$ is the matrix corresponding to precedence arcs P ∪ Q $P\cup Q$ ; hence, it is a totally unimodular (TU) matrix (Hoffman and Kruskal, 2010). Moreover, [ A P 0 A Q − I ] $[ \def\eqcellsep{&}\begin{array}{cc}A_P & 0 \\ A_Q & -I \end{array} ]$ is also a TU. To prove this, consider any TU matrix M and let u be a column vector such that u k = 0 $u_k=0$ if k ≠ ℓ $k \ne \ell$ and u k = − 1 $u_k=-1$ if k = ℓ $k=\ell$ (for some fixed row ℓ). We have that matrix M ′ = [ M , u ] $M^{\prime }=[M,u]$ is TU. Indeed, any submatrix N of M ′ $M^{\prime }$ either: (i) does not intersect u, in which case det ( N ) ∈ { − 1 , 0 , 1 } $\det (N) \in \lbrace -1,0,1\rbrace$ or (ii) is such that its jth column consists of some rows of u. We can compute det ( N ) $\det (N)$ using this column. Then, either all entries are zero (in which case det ( N ) = 0 $\det (N)=0$ ) or the only non-zero entry corresponds to u ℓ = − 1 $u_{\ell }=-1$ and det ( N ) = ( − 1 ) σ det ( N ℓ ) $\det (N)=(-1)^{\sigma }\det (N_{\ell })$ for some integer σ and N ℓ $N_{\ell }$ a submatrix of M that does not intersect u, thus det ( N ℓ ) ∈ { − 1 , 0 , 1 } $\det (N_{\ell })\in \lbrace -1,0,1\rbrace$ . In any case, we obtain that det ( N ) ∈ { − 1 , 0 , 1 } $\det (N)\in \lbrace -1,0,1\rbrace$ and the result follows. ▪ $\blacksquare$

Following Proposition 1, we observe that the integrality constraints can be relaxed for UPIT+, meaning that it can be solved directly using the simplex method, as the solutions will always be integral. In particular, the problem can be solved in polynomial time (Karmarkar, 1984).

As indicated before, a critical property of the ultimate pit is that the solutions are nested with regard to the economic value. Now we show that UPIT+ satisfies the same property. More precisely, for the definition of UPIT adopted in this paper, there is no guarantee that the solution is unique; thus, the nestedness property of UPIT states that if p ≤ p ′ $p \le p^{\prime }$ then there exists a solution of UPIT( p ′ $p^{\prime }$ ) such that it contains any solution of UPIT(p). Notice that this is only a theoretical issue, as it is easy to adapt algorithms to ensure that the solutions are maximal with regard to the inclusion.

Proposition 2. (Nestedness)Let p ≤ p ¯ $p\le {\bar{p}}$ be two value vectors and assume that x , x ¯ $x, {\bar{x}}$ are the optimal solutions of UPIT+(p) and UPIT+( p ¯ ${\bar{p}}$ ), respectively. Then, the solution defined as x ′ = max { x , x ¯ } $x^{\prime }=\max \lbrace x,{\bar{x}}\rbrace$ is also optimal for UPIT+( p ¯ ${\bar{p}}$ ).

Proof.First, we observe that if i 0 ∈ B $i_0\in B$ is such that increases its value, that is, p ¯ i 0 > p i 0 ${\bar{p}}_{i_0}>p_{i_0}$ and x i 0 = 1 $x_{i_0}=1$ , then x ¯ i 0 = 1 ${\bar{x}}_{i_0} = 1$ . To check this, with some abuse in the notation, let c , y $c,y$ be vectors representing the costs and penalization variables y i j $y_{ij}$ . Thus, the objective function can be shortly written as

p T x − c T y = ∑ i ∈ B p i x i − ∑ ( i , j ) ∈ Q c i j y i j . $$\begin{equation*} p^T x - c^T y=\sum _{i\in B} p_i x_i - \sum _{(i,j)\in Q} c_{ij} y_{ij}. \end{equation*}$$
Then
p ¯ T x ¯ − c T y ¯ = p T x ¯ − c T y ¯ ≤ p T x − c T y = p ¯ T x − e − c T y ≤ p ¯ T x ¯ − c T y ¯ − e . $$\begin{equation*} {\bar{p}}^T {\bar{x}} - c^T {\bar{y}} = p^T {\bar{x}} - c^T {\bar{y}} \le p^T x - c^T y = {\bar{p}}^Tx - e-c^T y \le {\bar{p}}^T {\bar{x}} - c^T {\bar{y}} - e. \end{equation*}$$

The first equality is because x i 0 = 0 $x_{i_0}=0$ , and the first inequality comes from the optimality of ( x , y ) $(x,y)$ . The second equality is because p ¯ i 0 = p i 0 + e ${\bar{p}}_{i_0}=p_{i_0}+e$ and x i 0 = 1 $x_{i_0}=1$ , and the second inequality follows from the optimality of ( x ¯ , y ¯ ) $({\bar{x}},{\bar{y}})$ . We obtain that e ≤ 0 $e \le 0$ , which is a contradiction. It follows that the set { i ∈ B : p ¯ i > p i ∧ x i > x ¯ i } $\lbrace i \in B : {\bar{p}}_i>p_i \wedge x_i>{\bar{x}}_i\rbrace$ is empty.

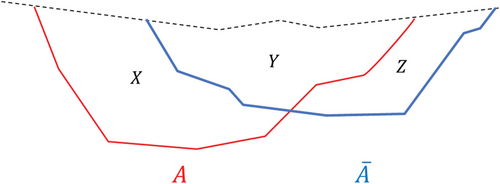
For the second part of the proof, it will be convenient to consider the sets A = { i ∈ B : x i = 1 } $A=\lbrace i \in B : x_i=1\rbrace$ , A ¯ = { i ∈ B : x ¯ i = 1 } ${\bar{A}} = \lbrace i \in B : {\bar{x}}_i=1\rbrace$ and from them to define X = A ∖ A ¯ , Y = A ∩ A ¯ $X=A\setminus {\bar{A}},Y = A \cap {\bar{A}}$ , and Z = A ¯ ∖ A $Z={\bar{A}}\setminus A$ (see Fig. 3 for a conceptual drawing of these sets). Moreover, to simplify the notation, we define for any sets U , V ⊆ B $U,V\subseteq B$ the values p ( U ) = ∑ i ∈ U p i $p(U)=\sum _{i \in U} p_i$ , c ( U , V ) = ∑ ( i , j ) ∈ Q ∩ U × V c i j $c(U,V)=\sum _{(i,j) \in Q \cap U \times V} c_{ij}$ , and β ( U ) = p ( U ) − c ( U , B ∖ U ) $\beta (U)=p(U)-c(U,B\setminus U)$ . p ( U ) $p(U)$ is the income of blocks in U considering block values p and p ¯ ${\bar{p}}$ , respectively; c ( U , V ) $c(U,V)$ is the cost of violated weak precedence constraints between U and V; and β ( U ) $\beta (U)$ is the value of the objective function if U is a pit, for the corresponding block values p and p ¯ ${\bar{p}}$ . Further on, we consider analogous definitions for p ¯ ( U ) ${\bar{p}}(U)$ and β ¯ ( U ) ${\bar{\beta }}(U)$ .

Notice that, from these definitions and the first part of the proof, we have that X does not contain any block i such that p i < p ¯ i $p_i &lt; {\bar{p}}_i$ and therefore p ( X ) = p ¯ ( X ) $p(X)={\bar{p}}(X)$ .

The optimality of A implies that

β ( A ) − β ( Y ) = p ( X ) − c ( X , ( A ∪ A ¯ ) c ) − c ( X , Z ) + c ( Y , X ) ≥ 0 . $$\begin{equation*} \beta (A)- \beta (Y)=p(X)-c(X,(A \cup {\bar{A}})^c )-c(X,Z)+c(Y,X) \ge 0. \end{equation*}$$

Similarly, from the optimality of A ¯ ${\bar{A}}$ ,

β ¯ ( A ¯ ∪ A ) − β ¯ ( A ) = p ¯ ( X ) − c ( X , ( A ∪ A ¯ ) c ) + c ( Z , X ) + c ( Y , X ) ≤ 0 . $$\begin{equation*} {\bar{\beta }}({\bar{A}} \cup A)- {\bar{\beta }}(A)={\bar{p}}(X) - c(X,(A \cup {\bar{A}})^c )+c(Z,X)+c(Y,X) \le 0. \end{equation*}$$

However, p ( X ) = p ¯ ( X ) $p(X)={\bar{p}}(X)$ and so − c ( X , Z ) ≥ c ( Z , X ) $-c(X,Z) \ge c(Z,X)$ , that is, c ( X , Z ) = c ( Z , X ) = 0 $c(X,Z)=c(Z,X)=0$ . We conclude that β ¯ ( A ∪ A ¯ ) − β ¯ ( A ¯ ) = β ( A ) − β ( Y ) ≥ 0 ${\bar{\beta }}(A \cup {\bar{A}}) - {\bar{\beta }}({\bar{A}})= \beta (A)- \beta (Y) \ge 0$ , that is, the set A ∪ A ¯ $A \cup {\bar{A}}$ which corresponds to the solution x ′ , x i ′ = max { x i , x ¯ i } $x^{\prime }, x^{\prime }_i = \max \lbrace x_i,{\bar{x}}_i\rbrace $ for i ∈ B $i \in B$ is optimal for UPIT+( p ¯ ${\bar{p}}$ ). ▪ $\blacksquare$

Details are in the caption following the image
Fig. 3
Open in figure viewerPowerPoint
Conceptual drawing of a section of two optimal pits A (for block values p) and A ¯ ${\bar{A}}$ (for block values p ¯ ${\bar{p}}$ , and partition of A ∪ A ¯ $A \cup {\bar{A}}$ into subsets X , Y $X, Y$ , and Z.

3 Algorithmic approaches

Because UPIT+ is equivalent to a continuous linear program, it can be solved using an off-the-shelf solver directly. However, we propose two alternative methods for solving UPIT+.

Using lazy constraints

Considering the application to open pit mining, it is reasonable to expect that only blocks located at the pit's borders may violate weak precedence constraints. These blocks represent a relatively small part of the whole block model; thus, the weak precedence constraints would not be necessary for most of the blocks. Therefore, we declare all constraints related to weak precedence arcs as lazy, letting the solver add them as necessary.

Iterative method based on the nestedness of the pits

Because of the nestedness property, given two value vectors p ′ ≤ p $p^{\prime } \le p$ , the optimal solution of UPIT+( p ′ $p^{\prime }$ ) can be used to potentially speed up solving the problem for UPIT+(p) because blocks extracted in the solution for p ′ $p^{\prime }$ can be removed and the optimization for p can be performed considering the remaining blocks only.

As mentioned before, in practice either computing the ultimate pit or a sequence of nested pits has a practical interest; thus, we can consider that value vectors are 0 < p 1 ≤ p 2 ≤ ⋯ ≤ p K $0 &lt; p^1 \le p^2 \le \cdots \le p^K$ . The algorithm to solve UPIT+( p K , B , P , Q $p^K,B,P,Q$ ) is straightforward:
  • 1. Let S1 be the set of blocks extracted by an optimal solution of UPIT+( p 1 , B , P , Q $p^1,B,P,Q$ ). Let also B 1 = S 1 $B^1 = S^1$ .
  • 2. For k = 2 , … , K $k=2, \ldots , K$
    • (a) Solve UPIT + ( p k , B ∖ B k − 1 , P , Q ) $\textrm {UPIT}^+(p^k,B\setminus B^{k-1},P,Q)$ , and let S k $S^k$ be the blocks extracted in its optimal solution.
    • (b) Let B k = S k ∪ B k − 1 $B^k=S^k \cup B^{k-1}$ .
  • 3. Return x , x i = 1 ⇔ i ∈ $x, x_i=1 \Leftrightarrow i \in$ B K $B^K$ as the solution.

It is worth emphasizing that both methods are exact, that is, they find the optimal solution of UPIT+.

4 Numerical experiments

In this section, we consider three block models of different sizes: “KD,” “Marvin,” and “Model3.” We are unable to undisclose Model3, but KD and Marvin are publicly available in MineLib (Espinoza et al., 2013).

We will consider a sequence of value vectors parameterized by a revenue factor. Therefore, the economic value of each block is computed as p i = max { α λ g i t i − ( γ m + γ p ) t i , − γ m t i } $p_i=\max \lbrace \alpha \lambda g_i t_i -(\gamma _m+\gamma _p) t_i, -\gamma _m t_i\rbrace$ , where α is the net income per ton of mineral, g i $g_i$ is the ore grade of the block, t i $t_i$ is the corresponding tonnage, γ m $\gamma _m$ is the cost of mining one tonne, γ p $\gamma _p$ is the cost of processing one tonne, and λ ∈ ( 0 , 1 ] $\lambda \in (0,1]$ is the revenue factor, that is, the value λ = 1 $\lambda =1$ corresponds to the ultimate pit. The maximum is computed over two possible destinations for the block: processing and selling it, which yields a net profit of α λ g i t i − ( γ m + γ p ) t i $\alpha \lambda g_i t_i-(\gamma _m+\gamma _p) t_i$ , or storing it in a waste dump, which has a negative profit equal to − γ m t i $-\gamma _m t_i$ .

We assume that the costs of violating weak precedence arcs are given in dollars per ton, that is, c i j = c t i $c_{ij}= c t_i$ , and consider three scenarios: c = 0.5 , 1.0 $c=0.5, 1.0$ , and 1.5 ($/t). These values are realistic and can be regarded as “low,” “medium,” and “high” cost scenarios.

Blocks in each block model have all the same size, and we denote d x , d y $d_x,d_y$ , and d z $d_z$ as the dimensions of blocks in each axis, respectively. An overall slope angle of 45° is used to generate the strong precedence arcs. The weak predecessors of a block with coordinates ( r x , r y , r z ) $(r_x,r_y,r_z)$ are those that are not strong predecessors of the block and have coordinates ( r x ′ , r y ′ , r z + d z ) $(r_x^{\prime },r_y^{\prime },r_z+d_z)$ such that ( r x − r x ′ ) 2 + ( r y − r y ′ ) 2 ≤ Δ 2 $(r_x-r_x^{\prime } )^2+(r_y-r^{\prime }_y)^2 \le \Delta ^2$ , that is, they are located at the level immediately above and within a given radius Δ. We consider three different values for Δ for each block model. They are summarized in Table 2, together with the number of strong and weak precedence arcs for each block model. Given all possible values of Δ and c, we analyze a total of nine scenarios per block model, that is, 27 instances in total for each revenue factor.

Table 2. Summary of block models dimensions and number of arcs for different values of Δ.
# Blocks d x × d y × d z $d_x \times d_y \times d_z$ # Strong arcs Δ # Weak arcs
KD 50,472 20 × 20 × 15 3,736,279 80 3,472,864
100 5,110,205
120 7,016,412
Marvin 53,271 30 × 30 × 30 6,425,028 60 946,293
90 2,048,874
120 3,480,709
Model3 58,240 20 × 20 × 15 2,949,826 80 3,864,140
100 5,726,490
120 7,920,066

All experiments were run on an AMD Ryzen 5 3600 CPU with 20 GB of RAM executing Windows 10. The optimization models were implemented in JuMP (Dunning et al., 2017) and Julia 1.7 (Bezanson et al., 2017). Gurobi 9.1 (Gurobi Optimization, 2023) was used to find the optimal solutions to the optimization problems.

4.1 Nested pits without bottom space penalization

This section summarizes the results for the classic UPIT problem. Table 3 presents, for each of the instances, the economic value and tonnage obtained for revenue factors λ = 0.2 , 0.4 , 0.6 , 0.8 $\lambda = 0.2, 0.4, 0.6, 0.8$ , and 1.0. Computing each of these pits required a few seconds using an implementation of the pseudo-flow algorithm available in Pyramp (Morales et al., 2021). These values are relevant because any solution x of UPIT is feasible for UPIT+. Indeed, if the value of x regarded as a solution of UPIT is p T x $p^Tx$ , then its value regarded as a solution of UPIT+ is p T x − C ( x ) $p^Tx-C(x)$ , where C ( x ) $C(x)$ is the cost of violated weak precedence arcs.

Table 3. Economic value and tonnage of optimal solutions of UPIT depending on the data set and λ.
Instance KD Marvin Model3
λ UPIT UPIT UPIT UPIT UPIT UPIT
(MM$) (MMt) (MM$) (MMt) (MM$) (MMt)
0.2 6.60 0.18 0.00 0.00 129.74 2.19
0.4 1,642.96 93.46 0.00 0.00 2,074.58 58.47
0.6 2,287.62 178.45 3,163.19 376.19 2,348.57 80.81
0.8 2,313.80 188.99 3,495.02 494.87 2,596.12 126.88
1.0 2,315.69 192.80 3,538.80 562.33 2,699.11 195.85

4.2 Comparison of ultimate pits ( λ = 1 $\lambda =1$ )

Tables 4, 5, and 6 summarize the results for each of the three block models, respectively. Each table presents all the scenarios of Δ and c and the columns described below.
  • The “Penalized UPIT” column contains the economic value of the solution of UPIT if regarded as a solution of UPIT+, that is, it shows the value p T x − C ( x ) $p^Tx-C(x)$ , where x is the solution corresponding to row λ = 1 $\lambda =1$ in Table 2 and C ( x ) $C(x)$ is the cost due to violated weak precedence arcs incurred by that solution.
  • Column “UPIT value loss” presents the difference between the economic value of the ultimate pit in Table 2 and column “Value of UPIT,” as a percentage, that is, 100 · C ( x ) / p T x $100 \cdot C(x)/p^Tx$ .
  • “UPIT+ value” and “UPIT+ tonnage pit” contain the value of the optimal solution of UPIT+ and its tonnage, respectively.
  • Column “Diff. in value” is the difference between the “UPIT+ value” and “Penalized UPIT” columns.
  • “Diff. in tonnage” is the difference between the “UPIT+ tonnage” column and the tonnage of the ultimate pit from Table 2.
  • “Solver runtime” is the execution time necessary for solving the corresponding instance of UPIT+ using an off-the-shelf linear programming solver.
Table 4. Comparison of ultimate pit economic values and tonnages, KD case.
Δ c Penalized UPIT UPIT+ UPIT+ Diff. Diff. Solver
UPIT value value tonnage in value in tonnage runtime
(m) ($/t) (MM$) loss (%) (MM$) (MMt) (%) (%) (s)
80 0.5 1,547.37 −33 1,810.12 305.34 15 37 1,771.5
1.0 779.42 −66 1,695.65 441.64 54 56 4,843.8
1.5 11.46 −99 1,670.41 473.47 99 59 5,837.9
100 0.5 817.36 −64 1,653.48 454.98 51 58 8,802.7
1.0 −680.62 −129 1,609.05 501.89 142 62 10,122.8
1.5 −2,178.59 −194 1,597.31 501.97 236 62 9,569.6
120 0.5 −254.14 −110 1,579.90 503.27 116 62 23,878.4
1.0 −2,823.61 −221 1,561.79 517.92 281 63 14,553.3
1.5 −5,393.09 −332 1,556.33 524.78 447 63 11,312.2
Table 5. Comparison of ultimate pit economic values and tonnages, Marvin case.
Δ c Penalized UPIT UPIT+ UPIT+ Diff. Diff. Solver
UPIT value value tonnage in value in tonnage runtime
(m) ($/t) (MM$) loss (%) (MM$) (MMt) (%) (%) (s)
60 0.5 3,350.1 −5.0 3,368.2 545.3 1.0 −3.0 152.8
1 3,161.4 −11.0 3,224.3 557.6 2.0 −1.0 196.4
1.5 2,972.7 −16.0 3,098.4 572.8 4.0 2.0 181.4
90 0.5 2,810.1 −21.0 2,935.9 564.8 4.0 0.0 282.6
1 2,081.3 −41.0 2,492.9 613.9 17.0 9.0 374.8
1.5 1,352.6 −62.0 2,160.2 693.3 37.0 23.0 664.8
120 0.5 1,712.9 −52.0 2,189.9 618.1 22.0 10.0 569.7
1 −113.0 −103.0 1,478.7 814.5 108.0 45.0 1,401.7
1.5 −1,938.9 −155.0 1,222.6 1,082.2 259.0 92.0 3,725.7
Table 6. Comparison of ultimate pit economic values and tonnages, Model3 case.
Δ c Penalized UPIT UPIT+ UPIT+ Diff. Diff. Solver
UPIT value value tonnage in value in tonnage runtime
(m) ($/t) (MM$) loss (%) (MM$) (MMt) (%) (%) (s)
80 0.5 2,480.1 −8.0 2,611.3 224.5 5.0 15.0 169.3
1 2,261.1 −16.0 2,586.0 240.6 13.0 23.0 163.3
1.5 2,042.1 −24.0 2,576.6 252.3 21.0 29.0 182.7
100 0.5 2,281.6 −15.0 2,572.2 243.4 11.0 24.0 240.1
1 1,864.1 −31.0 2,554.8 261.8 27.0 34.0 260.5
1.5 1,446.6 −46.0 2,548.5 265.4 43.0 36.0 307.8
120 0.5 1,994.8 −26.0 2,542.9 264.0 22.0 35.0 441.6
1 1,290.4 −52.0 2,529.9 275.8 49.0 41.0 461.2
1.5 586.1 −78.0 2,525.1 282.5 77.0 44.0 725.8

As expected, “Penalized UPIT” values decrease as the penalization cost c and the space requirement Δ increase. However, the magnitude of this variation is very significant. When comparing the values obtained for the ultimate pits (Table 2, λ =1), the economic value falls between 33% and 332% for KD, 5% and 155% (it becomes negative) for Marvin, and between 8% and 78% for Model3. These differences in economic value, together with the results from the column “Difference in tonnage,” have important implications in practice, due to the current practice of using the ultimate pit as a guide for the mine design which must incorporate geometric constraints such as minimum bottom width. The results in Tables 4–6 indicate that using the ultimate pit as a reference for design may not be a good practice, which is consistent with theoretical examples in Nancel-Penard and Morales (2022).

The increase in tonnages (column “UPIT+ tonnage”) for higher values of Δ and c is also expected, as higher penalties and more weak precedence arcs translate into larger pits to reduce the cost due to violated weak precedence arcs. However, it is very interesting to observe that the reduction in economic values of solutions of UPIT+ is smaller than those of the ultimate pits. The difference in economic values between the cases Δ = 80 , c = 0.5 $\Delta =80, c=0.5$ , and Δ = 120 $\Delta =120$ , c = 1.5 $c=1.5$ are −14% for KD, −64% for Marvin, and −4% for Model3.

Regarding the execution times, the instances become harder to solve when c , Δ $c, \Delta$ increase, even though in most cases the total time is only minutes. This contrasts with UPIT, which requires only a few seconds to be solved.

While Tables 4–6 report the results only for the ultimate pits ( λ = 1 $\lambda =1$ ), consistent figures are obtained if the analysis is done for all revenue factors. The appendix presents these comparisons for all values of c , Δ $c, \Delta$ , and λ and each of the block models.

The large difference in economic value and tonnage suggests that the ultimate pit does not provide a good guide for mine design. However, it is worth noting that all the results and differences presented in this section depend on the parameters c and Δ but also on the definition of Q. We briefly discuss this in Section 4.4.

4.3 Nested pits and running times

In this section, we provide some results related to the execution time for the ultimate pit and nested pits.

We evaluate the performance of solving the monolithic version of UPIT+|referred to as the “Direct method”|plus the two proposed approaches described in Section 3: “Lazy constraints” and “Iterative method.” Figures 4-6 present the running times for all the instances, separated by block model. The X axis contains the 45 combinations of Δ , c , λ $\Delta , c, \lambda$ sorted by the time required by the off-the-shelf solver to find the optimal solution of UPIT+ (i.e., the direct method). Running times are displayed using the primary axis while the right axis represents the “time difference” computed as the execution time of the iterative method minus the fastest of the other two algorithms; thus, a negative time gain means that the iterative method was not the best performing of the three. Notice that the instances include nested pits corresponding to 1 ≤ k ≤ 5 $1 \le k \le 5$ ; and that the iterative method uses results for smaller values of k. Thus, for this method, the graph reports the total time required to solve all instances k ′ = 1 , … , k $k^{\prime }=1, \ldots , k$ , including the time to process intermediate block sets.

Details are in the caption following the image
Fig. 4
Open in figure viewerPowerPoint
KD data set: comparison of runtimes for the direct, lazy constraints, and iterative methods.
Details are in the caption following the image
Fig. 5
Open in figure viewerPowerPoint
Marvin data set: comparison of runtimes for the direct, lazy constraints, and iterative methods.
Details are in the caption following the image
Fig. 6
Open in figure viewerPowerPoint
Model3 data set: comparison of runtimes for the direct, lazy constraints and iterative methods.

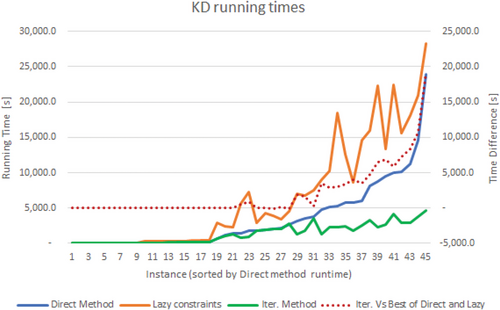
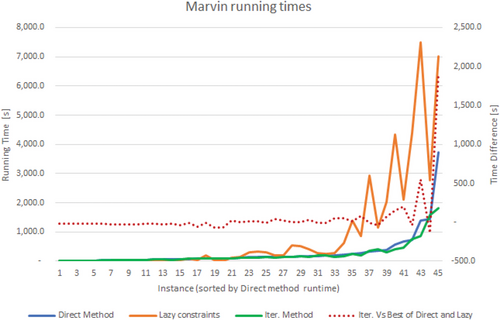
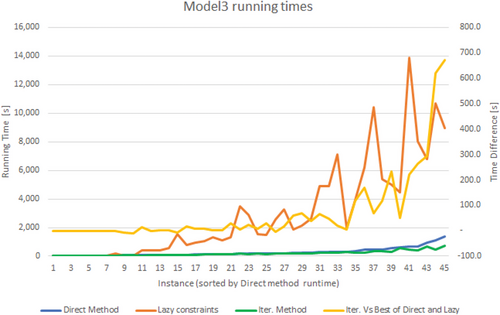
As seen in Figs. 4-6, the iterative approach scales significantly better than the other methods; however, there are cases in which the iterative method runs slower than the direct or the lazy constraints approach. We analyze both aspects in more detail next.

Table 7 presents runtimes for each of the block models. The table contains the average over the nine instances obtained for each data set by varying c and Δ. The reported values are the following: “Solver's best” is the time in seconds of the fastest approach between using the solver directly or adding lazy constraints. “Iter. method” is the time in seconds required by the iterative method to solve the instances. “Time Diff (s)” and “Time Diff (%)” present the difference in time between the solver's best algorithm, in seconds and percent, respectively.

Table 7. Comparison of runtimes between off-the-shelf solver and the iterative method.
λ 0.2 0.4 0.6 0.8 1.0
KD Solver's best (s) 36.9 148.5 1,957.4 5,394.7 10,076.9
Iter. method  (s) 40.0 144.6 1,915.2 2,320.2 2,588.9
Time Diff  (s) 4.5 −3.9 −42.3 −3,074.5 −7,488.1
Time Diff  (%) 10.8 −2.0 −1.8 −55.1 −70.8
Marvin Solver's best (s) 3.5 26.9 135.7 416.9 838.9
Iter. method  (s) 25.2 65.3 136.0 427.5 496.0
Time Diff  (s) 21.7 38.4 0.3 10.7 −342.9
Time Diff  (%) 705.7 144.4 0.4 −4.7 −28.6
Model3 Solver's best (s) 36.6 130 244.2 375.6 562.0
Iter. method  (s) 38.8 126.7 214.9 276 328.0
Time Diff  (s) 2.6 −3.4 −29.3 −99.5 −234.0
Time Diff  (%) 6.2 −2.8 −9.8 −21.2 −33.1

The cells in boldface represent negative results in which the iterative method took longer than the best solver's approach. However, these few cases are limited to small values of λ, that is, they correspond to small solutions (in a number of blocks). More importantly, even though the relative difference may be large (705.7% for Marvin), these cases have small runtimes. In fact, when the iterative method was slower, the gap was always less than three minutes. This contrasts with the cases in which the iterative method is better, which happens in most of the cases with long runtimes and greater absolute gains in time. A full report of all runtimes for each λ , Δ $\lambda , \Delta$ , and c can be found in the Appendix.

4.4 Comparison of geometries

To conclude the analysis of the approach, we compare the geometry obtained using UPIT and UPIT+. Figure 7 shows several section views of solutions for the Marvin data set. From top to bottom, the figure displays: the solution of UPIT and the solutions of UPIT+ for c = 0.5 , Δ = 60 $c=0.5, \Delta =60$ and c = 0.5 , Δ = 90 $c=0.5, \Delta =90$ . The left figures correspond to the XZ section  Y = 19 $Y=19$ , and the right figures correspond to the YZ section  X = 28 $X=28$ .

Details are in the caption following the image
Fig. 7
Open in figure viewerPowerPoint
Sections (left: Y = 19 $Y=19$ , right: X = 28 $X=28$ ) of solutions for the Marvin data set. Top row: UPIT solutions. Middle row: UPIT with c = 0.5 . Δ = 60 $c=0.5. \Delta =60$ . Bottom row: UPIT+ with c = 0.5 , Δ = 90 $c=0.5, \Delta = 90$ .

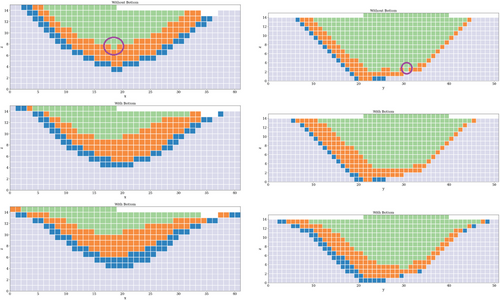
It is clear from these results that the model enforces more operational spaces at the bottom of the pit, making the resulting geometries more amenable for large pieces of equipment. Indeed, a shovel may require about 50 m of space for operation (for loading a truck at one side) to ideally 100 m or more (for two-sized loading). For Marvin, this means that a one-block bottom is not viable for such equipment, that a two-block bottom is feasible, but that at least three to four blocks are desirable for maximum productivity. Therefore, as the figure shows, both UPIT solutions have bottoms that do not have enough space for a shovel (marked in purple); however, the bottoms obtained using UPIT+ all are two or more blocks wide.

Finally, Fig. 7 also shows that there may be an impact on the overall slope angles, making them gentler when compared with the solutions of the ultimate pit (first row in the figure). This impact depends on the definition of Q and c. Practical use of UPIT+ may consider weak arcs starting at a certain level or in parts of the ultimate pit that are too narrow. As this paper focuses on the theoretical aspects of the model, a detailed study is outside of the scope of this work.

5 Conclusions

This paper presents a novel mathematical model for the problem of the optimal pit with minimum operational bottom pit space in strategic mine planning, some algorithmic ideas to solve the problem, and their application in realistic data sets.

The novelty of the mathematical model is that instead of considering complex constraints for requiring a minimum bottom space, it penalizes the narrow bottom of pits, which is compatible with the operational option of using more expensive but smaller equipment for this task. The resulting model is significantly simpler than previous efforts, but it also has interesting theoretical properties. First, the constraint matrix is unimodular; thus, the binary constraints of the variables can be relaxed, and the problem can be solved in polynomial time. Second, the optimal solutions to the problem are monotonic with regard to the economic value vector, which is a critical characteristic to be used in practical applications. A consequence of these results is that our model is the first that considers geometrical constraints beyond overall slope angles, ensures the generation of nested pits, and that is proven to be solvable in polynomial time.

The theoretical properties are used to propose a simple iterative method to speed up the computations, and the model is applied in three different data sets and several combinations of cost and geometric penalty configurations.

In practical terms, the results show that traditional UPIT, which does not consider costs of narrow pit bottoms, may produce very low-quality pits, even with negative economic values, if these costs are included in the economic evaluation. Conversely, the best solution for UPIT+, which takes these costs into account in the formulation, can be over 400% higher in some cases. This validates the proposed model as it suggests that solutions may change significantly if more detailed costs are considered.

In terms of computation times, the nestedness property is used to solve the problem of UPIT+ incrementally, that is, solving smaller pits first and then using these solutions to reduce the set of blocks. This technique is shown to reduce the computation time by about a 28% average on all tested instances, and more than 70% in some specific cases when compared to runtimes of an off-the-shelf solver.

From the theoretical point of view, future research should be oriented to improve the computation times because the speed-up obtained using the nestedness property is significant but computation times for larger data sets may still be too long. From the practical point of view, because the set Q of weak precedence arcs may have a huge impact on the resulting geometries and economic value, it is necessary to study what is the best approach for its definition and utilization. For example, Q may contain arcs corresponding to the deepest parts of the block model only.

Acknowledgments

The authors acknowledge the support of the Chilean National Agency for Research and Development (ANID) through the following programs. Jorge Amaya: Fondef Program, grant ID22I10199 and Basal Program CMM-FB210005. Gonzalo Nelis: Fondecyt de Iniciación, Project 11230022.

    Appendix

    This appendix provides detailed information about the numerical results for each of the 135 instances when solved by the three methods (direct, lazy constraints, and incremental) and comments on other potential algorithmic approaches.

    As reported in the body of the paper, using the nestedness property reduced the running time significantly. To further support these conclusions, detailed results obtained from applying this method are presented in Table A1, which contains, for each block model and combination of the parameters Δ , c $\Delta , c$ , and revenue factor λ, the “Solver” time that is required to solve the instance of UPIT+ using the off-the-shelf solver, the “Lazy” time required to solve the instance using the Lazy constraints approach, and the “Iter.” which is the time necessary for solving the instance iteratively by profiting of the nestedness property. The “Diff.” column presents the percentage gain of using the iterative method over the solver algorithm (i.e., 100 · ( S o l v e r T i m e − I t e r T i m e ) / S o l v e r T i m e $100\cdot (SolverTime-IterTime)/SolverTime$ ). Notice that the values of Δ = 80 , 100 , 120 $\Delta =80,100,120$ apply to KD and Model3 while for Marvin the corresponding values are Δ = 60 , 90 , 120 $\Delta =60,90,120$ . Values in bold are the fastest algorithm for the corresponding instance.

    Table A1. Comparison of execution times for KD, Marvin, and Model3 data sets. Values in bold correspond to the fastest algorithm for the given instance.
    KD Marvin Model3
    Δ c λ Solver Lazy Iter. Diff. Solver Lazy Iter. Diff. Solver Lazy Iter. Diff.
    (m) ($/t) (s) (s) (s) (s) (s) (s) (s) (s) (s) (s) (s) (s)
    60/ 80 0.5 0.2 22 33 22 0.0 20 2 20 −710.7 24 24 24 0.0
    0.4 63 367 62 1.0 42 24 51 −112.2 52 190 52 −0.6
    0.6 654 2905 669 −2.4 75 104 87 −16.4 83 378 82 0.6
    0.8 1417 5688 847 40.2 114 152 109 4.4 135 1029 127 5.4
    1.0 1772 7288 884 50.1 153 200 134 12.5 179 1553 169 5.3
    1.0 0.2 33 31 33 −5.8 20 2 20 −754.7 26 24 26 −7.2
    0.4 97 288 101 −3.5 62 24 41 −72.9 62 381 50 20.3
    0.6 1127 2379 1038 7.9 102 126 80 21.3 102 797 83 18.3
    0.8 3131 7074 1267 59.5 152 209 111 26.8 160 1300 129 19.0
    1.0 4844 8959 1291 73.3 196 267 140 28.7 223 1859 163 26.6
    1.5 0.2 27 29 27 0.0 17 2 17 −635.9 25 24 25 −2.9
    0.4 141 316 141 −0.2 42 24 43 −80.3 67 379 69 −3.2
    0.6 1388 2309 1334 3.9 85 206 89 −5.1 114 961 106 6.7
    0.8 3522 6775 1823 48.2 133 322 119 10.5 180 1481 149 17.1
    1.0 5838 8652 1854 68.2 181 419 146 19.3 251 2121 183 27.1
    90/100 0.5 0.2 36 35 36 −4.9 25 5 25 −362.3 39 36 39 −7.2
    0.4 108 288 109 −1.2 56 31 52 −69.0 84 573 84 0.6
    0.6 1865 4338 1869 −0.2 132 306 124 6.0 135 1344 132 2.4
    0.8 5337 18454 2276 57.4 212 626 164 22.6 208 3279 192 8.0
    1.0 8803 22382 2315 73.7 283 861 200 29.2 289 4922 240 16.9
    1.0 0.2 36 35 36 −2.7 27 5 27 −401.9 34 36 34 0.0
    0.4 128 249 121 6.2 69 31 68 −121.6 92 1550 98 −6.5
    0.6 2186 3455 2064 5.5 158 544 153 2.8 167 3511 161 3.5
    0.8 5763 12587 2423 58.0 264 1399 257 2.9 281 4880 215 23.5
    1.0 10123 15628 2883 71.5 375 2022 301 19.7 431 6213 261 39.6
    1.5 0.2 40 35 40 −14.8 22 5 22 −306.7 37 36 37 −4.5
    0.4 185 245 186 −0.6 59 31 62 −98.1 138 1087 136 1.8
    0.6 1841 2877 1824 0.9 134 306 141 −5.8 251 2636 213 15.1
    0.8 5194 10302 2301 55.7 366 1162 401 −9.6 374 3937 257 31.2
    1.0 9570 13323 2684 72.0 665 2117 462 30.5 542 5017 308 43.2
    120 0.5 0.2 55 45 55 −21.3 32 3 32 −1069.7 61 50 61 −21.8
    0.4 194 433 182 6.4 79 26 81 −206.7 171 2905 148 13.2
    0.6 3849 7500 3561 7.5 163 510 158 3.1 289 7138 268 7.3
    0.8 10035 22500 4111 59.0 341 2941 345 −1.1 435 10427 367 15.7
    1.0 23878 28257 4721 80.2 570 4332 418 26.6 663 13886 442 33.4
    1.0 0.2 51 44 51 −17.9 32 3 32 −1004.5 49 50 49 0.0
    0.4 213 407 194 8.8 89 27 96 −254.4 205 2579 208 −1.8
    0.6 2711 4566 2846 −5.0 182 276 190 −4.9 448 5363 330 26.4
    0.8 8146 15998 3334 59.1 732 4402 766 −4.6 665 8028 400 39.9
    1.0 14553 20905 3769 74.1 1402 7503 849 39.4 1082 10684 461 57.4
    1.5 0.2 59 46 59 −29.8 34 3 34 −1105.0 56 49 56 −12.5
    0.4 208 397 206 1.0 93 24 94 −284.2 301 1961 296 1.4
    0.6 1997 3865 2033 −1.8 192 254 201 −4.6 610 4475 560 8.3
    0.8 6008 14633 2500 58.4 1438 2776 1576 −9.7 943 6776 649 31.2
    1.0 11312 18082 2899 74.4 3726 7017 1813 51.3 1399 8958 726 48.1

    As seen in Table A1, the iterative method is the fastest for the vast majority of the cases. For small values of λ, the direct approach can be faster than the iterative method, as the latter method requires to work with the data (removing blocks) and setting up intermediate optimization instances. This advantage over the direct method could be reduced, for example, by using more efficient data structures. However, for greater values of λ, the iterative method can improve the execution time significantly, above 80% in some cases.

    When fixing the x variables in UPIT+ the optimal value of y is given by y i j = max { 0 , x i − x j } $y_{ij} = \max \lbrace 0,x_i-x_j\rbrace$ for each ( i , j ) ∈ Q $(i,j) \in Q$ . Thus, it makes sense to apply Bender's decomposition (Benders, 1962; Rahmaniani et al., 2017) to solve the problem. However, this approach proved to be slower than others. Another approach that can be suitable for the problem is similar to using lazy constraints but adding violated weak arcs iteratively. Unfortunately, this approach also became too slow.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.