Body sizes and diversification rates of lizards, snakes, amphisbaenians and the tuatara
Abstract
Aim
Size is one of the most important and obvious traits of an organism. Both small and large sizes have adaptive advantages and disadvantages. Body size–frequency distributions of most large clades are unimodal and right skewed. Species larger than the mean or range midpoint of body sizes are relatively scarce. Theoretical models suggest evolutionary rates are higher in small organisms with short generation times. Therefore diversification rates are usually thought to be maximal at relatively small body sizes. Empirical studies of the rates of molecular evolution and clade diversification, however, have usually indicated that both are unrelated to body size. Furthermore, it has been claimed that because snakes are longer than lizards, the size–frequency distribution of all squamate species is bimodal overall. We examined the shape of the size–frequency distribution of nearly all Squamata and Rhynchocephalia species, and investigated how size affected diversification rates.
Location
Global.
Methods
We collected data on maximum body length for 9805 lepidosaur (squamates and the tuatara) species (99.7% of all species) and converted them to mass using clade-specific allometric equations. Using methods that test for relationships between continuous traits and speciation and extinction rates on a large, dated phylogeny (4155 species), we investigated the relationship between diversification rates and body size.
Results
Living squamates span six orders of magnitude in body size, eight when giant extinct snakes and mosasaurs are included. The body size–frequency distributions of snakes and lizards separately, and of all lepidosaur species combined, are unimodal and right skewed. Nonetheless, we find neither linear nor hump-shaped relationships between size and diversification rates, except in snakes, where speciation and diversification are hump shaped.
Main conclusions
Despite a clear modality and skew in the body sizes of lepidosaurs, we find little evidence for faster diversification of modal-sized taxa, perhaps implying that larger-sized clades are relatively young.
Introduction
‘Size has a fascination of its own’ (Julian Huxley)
Body size is perhaps the most important attribute of an organism. Size dominates multiple aspects of morphology, ecology, physiology and life history (Haldane, 1928; Gould, 1966; Schmidt-Nielsen, 1984; Brown et al., 2004). Size plays a major role in shaping behaviour, extinction risk and evolutionary trajectories, such as the rate of molecular evolution (Fontanillas et al., 2007; Wollenberg et al., 2011) and the propensity for speciation (Stanley, 1973; Cardillo et al., 2005; Etienne et al., 2012). In fact, the systematic effects of size are so prevalent in comparative biology that when some attributes (such as overall population metabolic rates, the ratio between weaning mass and adult mass and the lifetime number of heartbeats) are found to be independent of size they are sometimes referred to as ‘invariant’ (Damuth, 1981; Nee et al., 2005; Etienne et al., 2012).
Hutchinson & MacArthur (1959) claimed that the size structure of ‘the fauna of any area’ has an overarching form: ‘groups containing the largest numbers of species are for the most part groups of small animals’. They derived a model according to which species numbers are determined by the mosaic of elements comprising the ecological niche, and whereby the greatest diversity of niches correspond to ‘some intermediate size’ [of organism] (Hutchinson & MacArthur, 1959). To test this, they drew some of the first histograms based on the sizes of large groups of closely related species over large geographic areas (Odonata of the north-eastern USA and Mammalia of Europe and Michigan). These histograms were characterized by unimodal size–frequency distributions when size was logarithmically transformed, a transformation which became a statistical convention from then on. Hutchinson & MacArthur (1959) predicted that, in taxa showing considerable size variation, the most common size class will be of relatively small, but not the smallest, species. May (1978) likewise equated the number of available niches with species numbers, but viewed the number of such niches, and hence the number of species, as a monotonically decreasing function of body size. He presented similar (unimodal and right skewed) body size–frequency distributions for lepidopterans, beetles, birds and mammals. He further boldly predicted, based on ‘crude approximations and outright guesses’, that the size distribution of all terrestrial organisms has a similar shape. However, he viewed the decline of species numbers at the smallest sizes as a potential artefact of poor taxonomic practices applied to minute animals.
Stanley (1973) arrived at a similar conclusion with regard to the shape of size–frequency distributions, from very different premises. He argued that speciation in the fossil record mainly occurs at small body sizes, whereas larger sizes are evolutionary ‘dead ends’, which do not give rise to major new taxa. The greater species numbers at small sizes are therefore a consequence of higher speciation rates of smaller organisms. Stanley (1973) explained the scarcity of very small species by evolutionary constraints on miniaturization (e.g. food acquisition rates in endotherms). These evolutionary and ecological mechanisms, of course, are not contradictory, and the latter may well explain the former, although faster evolution at smaller sizes can also be attributed to a faster mutation rate or to shorter generation times of small animals (e.g. Fontanillas et al., 2007; Etienne et al., 2012).
The unimodal, right-skewed shape of animal size–frequency distribution has been found in many taxa (e.g. mammals, Gardezi & da Silva, 1999; lizards, Meiri, 2008; fishes, Albert & Johnson, 2012; snakes, Burbrink & Myers, 2014; see Gaston & Chown, 2013, for a review of such patterns in insects). It is nowadays viewed as almost canonical, such that theoretical models have been designed to replicate it (e.g. Clauset & Erwin, 2008). Such a distribution suggests important size-related ecological and evolutionary constraints. The numerical dominance of medium-sized taxa was variably explained as stemming from them having greater reproductive potential (e.g. Brown et al., 1993; cf. Jones & Purvis, 1997) or ecological dominance in terms of population density (Damuth, 1993). Alternatively, such distributions were claimed to stem from the fact that medium-sized species have small geographic range sizes, and thus high spatial turnover, whereas larger- and smaller-sized species have larger ranges (e.g. Brown & Nicoletto, 1991; Agosta & Bernardo, 2013), or from the greater variety of ecological niches available to medium-sized species (e.g. Hutchinson & MacArthur, 1959).
Not all taxa, however, display such distributions. Bimodal size distributions (albeit usually with a higher mode at smaller sizes) have been detected in taxa as diverse as marsupials, hymenopterans, chameleons and placental mammals (Gardezi & da Silva, 1999; Ulrich, 2006; Meiri, 2008; Kelt & Meyer, 2009, respectively). Dinosaur size–frequency distributions (summed across their evolutionary history) are left skewed (O'Gorman & Hone, 2012). Furthermore, distributions tend to lose their skewness at low taxonomic and spatial scales (Brown & Nicoletto, 1991; Gardezi & da Silva, 1999; Meiri, 2008; Cox et al., 2011; Burbrink & Myers, 2014) or when assemblages include fewer species (e.g. at high latitudes; Olson et al., 2009).
Cox et al. (2011) claimed that squamates are an obvious exception to the unimodal, right-skewed pattern. They asserted that because snakes are generally larger than lizards and these are the two major squamate clades then combining their size–frequency distributions will result in a bimodal pattern, with lizards contributing mostly to a mode at small sizes and snakes mostly contributing to a mode at larger sizes. Using the maximum lengths of all species in Canada and the United States, they showed that the length–frequency distribution was, indeed, bimodal (Cox et al., 2011). While snakes are undoubtedly longer than lizards in general (see below and Appendix S1 in Supporting Information), they are also usually lighter for a given length [e.g. at a snout–vent length (SVL) of 100 mm our general snake and general lizard equations predict weights of 0.5 and 20.9 g, respectively]. Even within snakes (Feldman & Meiri, 2013) and lizards (Greer & Wadsworth, 2003; Meiri, 2010) there is considerable shape variation, which makes body length a very problematic measure of size at large taxonomic scales (Appendix S2c). The shape of the squamate size–frequency distribution is therefore poorly known.
The relationship between body size and diversification rates is mostly unresolved, despite being intensively studied. From early efforts to quantify speciation and extinction with respect to size in the fossil record (e.g. Stanley, 1973; Jablonski, 1997), research has mostly shifted to the study of diversification based on phylogenies and body sizes of extant taxa alone. Studies based on contrasts of the body sizes and species richness of different taxa usually yielded no directional patterns across a diverse array of organisms (Orme et al., 2002a,b). This remains the case even when body size–frequency distributions are right-skewed, and body size and richness are negatively correlated in non-phylogenetic analyses (Purvis et al., 2003). This apparent paradox may indicate that large-bodied taxa are, on average, simply younger than smaller-bodied ones (Purvis et al., 2003; Etienne et al., 2012), but diversify as fast as them, or faster. Alternatively, it may mean that the relationship between diversification rates and size is not linear, or that extinction plays a complex role at different body sizes.
To date, relationships between diversification rates and body size in large phylogenetic datasets were mostly restricted to vertebrates, with studies of invertebrates limited to lower taxonomic ranks in groups with fewer species (e.g. Orme et al., 2002b). In birds and mammals, size was mostly unrelated to diversification rates (Gittleman & Purvis, 1998; Owens et al., 1999; Isaac et al., 2005). In freshwater fishes and mantellid frogs, however, small sizes seem mostly associated with fast diversification rates (Knouft & Page, 2003; Wollenberg et al., 2011). Studies at the regional and community scale in North American snakes have shown a complex relationship, but do not suggest that higher speciation rates near the mode drive the observed distributions at local scales (Burbrink & Myers, 2014).
Methods for testing direct relationships between size and diversification on phylogenies have only recently become available (FitzJohn, 2010), thus earlier studies may have been confounded by methodological artefacts (Maddison, 2006). Our aim is threefold: (1) to describe the variation of body masses within lepidosaurs (Lepidosauria: the clade containing Squamata and Rhynchocephalia), (2) to examine the shape of lepidosaur body-mass distribution and test whether it is bimodal, and (3) to investigate the relationships between body size and diversification rates in squamates. This will allow us to determine, at least at a basic level, how body sizes are distributed across lepidosaur groups, and if a historical interplay between size and diversification is responsible for present-day patterns.
Methods
Data
We assembled data on the maximum sizes of nearly all extant (and extinct in historical times) lepidosaur species, using the taxonomy of the March 2015 version of the reptile database (Uetz, 2015) and a few species described since. Data are from an extensive literature search of over 9000 published works. These were supplemented, in a few cases, by measuring live individuals in the field and in captivity, and measuring preserved specimens in natural history museums (c. 1500 specimens belonging to c. 130 species), and by obtaining measurements through personal communications with museum collection managers. We used size maxima, as they are good proxies of the potential sizes attained by individuals with indeterminate growth, such as reptiles. Furthermore, maxima are by far the most readily available data in the literature. We were able to obtain maxima for virtually all species (9805, see below), whereas data on mean sizes were only available for c. 5350 species. Data comprise SVL for lizards and amphisbaenians, while for snakes most of the data (c. 90%) comprises total lengths (TL) and the rest SVL. The dataset (n = 9805; Appendix S1) is the largest dataset presented so far for size data of amphisbaenians, lizards and snakes.
In order to obtain a size measure that is comparable across all taxa, we converted all lengths to masses using 65 clade-specific allometric equations (Appendix S2a) – developing equations for the smallest clades for which we had sufficient mass data. These equations are based on specimens of known mass and length. They allow us to infer masses for species for which no mass data are available from mass–length relationship of close relatives. The different equations (27 for snakes, 36 for lizards, 2 for amphisbaenians; Appendix S2a) enable us to infer masses while accounting for differences in shape of species of different phylogenetic affinities, and, in lizards, varying degrees of leg development (Meiri, 2010; Pincheira-Donoso et al., 2011; Feldman & Meiri, 2013; Meiri et al., 2013; Novosolov et al., 2013; Scharf et al., 2015; and new equations developed here: Appendix S2b). The use of clade-specific equations is imperative as for a given length squamates can easily span two orders of magnitude in mass, and even snakes of the same length often differ in mass by a factor of 15 or more (Appendix S2c). We only used actual weight for the tuatara, Sphenodon punctatus.
Mass-dependent diversification
Non-random diversification processes, such as higher or lower speciation or extinction rates at different masses, could produce unimodal size–frequency distributions (Stanley, 1973). Such a process would affect the distribution of masses in extant taxa, as well as the shape of the tree (Maddison, 2006; Paradis, 2008). To test this, we used mass data of the squamate species represented in a recent large-scale chronogram (Pyron & Burbrink, 2014), resulting in a phylogeny spanning 4134 species (2828 lizards, 1255 snakes and 51 amphisbaenians).
We use the ‘QuaSSE’ (Quantitative State Speciation and Extinction) algorithm (implemented in the R package ‘diversitree’; FitzJohn, 2012) to test for a relationship between diversification rates (speciation, λ; extinction, μ; net diversification, r = λ − μ) and size (FitzJohn, 2010). We examined normal (humped) and sigmoidal (increasing or decreasing) responses of both rates to body mass. These are contrasted against a null model where diversification rates are not affected by body mass (mass-independent model). We then compared these models using the corrected Akaike information criterion (AICc) scores using Akaike weights (AICcw) calculated using the R package ‘qpcR’. The model receiving the highest AICcw score was considered the best. The QuaSSE analysis was performed for Squamata as a whole and separately for the three suborders (amphisbaenians, lizards and snakes), to account for rate heterogeneity across clades.
The QuaSSE algorithm accounts for missing species using a sampling proportion (FitzJohn et al., 2009), which we defined as 4134/9804 for squamates (the total number of squamate species in the tree divided by the total number in the entire dataset), and 2828/6086, 1255/3529 and 51/189 for lizards, snakes and amphisbaenians, respectively. We note that this only accounts for the existence of the missing extant lineages, not their known trait values, but the branches in our phylogeny cover essentially the entire range of extant squamate masses (i.e. the dwarf Sphaerodactylus geckos to the green Anaconda Eunectes murinus, 0.1 g to 345 kg; Table 1), so no major variation is unaccounted for by our present phylogenetic sampling.
| Taxon | Size | Species | Maximum length (mm) | Calculated mass (g) |
|---|---|---|---|---|
| Amphisbaenians | Smallest | Amphisbaena talisiae | 105 | 0.28 |
| Cynisca degrysi | 107 | 0.31 | ||
| Amphisbaena tragorrhectes | 110 | 0.34 | ||
| Largest | Monopeltis schoutedeni | 660 | 448 | |
| Dalophia gigantea | 705 | 583 | ||
| Amphisbaena alba | 810 | 1017 | ||
| Lizards | Smallest | Sphaerodactylus elasmorhynchus | 17 | 0.12 |
| Sphaerodactylus ariasae | 17.9 | 0.14 | ||
| Sphaerodactylus parthenopion | 18 | 0.14 | ||
| Largest | Varanus niloticus | 980 | 23,700 | |
| Varanus salvator | 1170 | 42,100 | ||
| Varanus komodoensis | 1540 | 102,500 | ||
| Snakes | Smallest | Indotyphlops veddae | 91 | 0.17 |
| Amerotyphlops yonenagae | 101 | 0.25 | ||
| Indotyphlops malcolmi | 107 | 0.30 | ||
| Largest | Python bivittatus | 9200 | 197,700 | |
| Malayopython reticulatus | 10,000 | 246,600 | ||
| Eunectes murinus | 10,000 | 345,100 | ||
| Rhynchocephalia | Only species | Sphenodon punctatus | 285 | 1020 |
- Masses are calculated from the length data using equations in Appendix S2 and a back transformation from logarithms. Lizard and amphisbaenian lengths are snout–vent lengths, snake lengths are total lengths. Masses > 10 kg are rounded to the nearest 100 g.
Running QuaSSE requires an estimate of a standard deviation (SD) for the continuous trait (here, body size) within species. To estimate this, we obtained the body mass of 7693 individuals belonging to 102 species (in 17 squamate families) from the database of the Steinhardt Museum of Natural History, and field measurements of one of us (S.M.). For each species (minimum 10 individuals per species) we calculated the log(mass) and the SD over all individuals. We then found the median SD value over the 102 species (0.19; Appendix S3).
Rabosky & Goldberg (2015) have recently shown that speciation and extinction models tend to be too liberal in rejecting the null model (specifically, this was shown on a model where traits are assumed to be categorized into binary states) when applied to empirically derived phylogenies. We thus used a parametric bootstrap approach and simulated 100 or more sets (see below) of random trait values along the tree (using the sim.character function in the ‘diversitree’ R package; FitzJohn, 2012) with the diffusion parameter estimated by the null model (see below) and ancestral value at the root estimated from maximum-likelihood ancestral reconstruction (using fastAnc method in the ‘phytools’ R package; Revell, 2012). These simulations assumed no direct effect of the character on speciation or extinction.
Similar to the analysis of the true data, the simulated state data were then subjected to the same QuaSSE procedures. In each clade we compared the best-fitted model and obtained the log-likelihood difference (ΔLL) between the two models. We used the distribution of simulated ΔLL values to calculate a P-value as the proportion of simulated values that are as extreme as the ΔLL observed for the real data in each group. A P-value of less than 0.05 can be interpreted as significant support for the hypothesis that mass affects net diversification in the examined group (Rabosky & Goldberg, 2015). In cases of marginally significant P-values (0.1 > P > 0.025) we ran another 100 stimulations, to have a more robust estimate of the actual probabilities (see Results).
As an alternative to the model-based QuaSSE analysis we used the MacroCAIC method (Agapow & Isaac, 2002), implemented in the R package ‘caper’ (Orme et al., 2014), to test for a correlation between mass and species richness under the phylogenetically independent contrast paradigm (Felsenstein, 1985). The method produces contrasts across a clade, including only contrasts with a minimal number of species (MNS), and regressions (quadratic and linear) are then fitted to these contrasts (e.g. using MNS = 20, the mean size and richness value of all contrasts in the clade that have at least 20 species are calculated). However, this method was criticized for having low power when extinction is correlated with the trait in question (Freckleton et al., 2008), and as it gives similar quantitative results to the QuaSSE analyses we only report them in Appendix S4.
Results
Dataset and body mass distribution
We obtained maximum body size data for 9805 of 9837 extant (and recently extinct) species of lepidosaurs (99.7%; Appendix S1). Of the remaining 32 species, 25 are known only from juveniles, Typhlops cariei is known from fossils and its length has never been estimated and Amphisbaena acrobeles is known only from the anterior part of the unique type specimen (Ribeiro et al., 2009). We lack size measures for five other species (Chalcides pentadactylus, Cyrtopodion mansarulus, Leiolopisma fasciolare, Dipsas petersi and Varanus samarensis). Most of these 32 species are known only from the types. Some of them may not be valid (e.g. Oligodon wagneri, L. fasciolare, Chalcides pentadactylus).
The mean SVL of lizard species in our dataset is 91.4 mm and that of amphisbaenid species is 265.6 mm (n = 6086 and 189, respectively). The mean SVL of the 250 snake species for which we used SVL as a size measure is 689.2 mm and the mean total length of the 3279 snake species for which we have used TL is 809.2 mm. As snake tails are usually much shorter than their body length, snake SVLs are still likely to be, on average, much longer than those of lizards.
Lepidosaur masses span six orders of magnitude, from the smallest lizard (Sphaerodactylus elasmorhynchus, 0.12 g) to the largest snake (the green Anaconda, Eunectes murinus, 345 kg; Appendix S1, but see below). While the three smallest lepidosaurs are Caribbean Sphaerodactylus geckos, and the largest five are constrictor snakes (Table 1, Appendix S1), both lizards and snakes span a similar six orders of magnitude variation in size, ranging from well under 1 g to over 100 kg. Amphisbaenians can be as small as the smallest snakes and lizards, but only grow to about 1 kg – roughly the size of the largest Sphenodon individuals (Table 1). We note that some of the maximum lengths (and hence calculated masses) reported in the literature for the largest snake species (pythons and anacondas) are probably unrealistically high. Even though 10-m long snakes are regularly reported in reputable herpetological literature (e.g. Perez-Santos & Moreno, 1991; Whitaker & Captain, 2007), we seriously doubt whether extant snakes grow that long, as such reports rarely stand up to scientific scrutiny (e.g. Barker et al., 2012).
Extreme sizes, in any case, are rare. The mean body size of extant Lepidosauria species (back-transformation of the average log value) is 18.7 g and the median size is 14.8 g. The lepidosaurian body size–frequency distribution is unimodal and right skewed (after logarithmic transformation; Fig. 1), with a distinct node at 1–1.2 (10–16 g).
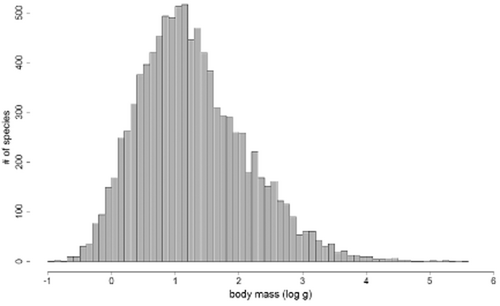
Frequency distribution of calculated maximum body mass of lepidosaur species (log10 of masses calculated from logarithms of maximum lengths). Underlying data are provided in Appendix S1.
The squamate suborders (amphisbaenians, lizards and snakes) differ in all size attributes (Fig. 2, Table 2). Mean, modal and median sizes of lizards and amphisbaenians are similar. Amphisbaenians have the smallest size range, but the highest coefficient of variation and the most platykurtic (i.e. the flattest), bimodal body size–frequency distribution, and their size distribution is bimodal and not skewed. Lizards have the most skewed and leptokurtic size distribution. Snakes are, on average, seven times as heavy as lizards and amphisbaenians, and the modal snake is ten times heavier than the modal lizard. The snake size–frequency distribution is weakly, but significantly, right skewed, and the mass coefficient of variation for snakes is much lower than that of amphisbaenians and lizards (Table 2). The species-rich clades (lizards and snakes) and all Lepidosauria are thus characterized by unimodal, leptokurtic and right-skewed body mass–frequency distributions (although the snake distribution is relatively flat over a size range of roughly 20 to 300 g; Appendix S5).
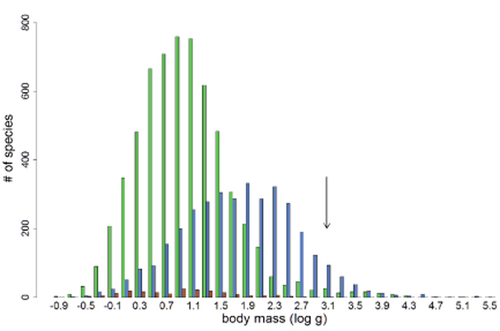
Frequency distribution of calculated maximum body mass of lepidosaur species as in Fig. 1, but divided into the three extant lepidosaur sub-orders: Sauria (lizards, green/grey*), Serpentes (snakes, blue/white*) and Amphisbaenia (‘worm-lizards’, red/black*); the size of the sole rhynchocephalian, Sphenodon punctatus, is marked with an arrow. (*Colour is in the online edition and greyscale in the printed edition.)
| Lepidosauria | Amphisbaenia (worm lizards) | Sauria (lizards) | Serpentes (snakes) | |
|---|---|---|---|---|
| No. of species | 9805 | 189 | 6086 | 3529 |
| Mean | 18.7 | 8.5 | 9.6 | 61.7 |
| Median | 14.8 | 8.7 | 8.5 | 63.9 |
| Mode | 14.1 | 7.5 | 7.9 | 79 |
| SD | 7.1 | 5.5 | 5.0 | 7.0 |
| CV | 38% | 65% | 52% | 11% |
| Skew | 0.64 ± 0.02 | 0.34 ± 0.18 | 0.94 ± 0.03 | 0.14 ± 0.04 |
| Kurtosis | 0.52 ± 0.05 | -0.30±0.36 | 2.29 ± 0.06 | 0.26 ± 0.08 |
- All mass values are in grams. Mean, median mode, sd values are back transformed from logarithms and CV (coefficient of variation) is calculated from the back-transformed figures. The mode is based on 0.2 log bins (Fig. 2). The values of skewness, kurtosis and their SDs are based on the log-transformed data.
Body size and diversification rates
The QuaSSE analyses resulted in different best-fitted models across the four examined clades ( Table 3). Across the whole squamate clade, the best-fit model (highest AICcw) had speciation and diversification rates as sigmoid functions of body mass (Fig. 3). A humped speciation (and diversification) model was chosen for snakes, with a maximum slightly above the modal size (Fig. 3, Table 3). A humped speciation (and diversification) model was the best-fitted model in lizards as well, but, unlike snakes, this was non-significant. The null model was chosen in amphisbaenians (Fig. 3, Table 3). Importantly, running 100 simulations, only the snake model was marginally significant (P = 0.05). Thus, for snakes only, we added 100 stimulations (see above). This continued to result in a marginally significant result as assessed using the parametric bootstrapping approach (P-value = 0.045; Table 3, Fig. 4). Neither the squamate nor the lizard model was significant when compared with the results of the simulations, suggesting that no strong effect of mass on diversification rates is apparent in any clade, except possibly snakes. The results of the MacroCAIC models are reported in Appendix S4, and generally show little association between size and diversification rates across clades.
| Squamates | Lizards | Snakes | Amphisbaenians | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | d.f. | AICc | AICcw | AICc | AICcw | AICc | AICcw | AICc | AICcw |
| Constant | 3 | 31,474.2 | 0 | 21,661.1 | 0 | 9062.8 | 0 | 426.4* | 0.45 |
| Sigmoid λ | 6 | 31,381.7* | 0.95 | 21,666.4 | 0 | 8955.8 | 0 | 427.3 | 0.29 |
| Hump λ | 6 | 31,476.7 | 0 | 21,622.8* | 0.97 | 8895.5* | 1 | 429.1 | 0.12 |
| Sigmoid μ | 6 | 31,475.6 | 0 | 21,666.9 | 0 | 9020.2 | 0 | 433.8 | 0.01 |
| Hump μ | 6 | 31,481.1 | 0 | 21,660.0 | 0 | 8958.7 | 0 | 428.9 | 0.13 |
| Sigmoid λ/hump μ | 9 | 31,387.5 | 0.05 | 21,650.7 | 0 | 8936.8 | 0 | 437.1 | 0 |
| Sigmoid λ/sigmoid μ | 9 | 31,393.4 | 0 | 21,630.0 | 0.03 | 8955.6 | 0 | 434.8 | 0.01 |
- P values (generated using simulations: the proportion of simulated values that are as extreme as the log-likelihood difference (ΔLL) observed for the real data, see Methods) are 0.24 for squamates, 0.32 for lizards and 0.045 for snakes (100 simulations for squamates and lizards, 200 for snakes, none for Amphisbaenia where the null is the preferred model). Asterisks mark the best model for each taxon.
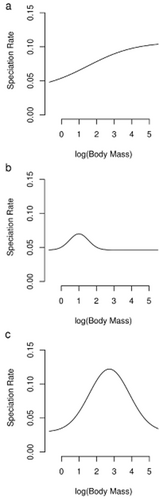
Illustration of the best QuaSSE models for speciation, extinction and net diversification rates in response to log(body mass), estimated using the best-fitted model (Table 3) in Squamata (a), Sauria (lizards, b) and Serpentes (snakes, c). The best model for Amphisbaenia was the null. Note that the best models included no extinction terms and hence speciation equals diversification.
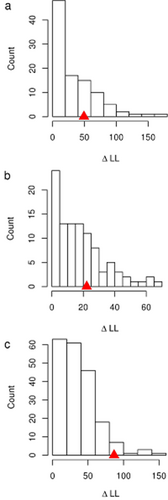
QuaSSE simulation results for Squamata (a), Sauria (lizards, b) and Serpentes (snakes, c). The log-likelihood difference (ΔLL) between the best-fitted model and the null model is shown for 100 simulations and assumed no direct effect of the character on speciation or extinction. In snakes, the results were marginally significant and thus we ran another 100 stimulations to get a more robust estimate of the actual P-value. The ΔLL of the true data for the best-fitted model is shown by a red/grey triangle. We used the distribution of simulated ΔLL values to calculate a P-value as the proportion of simulated values that are as extreme as the ΔLL observed for the real data in each group (0.24, 0.32 and 0.045, for squamates, lizards and snakes, respectively). In amphisbaenians the best model is the null model and thus no simulations are needed.
Discussion
We obtained mass estimates for nearly all extant lepidosaur species – by far the most complete dataset of body sizes for the major vertebrate classes. Despite great variation in shape and a discrepancy between the size distributions of the two major lepidosaur taxa (lizards and snakes), the overall body size–frequency distribution of virtually all extant (and recently extinct) species is unimodal and right skewed (Fig. 1). The bimodal distribution of amphisbaenian taxa shows that the classical distribution is only ubiquitous at very large scales. Lepidosaurs are relatively small terrestrial vertebrates: their mean and median sizes (18.7 and 14.8 g, respectively; Table 2) are much smaller than those of birds (33 and 47 g, n = 7551) and mammals (261 and 112 g, respectively, n = 4213; Meiri et al., 2011). Snakes are, on average, six to seven times heavier than lizards (mean and median c. 62–64 g versus c. 10 and 8.5 g; Table 2), a smaller difference than some earlier assessments have suggested (Boback & Guyer, 2003). This is perhaps because easily obtained size data in partial datasets are biased towards large snakes.
We note, however, that current size limits are not necessarily representative of the entire range of size variation in lepidosaur history. While we know of no fossils of lepidosaurs that are smaller than the smallest extant lizards or snakes, larger forms certainly existed. Snakes, such as the Palaeocene Titanoboa and Eocene Gigantophis, and the end Pleistocene lizard Megalania prisca (Head & Polly, 2004; Molnar, 2004; Head et al., 2009) would dwarf today's largest forms. We estimate the maximum weight of M. prisca [based on a maximum SVL of 3.8 m from Molnar (2004) and our allometric equation for size/SVL relationship in Varanus] as 1900 kg (compared with an estimated 102 kg for the Komodo dragon Varanus komodoensis). This is similar to the maximum masses of extant crocodiles of similar size (Britton et al., 2014), suggesting that the estimates are not out of proportion. Our estimate for the maximum weight of Titanoboa [based on a 13 m estimate for total length (Head et al., 2009) and our equation for Boidae] is 730 kg (compared with an estimate of 345 kg for the green anaconda Eunectes murinus). Head et al. (2009) estimated that Titanoboa was even heavier at 1135 kg. Thus historical size variation of lepidosaurs was up to an order of magnitude larger than it is today.
Yet even much larger, crown-group, lepidosaurs (indeed, squamates) existed: the Cretaceous mosasaurs, a group of highly derived marine squamates attained lengths of up to 17 m (see Fig. 6 in Polcyn et al., 2014). While the masses of mosasaurs are unknown, such lengths are only attained today by some of the largest whales (e.g. humpback and sperm whales, both of which can weigh well over 10 tons; Jones et al., 2009). Not only does the modern-day size range and frequency distribution give no indication for such sizes, but methods that derive diversification rate–size relationships, and methods relying on ancestral-state reconstruction, are unable to retrieve them. The extent to which this is likely to bias the results of studies such as ours is unknown, but could be fascinating to simulate. Overall, this suggests that, if fossils are included, mass variation in squamates is among the largest of all animal taxa.
Using the QuaSSE algorithm, increases in speciation and decreases in extinction result in a spike in net diversification rates near the mode for lizards (Fig. 3), in agreement with several previous models for the modality of body size (e.g. Stanley, 1973). In snakes, and in squamates overall, however, diversification is apparently highest for masses well above the mode. Nonetheless, high-mass taxa have not accumulated significant diversity in extant faunas. The high Type I error rates of the QuaSSE method seriously undermine our ability to draw definite conclusions regarding the interplay between body mass and net diversification rates. Our simulations suggest low power for differentiating between these models, and that such inferences could equally be obtained for a trait that does not affect diversification, except, perhaps, for snakes. The results of the MacroCAIC analyses (Appendix S4) also do not suggest any strong size-related diversification patterns, either linear or quadratic.
Given that we did not detect strong patterns suggesting faster diversification at modal sizes, the existence of more intermediate-sized taxa may reflect greater time for speciation for modal-sized lineages, with the largest species (experiencing the highest rates of speciation) arising only recently. The presence of very large, yet ancient, fossil species (e.g. mosasaurs, Titanoboa), however, argues against this latter possibility. Turnover may be highest for species with the smallest masses. This suggests that speciation and extinction dynamics are highest in those size classes, as expected under classical models.
We note that there are several important limitations to our diversification analyses. They assume that rates exhibit a constant response to mass across time and across lineages. The phylogeny is not fully sampled, and the algorithm cannot incorporate trait values for unsampled taxa. The power to estimate extinction rates may be particularly low. Furthermore, we did not account for uncertainties in the phylogeny or estimated parameters, such as using Markov chain Monte Carlo sampling. Coupled with the high Type I errors of the QuaSSE method (Rabosky & Goldberg, 2015; and our simulation results), we were only able to detect biologically meaningful associations between body size and diversification rates in snakes.
Incorporating fossil lineages into such analyses can be especially illuminating, revealing previously hidden patterns of evolutionary history (e.g. Betancur-R et al., 2015). It will enable us to determine whether changes in mass are related to the colonization of new areas, or facilitate the invasion of new adaptive zones (e.g. the marine environment in mosasaurs, or possibly the subterranean environment for small scolecophidian snakes). It will also enable us to detect possible changes in overall rates of extinction and diversification along the clade history (Raup et al., 1972; Gould et al., 1977, 1987) and include entire clades that are now extinct.
Acknowledgements
This research was funded, in part, by a Binational Science Foundation grant no. 2012143 to S.M. and in part by U.S. NSF grants DBI-0905765 and DEB-1441719 to R.A.P. Anat Feldman is supported by an Israel Science Foundation grant no. 1005/12 to S.M. We thank Dave Orme for valuable discussion and Tom Dowe and Miguel Olalla-Tárraga for help with amphisbaenian measurements. We thank museum collection managers for measuring some neglected species for us – or allowing us to measure them. We are indebted to many museum collection managers and herpetologists, especially to Aaron Bauer and Peter Uetz, and other members of the GARD initiative for huge help with taxonomic issues and in obtaining obscure papers and data. Yuval Itescu, Gavin Thomas and four anonymous referees provided very helpful comments on earlier versions of this manuscript.
References
Anat Feldman is a post-doctoral research fellow interested in the biogeography and macroecology of snakes.




