What can and can't we say about indirect land-use change in Brazil using an integrated economic – land-use change model?
Abstract
It is commonly recognized that large uncertainties exist in modelled biofuel-induced indirect land-use change, but until now, spatially explicit quantification of such uncertainties by means of error propagation modelling has never been performed. In this study, we demonstrate a general methodology to stochastically calculate direct and indirect land-use change (dLUC and iLUC) caused by an increasing demand for biofuels, with an integrated economic – land-use change model. We use the global Computable General Equilibrium model MAGNET, connected to the spatially explicit land-use change model PLUC. We quantify important uncertainties in the modelling chain. Next, dLUC and iLUC projections for Brazil up to 2030 at different spatial scales and the uncertainty herein are assessed. Our results show that cell-based (5 × 5 km2) probabilities of dLUC range from 0 to 0.77, and of iLUC from 0 to 0.43, indicating that it is difficult to project exactly where dLUC and iLUC will occur, with more difficulties for iLUC than for dLUC. At country level, dLUC area can be projected with high certainty, having a coefficient of variation (cv) of only 0.02, while iLUC area is still uncertain, having a cv of 0.72. The latter means that, considering the 95% confidence interval, the iLUC area in Brazil might be 2.4 times as high or as low as the projected mean. Because this confidence interval is so wide that it is likely to straddle any legislation threshold, our opinion is that threshold evaluation for iLUC indicators should not be implemented in legislation. For future studies, we emphasize the need for provision of quantitative uncertainty estimates together with the calculated LUC indicators, to allow users to evaluate the reliability of these indicators and the effects of their uncertainty on the impacts of land-use change, such as greenhouse gas emissions.
Introduction
Governments throughout the world have set mandatory biofuel targets for the transport sector, aiming at mitigating climate change, improving energy security, and stimulating rural development (Sorda et al., 2010). Currently, one of the central problems in the biofuel arena is the premise of biofuel-induced land-use change (IPCC, 2011; Creutzig et al., 2012; Finkbeiner, 2014; Warner et al., 2014). These land-use changes can have negative impacts such as carbon stock loss, rising food prices, loss of biodiversity, and water scarcity, reducing the eligibility of the feedstock as a sustainable source for biofuels. An increased demand for biofuel feedstocks can lead to direct land-use change (dLUC): land use is changed from some previous use to the biofuel feedstock. This, in turn, can lead to indirect land-use change (iLUC): a change of land use outside the biofuel feedstock cultivation area, induced by a change in use or production quantity of that biofuel feedstock. This can happen either when the agricultural land-use type converted to the biofuel feedstock is displaced to elsewhere, in order to continue to meet the demand for its agricultural products, or when the direct conversion triggers a change in the price of agricultural products, causing land to be taken into (or out of) production elsewhere (Wicke et al., 2012). The question to be tackled is to what extent the global increase in demand for biofuels (Broch et al., 2013) leads to dLUC and iLUC and how the negative effects can be minimized.
Direct land-use changes are unambiguously visible in both historical data and spatial land-use change model results. DLUC takes place wherever a bioenergy crop field appears and consequently displaces the previous land use. On the contrary, iLUC cannot be directly observed (Finkbeiner, 2014), because if, for example, pasture displaces forest in the presence of an expansion of bioenergy cropland over pasture, this does not necessarily mean that the pasture displacement is caused by the expansion of bioenergy cropland. The pasture might have caused deforestation for a reason unrelated to bioenergy. In other words, the indirect effects of a particular demand increase cannot be identified from historical data because the effects are intertwined with a wide range of processes from which the effects are also present in these data (O'Hare et al., 2011; Overmars et al., 2011). Separate identification is only possible by comparing all land-use changes with and without the demand increase for bioenergy, which can be performed using a simulation model (Creutzig et al., 2014).
The processes governing dLUC and iLUC range from global to local scale. For example, the impact of the biofuel targets on demands for feedstocks in different parts of the world is a global market issue. On the other hand, at which location the land-use changes and which previous land use is replaced is primarily steered by local factors, such as accessibility and biophysical conditions (Meyfroidt et al., 2013). Likewise, the impacts of the land-use change are highly location-dependent (e.g. van der Hilst et al., 2014). Therefore, a sound approach to model iLUC is by using a global economic model coupled to a spatially explicit land-use change (LUC) model to take both the global- and local-scale level into account, as, for example, demonstrated by Lapola et al. (2010).
It is commonly recognized that there is a large uncertainty in modelled iLUC (Mathews & Tan, 2009; Wicke et al., 2012; Malins, 2013; Creutzig et al., 2014; Finkbeiner, 2014). The uncertainties arise from model structure uncertainty (Refsgaard et al., 2006; Verstegen et al., 2015), from data (inputs, calibration data set and initial system state) (Dendoncker et al., 2008), and from model coupling (Ray et al., 2012). For iLUC in particular, uncertainty in reported values also stems from the fact that the assumptions, the employed models, and the validity of these models are often not clearly communicated (Mathews & Tan, 2009). Information quantifying uncertainty in iLUC is critical to evaluate whether or not iLUC indicators are reliable enough to be included in legislation, to identify which parts of the modelling chain have the highest priority for improvement, that is cause most uncertainty, and to assess how this uncertainty propagates to the impacts of iLUC, such as greenhouse gas (GHG) emissions (e.g. Plevin et al., 2015). Uncertainty information can be obtained by (1) being explicit about the applied models, the processes included in these models, and the parameter settings used, as well as the uncertainty in the various model components and the performance of these models (Mathews & Tan, 2009; Broch et al., 2013), and (2) assessment of the magnitude of the output uncertainty by, for example, doing Monte Carlo analyses of iLUC (Wicke et al., 2012, 2015; Nelson et al., 2014; Warner et al., 2014; Plevin et al., 2015). Uncertainty should be assessed at different spatial scales because different types of impacts play a role at different scales and it is known that uncertainty is highly scale-dependent (e.g. Pontius Jr. and Spencer; Verstegen et al., 2012). Yet, such information is currently scarcely reported for iLUC; a status we aim to improve with this study.
We have set up a model study with the global Computable General Equilibrium (CGE) model MAGNET (e.g. Kavallari et al., 2014; Woltjer & Kuiper, 2014), integrated with the spatially explicit land-use change model PLUC (e.g. Verstegen et al., 2012). With this integrated model, we project land-use change caused by an increasing demand for biofuels up to 2030 for Brazil, one of the main bioethanol producers in the world. As Brazil holds the world's major potential for agricultural expansion (Alexandratos & Bruinsma, 2012), production and export of bioethanol are likely to increase in the future (IEA, 2013; OECD/Food and Agriculture Organization, 2014, Walter et al., 2014). Yet, the country also maintains the largest area of natural remnants, with high carbon stocks and high levels of biodiversity, stressing the need to assess potential negative impacts. For this case study, we seek to answer the following research questions: (1) What are the dLUC and iLUC projections for Brazil up to 2030 at different spatial scales and what is the uncertainty herein? (2) What are the sources of uncertainty for each step in the model chain and how do these uncertainties influence dLUC and iLUC projections? (3) What is the contribution of the economic and land-use change model to the uncertainty in dLUC and iLUC at the different spatial scales?
The next section introduces the Brazilian case study, presents the LUC model, the CGE model, and the way they are coupled, describes the calibration method, defines the projection scenario for the increased demand for biofuels, and explains how iLUC is derived from the results. Section three illustrates the results for the three research questions. The final section discusses these results in the light of the research questions and gives suggestions for further research.
Materials and methods
Overview
The projection of dLUC and iLUC in Brazil caused by an increasing demand for biofuels and the uncertainty herein is performed using MAGNET (Woltjer & Kuiper, 2014), a global Computable General Equilibrium (CGE) model, connected to the land-use change model PLUC (e.g. Verstegen et al., 2012), tailored to Brazil (Fig. 1). For 2006, an initial land-use map is created by combining tabular area data per land-use type and land-use maps with satellite data. This map is used as the initial system state for PLUC. Next, PLUC is calibrated from 2007 until 2012 based on trends per land-use type from agricultural statistics databases. To project the dLUC and iLUC effects of the biofuel mandates, we define both a ‘biofuel scenario’ that includes these mandates and a ‘reference scenario’ that does not include them. For both scenarios, MAGNET determines the supply and demand of all commodities in all world regions up to 2030 and, related to that, the areas they occupy. This 2013–2030 time series of land area demands per land-use type for Brazil is then input for the spatially explicit land-use change projection up to 2030 by PLUC. The PLUC outputs are a time series of land-use maps. By comparison of the maps of the two scenarios, dLUC and iLUC are assessed.
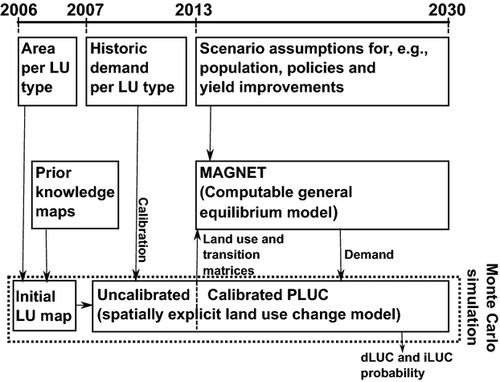
In the model chain, uncertainties in the inputs, calibration data set, initial system state, and model structure are quantified, part of which propagates through the model coupling (Fig. 1). To quantify uncertainty in MAGNET, it is run with two different parameter sets, resulting in an upper and a lower demand limit. PLUC, including the generation of the initial land-use map, the calibration, and the demand coming from MAGNET, is used stochastically by running it in Monte Carlo mode (Fig. 1).
Case study
Brazil has been producing bioethanol from sugar cane since the beginning of the 20th century and has been exporting the ethanol since 1989 (Andrade de Sá et al., 2013). Sugar cane currently occupies the third largest area of all crops in Brazil, topped only by soya and maize (although a large quantity of the maize is cultivated as second crop) (IBGE, 2013b). The main sugar cane production areas are the Central South region and the north-east region. Recent expansion has mainly taken place in the Central South region: in the past decade, the total area dedicated to sugar cane cultivation has more than doubled in that region (Rudorff et al., 2010). It expected that future expansion will also predominantly occur in the Central South region (Nassar et al., 2008; Lapola et al., 2010). According to Adami et al. (2012), over 99% of all sugar cane expansion in the last decade has taken place over existing agricultural land, signifying that the direct effect of increasing ethanol demand on deforestation is negligible. However, deforestation can still take place through iLUC, which is also shown by others (Lapola et al., 2010; e.g., de Souza Ferreira Filho & Horridge, 2014).
Initial land-use map and land-use change model
We distinguish 11 different land-use types n, where n = 1, 2, …, 11: urban, water, natural forest, rangeland, planted forest, crops (excluding sugar cane), grass and shrubs, sugar cane, planted pasture, bare soil, and abandoned agricultural land. Planted pasture and natural pasture (rangeland) are modelled separately because the extensively managed, naturally vegetated rangelands have a stocking rate of about 70% lower than the intensively managed planted pastures (IBGE, 2006, Aguiar & d'Athayde, 2014). Cropland includes both annual and permanent crops. Sugar cane is modelled as a separate land-use type to be able to evaluate where sugar cane expands in reaction to the increased ethanol demand and which other land uses it replaces.
PLUC (PCRaster Land Use Change model) (van der Hilst et al., 2012, 2014; Verstegen et al., 2012; Diogo et al., 2014) is founded on the separation between the quantity of change per land-use type and the spatial allocation of this change, like many other land-use change models (Pontius Jr. and Neeti, 2010). The quantity of land demanded per land-use type n is called ‘demand’ dn,t, in which t is the time step in years, with t = 1, 2, …, T. The total area per land-use type in the demand time series (tabular area data from agricultural statistics) for the initial year of the simulation should match the total area per land-use type in the initial land-use map, that is the initial system state of the model. If the time series and initial map are coming from different sources, which is likely, a perfect match is obviously never going to be the case. You & Wood (2005) provide a deterministic method to create a land-use map that matches the time series, by spatially disaggregating land-use areas per administrative region from the time series into raster cells within that region, using prior knowledge maps. We apply this procedure, using municipalities as administrative regions (5566 in total for Brazil), to create an initial land-use map for Brazil with a cell size of 5 × 5 km2 for the year 2006. This year is chosen because it was the year in the recent past (to have a calibration period) with the best data availability for both the tabular and prior knowledge map data. Compared to You & Wood (2005), we do a few things differently, most importantly adding a method to make a stochastic map instead of a deterministic map, in order to include uncertainty arising from errors in the initial land-use map into the model chain, as explained in Methods S1.
Of the eleven land-use types considered in PLUC, five are assumed to respond to changes in the economy by expanding or contracting: rangeland, planted forest, crops, sugar cane, and planted pasture. These active land-use types are demand-driven (Table 1). The other six land-use types do not have demands. They are either passive, meaning that they can contract or expand due to the dynamics of the active land-use types, or static, meaning that they cannot change and are thus fixed on the map. Passive land-use types are natural forest, grass and shrubs, bare soil, and abandoned agricultural land. Abandoned land originates when an active land-use type contracts; it is not present in the initial land-use map. Static land-use types are urban and water.
| n | Land-use type | k | Process represented | Suitability factor |
|---|---|---|---|---|
| 4 | Rangeland | 1 | Economies of scale | n in the neighbourhood |
| 2 | Transportation costs | Distance to roads | ||
| 3 | Potential profits per hectare | Potential yield of n | ||
| 5 | Planted forest | 1 | Economies of scale | n in the neighbourhood |
| 2 | Transportation costs | Distance to roads | ||
| 3 | Potential profits per hectare | Potential yield of n | ||
| 6 | Crops | 1 | Economies of scale | n in the neighbourhood |
| 2 | Transportation costs | Travel time to hubs for n | ||
| 3 | Potential profits per hectare | Potential yield of n | ||
| 4 | Costs to make the land cultivatable | Conversion elasticity | ||
| 5 | Double-cropping potential | Growing season length | ||
| 8 | Sugar cane | 1 | Economies of scale | n in the neighbourhood |
| 2 | Transportation costs | Travel time to hubs for n | ||
| 3 | Potential profits per hectare | Potential yield of n | ||
| 4 | Costs to make the land cultivatable | Conversion elasticity | ||
| 9 | Planted pasture | 1 | Economies of scale | n in the neighbourhood |
| 2 | Transportation costs | Distance to hubs for n | ||
| 3 | Potential profits per hectare | Potential yield of n |
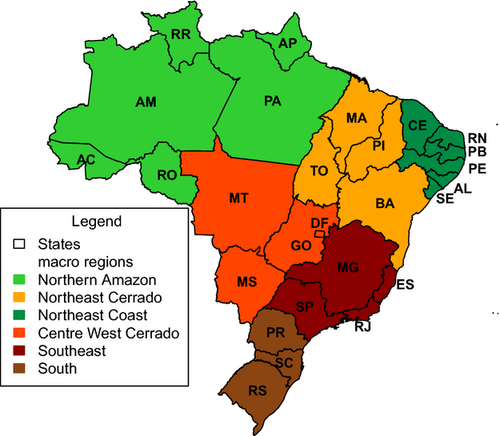
The demands for the five dynamic land-use types over time in Brazil have been subdivided into six regions (Fig. 2), corresponding to the macroregions defined by the Brazilian Institute of Geography and Statistics (IBGE). We added one region by splitting the north-eastern macroregion into two regions, as suggested by Nassar et al. (2010), because the north-east coast differs significantly from the north-east Cerrado (savannah) in terms of agricultural production.
In PLUC, the spatial allocation is regulated by spatial attributes that serve as proxies for important drivers of location, that is processes that determine where a land-use type expands or contracts. These are called suitability factors k, with k = 1, 2, …, Kn (each active land-use type n can have a different number of suitability factors). For each n defined as active, a weighted sum of these suitability factors forms the total suitability map. In one model time step, representing 1 year, the demands of the active land-use types are allocated sequentially for each macroregion, as follows. For the first active land-use type n, the total suitability map is sorted, and cells are allocated to n, starting with the cell with the highest suitability value that is not yet of type n, until dn,t is fulfilled. Next, the same is performed for the second land-use type in the sequence, with the exception that cells occupied by the first land-use type cannot be changed. This procedure continues until the demands of all active land-use types in all macroregions have been allocated (see also Methods S2).
The suitability factors for the Brazilian case study are given in Table 1. To represent economies of scale (k = 1), the number of neighbours of the same land-use type is counted in a square window of 5 by 5 cells (25 × 25 km2). For transportation costs (k = 2), the travel time to hubs is used as a proxy. This is the time it takes to transport the products originating from the land-use type to the nearest production facility. For planted forest, we have no data about the location of hubs (e.g. saw mills), and for rangelands, we believe that the livestock hubs are of lower importance, because livestock from rangeland is often ‘finished’ elsewhere before being slaughtered. Therefore, for these two land uses, we apply distance to roads as the proxy for transportation costs. Potential profits per hectare (k = 3) are represented by potential yield maps, using IIASA's GAEZ data (Tóth et al., 2012). As, to our knowledge, no potential yield map exists for woody biomass, we use IIASA's map of the length of the growing season as a proxy for the potential yield of planted forest. The costs to make the land cultivatable (k = 4) are estimated using a conversion elasticity, that is a fraction indicating the ease with which a certain land-use type can be transformed into the land-use type that implements the suitability factor, especially relevant for crops. Double-cropping potential (k = 5) is an important suitability factor in Brazil, indicated by the rapid increase in double-cropped area or even triple-cropped area over the last decade (Galford et al., 2008, Conab, 2014). We do not have a map of double-cropping potential, so we use the growing season length as a proxy, which is supported by an analysis of the relation between these two by Arvor et al. (2014).
The no-go map, that is areas where expansion is not allowed, is an overlay of military areas, areas of indigenous people, and federal and state conservation units (Gurgel et al., 2009). Conservation policies or initiatives which have historically not been well enforced, such as the Forest Act (Sparovek et al., 2012), the soy moratorium (Rudorff et al., 2011), and the sugar cane zoning (Padua Junior et al., 2012), are not taken into account in this simulation. We are preparing another study, in which we include more scenarios with, among other things, stricter nature conservation rules (F. van der Hilst, J.A. Verstegen, G. Woltjer, E.M.W. Smeets, A.P.C. Faaij, unpublished results).
We use a Monte Carlo simulation with 5000 realizations. The weights of the suitability factors and the order of allocation are modelled stochastically. Their prior probability distributions are uninformed (see Methods S2).
Calibration
The aim of the calibration phase, 2007 to 2012, is to narrow the probability distributions of all stochastic elements: the order of the land-use types and all weights of the suitability factors (Table 1). The model calibration is performed using a Bayesian data assimilation technique, the sequential importance resampling (SIR) particle filter (van Leeuwen, 2009). In short, the SIR particle filter compares the land-use system simulated by PLUC and observations of the land-use system from the real world, taking into account the uncertainty in these observations. Next, it updates the Monte Carlo ensemble in such a way that well-performing realizations are progressed and poorly performing realizations are discarded. An extensive explanation of this model structure identification and calibration method for a case study in the São Paulo state is provided by Verstegen et al. (2014).
For calibration, a time series of land-use/cover data is required as observational data. For Brazil, we use time series of areal data per land-use type per state (Fig. 2). These time series are derived using information from agricultural statistics databases (IBGE, 2013a,b, ABRAF, 2013, see F. van der Hilst, J.A. Verstegen, G. Woltjer, E.M.W. Smeets, A.P.C. Faaij, unpublished results). These observational data are not error free. Between the yearly (IBGE, 2013b (for crops), IBGE, 2013a (for livestock)), and the 10-yearly (IBGE, 2006) census data sources, areas and area increases differ from zero up to more than 100%. As one cannot calculate a standard deviation based on two values, we make an educated guess of the average error based on these data sources. Under the assumption that the observational errors are uncorrelated over space and time, we assign an observation error to the observed increase in area with a standard deviation of 20% of the observed increase in that time step.
After calibration, a land-use matrix, summarizing the total areas per land-use type in 2012, is computed per macroregion, representing the initial system state for MAGNET (Fig. 1). In addition, a land transition matrix is calculated per macroregion, to be used for the calibration of MAGNET. These six land transition matrices show the average area of conversion from every land-use type to every other land-use type derived from PLUC over the whole calibration period.
As a measure of model performance, we calculate root-mean-squared error (RMSE), the root of the summed squared differences between the median of the modelled area and observed area over all states. We determine the reduction in RMSE (%) for the results of the calibrated model, that is with uncertainty reduced by the SIR particle filter, compared to the non-calibrated model. To evaluate the effect of calibration, we apply a split-sample approach: PLUC is calibrated using data from 2007 to 2009, and the model reduction in RMSE is evaluated from 2010 to 2012. This split-sample approach is used only to evaluate the effect of calibration. The model parameters we use for the projection, integrated with the MAGNET model, are calibrated based on all available observational data (2007–2012).
Economic (CGE) model
The growing demand for food, feed, fibre, and bioenergy requires an increased agricultural output. This can be reached by raising inputs such as fertilizers, machinery and labour (bound by technological limitations), that is expansion at the intensive margin, or by converting new land to agriculture, that is expansion at the extensive margin (Hertel, 2011), which can result in iLUC. At what ratio both alternatives are applied in face of a growing demand depends on, for example, land availability, prices, and policies that vary worldwide. To evaluate how demand grows over time and to assess to what extent this demand is fulfilled by expansion at the intensive and extensive margins, we use a global Computable General Equilibrium (CGE) model (Rose, 1995). Key parameters in CGE models are the elasticities, simulating behavioural responses, for example the response of the demand for a commodity to a change in price or the response of consumption to a change in GDP per capita.
The CGE model used is MAGNET (Modular Applied GeNeral Equilibrium Toolbox) (see for an extensive explanation Woltjer & Kuiper, 2014). This is the modularized and improved version of LEITAP (e.g. Banse et al., 2011; Hoefnagels et al., 2013). MAGNET uses the GTAP database version 8 (Narayanan et al., 2012), in an extended and adaptable form. For this case study, we use the database with 42 sectors (including various ethanol sectors that take into account co- and by-products such as molasses and electricity, and a difference between planted pasture and rangeland), 45 commodities and 15 regions, of which Brazil is one. Brazil has been subdivided into six regions, matching the input macroregions for PLUC (Fig. 2). These six macroregions are a subdivision in MAGNET in terms of agricultural production and land area only; for international trade, Brazil is considered as one region. Total land availability per macroregion is calculated from the no-go map.
To model land cover change, a regional land transition approach has been developed that is inspired on the work of de Souza Ferreira Filho & Horridge (2014) and further developed by Woltjer (2013). Herein, the area of land that is changed from one particular land-use type n to another one m depends on the land transition elasticity en,m. Using expert knowledge and trial and error, we test for all combinations of n and m for what values of en,m MAGNET can best reproduce the 2012 system state given by the land-use matrix from PLUC, and the transitions given by the land transition matrix.
 (1)
(1)Equation 1 shows that the demand input of PLUC dn,t in the projection phase has an error model based on a uniform distribution between du,n,t and dl,n,t.
Projection
In the projection from 2013 to 2030, the socio-economic developments are based on the Shared Socioeconomic Pathways (SSPs) (O'Neill et al., 2014). The SSPs quantify global drivers of the energy–economy–land-use system such as demographics and economic development. In these pathways, projections are included on population and GDP growth. We use SSP2, the Middle of the Road pathway with some additional assumptions on, for example, the agricultural intensification over time (see F. van der Hilst, J.A. Verstegen, G. Woltjer, E.M.W. Smeets, A.P.C. Faaij, unpublished results).
Using SSP2 and these assumptions, MAGNET is run up to 2030, providing total land areas occupied by all land-use types for all world regions and the six macroregions in Brazil for the years 2013, 2015, 2020, 2025, and 2030. Yearly demand time series for the six macroregions to serve as an input for PLUC are obtained by a linear interpolation between these years and an aggregation of the areas of all individual crops, except sugar cane, into the single class cropland.
To evaluate the future dLUC and iLUC effects caused by current and planned ethanol mandates worldwide, we define both a ‘biofuel scenario’ including these mandates and a ‘reference scenario’ excluding them. This does not mean that there is no increase in the demand for sugar cane in the reference scenario, only that there is no (additional) increase originating from the increased ethanol demand. All other inputs and parameters of both models are kept the same as in the biofuel scenario.
Direct land-use change (dLUC) and indirect land-use change (iLUC)
Normally, direct land-use change can be assessed using one scenario, as the difference between current and projected land use. In our case, however, we want to assess dLUC from sugar cane caused by the biofuel mandates, that is, only sugar cane expansion for ethanol. Therefore, we want to exclude sugar cane expansion that is a result of an increased demand for sugar over time. Hence, both dLUC and iLUC originating from the mandates are assessed through the difference between the reference and the biofuel scenario (Table 2) in 2030. A grid cell that is sugar cane in the biofuel scenario, and something else in the reference scenario, is considered dLUC, that is sugar cane expansion resulting from the biofuel mandates. A grid cell that is nature in the reference scenario and agricultural land but not sugar cane is considered iLUC. The opposite effects exist as well. A grid cell that is sugar cane in the reference scenario and something else in the biofuel scenario is negative dLUC (neg_dLUC), and a grid cell that is agriculture in the reference scenario and nature or abandoned land in the biofuel scenario is negative iLUC (neg_iLUC).
| Reference scenario | Biofuel scenario | ||
|---|---|---|---|
| Sugar cane | Other agriculture | Nature | |
| Sugar cane | 0 | neg_dLUC | neg_dLUC |
| Other agriculture | dLUC | 0 | neg_iLUC |
| Nature | dLUC | iLUC | 0 |
Especially for iLUC, this opposite effect might appear in the real world. If, for example, an area of 10 000 ha of wheat fields is present, and 80% of this area is taken over by sugar cane for ethanol, then the remaining 20% of wheat land might be abandoned because the advantages of economies of scale have disappeared. The 8000 ha of displaced wheat land and the 2000 ha of wheat land now grown elsewhere make 10 000 ha of iLUC. In our methodology, we count the abandoned land as −2000 ha of iLUC [and therefore, we call it neg_iLUC (Table 2)], coming to a total of 8000 ha iLUC, which was indeed the area of land shifted by sugar cane.
To compare outcomes at different spatial scales, we focus our analysis on local, regional, and national level, calculated from output of PLUC. At the regional level, we use 250 × 250 km2 blocks. We do not use administrative levels, like states, because these differ in size and are thus problematic to compare. The coefficient of variation (cv) (standard deviation of dLUC or iLUC area over all Monte Carlo realizations divided by the mean of dLUC or iLUC area over all Monte Carlo realizations) is used as the measure of uncertainty. As this measure of uncertainty is standardized by the mean, the cv is comparable between dLUC and iLUC and between regions with different magnitudes of dLUC or iLUC. As the local level, we use probabilities of dLUC and iLUC in single cells (5 × 5 km2).
Contribution of the two models to total output uncertainty
We compare the contribution of the two models to the total output uncertainty, by running the projection until 2030 three times, all three with 5000 realizations. One Monte Carlo run is with both models stochastic (the default run used in all analysis described above). One run is with only PLUC stochastic (including the uncertainty in the initial land-use map and calibration time series). In this run the demand dn,t is fixed at the mean between the upper and lower time series, by setting Zd (equation 1) to 0.5 for all Monte Carlo realizations to exclude uncertainty from MAGNET. The uncertainty in the output of this run is thus caused by uncertainty in PLUC only. The final run is with only MAGNET stochastic. In PLUC, the weights, the order of allocation, and the land-use map for 2012 are fixed by taking the medians hereof from the calibrated model, to exclude uncertainty from PLUC. This run results in information about output uncertainty caused by MAGNET. For the three runs, we compare the mean and the coefficient of variation in dLUC and iLUC area at the different spatial scales.
Results
Sources of uncertainty for each step in the model chain and their influence on dLUC and iLUC projections
Initial land-use map
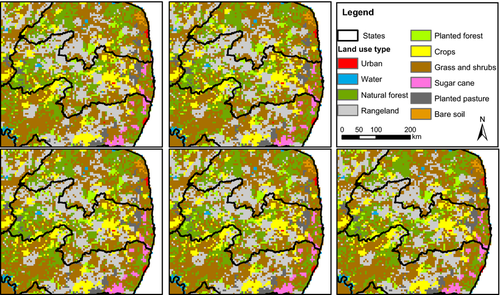
For the initial year, 2006, a land-use map was created for each Monte Carlo realization to serve as the initial system state (Fig. 3). The total area per land-use type per macroregion is the same for all realizations and also the locations of individual patches within the macroregion are the same, but the shape of these patches differs slightly, see, for example, the patch of sugar cane at the bottom of the map view in Fig. 3. The patches of land-use types that were assumed to be known precisely, being urban, water, and bare soil (see Methods S1) always have the same shape, see, for example, the shape of the city Natal, in the north-east of the map. We can conclude that the uncertainty in the initial land-use map is very local, important only at cell level. The effect for projected iLUC will mainly be that when sugar cane expands in a certain grid cell, uncertainty in the initial land-use map makes that in some realizations, it expands over agricultural land, which may result in iLUC through displacement (depending on the demand trend for the displaced agricultural land-use type), and in other realizations over nature, not resulting in iLUC, because there is no displacement effect.
Land-use change model, calibration
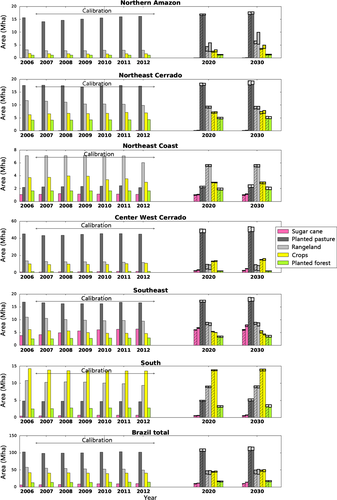
The input demand time series that were constructed from agricultural statistics for calibration are shown in Fig. 4 (2007–2012, indicated by an arrow). After calibration using this demand and the observations, of the 120 possible sequences (see Methods S2) for the order of allocation of the land-use types, 72 obtain a posterior probability of zero, that is they are not present anymore in the ensemble. So, 48 unique sequences remain, with posterior probabilities ranging between 0.002 and 0.19. The land-use sequence with the highest posterior probability is planted pasture–planted forest–sugar cane–rangeland–crops. An analysis of all other sequences and their posterior probabilities reveals that there is a dichotomy in this most common sequence. Planted pasture, planted forest, and sugar cane usually (in about 80% of the realizations) come in the first part of the sequence, and rangeland and crops in the last part, but the order among them fluctuates.
Sugar cane can only displace land-use types coming after it in the sequence. So, in 80% of the realizations, it predominantly replaces crops and rangeland. An important consequence of this calibration result with regard to iLUC is that the iLUC within a macroregion will originate mainly from the displacement of crops and rangeland, which is in line with the findings of Lapola et al. (2010).
The weights of the suitability factors have been calibrated as well (Table 3). In general, suitability factor k = 1, representing n in the neighbourhood, obtains a high weight. This means that a land-use type is likely to expand in regions in which it is already cultivated. This factor has the highest median posterior weight for rangeland, sugar cane, and planted pasture. Accordingly, dLUC will take place close to existing sugar cane patches. For cropland, the double-cropping potential (k = 5) is the most important suitability factor for expansion. Galford et al. (2008) have found in a case study in Matto Grosso (an important expansion region, see Fig. 2) by means of remote sensing that newly established cropland is usually single cropped, but is converted to double cropping after 2–3 years. The high weight for the double-cropping potential factor indicates that this potential already plays a role at the establishment of the cropland, while the actual implementation of double cropping takes place a few years later. As a consequence, the location of iLUC in the case of displaced cropland is likely to be a location with a high double-cropping potential. In conclusion, the calibrated land-use change model mainly influences the location of dLUC and iLUC within the macroregion, that is distribution between and also within states in a macroregion.
| n | Name | k | Suitability factors | First quartile | Median | Third quartile |
|---|---|---|---|---|---|---|
| 4 | Rangeland | 1 | n in the neighbourhood | 0.35 | 0.46 | 0.60 |
| 2 | Distance to roads | 0.24 | 0.35 | 0.45 | ||
| 3 | Potential yield of n | 0.03 | 0.19 | 0.28 | ||
| 5 | Planted forest | 1 | n in the neighbourhood | 0.19 | 0.29 | 0.36 |
| 2 | Distance to roads | 0.27 | 0.34 | 0.37 | ||
| 3 | Potential yield of n | 0.32 | 0.37 | 0.51 | ||
| 6 | Crops | 1 | n in the neighbourhood | 0.11 | 0.22 | 0.36 |
| 2 | Travel time to hubs for n | 0.05 | 0.14 | 0.22 | ||
| 3 | Potential yield of n | 0.05 | 0.11 | 0.20 | ||
| 4 | Conversion elasticity | 0.12 | 0.23 | 0.33 | ||
| 5 | Growing season length | 0.21 | 0.30 | 0.36 | ||
| 8 | Sugar cane | 1 | n in the neighbourhood | 0.23 | 0.29 | 0.36 |
| 2 | Travel time to hubs for n | 0.21 | 0.28 | 0.33 | ||
| 3 | Potential yield of n | 0.15 | 0.22 | 0.26 | ||
| 4 | Conversion elasticity | 0.17 | 0.21 | 0.24 | ||
| 9 | Planted pasture | 1 | n in the neighbourhood | 0.40 | 0.53 | 0.66 |
| 2 | Distance to hubs for n | 0.33 | 0.45 | 0.56 | ||
| 3 | Potential yield of n | 0.00 | 0.02 | 0.03 |
The results above were based on calibration over 2007–2012. To show the effect of calibration, we have applied a split-sample approach, with calibration only from 2007 to 2009, to allow a comparison with observational data in the validation period from 2010 to 2012. We compare the modelled against observed area of cropland (Fig. 5), because this land-use type gives the most information on model performance as it both expands and contracts in the calibration period. For most states without a clear break in their trend, for example Roirama (RR), Ceará (CE), and Mato Grosso (MT), the modelled median remains good in the validation period. However, the areas of states that do show a trend break, for example Maranhão (MA) and Rio de Janeiro (RJ), are poorly simulated, although at least for Maranhão, the observed cropland area falls within the 95% confidence interval of the modelled area.
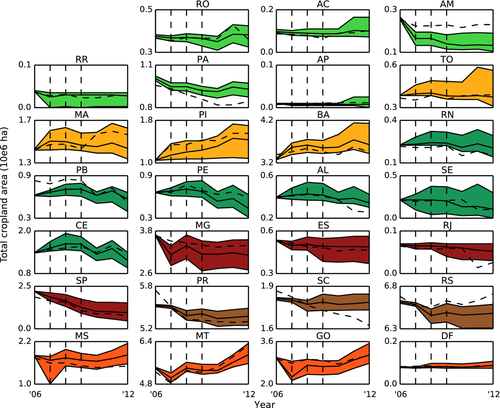
To summarize the effect of calibration for all land-use types, we compare the root-mean-squared error (RMSE) in area summed over all states of the calibrated and noncalibrated model (Table 4). For crops, sugar cane, and planted pasture, a considerable RMSE reduction is achieved. The highest reduction is achieved for crops, with a maximum of 53% in 2010. For sugar cane, the average reduction is 24%. A significant reduction for sugar cane is important, as it is the land-use type of main interest. Being able to correctly project the location of sugar cane expansion connotes correct modelling of dLUC, which is the first step in also correctly projecting iLUC as the two are chained. For rangeland and planted forest, the calibration does not bring the modelled median area per state closer to the observed area. The modelled median even becomes worse, although not significantly, only a few percentage. The reason why PLUC cannot find weights for the suitability factors that result in a correct projection is probably the poor data availability for these two land-use types. For example, for the initial land-use map, no good prior knowledge maps were available (see Methods S1), and for the suitability factors, we have no information about the locations of the hubs for these land-use types.
| n | Land-use type | Year | ||
|---|---|---|---|---|
| 2010 | 2011 | 2012 | ||
| 4 | Rangeland | −1 | −2 | −4 |
| 5 | Planted forest | −6 | 0 | 2 |
| 6 | Crops | 53 | 50 | 42 |
| 8 | Sugar cane | 26 | 21 | 24 |
| 9 | Planted pasture | 33 | 35 | 25 |
Economic model, projection
Demands are projected by MAGNET per land-use type for 2013, 2015, 2020, 2025, and 2030. To illustrate the trend, the demands for 2020 and 2030 for the reference and the biofuel scenario and the uncertainty herein are shown in Fig. 4. An interesting result is that the uncertainty within a scenario is often higher than the difference between the scenarios. This indicates that it can be problematic to draw conclusions about the effect of, for example, a policy by means of comparing scenarios from the CGE model. If the land transition elasticities are uncorrelated between the two scenarios, the large uncertainty makes that the policy effects might be negative as well as positive. Yet, we believe that although the elasticities are uncertain, they are correlated between the two scenarios, as these scenarios represent the same system, as long as the difference between scenarios is not too large. Others doubt this; a discussion that is known in economic modelling as the Lucas critique. Lucas (1976) argues in his work that the parameters in economic models are not policy-invariant and that they would therefore change when a policy is implemented. This discussion is interesting, but goes beyond the scope of this study. Nevertheless, we should be aware, that if Lucas is correct, the uncertainties in dLUC and iLUC shown in the next sections might be significantly higher.
In the reference scenario, sugar cane mainly expands in the Centre West Cerrado and the South-east (together called the Central South). The extra demand for sugar cane for ethanol from the mandates (biofuel scenario) also mainly ends up in these two regions. In the biofuel scenario, the total area of sugar cane in the Centre West Cerrado almost triples by 2030 compared to 2012.
The difference between the reference scenario and the biofuel scenario for the other land-use types within Brazil is the largest in the South-east (Fig. 4). In this macroregion, the areas of crops and rangeland are significantly smaller in the biofuel scenario than in the reference scenario. As the productivity of all land-use types are roughly the same in these two scenarios, this decrease in area means that MAGNET assumes that these areas of crops and rangeland are displaced by sugar cane. The displaced land uses are shifted to the north-east Cerrado and the Northern Amazon: here, crops and rangeland occupy a larger area in the biofuel scenario than in the reference scenario (Fig. 4, difference between the hatched and plain bars).
Conceptual differences between the two models
Despite the ‘shared’ conversion matrix between MAGNET and PLUC and despite the fact that MAGNET provides the demand as an input for PLUC, the conversion dynamics between the two models differ because of conceptual differences between the models. A result of this is that the area of iLUC for the whole of Brazil calculated from MAGNET differs from the area calculated by PLUC (further discussed later on), although ideally these two would be the same. This problem does not occur for dLUC, only for iLUC, and in the following we explain why.
The origin of the problem is that in PLUC sugar cane expands in the projection period, besides over cropland and rangeland, also often over planted pasture; a displacement also observed in other studies (e.g. Rudorff et al., 2010; Adami et al., 2012). In MAGNET, however, the area of conversion from planted pasture to sugar cane is negligible. This displacement of planted pasture in PLUC, not present in MAGNET, has two effects. One is that in PLUC, the area of planted pasture is decreased in a region, such that, in that same year, planted pasture should expand (in addition to the expansion caused by a potential increase in demand already given by MAGNET) elsewhere in that region in order to make up for the lost acreage. This causes iLUC in the region, not anticipated by MAGNET. Another effect is that the areas of rangeland and/or crops in PLUC are larger than dictated by the demand in MAGNET for that year, so that these land uses will contract, resulting in abandoned land. This causes negative iLUC, which by definition never occurs in MAGNET. It can be debated which of the two models, if any, is correct. But the most important implication for our study is that uncertainty in iLUC projections does not only stem from uncertainties of parameters and model structure within one model component, but also from the dissimilarity in model concepts between the two models within the integrated model chain.
DLUC and iLUC projections for Brazil up to 2030 at different spatial scales and the uncertainty herein
The direct land-use change as a result of an increased ethanol production from 2013 to 2030 mainly takes place in the Central South region. The highest (5 × 5 km2) cell-based probabilities, up to 0.77, exist in the south of Mato Grosso do Sul and the west of São Paulo (Fig. 6, frame 1). The highest probabilities of indirect land-use change, with a maximum of 0.43, occur in the Amazonian states Rondônia, Amapá, and Roirama (Fig. 6, frame 2). Probabilities in these three small states are high because they are the only places in the northern Amazon where any agricultural land-use type can expand, as the rest of the northern Amazon has very few roads, almost no existing agriculture and thus few hubs, and many protected areas. Implementation of new roads in the Amazon could change the spatial distribution drastically, but this is not included into the model due to limited spatial planning data availability. In the other macroregions, there are more options for expansion, and there is more variation in the suitability maps (best locations for expansion) between the different land-use types and between the individual Monte Carlo realizations, that is more uncertainty. In these other macroregions, iLUC locations with high probabilities are the frontier of the sugar cane expansion area (Goiás, Mato Grosso do Sul, and Mato Grosso) as well as the ‘arc of deforestation’, the transition area from cultivated land to mainly natural vegetation (Mato Grosso, Pará, and Rondônia).
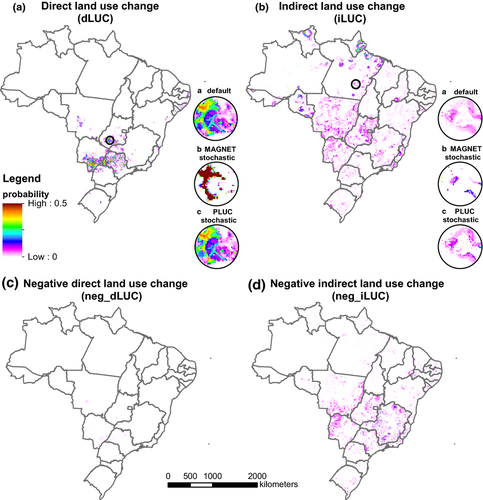
As expected, there are only very few cells experiencing negative dLUC, and with negligibly low probabilities, with a maximum of 0.07 (Fig. 6, frame 3). Conversely, negative iLUC (land abandonment in the biofuel scenario and not in the reference scenario, Fig. 6, frame 4) does appear, with probabilities up to 0.48, mainly in Espírito Santo, Minas Gerais, and the Pantanal, which is the wetland area in the west of Mato Grosso do Sul and the south of Mato Grosso. These are areas where the suitability for most agriculture is low, resulting in land abandonment when the demand in the biofuel scenario is lower than in the reference scenario (see also the discussion in the previous section). With lower probabilities, up to 0.1, this effect also occurs in the rest of the Central South.
In the following, we add up dLUC and negative dLUC, and iLUC and negative iLUC, obtaining net dLUC and net iLUC. Scaling up to 250 × 250 km2 blocks (Fig. 7), we can calculate the coefficient of variation (cv), indicating relative uncertainty in dLUC and iLUC. Clearly, the uncertainty in iLUC is generally larger than in dLUC. The median cv over all selected blocks for dLUC is 0.91, while for iLUC, it is 1.61. This is caused by the fact that dLUC is affected by the dynamics of sugar cane only, while iLUC is an effect of the interplay of all land-use types, thereby being subjected to the uncertainties in all weights of all suitability factors (Table 3) and the order of allocation. The maximum cv value of dLUC is 4. The maxima occur at the expansion frontier of sugar cane, through Mato Grosso, Goiás, and Minas Gerais. The maximum cv value of iLUC is 6. This means that, when considering the 95% confidence interval, mean iLUC values might be as much as 13 times as high or as low. In a nutshell, the uncertainty in these blocks is so high that we can say practically nothing about expected iLUC there, except when mean iLUC is (very close to) zero (13 times zero is still zero). Coefficients of variation in the arc of deforestation generally range from 1 to 3, which is a bit better, but still very uncertain.
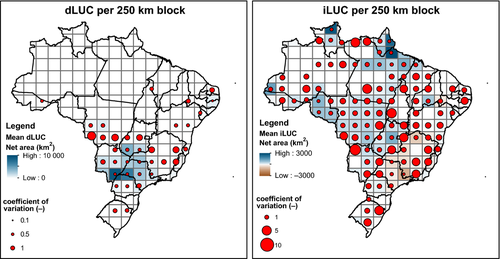
Comparing Figs 6 and 7, it becomes apparent that blocks of maxima in cv of iLUC area correspond to regions where both iLUC and negative iLUC might appear. When some Monte Carlo realizations have negative iLUC values and others positive iLUC values, the standard deviation is large, and correspondingly the cv. In these blocks, the net iLUC effect might be positive as well as negative, so that the impacts on, for example, biodiversity, might be negative as well as positive, respectively.
When looking at the cv for dLUC and iLUC area for Brazil as a whole (Table 5, both models stochastic), the values are many times smaller. The total amount for the whole of Brazil can be determined about nine times as precise for dLUC and about two times as precise for iLUC compared to the median of the 250 × 250 km2 blocks, because small-scale errors balance each other out when aggregating.
| Run | Mean dLUC | SD dLUC | cv dLUC | Mean iLUC | SD iLUC | cv iLUC |
|---|---|---|---|---|---|---|
| Both models stochastic | 4.20 | 0.10 | 0.02 | 3.13 | 2.25 | 0.72 |
| PLUC stochastic | 4.21 | 0.00 | 0.00 | 3.15 | 0.61 | 0.06 |
| MAGNET stochastic | 4.20 | 0.10 | 0.02 | 2.62 | 2.19 | 0.84 |
Contribution of the economic and land-use change model to the uncertainty in dLUC and iLUC at different spatial scales
The cv of the dLUC area at national level is for 100% caused by MAGNET (Table 5), which is logical, as MAGNET determines the total demand for sugar cane, and PLUC only allocates it within the macroregions. For iLUC area, this is not the case. The cv value of iLUC area for the run with only MAGNET stochastic is about sixteen times higher than cv value of iLUC area for the run with only PLUC stochastic, so about 93% of uncertainty in iLUC stems from MAGNET. Yet, the exact contribution of both models cannot be determined, because errors from the two models partly compensate each other (the cv values of the two runs do not add up to the cv value of 0.72 found in the default run). The reason that uncertainty in iLUC at national level is not fully determined by MAGNET is that in PLUC iLUC can occur within a macroregion that is additional to the iLUC between macroregions from MAGNET.
At the grid cell level, many cells have some probability of experiencing dLUC or iLUC when both models are stochastic (Fig. 6, detail frame 1a). With only PLUC stochastic and MAGNET deterministic, there is in general not much difference with the results of the default run (Fig. 6, panel 1c), although somewhat fewer cells have a probability above zero on dLUC and iLUC. This indicates that only a small part of the uncertainty at cell level is caused by MAGNET. With only MAGNET stochastic and PLUC deterministic, compared to the default run less than half of the cells have a probability above zero on dLUC and iLUC, and the ones that have, have a relatively high probability, indicating much lower uncertainty (Fig. 6, panel 1b). The uncertainty now mainly exists at the edges of the expansion patches, caused by the variation in demand from MAGNET. For iLUC (Fig. 6, panels 2a–c), the same reasoning applies. In conclusion, uncertainty at grid cell level is mainly caused by uncertainty in PLUC, for both dLUC and iLUC.
Discussion
In this study, we have demonstrated a general methodology to calculate direct and indirect land-use change (dLUC and iLUC) stochastically with an integrated economic – land-use change model, taking into account the important uncertainties in all components of the modelling chain. The proficiencies of this methodology were shown for a case study of land-use change in Brazil up to 2030, steered by the current and planned ethanol mandates worldwide. Here, we shortly discuss the answers to our three research questions and give recommendations for further studies.
What are the dLUC and iLUC projections for Brazil up to 2030 at different spatial scales and what is the uncertainty herein?
Cell-based (5 × 5 km2) probabilities of dLUC range from 0 to 0.77, and of iLUC from 0 to 0.43. Thus, given our scenario assumptions, there is no single cell in Brazil for which it can be said with certainty that dLUC or iLUC will take place up to 2030. So, it is difficult to project exactly where dLUC and iLUC will occur, but it is certain that it will occur (there are no Monte Carlo realization without dLUC or iLUC effects). Yet, overall locations of iLUC are in line with the locations projected by Lapola et al. (2010). For dLUC, our study shows some locations with high probabilities in Mato Grosso do Sul and Goiás, where Lapola et al. (2010) do not project dLUC. As there are the ‘new’ expansion areas, this inconsistency is likely caused by the fact that their projection is for 2020, while we project up to 2030. Also, in our projections, there are many cells for which it can be concluded with certainty that no dLUC or iLUC will take place in 2030, which is surely relevant information. In 250 × 250 km2 blocks, the coefficient of variation (cv) ranges from 0 to 4 for dLUC and from 0 to 6 for iLUC. Large cv values for dLUC occur at the frontier of sugar cane expansion. High cv values for iLUC occur where both iLUC and the opposite effect (agriculture in the reference scenario is abandoned land in the biofuel scenario), introduced in this study, might take place.
The uncertainty in iLUC area and location is generally higher than in dLUC, because iLUC is caused by the interplay of various land-use types that each have their uncertain model parameters, while dLUC is mainly affected by the parameters for sugar cane. Uncertainty in dLUC and iLUC is lower at higher aggregation levels. For iLUC, the decrease in uncertainty by aggregation is smaller. At country level, the cv for iLUC is 36 times higher than for dLUC in our case study. At this level, dLUC can be projected with high certainty, having a cv of only 0.02, while iLUC is still uncertain, having a cv of 0.72. Thus, to answer the question posed in the title, what we can and cannot say about iLUC: we can merely say things about iLUC with high uncertainties. Estimated iLUC areas, even at country level, might as well be 2.4 times as high or as low, given the 95% confidence interval.
What are the sources of uncertainty for each step in the model chain and how do these uncertainties influence dLUC and iLUC projections?
Uncertain components in the land-use change model are (1) the initial land-use map, causing uncertainty at cell level, (2) the order of allocation of the land uses, causing uncertainty in especially iLUC, and (3) the selection and weights of the suitability factors for allocation of the land-use types, causing mainly uncertainty at intermediate aggregation levels, like states. The reduction in root-mean-squared error in the modelled median land-use areas per state by model calibration, compared to a noncalibrated model is on average 20%. Poor-performing land-use types are rangeland and planted forest, probably due to poor data availability for the drivers of location of land-use change.
For the economic model, we have assessed only the effect of one of the most critical parameters: the land transition elasticities that simulate the likelihood of particular land transitions. The uncertainty caused by varying these elasticities mainly plays a role at national level. At the cell level, it only causes uncertainty at the edge of the patch of expansion.
The final aspect generating uncertainty in the output is the difference in the conceptual model between the economic and the land-use change model concerning the reclaiming of abandoned land. This conceptual difference affects the total amount of iLUC and the opposite iLUC effect.
What is the contribution of the economic and land-use change model to the uncertainty in dLUC and iLUC at the different spatial scales?
At the cell level, uncertainty is primarily determined by the land-use change model. Going to higher aggregation levels, the influence of the uncertainty in the Computable General Equilibrium (CGE) model on output uncertainty increases. At national level, the cv of dLUC is caused by the CGE model for 100%. The contribution of the economic model to the cv of iLUC at this level is about 93%, although this cannot be determined precisely, because errors from the two models partly compensate each other.
Implications and recommendations
From the above, we can conclude that projected iLUC areas and locations are highly uncertain. Based on the case study, our opinion is that threshold evaluation for iLUC indicators should not be implemented in legislation. Thresholds (cf. Malins, 2013) have no use when the model, used to check whether an indicator for a specific case is above or below this threshold, gives an output confidence interval that straddles the threshold. This is likely to happen considering the high uncertainties found in our study. As most iLUC (or LUC) indicators in legislation are provided in terms of greenhouse gas (GHG) emissions generated, the impacts of the uncertainty in dLUC and iLUC projections on GHG emissions should be assessed to underpin our conclusion. Error propagation assessment for other impacts, such as biodiversity and water availability, is also desirable. Our opposition to thresholds for iLUC factors in legislation does not mean we favour negligence of biofuel-induced land-use change. We propose, in line with, for example, Finkbeiner (2014) and Mathews & Tan (2009), a change of focus from quantifying iLUC to taking proactive measures to mitigate iLUC, even though the effectiveness of these measures might be difficult to quantify.
Our quantification of the sources of uncertainty allows identification of the parts of the modelling chain having the highest priority for improvement. If one wants better estimates of dLUC and iLUC at cell level for a given case study, for example to be able to better quantify local GHG emissions caused by the biofuel targets, one should focus on improving the land-use change model. Spatially explicit input data could be improved, especially for land-use types that are problematic to derive from remote sensing: rangeland (problematic to distinguish from natural savannah) and planted forest (problematic to distinguish from natural forest). And data that are now only included at an aggregate level, such as land management and yield level, could be included spatially to account for spatial variation. Also, better information on data accuracy would be helpful. Due to the lack of accuracy information we had to make strong assumptions on the errors in the maps used to create the initial land-use map and the observational data used for calibration.
If one wants better estimates of dLUC and iLUC at country level, one should focus on improving the economic model. Our current estimates of uncertainty in the CGE model might be underestimated, because we have evaluated the uncertainty from the and transition elasticities only, while land-use changes might be sensitive to other parameters as well (Kavallari et al., 2014). Yet, making other parameters stochastic could also reduce uncertainty, when they cancel out each other's errors. It would be good if making parameters stochastic and running Monte Carlo simulations would become common practice in economic modelling. Another option for better country level estimates might be the usage of a whole different type of model or tool, obviously also stochastic, although our current study gives cannot ascertain whether and to what extent that could reduce uncertainty.
One thing that could improve iLUC estimates at all spatial scales is a better match between the economic and land-use change model. The best solution would be to link the economic and the land-use model with a hard link that includes a feedback, as also suggested by Wicke et al. (2015). However, there is an inherent risk that this feedback loop is infinite, meaning that the land-use dynamics cannot be resolved, and there are many technical obstacles that complicate hard linking.
Yet, even if improved models, or improved model connections are used, in all cases, we strongly advise to provide quantitative uncertainty estimates together with the calculated dLUC, iLUC, or LUC indicators so that users of these indicators can evaluate the reliability of the indicators.
Acknowledgements
This work was carried out within the BE-Basic R&D Program, which was granted a FES subsidy from the Dutch Ministry of Economic Affairs, Agriculture, and Innovation (EL&I). We thank two anonymous reviewers for their valuable comments.




