A framework for understanding climate change impacts through non-compensatory intra- and interspecific climate change responses
Abstract
Understanding and predicting population responses to climate change is a crucial challenge. A key component of population responses to climate change are cases in which focal biological rates (e.g., population growth rates) change in response to climate change due to non-compensatory effects of changes in the underlying components (e.g., birth and death rates) determining the focal rates. We refer to these responses as non-compensatory climate change effects. As differential responses of biological rates to climate change have been documented in a variety of systems and arise at multiple levels of organization within and across species, non-compensatory effects may be nearly ubiquitous. Yet, how non-compensatory climate change responses combine and scale to influence the demographics of populations is often unclear and requires mapping them to the birth and death rates underlying population change. We provide a flexible framework for incorporating non-compensatory changes in upstream rates within and among species and mapping their consequences for additional downstream rates across scales to their eventual effects on population growth rates. Throughout, we provide specific examples and potential applications of the framework. We hope this framework helps to enhance our understanding of and unify research on population responses to climate change.
1 INTRODUCTION
Global climate change is altering mean temperatures, temperature variances, precipitation regimes, and extreme weather events (IPCC, 2021). Understanding how species respond to these changes is crucial for managing and forecasting the ecological impacts of climate change. Furthermore, understanding species' responses to climate change is also critical due to the potential consequences for ecosystem services, disease transmission, and food production (IPCC, 2022). However, predicting species responses to climate change remains difficult because this requires an understanding of both direct physiological effects and impacts on intra- and interspecific interactions (Blois et al., 2013; Gilman et al., 2010; Sutherst et al., 2007).
Our goal here is to provide a framework for understanding and predicting how populations will respond to climate change through non-compensatory effects of climate change on rates determining species' population demographics. We define a non-compensatory effect as the case in which a focal ‘downstream’ rate of interest changes because changes in ‘upstream’ processes influencing the focal rate do not cancel one another out (see Box 1 for an in-depth explanation and mathematical definition, and see Box 2 for a glossary of terms in bold throughout the manuscript). Non-compensatory effects with respect to climate change are those in which the ‘upstream’ components respond in a non-compensatory manner to some aspect of climate (e.g., precipitation, temperature, pH, etc.) to drive a change in a ‘downstream’ focal rate. For example, changing temperatures can alter population growth rate (a downstream rate) through non-compensatory effects of changes in birth and death rates (upstream rates; Amarasekare & Savage, 2012). Such non-compensatory effects can occur at any level of biological organization, from the molecular level to population growth rate, and a key to understanding them is to identify a focal rate, to evaluate how upstream components combine to generate the focal rate, and to assess the response of upstream components to climate change.
BOX 1. What is a non-compensatory effect?
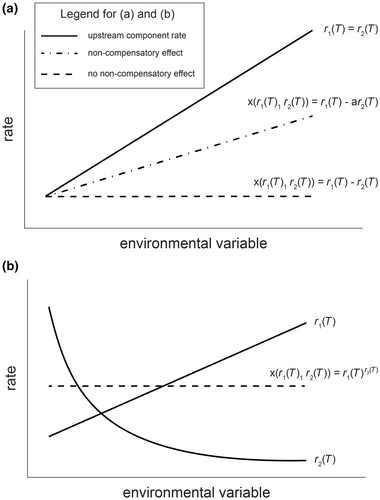
A non-compensatory effect is a case in which some focal rate, say, rate X, changes in response to some driving factor (e.g., temperature) because two or more determining components change in response to that driving factor in such a way that their effects on the focal rate are not canceled out. In contrast, changes in upstream components may lead to no change in a downstream rate if their effects perfectly cancel out in how they determine the downstream rate (Box Figure 1). Thus, non-compensatory effects focus not on whether changes in the upstream components are proportionally different, but whether the effects of those changes drive further change in the downstream rate. It is both possible that (1) two upstream components respond to a climate driver in the same proportional way but still cause a non-compensatory effect because they come together to influence the downstream rate in different ways (Box Figure 1a) and that (2) two upstream components change in a disproportionate way and do not lead to a change in the downstream rate because the way they come together cancels out their effects on the downstream rate (Box Figure 1b). Thus, non-compensatory effects are only detectable in the change in the downstream rate or by knowing how the upstream components combine to determine the downstream rate. We suggest that these special cases will mostly be rare and that differential changes in upstream components will most likely have downstream consequences.
To define non-compensatory effects mathematically, assume that our rate X is a function of two or more components that are themselves a function of an environmental variable such as temperature . Then, a non-compensatory effect will alter when differences in between temperatures change the value of . For example, the rate of change in population size is a function of birth and death rates, which vary with temperature (in this case, ). So, non-compensatory effects occur between two temperatures when the birth and death rates change differentially with temperature such that .
We can consider non-compensatory effects at a single temperature, between two temperatures, or over a range of temperatures. At a single temperature, non-compensatory effects occur if instantaneous changes in result in . In the case of a rapid shift between two temperatures, non-compensatory effects occur if . When considering a range of temperatures (or , an open interval between two temperatures), there is a non-compensatory effect if there exists such that . In other words, there is no non-compensatory effect over an interval if and only if, over all intervals .
BOX 2. Glossary
Non-compensatory effect/response—A change in a focal downstream rate due to non-cancelling changes in the effects of upstream rates on the downstream rate.
Asymmetry—The term asymmetry is used in several ways in the climate change literature: (1) Asymmetry describes when a curve such as a thermal performance curve exhibits skew or is not symmetric around its peak. (2) Asymmetry describes when two rates have different thermal sensitivities. (3) Asymmetry describes when two species' thermal performance curves are not equivalent (differ in their optima). Here we focus on the second and third definitions when using the term.
Mismatch—The term mismatch is used in several ways in the climate change literature: (1) Mismatch describes when the thermal performance curves of two species are not equivalent (differ in their optima). (2) Mismatch describes when a process was ‘matched’ at some point but has become ‘mismatched’ with climate change (e.g., phenological mismatches). We note that phenological mismatches can be viewed as non-compensatory effects/responses (see Interspecific non-compensatory effects section).
Demographic non-compensatory effect/response—A non-compensatory effect in which a change in population growth rates occurs due to non-cancelling changes in birth and death rates in response to a change in climate.
Fecundity-maturation non-compensatory effect—A non-compensatory effect that alters population birth rates through non-cancelling changes in the allocation of resources to reproduction or fecundity and organismal growth in response to climate change.
Growth-maintenance non-compensatory effect—A non-compensatory effect that alters population death rates through non-cancelling changes in the allocation of resources to organismal growth and maintenance in response to climate change.
Predator–prey non-compensatory effect—A non-compensatory effect in which climate change leads to non-cancelling changes in the underlying processes determining foraging success rates of predators on their prey.
Movement non-compensatory effect—A specific form of predator–prey non-compensatory effect that is due to non-cancelling changes in predator and prey movement velocities in response to climate change, which in turn alter predator–prey encounter rates and, thus, foraging rates.
Uptake rate non-compensatory effect—A non-compensatory effect that can occur in host–parasite or mutualistic interactions in which one interaction partner's uptake rate is dependent on the uptake rate of the other interaction partner (e.g., a gut macroparasite and host or photosynthetic symbiont and host) and there are non-cancelling changes in uptake rates of the two species in response to climate change.
We focus on non-compensatory climate change effects for two principal reasons. First, at the population level, a crucial climate change response is the extent to which a population might grow or decline in response to climate change. In general, barring changes in immigration or emigration, changes in population abundances must reflect non-zero population growth rates (i.e., birth rates minus death rates; note that our framework can be expanded to incorporate the climate-dependence of immigration and emigration, but we do not discuss these here for the sake of simplicity). For example, a change to a negative growth rate from a positive one with a change in the environment implies that birth and death rates have changed with the environment such that the death rate now exceeds the birth rate. Thus, this fundamental non-compensatory effect is central to understanding population demographic changes in response to climate change, as well as all other dynamic changes in population abundance. Second, there exists a large and growing list of so-called ‘asymmetries’ and ‘mismatches’ that have been identified both within and among species. These asymmetries and mismatches describe cases in which multiple biological rates respond differently to climate change, suggesting that non-compensatory climate change effects could be nearly ubiquitous (See Box 3 Figure: Non-compensatory effects, asymmetries, and mismatches for a critical comparison of the three concepts). For example, studies have identified asymmetric responses to temperature: among different rates within species (Bozinovic et al., 2020; Huey & Kingsolver, 2019; Johnson et al., 2023; Jørgensen et al., 2022; Pawar et al., 2024; Wang et al., 2020), in consumer-resource interactions (Álvarez-Codesal et al., 2023; Bideault et al., 2021; Dell et al., 2014; Gibert et al., 2022; Gilbert et al., 2014), and in host–parasite systems (Cohen et al., 2017; Kirk et al., 2022; Mordecai et al., 2013, 2019; Taylor et al., 2019). However, we currently lack a cohesive framework with which to conceptualize how these responses might lead to non-compensatory climate change effects and how those effects fit together and interact to ultimately produce changes in populations. Furthermore, a common framework to understand these non-compensatory effects across systems would provide a powerful tool for synthesizing climate change impacts.
BOX 3. Non-compensatory effects, asymmetries, and mismatches
A current difficulty in navigating the literature on asymmetries, mismatches, and climate change is the ambiguity with which these terms are used. For example, asymmetries and mismatches are often treated as synonymous, and the term mismatch is used to refer to several distinct effects of climate change (cf. Cohen et al., 2017; Stenseth & Mysterud, 2002). Here, we hope to clarify the language that is used around asymmetries and mismatches and explain why we think a focus on non-compensatory effects is more useful in most cases.
Asymmetry in the context of climate change responses is currently widely used in three contexts. First, asymmetry is used to describe when a thermal performance curve is skewed (i.e., non-symmetric around its peak; Buckley et al., 2022). Second, asymmetry is used to describe when two or more rates have different thermal sensitivities (Gibert et al., 2022). Third, asymmetry is also used to describe the case where the thermal performance curves of two species are not equivalent (also referred to by some authors as mismatch; e.g., Cohen et al., 2017). We believe that the first definition is appropriate language for describing thermal performance curves, but that the other definitions are inadequate when the goal is to understand how a process of interest is likely to change with climate due to changes in component processes or rates. Our focus on non-compensatory effects does not depend on whether the components change in the same manner or not with climate change, but whether the changes in the components with climate change subsequently alter a process of interest (Box 1). This is because it is possible that the components change with the environment proportionally in exactly the same way and generate effects on a rate of interest (Box Figure 1a), and for the components to change with the environment in different ways and generate no effect on a process of interest (Box Figure 1b). Crucially, it is how these components specifically combine that determines whether a non-compensatory effect occurs.
We also take issue with the use of the term mismatch as a synonym for asymmetry. We view the term mismatch as implying that there must be some optimum constituting a ‘match’, with a ‘mismatch’ describing when this optimum is not occurring (Cushing, 1990; Cushing & Dickson, 1977). This definition fits the case where mismatch is used in the climate change literature to describe when some interaction process was ‘matched’ at some point in time, but climate change has led to the development of a discrepancy (e.g., phenological mismatches). However, we believe that using mismatch to describe, for example, differences in thermal performance curves among species, generates confusion because: (1) it conflates multiple usages of the word mismatch, (2) what would often be a ‘match’ in terms of an optimum for one species is likely to be a ‘mismatch’ for the other species if they interact antagonistically, and (3) the optimal situation for one species (also known as a ‘match’) may often be to have a ‘mismatch’ in terms of, say, thermal optima (Casas Goncalves & Amarasekare, 2021; Smith & Amarasekare, 2018). If differences in climate change responses lead to downstream effects, we believe that non-compensatory effect is a much better description.
Last, we note that mismatches, such as phenological mismatches, may arise due to non-compensatory climate change effects and can generate additional non-compensatory effects in the framework we introduce here. For example, the timing of the peak activity of predators and prey, such as birds and insects, may show differential responses to temperature generating a phenological mismatch (Damien & Tougeron, 2019; Reed et al., 2013; Box Figure 3a). This phenological mismatch could then alter bird-feeding rates through the non-compensatory effects of peak activity changes in birds and insects on the abundance of insects experienced by the birds through reduced temporal overlap (Box Figure 3b). Lowered feeding rates, in turn, may lead to non-compensatory changes in birth and death rates in bird or insect populations thus generating yet another non-compensatory effect.
Below, we first provide an in-depth explanation of a framework for understanding non-compensatory climate change effects that provides a flexible, hierarchical approach for linking multiple non-compensatory effects, tracking their consequences for populations, and connecting both intra- and interspecific processes. Throughout our explanation of the framework, we provide empirical examples of non-compensatory climate change effects across single-species systems, consumer-resource interactions, parasite–host interactions, and others to illustrate the generality of the framework and how it can be applied to understanding climate change responses in particular systems. We then conclude by providing some suggestions for how researchers might apply this framework in their own systems and offer guidance on how future studies might combine this framework with experiments and observational data to better understand species' responses to climate change.
2 A FRAMEWORK FOR NON-COMPENSATORY EFFECTS AND CLIMATE CHANGE IMPACTS
2.1 A minimal, rate-hierarchy model of emergent climate change effects
Our framework (Figure 1) starts with the recognition that the most concerning species' responses to climate change generally come in the form of changes in population size through the population growth rate. Thus, we focus primarily on the population growth rate (r; note that this is the net growth rate encompassing births and all sources of mortality rather than a maximum or intrinsic growth rate). All factors that feed into population growth within our framework are also rates. By definition, in a closed population, changes in growth rates are driven by changes in the demographic rates of births (b) and deaths (d). Thus, a demographic non-compensatory effect arises when birth and death rates respond to some aspect of climate change (e.g., temperature) in a non-compensatory way thus altering the population growth rate. Demographic non-compensatory effects form the top-level effect and all other non-compensatory effects must feed into the demographic non-compensatory effect to affect the population growth rate.
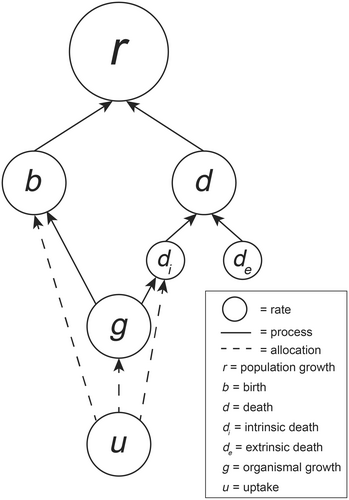
Changes in birth rates arise through two general pathways. First, net resource uptake (of any form from light to prey; designated as u) determines the amount of energy and biosynthetic metabolites available for allocation to reproduction (b), organismal growth (g), and maintenance (di, with allocations described by dashed lines in Figure 1). Allocation of resources to reproduction is a principal driver of birth rates, given variation in life history that determines offspring size, fecundity, and reproductive effort. Indirectly, birth rates at the population level are also determined by the timing of maturation based on the development rate. Thus, organismal growth feeds into the rate of births at the population level by influencing the number of adults.
Changes in death rates (d) arise through both internal (di) and external forces (de). External forces include risks from environmental conditions, competitors, predators, or pathogens generating a rate of extrinsic mortality. Internal forces, such as aging, will generate an intrinsic rate of mortality. This intrinsic rate will depend on the allocation of resources to maintenance, including repair, immune function, and basal metabolic costs. Intrinsic and extrinsic death rates are, in principle, additive. Although one could influence the other through density dependence and compensatory mortality (i.e., when extrinsic mortality reduces density-dependent mortality; Anderson & Burnham, 1976).
This minimal model represents a single species and can be broken into life stages if needed as different life stages may have different responses to climate variables and accounting for stage structure may be necessary to understand overall population patterns (Coulson et al., 2001; Davidson et al., 2024; Johnson et al., 2023). It can also be connected to other species via connecting rates, such as the predator functional response, which, for example, would link the uptake rate for the predator and the extrinsic death rate for the prey (see the Interspecific Non-compensatory Effects section below). Species interactions can connect two or more rate hierarchies in a variety of ways, depending on whether the interaction alters mortality, resource uptake, or allocation of resources. For example, a vector-borne pathogen may be connected to both the vector and the host through the rate at which the vector bites hosts.
Critically, the framework is intended to be a minimal but general depiction of how core organismal-level rates interact to drive changes in population size. All populations have individuals that uptake and allocate resources for maintenance, growth, and reproduction. These allocations, in all cases, are used to support physiological processes determining development rates, fitness, and demographics. Thus, we intend that any species can be described through the minimal model, with appropriate expansions of rates and processes as needed for a particular problem. For example, a prey species with anti-predator defenses may require an allocation arrow from the uptake rate to extrinsic mortality, or if one is studying multiple sources of extrinsic mortality and their responses to climate change, one may need to split up the extrinsic mortality rate into multiple rates. Note, this model is not a food-web model or a network; the arrows describe how upstream rates lead to downstream rates following a chain of effects from resource uptake to the change in population growth rates. Thus, we refer to this structure as a rate hierarchy.
3 INTRASPECIFIC NON-COMPENSATORY EFFECTS
Within the rate-hierarchy framework, non-compensatory effects altering population growth rate can arise at multiple levels of biological organization. At the highest level are the aforementioned demographic non-compensatory effects that directly change population growth rates (and therefore mean fitness; Lande, 1982) when climate change alters birth and death rates in a way that does not cancel. Population growth will be promoted when birth rates increase faster with climate change than death rates, while population declines will result when death rates increase faster with climate change than birth rates. Given the nonlinearity or unimodality of some climate change responses, such as many thermal functions, population growth may increase or decrease with changes in climate. A commonly assumed form of the demographic non-compensatory effect comes from Amarasekare and Savage (2012), in which birth rates are a unimodal function of temperature and death rates are an exponentially increasing function of temperature (Figure 2a). The difference between these two functions generates the canonical left-skewed population growth rate thermal performance curve (TPC; Amarasekare & Savage, 2012; Ratkowsky et al., 1982, 1983) through the non-compensatory changes in birth and death rates with temperature.
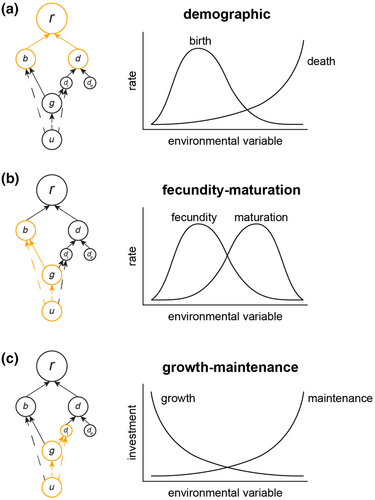
At lower levels of the rate hierarchy, the proportional allocation of resources acquired through uptake rates to organismal growth, maintenance, and reproduction also may shift in response to changing environmental conditions (Atkinson, 1994; Brett et al., 1969; Roff, 2001). These changes often will manifest in life history trade-offs, and their potential consequences may be complex, as resources are split into multiple competing ends. It is worth noting that an allocation change may not immediately result in a change in a specific rate if changes in uptake rates counteract the effect of the allocation. Below we discuss the two non-compensatory effects at lower levels in our rate hierarchy, fecundity-maturation and growth-maintenance non-compensatory effects, which arise from resource uptake rate and allocation changes.
The total birth rate (b) is the product of the number of mature adults (A) and the fecundity per time of individuals (F). The number of mature adults in the population depends on the organismal growth rate (or inversely, maturation time). Faster development and shorter maturation times resulting from increases in resource acquisitions and allocations to organismal growth will lead to a subsequent increase in the number of reproducing adults, so one of the upstream contributors to b passes through organismal growth to a change in A. Fecundity (F) is determined by a combination of factors including resource allocations to reproduction (ur) and the costs per offspring (c), following a typical Smith-Fretwell quantity-quality trade-off (Smith & Fretwell, 1974). Thus, the other upstream contributor to b is straight from the uptake rate given the fraction of the uptake rate allocated to reproduction. Given that the cost per offspring could also be climate-dependent, there are at least three ways in which birth rates change due to non-compensatory effects on the upstream component rates (i.e., the number of adults, resource allocation to reproduction, and cost per offspring).
A common example of potential fecundity-maturation non-compensatory effects in ectotherms is the relationship between temperature, size at maturity, and fecundity. At cooler temperatures, ectotherms tend to grow more slowly, reach maturity at a larger size, and, due to their larger size, produce a larger number of eggs (Atkinson, 1994; Roff, 2001). Thus, birth rates may change with temperature because of the simultaneous changes in A and F. Whether or not these changes lead to a decrease in birth rates with increasing temperatures can be complex, depending on, for example, whether the relationship between size and fecundity itself is temperature dependent (Arendt, 2011).
The mortality rate is the inverse of survival, and survival depends on the allocation of resources to maintenance and the size of the organism that is being maintained. Thus, survival (s) is proportional to the product of the per mass availability of maintenance resources (um/cm: allocation of resources to maintenance over maintenance cost) and the mass of the organism (B). In this way, maturation and growth form one part of the upstream rate effect on mortality, and allocation of resources forms the other part. As body mass may change with climate, for example, through the impact of temperature on growth, and allocation decisions and overall uptake rates may vary with temperature, there are several ways in which the climate dependence of upstream rates will have non-compensatory effects on survival.
For example, across ectothermic taxa, increases in environmental temperatures drive elevated maintenance metabolic rates, up to a point, influencing the cost of maintenance (cm), and correspondingly necessitating higher rates of resource allocation requirements for maintenance (um; Amarasekare & Savage, 2012). If not compensated for by changes in the uptake rate, increasing metabolic rates will result in concurrent decreases in resource allocation to organismal growth. Huey and Kingsolver (2019) proposed the “metabolic meltdown hypothesis” suggesting that growth-maintenance non-compensatory effects will frequently arise, given direct negative effects of climate change on resource and nutrient availability or indirectly by negative effects of higher temperatures on locomotion and foraging rates. This hypothesis is supported by empirical studies demonstrating combined negative effects of temperature and resource availability on organismal and population growth rates (Brett et al., 1969; Thomas et al., 2017).
4 INTERSPECIFIC NON-COMPENSATORY EFFECTS
Although intraspecific physiological and life history responses to climate change play an important role in how populations will respond to climate change, it is also necessary to understand how the interactions among species are likely to change and how these changes can feed into the intraspecific rates. To understand how non-compensatory changes occurring among interacting species will impact populations, we expand our framework from the single species to multi-species cases. To do so, we connect two or more species' rate hierarchies via an appropriate connecting rate (e.g., predator functional response, mosquito biting rate, plant pollination rate) dictating their interactions. Critically, changes in connecting rates will have cascading consequences across pairs of species that can result in demographic shifts in one or both interacting species. Furthermore, the connecting rate itself can depend on possible non-compensatory changes in upstream mechanisms that generate the rate. Below, we show how the addition of connecting rates can allow us to examine how non-compensatory climate change responses might influence predator–prey, host–parasite, and mutualistic interactions and the resultant consequences for populations.
4.1 Predator–prey interactions
Feeding rates connect predators and prey as they determine the uptake rate of the predator and influence the extrinsic death rate of the prey. We define a predator–prey non-compensatory effect as the case when the foraging rate changes with climate due to the non-cancelling effects of upstream factors related to both the predator/consumer (xc) and prey/resource (xr) that respond to climate (Figure 3). As predation events depend on movement and encounters between predator and prey, the detection of prey by the predator, and the successful attack by the predator (DeLong, 2021; Jeschke et al., 2002; Wootton et al., 2023), there are many ways in which climate change may alter the emergent foraging rate (f).
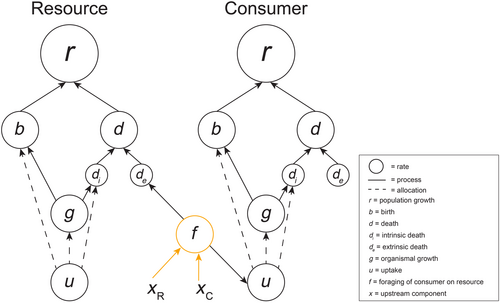
One of the earliest recognized drivers of climate change effects on interspecific interactions are phenological mismatches, which can be viewed as a predator–prey non-compensatory climate change effect. Predators and prey must be in the same area at the same time for predation to occur, and environmental factors like temperature may influence the likelihood of this co-occurrence, especially in highly seasonal habitats (Damien & Tougeron, 2019). In a classic case of phenological mismatch, differential changes in the timing of breeding activity of insectivorous great tits (Parus major) and their caterpillar prey affects foraging rates of the birds (Reed et al., 2013). The migration of great tits is triggered by day length and temperature, but caterpillar phenology advances more quickly with warming than egg laying phenology of the birds (Burgess et al., 2018; Reed et al., 2013), resulting in non-compensatory phenological changes that reduce availability of prey during peak resource demand for the birds. As foraging rates depend on prey availability through the functional response, this disparity in timing lowers the foraging rates and can also generate a demographic non-compensatory effect for the birds by reducing reproductive rates and/or increasing death rates due to resource shortage. As phenological changes are widely documented with climate change, this may be a common source of predator–prey non-compensatory climate change effects.
Predation events also depend on the ability of predators to detect prey. Climate change may alter the ability of predators to detect prey or for prey to avoid detection by predators. For example, changes in temperature regimes can alter the effectiveness of camouflaging phenotypes, creating a camouflage mismatch that changes the risk of predation. In a classic case, snowshoe hares (Lepus americanus) change coat color to blend in with the seasonally changing environment, with a white coat in the winter to reduce contrast with the snowy ground and a brown coat in the summer to reduce contrast with soils and plants. The timing of the color switch is temperature independent, but changing precipitation patterns resulting in delayed snowfall and early snowmelt result in windows during which hare have a visual mismatch with the background, causing easier detection by predators such as lynx (Lynx canadensis; Ferreira et al. 2023). Thus, the mismatch increases foraging rates because of an effect on the upstream process of detecting prey (xc), which depends on both predator and prey traits. Climate change also may alter prey detection of predators in chemically mediated interactions (Roggatz et al. 2022). For example, increases in acidity in aquatic environments can alter the olfactory ability of fish to detect predators or alarm cues potentially making fish more susceptible to predation (Ou et al., 2015; Porteus et al., 2018).
4.2 Host–parasite interactions
Given the diversity of types of host–parasite interactions, hosts and parasites may be connected in a variety of ways resulting in several types of host–parasite-specific non-compensatory effects. For example, for parasites that primarily draw off resources of the host (e.g., tick, tapeworm, etc.), the host and parasite rate hierarchies would be directly connected through the two uptake rates, without need for a distinct intermediate connecting rate (Figure 4). That is, the parasite gathers resources out of the host's resource stream, impacting the host's available resources. Thus, we draw an arrow toward the host's uptake rate from the parasite's uptake rate. The host's realized net uptake rate, then, is generated by the interacting effects of their own resource gathering activity (f) and the parasite's resource extracting behavior. In this way, a non-compensatory uptake rate effect can arise when the changes in host and parasite foraging do not cancel. If warming, for example, increases the rate of resource uptake of a parasite more quickly than that of its host, there would be a net decline in the realized net uptake rate of the host. This change in uptake rate would cascade up to host demography and also potentially would feed back to alter the demography of the parasite. Further, a transfer of resources from host to parasite may or may not be compensatory depending on whether the fraction of resources passing through the gut varies with resource flow. A parasite that has an uptake rate that saturates with increasing flow through would have a different proportional effect on host resource assimilation, and the emergence of a non-compensatory effect would depend on whether or not host uptake rate was altered by climate change. Additionally, parasite-induced anorexia or hyperphagy in its host (Hite et al., 2020; Hite & Cressler, 2019) could also mediate a non-compensatory uptake rate effect.
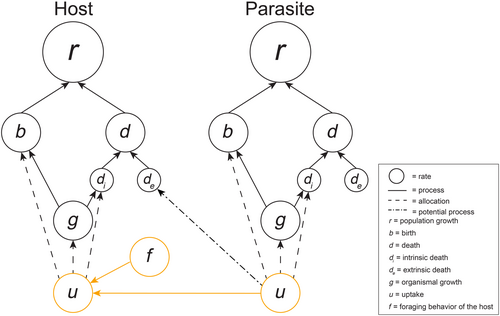
Outside of direct effects of parasites on host uptake rates, endoparasites also may increase host extrinsic mortality directly by triggering cell death, releasing toxins, or instigating extreme immune responses (Figure 4). As parasite pathogenicity and host immune responses can both be dependent on the environment (Thomas & Blanford, 2003; Wright & Cooper, 1981), environmental changes could lead to non-compensatory changes that alter the death rate of the host. In sub-lethal infections, the presence of the endoparasite could necessitate increased host allocations to immune function, leading to non-compensatory fecundity-maturation or growth-maintenance effects. In particular, all of these processes could be temperature dependent if the host's decision to tolerate or fight the endoparasite depends on temperature, or if the host is an ectotherm, making uptake, allocation, and demographic processes temperature dependent.
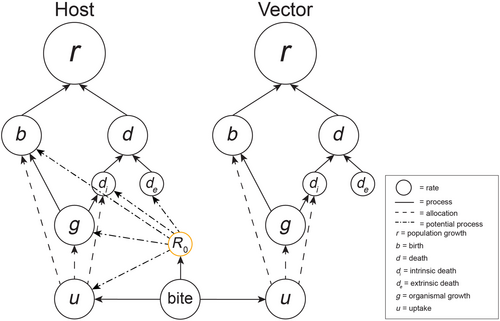
For ectoparasites that are vectors (e.g., mosquitos), the presence of a vectored pathogen generates new possible avenues of non-compensatory changes (Figure 5). Here the biting rate would serve as an intermediate connecting rate between the host, pathogen, and vector. This is an expansion of the non-compensatory uptake rate effect, as some form of ‘biting’ would be involved in any such host–parasite interaction. Thus, the biting rate could cause a demographic non-compensatory effect by increasing reproduction of the vector, decreasing reproduction of the host, and increasing death rate of the host caused by pathogen transmission, and altering the states (susceptible or infected with pathogen carried by the vector) of individuals in the host population. The biting rate is also a critical connecting rate determining the net reproductive rate (R0) of vectored pathogens themselves. A seminal study by Mordecai et al. (2013) makes clear how R0 is dependent on numerous upstream rates (e.g., vector development rate and competence), creating a wide range of potential non-compensatory changes in upstream rates. As most of these upstream rates are dependent on climate, including temperature, the non-cancelling nature of responses in upstream rates make R0 temperature dependent as well (Mordecai et al., 2013, 2019).
4.3 MUTUALISTIC INTERACTIONS
As for host–parasite and consumer-resource interactions, we can incorporate mutualistic interactions into the framework through the addition of direct or intermediate connecting rates between the mutualists based on how the mutualism operates. For example, plants and their pollinators can be connected through a visitation rate that links the birth rate of the plant to the uptake rate of the pollinator (often through pollen or nectar consumption for the pollinator; Figure 6). This visitation rate is a downstream rate that could be affected by upstream features of the pollinator (xpo) and the plant (xpl), such as pollinator energy demands or plant attractiveness. A protective mutualism, such as ant-acacia mutualisms, would have a connecting rate linking the uptake rate for the ants from resources provided by the acacia to the extrinsic death rate or uptake rate of the acacias as the ants prevent defoliation (Janzen, 1966). Endosymbiotic mutualists may have similar or more complex relationships between connecting rates than other mutualisms. For example, the protist Paramecium bursaria hosts an algal Zoochlorella symbiont. The paramecium in this interaction receives sugars provided from algal photosynthesis while the paramecium both provides protection and nutrients for the algae (Brown & Nielsen, 1974; Karakashian, 1963). Thus, this system might be described by a connecting rate that links the uptake rate of the paramecium and the uptake rate and extrinsic death rate of the algae.
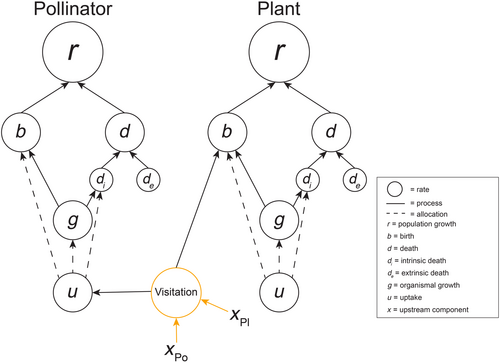
There are many ways in which differing responses of mutualistic partners to climate change can lead to non-compensatory uptake rate effects, phenological mismatches, or other non-compensatory effects that alter the connecting rate with potential cascading effects for either or both mutualistic partners. In a recent review, Cruz et al. (2023) highlighted how differing thermal performance curves of mutualistic partners in traits related to the interaction among partners can generate an overall mutualism thermal performance curve, making the mutualism itself temperature dependent. Given that mutualistic interactions generally involve connections to rates such as uptake rates and extrinsic death rates, the temperature dependence of mutualisms generated by non-compensatory effects can potentially lead to changes that could scale up to a non-compensatory demographic effect and population growth or decline. For example, in an experimental plant-pollinator system, increasing temperatures led to fewer flowers per plant and lower nectar volume, but higher nectar concentration (de Manincor et al., 2023). However, the net effect of these changes with temperatures led to reduced visitation rates and shorter bee handling times with negative consequences for flower seed set under warmer conditions (de Manincor et al., 2023). The negative effect on plant reproduction would not have been expected had consequences for pollinators not also been considered. Thus, this example also highlights the importance of accounting for non-compensatory effects arising from interspecific interactions for understanding population responses to climate change.
Under some circumstances, non-compensatory climate change effects on mutualisms may shift these interactions along the so-called mutualism–parasitism continuum (Bronstein, 1994; Johnson et al., 1997). For example, in the aforementioned Paramecium bursaria–Zoochlorella system, at high temperatures ‘ghost’ Paramecium without algal symbionts have higher fitness than Paramecium that contain Zoochlorella symbionts (Salsbery & DeLong, 2018). A potential explanation for this is that the paramecia are mixotrophs that receive energy from both their algal symbionts and through bacterivory. At higher temperatures, bacterivory may lead to greater fitness for Paramecium without symbionts relative to those with symbionts because the energy gained from the algae at high temperatures is less than the potential energy that could be gained from bacteria. This is because the space within a cell is finite, generating a trade-off between allocating that space to algae or food vacuoles. In this case, changes in the relative potential benefits of bacterivory and photosynthates from the algae with temperature generate a non-compensatory effect on uptake rates that switches the presence of algae from beneficial to detrimental. Given the potential for the costs and benefits or symbioses to be environmentally dependent (Bronstein, 1994; Cruz et al., 2023; Hoeksema & Bruna, 2015; Johnson et al., 1997), non-compensatory climate change effects may play a particularly important role in moving host-symbiont relationships along the mutualism–parasitism continuum.
5 NON-COMPENSATORY EFFECTS AND INDIRECT INTERACTIONS
Thus far, we have focused on how the framework can be used to understand non-compensatory climate change impacts on rates within species and species with direct interactions. By combining modules representing single species or pairwise species interactions, we can apply the framework to larger groups of species and communities more generally. For example, a key indirect interaction in ecology is resource competition (Tilman, 1982). Although often modeled phenomenologically as a direct interaction between two species, competition can be understood more mechanistically as two or more consumers using the same resource (Abrams, 2022). In our framework, this can be represented by two consumers with uptake rates that are connected to a single resource through feeding rate links for a biotic resource or utilization rate links for an abiotic resource. Armed with this new module, one can then track how non-compensatory changes in rates within and among species might influence the entire competitive system. Similarly, one could construct a module with two resources consumed by a single consumer to examine apparent competition (Holt, 1977) or a module with a predator connected to a consumer connected to a resource to examine trophic cascades (Paine, 1980).
6 APPLYING THE FRAMEWORK
If one is simply interested in whether a population is declining or increasing in response to climate change, it may suffice to monitor population sizes and growth rates and examine trends over time or space. However, if one wants to know why a population is changing in response to climate change and therefore develop possible interventions, then it is necessary to know how the rates that ultimately determine birth and death rates come together to lead to non-compensatory demographic effects. Therefore, we built the framework presented here with that goal in mind.
We can imagine a number of ways in which the framework presented here can be combined with data to either predict how a species might respond to ongoing and future climate change or to dissect why populations are currently increasing or declining with climate change. For many species—especially those amenable to experimental study—the climate change dependence of upstream rates within the framework can be measured directly. For example, studies of arthropods have measured the temperature dependence of a variety of intraspecific upstream rates such as maturation rates, mortality rates, and organismal growth rates in the laboratory that can be combined with mathematical models of population growth to examine how these rates combine and potential responses to climate change (Johnson et al., 2023; Richard et al., 2023; Simon & Amarasekare, 2024). For interspecific interactions, the dependence of interaction rates on environmental factors likely to change with climate also can be measured experimentally or with observational data both in the lab and field (e.g., Coblentz et al., 2022; Englund et al., 2011; Kirk et al., 2022; Mordecai et al., 2019). For species that are not amenable to experimental manipulation, the environmental dependence of upstream rates that ultimately influence population birth and death rates can potentially be measured using appropriate field observations and their dependence spatially or temporally on environmental factors likely to be affected by climate change (e.g., Coulson et al., 2001; McLean et al., 2016; Wang et al., 2020). One also may be able to make assumptions or perform sensitivity analyses regarding particular rates and how they are likely to respond to climate change for rates that are difficult to measure directly. Last, knowing the life history and ecology of one's study system is invaluable in understanding how the minimal framework presented here should be modified to match a particular system and which rates within the rate hierarchy and interactions with other species might be the most important to include or focus on.
7 CONCLUSIONS AND FUTURE PROSPECTS
Here we provide a framework for understanding how non-compensatory effects of climate change in rates within and among species combine to impact populations. Although most of the examples we used throughout have focused on non-compensatory responses to mean temperatures, we believe that this framework is equally applicable to other environmental impacts of climate change. For example, in a study of Sonoran Desert plant community change over 25 years, Kimball et al. (2010) showed how later winter rains in colder conditions alter germination rates across annual plants leading to community change. When put in the context of our framework, the germination response to the timing of precipitation of each plant species could be viewed as altering birth rates and causing non-compensatory demographic effects leading to declines or increases in population growth. Our focus on temperature is largely a reflection of the fact that this has been the most widely studied component of climate change, particularly with regard to asymmetries in rates and mismatches. Expanding research to include non-compensatory effects in response to a greater number of changing climatic features, including the variance of those features (IPCC, 2021; Vasseur et al., 2014), will provide a more holistic view of how climate change is likely to influence populations.
Our framework makes it apparent that there is potential for non-compensatory effects generated at one level to be canceled out by another rate response to climate change, indicating that caution should be taken when directly interpreting how effects at one level scale to influence population growth or decline. For example, using data across 35 species of birds, (McLean et al., 2016) showed that warmer temperatures were associated with earlier lay dates and earlier lay dates were associated with higher reproductive rates. However, despite these changes suggesting higher reproduction rates with higher temperatures, they found no relationship between temperature and population growth, suggesting that some negative effect of temperature must be compensating for the increase in reproduction (McLean et al., 2016). We believe that the framework herein may be particularly useful in helping to identify where effects cancel and therefore provide target rates to be measured to determine whether a particular non-compensatory effect at one level is likely to influence the population growth rate. Another possible way non-compensatory effects could be canceled out is through feedbacks that are not currently incorporated into the minimal rate hierarchy model. For example, consider a predator–prey interaction in which a non-compensatory climate change effect increases the predator feeding rate which, in turn, increases prey extrinsic mortality and decreases the prey population growth rate and density. As predator feeding rates are increasing functions of prey densities, lower prey densities could feedback to lower predator feeding rates or could lead to reduced density dependence in the prey, which could alter birth or death rates. Although this increases the complexity of understanding non-compensatory climate change impacts, applying the framework to think through these possibilities makes clear where these feedbacks might emerge and how they might ultimately affect population growth rates. The framework also facilitates the identification of rates researchers should focus on measuring to understand population-level climate change responses.
One impetus for the development of the framework herein was that there is often a disconnect in the literature between traits measured and their inferred effects on downstream climate change responses of interest. For example, differences among species in thermal performance curve properties are often used to suggest the existence of differential responses to temperature that will impact the system (Cohen et al., 2017; Gsell et al., 2023; Meehan & Lindo, 2023). Yet, applying the framework here, it becomes clear that the relevance of differences in thermal performance curves and whether they lead to non-compensatory climate change effects is dependent on what trait is being compared among species, where the response of interest occurs within the rate hierarchy, and how ‘performance’ at that position in the rate hierarchy translates to the downstream rate of interest. For example, in seeking to explain the temperature dependence of chytrid prevalence in frogs, Cohen et al. (2017) performed an experiment comparing frog-preferred temperatures, chytrid growth rates in culture, and chytrid growth rates on frogs. Although chytrid growth rates on frogs are indeed likely to be a determinant of prevalence, applying the framework to this problem would suggest that the temperature dependence of several other processes should also be considered, such as the susceptibility of the frogs to infection and chytrid spore survival. If the temperature dependencies of these processes are well-correlated, these extra considerations may not be necessary, but, in general, this will be an assumption that requires testing. As another example, the relationship between sprint speed and temperature is commonly measured in the literature (Hertz et al., 1983; van Berkum, 1988) and often taken to be correlated with overall organismal performance. However, in our framework, sprint speed is likely to be a trait near the base of the hierarchy that may or may not alter feeding rates depending on how sprint speeds, predator attack or prey escape rates, and their relationships with temperature combine (Öhlund et al., 2015). Further, as a rate near the base, taking into account all of the other possible temperature responses in the rate hierarchy, it becomes clear that differences in temperature effects on sprint speeds of predator and prey need not result in non-compensatory demographic effects or be directly correlated with the overall relationship between temperature and population growth (fitness) at the highest level of the hierarchy. Overall, we hope that this framework can help researchers identify which rates are important to measure for a particular process of interest and for making inference on how or if those rates are likely to scale to bring about population-level changes.
Throughout, we also have assumed that non-compensatory climate change responses and their potential impacts are constant. However, individual variation in sensitivity to climate change creates the opportunity for natural selection to lead to an eco-evolutionary feedback (Palkovacs & Hendry, 2010; Yoshida et al., 2003) that in turn could alter the prevalence and consequences of non-compensatory effects. This also highlights the potential role that plasticity may play in moderating non-compensatory climate change effects. As mentioned above, effects on population density from non-compensatory climate change responses could alter the environments to produce additional feedbacks or phenotypic plasticity that counteract or generate new non-compensatory effects. Such changes are likely to depend on the specifics of systems (e.g., is there heritable variation in a particular climate change response involved in affecting a downstream rate?), but studies focusing on these processes will provide important information on how organisms might adapt to the consequences of non-compensatory climate change responses and climate change more generally.
Understanding how species are responding to climate change is pressing. Non-compensatory effects of climate change on intra- and interspecific biological rates are likely to be playing a critical role in determining consequences for population growth rates. Here we provide a broadly applicable and flexible rate-hierarchy framework that we hope will allow researchers to identify critical areas and traits within their study systems in which non-compensatory climate change effects may occur and to place identified effects within the framework to predict when non-compensatory effects will influence population-level responses to climate change.
AUTHOR CONTRIBUTIONS
Kyle E. Coblentz: Conceptualization; investigation; project administration; supervision; writing – original draft; writing – review and editing. Lisa A. Treidel: Conceptualization; investigation; writing – original draft; writing – review and editing. Francis P. Biagioli: Conceptualization; investigation; writing – original draft; writing – review and editing. Christina G. Fragel: Conceptualization; investigation; writing – original draft; writing – review and editing. Allison E. Johnson: Conceptualization; investigation; visualization; writing – original draft; writing – review and editing. Dinelka D. Thilakarathn: Conceptualization; investigation; writing – original draft; writing – review and editing. Liuqingqing Yang: Conceptualization; investigation; writing – original draft; writing – review and editing. John P. DeLong: Conceptualization; investigation; project administration; writing – original draft; writing – review and editing.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflicts of interest.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no data were created or analyzed in this study.