Population variability complicates the accurate detection of climate change responses
Abstract
The rush to assess species’ responses to anthropogenic climate change (CC) has underestimated the importance of interannual population variability (PV). Researchers assume sampling rigor alone will lead to an accurate detection of response regardless of the underlying population fluctuations of the species under consideration. Using population simulations across a realistic, empirically based gradient in PV, we show that moderate to high PV can lead to opposite and biased conclusions about CC responses. Between pre- and post-CC sampling bouts of modeled populations as in resurvey studies, there is: (i) A 50% probability of erroneously detecting the opposite trend in population abundance change and nearly zero probability of detecting no change. (ii) Across multiple years of sampling, it is nearly impossible to accurately detect any directional shift in population sizes with even moderate PV. (iii) There is up to 50% probability of detecting a population extirpation when the species is present, but in very low natural abundances. (iv) Under scenarios of moderate to high PV across a species’ range or at the range edges, there is a bias toward erroneous detection of range shifts or contractions. Essentially, the frequency and magnitude of population peaks and troughs greatly impact the accuracy of our CC response measurements. Species with moderate to high PV (many small vertebrates, invertebrates, and annual plants) may be inaccurate ‘canaries in the coal mine’ for CC without pertinent demographic analyses and additional repeat sampling. Variation in PV may explain some idiosyncrasies in CC responses detected so far and urgently needs more careful consideration in design and analysis of CC responses.
Introduction
Populations of all organisms, animals to plants and aquatic to terrestrial, exhibit natural variability in abundance year to year, often fluctuating tremendously (Fig. 1a, b; Ariño & Pimm, 1995; Cyr, 1997; Pimm & Redfearn, 1988). Amidst these natural population peaks and troughs, researchers seek to determine how often and in what ways species are responding to anthropogenic climate change (CC). Despite the intricate links between population dynamics and CC responses, effects of interannual population variability have been understudied and underestimated in the CC literature. Here we demonstrate just how critical population stochasticity is to the accuracy of detected CC responses.
Individual and comparative population dynamics, population cycling, and the underlying trends in environmental, demographic, and inherent population variability are the empirical basis of population biology (Elton, 1924; Andrewartha & Birch, 1954; Ricklefs, 1990; Begon et al., 1996). Thus, interannual population variability has an extensive history of study. Some species are known to exhibit extreme population variability with sequential years of moderate fluctuations followed by extreme outbreaks and crashes, for example, shrews (Matlack et al., 2002), field mice (Brady & Slade, 2004), moths (Varley, 1949), grasshoppers (Uvarov, 1977), desert annual plants (Huxman et al., 2008), and phytoplankton (Davis, 1964). Often the most conspicuous examples of such patterns are insect pests (e.g., Davidson & Andrewartha, 1948; Varley, 1949; Uvarov, 1977), but long-term, frequent monitoring of various communities (e.g., Matlack et al., 2002; Brady & Slade, 2004; Wittwer et al., 2015) has shown a wide range of population variability across vertebrate species. Generally, population variability decreases with increasing body size (Ricklefs, 1990; Morris & Doak, 2003; Begon et al., 1996). Large, long-lived species exhibit little population variability year to year, including ungulates (Davidson, 1938; Nicholls et al., 1996; Clutton-Brock et al., 1997), perennial plants and trees (Harper, 1977), and large birds (Perrins et al., 1991).
Population variability is also a key component of conservation biology and critical to estimations of extinction risk (e.g., Vucetich et al., 2000; Morris & Doak, 2003). Populations prone to dramatic peaks and crashes are at greater risk of extinction (e.g., Lande & Orzack, 1988; Vucetich et al., 2000). Similarly, metapopulation dynamics emphasize how the population dynamics of individual patches are influenced by varying degrees of population variability – higher population variability increases both the probability of patch extirpations at population lows and of recolonizations at population highs (e.g., Hanski & Gilpin, 1997 and references therein). At geographic range limits, range edges expand and contract as populations experience population highs and lows concordantly (e.g., MacArthur, 1972; Brown et al., 1996; Sexton et al., 2009). Given the empirically and theoretically demonstrated importance of population variability to many fields of biology and conservation, population variability must play an important role in our ability to detect CC responses.
Studies testing how species are responding to CC examine range and abundance changes, local extirpations, and phenological and genetic shifts by comparing historical and contemporary populations (resurvey studies) or by repeated surveys over many years (Parmesan & Yohe, 2003; Lenoir et al., 2008; Moritz et al., 2008; Chen et al., 2011; Rowe et al., 2011). Our assumption in these repeat surveys is that our ability to detect the CC signal is primarily a property of sampling quality – the consistency of methods between surveys, a strong sampling effort, and little disturbance of the sites between samples (e.g., Lenoir et al., 2008; Moritz et al., 2008; McCain & King, 2014; Bates et al., 2015). For a negative abundance response to CC, population size or population indices are predicted to decline between pre- and post-CC surveys or across multiple years of resampling (e.g., Mieszkowska et al., 2006; Rowe et al., 2011). But how often do such sampling windows fall within a natural population peak or trough (e.g., Fig. 1a, yellow sampling windows), and how might that influence the pattern detected? In a stochastically low-abundance year, we are less likely to detect that species in surveys (Fig. 1b; e.g., Seber, 1982). How do we assess whether what appears to be a local extirpation is a natural population fluctuation or a negative response to CC? Similarly for latitudinal or elevational ranges, if edge populations exhibit high population variability year to year (Fig. 1c; e.g., Sexton et al., 2009 and references therein), there may be natural range shifts, contractions, and expansions resulting from changes in population sizes and detectability. How often are shifts and changes in range size related simply to natural stochasticity rather than CC? How often are underlying responses to CC masked by natural stochastic noise? Such questions remain unexplored and untested, but may significantly influence the accuracy of our detected CC responses.
The highly idiosyncratic nature of responses documented to date indicates that such stochastic impacts may exist within current CC studies. Roughly half of studied species are responding negatively (e.g., declines in abundance, local extirpations, range contractions), another quarter positively (e.g., increasing in abundance, range expansions), and the final quarter exhibit no significant responses. For example, in the 73 mammals examined across studies, these percentages were 52% negative, 7% positive, and 41% no significant response (McCain & King, 2014). In only three of those cases were influences of population dynamics considered (Post & Forchhammer, 2008; Ozgul et al., 2010; Towns et al., 2010). In five resurvey studies of bird elevational ranges along the Californian Grinnell transects (Tingley et al., 2012) and the Papua New Guinea transects (Freeman & Class Freeman, 2014), these percentages were about 45%, 30%, and 26%, respectively. Among nine resurvey studies of plant, insect, and vertebrate ranges, these percentages were 65%, 24%, and 11%, respectively (Lenoir et al., 2010). Like most mammal studies, none of these resurveys considered the underlying population dynamics of the focal species.
We propose that since a large proportion of studies of organismal responses to CC have not considered the impacts of population variability, some results may be misleading, both overestimating and underestimating responses. Ideally, we would assess the influence of population variability by testing each CC response with empirical data from multiple species at different levels of population variability while manipulating the amount of CC. Such analyses would require not only years of demographic data per species to estimate population variability, but also a variety of species to capture a broad range of population variability in addition to various trends in CC impacts and responses. Long-term population studies of this type are vanishingly rare and nonexistent for all the myriad of CC scenarios and responses. Thus, robust, quantitative simulations across empirically-based parameter ranges are the only viable method to assess the severity of population variability consequences to a broad swath of our CC studies. Here we explored such sets of population simulations (Ricker models: Morris & Doak, 2003; Ricker, 1954) to investigate the influence of natural population variability on our ability to accurately detect three of the most commonly measured CC responses: population declines, local population extirpations, and range contractions.
Materials and methods
Population model structure
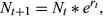
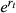. To introduce stochastic population variability, this growth rate was chosen each year from a normal distribution:
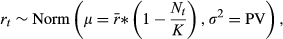
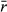, modified by density dependence with carrying capacity K, and variance equal to the population variability (Ricker, 1954; Morris & Doak, 2003). Thus, population variability is the variance of the log population growth rate across years due to environmental stochasticity (Morris & Doak, 2003). We ran sets of simulations to explore a reasonable span of natural population values that encapsulate the basic dynamics of a broad range of species (Table 1; e.g., Herrera, 1998; Liebhold, 1992; Morris & Doak, 2003; Nicholls et al., 1996; Sæther & Engen, 2002; Wang et al., 2013). Ranges of population variability (0–2) are based on known variability from the literature (e.g., Davidson, 1938; Davidson & Andrewartha, 1948; Varley, 1949; Davis, 1964; Harper, 1977; Uvarov, 1977; Perrins et al., 1991; Liebhold, 1992; Nicholls et al., 1996; Clutton-Brock et al., 1997; Herrera, 1998; Matlack et al., 2002; Sæther & Engen, 2002; Morris & Doak, 2003; Huxman et al., 2008) as well as empirical population variability calculated among small mammals from a 30-year mark and recapture study in Kansas (Brady & Slade, 2004; Wang et al., 2013; Slade pers. comm.: population variability = 0.59–1.88). Higher values than we investigated are possible (e.g., highly eruptive insect dynamics or unpredictable aquatic bacterial fluxes), but the asymptotic or linearly increasing nature of the current results is easily extrapolated to more extreme stochasticity. From this literature, we found it is somewhat rare to be on the extremes of little or maximum population variability, while most organisms exhibit intermediate values. Under the range of parameters explored, the deterministic version of the Ricker model exhibits damped oscillations and stability at the carrying capacity (Morris & Doak, 2003). Additionally, we chose the Ricker models because they are general, simple to understand, do not make additional assumptions about population dynamics as do more complicated models, and are commonly used in the population, conservation, and theoretical biology literature (e.g., Seber, 1982; Morris & Doak, 2003; Melbourne & Hastings, 2008).| Parameter | Symbol | Values/range |
|---|---|---|
| Abundance changes | ||
| Average log intrinsic growth rate |
|
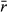
0.25, 0.75, 1.25 |
| Population variability (PV = variance in r) | σ 2 | 0.005–2.0 |
| Initial pop. size | N 0 | 100 |
| Initial carrying capacity | K 0 | 102 |
| Final carry capacity, no CC | K final,none | 102 |
| Final carry capacity, negative CC impact | K final,neg | 30.6 (−70%), 81.6 (−20%) |
| Final carry capacity, positive CC impact | K final,pos | 173.4 (+70%), 122.4 (+20%) |
| Survey length | w | 1, 3, 5 years |
| Number of surveys | # | 2, 5, 7, 10, 20 |
| Local extirpations | ||
| Average log intrinsic growth rate |
|
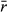
0.25, 0.75, 1.25 |
| Population variability (PV = variance in r) | σ 2 | 0.005–2.0 |
| Initial pop. size | N 0 | 100 |
| Carrying capacity | K | 50, 100, 500, 1000 |
| Individual detection rate | r d | 0.02–0.40 |
| Survey length | w | 1, 3, 5 years |
| Range contractions | ||
| Average log intrinsic growth rate |
|
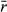
0.75 |
| Constant, high PV |
|
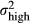
1.5 |
| Constant, low PV |
|
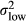
0.05 |
| Increasing PV: edge to center populations |
|
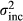
0.05–1.5 |
| Decreasing PV: edge to center populations |
|
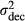
1.5–0.05 |
| Number of populations | n | 15 |
| Initial pop. size | N 0 | 100 |
| Constant and center population sizes | K c | 100 |
| Decreased edge populations (3 low, 3 high) | K e | 25, 50, 75 |
| Among-population correlation | Pop. Corr. | 0–1 |
| Survey length (cons. or alter.) | w | 1–5 years |
- All possible combinations of the listed parameters were simulated.
Detecting abundance change
To assess the influence of population variability on the ability to detect underlying abundance responses to climate change (CC; e.g., Fig. 1a), populations were simulated each for 50 time steps (i.e., 50 years), with steps 0–20 as a pre-CC stage, and steps 21–50 a post-CC stage. In all cases, the starting carrying capacity (K0 = 102) was constant during the pre-CC stage. Across the post-CC stage, the carrying capacity changed linearly each year, ending at a moderate decrease (−20%), a large decrease (−70%), a moderate increase (+20%), a large increase (+70%), or no change (K0). In these simulations, we varied population variability (σ2),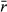 
, Kfinal, the survey length, and the number of surveys, and ran 3000 simulations for each combination of parameter values (Table 1). We chose values for 
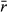to represent populations with slow, medium, and fast average annual growth rates (0.25, 0.75, and 1.25, respectively). Population variability is bounded theoretically by 0, representing a population with no stochasticity in the growth rate. We modeled up to population variability = 2.0 which depicts marked and frequent peaks and troughs in population sizes year to year (Fig. S1).
In resurveys, to assess the abundance shifts between pre- and post-CC surveys, yearly abundances were extracted without sampling error starting at step 10 in the pre-CC stage and ending at step 50 for the post-CC stage in each simulation. We reran all simulations varying both survey lengths as 1, 3, or 5 years. The longer survey lengths encompassed more population variability, potentially dampening its effects on CC response detection. The average abundance was calculated for each survey period, and percentage change in abundance (and change in estimated K, for 5 year samples) was calculated between samples. We recorded abundance decreases or increases using three threshold levels of change (±10%, 15%, or 20%); if the change was below the threshold, the population was considered to show no abundance response to CC. These thresholds span a range of liberal to conservative abundance change; higher thresholds were not included as the lower limit of modeled CC was 20% change. Each simulation result was then compared to the underlying modeled CC trend of decreasing, increasing, or stable carrying capacity. Finally, the probability of correctly detecting CC trends was calculated as the proportion of simulations that revealed the underlying trend for each scenario at the various survey lengths.
In time-series surveys, the same simulations were used, but in this case 5, 7, 10, or 20 evenly spaced, single-year populations were extracted across pre- and post-CC stages starting at year 10 and ending at year 50. Linear regressions assessed whether the population trend was declining, increasing, or steady at two levels of significance: P ≤ 0.05 to be strict in trend detection and P ≤ 0.10 to be liberal in trend detection. The probability of correctly detecting CC trends was calculated as above from all 3000 simulations for each scenario and set of parameters.
Detecting local extirpations
To assess the likelihood of local extirpations due to population variability, we used Ricker models as described above, but included individual detection rates (e.g., difficult or easy to capture, sample, or sight) based on a known range of values from the literature (e.g., Otis et al., 1978; Seber, 1982; Lebreton et al., 1992; Alexander et al., 1997; Williams et al., 2002). In these simulations, we did not impose a CC trend, but only assessed the influence of population variability on population detection within a single snapshot of the population rather than trends over time. Nonetheless, the results are indicative of any comparison among surveys across time with or without CC imposed. Simply, these simulations depict how often a population is undetectable even without a negative CC impact, but due to population dynamics alone (e.g., Fig. 1b). Such population variability-induced nondetections would be difficult to discern from CC-induced extirpations.
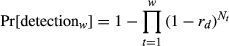
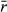= 0.25, 0.75, 1.25), a range of underlying population variability (0.0–2.0), and three survey lengths (w = 1, 3, 5 years).Detecting range contractions
Range contraction simulations (e.g., Fig. 1c) were constructed as Ricker models for each of 15 closed populations across a hypothetical elevational gradient of 1500 m (i.e., a population every 100 m). The modeled elevational range and spacing between populations is hypothetical and could just as easily be depicting populations every 300 m elevationally, 100 km latitudinally, or any set of equidistant populations across a gradient of interest. Rather than exploring a broad parameter space, we chose a smaller range of illustrative parameter sets due to the unwieldy range of possible parameter combinations and individual population dynamics. Thus, we investigated four patterns of population variability across the gradient and two patterns of K (see insets in Fig. 5). Population variability scenarios include the following: equally high (1.5) or low (0.05) population variability in all populations, and increasing (0.05–1.5) or decreasing (1.5–0.05) population variability from the range edges to the center population. Although previous simulations included more extreme values, we chose these values to be more representative of a range in typical species. K was modeled either as constant in all populations (K = 100) or decreasing toward the range edges (each three edge populations: K = 25, 50, 75). Populations are often smaller and more variable at range edges (e.g., Brown, 1984; Brown et al., 1996; Sexton et al., 2009), and thus, these scenarios explore range-edge dynamics and constancy across the hypothetical gradient. We used the medium average growth rate (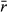
) for all populations. Lastly, to represent the potential for populations along a gradient to experience the same good or bad years, we explored a range of correlation in the population variability of the populations: no correlation (0) where the growth rate stochasticity of each population is independent of all other populations, total correlation (1) where that stochasticity is perfectly correlated among all populations, and an intermediate correlation (0.5) where dynamics are related but have some level of divergence among years.
For each combination of parameters, the 15 populations were surveyed at 3000 time steps (‘survey points’) to measure whether individual populations fell below a single individual, indicating an extirpation. Then using range interpolation, we assumed presence at all sites between the lowest and highest extant populations, and calculated the size of contraction from the initial range of 1500 m at each survey point (see Animation S2). To examine the effect of repeat surveys on the detection of stochastic range contractions, we reassessed these models with a sampling scheme of multiple consecutive years (years 1–2, 1–3, or 1–5) and multiple alternating years (years 1 and 3 or 1, 3, and 5). In all cases, absolute abundances were used rather than incorporating sampling and detection error. Although the latter may be more realistic, it would proportionally exacerbate the impact of population variability.
Results
Among the simulated parameters (Table 1) for the three commonly measured responses to climate change (CC) – abundance changes, local extirpations, and range contractions – the amount of interannual population variability had the largest impact on accurate detection of response. Surprisingly, survey length and number, average population growth rate, carrying capacity, and individual detection rate were much less impactful.
Detecting abundance change
Pre- and postclimate change resurveys
The probability of correctly detecting an abundance change in concordance with the underlying CC – whether positive or negative – drops precipitously to around 50–60% accuracy with only moderate population variability year to year (Figs 2a–f and S2a–d). Only very stable populations with population variability <0.1 have a greater than 80% likelihood of detecting an abundance shift in concordance with the actual CC response, but only if the CC response is large (i.e., 70% increase or decrease in carrying capacity; solid thick lines). Under the low CC response (20%; dashed thin lines), the probability of correct detection of an abundance change drops extremely rapidly and asymptotes near 50–50 accuracy at a relatively low population variability (<0.5). It is nearly impossible in this two-survey comparison to detect no abundance change (Fig. 2g–i). When no change in carrying capacity is modeled, all detect an erroneous positive or negative change in abundance with the exception of populations with almost no variability (<0.1; Fig. S2e). Thus, due to repetitive, stochastic population peaks and troughs, nearly all tests between two sampling periods detect a significant abundance shift regardless of the modeled CC impacts, with roughly half detecting increases and half detecting decreases (Fig. S2a–e). Only populations with population variability approaching zero allow reliable detection of underlying population change in the resurvey comparisons.
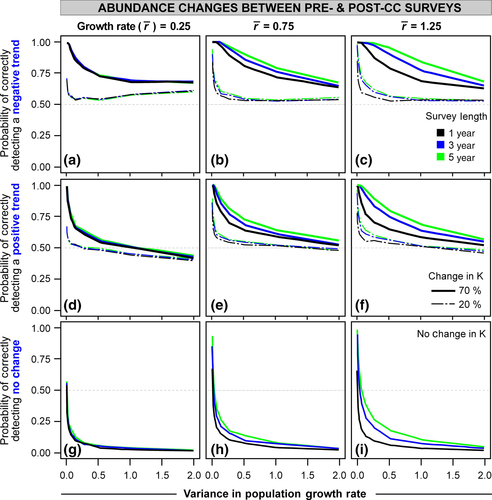
Survey sampling length had relatively little impact despite our methodological assumptions that more sampling will always improve accuracy. Likewise, intrinsic growth rate (Fig. 2 columns) did not substantially affect results, nor did changing the threshold for detection of change (10%, 15%, 20%; Fig. S3). For 5-year sampling windows, estimating K in each sample did not produce qualitatively different results.
Time series of population surveys
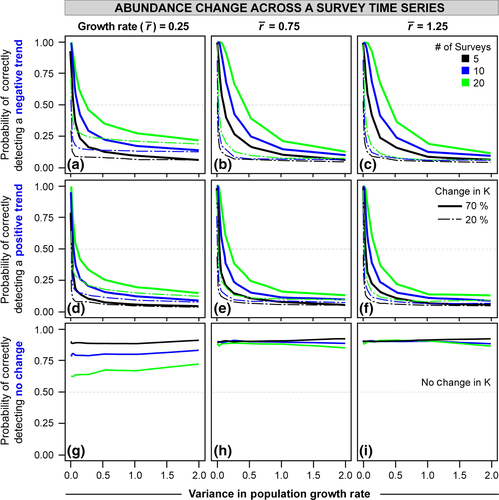
In the population time-series scenario, correctly detecting a significant underlying positive or negative trend is quite improbable even with modest amounts of population variability (Fig. 3a–f). The probability of correct detection of the CC response declines rapidly in all scenarios even with a small amount of population variability (<0.5) and then asymptotes quickly thereafter between 0 and 25% probability of accuracy. The population trajectory erroneously identified in these cases is no change (stasis; Fig. S2f–i). The probability of correctly identifying stasis is nearly 100% (Fig. 3g–i). The exceptions to accurate stasis are the scenarios at lowest growth rate and 10–20 surveys where occasionally significant, but erroneous, positive, or negative population trends are detected (Figs 3g and S2j). A larger magnitude of carrying capacity change (K = 70% vs. 20% change due to CC) increases the probability of correct pattern detection. But this impact is most evident at low to mid-population variability values (Fig. 3 line weights and dashes). The number of sampling surveys and variation in average growth rate had relatively little impact (Fig. 3, line colors and columns, respectively). These results (Fig. 3) are for a liberal trend detection (P = 0.10); the results are almost identical with a more conservative trend detection (P = 0.05), although the latter has more rapid decreases and plateaus closer to zero probability. Overall in time series, even with occasional peaks and troughs in the population, most underlying CC response is undetectable even if the underlying carrying capacity has declined drastically.
Detecting local extirpations
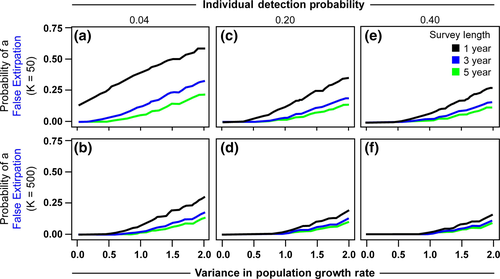
Across the parameter space, apparent extirpations increase with more population variability (Fig. 4; Animation S1). Overall, 10–60% of local population simulations result in a false extirpation at moderate to high population variability. Such false extirpations, indistinguishable from extirpations caused by CC, are most common when individuals are hardest to detect (Fig. 4a, b), when populations are small (upper panels), and when the sampling window is short (black lines). Surveying the populations among multiple years (blue and green lines) decreases the likelihood of falsely attributed CC extirpations, particularly for harder to detect species. For results of all parameter space explored in local extirpation simulations, see Animation S1.
Detecting range contractions
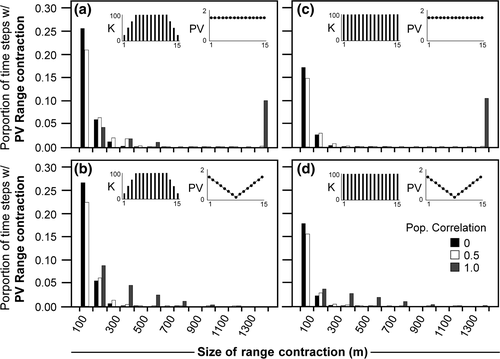
Range contractions are detected at significant levels (20–33%) for those scenarios of constant high population variability at all sites (Fig. 5a, c) and increasing population variability toward the range edges (Fig. 5b, d). See Animation S2 for examples of these simulations. Stochastic range contractions are not detected for scenarios of uniformly low population variability or low population variability at range edges. Highly correlated dynamics (i.e., all populations experience bad and good years similarly; 1.0 in gray in Fig. 5) lead to larger range contractions, including total range collapse, whereas less correlated dynamics (each population experiencing at least some independent stochasticity; 0 in black and 0.5 in white in Fig. 5) lead to smaller contractions, mostly 100–300 m. Small percentages of all simulations result in larger range contractions (400–1400 m: ~0.5–2% each; Fig. 5 small bars near unit line). All of these population variability-induced range contractions, regardless of size, would be difficult to distinguish from a CC response.
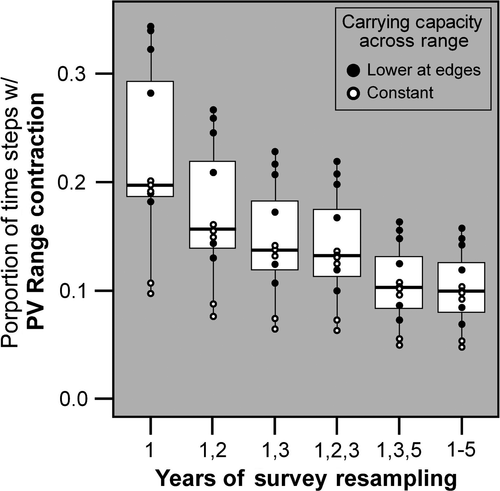
The size and frequency of population variability-induced, detected range contractions are reduced by various years of repeat sampling (Fig. 6). As in Fig. 5, smaller population sizes at range edges lead to a greater proportion of range contractions (solid black circles) compared to constant high populations across the gradient (white circles). Two, three, and five years of repeat sampling lead to increasingly fewer population variability-induced range contractions. For the same number of sampling bouts, alternating years of sampling (1 and 3; 1, 3, and 5) led to a more rapid drop in population variability-induced, range contractions than consecutive repeat sampling (1 and 2; 1–3).
Discussion
Our simulations display how easily interannual population variability alone can lead to the same patterns we are trying to detect in assessing climate change (CC) impacts (Figs 2-6). Accurate detection of CC responses necessitates the consideration of underlying population variability effects. The influence of population variability extends beyond species with extreme abundance fluctuations, as most scenarios reached critical differences at population variability values as low as 0.25–0.50. Abundance responses were the most obscured by population variability, with either nearly half incorrect (resurveys) or uniformly underestimating any CC effect (time series). Local extirpations for single populations and at range edges occurred regularly due to population variability. Such fluctuations in population detection occurred more often with greater population variability, but would be more exaggerated for species that are difficult to detect, occur in low abundances, and/or were surveyed for a short snapshot of time. Our simulations were constructed with perfect knowledge of the abundance and in all cases except local extirpation, every individual was perfectly detectable. Including the sampling realism of field studies (sampling error, lower detection probabilities, population indices) would further obfuscate the potential responses to CC (Seber, 1982; Begon et al., 1996 and references therein). Adding to this complexity is the potential that a species’ population variability itself may be modified by anthropogenic climate change as environmental stochasticity is altered. Overall, our results highlight the dramatic effect of natural population variability on the ability to accurately detect responses to CC. More study design and analysis precautions are urgently needed to distinguish CC impacts from effects of natural population fluctuations.
Pre- and postclimate change resurveys
Given that the accuracy of two-survey comparisons is nearly equal to a coin toss, we suggest they are unwise estimates of organismal responses to CC. In most field studies, there will be greater error than these simulations due to short sampling periods, use of population indices, and different sampling methods between surveys (e.g., museum specimens vs. live trapping; sighting records vs. call point counts; citizen scientists vs. field biologist records). The only cases where resurvey abundance comparisons could be potentially robust are for populations that are very stable across time, particularly long-lived, large vertebrates, trees, and shrubs.
Possibly due to these inherent drawbacks of resurvey abundance, there are fewer of these assessments in the literature. But given the historical databases of surveys, specimen records, bird counts, and citizen scientist logs, these types of abundance data are relatively available. Such resurveys for CC response are therefore tempting. But we urge caution. For example, in a resurvey of Great Basin small mammals (Rowe et al., 2011), which have moderate to high population variability, our simulation results would predict probabilities of 40–60% decline and increase, and 5–10% no change. Their detected percentages were nearly identical: 41% increased, 50% decreased, and 9% did not change. Additionally, analyses of other aspects of a species’ biology between pre- and post-CC surveys – phenology changes or genetic diversity changes (e.g., Bradley et al., 1999; Mieszkowska et al., 2006; Taylor et al., 2014) – can be highly influenced by the underlying differences in abundance shown here. For example, in years of high abundance, more individuals are detected, increasing both the detected and the real interindividual variance in phenology, making earlier occurrences more likely, and more likely to be detected. So careful consideration of how underlying population variability could influence results in those cases is also warranted.
Time series of population surveys
Only populations with very low population variability (<0.25) provide accurate assessments of abundance change over time and usually only if the CC impact is strong. Otherwise, it is difficult to detect any significant changes even if they are occurring and putting species at high risk. Some of the species thought to be declining in response to CC, for example, polar bears (Towns et al., 2010) and caribou (Post & Forchhammer, 2008), are large, long-lived and exhibit low population variability, and are thus likely to be quite accurate, whereas studies of multiple species of various body sizes and levels of population variability (e.g., Inouye et al., 2000; Koontz et al., 2001; Myers et al., 2009) may have a higher risk of erroneous results particularly if no change has been detected. In cases of long-term population monitoring, estimates of population variability, juvenile and adult survival, or growth rates in a more sophisticated demographic framework (e.g., structured population models) are possible and much more statistically powerful in detecting change than regressions. Therefore, such long-term, robustly collected data have the capability of much more robust results if handled carefully and quantitatively, even with moderate population variability (e.g., Post & Forchhammer, 2008; Ozgul et al., 2010). But in cases of heterogeneously collected abundance data (e.g., not standardized monitoring programs), claims of minimal CC response should be treated with caution for all but the low population variability populations unless quantitative assessments or simulations of error potential are evaluated.
Local extirpations
Based on the empirical support for source–sink and metapopulation dynamics, we know populations come and go stochastically at single localities (e.g., Ricklefs, 1990; Hanski & Gilpin, 1997; Hanski & Simberloff, 1997; Begon et al., 1996 and references therein). Our population variability simulations also exhibit how tightly linked local extirpations are to population fluctuations, and how easily such extirpations are exacerbated by low detection probabilities, low population sizes, and short-term surveys. Such abundance fluctuations lead to local extirpations or populations too low for detection, which are difficult to distinguish from a CC-induced extirpation. Many CC-extirpation studies could include this potential influence (Parmesan, 1996; Beever et al., 2003; Epps et al., 2004; Floyd, 2004; Hickling et al., 2005; Larrucea & Brussard, 2008; Erb et al., 2011; Hubbard et al., 2014). Most did not conduct multiple resurveys of extirpated populations, but those that did documented extirpations that had been recolonized or populations that rebounded naturally (Beever et al., 2011; Erb et al., 2011). Thus, in CC-extirpation studies, the key is multiple repeat sampling (Fig. 4) to document a longer-term, local extirpation which has a stronger signature of CC impact. Additionally, caution should be used when evaluating species that are difficult to detect, when historical and contemporary surveys use different indices of detection, or different detection methodologies. Extirpations in populations within the well-established and persistently occupied central portions of ranges, rather than range-edge populations may also be a better indicator of CC responses.
Range contractions
Elevational and latitudinal range contractions and shifts are the most common CC responses measured in the literature (Lenoir et al., 2010; Chen et al., 2011; McCain & King, 2014 and references therein). In a recent review (Chen et al., 2011), the median upward shifts were ~40 m in elevation and 45 km in latitude, respectively, across arthropod, plant, and vertebrate datasets (# of studies = 31 (elevation), 22 (latitude)) regardless of the expected shift given the amount of warming. In fact, among the datasets, four exhibited small average range expansions, and only one averaged over 100 m elevational shift upward (108.6 m for butterflies in Spain). Many detected negligible changes in terms of the scale of field studies along latitudinal or elevational transects which tend to be conducted at 100 m/100 km bands or greater (25% were <25 m or 25 km of change). Although these constitute a significant amount of change taken together and a coherent fingerprint of CC, this average change is quite small. One reason the averages are smaller is because some species’ ranges are contracting or shifting whereas others are expanding or not changing. There is a high probability given the results of population variability simulations presented here that some of that variability and some amount of range fluctuation over time are due to natural population dynamics at or near range edges (Figs 5 and 6).
Higher population variability at range edges is the norm according to a recent review (Sexton et al., 2009) and is the likely scenario for many range shift studies. In some cases, populations at or approaching range edges are smaller (Brown et al., 1996; Sexton et al., 2009 and references therein). These two conditions lead to the greatest proportion of range contraction exhibited in our simulations (Figs 5 and 6). Although we did not simulate range shifts, expansions, or changing weighted elevational midpoints (Lenoir et al., 2008), similar results would be expected due to the high probability of intermittent population lows and highs, and temporary local extirpations associated with population variability across a range and at range edges.
In studies where the historical surveyors collected all individuals in each population or kept detailed notes of population sizes at the identical sites of resurvey (e.g., Moritz et al., 2008; Tingley et al., 2009), the influence of population variability can be reduced by employing occupancy modeling techniques. But even in those cases, each survey necessarily captures a small time slice of variable populations; the probability that some populations were at stochastic abundance peaks or troughs is substantial and unavoidable. In cases where the historical surveys occurred during population lows, particularly at range edges, some proportion of range expansions with modern resurveys would also be expected due to population variability alone. Since improving modern resurvey data is the only option, including multiple consecutive (2, 3 and 5 years) and alternating years of sampling (years 1 and 3, or 1, 3, and 5) decreases the proportion of resurveys with range contractions. Nonconsecutive years of sampling had a larger impact for the same number of years sampled (false contractions <10%) due to the greater variability captured among more widely spaced years. Thus, like local extirpations, geographic range change studies should adopt repeat sampling designs, ideally nonconsecutive years for efficiency, to ensure robust detection of a CC trend rather than a demographic trend. So far, repeat sampling of range shift data is exceedingly rare (e.g., Beever et al., 2011).
How can we modify our field studies to reduce population variability effects?
To confidently assess responses to CC, the population variability of the populations of interest must be known at least as a rough estimate. True estimates of population variability differ for species across their range and among populations, so like other population parameters are difficult to assess accurately (e.g., Morris & Doak, 2003; Gonzalez-Suarez et al., 2006; Begon et al., 1996; and references therein). They are generally underestimated with short time spans of demographic data (e.g., Gerber et al., 1999; Morris & Doak, 2003 and references therein). Thus, a valuable rule of thumb would be to estimate a potential range of population variability within which your population, species, or clade falls (e.g., very low (<0.25), low (0.25–0.50), moderate (0.50–1.0), or high (>1.0)). As can be seen in most of the simulations, population variabilities below 0.50 have decreasing probabilities of error as they approach zero, whereas above 0.5 the error probabilities start to plateau. Unless a population has very low population variability, conclusions likely need a strong consideration of a potential population variability effect. Additionally, for assessments across species’ elevational and latitudinal ranges, it is likely that population variability is higher near range edges and possible that carrying capacities are lower. Once the estimate of population variability error is established, consider carefully how intermittent peaks and troughs in your population may influence the measured response and how it may be compounded by your sampling design (greater influences with the two-window resurveys) and your sampling error (indices, individual detectability, differences in methodology historically vs. contemporarily). Do you have additional lines of evidence that these changes are CC vs. demographic?
Recent state-space models to detect population trends and extinction probabilities, including approaches that use multi-population data, could be adapted to improve the detection of CC effects (Dennis & Ponciano, 2014; See & Holmes, 2015). Additionally, simulations constructed specifically for your system, similar to those here, could be used to estimate probabilities of error for each species, clade, and/or response. One lesson from these new state-space methods is that repeated sampling is necessary to draw strong conclusions about population dynamics (Dennis & Ponciano, 2014; See & Holmes, 2015). Similarly, sampling several years, ideally nonconsecutively, reduces false CC signal for local extirpation and range change studies by capturing more interannual fluctuation (Figs 4 and 6; Animation S1). We urge more repeat sampling, particularly for presence–absence studies of local extirpation and range changes, to increase the confidence that detected responses are the result of CC impacts rather than an effect of short-term stochastic fluctuation. Lastly, for published results, a re-evaluation in light of population variability influences may be warranted. Clearly, CC is impacting species as multiple reviews show convincingly (e.g., Parmesan & Yohe, 2003; Walther et al., 2005; Thomas et al., 2006; McCain & King, 2014, and references therein), but the strength of individual signals detected so far for abundance, extirpation, and range changes may be overly simplistic and possibility misinterpreted as either overly dire or severe underestimates. Thus, the impacts of interannual population variability urgently need more careful consideration in design and analysis of CC responses.
Acknowledgements
This work was supported by the US National Science Foundation (McCain: DEB 0949601). We thank Norm Slade for access to his 30-year dataset on small mammal populations in eastern Kansas, and Daniel Doak, Jan Beck, and three thoughtful reviewers for feedback on manuscript drafts.
