Leaf and stem economics spectra drive diversity of functional plant traits in a dynamic global vegetation model
Abstract
Functional diversity is critical for ecosystem dynamics, stability and productivity. However, dynamic global vegetation models (DGVMs) which are increasingly used to simulate ecosystem functions under global change, condense functional diversity to plant functional types (PFTs) with constant parameters. Here, we develop an individual- and trait-based version of the DGVM LPJmL (Lund-Potsdam-Jena managed Land) called LPJmL- flexible individual traits (LPJmL-FIT) with flexible individual traits) which we apply to generate plant trait maps for the Amazon basin. LPJmL-FIT incorporates empirical ranges of five traits of tropical trees extracted from the TRY global plant trait database, namely specific leaf area (SLA), leaf longevity (LL), leaf nitrogen content (Narea), the maximum carboxylation rate of Rubisco per leaf area (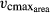
), and wood density (WD). To scale the individual growth performance of trees, the leaf traits are linked by trade-offs based on the leaf economics spectrum, whereas wood density is linked to tree mortality. No preselection of growth strategies is taking place, because individuals with unique trait combinations are uniformly distributed at tree establishment. We validate the modeled trait distributions by empirical trait data and the modeled biomass by a remote sensing product along a climatic gradient. Including trait variability and trade-offs successfully predicts natural trait distributions and achieves a more realistic representation of functional diversity at the local to regional scale. As sites of high climatic variability, the fringes of the Amazon promote trait divergence and the coexistence of multiple tree growth strategies, while lower plant trait diversity is found in the species-rich center of the region with relatively low climatic variability. LPJmL-FIT enables to test hypotheses on the effects of functional biodiversity on ecosystem functioning and to apply the DGVM to current challenges in ecosystem management from local to global scales, that is, deforestation and climate change effects.
Introduction
The links between biodiversity effects and ecosystem functioning (hereafter BEF) (Hooper et al., 2012; Naeem et al., 1994) are still insufficiently understood and are therefore in the spotlight of ecological research (Loreau et al., 2001; Naeem & Wright, 2003; Hooper et al., 2005; Balvanera et al., 2006). In particular, functional diversity supports ecosystem functioning (Violle et al., 2007; Suding et al., 2008; Sterk et al., 2013), stability and productivity (McCann, 2000; Diaz & Cabido, 2001; Morin et al., 2011), and resilience against disturbances and environmental variability (Mori et al., 2013).
To predict ecosystem functioning at regional to global scales (Sitch et al., 2008), dynamic global vegetation models (DGVMs) (Prentice et al., 1992) simulate processes of vegetation dynamics and hydrology. However, most current DGVMs condense functional diversity to the smallest scale possible using plant functional types (PFT) (Woodward & Kelly, 1997) in a monoculture-like approach at the biome level (Poulter et al., 2011; Scheiter et al., 2013) with fixed bioclimatic limits and often calibrated parameters which prescribe their simulated performance under varying environmental conditions. This reductionist PFT approach eliminates sources of natural trait variability which, at the time of model design, was inevitable due to the lack of plant trait data and computational power.
With increased computational capabilities, the preconditions to better acknowledge natural functional diversity and plant trade-offs in DGVMs are generally fulfilled (Van Bodegom et al., 2012). At the same time, there is a recent boost in trait-based ecology that aims to identify leading axes of plant strategy variation (Westoby & Wright, 2006), and a growing theoretical and empirical body on global plant trait spectra related to the economics of leaves and stems (Wright et al., 2004; Chave et al., 2009; Baraloto et al., 2010; Kattge et al., 2011). Bridging the gap between the research fields of DGVMs and functional ecology by modeling trait variability is crucial to disentangle the influence of abiotic factors from BEF in a spatiotemporally heterogeneous environment (Hector & Bagchi, 2007; Hillebrand & Matthiessen, 2009; Reiss et al., 2009). Such an approach would also take the empirical trait-based approach important steps further by 1) scaling up from individual tissue traits to whole-plant performance, ecosystem processes and services and 2) providing a better predictive framework for ecological patterns and their societal consequences at larger spatial and temporal scales (Van Bodegom et al., 2012).
We re-implemented the existing DGVM LPJmL (Lund-Potsdam-Jena managed Lands) (Sitch et al., 2003; Bondeau et al., 2007) with flexible individual traits (LPJmL-FIT) as an individual-based gap model (Bugmann, 2001; Taylor et al., 2009). This allows simulating individual trees with unique trait combinations which compete for resources within a distinctive patch. We applied LPJmL-FIT to generate plant trait maps for the Amazon region because the Amazon is the largest remaining forest with high tree functional diversity on Earth (Kraft et al., 2008) and of critical importance for the global carbon cycle and carbon cycle–climate feedbacks (Cox et al., 2013). This is the first study, where detailed, basin-wide patterns in trait distributions and diversity of functional plant traits are quantified applying a trait-based DGVM. We conducted a series of simulation experiments to assess the effects of model complexity on the resulting trait distributions, diversity of plant traits, and vegetation carbon.
LPJmL-FIT features five variable plant traits connected via trade-offs derived from global plant trait data. This opens up a realistic global trait space. We focus on the traits specific leaf area (SLA), leaf longevity (LL), leaf nitrogen content (Narea), the maximum carboxylation rate of Rubisco per leaf area (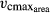
) and wood density (WD) because these traits determine the individual performance of tree individuals through their effects on growth and mortality (Violle et al., 2007). The leaf traits are linked by empirically established trade-offs based on the leaf economics spectrum (LES) (Reich et al., 1997, 1999; Wright et al., 2004; Shipley et al., 2006) which describes a set of leaf trade-offs explaining worldwide leaf investment strategies. WD is linked to tree mortality following the idea of the stem economics spectrum (SES, Baraloto et al., 2010).
The main objective of this study is to develop a generalizable approach which incorporates continuous plant traits and their respective trade-offs in DGVMs (1) to add ecological realism to DGVMs by improving their representation of functional diversity by plant trait distributions and (2) to predict observed plant trait distributions and biomass. This way, we lay the foundations to test BEF-related hypotheses, for example, the insurance hypothesis, by associating changes in trait means, ranges and trade-offs with their effect on functional diversity and ecosystem-level indicators of plant performance, for example, biomass. Principally globally applicable, such a DGVM may complement the existing empirical knowledge of functional diversity and its relation to ecosystem functions.
Few other vegetation models such as the JEDI-DGVM (Reu et al., 2011a,b; Pavlick et al., 2012), the aDGVM2 (Scheiter et al., 2013), the trait-based version of the JSBACH model (Verheijen et al., 2013), and most recently, the Traits-based Forest Simulator (TFS) (Fyllas et al., 2014) also build upon trait-based growth strategies. Our DGVM approach differs from those models or their specific components for several reasons: LPJmL-FIT establishes individual trees with a number of variable traits. These traits range within their globally observed boundaries in natural ecosystems because their ranges are constrained by empirically derived trade-offs following the theory of LES and SES. This opens a multidimensional trait space including all ecologically reasonable trait combinations. Each of these trait combinations has the same probability to be assigned at tree establishment because no preselection (e.g., due to bioclimatic limits) is applied. During simulated vegetation dynamics, all possible trait combinations compete for light and water within the study area. The trait combinations which are best adapted to local environmental conditions survive and represent a subset of the initialized trait space which is then validated against observed trait data.
We discuss the relevance of our findings for ecosystem theory and its applications, that is, upscaling effects of continuous traits to whole-plant performance and their influence on trait distributions at the regional scale, thereby accounting for spatiotemporal heterogeneity, and conclude with an outlook on future DGVM applications in the prediction of future ecosystem transitions under global change such as the uncertain future of the Amazon rainforests (Cox et al., 2000, 2013; Malhi et al., 2009; Rammig et al., 2010).
Materials and methods
LPJmL-FIT: a new gap model version of LPJmL with flexible individual traits
Standard LPJmL is a process-based DGVM with nine generic PFTs representing natural vegetation at the level of biomes (Sitch et al., 2003; Gerten et al., 2004; Schaphoff et al., 2013), 12 crop functional types (CFTs) and managed grass (Bondeau et al., 2007). We re-implemented LPJmL in a gap model approach to account for the competitive effects between tree individuals with unique key trait combinations forming a highly diverse community of possible tree growth strategies. We deliberately model tree individuals with unique trait combinations, but not species, to elucidate how selective processes (i.e., environmental filtering and local competition) influence the performance of tree growth strategies. This level of abstraction allows to investigate how functional diversity influences community assembly, functional composition, and ecosystem functioning in a computationally feasible and spatially scalable approach.
To provide an overview about the structure of the new LPJmL-FIT model (cf. Fig. 1), we first discuss 2.2, 2.3 and 3, and then shortly describe the 4 and 5. All data processing and statistical analysis described in the methods sections were performed with the commercial software matlab® (MATLAB and Statistics Toolbox Release 2012b; The MathWorks, Inc., Natick, MA, USA).
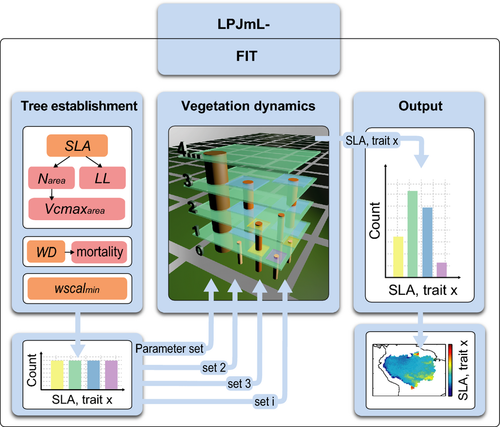
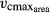give every possible trait combination within the parameter space the same chance to establish at a given location. (b) Vegetation dynamics: Trees compete for light and water while passing through distinct canopy layers during growth. A bottom layer (0) represents the C3- and C4-grass plant functional types (see video visualization of model output under: http://www.pik-potsdam.de/~borissa/video; documentation in Fig. S7). The location of individual trees within a patch is not spatially explicit so that total leaf area within a canopy layer is mixed. (c) Output: Individual trees above 5 m in height and their respective trait combinations are recorded each year. More competitive trait combinations show a higher contribution to the growing data set. A histogram of the simulated trait distribution (e.g., SLA) is established from a sufficient number of patches and simulation years (cf. 2). Local trait distributions enable to compile trait maps for a whole region.Tree establishment
Selection of key plant traits to be diversified in LPJmL-FIT
All empirical plant trait data were obtained from the global plant trait database TRY (Kattge et al., 2011) and were filtered for worldwide broad-leaved tree entries to investigate worldwide tree trait interrelations. We used worldwide data to create a generalizable approach enabling to make worldwide simulations. Rather than using averaged species trait values, we used all observations of broad-leaved trees recorded in the TRY database to conserve the intraspecific variability of traits. We focused on five key traits that are thought to capture the major axes of strategy variation across land plants, as they are related to the LES (Wright et al., 2004) and the SES (Baraloto et al., 2010). Traits included are SLA (leaf area per unit leaf mass, mm2 mg−1), LL (average lifespan of leaves, in months), leaf nitrogen content per leaf area (Narea, mg g−1), maximum carboxylation rate of Rubisco enzyme per leaf area (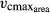
, μmol CO2 m−2 s−1), and WD (wood dry mass per unit of green volume, g cm−3). All TRY data we used relates to the following original references: (Cornelissen, 1996; Cornelissen et al., 1996, 2003, 2004; Castro-Diez et al., 1998; Atkin et al., 1999; Medlyn et al., 1999; Fonseca et al., 2000; Niinemets, 2001; Shipley, 2002; Shipley & Vu, 2002; Loveys et al., 2003; Ogaya & Penuelas, 2003; Quested et al., 2003; Xu & Baldocchi, 2003; Diaz et al., 2004; Wright et al., 2004, 2007, 2010; Preston et al., 2006; Campbell et al., 2007; Garnier et al., 2007; Swaine, 2007; Cornwell et al., 2008; Kleyer et al., 2008; Kurokawa & Nakashizuka, 2008; Reich et al., 2008, 2009; Shiodera et al., 2008; Chave et al., 2009; Fyllas et al., 2009; Kattge et al., 2009; Poorter et al., 2009; Freschet et al., 2010; Laughlin et al., 2010; Messier et al., 2010; Ordonez et al., 2010; Penuelas et al., 2010; Willis et al., 2010; Gutierrez & Huth, 2012).
Implementing trade-offs and diversifying model parameters
LPJmL-FIT implements three trade-offs (a–c), two of which (a–b) are part of the LES (Wright et al., 2004). The third trade-off (c) is part of the SES and accounts for the empirically observed negative relationship between wood density and tree mortality (see e.g., Chave et al., 2009 and references below). Detailed information on all derived regression functions, underlying composition and geographical origin of data, is given in Data S1 (Eqns 1–3; Figs S1–S4).
(a). The SLA-LL trade-off and its relation to Narea and tree phenology
There is a spectrum in leaf traits, running from productive short-lived leaves with high carbon returns and nutrient investments, to conservative, long-lived leaves with slow returns on investments. This implies a trade-off between potential rates of carbon return and the respective duration of return along the SLA-LL spectrum (Kikuzawa, 1995; Reich et al., 1997; Westoby et al., 2000, 2002). Thin and/or soft leaves (i.e., with a high SLA) generally require little carbon investment per unit leaf area and are physiologically more active. In contrast, leaves with low SLAs have higher LLs, because they invest more carbon per unit leaf area in defense structures making them more durable against physical stress and herbivory. This general pattern also holds for trees in the Amazon region (Reich et al., 1991, 2004; Poorter & Bongers, 2006), and scales up to a growth–survival trade-off at the whole-plant level (Poorter & Bongers, 2006; Sterck et al., 2006; Poorter et al., 2008; Kikuzawa & Lechowicz, 2011; Ruger et al., 2012).
In seasonal environments, periodical unfavorable conditions, for example, drought or cold, force trees to shed their leaves, thereby setting an upper limit to LL. A high SLA is advantageous in such a seasonal environment, as it optimizes carbon gain during the short growing season. However, a low LL is not only the result of climatic forcing, but also occurs due to the often higher palatability of high SLA leaves which tend to have high nutrient concentrations per unit leaf mass (Poorter & Evans, 1998) and smaller investments in leaf defenses (Kitajima & Poorter, 2010).
A low SLA is usually the response to stable climatic conditions and shaded conditions as in tropical rainforests. Here, a low SLA can bear an advantage, because the nutrient-poor soils and low-light environment of tropical rainforests favor leaves which store nutrients and carbon for a longer time period. A high LL increases the residence time of nutrients and carbon in the plant and therefore enhances the photosynthetic revenue stream of carbon and nutrient investment in leaves (Kikuzawa & Lechowicz, 2011).
In standard LPJmL, LL is a fixed empirical parameter for each PFT from which the PFT's SLA value is derived. In LPJmL-FIT, in contrast, we infer LLs from the empirical SLA range in the TRY database via regression functions (Data S1) to account for the continuum of LLs observed in nature (Chabot & Hicks, 1982; Kikuzawa & Lechowicz, 2011; van Ommen Kloeke et al., 2012).
Standard LPJmL describes two phenology types in the tropics, ‘evergreen’ and ‘deciduous’. A fixed LL for evergreen and deciduous trees is accompanied by a PFT-specific minimum water stress scalar wscalmin. LPJmL-FIT simulates a large range of LLs as found in nature and does not prescribe wscalmin to enforce a specific phenology. Instead, LPJmL-FIT assigns each individual tree a random wscalmin at establishment. This approach tests all conceivable wscalmin values and supports individuals with the best adapted wscalmin in a specific simulated environment (Data S1).
In conjunction with the SLA-LL trade-off, the effect of the randomized wscalmin is that deciduous behavior is advantageous in dry regions because trees which do not invest much carbon into their leaves per unit dry mass (higher SLA) may shed them (lower LL) during the dry season. Conversely, evergreen behavior is advantageous in wet regions as the longer LLs allow achieving a constant carbon gain from photosynthesis throughout the year.
(b). The trade-off between SLA and the maximum carboxylation capacity of Rubisco (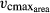
) mediated by Narea
Empirical evidence shows a strongly positive relationship between a leaf's nitrogen content and its photosynthetic capacity (Field & Mooney, 1982; Reich et al., 1994). Interconnected with SLA, these leaf traits are part of the LES (Wright et al., 2004) and introduce an additional source of variability in the spectrum of tree growth strategies of LPJmL-FIT.
Trees with high SLA not only have higher nitrogen content per unit mass, but also a higher photosynthetic nitrogen use efficiency (PNUE = rate of photosynthesis/amount of leaf nitrogen) (Poorter & Evans, 1998) as relatively more leaf nitrogen is invested into the photosynthetically active molecular structures within the chloroplasts (Evans & Seemann, 1989). On an area basis, however, thicker leaves with lower SLA have a higher photosynthetic capacity per area than thin leaves with high SLA.
Standard LPJmL ignores these functional relationships between SLA, nitrogen content, and photosynthetic rates. Photosynthesis of PFTs is explicitly calculated depending on temperature, atmospheric CO2 concentration, photosynthetically active radiation (PAR), and water availability (Farquhar et al., 1980; Haxeltine & Prentice, 1996). One crucial variable in standard LPJmL's photosynthesis calculation is the maximum carboxylation rate of Rubisco per leaf area (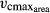
),which is calculated on a daily basis (Sitch et al., 2003).
In LPJmL-FIT, we account for the influence of SLA on Narea and the influence of Narea on photosynthetic capacity by introducing an SLA-dependent Narea and a Narea-dependent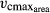 
(Data S1).
(c). Trade-off between WD and mortality
Wood density is a species-specific key trait determining the carbon storage capacity per unit volume as tree stems constitute about 2/3 of the aboveground tree biomass (Segura & Kanninen, 2005). Apart from affecting vegetation carbon, WD also influences the forest's age structure and maximum tree heights (Iida et al., 2012).
In LPJmL standard, WD is a constant parameter for all tree PFTs. LPJmL-FIT now varies WD because several mechanisms have been empirically established which link higher WD to higher construction costs and lower growth rates, but greater resistance against mechanical and drought stress (Baker et al., 2004; Chave et al., 2006; Chao et al., 2008; Kraft et al., 2008; Markesteijn et al., 2011) and therefore, overall lower mortality (Swenson & Enquist, 2007; Anten & Schieving, 2010; Kraft et al., 2010; Niklas & Spatz, 2010). Analogously to the LES (Wright et al., 2004), the SES links WD-dependent traits with particular growth strategies (Chave et al., 2009; Baraloto et al., 2010). WD is mechanistically separated in LPJmL-FIT from the traits involved in the LES (Data S1), because leaf and stem trade-offs operate largely independently (Baraloto et al., 2010). We incorporated the WD-mortality trade-off using an equation derived by King et al. (2006) which assigns a WD-dependent annual mortality rate mortWD to each individual tree at tree establishment. mortWD is then used as the maximum of the growth efficiency-dependent mortality from standard LPJmL (Data S1). While a high WD decreases the growth rate of an individual, it also decreases the performance-related mortality. Therefore, a high WD tree generally grows slower, but also lives longer. This trade-off enables many different WDs to establish and therefore balances the variety of coexisting WDs.
Trait variability corridor
To conserve the natural variability of plant trait interrelations, we introduce the novel concept of a trait variability corridor in LPJmL-FIT which we apply to the log-log-SLA-LL regression (Fig. S5). Each value of an independent variable can now yield a range of values for the dependent variable, and within this range, each value is assigned a certain probability. The range and probabilities are determined by normal distributions with a mean μα equal to the outcome of the original regression function and a standard deviation σα equal to half of the 50% prediction bounds of the original regression (Fig. S5). This approach is used at tree establishment when each sapling is assigned parameters which are drawn from the trait space within the trait variability corridor (see next section). We only applied this approach to the SLA-LL regression, because the introduced variability propagates to the derived trait values under the assumption that SLA, LL, Narea, and Ncmax are interconnected directly or indirectly via the trade-offs of the LES.
Assignment of trait values to tree individuals
Each individual tree obtains a unique set of the trait values for SLA, LL, WD, Narea,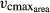 
, and wscalmin (Fig. 1). To obtain these sets, we first fit a probability density function (pdf) of a log-normal distribution (Data S1; Fig. S6) to the worldwide SLA recordings of broad-leaved trees in the TRY database (Kattge et al., 2011). The range between the 1% and 99% percentiles of this pdf determines the SLA range tested in LPJmL-FIT (SLA = 2.25–27 mm2 mg−1). Within this range, 100 uniformly distributed SLA values determine the spectrum of 100 possible plant types regarding SLA (Fig. S6). According to the empirically based regression functions, each SLA value then leads to the calculation of a particular LL (Data S1 Eqn. 1), Narea (Data S1 Eqn. 2), and 
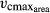(Data S1 Eqn. 3). We apply the trait variability corridor to the calculation of LL. Analogously to SLA, the potential range of WDs between 0.14 and 1.3 g cm−3 was calculated from the pdf of the empirical WD distribution. Whereas the SLA and WD ranges were derived from empirically observed trait variation in the TRY database, the possible values of the minimum water scalar wscalmin fall between 0 and 1. From within this range, wscalmin values are drawn randomly assuming a uniform distribution. The resulting 100 unique sets of trait values are assigned to respective 100 new tree saplings every five simulation years.
Vegetation dynamics
In LPJmL-FIT, 50 simulation patches, each 100 m² in size, are introduced into each grid cell (Fig. S7). Within each patch, individual trees are simulated. Each individual tree is a representative of a certain plant type. All plant types are allowed to grow in each patch. Resulting tree communities are scaled up to cover half-degree grid cells.
Light competition of individual trees
The basic light competition scheme is adapted from Smith et al. (2001) as in LPJ-GUESS. Within a patch, light competition occurs in distinct canopy layers each 100 m² in size according to the patch area. The locations of these layers are prescribed starting at the maximum tree height (50 m) followed by additional layers every 2 m down to a height-specific bole height, but not lower than 2 m. Tree bole height is a yearly calculated variable depending on tree height (Thonicke et al., 2010). If a tree is smaller than 2 m (e.g., true for saplings), a respective fraction of its leaf mass is transferred to the first leaf layer where photosynthesis is possible (Fig. 1). An additional bottom layer enables the C3- and C4-grass PFTs of standard LPJmL to establish. Trees pass through the canopy layers during growth and distribute their leaf mass equally to the amount of layers they have reached above their bole height. The total amount of leaf area within each leaf layer determines the fraction of absorbed photosynthetic active radiation (fAPARLayer) according to the Lambert–Beers law (Data S1).
Output
Output trait distributions and trait maps
For the key traits SLA, LL, and WD, we fitted log-normal probability density functions (PDFs) to the trait distributions simulated in each grid cell in the Amazon region. The distributions were fitted with the same type of probability density function (log-normal distribution) as was used for fitting the empirical TRY histograms. The investigated model output comprises averaged data from the last 600 of 900 simulation years, since a 300-year initial phase was sufficient for trait distributions to reach equilibrium. Trait and trait variability maps were compiled by plotting the expectation value E and scale parameter σ of each log-normal PDF within each grid cell in the Amazon region (Data S1).
For evaluation, E is the most common trait value, while σ is a measure of trait variability. We chose E, because trait expectation values are important for the magnitude of ecosystem processes, whereas σ determines the variety of viable growth strategies and may therefore be used as an indicator of the forest's capacity to adapt to environmental change (Isbell et al., 2011; Mori et al., 2013).
Output vegetation carbon
Carbon stored in the vegetation (gC m−2) for the Amazon region was derived from LPJmL-FIT output data by averaging vegetation carbon in each grid cell across all surviving tree individuals including the grass PFTs over the last 600 years of the simulation.
Modeling protocol
Environmental drivers
Simulations are carried out for the Amazon basin. The model is driven by monthly climate data (temperature, precipitation, cloudiness, and number of wet days) from the CRU TS 3.10 compiled by the Climate Research Unit (Harris et al., 2013). These are calculated on high-resolution (0.5°×0.5°) grids which are based on an archive of monthly mean temperatures (Mitchell & Jones, 2005). To reach an equilibrium state of the vegetation, climate data from 1961 to 1990, which are interpolated to a daily time step, are constantly repeated for 900 years. The interval of 1961–1990 is chosen because the accuracy of input data for the Amazon basin is better than in previous years. To exclude CO2-fertilization effects, the atmospheric CO2 concentration is kept constant at the pre-industrial level of 288 ppm. Soil input data are based on the updated hydrology scheme for standard LPJmL (Schaphoff et al., 2013). The soil types remain constant over time as we do not aim to disentangle climate and soil effects on trait distributions.
Three modeling experiments A–C reveal the effects of different model complexity on trait distributions and vegetation carbon.
Simulated experiments A-C
- Experiment A. This simulation includes all three trade-offs listed above. The trait variability corridor is applied to the SLA-LL trade-off. We hypothesize that incorporating key traits and their trade-offs in a mechanistic framework successfully predicts observed plant trait distributions along a climatic gradient of the Amazon region (e.g., precipitation patterns and seasonality; Fig. S9) as well as vegetation carbon stocks which should fall in the observed ranges.
- Experiment B. In this simulation, we exclude the trait variability corridor of the SLA-LL trade-off, and use paired input values that were strictly derived from the SLA-LL regression function. We hypothesize that the resulting trait distributions should reflect a tree community with less diversity in functional traits because a large part of the natural variability is excluded from the trait space.
- Experiment C. In addition to the changes made in experiments A and B, this experiment excludes the trade-off between SLA and LL and each tree is assigned a random LL within the LL range resulting from Eqn. 1. We expect that without this essential trade-off, the resulting SLA and LL trait distributions should be shifted toward the thinner leaves with high leaf longevities, because both features increase the competitiveness.
Computational intensiveness
Simulations of LPJmL-FIT have relatively high computational costs compared to standard LPJmL. LPJmL-FIT accounts for light competition within the canopy as a compromise between the traditional PFT-representation (average individual approach) and representing individual trees with single stems and leaves in a spatially explicit manner. Diversifying former constant plant traits requires simulating a high number of different individuals. Under the settings described in this work, 900-year simulation years of the Amazon region take 3–4 days on 256 central processing units.
Model validation
Trait distributions
Simulated local trait distributions are evaluated at 12 selected locations (Fig. S8) where sufficient TRY data are available. We compare the expectation value E and the scale parameter σ of the fitted probability density functions (log normal) of TRY data vs. LPJmL-FIT output to determine the difference between empirical vs. modeled trait distributions for SLA. Moreover, we calculate the percentage overlap (ov) of the two (empirical vs. modeled) probability density functions within the investigated SLA range (Data S1). This strategy has the advantage of comparing local distributions which contain information on both trait abundances and ranges instead of mean values. We focused on SLA, because this was the only trait where TRY offered sufficient empirical data for several locations in the Amazon region making location-specific model validation possible. Moreover, SLA distributions are representative for the other variable leaf traits as they are derived from SLA in LPJmL-FIT.
Vegetation carbon
Modeled vegetation carbon is compared to vegetation carbon estimates and associated uncertainties for the Amazon region based on remote sensing (Saatchi et al., 2011) corrected for vegetation carbon of herbaceous cover (Carvalhais et al., 2014).
Results
Comparing the experiments A–C at specific test locations
We show detailed results for 4 (L1-L4) of 12 (L1-L12) validation locations (cf. 2, Fig. S8). The complete results for all 12 locations are given in the SI (Tables S1 and S2; Figs S10–S13).
In experiment A with the trait variability corridor included, the empirical and modeled distributions of SLA (Fig. 2a–h, Figs S10 and S11) and their fitted log-normal probability functions (Fig. 2i–m, Fig. S12) agree very well at all four locations. The four selected sites L1-L4 (all 12 sites L1-L12) show a mean overlap between the modeled and observed PDFs of 88% (83%) with a 0.3–12.6% (0.3–23.7%) and 2.6–30.1% (1.5–31.5%) range of absolute difference between modeled and observed values of E and the scale parameter σ, respectively (Tables S1 and S2). The variability in SLAs as indicated by σ is largest in experiment A.
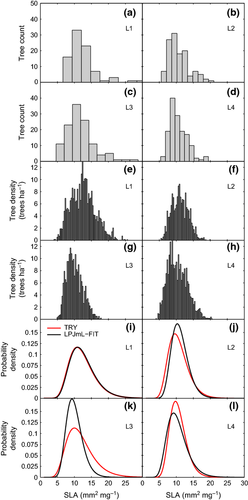
In experiment B, the correlation corridor is not applied. Excluding the natural variability of the SLA-LL trade-off decreases the viable range of SLAs able to survive and compete successfully at a given location within a particular simulated environment. E values of SLA are shifted toward the lower SLA range, and the respective distributions are narrower than in experiment A indicated by a smaller σ (Fig. 3, Fig. S13). The four selected sites L1-L4 (all 12 sites L1-L12) show a mean overlap of 63% (66%) between the modeled and observed PDFs (Table S2; Fig. S13).
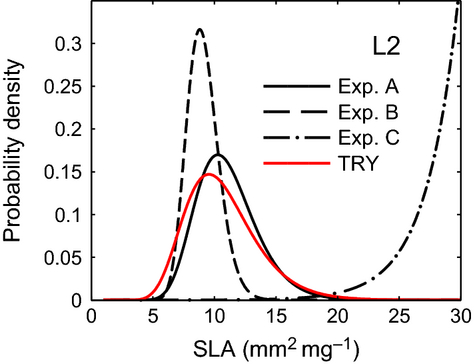
In experiment C, the SLA-LL trade-off is excluded. The resulting SLA distribution is shifted strongly toward an unrealistically high range. The resulting SLA histograms do not follow a log-normal distribution. The fitted PDFs increase exponentially toward the higher SLAs (Fig. 3, Fig. S13). Consistently, the four selected sites L1-L4 (all 12 sites L1-L12) show a mean overlap of 4% (5%) between the modeled and observed PDFs (Table S2; Fig. S13).
Overall, the comparison of the experiments A-C indicates that the modeled SLA distributions strongly depend on the SLA-LL trade-off and the trait variability corridor (Fig. 3, S13). While the trade-off itself constrains SLA distributions to the biological realistically range, the trait variability corridor ensures that establishing phenotypes cover this range.
Trait maps simulated for the Amazon region
The geographical pattern of SLA based on experiment A (Fig. 4) shows low expected SLA values in the northwestern wetter parts of the Amazon and high SLAs in the southeastern drier parts of the Amazon region (Fig. 4a). This indicates that a combination of low SLA and high LL, which is characteristic for an evergreen phenology, is the most successful growth strategy in wet per-humid regions, whereas deciduous species with high SLA and low LL establish in dry regions with stronger rainfall seasonality. The variability in SLA (as indicated by the σ of the SLA probability density functions) is higher in drier and more seasonal areas (Fig. 4b). This indicates higher trait diversity in dry areas because of greater environmental variability.
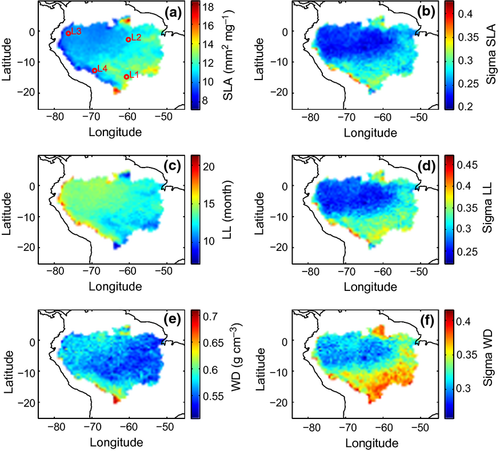
The geographical patterns of LL (Fig. 4c) and SLA (Fig. 4a) are approximately inverted because SLA and LL are negatively correlated by the SLA-LL trade-off. Higher LLs are found in wetter per-humid areas because evergreen trees do not suffer from water stress (Fig. 4c). Such trees have LLs >14 months, while deciduous trees in dry regions have LLs <12 months, because they drop their leaves during the dry season. As for SLA, the σ of the LL distribution (Fig. 4d) is higher in the drier, more seasonal areas.
The geographical pattern of WD (Fig. 4e) differs from the other two traits in that it does not represent a clear northwest to southeast gradient, but rather shows a crescent-shaped distribution. Highest WD values are found in the driest, most seasonal regions at the fringes of the Amazon, for example, in the South, but also in wet regions in the northwest with low intra-annual variability in precipitation (Fig. 4e).
Carbon stocks in the vegetation
In experiment A, vegetation carbon (Fig. S14) of 79% (41%) of all grid cells falls within the 5–95% (25–75%) uncertainty percentile range of one of the most recent and detailed map of vegetation carbon for the Amazon region (Saatchi et al., 2011). Over- and underestimation of vegetation carbon are well balanced with a mean difference of 0.11 and a standard deviation of ±4.93 kgC m−2 across all grid cells between LPJmL-FIT and mean observed values. Excluding the trait variability corridor in experiment B not only reduces diversity of SLA (cf. Fig. 2), but also reduces the average vegetation carbon of the whole study area by 15% compared to experiment A (Fig. S14). In experiment B, vegetation carbon appears generally underestimated with the mean absolute difference of −1.75 and a standard deviation of ±4.79 kgC m−2 across all grid cells between LPJmL-FIT and observed mean values.
Discussion
This study demonstrates a generalizable approach to (a) improve the representation of functional diversity in a DGVM by incorporating empirically based trait distributions and (b) employ a mechanistic framework of trade-offs to enable the coexistence of uniquely parameterized tree individuals with realistic growth strategies as defined by their trait combinations. A major advance of the individual- and trait-based DGVM LPJmL-FIT model is that the uniform input of trait values ensures that each trait combination gets the same chance to establish in a certain location. This flexible parameterization method avoids the preselection of tree types by bioclimatic limits as well as the model-specific calibration of plant traits. As a result, LPJmL-FIT replaces PFTs with numerous plant types representing functional spectra instead of constant plant parameters.
The study design with three simulated experiments A-C provides new insight into the mechanisms and selective forces shaping modeled and natural trait distributions in tree communities with different levels of functional diversity along a climatic gradient. Only the simulation experiment A with all trade-offs and the trait variability corridor included successfully reproduces empirical leaf trait distributions and vegetation carbon. Two further experiments B-C which lack functional components of the SLA-LL trade-off fail to do so. Here, we first discuss the modeling implications, and then the ecological implications of this study.
Continuum of tree growth strategies replaces PFTs
From the climate of wetter and less seasonal tropical rainforests to the climate of drier and more seasonal closed and open dry deciduous forests, LPJmL-FIT produces a continuous gradient of tree growth strategies, replacing the strict classification of the ‘evergreen’ and ‘raingreen’ tropical broad-leaved tree PFTs.
The results of experiment A show a large trait diversity in heterogeneous environments which implies that the SLA-LL trade-off has a decisive influence on the realized functional diversity in LPJmL-FIT as quantified by the expectation value E and width (scale parameter σ) of the modeled trait distributions. For example, the model predicts a high trait diversity at the fringes of the Amazon (Fig 4, right panels), where drought-avoiding deciduous species and drought-tolerant evergreen species coexist (Markesteijn & Poorter, 2009). Here, niche differentiation (Macarthur & Levins, 1967) due to climatic variability (seasonal and interannual) leads to coexistence of more growth strategies (Mori et al., 2013; Sterk et al., 2013). This suggests that climatic variability acts as a major driver shaping the realized niche (McGill et al., 2006) of trees. The resulting trait divergence is also observed in natural communities (Brousseau et al., 2013; Laurans et al., 2012; Pillar et al., 2009) where niche separation in a heterogeneous environment prevents competitive exclusion. The large trait variation should also make forests more resilient to environmental change due to higher response diversity (Mori et al., 2013). Other studies have predicted that increased droughts could lead to the replacement by savanna vegetation (Hirota et al., 2011; Nobre & Borma, 2009), or even forest collapse (Cox et al., 2000, 2013; Phillips et al., 2009). LPJmL-FIT provides a tool to test which outcome is more likely in dependence of functional diversity, especially at the fringes of the Amazon, where climatic extremes are now more commonly observed (Marengo et al., 2011; Saatchi et al., 2011).
Conversely, a lower σ for all considered leaf and stem traits is simulated in areas with low climatic variability where trait convergence (Shipley et al., 2006) occurs due to environmental filtering. Here, our model predicts a lower diversity of SLA and LL in the northwestern Amazon, despite the high observed species diversity in this area (Baker et al., 2004; ter Steege et al., 2003). Due to functional redundancy, plant trait diversity cannot be directly translated into species diversity. However, the model results suggest that the lower plant trait diversity in this area may render it especially vulnerable to climatic changes.
Overall, the modeled trait distributions for SLA are very similar in expectation value E and scale parameter σ to the empirically derived ones at all 12 tested locations in experiment A (mean overlap of PDFs: 86.7%, cf. Fig. 2, Fig. S12, and Tables S1 and S2). The key to this successful model approach is that LPJmL-FIT selects for the best adapted growth strategies under different environmental conditions so that tree individuals optimize gains from photosynthesis per gram carbon investment into their leaves.
All viable growth strategies are based on trait combinations, which lie within a multidimensional trait space constrained by trade-offs. Higher carbon investment per leaf area (lower SLA) is connected with higher possible carbon return time (LL) and higher possible return rate (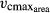
). These trade-offs enable a continuum between the extremes of short-lived, thin and less dense leaves and thicker, long-lived leaves as implied by the LES. Without this continuum, DGVMs are likely to misrepresent the seasonality of tree phenology and may therefore fail to predict future responses of forests to climate change (Richardson et al., 2013). By including these trade-offs with the trait variability corridor and randomizing the threshold value for leaf abscission (minwscal) in LPJmL-FIT, we have achieved to reproduce the observed continuum of phenological strategies from evergreen to raingreen trees. This is a considerable advance over the simplified representation of phenology in existing DGVMs, which prescribe either evergreen or deciduous PFTs.
Using the successful modeling approach from experiment A to model SLA distributions across the entire Amazon region, we find that the SLA expectation values agree well with the SLA map from Castanho et al. (2013) which interpolates field data. Few empirical data are available for the basin-wide validation of the modeled LL. Independent data on estimated leaf longevities (Caldararu et al., 2011) based on satellite images of the leaf area index from the MODIS product series (MOD15) support our simulated pattern with high LLs in the northwestern part of the Amazon region and lower LLs in the southeastern part.
The northwestern part of the Amazon is characterized by high rainfall and irradiation as well as low climatic variability (Fig. S9). Here, the simulated SLAs are lowest and the most abundant LLs are >14 months. The favorable and comparatively stable growing conditions throughout the year promote the growth of trees with high LLs, as leaf shedding due to seasonal drought is not necessary. A high LL improves the carbon balance, increasing the competitiveness of an individual. A corresponding, low SLA entails a high VcN which can compensate for the higher carbon investment per leaf area of thicker and/or denser leaves. Together, these advantages let plant types with low SLAs prevail in high and aseasonal rainfall areas in our simulations. In contrast, slow-growing, drought-resistant, long-lived trees with high SLAs, LLs <12 months, and high WD are more abundant in drier areas with higher climatic variability, for example, in the eastern to southern parts of the Amazon region.
Generally, the WD-mortality trade-off enables to simulate a continuum of competing WDs because it counteracts the higher growth rates of trees with low WD. The continuous WD distribution is an advance over setting constant WD for all tree types and contributes to a reasonably good match of simulated vegetation carbon with remote sensing data (Saatchi et al., 2011). This implies that the WD-mortality trade-off is important for modeling ecosystem functioning, as WD influences the carbon storage capacity of the forest (Malhi et al., 2009; Stegen et al., 2009).
More specifically, the modeled WD pattern generally reflects the observed gradient from drier (higher WD) to wetter (lower WD) areas in Chave et al. (2009). However, at sites with pronounced nutrient wash-out (e.g., Guyana shield), LPJmL-FIT simulates evergreen trees with low WD, although field observations show a stronger northeast to southwest gradient (Quesada et al., 2012; ter Steege et al., 2006). This is because the simulated trait distributions are a result of climatically forced forest communities under competition, whereas other factors influencing tree growth such as nutrient availability (Quesada et al., 2012; Fisher et al., 2012) are still being ignored. In LPJmL-FIT, dry and seasonal climates as at the fringes of the Amazon promote higher WDs and wider WD distributions because a relatively low growth efficiency promotes trees with high WD, reflecting their physiological advantage under water stress (Data S1 Eqns 6–7). In contrast, relatively high and constant annual rainfall as in the northwestern part of the Amazon leads to a low growth efficiency-related mortality for all simulated tree types. In such areas, E values of WDs are intermediate to high because trees may invest carbon both into higher WD and into height growth at the same time. Notably, the constant rainfall also decreases the range of the WD distributions (Fig. 4f). In climates with intermediate rainfall and high seasonality as in the central and eastern part of the Amazon, the E values of WD are lowest because the two mechanisms promoting higher WD as described above are less effective.
Trait corridors enhance the number of growth strategies and the performance of tree individuals in trait-based models
Experiment B excludes the trait variability corridor around the SLA-LL trade-off. The corridor broadens the possible range of trait combinations at establishment time and is therefore essential to enlarge the width of the resulting trait distributions in the model. Within the spectrum of possible trait combinations in experiment A, there are combinations which outperform those in experiment B. In general, the trait variability corridor produces tree individuals with a higher performance, because trees with a certain SLA can adapt a variety of LLs, therefore, partially capturing the variability within the SLA-LL trade-off. The magnitude and direction of this trait offset depends on the local environmental conditions. Hence, a higher trait variability as model input and a resulting higher adaptability leads to more productivity and an overall better C-balance of trees in LPJmL-FIT. This result suggests that the natural variability around empirically based linear regressions of traits should be incorporated in trait-based models, which contrasts sharply with the fixed PFTs in most DGVMs.
Inclusion of trade-offs is essential to provide ecological realism
Experiment C completely excludes the SLA-LL trade-off. The resulting SLA expectation values become unrealistically high. High SLAs are much more competitive than lower ones in all regions, because they invest less carbon into their leaves per area (thin or less dense leaves), while they are also able to maintain high LLs. Therefore, they achieve unrealistically high returns from photosynthesis. This result implies that just varying trait parameters without constraining them by an ecophysiologically motivated trade-off is insufficient to replace the fixed PFT approach and fails to reproduce natural patterns of plant trait diversity and indicators of ecosystem functioning.
Potential of LPJmL-FIT to model the effects of functional diversity on ecosystem functioning
According to our knowledge, the links between BEF were neither be tested systematically nor quantitatively established with DGVMs. LPJmL-FIT advances in this direction because it improves the representation of functional diversity by combining three modeling strategies: (a) the gap model approach with simulation of individual trees which enables unique trait combinations and local competition for resources, (b) parameter assignment to these trees based on empirical trait ranges publicly available from the TRY plant trait database (Kattge et al., 2011), and (c) the empirically grounded constriction of the trait parameter space by the implemented trade-offs and the trait variability corridor based on the LES. This methodology directly address several calls (Adler et al., 2013; Quillet et al., 2010; Webb et al., 2010) to better quantify the influence of continuous multiple traits on ecosystem functions by testing their functional redundancy and complementarity with empirical data and vegetation models. The combination of a strong theoretical core, mechanistic relationships, and the empirically derived knowledge on trait correlations makes LPJmL-FIT a powerful modeling tool for testing of leading BEF-related hypotheses, for example, the insurance hypothesis (Walker, 1992; Yachi & Loreau, 1999) and the mass-ratio hypothesis (Grime, 1998), at different spatial scales.
As a future outlook, LPJmL-FIT could be extended to needle-leaved and herbaceous plants to model other natural ecosystems. For forests, LPJmL-FIT lends itself to simulate the effects of different logging schemes on the trait diversity of trees and the carbon cycle in exchange with the atmosphere. LPJmL-FIT may also predict the effects of global warming and CO2 fertilization on individual tree physiology to reduce model uncertainty (Rammig et al., 2010) and to better understand processes leading to biodiversity loss, for example, by identifying ecological tipping points in scenarios of global change.
Acknowledgements
We thank Nuno Carvalhais and Matthias Forkel from the Max Planck Institute for Biogeochemistry (Jena, Germany), Jörg Asmus (University of Bergen, Norway), and Jasmin Joshi (University of Potsdam, Germany) for lively discussions about an earlier version of this manuscript. Many thanks to Dennis Drechsler for helping with the figure design. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement n° 283093 – The Role of Biodiversity In climate change mitigatioN (ROBIN). We thank Christopher Baraloto and one anonymous reviewer for constructive comments on an earlier version of the manuscript. The study has been supported by the TRY initiative on plant traits (http://www.try-db.org). The TRY initiative and database is hosted, developed and maintained by J. Kattge and G. Bönisch (Max Planck Institute for Biogeochemistry, Jena, Germany). TRY is/has been supported by DIVERSITAS, IGBP, the Global Land Project, the UK Natural Environment Research Council (NERC) through its program QUEST (Quantifying and Understanding the Earth System), the French Foundation for Biodiversity Research (FRB), and GIS ‘Climat, Environnement et Société’ France.
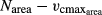regression (Data S1 Eqn. 3).
