Carbon accumulation of tropical peatlands over millennia: a modeling approach
Abstract
Tropical peatlands cover an estimated 440 000 km2 (~10% of global peatland area) and are significant in the global carbon cycle by storing about 40–90 Gt C in peat. Over the past several decades, tropical peatlands have experienced high rates of deforestation and conversion, which is often associated with lowering the water table and peat burning, releasing large amounts of carbon stored in peat to the atmosphere. We present the first model of long-term carbon accumulation in tropical peatlands by modifying the Holocene Peat Model (HPM), which has been successfully applied to northern temperate peatlands. Tropical HPM (HPMTrop) is a one-dimensional, nonlinear, dynamic model with a monthly time step that simulates peat mass remaining in annual peat cohorts over millennia as a balance between monthly vegetation inputs (litter) and monthly decomposition. Key model parameters were based on published data on vegetation characteristics, including net primary production partitioned into leaves, wood, and roots; and initial litter decomposition rates. HPMTrop outputs are generally consistent with field observations from Indonesia. Simulated long-term carbon accumulation rates for 11 000-year-old inland, and 5 000-year-old coastal peatlands were about 0.3 and 0.59 Mg C ha−1 yr−1, and the resulting peat carbon stocks at the end of the 11 000-year and 5 000-year simulations were 3300 and 2900 Mg C ha−1, respectively. The simulated carbon loss caused by coastal peat swamp forest conversion into oil palm plantation with periodic burning was 1400 Mg C ha−1 over 100 years, which is equivalent to ~2900 years of C accumulation in a hectare of coastal peatlands.
Introduction
Tropical peatlands, covering approximately 440 000km2 or ~10% of the global peatland area (Page et al., 2011), have been persistent carbon sinks through the Holocene (from about 11 600 years ago to the present), contributing a significant influence on the global carbon budget (Yu, 2011). Southeast Asia contains about 60% of the tropical peat area, with about 210 000 km2 in Indonesia, and 26 000 km2 in Malaysia (Page et al., 2011). Tropical peatlands store about 40–90 Gt C overall, and Southeast Asian peatlands account for 77% of that stock (Yu et al., 2010; Page et al., 2011). Data collected from 26 sites throughout the tropics indicate that the tropical peatlands long-term mean carbon accumulation rate during the Holocene averaged 12.8 g C m−2 yr−1, although rates as high as 56.2 g C m−2 yr−1 are reported from Central Kalimantan, Indonesia (Page et al., 2004; Yu et al., 2010). High rates of organic matter accumulation as peat are generated by high productivity of tropical peat swamp forests (PSFs) and low decomposition rates due to soil saturation (Chimner & Ewel, 2004). Low drainage gradients and high precipitation result in soil saturation and anaerobic conditions necessary for tropical peat development, and the acidic, nutrient poor conditions common in ombrotrophic peatlands further impede decomposition (Chimner & Ewel, 2005; Dommain et al., 2011).
In Southeast Asia, inland peat formation began as early as 20–30 thousand calendar years before present (hereafter kBP; Anshari et al., 2004), though most peatlands initiated in the early Holocene, around 11–8 kBP (Neuzil, 1997; Yu et al., 2010). Coastal peatland development initiated later, around 7 kBP (Dommain et al., 2011), with the youngest peatlands beginning from <2 kBP (Yu et al., 2010). However, the rate of peat accumulation in coastal peatlands has been faster than for inland peatlands, averaging 1.8 and 0.5 mm yr−1, respectively, apparently due to a weaker coastal influence of decreased precipitation and higher ENSO (El Niño Southern Oscillation) intensity over the past several millennia (Dommain et al., 2011). Rieley et al. (2008) reported peat accumulation rates in tropical peat swamp ecosystems, especially in Southeast Asia, to vary between 0–3 mm yr−1, with a median value of 1.3 mm yr−1. Using a mean tropical dry peat density of 90 kg m−3 and carbon concentration of 0.56 kg C kg−1 (Page et al., 2011), this is equivalent to about 70 g C m−2 yr−1.
Recently, tropical peat swamp forests have been heavily impacted by increased rates of deforestation and land conversion. During 2000–2010, the upland deforestation rate in Southeast Asia was 1% yr−1, while PSF deforestation was 2.2% yr−1 (Miettinen et al., 2011). Tropical PSF deforestation releases carbon to the atmosphere not only from the loss of aboveground biomass (Miettinen & Liew, 2010) but also from enhanced peat decomposition due to the lowering of the water table level (Hooijer et al., 2010), and peat combustion from fire (Page et al., 2002; Heil et al., 2006). PSF conversion into oil palm plantations (a dominant land-use change in the region) results in loss of about 16 Mg C ha−1 yr−1, mostly as CO2 (Hergoualc'h & Verchot, 2011; Koh et al., 2011). This C loss rate from land conversion is about 20 times the mean C uptake rate, and includes emissions from peat burning, changes in aboveground biomass, and peat oxidation (Murdiyarso et al., 2010).
Relative to northern temperate peatlands or upland tropical forests, limited carbon-related field research has been conducted in tropical PSF, thus the influence of climate and land use on tropical PSF carbon are not well understood (Farmer et al., 2011). Ecosystem modeling is one tool that can be utilized to represent and understand dynamic processes in tropical PSFs and, in turn, can be used for assessing the impact of climate change and land-use pressure on peatlands. Several ecosystem models have been developed for simulating carbon dynamics in northern temperate peatlands; however, very few models have been applied for tropical PSF systems (Farmer et al., 2011). Recent work by Mezbahuddin et al. (2014) has focused on hourly to seasonal carbon and water dynamics using the detailed, process-based ecosys model over 4 years at a drained PSF in Central Kalimantan, Indonesia. Consistent with flux tower data from the site (Hirano et al., 2007), ecosys modeling showed that the PSF lost substantial C (~100 g C m−2 month−1) when the water table was deeper than 1 m, due to strong increases in ecosystem respiration and a relatively weak sensitivity in C uptake (photosynthesis) to water table (WT) depth (Mezbahuddin et al., 2014). In this article, we present a new, simple model of long-term tropical PSF carbon cycling, to explore whether limited existing field data of contemporary carbon dynamics (e.g. net primary productivity, litter decomposition) are consistent with long-term carbon accumulation rates inferred from peat core analysis. We modified the Holocene Peat Model (HPM; Frolking et al., 2010) to simulate carbon accumulation in tropical PSF. Using this modified model, we assess impacts of annual and seasonal precipitation variability on carbon accumulation over millennia, and simulate impacts of land-cover change from pristine forests to oil palm plantations on peatland carbon dynamics.
Materials and methods
Overview of HPMTrop
The Holocene Peat Model is a one-dimensional and annual time step model for estimating the carbon cycle in northern temperate peatlands that has been applied to field studies (Frolking et al., 2010; Tuittila et al., 2012; Quillet et al., 2014) and qualitative analysis (Turetsky et al., 2012). The model integrates a peat decomposition model (Frolking et al., 2001) and dynamic peat accumulation model that couples carbon and water balances (Hilbert et al., 2000). Holocene peat model estimates characteristics of the vegetation and peat column such as litter production, litter decomposition, peat accumulation, hydrological properties of peat, and water table depth.
To apply HPM to tropical peatlands, we developed a new version: HPMTrop, which uses the basic functionalities of HPM to calculate long-term (millennial) carbon dynamics, but with three fundamental changes – plant functional types (PFTs), monthly time step, and water balance calculation – along with some modified parameter values. HPM's northern temperate peatlands PFTs include mosses, sedges, herbs, and shrubs. However, primary production in intact tropical PSF is dominated by trees, while contributions from mosses and other PFTs are negligible (Phillips, 1998). Hence, HPMTrop considers only a tree PFT, with tree net primary productivity (NPP) partitioned into three components (leaves, wood, and roots) that are tracked separately. Tropical climates are warm year-round, with precipitation patterns that can be partitioned into rainy and dry seasons if not uniform throughout the year. To capture the impact of the precipitation seasonality on tropical peat development, HPM was modified from an annual time step to a monthly time step. Tropical PSF water balance models are site-specific and not well developed for general application, (e.g. Susilo et al., 2013; Mezbahuddin et al., 2014) and because few data exist for run-on, runoff, or water table depth in tropical PSF, HPMTrop does not calculate a monthly water balance. Instead HPMTrop uses an empirical relationship between WT and monthly water deficit to set the monthly WT for NPP and decomposition calculations.
Model Structure
Vegetation
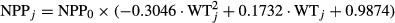 (1)
(1)| Parameter | Description | Value | Units | References |
|---|---|---|---|---|
| Monthly NPP | ||||
| leaves | Monthly leaf production/litterfall | 0.079 | kg m−2 month−1 | Hergoualc'h & Verchot (2011) |
| wood | Monthly wood production/litterfall | 0.057 | kg m−2 month−1 | Chimner & Ewel (2005) |
| roots | Monthly root production/litterfall | 0.025 | kg m−2 month−1 | Hergoualc'h & Verchot (2011) |
| k0 (initial litter decomposition rate) | ||||
| leaves | Initial leaf decomposition mass loss rate | 0.1055 | Month−1 | Brady (1997); Chimner & Ewel (2005); Shimamura & Momose (2005); Yule & Gomez (2008) |
| wood | Initial wood decomposition mass loss rate | 0.0224 | Month−1 | Chimner & Ewel (2005) |
| roots | Initial root decomposition mass loss rate | 0.0685 | Month−1 | Chimner & Ewel (2005) |
| Anoxia scale length | ||||
| Coastal | e-folding length for anoxia below WT | 0.23 | m | |
| Inland | e-folding length for anoxia below WT | 0.30 | m | |
| Root depth (min) | 0.5 | m | ||
| Peat water content parameters | ||||
| Wmin | Minimum peat pore water content | 0.03 | m3 m−3 | Frolking et al. (2010) |
| c1 | Peat water content parameter | 0.5 | — | Frolking et al. (2010) |
| c2 | Peat water content parameter | 20 | kg m−3 | Frolking et al. (2010) |
| Saturation factor for the decomposition rate | ||||
| Wopt | Peat pore water content for optimum decomposition | 0.45 | m3 m−3 | Frolking et al. (2010) |
| Wsat | Peat pore water content at saturation | 1 | m3 m−3 | Frolking et al. (2010) |
| fmax | Maximum decomposition rate multiplier | 1 | — | Frolking et al. (2010) |
| fsat | Saturation decomposition rate multiplier | 0.3 | — | Frolking et al. (2010) |
| fmin | Minimum decomposition rate multiplier | 0.001 | — | Frolking et al. (2010) |
| Bulk density function parameters | ||||
| c5 | Bulk density function parameter | 0.2 | — | Frolking et al. (2010) |
| c6 | Bulk density function parameter | 0.1 | — | Frolking et al. (2010) |
| ρ min | Minimum peat bulk density | 90 | kg m−3 | Warren et al. (2012) |
| Δρ | Maximum increase in bulk density | 40 | kg m−3 | Warren et al. (2012) |
Decomposition, peat mass balance, and peat bulk density
HPMTrop peat decomposition follows HPM (Frolking et al., 2010), however with a monthly time step, and PSF tissue decomposition parameters are based on several studies (e.g. Brady, 1997; Chimner & Ewel, 2005; Shimamura & Momose, 2005; Yule & Gomez, 2008; Table 1). Leaves, wood, and root litter/peat decompose independently in each annual peat cohort (and the surface litter layer). Decomposition rates, k, decline linearly from their initial value, k0, as the cohort loses mass, k = k0(m/m0) (Clymo et al., 1998; Frolking et al., 2001). There is a water content rate multiplier for cohorts above the water table and a different rate multiplier for cohorts below the water table (Frolking et al., 2010). Above the water table, the degree of saturation of a peat cohort (Wl) is determined by two factors: cohort bulk density and cohort distance from the water table, following the formulation in HPM (Frolking et al., 2010). Mass remaining of peat and surface litter cohorts are calculated each month, as the balance of litter input (to the surface litter pool and to the peat cohorts in the root zone) and loss via decomposition. The root input density profile was assumed to be uniform from the surface of the peat down to 0.5 m or the water table depth, whichever depth is greater. Bulk density increases nonlinearly with peat mass loss as in HPM (Frolking et al., 2010), and is computed for each annual cohort. The thickness of each annual peat cohort is calculated as the ratio (cohort mass remaining)/(cohort bulk density). Total peat depth is the sum of all cohort thicknesses. Peat carbon content is set to 0.5 kg C kg−1.
Water table reconstruction
HPMTrop simulates thousands of years of peat accumulation (or loss), and so requires a monthly water table depth reconstruction for the simulation period. We used three steps for generating the water table over the Holocene: (i) developing a linear relationship between monthly water deficit and measured water table, (ii) analyzing 20th century precipitation to generate different monthly precipitation patterns with probabilities related to El Niño, ‘normal’, and La Niña conditions, and (iii) using proxies to generate long-term (millennial) variability in El Niño probability and total annual precipitation.
Empirical water table model
 (2)
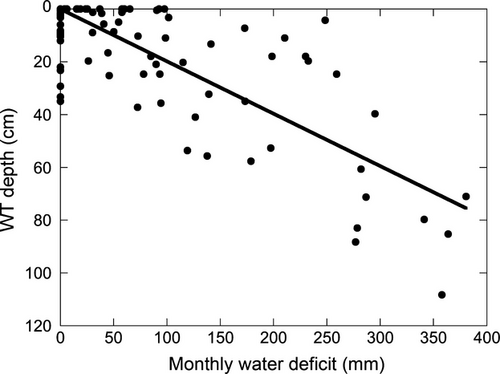
(2)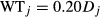 (3)
(3)
Generating stochastic monthly precipitation for El Niño, normal, and La Niña years
El Niño/La Niña dynamics exert a strong control on dry season precipitation in Indonesia (Aldrian & Dwi Susanto, 2003), and this was the basis of our reconstruction. First, 1900–2010 annual precipitation in Sebangau, Kalimantan (Matsuura & Willmott, 2012) was disaggregated into three classes based on each year's southern oscillation index (SOI): El Niño, normal, or La Niña (McKeon et al., 2004), with about half of the years classified as normal years and the remainder divided between El Niño and La Niña. A cluster analysis of monthly precipitation was done for all years in each class – El Niño, normal, and La Niña – using Ward's method for clustering the monthly data based on the dissimilarity matrix calculated using Euclidian distance. The cluster analysis, done with the JMP pro 10 software, resulted in 12 precipitation groups, four in each class. A dendrogram graph showing the precipitation grouping was generated by using dissimilarity distance (Figures S1–S3 in supporting document). The probability of each precipitation group was calculated as the ratio of the number of years within the group generated by cluster analysis to the number of years in its precipitation class. This generated contemporary probabilities for precipitation class (El Niño, normal, and La Niña) and, within class, four different monthly precipitation patterns (Figure S4; Kurnianto, 2013). Predicted monthly precipitation could then be used with the empirical WT model to generate monthly WT values to drive HPMTrop simulations.
Holocene variability in precipitation/water table depth
Precipitation class probabilities and magnitudes through the Holocene were modified from 20th century values based on paleoclimate reconstruction. Reconstructions from the region indicate that the intensity and frequency of El Niño Southern Oscillation (ENSO) were low early in the Holocene, increased substantially around 4 kBP, and further intensified up to the present (Sandweiss et al., 2001; Conroy et al., 2008; Cobb et al., 2013). In addition, oxygen isotope content (δ18O) sampled from cave stalagmites in northern Borneo indicates wetter conditions around 5 kBP relative to both earlier and later in the Holocene (Partin et al., 2007; Griffiths et al., 2009).
We modified El Niño probabilities through the Holocene based on the time series of El Niño frequency in 100-year overlapping windows through the Holocene (Moy et al., 2002). These data were averaged in 1000-year intervals and probabilities were standardized by using the frequency of El Niño in the 20th century. For each year of the simulation, we randomly chose a precipitation class (El Niño, normal, or La Niña) based on the reconstructed probabilities, then selected one of the four monthly precipitation time series (see Figure S4) for that class, based on the 20th century probabilities. We then scaled the magnitude of annual (and equivalently, monthly) precipitation throughout the Holocene based on the pattern of oxygen isotope content (δ18O) from stalagmite samples from Borneo (Partin et al., 2007). Thus, a complete monthly precipitation time series was generated by combining these two long-term trends (El Niño probability and annual precipitation) with the interannual variability based on the ENSO probabilities and monthly precipitation probability in 20th century generated by the cluster analysis. We then used Eqns (2,3) to generate monthly water table depths for the entire simulation. Note that El Niño intensity – represented by the four possible monthly precipitation scenarios and their relative probabilities (see Figure S4) – was not changed over the simulation.
Model Calibration
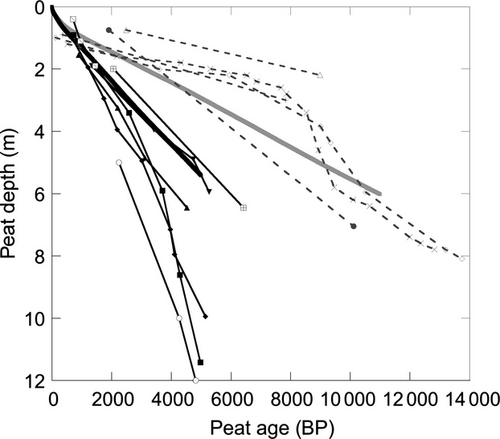
A simple model calibration between simulated peat age–depth profiles and field data from peat cores in South East Asia, particularly in Sumatra, Borneo, and peninsular Malaysia (Dommain et al., 2011), was used to set the values of the anoxia scale length parameter and a water table offset for coastal peatlands. Based on the characteristics of peat development and their distance to the sea, Dommain et al. (2011) distinguished peat profiles as coastal (N = 15 cores), inland peatlands (N = 11), and Kutai peatlands (N = 4). The Kutai peatlands were excluded from this study as they are a disjunct peat formation in East Kalimantan, Indonesia and data necessary to calibrate HPMTrop to this type of peatland are not available. We simulated peat profiles for both coastal and inland types by (i) using different anoxia scale length values (Table 1), (ii) adjusting the water table for coastal peatlands 25% closer to the peat surface compared to inland peat, and (iii) using different peat initiation times of 5 and 11 kBP for coastal and inland peatlands, respectively (Dommain et al., 2011). Anoxia scale length is a constant model parameter that controls how steeply decomposition rates decline to full anoxia (minimum decomposition rate) with depth below the water table (Frolking et al., 2010); i.e. it represents an effective redox gradient. We calibrated the anoxia scale length parameter in the model simulation to generate typical accumulation rates for coastal and inland peatlands, based on the age–depth data of Dommain et al. (2011).
Sensitivity analysis
We conducted basic sensitivity simulations, adjusting individual parameters (typically by ±25%; Table 2) using peat depth and peat mass at the end of the simulation as the model response. Parameters adjusted were NPP0 and k0 values for plant components (leaves, wood, and roots), anoxia scale length, bulk density parameters, and monthly precipitation. We also simulated different moisture seasonality for a set of coastal PSF scenarios with mean annual WT of 0.1 m.
| No | Parameter | Value | Peat carbon (Mg C ha−1) | Depth (m) | total NPP | C/NPP (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| leaves | wood | roots | C (total) | |||||||
| 1 | base run | 480 | 1810 | 920 | 3210 | 6.0 | 47900 | 6.7 | ||
| 2 | NPP | Leaves | 0.099 | 667 | 2000 | 976 | 3640 | 6.8 | 53700 | 6.8 |
| 3 | 0.059 | 311 | 1580 | 848 | 2740 | 5.1 | 42000 | 6.5 | ||
| 4 | Wood | 0.071 | 635 | 2930 | 1090 | 4650 | 8.7 | 52100 | 8.9 | |
| 5 | 0.043 | 327 | 937 | 725 | 1990 | 3.7 | 43600 | 4.6 | ||
| 6 | Roots | 0.031 | 507 | 1900 | 1220 | 3620 | 6.7 | 49700 | 7.3 | |
| 7 | 0.019 | 455 | 1720 | 650 | 2820 | 5.2 | 46000 | 6.1 | ||
| 8 | total | 0.246 | 916 | 3320 | 1490 | 5720 | 10.7 | 59800 | 9.6 | |
| 9 | 0.147 | 192 | 736 | 444 | 1370 | 2.5 | 35900 | 3.8 | ||
| 10 | k | Leaves | 0.132 | 326 | 1620 | 860 | 2810 | 5.2 | 47900 | 5.9 |
| 11 | 0.079 | 770 | 2050 | 994 | 3810 | 7.1 | 47900 | 8.0 | ||
| 12 | Wood | 0.028 | 393 | 1200 | 807 | 2400 | 4.4 | 47900 | 5.0 | |
| 13 | 0.017 | 610 | 2920 | 1090 | 4620 | 8.6 | 47900 | 9.6 | ||
| 14 | Roots | 0.086 | 457 | 1730 | 720 | 2910 | 5.4 | 47900 | 6.1 | |
| 15 | 0.051 | 488 | 1840 | 1200 | 3530 | 6.6 | 47900 | 7.4 | ||
| 16 | total | 0.246 | 244 | 992 | 570 | 1810 | 3.3 | 47900 | 3.8 | |
| 17 | 0.147 | 976 | 3270 | 1470 | 5720 | 10.8 | 47900 | 12.0 | ||
| 18 | anoxia scale length | 0.29 | 340 | 1300 | 551 | 2190 | 4.1 | 47900 | 4.6 | |
| 19 | 0.17 | 681 | 2490 | 1420 | 4590 | 8.6 | 47900 | 9.6 | ||
| 20 | minBD | 112.5 | 313 | 1210 | 689 | 2210 | 3.4 | 47900 | 4.6 | |
| 21 | 67.5 | 749 | 2710 | 1210 | 4670 | 11.1 | 47900 | 9.8 | ||
| 22 | deltaBD | 50 | 447 | 1690 | 875 | 3020 | 5.4 | 47900 | 6.3 | |
| 23 | 30 | 504 | 1900 | 953 | 3350 | 6.5 | 47900 | 7.0 | ||
| 24 | BD_c1 | 0.25 | 489 | 1840 | 926 | 3260 | 6.1 | 47900 | 6.8 | |
| 25 | 0.15 | 468 | 1770 | 915 | 3150 | 5.8 | 47900 | 6.6 | ||
| 26 | BD_c2 | 0.125 | 466 | 1760 | 906 | 3140 | 5.8 | 47900 | 6.6 | |
| 27 | 0.075 | 504 | 1890 | 949 | 3340 | 6.3 | 47900 | 7.0 | ||
| 33 | P multiplier | 1.25 | 572 | 2130 | 1030 | 3730 | 6.9 | 47900 | 7.8 | |
| 34 | 0.75 | 307 | 1180 | 660 | 2150 | 4.0 | 47900 | 4.5 | ||
| 35 | WT multiplier | 1.25 | 417 | 1590 | 805 | 2810 | 5.2 | 47900 | 5.9 | |
| 36 | 0.75 | 551 | 2060 | 1020 | 3620 | 6.8 | 47900 | 7.6 | ||
Land-cover change scenario
- The palm plantation continues for the final 100 years of the coastal simulation, with a 25-year crop rotation.
- Drainage ditches were installed to lower monthly WT by 60 cm (Melling et al., 2005); these drainage ditches were ‘maintained’ so the lower water table persisted even as the peat surface lowered due to decomposition (net mass loss). While drainage ditches will have a variable impact on the increase in water table depth across a peatland, with decreasing impact laterally away from the ditch (e.g. Verry et al., 2011), this is not considered in these simulations, as HPMTrop has only a vertical peat profile.
- At the beginning of each 25-year oil palm rotation, the site was burned, removing the upper 20 cm of peat and all remaining aboveground biomass (Hergoualc'h & Verchot, 2011).
- During oil palm rotations, constant leaf litter (0.025 kg m−2 month−1) and root input rate (0.06 kg m−2month−1) values were used (Hergoualc'h & Verchot, 2011).
Changes in peat volume due to compaction and consolidation following drainage are not included in the model.
Results
Long-term apparent carbon accumulation rates
The simulated apparent peat accumulation rate for any year, which can be compared to accumulation rates measured in peat cores, is equal to annual peat cohort thickness at the end of simulation (as if the simulated peat were ‘cored’ at 0 kBP). For coastal peatlands, the simulated peat accumulation rate was initially about 1.1 mm yr−1 and dropped quickly to about 0.9 mm yr−1 at 3.5 kBP, then increased to about 1.1 mm yr−1 at 2.2 kBP (Fig. 2). In recent years, the apparent peat accumulation increased to ~1.6 mm yr−1 due to recent peat cohorts being less fully decomposed than older, deeper cohorts. Overall, the long-term carbon accumulation rate in the coastal peatlands, calculated as the average yearly cohort thickness is 1.1 mm yr−1 or ~0.59 Mg C ha−1 yr−1 and it yields a total carbon accumulation of about 2900 Mg C ha−1 at the end of the 5000-year simulation (Fig. 3).
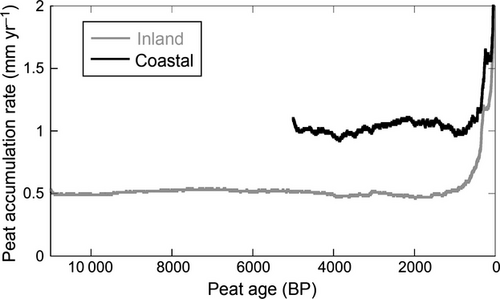
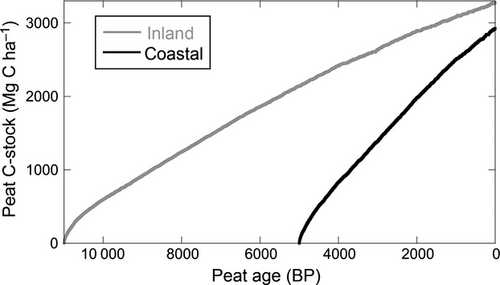
Over an 11000-year simulation, the inland peatlands had a lower peat accumulation rate compared to coastal peatlands, ranging from 0.4 to 1.4 mm yr−1 (Fig. 2) with a simulated long-term apparent peat accumulation rate of 0.5 mm yr−1 (0.3 Mg C ha−1 yr−1). The simulated carbon storage in inland peat that accumulates over 11 000 years is about 3300 Mg C ha−1 (Fig. 3).
The high apparent accumulation rates for the youngest peat cohorts, less than a few hundred years old (Fig. 2), reflect the incomplete decomposition of the young, surface peat. This generates a slightly steeper simulated age–depth profile near the surface (Fig. 4). Aside from this young-peat artifact, the simulated variability in peat accumulation rate in inland peatlands over 11 000 years was generally low (Fig. 2), resulting in a slow decline in overall peat mass accumulation rate (Fig. 3) and a relatively linear age–depth profile that reaches a depth of 6.0 m (Fig. 4). The coastal PSF simulation had higher variability in peat accumulation rate than the inland peatlands (Fig. 2), but again this did not lead to significant curvature in the age-C mass profile (Fig. 3). Over 5000 years, there was a relatively linear relationship between peat age and depth, and a maximum depth of about 5.4 m (Fig. 4). The simulated decay rate of the deep peat was about 7 × 10−5 yr−1.
Sensitivity analysis
Sensitivity runs were done for the coastal PSF (Table 2). Increasing total tree litter production (leaves, wood, and roots) by 25%, while leaving the decomposition parameters and water table depths unchanged, increased the peat carbon after 5000 years by about 80% and, hence, increased the final peat depth to 10.7 m at the end of simulation. The fraction of total NPP remaining as peat carbon at the end of the simulation increased by about 40% from 6.7% in the base run to 9.6%, so the final peat storage increase both in absolute magnitude and as a fraction of NPP, with about 20% of the additional NPP stored as peat due to more rapid burial in the permanently saturated zone. Conversely, decreasing the total tree productivity by 25% reduced the peat mass remaining by about 60%, and the peat depth by about 60%.
Litter quality, represented by k0, is the main factor of the decomposition component of the mass balance equation. Increasing the k0 for all three tree components by 25% reduced the coastal PSF peat accumulation at the end of the simulation by ~45%, due to the higher decomposition rate, and hence reduced the final peat depth 45%. Total NPP was the same in all k0-sensitivity simulations as it was only influenced by the water table. Therefore, the fraction of the total NPP that remains as peat, C/NPP, reduced with an increase of ko. Among three litter components, the model is most sensitive to the change of the k0 of wood; reducing wood's k0 to 0.017 month−1 (25%) resulted in an increase ~45% of both peat carbon and peat depth.
The anoxia scale length regulates simulated peat accumulation by affecting the decomposition rate of peat cohorts located near to, but below the water table. Increasing the anoxia scale length by 25% reduced the coastal PSF peat carbon, depth, and the ratio of peat carbon to NPP by about 30%. Decreasing the value of anoxia scale length to 0.17 m led to an increase of about 45% in peat carbon, depth, and C/NPP after 5000 years.
Sensitivity analyses on the multiplier of the precipitation pattern based on δ18O of cave stalagmites and the linear relationship for estimating water table were also performed. Increasing monthly precipitation by 25% generated an increase in coastal PSF peat mass remaining of ~15%, and also increased the peat depth by the same magnitude, due to unchanged bulk density parameters. Simulating a drier climate over 5000 years by reducing the precipitation multiplier by 25% reduced the peat mass and peat depth about 30%. Increasing the monthly water table depth by 25% resulted in a decrease in peat mass remaining and peat depth by ~15% at the end of the simulation.
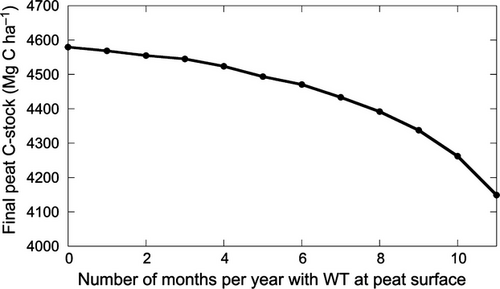
Finally, we conducted a set of sensitivity simulations with mean annual water table of 0.1 m, but with different precipitation seasonality, from none (setting the monthly water table to a constant value of 0.1 m) to extreme (1 month with 1.2 m WT and 11 months with 0.0 m WT). Coastal PSF peat C accumulation over 5000 years decreased with increasing precipitation seasonality by about 10% across this range (Fig. 5).
Land-cover change scenario
The simulated coastal PSF accumulated 2870 Mg C ha−1 prior to conversion into oil palm, and then rapidly lost nearly half that mass in the 100 years following forest conversion (Fig. 6). The simulated carbon loss of 1370 Mg C ha−1 over the period of 100 years generated by land-cover change and current management practices was equivalent to peat accumulation over the previous 2900 years. Put differently, in 1 year it would require an area of about 2300 ha of pristine coastal PSF to sequester the amount of carbon lost over 100 years from just one hectare of converted area. Despite ongoing litter inputs from the oil palm, periodic burning resulted in a truncated peat age–depth profile, with the near-surface peat dating to about 2400 BP after 4 oil palm rotations with burning. At the end of the simulation with four, 25-year rotations of oil palm planting and burning, the peat depth was about 2.6 m, down ~3 m from the simulation run without forest conversion. Burning directly removed 0.8 m of peat (0.2 m per burn in each rotation); about 2 m of peat was lost to oxidation. Aside from direct removal via burning, peat subsidence simulated from HPMTrop was only caused by peat oxidation (i.e. mass loss) and a resulting increase in bulk density with peat humification (though much of the lower density surface peat was burned off every 25 years), but neglected any consolidation and compaction components of subsidence that arise directly from dewatering the peat, which can be particularly significant in the initial few years after drainage (e.g. Couwenberg et al., 2009; Hooijer et al., 2010; Jauhiainen et al., 2012).
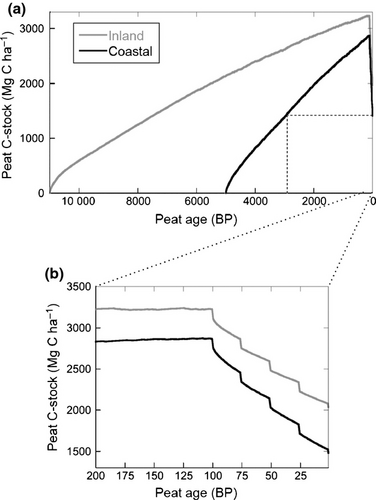
For the simulated inland PSF, accumulated peat mass reached about 3240 Mg C ha−1 before forest conversion and reduced to 2080 Mg C ha−1 due to oil palm conversion (Fig. 6). The carbon loss resulting from that scenario was about 1 160 Mg C ha−1 over 100 years (~12 Mg C ha−1 yr−1; averaging over episodic burning); it required about 5500 years to accumulate the final 1160 Mg C ha−1. The peat depth at the end simulation was 3.6 m, down about 2.4 m from the pristine scenario (again with 0.8 m lost directly to burning), generating a truncated peat age–depth profile. For the inland scenario, annual C sequestration from 3900 ha of pristine Southeast Asian PSF would be required to offset the C lost from 100 years cultivation of a single hectare.
Discussion
HPMTrop is the first process-based model to simulate long-term (decadal to millennial) carbon accumulation dynamics in tropical peat ecosystems. Using a simple carbon balance as the difference between tree productivity and decomposition rates, and including the effects on decomposition rates of a water table that varies seasonally and interannually, HPMTrop simulates (i) annual peat cohort mass and thickness and (ii) total peat profile carbon stocks and peat depth.
Carbon accumulation rates in tropical PSF during the Holocene
There were two dominate regional changes during the late Pleistocene and Holocene that influenced the regional hydrology of Indonesian peatlands – changes in sea level and changes in precipitation. The abrupt rise in sea level in the early Holocene led to inundation of the Sunda Shelf, which had been exposed during the last glacial maximum (Smith et al., 2011) and, hence, increased the regional evaporating area as a source of moisture. This, coupled with an increase in sea surface temperature (SST) in the western equatorial Pacific (Rosenthal, 2003), may have increased convective forcing, resulting in higher precipitation in Southeast Asia. Although sea-level rise would also have affected the rate of continental runoff, and thus perhaps inundation depths and duration in flat coastal plains (Dommain et al., 2011), we did not consider this in the HPMTrop simulations reported here.
During the Holocene, Southeast Asian precipitation varied, influenced by multiple factors: northern summer insolation, mean position of Intertropical Convergence Zone (ITCZ), sea surface temperature, and sea-level rise (Wang et al., 2005; Griffiths et al., 2009). Precipitation reconstruction based on δ18O speleothems sampled from cave stalagmite calcite in northern Borneo (Partin et al., 2007) and Liang Luar, Flores, Indonesia (Griffiths et al., 2009), demonstrated that annual precipitation in the mid-Holocene was higher than in both the late Pleistocene/early Holocene and the present. However, the two paleo-reconstructions show different patterns: stalagmite δ18O from northern Borneo indicate a precipitation maximum occurred ~4 kBP; while at Liang Luar it was ~7 kBP. In addition, El Niño began to intensify about 6 kBP (Sandweiss et al., 2001; Conroy et al., 2008; Cobb et al., 2013), which probably caused a decrease in precipitation, at least in some years, in the Indonesian region (Aldrian & Dwi Susanto, 2003).
In the early Holocene, 11–10 kBP, inland peatlands were in early phases of development, possibly caused by sea-level rise on the Sunda Shelf associated with the last deglaciation (Steinke et al., 2003; Dommain et al., 2011). HPMTrop simulated an initial peat accumulation rate for inland peatlands of about 0.49 mm yr−1 (~0.26 Mg C ha−1 yr−1). This value is slightly lower than published peat accumulation rates ranging between 0.6 and 0.8 mm yr−1 recorded from inland peatland cores collected in the Sebangau catchment, Kalimantan, dated from 13 to 10 kBP, and the Palangkaraya peatlands dated at 9 kBP (Neuzil, 1997; Page et al., 2004). C accumulation rates recorded from a core sampled in the Sebangau catchment ranged from 0.18 to 0.33 Mg C ha−1 yr−1 (Page et al., 2004) which is lower than 0.5 to 0.7 Mg C ha−1 yr−1 measured from adjacent peatlands in Palangkaraya, Kalimantan (Neuzil, 1997). Around 8 to 7 kBP, simulated peat accumulation rates for the inland peatland scenario were about 0.5 mm yr−1, equivalent to a carbon accumulation rate of 0.29 Mg C ha−1 yr−1. This value is consistent with accumulation rates for the same time period measured from a peat core sampled in the Sebangau catchment, which ranged from 0.4 to 0.9 mm yr−1 (0.2 to 0.5 Mg C ha−1 yr−1), however higher values were observed in a core from the Palangkaraya peatlands where the accumulation rate was 1.2 mm yr−1 (Neuzil, 1997).
From 6 to 5 kBP, the mean peat accumulation rate in Sebangau was 0.23 mm yr−1, with an average carbon accumulation rate of 0.1 Mg C ha−1 yr−1 (Page et al., 2004). Based on peat cores sampled from an inland peatland in Kalimantan, peat accumulation rates were reduced from ~0.8 mm yr−1 circa 8 kBP to about 0.5 mm yr−1 around 5 kBP (Dommain et al., 2011). Simulated rates were consistent with this trend, with a peat accumulation rate of 0.51 mm yr−1 at 5 kBP, which is equivalent to carbon accumulation of 0.28 Mg C ha−1 yr−1.
In coastal Sumatra and Kalimantan, however, peat initiation began at higher accumulation rates in the period after 7 kBP. A core taken from Bengkalis Island, near Sumatra shows that the onset of peatland development in this area was 5.8 kBP, with an initial accumulation rate of about 2.5 mm yr−1 and carbon accumulation of about 5.7 Mg C ha−1 yr−1 (Neuzil, 1997). Dommain et al. (2011) also reported that the accumulation rate during the initial development of coastal peatlands in Sumatra, peninsular Malaysia, and Borneo was about 1.7 mm yr−1 at 6 to 5 kBP. HPMTrop simulated rates for the coastal peatlands scenario were lower, with about 1.0 mm yr−1 of peat accumulation in the early stage of development (~5 kBP).
After 5 kBP, sea level gradually decreased from 5 m above present mean sea level (MSL) to the present MSL (Steinke et al., 2003). Decreasing precipitation in the western part of Indonesia was probably associated with the weakening of both the East Asian summer monsoon (Wang et al., 2005) and the Australian-Indonesian summer monsoon (Griffiths et al., 2009) as well as more frequent El Niño (Cobb et al., 2013). Slowly declining sea level, combined with decreasing precipitation, led to a decline in the water table and enhanced organic matter decomposition, and thus a lower peat accumulation rate. From ~5 kBP onward, declines in HMPTrop-simulated peat accumulation rates were minimal in both inland and coastal peatlands; HPMTrop would respond to changes in precipitation only, as the impact of sea-level decline on continental runoff and groundwater levels was not incorporated into HPMTrop. Peat accumulation rates were 0.46 mm yr−1 (0.25 Mg C ha−1 yr−1) and 1 mm yr−1 (0.54 Mg C ha yr−1) in inland and coastal peatlands, respectively. A variable but probably slightly decreasing pattern of accumulation rate was measured from peat cores taken in Southeast Asia, with mean values ~0.3 mm yr−1 for inland peatlands and ~1.5 mm yr−1 for coastal peatlands (Dommain et al., 2011).
Impact of land-cover change on PSF carbon dynamics
Tropical PSF are now experiencing strong land-use pressure, including conversion into agriculture or plantation forestry (Koh et al., 2011; Miettinen et al., 2012), which usually includes canal development for lowering the water table (Hooijer et al., 2010) and results in more common peat fires (Page et al., 2002; Saharjo & Munoz, 2005). Both drainage and fires release peat carbon to the atmosphere, and emission factors and process models are needed to inform the development of REDD+ mechanisms (e.g. Murdiyarso et al., 2010) by estimating some of the carbon losses that contribute to the total emissions from land-cover changes occurring on tropical peatlands. In coastal peatlands, the simulation of a 100-year conversion with periodic peat burning reduced the peat carbon by about 1400 Mg C ha−1 or ~14 Mg C ha−1 yr−1 carbon emission due to both peat oxidation and fires (Table 3). The mean annual carbon loss is equivalent to about 30 years of peat accumulation. For inland peatlands, a net carbon loss of ~12 Mg C ha−1 yr−1 was estimated for the same land-cover change scenario (Fig 6). These carbon loss estimations are conservative values as we did not include the loss from aboveground biomass (e.g. Hergoualc'h & Verchot, 2011). A similar rate of carbon loss of about 10.8 Mg C ha−1 yr−1 was estimated using a flux change method proposed by IPCC (Hergoualc'h & Verchot, 2011). Based on several years of eddy flux tower data, Hirano et al. (2012) reported a ~3 Mg C ha−1 yr−1 increase in CO2 emissions in a disturbed and burned site (fern and sedge vegetation, with no remaining trees) compared to a secondary PSF (secondary forest) in Central Kalimantan, Indonesia.
| Area of peat burnt (ha) | 1 450 000 | Page et al., 2002 |
| 2 441 000 | ||
| 6 804 688 | ||
| 1 909 200 | Heil et al., 2006 | |
| 2 300 500 | ||
| 1 331 367 | Ballhorn et al., 2009 | |
| Thickness of peat burnt (cm) | 51 ± 5 | Page et al., 2002 |
| 33 ± 18 | Heil et al., 2006 | |
| 20 | Hergoualc'h & Verchot, 2011 | |
| Carbon stock at end of simulation (Mg C ha−1) | ||
| No LCa | 2900 | This study |
| LC onlyb | 2000 | This study |
| LC + fire (20 cm)c | 1500 | This study |
| Carbon loss (Mg C ha−1) | ||
| LC onlyd | −900 | This study |
| LC + fire (20 cm)e | −1400 | This study |
| Carbon loss due to fire (Mg C ha−1)f | −125 | This study |
| Total carbon loss (Gt C)g | ||
| Lower estimate | −0.22 | This study |
| Upper estimate | −1.02 | This study |
- a Simulation without land-cover change.
- b Land-cover change simulation – 100 years of drainage, but without peat burning.
- c Land-cover change and peat burning simulation with 20 cm of peat burnt every 25 years.
- d Calculated as carbon stock of LC only (2) minus no LC (1).
- e Calculated as carbon stock of LC + fire (3) minus no LC (1).
- f Calculated as carbon loss of LC + fire (5) – LC only (4) divided by the number of fire occurrences–four in this study.
- g Product of carbon loss due to fire (6) and minimum and maximum areas of peat burnt.
Forest conversion into agriculture, including oil palm plantations, frequently involves burning for land preparation (Saharjo & Munoz, 2005). HPMTrop results showed that total peat carbon at the end simulation following forest conversion without burning is about 2000 Mg C ha−1. The estimated total carbon stock before conversion is 2900 Mg C ha−1, therefore carbon loss from heterotrophic oxidation is 900 Mg C ha−1 over 100 years, equivalent to a rate of 9 Mg C ha−1 yr−1. The total carbon loss from simulated forest conversion with burning was 1400 Mg C ha−1, assuming 20 cm of peat is consumed by fire every 25 years. Over 4 rotations (100 years), the simulated peat loss from burning releases about 500 Mg C ha−1, equivalent to 125 Mg C ha−1 for each fire. A much higher carbon loss per unit area of 250–320 Mg C ha−1 was estimated from the severe 1997 peat fires in the Mega Rice Project, West Kalimantan due to deeper peat burning of 51 ± 5 cm (Page et al., 2002). Using the reported range in peat burned area in Indonesia estimated for two different fire seasons, (Table 3), peat burning to 20 cm would release carbon in the range of 0.22 – 1.02 Gt C per fire season.
Our simulation results show that land conversion with burning led to 2.4–2.8 m reductions in peat depth over 100 years, at a fairly constant rate, from 5.4 m to 2.6 m in coastal peatlands and 6.0 m to 3.6 m in inland peatlands; equivalent to mean peat decomposition loss rates of 24 and 28 mm yr−1 for inland and coastal, respectively. Measured peat subsidence rates in oil palm were 54 ± 11 mm yr−1 when burning was used for land clearing, and about 50 ± 22 mm yr−1 in Acacia plantations in Sumatra without burning activities (Hooijer et al., 2012). These measured values, however, are total subsidence rates, comprising several components: burning (oil palm case), oxidation, compaction (due to heavy machinery and to shrinkage in the aerated zone with drying), and consolidation (of the saturated peat due to changes in overlying buoyancy); oxidation is the dominant component (75% to 90% of total subsidence), although compaction and consolidation dominate the subsidence in the initial few years (Hooijer et al., 2012). Similar research from peninsular Malaysia reported an average subsidence rate of 20 mm yr−1, of which 60% was due to peat oxidation and the remaining portion caused by shrinkage (Wösten et al., 1997). In the HPMTrop simulations, the subsidence rates were generated by direct burning losses and peat oxidation (plus any resulting increases in bulk density), but with no compaction or consolidation due to dewatering, and were generally about 50–100% of reported total subsidence rates.
Model uncertainty
Tropical PSFs are relatively poorly understood ecosystems, with limited data on various carbon and water cycle processes, and no sites (yet) with comprehensive ecosystem-scale continuous measurements of the different components of carbon balance, as exist for northern peatlands (e.g. Roulet et al., 2007; Nilsson et al., 2008). On developing a first model to simulate long-term peat accumulation in tropical PSF, HPMTrop was designed to capture each of the fundamental processes – carbon (peat mass) gain through vegetation litter inputs, carbon loss through decomposition, and hydrological controls on the rates of C gain and loss – in a very simple way, thus setting up a framework for improvements as more data become available. This simplicity, coupled with very limited field data, produces several sources of uncertainty inherent to the simulations.
Vegetation NPP and its partitioning into leaf, wood, and root litter fractions (Table 1) come from a limited number of studies (e.g. Chimner & Ewel, 2005; Hergoualc'h & Verchot, 2011). As a result, variation in simulated litter inputs through the Holocene simulations was small. HPMTrop peat accumulation is sensitive to NPP, so improved estimates of PSF NPP and above- and belowground litter production, including their variability in space (e.g. inland vs. coastal peatlands) and time (e.g. El Niño vs. La Niña years), could be used to refine the representation of this process. Long-term observations of tree productivity in PSF are needed to understand the impact of precipitation seasonality on productivity. Similarly, the fundamental decomposition rates come from a single, 12-month litter bag study from Micronesia (Chimner & Ewel, 2005), and it is therefore difficult to even characterize the uncertainty in these parameters, particularly for decomposition over millennia. Note that much of total decomposition occurs in the first few years, and most mass is lost within the first few decades (Moore et al., 2005). As the only literature for decomposition rate for wood and roots are from a Micronesian peatlands (Chimner & Ewel, 2005), it is unknown how well this represents conditions and litter qualities in other tropical peatlands, and in particular, PSF in Southeast Asia. Although trees are generally the dominant PFT, other vegetation types are found in tropical PSF, such as herbs, sedges, aroids, pandan, ferns, and epiphytes (Anderson, 1963; Wust & Bustin, 2004).
To accumulate organic matter, decomposition rates must be lower than vegetation productivity; in peatlands this is primarily due to water-logging that creates anoxic conditions. In HPMTrop, the extent of peat saturation was driven by water table position, which is a result of the hydrological interactions of climate conditions, local topography, and peat physical properties. A more robust precipitation reconstruction throughout the Holocene, incorporating both frequency and intensity of ENSO as well as long-term variations in total annual precipitation, and precipitation seasonality, would improve PSF water table simulations. Water table position is modeled as an annual site-level water balance in HPM (Frolking et al., 2010). However, due to uncertainty and lack of field data for model development and testing, HPM's water balance equations were not used in HPMTrop, and instead an empirical water table estimation based on a monthly water deficit was implemented. Improved modeling of water balance would allow for feedbacks between dynamic peat properties and water table variation (Belyea & Baird, 2006; Frolking et al., 2010). This may be particularly important in drainage simulations, where deeper, highly decomposed peat can have different hydraulic properties than surface peat (e.g. Belyea & Baird, 2006). Improved data on tropical peat hydraulic characteristics, including water retention and hydraulic conductivity are also needed to enhance modeling of water table position (Dommain et al., 2010; Rais, 2011). In addition, installation of a network of drainage ditches in a peatland will generate a predictable spatial pattern of impact on the water table (Verry et al., 2011), and the impact is likely to vary over time as the peat surface subsides and the ditches degrade or are maintained. The simulation results presented here do not take these factors into account.
HPMTrop did not vary NPP rates between inland and coastal peatland simulations, therefore more rapid accumulation in the coastal peatlands had to arise from slower decomposition. This was accomplished by two modifications – (i) a shallower water table, and (ii) a shorter anoxia scale length in the coastal peatlands. Anoxia scale length is a parameter that controls the exponential decline in the peat decomposition rate with depth below the water table to full anoxia with minimum decomposition rate. Anoxia scale length is a simple representation of several processes that could influence oxygen penetration below the water table – e.g. high frequency water table variability (i.e. submonthly), inputs of oxygenated rainwater, general diffusion, and plant-mediated gas transport. Based on an in situ experiment of peat drying-rewetting, lowering the water table generates oxygen penetration into the peat pores and thus the dissolved oxygen may still be detected below, but close to, the water table (Estop-Aragonés et al., 2012). In the scenario for simulating peat accumulation in inland and coastal peatlands, the anoxia scale length values are 0.3 and 0.23 m, respectively. Those values were obtained based on sensitivity tuning by comparing the simulated peat age–depth profiles with the measured profiles reported by Dommain et al. (2011). As we had only one set of multi-year water table data available (for an inland peatland), the water table depth adjustment for all noninundated months for coastal peatlands was also set by sensitivity tuning, to a value of 25% closer to the peat surface (shallower). Dommain et al. (2011) noted that, relative to inland peatlands in Indonesia, coastal peatlands were not strongly influenced by sea-level decline, or reduced precipitation and El Niño activity over the past several millennia. It was also shown in HPMTrop sensitivity analysis that changing the pattern of water table seasonality affects both carbon stocks and peat depth at the end of simulation (Table 2).
HPMTrop simulation results indicated that a large amount of carbon would be lost from tropical PSF converted to agriculture, due to draining, reduced litter inputs, and burning (Table 3). Nevertheless, this amount of carbon release was generated only by peat oxidation due to peat decomposition and burning. Other carbon forms that could be released from peat, such as methane and fluvial dissolved organic carbon, were not modeled in HPMTrop. A recent study in a disturbed Kalimantan peatland showed that total fluvial organic carbon (comprising dissolved organic carbon and particulate organic carbon) flowing out of a drained disturbed PSF ranged from 88 to 100 g C m−2 yr−1 (0.88 to 1.0 Mg C ha−1 yr−1), potentially increasing the peat carbon loss rate by about 20% (Moore et al., 2013). Including both methane emissions and fluxes of dissolved organic carbon are important next steps in model improvement for studying the carbon dynamics in tropical peatlands.
Despite uncertainties and the need for improved long-term ecological observations from tropical peatlands, HPMTrop reproduced observed century- to millennial-scale rates of peat carbon accumulation for inland and coastal PSF. In addition, results from the land-use change scenario emphasize the magnitude of carbon emissions associated with tropical peat swamp conversion, and the thousands of years necessary for hydrologically restored and reforested peatlands to regain the carbon lost in years and decades following conversion. HPMTrop provides the first platform for modeling long-term C dynamics in tropical peatlands, and the model can be modified to accommodate refined or additional inputs aimed to assess the impacts of climate, land management, disturbance, and their interactions on landscape scale peatland C dynamics. Provided adequate data for parameterization, the HPMTrop framework could also be used as a foundation for simulating C dynamics for tropical peatlands beyond Southeast Asia.
Acknowledgements
We thank R. Dommain for providing the peat core age–depth profile data, and for helpful comments on the model. We thank R. Birdsey, R. Kolka, S. Neuzil, and three anonymous reviewers for helpful comments on an earlier draft. This study was supported by a grant from the USDA Forest Service Indonesia Peatlands, Forest and Climate Change Initiative to SF (USDA-2011-67003-30373), a graduate tuition fellowship to SK from the University of New Hampshire, and the Center for International Forestry Research (CIFOR). Additional support from the USAID-funded Sustainable Wetlands Adaptation and Mitigation Program (SWAMP) was jointly implemented by CIFOR, the USFS, and Oregon State University.




