Residual stress relaxation induced by the application of mechanical loads is determined by the nature of residual stress, the elasto-plastic material properties, and the type of applied load. Despite the importance of the first load cycle, analytical models available in the literature generally assumed residual stress relaxation as a continuous process. Residual stress induced by machining on Inconel 718Plus superalloy cylindrical specimens was measured before and after the application of load cycles under strain control. Low-cycle fatigue tests were carried out at room temperature for different strain amplitudes, and X-ray diffraction measurements were performed before and after 10 and 100 cycles. A comprehensive analytical model was derived to describe the relaxation process associated with the initial cycles and that associated with the continuous application of load cycle, which is based on the plastic strain energy per cycle W and requires the evaluation of parameters that are only dependent on the material and not on the strain amplitude.

1 INTRODUCTION

The residual stress induced by machining is essentially caused by the mechanical and thermal effects associated with the severe plastic deformations experienced by the material. When these effects are particularly relevant, the phase and metallurgical transformations are non-negligible. The interaction and level of these factors determine the resulting residual stress field.¹ Two competitive phenomena result in a wide range of residual stress fields. The first one is a mechanical effect, which is essentially governed by strain hardening, whereas the second one can be considered a thermal effect, which originates from material softening at increasing temperature. By distinguishing the two effects and ignoring the thermal aspect, we can simplify the problem and better understand why residual stress occurs during machining. Considering only the mechanical effect, the material in the vicinity of the tip is initially deformed in compression during machining and then partially moved beneath the tool, resulting in superficial tensile plastic deformation. Consequently, the surrounding material tends to limit its inelastic deformation, generating a compressive residual stress state highly localized in the superficial layer. The thermal effect originating from the dissipative phenomena associated with the relevant plastic strain is also considered, which essentially consists of heat generation and the consequent local increase in the material temperature. Because plastic deformation determines a high thermal output in a thin superficial layer, the material suffers a relevant increase in temperature. If the temperature variation is particularly high and the mechanical properties are softened by the temperature, the material exhibits plastic deformation at high temperatures. When the temperature returns to room temperature, the thermal shrinkage generates a predominantly tensile residual stress.

No consensus has been reached in the literature regarding the relative contributions of mechanical and thermal effect during cutting. Several authors^2-5 have shown that the mechanical effect is predominant, and the thermal effect becomes relevant at higher cutting speeds.⁶ However, by limiting the observation to high strength metallic materials, it can be found that the superficial residual stress induced by machining is tensile in some cases^7-10 and compressive in others,^{11, 12} confirming that the final nature of the superficial residual stress is the result of contrasting phenomena.^{2, 13}

The initial residual stress state can undergo relaxation due to the mechanical loads. Understanding and accurately quantifying residual stress redistribution under cyclic mechanical loads remains an important technical challenge.

The importance of relaxation after the first load cycle (quasi-static loading) was reported in the comprehensive literature reviews by James¹⁴ and McClung.¹⁵ When the initial residual stress was relaxed, specifically after the first load cycle, the application of further cycles may produce only a gradual relaxation, as reported in previous studies.^16-18 In these cases, quasi-static and cyclic relaxation occur according to the von Mises yield criterion; the superposition of the initial residual stress and external load exceeds the local monotonic or cyclic yield stress of the material.^19-21 These considerations derived from experimental measurements are consistent with the results obtained by the finite element method numerical models of the relaxation phenomenon. ^22-24 In particular, the effect of the plasticization behavior of the material on the residual stress relaxation was found to be particularly evident after the first load cycle and negligible in subsequent load cycles. In certain cases,^25-29 residual stress measured after load application was found to be higher than the initial residual stress, and in others, the compressive residual stress became tensile. This effect is mainly observed when bending fatigue loads are applied.^{23, 25, 27} Other studies have considered the residual stress relaxation originating from constant and variable amplitude fatigue loads³⁰ and determined how the process is affected by the material characteristics and surface hardening state.^{17, 31} The importance of the relaxation near the crack tip was also considered.^{32, 33}

This phenomenon was analyzed also from a microscopic perspective by Qian et al. in three different types of steel.³⁴ The authors proposed a relaxation model based on the principle of creep dislocation movement individuating the three relaxation regimes as a function of the applied stress. Xie et al.,³⁵ in agreement with Morrow and Sinclair,³⁶ attributed the amount of relaxation to the plastic strain accumulation with the number of cycles. Concerning this aspect, relaxation can only occur if there is some degree of plasticity in the reverse loading, both in tension and compression.³⁷ In a recent study,³⁸ the authors analyzed the circumstances under which continuous relaxation could arise. They concluded that a continuous residual stress modification is possible if the production of new plastic strain takes place in both the loading and reverse loading parts of a cyclic loading. They further determined that the relaxation at a small load is limited to the first cycle depending on whether the stress ratio is positive or negative. In contrast, continuous relaxation occurs if the load is sufficiently high and the stress ratio is negative.

The significance of considering the influence of the cold working rate on different volumes of material and its influence on the local material properties and therefore on the role of gradient properties on the relaxation mechanism has been demonstrated in previous studies.^{39, 40} This is particularly true for all residual stress fields concentrated in a superficial layer, such as those introduced by shot peening, general surface mechanical treatments, and machining. These treatments and manufacturing phases introduce cold work in the surface layer, producing a local yield strength gradient. In particular, tensile cold working increases the tensile yield strength on the surface but reduces the compressive yield strength owing to the Bauschinger effect. Consequently, the surface layer, where compressive residual stress is introduced, easily reaches the yield limit and relaxes the residual stress.

This study focuses on the phenomenon of relaxation of residual stress induced by machining in a nickel-based superalloy, characterized by superior mechanical properties at room and at elevated temperature. This class of materials is widely used to realize high-value components subjected to particularly heavy thermal and mechanical load conditions. An improvement in the mechanical behavior of such components could lead to valuable economical and technical advantages.

This study aims to describe how the chip-forming residual stress induced by machining in a nickel-based superalloy is modified by applying a fatigue load cycle under strain control at different amplitudes. Based on experimental observations, a two-stage process has been proposed for the evaluation of the residual stress relaxation. Furthermore, identifying in plastic strain energy per cycle is a suitable parameter to define an analytical model for predicting the phenomenon in the considered class of material.

1.1 Residual stress relaxation models

Semi-empirical models have been developed to predict residual stress relaxation based on experimental assessments.^{16, 36, 41, 42} Relaxation is considered a continuous and gradual process that ideally occurs for the entire life of the component. In several cases, the authors recognized the importance of relaxation during the first load cycle but explicitly declared that this phenomenon was not covered by their proposed model.^{16, 36} Relaxation models are characterized by a common framework consisting of relatively simple analytical formulations, in which the main relevant parameters (initial residual stress, applied stress/strain amplitude, number of cycles, and cyclic hardening/softening behavior) are arranged with empirical factors to obtain a good fit with the experimental data. Therefore, the need to determine these empirical factors produces a lack of generality in these relaxation models, which are not directly applicable to cases that differ from those used for developing them.

Several models maintain a general approach and therefore could be suitable for application in different cases. Morrow and Sinclair³⁶ conducted fatigue tests on strain control. Considering the residual stress as the mean stress, they proposed the following relationship:

\frac{σ_{mN}}{σ_{m 1}} = \frac{σ_{y} - σ_{a}}{σ_{m 1}} - {(\frac{σ_{a}}{σ_{y}})}^{b} \log N

(1)

where σ_mN is the mean stress in the Nth cycle, σ_m1 is the mean stress in the first cycle, σ_a is the stress amplitude, σ_y is the yield stress, and b is a constant that depends on the material hardening and applied strain. This model is suitable only for a stress ratio R = −1, because in this case the residual stress can be considered the mean stress.

Similarly, Jhansale and Topper⁴¹ proposed a simple relationship between the mean stress relaxation and the number of cycles in strain control, given by

\frac{σ_{mN}}{σ_{m 1}} = {(N)}^{B}

(2)

where the symbols assume the same meaning as in Equation (1). Landgraf and Chernenkoff⁴² used this approach to evaluate the empirical factor B and introduced the concept of a threshold strain range for the mean stress relaxation.

Kodama¹⁶ performed residual stress measurements using X-ray diffraction on shot-peened specimens. Analyzing the results for different number of cycles, he obtained the following rule:

σ_{N}^{re} = A + m \log N

(3)

where σ_N^re is the residual stress after N cycles, and A and m are material constants that depend on the load amplitude σ_a. Experimental data show that this relation is only true after the first cycle; therefore, it is not suitable for cases where residual stress relaxation occurs immediately after the first load cycle, which is typically the case.

These few examples are based on simple analytical relations; however, they lead to prediction that could be very different. Moreover, a common framework does not exist, and it is difficult to define a general model of the residual stress relaxation, which is still a complex phenomenon. In several cases, only qualitative indications can be derived, and the proposed models are often inapplicable to different experimental conditions. To overcome these difficulties, the use of plastic strain energy per cycle as an indicator of residual stress relaxation was considered in this study.

2 MATERIALS AND METHODS

Superalloys are extensively used in the aeronautical and aerospace fields, mainly for turbines and compressors production, because of their high resistance at operating temperature. The polycrystalline superalloy Inconel 718Plus could be used for turbine disk applications, because of its high-temperature strength, good corrosion resistance, and excellent workability.

Inconel 718Plus is a precipitation-hardened nickel-based material that is normally subjected to thermal treatment, which consists of double vacuum melting or triple melting. The first process ensures a good degree of microcleanliness and tight compositional control. Triple melting minimizes the possibility of macrosegregation and enhances microcleanliness.^43-45

The analyzed specimens were obtained from a larger part of the forged disk using Electric Discharge Machining. After having cut three circumferential blocks, each block has been used to obtain a certain number of cylindrical bars having a diameter of 14 mm (Figure 1A). Finally, the bars were chip formed to obtain the typical geometry of the Low-Cycle Fatigue specimens, according to the ASTM E606 standard (Figure 1B). In this manner, all specimens were oriented in the circumferential direction with respect to the original forged disk. The specimens had a final diameter of 5 mm and a gauge length of 12.7 mm to prevent elastic instability. As the specimens were obtained from an Inconel 718Plus bar by turning, a residual stress state was introduced on the surface layer.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

(A) Disposition of specimens in the forged disk; (B) geometry of LCF specimens [Colour figure can be viewed at wileyonlinelibrary.com]

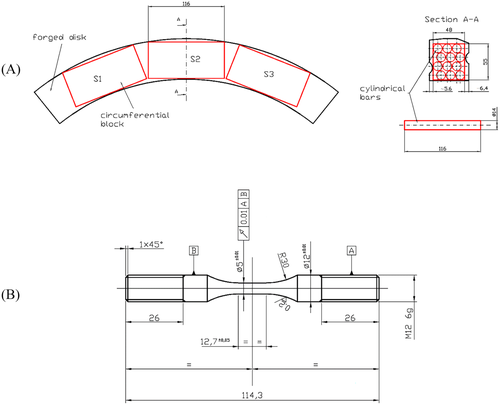
Low-cycle fatigue tests were performed using a servo-hydraulic test machine MTS810, with a load capacity of 100 kN. Triangular ramps were imposed in strain control at a frequency of 0.1 Hz to prevent specimen overheating. An axial extensometer with a gauge length of 10 mm was used to measure the longitudinal strain during tests. During the tests, the load and applied strain were acquired at 50 Hz to reconstruct hysteresis cycles. The level of the applied strain ε_a ranged from 0.76% to 1.33%. All tests were suspended after 10 and 100 cycles to measure the residual stress using X-ray diffraction. Finally, the test was continued up to failure, identified by a 10% drop of the maximum load of the stabilized cycle.

Residual stress in the longitudinal and circumferential directions was evaluated using X-ray diffraction in the as-machined specimens and after the application of 10 and 100 fatigue cycles to determine the residual stress relaxation. The X-ray diffraction measurement technique was selected because it is a non-destructive technique that allows the mechanical test to be suspended, and residual stress measurements can be carried out without introducing any change in the specimen geometry. The limitation of this technique is that measurement is possible only on the surface of the specimen.⁴⁶ The evaluation of the in-depth residual stress is, however, a feasible means to remove a thin layer of the material by electropolishing, without altering the surroundings residual stress. This possibility has not been considered in this study because the relevant residual stress introduced by machining is on the surface, and second, the residual stress profile over depth, independent of its surface value, goes rapidly to zero.^{9, 47}

A Rigaku ULTIMA IV diffractometer was used in the iso-inclination configuration with a Cu source (λ = 1.540562 ang.), spot size of 1 mm, voltage of 40 kV, and amperage of 40 mA. A collimator with a diameter of 1 mm was used to reduce the error induced in the circumferential direction by specimen curvature. Using a Cu source on Inconel 718, the Bragg angle 2θ = 90.4°, and the microscopic elastic constant (E/[1 + ν]) = 140 GPa.⁴¹ Under these measurement conditions, the residual stress measurement must be referred to a superficial layer of approximately 0.005 mm. For each measurement, six scans were performed for six different ψ angles, chosen in the range 0° to 30° to ensure that the values of sin²ψ are evenly spaced. The diffraction peak position was evaluated using the center of gravity method, followed by filtering and reduction of data scatter.

3 RESULTS

3.1 Static and fatigue results

A static mechanical test was performed to determine monotonic mechanical properties at room temperature (Figure 2A). Moreover, the material behavior under repeated plastic strain was evaluated. In this case, a single specimen was loaded in the strain control using blocks of 10 cyclic loads at increasing strain amplitudes up to failure. The data for the stabilized hysteresis cycle of each block were used to determine the cyclic curve (Figure 2B). The Ramberg–Osgood model was adopted for both static and cyclic behavior, which can be expressed as⁴⁸

ε = ε_{e} + ε_{p} = \frac{σ}{E} + {(\frac{σ}{K})}^{\frac{1}{n}},

(4)

\frac{∆ ε}{2} = \frac{∆ ε_{e}}{2} + \frac{∆ ε_{p}}{2} = \frac{∆ σ}{2 E} + {(\frac{∆ σ}{2 K^{'}})}^{\frac{1}{n^{'}}},

(5)

The parameters that describe the resultant monotonic and cyclic mechanical properties could be determined (Table 1), which are consistent with the values reported in the literature.⁴⁵

TABLE 1. Monotonic and cyclic mechanical properties of Inconel 718Plus

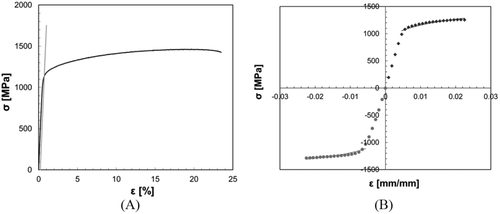
Tensile strength σ_R [MPa]	Yield stress σ_y [MPa]	Elastic modulus E [MPa]	Elongation at break A [%]	Strength coefficient K [MPa]	Strain hardening exponent n	Cyclic strength coefficient K′ [MPa]	Cyclic strain hardening exponent n′
1462	1136	219,160	23.5	1666.2 ± 1.00	0.0742 ± 0.0003	2079.1 ± 1.05	0.127 ± 0.0104

Finally, fatigue tests were outperformed by applying a constant strain amplitude. Data of all the tests are reported in Table 2, whereas Figure 3 shows the hysteresis cycles for specimens subjected to strain amplitudes of 0.9% and 1.33%. It can be observed that the experimental behavior was not affected by the test interruption. The hysteresis cycles show that the material exhibits a cyclic softening behavior, which is typical of this class of high-strength materials. The results of the fatigue tests were used to determine the strain-life curve. The Manson–Coffin relationship^{49, 50} accurately described the fatigue life behavior of the material, enabling the determination of the corresponding parameters (Figure 4):

\frac{∆ ε}{2} = \frac{∆ ε_{e}}{2} + \frac{∆ ε_{p}}{2} = \frac{σ_{f}^{'}}{E} {(2 N_{f})}^{b} + ε_{f}^{'} {(2 N_{f})}^{c},

(6)

TABLE 2. Detail of low-cycle fatigue tests of Inconel 718Plus

Specimen	Strain amplitude ε_a [%]	Number of cycles to failure N_f	Stress amplitude σ_a [MPa]	Mean stress σ_m [MPa]	Tangent modulus E_NT [MPa]	Elastic strain amplitude ε_ael [%]	Plastic strain amplitude ε_apl [%]
29G	0.760	2111	1034.4	21.1	207,364	0.472	0.288
27G	0.900	645	1110.7	−25.0	220,936	0.507	0.393
21F	1.000	337	1142.3	−37.8	205,819	0.521	0.479
22F	1.100	269	1189.5	−24.1	207,560	0.543	0.557
23F	1.200	374	1216.1	2.8	175,538	0.555	0.645
24F	1.250	374	1164.1	4.6	188,151	0.531	0.719
25G	1.330	167	1242.7	−3.9	187,290	0.567	0.763
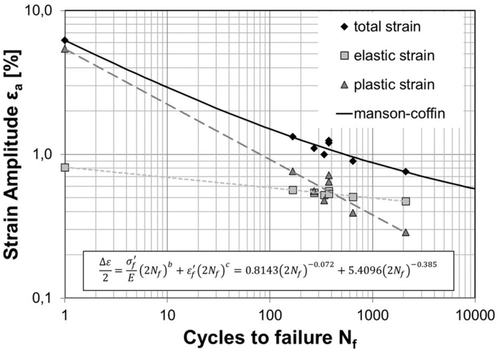
Static	6.2239	1				0.8143	5.4096

3.2 Residual stress results

Residual stress measurements in the longitudinal direction were characterized by a very low data dispersion of the sin²ψ straight line, confirming the reliability of the measurements, although the surface was not flat owing to the curvature of the specimen. As the effect of curved surface produces an asymmetry of the diffraction peak,⁵¹ the peak position evaluated by the center of gravity method differs from the maximum peak intensity. In the longitudinal direction, the difference between the two estimated peaks fell within 0.5%, which is considered acceptable. On the contrary, the high curvature of the specimen surface in the circumferential direction determined the difference in the peak position higher than 0.5% in a limited number of cases. Therefore, these data were discarded during the data-elaboration process. Table 3 lists the longitudinal and circumferential residual stress values σ_L(N) and σ_C(N) for each specimen, where the parameters N = 0, 10, and 100 indicate the number of load cycles applied before the residual stress evaluation. The scatter of the residual stress measurements was acceptable, considering the experimental difficulty in carrying out a correct measurement on the curved surface of the specimen. The NR (Not Reliable) measurement indicates the uncorrected evaluation of the sin²ψ straight line. The initial residual stress was compressive in both the longitudinal and circumferential directions suggesting that the residual stress field that originated from machining, as a result of the material properties and typical cutting parameters adopted, was dominated by the mechanical effect, as discussed in the section 1. The residual stress was higher in the longitudinal direction with exceptions in two cases. In general, the initial residual stress, especially in the longitudinal direction, can be considered fairly uniform between different specimens, which is a preferable prerequisite for the scope of this work.

TABLE 3. Longitudinal and circumferential residual stress

Specimen	Strain amplitude ε_a [%]	Longitudinal residual stress after N cycles σ_L (N) [MPa]			Circumferential residual stress after N cycles σ_C (N) [MPa]
Specimen	Strain amplitude ε_a [%]	σ_L(0)	σ_L (10)	σ_L(100)	σ_C(0)	σ_C (10)	σ_C(100)
29G	0.76	−414 (±189)	−545 (±73)	NR	−213 (±219)	NR	NR
27G	0.90	−437 (±163)	−563 (±116)	−357 (±139)	−650 (±56)	−245 (±88)	−649 (±72)
21F	1.00	−507 (±140)	−475 (±95)	−585 (±157)	−646 (±54)	−220 (±83)	N.R.
22F	1.10	−673 (±270)	−364 (±27)	−267 (±141)	−402 (±40)	−541 (±71)	−715 (±104)
23F	1.20	−796 (±85)	−163 (±77)	−164 (±50)	−314 (±44)	−277 (±73)	−317 (±61)
24F	1.25	−615 (±133)	−29 (±65)	−56 (±61)	−186 (±78)	−367 (±47)	NR
25G	1.33	−665 (±165)	−185 (±48)	−2 (±54)	NR	−188 (±104)	NR

4 DISCUSSION

The analysis of the relaxation phenomenon was restricted to the longitudinal residual stress, which is directly involved in the relaxation phenomenon because it is aligned with the direction of the applied load. In fact, the circumferential residual stress did not show a particular evolution trend with respect to the number of cycles. This is an expected behavior, as it is evident that applying a tensile load could produce a relaxation of the residual stress especially in the longitudinal direction. On the other hand, the circumferential residual stress measurements do not provide sufficient reliability to derive valid observations from a curved surface.

Despite the limited amount of experimental data, the relaxation phenomenon was observed only when the applied strain amplitude is above a threshold value ε_a,th, which is in agreement with the observation reported previously.⁴² This is evident if the longitudinal residual stresses are plotted against the number of cycles (Figure 5). In this figure, residual stress data have been presented in two separated graphs to improve readability and better interpret the data. Specimens subjected to strain amplitudes lower than 1% (Figure 5A) have been separated from those higher than 1% (Figure 5B). Thus, it is possible to ascertain that relaxation is practically absent if the applied strain amplitude is lower than the threshold value of approximately 1%. However, for the specimens subjected to a lower strain amplitude (ε_a < ε_a,th), the applied strain amplitude was sufficiently high to determine the cyclic plasticization of the material, as shown by the data reported in Table 2. Nevertheless, with cycle-by-cycle plasticization, the residual stress amount seemed to be stable against the number of cycle and did not change continuously (Figure 5A). From an empirical point of view and without any specific claim, it can be observed that the strain amplitude threshold is in good agreement with the value of the strain amplitude that corresponds to the yield stress, as described by the Ramberg–Osgood model, which has been previously suggested for the static behavior of the material.

ε_{a, th} = \frac{σ_{y}}{E} + {(\frac{σ_{y}}{K})}^{\frac{1}{n}} = 1.09 %,

(7)

This behavior was different (Figure 5B) when a strain amplitude higher than 1% was applied (ε_a > ε_a,th). Relaxation occurred, with the majority of it concentrated in the first 10 cycles. According to the findings present in the literature,^{15, 16} a large amount of this relaxation can be attributed to the first load cycle, even if no measurement has been carried out to support this statement. The application of further cycles after the first 10 cycles produces a slightly change in residual stress, which is significant in cases where it exceeds the inherent scatter of the measurement process.

The percentage variation in the residual stress after N cycles was calculated to quantify the relaxation phenomenon:

∆ σ_{L} (N) = \frac{σ_{L} (N) - σ_{L} (0)}{σ_{L} (0)} \cdot 100,

(8)

where σ_L(N) is the residual stress after N load cycles (N = 10, 100 cycles) and σ_L(0) is the initial residual stress. A general indication of the influence of the applied load on the residual stress relaxation can be derived by relating Δσ_L(N) to the applied strain amplitude ε_a (Figure 6). The curves show that the longitudinal residual stress was completely relaxed in specimens subjected to high strain amplitudes, particularly for strain amplitudes higher than 1.2%. For lower values of strain amplitude, but not lower than 1%, residual stress drops by approximately 50% without any relevant difference between 10 and 100 cycles. Finally, for strain amplitude lower than 1%, the relaxation falls into the scatter of the measurement and therefore must be considered as not significant.

Based on the experimental behavior described above and observations made in the past by other researchers (briefly reported in section 1), three hypotheses have been considered to formulate a model that could describe the complexity of the relaxation phenomenon.

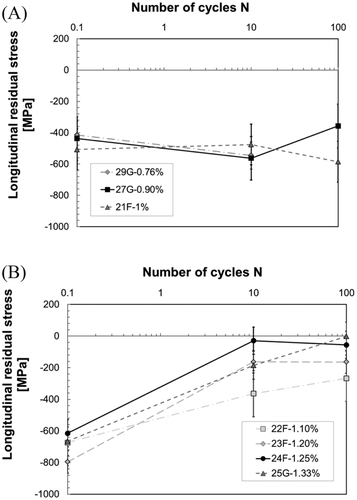
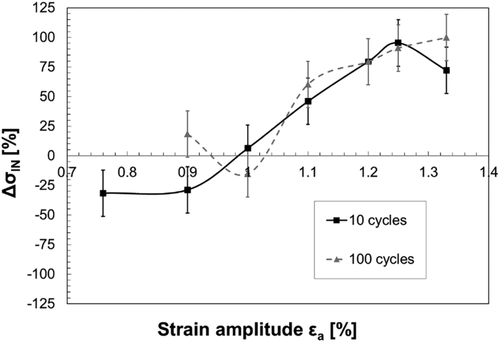
Residual stress relaxation appears only if the applied load condition is above a threshold value, expressed by a threshold strain amplitude ε_a,th, which has been previously identified and derived from the static behavior of the material (Equation 7).
Residual stress relaxation is concentrated in the first 10 cycles, most likely in the first cycle, as observed in several works in literature.
Residual stress relaxation continues after the first 10 cycles, even if this phenomenon is minimal with respect to the initial one, and the continuous relaxation after the first 10 cycles cannot be neglected especially for higher strain amplitudes.

Regarding the first statement, in a recent study,⁵² static four-point bending tests were performed to induce residual stresses in flat-bending specimens. Subsequently, specimens were subject to several constant cyclic strain-controlled bending loads, and the tests revealed almost cyclic stability of residual stresses for such loading, considering that the maximum strain amplitude applied was relatively low (0.20%).

Consequently, residual stress relaxation must be regarded as a two-stage evolution, activated only if a threshold stress–strain state is achieved. Moreover, each stage of relaxation can potentially be governed by different load cycle parameters.

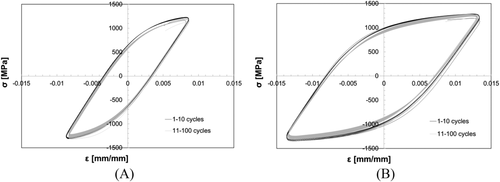
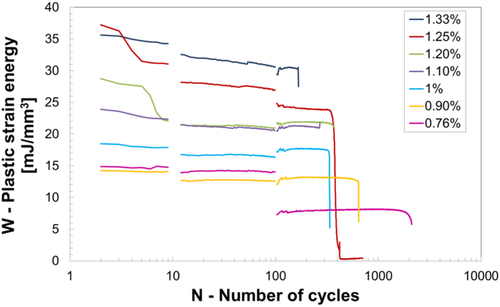
The model proposed in this study describes this two-stage process based on the evolution of hysteresis cycles against the number of cycles. The availability of the complete fatigue data of each specimen, which allows the reconstruction of all hysteresis cycles, makes it possible to discuss the relaxation phenomenon from an energy perspective. Considering a specific load cycle, the hysteresis area can be obtained by plotting the measured stress against the applied strain. The area W represents the plastic strain energy of a unitary material volume, which is evaluated through a numerical integration of the 500 experimental stress–strain datasets available per cycle. This value is averaged over the cylindrical volume corresponding to the gauge length of the extensometer and is referred to as the specific cycle considered. The plastic strain energy per cycle W has a relatively long tradition as a damage parameter to determine the fatigue behavior in several conditions.⁵³ In addition, the specific thermal energy per cycle Q was proposed by Meneghetti et al.⁵⁴ as a fatigue damage parameter.

Figure 7 shows the parameter versus the number of cycles for each specimen, excluding the data corresponding to the first and last cycles of the test block (cycles 1, 10, 11, 100, and 101) affected by transient effects due to the testing rig control system. Moreover, the need to stop the fatigue test for carrying the X-ray measurement introduces a step in the trends (Figure 7), because the repositioning of the extensometer always results in a change in the effective gage length. This change in the plastic strain energy is particularly significant in the case of 1.25% after 100 cycles. These data must be used with caution. Despite of these experimental effects, which potentially introduce errors in the evaluation of the energy parameter, W, three notable general behaviors were observed.

Specimens tested at higher strain amplitudes revealed an important reduction of the plastic strain energy W concentrated in the first 10 cycles. The reduction was quite regular and uniform; however, in two cases, the reduction was concentrated between two subsequent cycles, not necessarily in the initial phase.
The trend of the plastic strain was regular and uniform between 10 and 100 cycles. Furthermore, a reduction was associated with specimens tested at higher strain amplitudes, which seemed to disappear at lower strain amplitudes. Finally, the rate of decay was proportional to the applied strain amplitude.
The slope of the intermediate curves between 10 and 100 cycles was high at the maximum strain amplitude and decreased with a decrease in the strain amplitude ε_a.

These qualitative observations suggest the existence of a possible relationship between relaxation and plastic strain energy W: if the area of the hysteresis cycle does not change, no relaxation occurs. On the other hand, in cases in which relaxation occurs, a reduction in the hysteresis cycle is observed. Although the existence of a relationship is evident, it is not possible to establish whether the cause of the relaxation is a change in the hysteresis area or vice versa. Consequently, the plastic strain energy W can be used as an indicator to establish whether relaxation occurs. However, the experimental error associated with the measurement of the plastic strain energy W could be potentially high because its uncertainty is the product of the uncertainty of the measured stress and strain. Considering that a further error is introduced by the numerical integration of the hysteresis cycle, the values of the plastic strain energy W must be considered carefully in comparison with the stress and strain data.

Based on these considerations, parameter W was used to describe the residual stress relaxation. As previously assumed, residual stress relaxation must be considered a two-stage process. The first stage occurs primarily during the initial cycles. For this purpose, several authors have suggested that relaxation occurs primarily in the first cycle. However, a more convenient hypothesis is that this stage is concentrated in one of the initial cycles, not necessarily the first one. This phase is mainly governed by the absolute intensity of the stress–strain state. A corresponding alternative parameter is the absolute amount of plastic strain energy that characterizes the initial cycles, W_in. In particular, a linear trend is assumed between the relaxation amount of the first 10 cycles and the plastic strain energy of the initial cycle:

\frac{σ_{L} (10)}{σ_{L} (0)} = p W_{in} + q,

(9)

where parameters p and q solely depend on the material.

This hypothesis was confirmed by the experimental data reported in this study, as shown in Figure 8. However, Equation (9) was obtained using the data from cycle 2, which ignore the transient effect of the test control; however, the relaxation is governed by the plastic strain energy associated with the first reliable cycle.

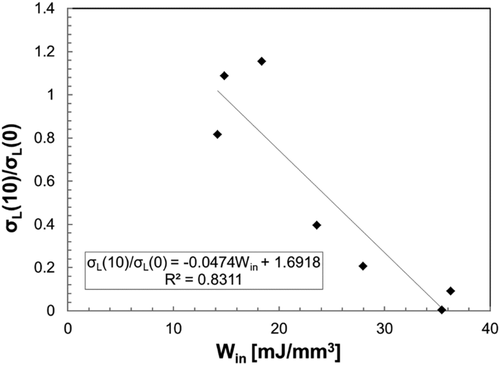
The second stage corresponds to the continuous relaxation associated with the application of several cycles. Practically, all the models proposed in the literature are concerned with this stage. In this phase, the amount of relaxation can be associated with the rate of change in the hysteresis cycles. As previously observed, the slope of the intermediate curves between 10 and 100 cycles (Figure 8) was high at the maximum strain amplitude. Moreover, it decreased with a decrease in the strain amplitude ε_a until the trend appeared horizontal for the test performed below the threshold value ε_a,th. This behavior can be quantified by calculating the absolute value of the plastic strain energy variation over 10 and 100 cycles (Figure 9). Accepting the hypothesis that the relaxation mechanism could be activated above a threshold value of the strain amplitude, it is reasonable to consider that the other mechanical parameters associated with that specific strain level, such as the plastic strain energy W, could act as a threshold value. Relaxation is absent when this parameter falls below the threshold value, whereas a higher relaxation amount corresponds to a higher variation in plastic strain energy. A threshold value for plastic strain energy can be determined by fixing the value of the plastic strain energy W_10th measured in correspondence with the test with strain amplitude ε_a = 1%, which is the nearest to the threshold value ε_a,th = 1.09% derived from the Ramberg–Osgood model (Equation 7). This choice allows the establishment of a threshold value for the plastic strain energy that can be evaluated simply by determining the monotonic curve of the material.

This threshold value W_10th can be used to calculate a normalized parameter for the reduction of plastic strain energy after 100 cycles as follows:

w_{100} = - \frac{W_{100} - W_{10}}{W_{10 th}},

(10)

The parameter w₁₀₀ represents the normalized reduction in the hysteresis cycle measured between 10 and 100 cycles. Using an exponential law, a simple relationship for the calculation of the amount of residual stress relaxation after N cycles can be obtained as follows:

\frac{σ_{L} (N)}{σ_{L} (0)} = A e^{β w_{N}},

(11)

where A and β are parameters depending on the material.

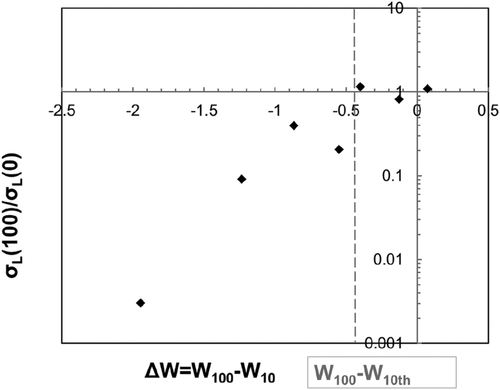
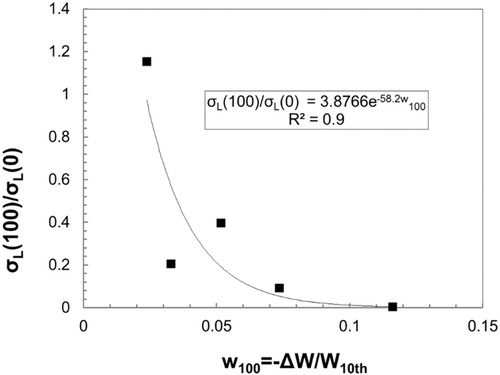
Applying Equation (11) to the experimental data reported in this study and considering only the specimens that were tested above the threshold strain amplitude, a good correlation of the data was obtained (Figure 10).

5 COMPARISON WITH ALTERNATIVE RESIDUAL STRESS RELAXATION MODELS

The experimental data reported in this study were used to validate the alternative models proposed in the literature. This allows comparison of the approaches especially with respect to their generality and the effective possibility of evaluating the material parameters involved. The models reported in the literature have been developed using theoretical considerations and experimental data that differ in terms of material, nature of residual stress, and applied load. Therefore, direct application of these models to general cases is not feasible. Another complication is the need to calculate specific parameters, which are often used in the models to obtain good agreement with the experimental data. However, the aim is to highlight the peculiarities and disadvantages of the most common models.

Let us firstly consider the model proposed by Morrow and Sinclair.³⁶ The application of the model requires the determination of the parameter b of Equation (1), which is dependent not only on the material properties but also on the applied strain. By adopting the notation used in this study to indicate the residual stress before and after N cycles, it is possible to rearrange Equation (1) to derive the analytical expression of the parameter b:

b = \frac{\log [\frac{1}{\log N} (\frac{σ_{y} - σ_{a}}{σ_{L} (0)} - \frac{σ_{L} (N)}{σ_{L} (0)})]}{\log \frac{σ_{a}}{σ_{y}}},

(12)

By substituting the experimental data into Equation (12), the value of b is obtained for each strain amplitude ε_a and for N = 10 and 100. The values of parameter b vary randomly with respect to ε_a and N (Figure 11). Therefore, we conclude that this model does not correspond with the experimental data reported in this study and it is, at least in this case, not verified.

The second model considered for the comparison was proposed by Jhansale and Topper.⁴¹ The analytical formulation of the model is expressed by Equation (2) and is particularly simple. Using the experimental data reported in this study, parameter B can be easily calculated for each strain amplitude. Plotting the values of B against the applied strain amplitude shows that B is equal to zero below a strain amplitude threshold, which indicates that no relaxation occurs (Figure 12A). This behavior was observed and proposed by Landgraf and Chernenkoff⁴² and is now confirmed by the experimental data of this study. Using the threshold value of strain amplitude ε_a,th = 1.09%, which has been calculated previously, it is possible to derive the expression of B, as shown in Figure 12B.

B = - 4.8972 \cdot (\frac{ε_{a}}{ε_{a, th}} - 1),

(13)

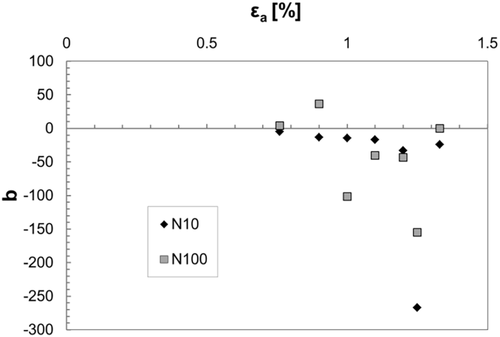
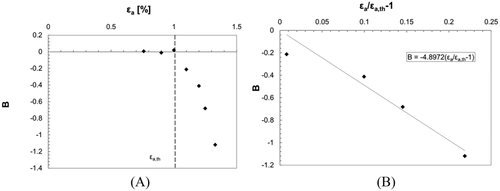
After determining parameter B, the model proposed by Jhansale and Topper can be used to predict residual stress relaxation for the experimental data of this study, with the strain amplitude threshold considered. Figure 13 clearly shows that the prediction values of this model were comparable to the experimental values. In this case, parameter B is dependent not only on the material but also on the strain amplitude, even if a simple correlation with the applied strain exists.

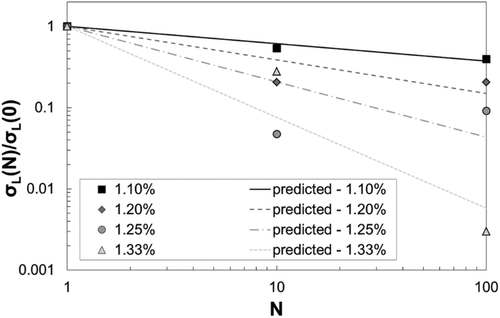
In summary, the residual stress relaxation reported in this study cannot be described using the model proposed by Morrow and Sinclair but is coherent with the model proposed by Jhansale and Topper, which was modified to consider the existence of a strain amplitude threshold for activating the relaxation process. However, both models require the derivation of experimental parameters for each applied strain amplitude, resulting in a poor generality.

6 CONCLUSIONS

In this study, the residual stress relaxation phenomenon, following the application of cyclic load in the low-cycle fatigue regime, was analyzed based on data derived from a series of experimental tests carried out on Inconel 718Plus round specimens.

Based on experimental data, the following conclusions can be drawn.

Relaxation occurs only if the threshold value of the stress–strain state is reached. This threshold condition can be evaluated based on the static curve of the material.
A two-stage relaxation process was observed owing to the availability of residual stress data after 10 and 100 cycles. The existence of two distinct relaxation stages was assumed as a starting point for defining a unique coherent model based on the evolution of the plastic energy per cycle W. The two-stage relaxation process has the merit of appropriately considering all the qualitative factors reported in the literature. Relaxation was considered a continuous phenomenon, governed by analytical formulation depending on the number of cycles N, integrated by the ascertainment that the relaxation is mainly concentrated in the initial cycles.
The two-stage relaxation model was successfully described using the plastic strain energy per cycle W, relating the amount of the residual stress relaxation to the initial extension of the hysteresis cycle W_in through a linear relation in the first stage and to the normalized decay of plastic strain energy w₁₀₀ in the second stage.
The proposed model has been proven to provide an accurate quantification of the residual stress relaxation by adopting parameters that are only dependent on the material and not on the strain amplitude.

ACKNOWLEDGEMENTS

Open Access Funding provided by Universita del Salento within the CRUI-CARE Agreement.

CONFLICT OF INTEREST/COMPETING INTEREST

The authors have no conflicts of interest to declare.

AUTHOR CONTRIBUTIONS

Conceptualization and methodology R.N.; experimental test M. De G. and R.N.; resources and supervision V.D.; data curation R.N.; writing—original draft preparation M. De G. and R.N.; writing—review and editing R.N.

All authors declare that the work described has not been published before; it is not under consideration for publication anywhere else, and its publication has been approved by all co-authors, as well as by the responsible authorities—tacitly or explicitly—at the institute where the work has been carried out.

Nomenclature

A, m: parameters of the Kodama model
A, β: parameters of the proposed model
b: parameter of the Morrow–Sinclair model
b, c: parameters of the Manson–Coffin relationship
B: parameter of the Jhansale–Topper model
E: Young's modulus
E_NT: tangent modulus
K: strength coefficient
K′: cyclic strength coefficient
n: strain hardening exponent
n′: cyclic strain hardening exponent
N: number of applied cycles
N_f: number of cycles to failure
p, q: parameters of the proposed relaxation model
Q: specific thermal energy
R: load ratio
sin²ψ: angular orientation of diffraction peaks
w₁₀₀: normalized plastic strain energy at the 100th cycle
W: plastic strain energy per cycle
W₁₀: plastic strain energy at the 10th cycle
W₁₀₀: plastic strain energy at the 100th cycle
W_10th: threshold plastic strain energy of the 10th cycle
W_in: plastic strain energy of initial cycles
2θ: Bragg angle
Δε_e: elastic strain range
Δε_p: plastic strain range
Δσ: stress range
ε: strain
ε_a: strain amplitude
ε_ael: elastic strain amplitude
ε_apl: plastic strain amplitude
ε_a,th: threshold strain amplitude
ε_e: elastic strain
ε_f′: true strain fracture
ε_p: plastic strain
σ_a: stress amplitude
σ_C(0), σ_C(10), σ_C(100), σ_C(N): circumferential residual stress at 0, 10, 100, and N cycles
σ_L(0), σ_L(10), σ_L(100), σ_L(N): longitudinal residual stress at 0, 10, 100, and N cycles
σ_f′: fatigue strength coefficient
σ_m: mean stress
σ_m1: mean stress during the first cycle
σ_mN: mean stress during the Nth cycle
σ_N^re: residual stress after N cycles
σ_R: tensile strength
σ_y: yield stress
ν: Poisson's ratio

Open Research

DATA AVAILABILITY STATEMENT

The experimental data presented in this study are available upon request from the corresponding author.

REFERENCES

1Brinksmeier E, Cammett JT, König W, Leskovar P, Peters J, Tönshoff HK. Residual stresses—measurement and causes in machining processes. CIRP Ann-Manuf Techn. 1982; 31(2): 491-510.
10.1016/S0007-8506(07)60172-3
Google Scholar
2Liu CR, Barash MM. Variables governing patterns of mechanical residual stress in a machined surface. J Manuf Sci E. 1982; 104(3): 257-264.
Google Scholar
3Lin ZC, Lin YY, Liu CR. Effect of thermal load and mechanical load on the residual stress of a machined workpiece. Int J Mech Sci. 1991; 33(4): 263-278.
10.1016/0020-7403(91)90040-A
Web of Science® Google Scholar
4Liu CR, Barash MM. The mechanical state of the sublayer of a surface generated by chip-removal process—part 1: cutting with a sharp tool. J Manuf Sci E. 1976; 98(4): 1192-1199.
Google Scholar
5Liu CR, Barash MM. The mechanical state of the sublayer of a surface generated by chip-removal process—part 2: cutting with a tool with flank wear. J Manuf Sci E. 1976; 98(4): 1202-1208.
Google Scholar
6Okushima K, Kakino Y. The residual stress produced by metal cutting, Defense Technical Information Center.
Google Scholar
7Madariaga A, Arrazola PJ, Esnaola JA, Ruiz-Hervias J, Muñoz P. Evolution of residual stresses induced by machining in a nickel based alloy under static loading at room temperature. In: Proc CIRP 13. 2014: 175-180.
Google Scholar
8Arrazola PJ, Kortabarria A, Madariaga A, et al. On the machining induced residual stresses in IN718 nickel-based alloy: experiments and predictions with finite element simulation. Simul Model Pract Th. 2014; 41: 87-103.
10.1016/j.simpat.2013.11.009
Web of Science® Google Scholar
9Kortabarria A, Madariaga A, Fernandez E, Esnaola JA, Arrazola PJ. A comparative study of residual stress profiles on Inconel 718 induced by dry face turning. Procedia Eng. 2011; 19: 228-234.
10.1016/j.proeng.2011.11.105
CAS Google Scholar
10Özel T, Ulutan D. Prediction of machining induced residual stresses in turning of titanium and nickel based alloys with experiments and finite element simulations. CIRP Ann-Manuf Techn. 2012; 61(1): 547-550.
10.1016/j.cirp.2012.03.100
Web of Science® Google Scholar
11Caruso S, Umbrello D, Outeiro JC, Filice L, Micari F. An experimental investigation of residual stresses in hard machining of AISI 52100 steel. Procedia Eng. 2011; 19: 67-72.
10.1016/j.proeng.2011.11.081
CAS Google Scholar
12Jacobus K, DeVor RE, Kapoor SG. Machining-induced residual stress: experimentation and modeling. J Manuf Sci E. 2000; 122(1): 20-31.
10.1115/1.538906
Web of Science® Google Scholar
13Wu DW, Matsumoto Y. The effect of hardness on residual stresses in orthogonal machining of AISI 4340 steel. J Eng Ind. 1990; 112(3): 245-252.
10.1115/1.2899582
Google Scholar
14James MR. Relaxation of residual stresses an overview. In: Advances in surface treatments: technology-applications-effects. Pergamon Books Ltd.; 1987: 349-365.
Google Scholar
15McClung RC. A literature survey on the stability and significance of residual stresses during fatigue. Fatigue Fract Eng Mater Struct. 2007; 30(3): 173-205.
10.1111/j.1460-2695.2007.01102.x
Web of Science® Google Scholar
16Kodama S. The behavior of residual stress during fatigue stress cycles. In: Proceedings of the international conference on mechanical behavior of metals II; Kyoto, Society of Material Science, 1972; 2: 111-118.
Google Scholar
17Statti G, Mehmanparast A, Biswal R, Rizzo CM. Evaluation of cyclic loading effects on residual stress relaxation in offshore wind welded structures. J Multiscale Model. 2021; 12(02):2150005.
10.1142/S1756973721500050
Web of Science® Google Scholar
18Jiang W, Xie X, Wang T, et al. Fatigue life prediction of 316L stainless steel weld joint including the role of residual stress and its evolution: experimental and modelling. Int J Fatigue. 2021; 143(3):105997.
10.1016/j.ijfatigue.2020.105997
CAS Web of Science® Google Scholar
19Farajian M, Nitschke-Pagel T, Dilger K. Mechanisms of residual stress relaxation and redistribution in welded high-strength steel specimens under mechanical loading. Weld World. 2010; 54(11–12): R366-R374.
10.1007/BF03266751
CAS Web of Science® Google Scholar
20Farajian M, Nitschke-Pagel T, Dilger K. Residual stress relaxation of quasi-statically and cyclically-loaded steel welds. Weld World. 2010; 54(1–2): R49-R60.
10.1007/BF03263484
Web of Science® Google Scholar
21Holzapfel H, Schulze V, Vöhringer O, Macherauch E. Residual stress relaxation in an AISI 4140 steel due to quasistatic and cyclic loading at higher temperatures. Mater Sci Eng A. 1998; 248(1-2): 9-18.
10.1016/S0921-5093(98)00522-X
Web of Science® Google Scholar
22Song X, Liu WC, Belnoue JP, et al. An eigenstrain-based finite element model and the evolution of shot peening residual stresses during fatigue of GW103 magnesium alloy. Int J Fatigue. 2012; 42: 284-295.
10.1016/j.ijfatigue.2012.01.019
CAS Web of Science® Google Scholar
23Yi H, Lee Y. Numerical analysis of welding residual stress relaxation in high-strength multilayer weldment under fatigue loads. Metall Mater Trans B. 2017; 48(4): 2167-2175.
10.1007/s11663-017-0958-0
CAS Web of Science® Google Scholar
24Dehkordi YG, Anaraki AP, Shahani AR. Comparative study of the effective parameters on residual stress relaxation in welded aluminum plates under cyclic loading. Mech Ind. 2020; 21(5): 505.
10.1051/meca/2020061
CAS Web of Science® Google Scholar
25Lambda research the effect of prior cold working on the development of tensile residual stress following bulk deformation. Diffr Notes. 2002; 28: 1-4.
Google Scholar
26Hornbach DJ, Prevéy PS. Tensile residual stress fields produced in austenitic alloy weldments, In: Proceedings of energy week conference & exhibition, Houston, TX, January 28-30 1997, ASME-API, 1997: 183-188.
Google Scholar
27De Giorgi M. Residual stress evolution in cold-rolled steels. Int J Fatigue. 2011; 33(3): 507-512.
10.1016/j.ijfatigue.2010.10.006
CAS Web of Science® Google Scholar
28Dalaei K, Karlsson B, Svensson LE. Stability of shot peening induced residual stresses and their influence on fatigue lifetime. Mater Sci Eng A. 2011; 528(3): 1008-1015.
10.1016/j.msea.2010.09.050
Web of Science® Google Scholar
29Prevey PS, Cammett JC. The effect of shot peening coverage on residual stress, cold work and fatigue in a Ni-Cr-Mo low alloy steel, In: Proceedings of Int. Conf. on Shot Peening, Garmisch-Partenkirchen, Germany, 2002 Sept. 16-20.
Google Scholar
30Zhong W, Ding Y, Song Y, Geng F, Wang Z. Residual stress relaxation of DRWDs in OSDs under constant/variable amplitude cyclic loading. Appl Sci. 2021; 11(1): 1-23.
CAS Google Scholar
31Yonezawa T, Shimanuki H, Mori T. Influence of cyclic loading on the relaxation behavior of compressive residual stress induced by UIT. Weld World. 2020; 64(1): 171-178.
10.1007/s40194-019-00821-1
Web of Science® Google Scholar
32Noghabi M, Sattari-far I, Hosseini Toudeshky H. The study of redistribution in residual stresses during fatigue crack growth. J Mech Eng Sci. 2021; 15(4): 8565-8579.
10.15282/jmes.15.4.2021.09.0675
CAS Web of Science® Google Scholar
33Jiang W, Yu Y, Zhang W, Xiao C, Woo W. Residual stress and stress fields change around fatigue crack tip: neutron diffraction measurement and finite element modeling. Int J Press Vessel Pip. 2019; 179:104024.
10.1016/j.ijpvp.2019.104024
Web of Science® Google Scholar
34Qian Z, Chumbley S, Karakulak T, Johnson E. The residual stress relaxation behavior of weldments during cyclic loading. Metall Mater Trans A. 2013; 44(7): 3147-3156.
10.1007/s11661-013-1688-9
CAS Web of Science® Google Scholar
35Xie XF, Jiang W, Luo Y, Xu S, Gong JM, Tu ST. A model to predict the relaxation of the weld residual stress by cyclic load: experimental and finite element modelling. Int J Fatigue. 2017; 95: 293-301.
10.1016/j.ijfatigue.2016.11.011
CAS Web of Science® Google Scholar
36Morrow J, Sinclair GM. Cycle-dependent stress relaxation. In Proceedings of symposium on basic mechanisms of fatigue, ASTM STP 237. American Society for Testing and Materials, 1958.
Google Scholar
37Chaboche JL, Kanouté P, Azzouz F. Cyclic inelastic constitutive equations and their impact on the fatigue life predictions. Int J Plasticity. 2012; 35: 44-66.
10.1016/j.ijplas.2012.01.010
CAS Web of Science® Google Scholar
38Qiang W, Xuesong L, Zhongjie Y, Zhibo D, Dejun Y. On the mechanism of residual stresses relaxation in welded joints under cyclic loading. Int J Fatigue. 2017; 105: 43-59.
10.1016/j.ijfatigue.2017.08.016
Web of Science® Google Scholar
39Zhuang WZ, Halford GR. Investigation of residual stress relaxation under cyclic load. Int J Fatigue. 2001; 23: 31-37.
10.1016/S0142-1123(01)00132-3
Web of Science® Google Scholar
40Smith DJ, Farrahi GH, Zhu WX, McMahon CA. Experimental measurement and finite element simulation of the interaction between residual stress and mechanical loading. Int J Fatigue. 2001; 23(4): 293-302.
10.1016/S0142-1123(00)00104-3
CAS Web of Science® Google Scholar
41Jhansale HR, Topper TH. Engineering analysis of the inelastic stress response of a structural metal under variable cyclic strains. In: Cyclic stress-strain behavior—Analysis, experimentation, and failure prediction. American Society for Testing and Materials; 1973: 246-270.
Google Scholar
42Landgraf RW, Chernenkoff RA. Residual stress effects on fatigue of surface processed steels. In Analytical and experimental methods for residual stress effects in fatigue, ASTM STP 1004, American Society for Testing and Materials, 1988; 1-12.
Google Scholar
43Du JH, Lu XD, Deng Q, Qu JL, Zhuang JY, Zhong ZY. High-temperature structure stability and mechanical properties of novel 718 superalloy. Internal report, Department of superalloy, Central Iron and Steel Resarch Institute, 2006; 452-453.
Google Scholar
44Kennedy RL. Allvac® 718plus™, superalloy for the next forty years. The Minerals, Metals & Materials Society, 2005.
Google Scholar
45 ATI 718Plus Technical Data Sheet, 2008.
Google Scholar
46Wither PJ, Bhadeshia HKDH. Residual stress Part 1—measurement techniques. Mater Sci Technol. 2001; 17(4): 355-365.
10.1179/026708301101509980
Web of Science® Google Scholar
47Prevey PS. X ray diffraction residual stress techniques. ASM Handbook, vol. 10.
Google Scholar
48Ramberg W, Osgood WR. Description of stress-strain curves by three parameters. Natl. Advis. Comm. Aeronaut. 1943; Technical Note No. 902.
Google Scholar
49Coffin LF. A study of the effects of cyclic thermal stress on a ductile metal. Trans ASME. 1954; 76: 931-950.
CAS Google Scholar
50Manson SS. Behaviour of materials under conditions of thermal stress, Natl. Advis. Comm. on Aeronaut. 1954, Report 1170, Cleveland, Lewis Flight Propulsion Laboratory.
Google Scholar
51Zhigachev AO. The effect of specimen surface curvature on x-ray diffraction peak profiles. Rev Sci Instrum. 2013; 84(9):095105.
10.1063/1.4820444
PubMed Web of Science® Google Scholar
52Repplinger C, Sellen S, Kedziora S, Zürbes A, Maas S. Analysis of residual stress relaxation of aluminum alloys EN AW 6061/-82 T6 under cyclic loading. Fatigue Fract Eng Mater Struct. 2021; 44(11): 3023-3041.
10.1111/ffe.13542
Web of Science® Google Scholar
53Ellyin F, Kujawski D. Plastic strain energy in fatigue failure. J Press Vess-T ASME. 1984; 106(4): 342-347.
10.1115/1.3264362
Web of Science® Google Scholar
54Meneghetti G. Analysis of fatigue strength of a stainless steel based on the energy dissipation. Int J Fatigue. 2007; 29(1): 81-94.
10.1016/j.ijfatigue.2006.02.043
CAS Web of Science® Google Scholar

Volume46, Issue1

January 2023

Pages 310-324

An experimental study on residual stress relaxation in low-cycle fatigue of Inconel 718Plus

Abstract