1 INTRODUCTION

Whether conscious visual perception unfolds continuously or as a series of discrete updates remains a topic of much debate (Anliker, 1963; Doerig et al., 2019; Fekete et al., 2018; Harter, 1967; Herzog et al., 2016; James, 1890; Kristofferson, 1967a; VanRullen, 2016; VanRullen & Koch, 2003; Varela et al., 1981; White, 1963; White, 2018). Vision appears continuous to introspection, yet a number of perceptual phenomena are difficult to reconcile with a continuously updating perceptual process (Herzog et al., 2020; Sokoliuk & VanRullen, 2019). The flash–lag effect and the Fröhlich effect are two such examples. In the flash–lag illusion, a brief stationary stimulus (the “flash”) is misperceived as lagging behind a moving stimulus when the two stimuli are, in fact, spatially aligned (Metzger, 1932; Murakami, 2001; Nijhawan, 1994). The Fröhlich illusion refers to the observation that the onset of a moving stimulus is often mislocalized as being further along the trajectory of motion than it really is (Fröhlich, 1923; Kerzel, 2010). Many variants of discrete sampling models have been proposed (for reviews, see Herzog et al., 2020; VanRullen, 2016; White, 2018), but recently, Schneider (2018) proposed a unifying account of both the flash–lag and Fröhlich illusions based on discrete sampling.

In the model, a repeating process of sampling followed by reconstruction occurs, with the sampling process lasting for a specified duration (a “perceptual moment”). At the end of the perceptual moment, stimuli are registered in their last-known positions and this estimate forms the basis of the conscious reconstruction of events. Because moving stimuli will be in a different position at the end of the moment than a stationary stimulus, this leads to the kind of discrepancy observed between the flash and motion stimulus (flash–lag) or between the onset of the motion and the position the stimulus is in when conscious perception was updated (Fröhlich). Thus, the duration of an individual's perceptual moment is the sole parameter in the model and half of this quantity corresponds to the average flash–lag and Fröhlich magnitude. This single-parameter model (Schneider, 2018) provided good fits to a large flash–lag dataset from Murakami, 2001.

At the neural level, oscillations in brain activity have long been speculated to be involved in discrete perceptual sampling. For instance, within- and between-subject variation in alpha-band frequency (7–14 Hz) is predictive of temporal properties of visual (Baumgarten et al., 2018; Coffin & Ganz, 1977; Coffin, 1977; Gray & Emmanouil, 2020; Gulbinaite et al., 2017; Kristofferson, 1967b; Minami & Amano, 2017; Ro, 2019; Samaha & Postle, 2015; Shen et al., 2019) and cross-modal perception (Cecere et al., 2015; Cooke et al., 2019; Keil & Senkowski, 2017), with higher-frequency oscillations being associated with finer-grained temporal resolution. Moreover, the phase of ongoing alpha activity predicts perception of near-threshold visual stimuli (Alexander et al., 2020; Busch et al., 2009; Dugué et al., 2011; Mathewson et al., 2009; Samaha et al., 2015; Samaha et al., 2017; Sherman et al., 2016). Indeed, it has been shown that trial-to-trial variability in the magnitude of the flash–lag effect is predictable by the phase of ~7-Hz oscillations prior to flash onset (Chakravarthi & VanRullen, 2012), consistent with the model proposed by Schneider (2018). And a recent experiment presented a luminance-modulating annulus at 10 Hz surrounding a flash–lag display and found that the flash–lag magnitude was correlated with the phase of the luminance modulation, suggesting that entraining brain activity at an alpha frequency causes changes in flash–lag perception at that frequency (Chota & VanRullen, 2019). Thus, discrete sampling at alpha frequencies has been advanced as a possible explanation for the flash–lag effect (Chakravarthi & VanRullen, 2012; Chota & VanRullen, 2019; Sokoliuk & VanRullen, 2019) and the Fröhlich effect has been argued to follow from the same underlying mechanism as the flash–lag (Eagleman & Sejnowski, 2007).

Importantly, variations in the flash–lag and Fröhlich effects, if driven by discrete sampling at alpha frequencies, should be seen across participants given that significant differences in individual peak alpha frequencies have been reliably observed (Grandy et al., 2013; Haegens et al., 2014). Individual alpha frequency has been described as a trait variable due to evidence linking it to genetic factors (Bodenmann et al., 2009). Additionally, an average standard deviation of 1 Hz has been reported for individual alpha frequency in age-matched participants, suggesting substantive variation across individuals (Klimesch, 1997). For these reasons, we expect that individual alpha frequency will vary within a random sample, even without having recorded EEG data.

The goal of this study was to test the proposition that, if the flash–lag and Fröhlich effects are driven by discrete sampling at the alpha frequency, then the magnitude of the illusion should be correlated across individuals. That is, given the relative stability of an individual's alpha frequency (Grandy et al., 2013; Haegens et al., 2014), an individual with a large flash–lag magnitude (putatively caused by a lower alpha frequency and thus less frequent updating) should also have a large Fröhlich effect. Alternatively, no correlation between illusion strengths could indicate either that the Fröhlich and flash–lag do not reflect the same discrete sampling mechanism, or that they do reflect discrete sampling but at different frequencies that are not meaningfully related to one another across individuals. This latter notion is supported by a general lack of convergence in the literature on a single time scale of the “perceptual moment” across tasks and stimuli, and a lack of a single oscillation frequency being related to temporal perception (Herzog et al., 2020; Ronconi et al., 2017; VanRullen, 2016). Thus, a correlation between illusion magnitudes is a necessary (but not sufficient) pre-condition for the theory that alpha sampling underlies both illusions. There is also a more general question of whether the flash–lag and Fröhlich effect are based on the same mechanism (whatever that may be), which remains controversial (Kreegipuu & Allik, 2003; Krekelberg & Lappe, 2000; Whitney & Cavanagh, 2000a, 2000b) but which can be informed by an individual differences approach.

We quantified the magnitude of the flash–lag and Fröhlich illusion psychophysically by determining the spatial offset required between a motion stimulus and a stationary reference stimulus to make the two stimuli appear spatially aligned (i.e., the point of subjective equality; PSE). Robust flash–lag and Fröhlich illusions were present in our displays and despite the two displays being highly similar, we observed no correlation between individual differences in the illusion magnitudes. A Bayesian analysis provided moderate support for the null hypothesis of no correlation. We conclude that either (1) our stimulus parameters were ill-suited to detect a true relationship, (2) these two illusions are supported by different mechanisms, perhaps based on sampling rates determined by different oscillatory frequencies in the brain, or (3) distinct mechanisms not based on discrete sampling underlie each illusion.

2 METHOD

2.2 Design

The experiment took place in a dimly lit room with participants positioned in a headrest to maintain a distance of 74 cm from the computer monitor. Stimuli were generated using Psychtoolbox-3 (Kleiner et al., 2007) running in the MATLAB environment (version 9.8) under the Ubuntu (version 18.04) operating system. Stimuli were presented on a middle-gray background of 50 cd/m² luminance on a gamma-corrected VIEWPixx EEG monitor (1920 × 1200 pixels, 120-Hz refresh rate). A central fixation, consisting of a gray crosshair superimposed over a black circle 0.4° of visual angle, was present on the screen throughout each task.

2.2.1 Flash–lag illusion

A 0.3° black dot moved horizontally outwards from the center in either the left or right hemifield (randomly determined on each trial with equal probability). The dot trajectory started at 2° from central fixation and moved horizontally away from fixation for 2000 ms at a speed of 6° per second. At a randomly selected interval between 500 and 1500 ms during the dot's trajectory, a set of vertical black bars (the “flash”) flashed above and below the dot for 8 ms. The two bars were 0.13° W × 0.83° H with a distance of 0.83° between them. The flash appeared at one of 8 offsets (randomly selected with equal probability on each trial) from the set [−0.70°, −0.40°, −0.24°, −0.08°, +0.08°, +0.24°, +0.40° + 0.70°] relative to the location of the moving dot, which translates to between 4.3° to 11.7° away from central fixation. This variation in offset caused the flash to appear “ahead of” or “behind” the dot to varying extents (see Figure 1).

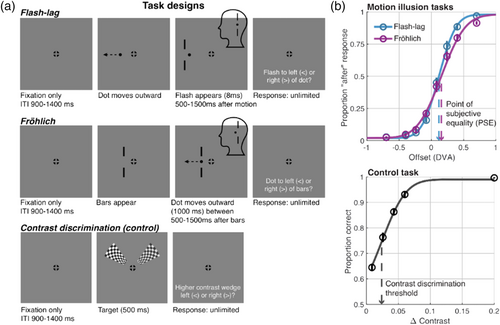
2.2.2 Fröhlich illusion

This task used the same parameters as the flash–lag for the moving dot and the set of bars except that the bars appeared first (either to the left or right if fixation, randomly determined), and remained on screen for 2000 ms. The dot then appeared midway into the 2000 ms (between 500 and 1500 ms) and immediately began moving (see Figure 1). The bars were placed using the same set of possible offsets between the onset of the dot trajectory ([−0.70°, −0.40°, −0.24°, −0.08°, +0.08°, +0.24°, +0.40° + 0.70°], randomly selected on each trial), which translates to between 5° to 11° from fixation. Similar to the flash–lag illusion, this offset caused the dot to appear “ahead of” or “behind” the set of bars to varying degrees.

2.2.3 Contrast discrimination (control) task

In addition to the two illusion tasks, we included a third control task that was intended to measure perceptual processes (here, contrast discrimination) different from those underlying the flash–lag and Fröhlich illusions. The control task was adapted using stimuli from Iemi et al. (2019) and presented two checkerboard wedges to the left and right of fixation (see Figure 1). The wedges corresponded to segments of an annular checkerboard with a spatial frequency of 5 cycles per degree. The two wedges appeared for 500 ms in either the upper or lower hemifield with the inner edge of the wedges 3° from central fixation and the outer edge 10° away. The right wedge was designated a “standard” and was held constant at 0.8 contrast (i.e., 80% Michelson contrast) and the left wedge varied randomly across the following 10 levels [0.60, 0.740, 0.757, 0.774, 0.791, 0.808, 0.825, 0.842, 0.860, 1.0]. This task was a control in the sense that the specificity of any correlation observed between the flash–lag and Fröhlich illusions could be tested by comparing this effect to the correlation obtained between the illusion PSEs and contrast discrimination thresholds (which, we hypothesized, would be uncorrelated).

3 RESULTS

We quantified the magnitude of the flash–lag and the Fröhlich illusion within the same individuals to assess their correlation. The data were well-described by a psychometric function (R² across all subjects in both tasks: mean = 0.98, range = [0.92, 0.99]; see Figures 1 and 2). As a first step, we tested whether illusory percepts consistent with the flash–lag and the Fröhlich effects were observed in our displays. Because each illusion was quantified as the PSE whereby the offset between the dot and bar stimuli would be judged as either “before” or “after” 50% of the time, a PSE of zero DVA would correspond to veridical perception, or a 0 ms difference between dot and bar stimuli. Consistent with illusory percepts, however, the mean (±SEM) PSE in the flash–lag task was 0.12 (±0.02) DVA or 20 (±3.33) ms (given a dot speed of 6 degrees per second), which was significantly different from zero, as assessed with a repeated-measures t-test (t[22] = 5.74, p < 0.0001). The mean Fröhlich PSE was 0.15 (±0.03) DVA or 25 (±5) ms, which also differed from zero (t[22] = 5.43, p < 0.0001). A positive PSE indicates, in the flash–lag case, that the bars needed to be flashed further from fixation than the moving dot by 20 ms (0.12 DVA) in order to be perceived as aligned with the dot (i.e., to offset the illusory lag of the flash). In the Fröhlich task, the bars needed to be 25 ms (0.15 DVA) further from fixation than the onset of motion in order for the motion onset to be perceived as aligned with the bars (consistent with a misperception of the motion stimulus as being advanced along the motion trajectory). Under comparable conditions to those used here, similar magnitude illusions have been reported for both the flash–lag and Fröhlich effect (Eagleman & Sejnowski, 2007). Additionally, Kanai et al. (2004) found flash–lag effects in the range of 20–60 ms, with the flash–lag magnitude increasing with increasing eccentricity of the moving stimulus, decreasing eccentricity of the flashing stimulus, and increasing distance between the stimuli, among other factors. Contrast thresholds from the control task were Δ0.024 (±0.002), indicating that observers could discriminate, on average, a contrast difference between wedges of 2.4% with 75% accuracy.

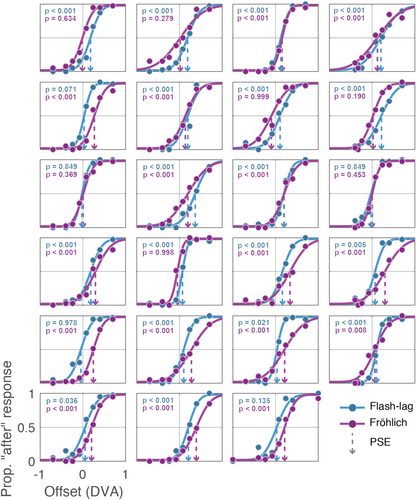
We also checked whether participants showed significant illusory percepts at the single subject level using a bootstrap method. A bootstrap analysis was performed on each participant's data where the total number of trials were randomly selected, with replacement, from each participant's trials. This means a trial could have been left out or included multiple times in any given bootstrap sample. The bootstrap sampling procedure was performed 5000 times to create a distribution of PSEs for each participant from their own data. Using these distributions, we calculated the proportion of bootstraps that had PSEs below zero, which would indicate the lack of an illusory percept. This was done to generate a p-value (one-tailed) for each participant for each illusion (Figure 2). A total of five and seven participants, for the flash–lag and Fröhlich illusions, respectively, did not have a significant illusory effect. These participants were not removed from the analysis, however, since all but two participants had a significant illusion effect in at least one of the illusions, and we are interested in the relationship (or lack thereof) between illusion PSEs in each subject.

We next directly compared the magnitudes of the two illusions as well as the split-half reliability of the PSE found for each illusion. The two illusions were of a comparable magnitude as they did not significantly differ from one another when assessed with a paired-samples t test (t[22] = 1.05, p = 0.304). To ensure reliability of our PSE measurement (an important prerequisite for detecting a correlation across subjects), we performed a split-half reliability analysis by fitting psychometric functions to all odd or even trials from each illusion and computing the Spearman–Brown split-half reliability to quantify the proportion of variance explained in PSE by random variation (Eisinga et al., 2013; Salkind, 2010). A repeated-measures t-test showed that the PSEs derived from each half of the data were not significantly different for either illusion task (flash–lag: t(22) = 1.26, p = 0.220; Fröhlich: t(22) = −1.31, p = 0.204) and a Spearman correlation showed the PSEs from each half of the data were strongly correlated for both illusions (flash–lag: r = 0.82, p < 0.001; Fröhlich: r = 0.91, p < 0.001). Finally, both tasks show high reliability according to the Spearman–Brown split-half reliability score, for which the flash–lag PSE was 0.915 and the Fröhlich PSE was 0.967. This indicates that only about 8.5% and 3.2% of the variance in our quantification of the flash–lag and Fröhlich illusion PSEs, respectively, is due to random variation.

Regarding our main hypothesis, we next asked whether the magnitude of an individual's flash–lag illusion (flash–lag PSE), was predictive of the magnitude of their Fröhlich illusion (Fröhlich PSE). A relationship between the flash–lag illusion PSEs and the Fröhlich illusion PSEs would be expected if the two illusions result from each individual's unique underlying oscillatory sampling frequency. However, the across-task correlation in PSEs was virtually zero (rho = −0.0089, p = 0.969, 95% bootstrap CI = [−0.41, 0.39]), indicating no evidence for a relationship between these illusions (Figure 3a). To appreciate the uncertainty associated with each correlation value, we conducted a bootstrap analysis that randomly sampled with replacement 23 PSEs from the pool of all participant data, meaning that the same participant may be represented multiple times in a sample. This was done 50,000 times to generate a distribution of samples. For each bootstrap sample, we correlated PSEs across tasks in order to also generate a distribution of correlations (Figure 3, right column), representing the uncertainty associated with the correlation between tasks. As evident from the bootstrap distributions presented in Figure 3a, the true correlation could plausibly span a wide range between ±0.4, though the mean of this bootstrap distribution is virtually zero (−0.006).

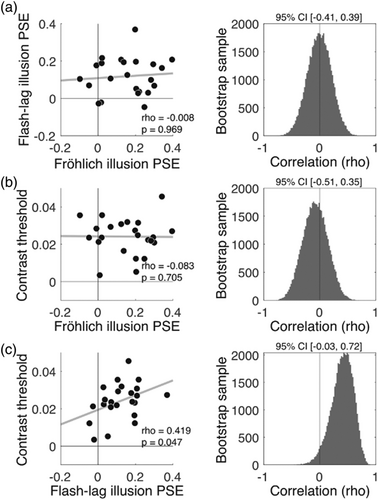
A Bayesian analysis (Dienes, 2014) that quantified the likelihood of the data belonging to the null hypothesis (H0) of no correlation versus the alternative hypothesis (H1) of a positive correlation (a weak version of the theory), indicated that the data are 5.56 times more likely to have been generated under the null (BF_{U(0, 0.9),0} = 0.179). Using a hard version of the theory to model H1, according to which the two PSEs are equal, resulted in a BF_{HN(0, 0.5),0} = 0.419, indicating that the null is 2.38 times more likely than the alternative. Thus, depending on the exact implementation of the theory, the data are approximately 2 to 5 times more likely under the null.

Next, we tested for associations between contrast discrimination thresholds and PSEs in each illusion task. As shown in Figure 3c, contrast thresholds were positively correlated with flash–lag PSEs (rho = 0.419, p = 0.0478, 95% bootstrap CI = [−0.03, 0.72]), indicating that individuals capable of discriminating smaller differences in contrast had smaller flash–lag illusions. (We speculate on the reason behind this correlation in the discussion.) No correlation was observed between contrast thresholds and the Fröhlich PSE (rho = −0.083, p = 0.706, 95% bootstrap CI = [−0.51, 0.35]). Because contrast thresholds unexpectedly explained variance in the flash–lag effect, we sought to test if an effect of Fröhlich PSE on flash–lag PSE emerged when controlling for the influence of contrast discrimination. However, a multiple regression model that predicted individual differences in the flash–lag PSE using the Fröhlich PSE and contrast thresholds (as a covariate) did not reveal an association between the two illusions (beta = 0.066, SE = 0.148, t = 0.447, p = 0.659), consistent with the results from the main correlation analysis.

For completeness, we also analyzed correlations between the slope of the psychometric functions from each task. Whereas the PSE in the illusion tasks capture the magnitude of each illusion (and is therefore the quantity of interest for the theory under consideration), the slope of the psychometric function reflects the general reliability or sensitivity of an individual's perceptual system as it captures the degree to which changes in the stimulus value translate to changes in behavior. We found a medium sized positive correlation between the flash–lag and Fröhlich slopes (rho = 0.414, p = 0.051), indicating that an individual who is more sensitive to changes in offset in the flash–lag illusion is also more sensitive to changes in offset in the Fröhlich illusion.

4 DISCUSSION

This study assessed the theory that the same mechanism of discrete perceptual sampling—oscillations at a given frequency—could explain the flash–lag and Fröhlich illusions. We induced illusory percepts in both the flash–lag and Fröhlich displays, yet the correlation between illusion sizes was virtually zero. A Bayesian analysis allowed us to determine the likelihood of our data being obtained from the hypothesized distribution according to alpha-based sampling theory. The BF indicated that responses to the flash–lag and Fröhlich illusion tasks were between 2.4–5.5 times more likely to come from the null distribution than various theory-derived alternatives. While additional research using EEG or MEG is needed to further support these conclusions, our current data suggest it is unlikely that a single oscillator, assumed to vary in frequency across subjects, is underlying individual variations in the flash–lag and Fröhlich effects, as this should drive a correlation between illusory percepts across tasks.

Although we observed moderate evidence for a null effect, there are several underlying reasons for obtaining null results. It could still be that discrete sampling theory is true and is neurally instantiated via oscillations, but that these two illusions rely on different frequencies which are themselves uncorrelated. A large body of work has linked alpha-band oscillations to temporal windows of processing (Cecere et al., 2015; Coffin & Ganz, 1977; Cooke et al., 2019; Grabot et al., 2017; Gray & Emmanouil, 2020; Kristofferson, 1967b; Minami & Amano, 2017; Samaha & Postle, 2015; Shen et al., 2019; Varela et al., 1981; Wutz et al., 2018) and even specifically to the flash–lag illusion (Chakravarthi & VanRullen, 2012; Chota & VanRullen, 2019). On the other hand, lower-frequency oscillations in the theta range are also often implicated in establishing temporal windows of perception (Nakayama et al., 2018; Wutz et al., 2016; for review see VanRullen, 2016). Indeed, even different tasks within the same subjects can reveal different frequencies related to the temporal parsing of visual stimuli (Ronconi et al., 2017), indicating that multiple and task-dependent rhythms may underlie the perceptual moment. Consistent with these variations in temporal parsing of visual stimuli is the problem of “multiple temporal resolutions”, as outlined by Herzog et al. (2020). Different perceptual phenomena attributed to discrete sampling have been explained by appealing to window sizes ranging from 3 ms up to 450 ms depending on the processing demands elicited from the particular visual features (Drissi-Daoudi et al., 2019; Holcombe, 2009). One possibility is that differential top-down attentional control is allocated during perception of the different tasks/stimuli, resulting in variations in duration of temporal integration windows. Our results are compatible with a model according to which the flash–lag and Fröhlich effect are driven by discrete sampling but at different frequencies or temporal sampling rates. However, on this theory, our finding that the two illusions were of very similar magnitude (Figure 1) may still require further explanation.

A second possible interpretation of our null effect is that these illusions do not rely on discrete sampling at all, contra Schneider (2018). Other viable accounts of the flash–lag and Fröhlich effects have been put forth and recently defended. Regarding the flash–lag, a recent review argues that motion extrapolation is currently the best account (Hogendoorn, 2020). Motion extrapolation refers to the prediction of a moving object's trajectory based on its recent past. This is distinct from discrete sampling (or the related postdiction account of the flash–lag) in that the motion percept is not reconstructed after the fact, but is instead based on a prediction about where the stimulus will be. Motion extrapolation mechanisms have been observed as early as the retina (in some species), and could therefore begin very early after motion onset to produce a percept of the motion stimulus that is advanced with respect to a stationary flash (Hogendoorn, 2020). Regarding the Fröhlich effect, it has been argued that metacontrast masking plays a crucial role (Kerzel, 2010). In metacontrast masking, the mask and target do not overlap and stimulus onset asynchronies between 40 and 100 ms between target presentation and mask presentation create strongest masking effects (Kerzel, 2010). It has been proposed that metacontrast masking suppresses the initial trajectory of the moving stimulus, thus creating the illusion that it begins farther ahead than its true starting location (Piéron, 1935). Because the moving dot is already along its trajectory when the flash appears in the flash–lag effect, this masking effect of the beginning trajectory would not affect perception in the flash–lag illusion. Thus, it remains an open possibility that these two illusions are based on different mechanisms, either one of which may not be discrete sampling.

A third possibility is that our stimulus design was suboptimal for detecting a true relationship. For instance, an unexpected correlation was found between PSEs in the flash–lag illusion and the contrast discrimination task. The control task was primarily administered to rule out the possibility that any observed correlation between the two illusion PSEs was a trivial reflection of any two tasks being correlated across individuals. Although this point is moot since no correlation was observed between the two illusion tasks, we speculate that the observed correlation between contrast thresholds and the flash–lag PSE might have occurred since the flash in our flash–lag display was very brief (8 ms) and perhaps having a lower contrast threshold could translate to more veridical flash localization and a smaller flash–lag effect. A longer flash should reduce variance in flash–lag estimates due to individual differences in contrast perception. However, a multiple regression model of our data that included contrast discrimination thresholds as a covariate still failed to find any relationship between the two illusions. Future studies should consider increasing the flash duration to facilitate perception of the flash, while also keeping in mind how the speed and proximity of the moving dot may interact with a longer flash and impact illusory effects. An additional stimulus consideration that may affect both the flash–lag and the Fröhlich effect is the interaction of each illusion with low-level motion processing. The flash–drag effect suggests that moving stimuli may distort the surrounding visual space and, thus, would affect perception of any nearby stationary stimuli (Whitney & Cavanagh, 2000b). Moving the bars farther away from the horizontal trajectory of the dot in both illusion tasks could help to mitigate any distortion caused by low-level motion processing.

Lastly, a lack of variation in individual sampling rates or illusion magnitudes could also produce no correlation between PSEs. That is, no correlation would be expected if for every subject the true magnitude of each illusion were the same and variability in PSEs were due solely to response bias or some other factor. However, this account would also violate the hypothesis that individual differences in peak alpha frequency are modulating individual differences in visual sampling rates, since the distribution of peak oscillation frequencies in a random sample of the population is known to vary (Grandy et al., 2013; Haegens et al., 2014), and the same should be expected of our sample. Additionally, the split-half reliabilities of our PSE estimates were each very large (>0.9), making it unlikely that random variation in PSE estimation was masking any true cross-task correlation.

Although it can be difficult to know the source of a null effect, even if evidence in support of the null can be shown (as with our Bayesian analysis), our data can inform future studies. The task parameters used in this study produced the expected illusory effects of the flash–lag and Fröhlich illusions on average (though not significantly for several subjects) and such parameters could be used to test other perceptual phenomena or mechanisms related to discrete sampling theory. Alternatively, adjusting these task parameters or comparing the PSE across additional tasks could provide further insight into how individuals sample visual information, or more specifically, what stimulus designs might better capture the hypothesized “perceptual moments.” Although our current data do not support the hypothesis that individual differences in perceptual moments are driving these two visual illusions, these findings are not sufficient to rule out discrete sampling theory altogether. They are also not sufficient to rule out the role of alpha oscillations or other frequencies in perceptual sampling in the two illusions in different ways, and future studies would benefit from measuring oscillatory activity during both tasks.

CONFLICT OF INTERESTS

The authors declare no conflicts of interest.