Packet randomized experiments for eliminating classes of confounders
Abstract
Background
Although randomization is considered essential for causal inference, it is often not possible to randomize in nutrition and obesity research. To address this, we develop a framework for an experimental design—packet randomized experiments (PREs), which improves causal inferences when randomization on a single treatment variable is not possible. This situation arises when subjects are randomly assigned to a condition (such as a new roommate) which varies in one characteristic of interest (such as weight), but also varies across many others. There has been no general discussion of this experimental design, including its strengths, limitations, and statistical properties. As such, researchers are left to develop and apply PREs on an ad hoc basis, limiting its potential to improve causal inferences among nutrition and obesity researchers.
Methods
We introduce PREs as an intermediary design between randomized controlled trials and observational studies. We review previous research that used the PRE design and describe its application in obesity-related research, including random roommate assignments, heterochronic parabiosis, and the quasi-random assignment of subjects to geographic areas. We then provide a statistical framework to control for potential packet-level confounders not accounted for by randomization.
Results
Packet randomized experiments have successfully been used to improve causal estimates of the effect of roommates, altitude, and breastfeeding on weight outcomes. When certain assumptions are met, PREs can asymptotically control for packet-level characteristics. This has the potential to statistically estimate the effect of a single treatment even when randomization to a single treatment did not occur.
Conclusions
Applying PREs to obesity-related research will improve decisions about clinical, public health, and policy actions insofar as it offers researchers new insight into cause and effect relationships among variables.
Glossary
-
- Experiment
-
- The systematic empirical observation of phenomena following the manipulation of some variable(s). True experiments must involve randomization to levels of the independent variable.
-
- Quasi-experiment
-
- A method in which the response of experimental subjects is compared to a control group; however, assignment to group is not presumed to be random or as if random 1.
-
- Natural Experiment
-
- A method in which the response of experimental subjects receiving a treatment is compared to a control group and assignment to group is random or as if random; however, the manipulation of the treatment is not under the control of the researcher 1.
-
- Randomized Controlled Trial
-
- An experimental design that involves at least one test treatment and one control treatment and in which treatments are randomly assigned by the experimenter 2.
-
- Confounder
-
- Any variable related to two factors of interest that falsely obscures or accentuates the relationship between the factors 2.
-
- Subject
-
- The unit of observation with the set of characteristics (W1…Wc) and randomized to a packet. Subjects could be humans, court cases, mice, etc.
-
- Packet
-
- The unit of analysis with the set of characteristics (X1…Xk), at least one of which is believed to exert a causal effect on the outcome of interest at the level of the subject.
-
- Dependent Variable
-
- A variable (Y) in which the expected value is presumed to be dependent on one or more other variables (independent variables) (X1, X2…) 3
Introduction
Two major methods for studying causality are ordinary association studies and randomized controlled experiments or trials (RCTs). Each has their advantages and disadvantages. The greatest disadvantage of association studies is that ‘association does not necessarily imply causation’ (to which we might add the less often acknowledged corollary that ‘a lack of association does not necessarily imply a lack of causation’). The reasons for this indeterminacy are also well known: the possible presence of confounding variables and the possibility that the cause–effect relationship could be reversed (i.e. that instead of X causing Y, Y causes X). RCTs overcome the problems of endogeneity and confounding by randomly assigning subjects to levels of the independent variable (e.g. X1), thereby assuring that the population distribution of X1 is independent of all known and unknown (measured and unmeasured) prerandomization variables that might otherwise be confounders 4. The greatest limitations of RCTs are that they are often impractical, prohibitively expensive, unethical or simply impossible because subjects cannot be randomly assigned to levels of X1.
Majumdar and Soumerai 5 have argued that a false dichotomy exists in which RCTs and association studies are often treated as the only alternatives; consequently, researchers do not consider other study designs that occupy an intermediary inferential position between the pure RCT and the ordinary observational association study. The result is that decisions about clinical, public health and policy actions are founded on a less-than-optimal understanding of the relationship between causes and effects, interventions and outcomes.
Herein, we introduce general principles of an intermediary experimental design that is inferentially stronger than an ordinary association because it can rule out entire classes of both measured and unmeasured potential confounders, but is not as inferentially strong as a pure RCT, which can rule out all potential confounders. Although specific cases of this design have been used in the past, including by us 6, a systematic explication of its general form and inferential properties has, to our knowledge, never been published.
As such, we: (a) introduce the idea of packet randomized experiments (PREs) and their inferential properties; (b) give examples of the use of PREs from both published and planned studies (Table 1); (c) discuss genetic linkage analysis as a special case of a PRE; (d) explain how, in some PREs, conditioning on particular covariates can indirectly and asymptotically control for some of the confounders left uncontrolled by the design; and (e) end with a general discussion.
| Design | Reference | Packet | Subject | Key independent variable | Results and comments |
|---|---|---|---|---|---|
| Randomized flatmate assignment | Yakusheva et al. 17 | Flatmate and dormitory | Student | Flatmate's weight | Subject's weight gain during freshman year of college is inversely related to flatmate's weight |
| Heterochronic parabiosis | Conboy et al. 25 | Young mouse | Old mouse | Circulatory factors in the blood | The muscle tissues of old mice paired with young mice recovered more quickly from injury |
| Randomized assignment of cases to judges | Anderson et al. 12 | Judge | Court case | Federal sentencing guidelines | Average sentencing differences between judges declined from 4·9 months to 3·9 months after implementation of federal sentencing guidelines |
| Holt adoptee analysis | Fontaine, et al. 6 | Adopters | Adoptee | Socioeconomic status | Biological and rearing environment contribute roughly equally to offspring obesity |
Introduction to PREs and their inferential properties
Let Si (for i = 1 to N) denote the subjects (units of observation) in a study, with N being the number of subjects. In biomedical and behavioural research, subjects most often will be individual humans or individual model organisms (e.g. mice) but in principle could be clusters of individuals (e.g. classrooms, cities, mouse litters and ant colonies) or inanimate objects (e.g. buildings, airplanes, etc.). Let Y be some outcome variable of interest measured on S1 to SN. Y could be continuous (e.g. height, BMI and IQ), dichotomous (e.g. dead or not dead), ordinal (e.g. number of sales made) or time to event (e.g. survival time). Let X1 denote some independent variable of interest – some variable hypothesized to have a causal effect on Y. X1 could be a characteristic of a blood sample with which a subject is transfused, a subject's college flatmate, a characteristic of a book one is assigned to read, a characteristic of a car one has rented, a dietary constituent of a fruit one is assigned to eat, and so on. Suppose that, for some reason, we are not willing or able to randomly assign S's to levels of X1 and only X1. However, we can randomly assign S's to objects or situations that differ in their values of X1, as well as in their values of other variables, X2 to XK, with the identities of X2 to XK not necessarily being known and, indeed, the value of K being unknown in most cases. We will refer to the objects or situations to which the S's can be assigned as ‘packets’ (P), because they are packets of the variables X1 to XK. For example, the random assignment of a subject to a flatmate constitutes a treatment that includes the myriad of characteristics of the assigned flatmate. Although our independent variable of interest may be the academic performance of the flatmate, we must also contend with the cleanliness, social habits or any other characteristic of the flatmate that may impact the outcome of interest.
One can easily imagine experiments in which each S was assigned to more than one P or more than one S was assigned to each P (see our example on altitude in section 4), but, for simplicity, for the remainder of this section, we will assume that each S is assigned to one and only one P. Hence, let Pi (for i = 1 to N) denote the packets in the experiment. Following our examples of potential variables for X1 above, packets could be blood samples with which subjects are transfused, subjects’ college flatmates, books subjects are assigned to read, cars subjects are assigned to rent, fruits subjects are assigned to eat, and so on. Let W1 to Wc denote characteristics of S that, by definition, are not within the set of X2 to Xk. Examples of W's could include intrinsic subject characteristics (e.g. genotypes, parental occupation, personality traits, wealth, tastes, preferences and behaviours) and contextual factors. When randomization of S's to X's is not used, the subject characteristics W1…C may be correlated with the levels of X1 to which S's were exposed (e.g. a correlation between academic achievement of the flatmate (X1) and prior valuation of academic achievement by the subject (W). If W1…c are observed and measured, they can be statistically controlled. If they are unobserved, as they often are, they may confound the relationship between X1 and the outcome of interest. In contrast, when S's are randomized to X's, the random assignment helps eliminates the possibility of confounding due to observed and unobserved W1…C variables. This is the key strength of PREs and distinguishes a PRE from an observational study. It does not, however, eliminate potential correlations between the treatment of interest X1 and other packet characteristics X2…k. This is the key limitation of PREs and distinguishes a PRE from a standard randomized controlled trial.
Suppose we were to study S-P pairings created by means other than random assignment (e.g. by allowing S's to choose packets with which to be paired) and fit a model of the form f(Yi) = g(X1,j) + ei where f(Y) denotes some link function of Y, g(X1) denotes some function of X1, and ei denotes an error term 7. Could we then assume that the fitted model represents a model of causation? No. This is because the true model might be f(yi) = g(X1,i) + h(X2,…XK) + m(W1,…Wc) +ei, where h and m are unspecified functions of packet and subject characteristics, respectively. Under such a model, if X2 to XK and W1 to WC are not independent of X1, then the observed relation between X1 and Y will be confounded and may not represent a causal effect. However, if we randomly assign S's to P's, then X1 must be independent of W1 to WC, and therefore, W1 to WC cannot be confounders of any relation between X1 and Y. This follows from the same logic of randomization that underlies the use of standard randomized controlled trials (RCTs) to eliminate confounders. PREs and standard RCTs do not differ in their use of randomization to eliminate the possibility of confounding due to subject variables; rather, they differ only in whether subjects are assigned to a single treatment or to a ‘packet’ of treatments. The degree to which PREs improve causal inferences via randomization is directly related to the proportion of any confounding that occurs which is due to W1…C. As the proportion of confounding due to W1…C approaches 1, so too do PREs approach the inferential strength (ability to rule out causation) possessed by standard RCTs. Unfortunately, the proportion of confounding due to W1…C vs. X1…k will usually be unknowable, thus one of the key limitations of PREs is that the exact degree of improvement in causal inferences will usually be unknown and variable among studies. Nonetheless, because PREs eliminate potential confounders (W1 to WC), they strengthen causal inferences relative to standard observational studies of associations between X1 and Y. An additional limitation of PREs is that they cannot rule out potential confounding from X2 to XK. As will be discussed later, sometimes such potential confounding can be mitigated using the more familiar methods of statistical adjustment in association studies, and in some situations, this potential confounding actually has utility. PREs have been used to improve causal inferences in a variety of disciplines, as discussed in the following section.
Examples of PREs
Holt adoptee analysis
For over 50 years, an inverse association between socioeconomic status (SES) and obesity has been observed. Multiple potential causal relations might underlie this association (e.g. lower SES causes obesity, obesity causes a decline in SES through factors related to the rearing environment), but randomly assigning children to families to articulate these potential causal relations is unethical. However, voluntary adoptions, in which young children are randomly assigned to rearing environments differing in SES, are essentially a natural experiment that can be used to estimate the possible causal effects of rearing environment SES on the development of obesity. In these studies, young children are subjects with a set of observed and unobserved characteristics (W1…Wc), randomly assigned to rearing environments that vary in level of SES (X1) as well as a range of observed and unobserved characteristics (X2…Xk). Association studies estimating the causal effect of SES on weight are limited by an inability to control for unobserved subject characteristics that plausibly affect weight, including genetic factors, sense of control, or ability to delay gratification, etc. PREs address this limitation by eliminating all possible subject confounders that could influence weight via randomization. Our group 6 used data from The Survey of Holt Adoptees and Their Families (HOLT) to investigate whether there might be a causal relationship between the SES of the rearing environment and obesity in the offspring. The HOLT data were derived from families who adopted a Korean–American child through Holt International Children's Services from 1970 to 1980.
Insofar as assignment of the adoptee to a family was independent of the adoptee's weight and all other variables, we can treat the family rearing environment as a ‘packet’ to which a subject has been randomly assigned. The association between the rearing family's SES and the weight of their children was then measured for both the biological and adopted children. While this association is usually confounded with the shared genetic background of the parent's and their offspring, in the case of the adopted children, neither shared genetic background nor any subject-level characteristic can confound the relationship. Thus, by comparing the magnitude of the association between the rearing family's SES on their biological and adopted children, we can get an estimate of the contribution of family environment's effect on weight. After controlling for relevant covariates (e.g. adoptee sex), the association between rearing family's SES and BMI of the adoptee was approximately half that of the association between family SES and BMI of the biological child. As such, biological factors and the rearing environment appear to contribute roughly equally to offspring obesity, a conclusion strengthened by the PRE design of the data.
Judges
PRE designs have been used in the analysis of judge- or court-level factors that influence case outcomes. In these designs, the judge or court is the packet of interest with a set of packet-specific characteristics (X1…Xk) such as average sentencing length handed down by the judge. In determining the causal effects of factors at the judge or court level, a key issue is comparability between cases – the subjects of this particular PRE design. Because each case will necessarily differ along innumerable factors, it is difficult to determine whether any observed effect of a judge is due to factors at the level of the judge or the level of the case. The random assignment of criminal cases to judges helps ensure that any differences in cases heard by judges are due to chance, strengthening causal inferences about the overall effect of court-level factors 8. Federal judges in the same location are randomly assigned cases to ensure fair procedures and to limit the ability to select judges with a reputation for leniency or strictness 9. Random assignment helps ensure that observed differences in sentence length, plaintiff win rate or recidivism are related to differences at the level of the court, not individual differences at the level of the case. Over time, the random assignment of cases to judges creates similar caseloads among judges, making it possible to compare averages of judge-level factors 10. Outcomes of interest have included plaintiff win rate 8 and sentencing disparities 11. In particular, researchers and policymakers have used PREs to determine whether federal sentencing guidelines have reduced sentencing differences among judges.
Nonetheless, the use of PREs in the criminological literature is limited by one factor that cannot be randomized – the distribution of offence types across time periods. Anderson, et al. 12 find that the share of drug offences increased over time with a concomitant decrease in other offences. If sentencing disparities in drug offences are lower relative to other offences, the observed effect of federal sentencing guidelines is confounded with the increasing share of drug offences. Packet randomization studies that depend on comparisons at two different time points must thus consider supra-packet effects, such as time, and whether they plausibly confound the independent variable of interest. Supra-packet effects are any effects independent from packet characteristics and are not controlled for via the randomization of subjects to a packet. When analysing the effect of federal sentencing guidelines on sentencing disparities, time is a supra-packet effect because it may confound the relationship between sentencing guidelines and sentencing disparities, is not accounted for via randomization, and is not a characteristic of the packet.
Human milk to mice
Significant ethical considerations in designing breastfeeding RCTs make it difficult to study the purported benefits of breastfeeding exposure while disentangling both genetic and environmental factors that influence (both directly and indirectly vis-à-vis maternal contact) breastfeeding behaviour and breast milk composition. Wide-ranging benefits of breastfeeding, including a protective effect against obesity, have been touted by public health and professional organizations throughout the world based primarily on observational evidence. The observed benefits, however, are diminished when known modulators are controlled (i.e. infant exposure to smoking, socioeconomic status, etc.) 13-15. Our conceptualized PRE specifically related to breast feeding studies offers a method to control for a significant number of modulators that breastfeeding studies to date have not, and ethically cannot, control for, namely eh (uncontrolled human external confounders with direct effects on the infant), τh (baby phenotype attributed to maternal factors), αh human maternal factors directly impacting the composition of breast milk); thus, the criteria to make causal claims about the effect of breast milk on obesity is not met (Fig. 1).
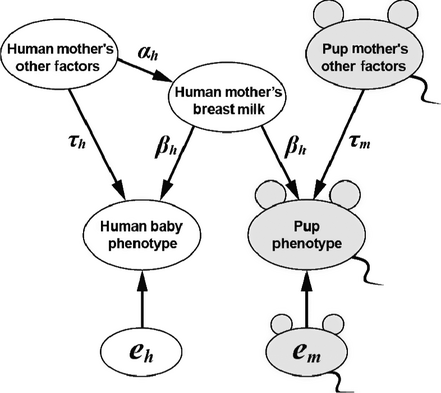
Our group (Fields and Allison) is proposing a breastfeeding PRE that eliminates ethical constraints while improving statistical inference that most studies cannot achieve by introducing a study design (Fig. 1) where mice will be randomized to human breast milk obtained from breastfeeding mothers who vary greatly in a diverse range of physiological (fatness), sociological (socioeconomic status, education, urban vs. rural) and genetic confounders that human correlational studies could not remove. By randomizing mice (subjects) to differing sets of human breast milk (packets), the PRE design eliminates τm (mouse phenotype attributable to mouse maternal factors given all mice have the same mother), αh (impact of human maternal factors on the composition of breast milk), and em (external confounders directly affecting the mouse phenotype, given all mice are housed and raised in the same tightly regulated/controlled environment). All three sources (τm, αh and em) of confounding cannot be eliminated in human studies; however, the proposed PRE allows for greater inferential power than associational inferences currently being conducting in human studies by eliminating all classes of confounders while retaining physiological relevance in the proposed animal study.
Flatmate randomization
Randomized flatmate assignments are natural experiments that have been used to examine peer influence on a range of student health and behavioural outcomes. In these studies, the flatmate is the packet of interest with a set of packet-specific characteristics such as flatmate weight or study habits. This type of study design addresses a key difficulty in making causal inferences about peer influence – selection. Random assignment to treatment groups helps ensure that the observed effect of a flatmate or peer is due to the treatment and not a consequence of selection. For example, a student who values academic performance may select peers who likewise value academic performance, confounding the effect of peer valuation of academics with that student's peer preferences. More generally, the nonrandomness of peer associations makes it possible (and likely) that unobserved factors that affect an individual outcome of interest (e.g. weight) also may be systematically related to the characteristics of one's chosen peers 16. This poses a serious challenge to research on peer influence; however, several studies have used PREs to eliminate potential subject-level confounders by utilizing the random assignment of flatmates.
Randomly assigning individuals to flatmates or dormitories helps ensure that unobserved subject characteristics (W1…Wc) are not confounded with the overall observed effect of a particular flatmate with the set of characteristics (X1…Xk). Taking advantage of flatmate randomization, Yakusheva et al. 17 found that the amount of weight gained by a subject during freshman year was inversely related to their flatmate's weight. Although randomization of subjects to flatmates helps to account for all observed and unobserved subject factors, it cannot control for unobserved factors at the level of the ‘packet’ – not all conceivable flatmate characteristics that might exert an influence on a subject's weight could be measured and included in the model. Thus, the observed effect of a flatmate's weight on a subject's weight is potentially confounded with flatmate characteristics not included in the model and associated with both the flatmate and the subject's weight.
Military relocation and altitude
Looking beyond a flatmate's influence, residential exposures that vary on a macrogeographic (regional, national or global) scale also may influence a range of outcomes. Previously, an inverse relationship between altitude of residence and obesity prevalence was found in the United States 18, but as in the case of peer influence, disentangling the causal order of residential exposure and health outcome is difficult. The semi-random assignment of US military service members to geographic locations is an opportunity to overcome many of these limitations. The US military assigns service members to geographic locations using a semi-random process similar to dorm room assignment, but on a much larger spatial scale. Although the assignment of service members to geographic locations does not follow a pure randomization process, it can be treated ‘as if’ random for the purposes of some analyses 1.
In the language of PRE, the packet of interest is the combination of observed and unobserved characteristics (X1…Xk) found at the service member's new residential location. The unit of (semi) randomization is the individual member assigned to a new duty station with the set of observed and unobserved characteristics (W1…Wc). To investigate the relationship between residential altitude and obesity, overweight service members at risk of transitioning to obesity could be followed as they are assigned from one duty location to the next 19. As obesity incidence shows spatial variation by altitude, causal inferences about the packet of exposures at each location are stronger than purely observational data. Semi-randomization of service members helps ensure that subject characteristics (W1…Wc) are not associated with packet characteristics (X1…Xk), eliminating the risk of confounding at the subject level. Although such an investigation would not isolate a specific exposure (e.g. high altitude), it virtually eliminates reverse causation as an explanation for the geographic variation in obesity incidence.
Old-young mouse parabiosis
Packet exposures need not exist solely outside the subject's physical body. Packet exposures also may include exposure to a set of factors within the body, such as the circulatory system. Parabiosis surgically pairs two subjects such that they develop a single circulatory system 20. In the language of packet randomization, each subject also contains a packet of interest (the circulatory system) with a set of packet-specific characteristics. Just as human subjects can be randomly paired with flatmates to share the same dormitory environment, animal subjects have been paired with other animals to share a circulatory system. Parabiosis has been used to study a range of health outcomes, including tumour growth 21, cholesterol 22 and diabetes 23. Parabiosis experiments helped lay the foundation for the discovery of leptin after work by Coleman 24 suggested that a satiety factor found in db/db mice but not ob/ob mice could regulate appetite.
More recently, researchers have used heterochronic parabiosis, pairing an old mouse with a young mouse, to study ageing. Conboy, et al. 25 hypothesized that factors in the circulatory system of a young mouse help regulate tissue regeneration, and that, by pairing an old mouse with a young mouse, the molecular pathways of the older mouse could be ‘rejuvenated’. The randomization of old mice to young mice controls for all subject-level characteristics (W1…Wc), ruling out the possibility that variation in the old mice, such as size or diet, accounts for the observed differences in tissue rejuvenation. Conboy, et al. 25 acknowledge that further experimental research is necessary to identify individual circulatory factors that regulate age-related processes. Such research is necessary because packet randomization does not control for packet-level characteristics that are correlated with the packet characteristic of interest (X1).
Genetic linkage and family-based association studies as special cases of PREs
In genetic studies, the potential sources of confounding are numerous, encompassing the entire genome. Within any genetic population – that is, a group of individuals who could theoretically mate randomly – actual matings are natural experiments that can be taken advantage of analytically. Two types of analysis do this, linkage analysis and family-based association testing. In both cases, the genomes of the two parents are the source of all possible genomes of any offspring. From a theoretical standpoint, we can consider the nuclear family to have been ‘randomized’ to the set of genomes determined by the parental genomes. These analyses are thus special cases of packet randomization in which the packet is identified with the nuclear family.
The practical difference between these types of studies and previously given examples of packet randomization is a matter of perspective. Previous examples considered the definition of a packet to be the primary variable of interest. In the cases of these types of genetic analysis, the primary variable of interest can vary over the genome. Linkage analysis seeks evidence that the inheritance of a particular chromosomal segment from a parent will be associated with some observable trait. Family-based association analysis seeks evidence that the inheritance of a specific allele at a specific locus from a parent will be associated with some observable trait. Central to both analyses is the packet: because all genomes in all children have to be derived from just the two genomes of the parents, there is always a probability of ½ that a particular allele or chromosomal segment came from the same parental source in two siblings. The analysis is thus performed on the background of this average sharing, giving us a powerful way of controlling for confounding on an immense scale.
Linkage analysis attempts to determine whether the degree of local genetic sharing at a specific position on a chromosome is correlated with the observed concordance of the trait of interest. We can consider this to be a question of the form, ‘All other (genetic) factors being (roughly) equal, does concordance of inheritance at one position correlate with concordance of some observed trait’? The degree of correlation of the trait is decomposed into a portion that is proportional to the overall sharing of the entire genome and a portion that is proportional to the degree of genetic sharing at a specific position in the genome. Thus, unlike previously discussed examples of packet randomization, the primary variable of interest in linkage analysis (the inherited chromosomal segment, which can include multiple variants that all influence the trait) believed to be associated with a particular phenotype is itself unobserved and must be inferred through statistical analysis.
Conditioning on particular covariates to control for packet confounders
The major limitation of PREs is the inability to eliminate confounders at the level of the packet. PREs are not alone in having this limitation – any nonrandomized analysis in which dependent variables are a function of independent variables is at risk of confounding due to unobserved independent variables not included in the model. In this section, we propose a method in which controlling for certain packet-level covariates can reduce the risk of confounding due to omitted variables.
Section 5 described a PRE in which service members were quasi-randomly assigned to a city, and change in weight was observed. The benefit of this research design is the elimination of endogeneity and subject factors as threats to the observed changes in weight. However, causal inferences about the effect of the new city's characteristics on weight can be made only for the city as whole, not for a specific characteristic of the city. Suppose that the effect of altitude (A) on weight change (Y) among subjects is of interest. Standard PREs are unable to distinguish between the effect of altitude and the myriad other city level characteristics that may affect weight. Temperature, sunlight exposure and cultural norms all vary across cities and plausibly confound the relationship between altitude and weight change. Even if we were to include all known or measured characteristics of a city, it is unlikely that we have accounted for all variables that vary across cities, are associated with altitude, and have an effect on weight.
Nonetheless, it may be possible to identify a variable that plausibly serves as a vector of all unobserved city level characteristics and can asymptotically control for all packet-level characteristics left uncontrolled by the design. In the case of investigating the effects of city characteristics on weight, we propose that mean weight of a city (Z) is such a variable (See Fig. 2). Mean weight of a city necessarily represents the average effect of all city characteristics on the weight of all individuals living within that city. This is true regardless of whether some city characteristics have an effect on the weight of only select individuals, or whether some residents have lived in the city longer than others. For example, some individuals may live in an area of a city more conducive to physical activity than others. Although these subjects are exposed to an array of city characteristics that other subjects living in the same city are not, the uneven distribution of city characteristics and their effects on weight will be reflected in average city weight. The same is true for length of residence – although some city residents will have been exposed to that city's environment for only a few weeks or perhaps even a few days, other city residents will have lived in the city their whole lives and therefore have been exposed to whatever aspects of the city influence weight. The uneven exposure to city characteristics due to varying lengths of residence will be reflected in the average city weight. The average city effect on weight also includes all individual-level effects on weight in that city, including average city socioeconomic status, demographics or any other aggregate of individual-level characteristics. One important aspect of using average city weight is that it is the average of the outcome variable and, as such, it equals the city level effect plus the average of the city level random variation, plus the average of independent level effects. Thus, it is the city level effect plus a term that is O(1/N), where N is the number of observed individuals. Finally, although distinctions between individual and neighbourhood-level characteristics are essential in associational studies of neighbourhood characteristics, such a distinction is less important in PREs. From the perspective of the randomized subjects, aggregate individual effects are simply another type of city characteristic, while the random assignment of subjects to cities assures that between-subject variation in weight is not due to omitted subject-level variables.
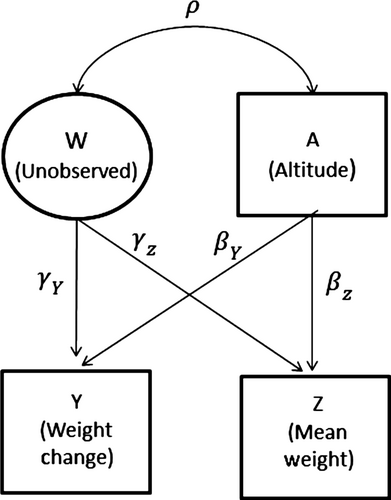
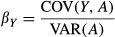
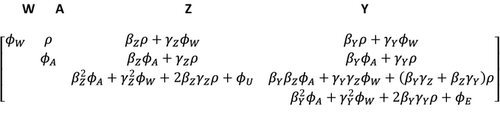
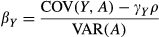
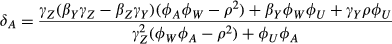
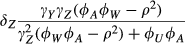
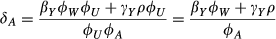

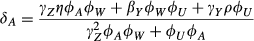
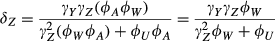
Conditioning on a particular covariate may thus help to adjust for packet-level factors not accounted for via randomization. Specifically, it may be possible to condition on a variable that represents the average of the outcome of interest over individuals who are within the packet but who are not themselves included in the experiment 27.
Discussion
This article had three goals. First, we sought to provide a general introduction to packet randomization, an experimental design, as an intermediary between observational studies and true randomized trials. The false dichotomy between association studies and the pure RCT obscures the potential of natural experiments to improve causal claims 5. Failure to consider intermediate designs between observational studies and true randomized trials limits the quality of evidence available to policymakers. Although the internal validity of packet randomized experiments cannot match that of randomized trials, it is a step above typical observational studies. Most notably, PREs greatly improve upon the strength of causal inferences by eliminating subject-level characteristics as potential confounders. In doing so, they compare favourably with other methods to control for confounding in nonexperimental research, including instrumental variable methods and propensity score matching.
Instrumental variable methods attempt to control for confounding via the identification of a variable (Z) whose effect on the outcome variable (Y) operates only through the independent variable of interest (X). Instrumental variable methods are an attempt to isolate and use the variation in X not correlated with the errors (U) 28. If the instrument is truly an exogenous predictor (uncorrelated with the error terms, U) of X, estimates of its effects on Y will be consistent (bias will reduce to zero as sample size increases 29). A limitation of instrumental variable methods is that it is not possible to empirically determine whether Z is exogenous to U; rather, this must be determined through judgment 30. In PREs, randomization rather than judgment is used to assure the treatment X is exogenous to U for the portion of covariance between X and Y due to subject factors W1…Wc. PREs cannot, however, assure that X is exogenous to U for the portion of covariance between X and Y due to unmeasured packet characteristics X2…Xk. Additional methods, including instrumental variable approaches, may be considered to potentially reduce confounding from packet characteristics.
Another method frequently used to improve causal inferences in observational studies is propensity score analysis. Propensity scores indicate the estimated probability that an individual has a particular level of the independent variable of interest conditional on other characteristics of that individual 30. Propensity scores can then be used reduce bias in the estimated independent variable effect by conditioning on differences among S's in propensity. This method is, in effect, an attempt to use a single scalar variable (the propensity score) to match participants as closely as possible on all covariates and who differ only on whether they received the treatment. The model used to match participants and estimate a propensity score can include a large number of covariates and interactions; allowing the analyst to estimate a simpler final model 31. Propensity score methods and more standard multiple regression methods will produce the same estimates of a treatment effect so long as the model used to estimate the propensity score is used in the multiple regression analysis 31. Despite the advantages of reducing bias in the estimated treatment effect using a single scalar variable, propensity score matching still depends on the inclusion of all relevant variables, measuring them without error, and modelling their functional form correctly to provide unbiased effect estimates. If relevant variables are unmeasured (or poorly measured) or unknown, confounding can remain despite use of propensity scores. In contrast, PREs use randomization to ensure that S's characteristics do not systematically differ in association with levels of the independent variable.
The second goal of this work was to describe the application of PREs across a range of disciplines and to demonstrate their potential to investigate any outcome within almost any discipline. PREs have been applied in animal, genetic and social scientific research. The lack of a general introduction to PREs makes it more likely that researchers within specific disciplines must spend unnecessary time reinventing for themselves a method that already has been employed and developed by researchers in multiple disciplines. With this comes the risk that insights of past researchers will be overlooked, or that old mistakes will be repeated. Relatedly, we hope that greater awareness of the PREs among researchers across all disciplines, especially those in human behavioural disciplines, will encourage the search for opportunities whereby PREs can be used to improve causal claims previously made using only observational data.
Third, this work sought to describe a situation in which conditioning on a covariate can plausibly control for packet-level confounders. Although such an approach cannot address packet-level confounding variables as convincingly as randomization of subjects to packets, it enables researchers to better isolate the effect of a single packet characteristic from the overall effect of the set of packet characteristics. The inability to isolate a single causal factor within a complex system is typically viewed as a limitation; however, we believe that, in some situations, it may be a strength. The interactions of variables within highly complex systems such as a brain or a city initially may require consideration of their effects as a whole rather than understanding the effect of any particular factor in isolation. Multifactorial outcomes such as obesity provide an excellent example of the utility in assessing a packet of exposures simultaneously. If the entire packet of exposures is beneficial, from a public health perspective, it may not be immediately necessary to isolate the specific exposure within the packet that is most helpful. Rather, the entire packet might be applied.
Although PREs combine many of the strengths of associational and true RCT studies, they are not a panacea. Researchers must continue to pay attention to the assumption of randomization, generalize causal claims only to the population of subjects for whom randomization actually occurred and consider the possibility of ‘supra-packet’ factors such as time – any factors not accounted for by randomization. The assumption of randomization is most important, and those who wish to use PREs in their own analyses may wish to follow the example of Anderson et al. 8, who provided both deductive and empirical evidence to support their assumption that randomization of cases to judges occurred. If evidence for randomization cannot be provided, PREs cannot be claimed to generate causal inferences superior to that of observational studies. Researchers must also be careful about generalizing claims (about either causation or association) beyond the population of subjects studied with a PRE, lest they introduce another confound into their analysis – whether or not subjects were randomized. Students who opt not to participate in the random assignment of flatmates, districts in which case randomization was more plausible than others, and service members randomized to a city to live, may, likely do, systematically vary from the students, districts and nonservice members where randomization did not occur. The usefulness of PREs, as with standard RCTS, thus depends on whether the assumption of randomization is correct for the population of interest, or whether those randomized resemble the population of interest. If randomization is plausible for the population of interest, and supra-packet factors such as time are accounted for, well-designed PRE's can offer inferentially superior and more useful results than association studies.
Acknowledgements
The views expressed in this article are those of the authors and do not necessarily reflect the official policy or position of the US Air Force, the Department of Defense or the US government.
We would like to thank Dr. Mikako Kawaii, at the University of Alabama at Birmingham, for making Fig. 1.
Disclosures
None.
Grant support
Research reported in this publication was supported by the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health under Award Numbers T32DK062710, P30DK056336 and R25DK099080. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Diabetes and Digestive and Kidney Diseases or the National Institutes of Health.
Address
Office of Energetics, Nutrition Obesity Research Center, University of Alabama at Birmingham, LHL 407, 1700 University Boulevard, Birmingham, AL 35294, USA (G. Pavela); Department of Epidemiology, University of Alabama at Birmingham, Ryals Building, Room 217D, 1665 University Boulevard, Birmingham, AL 35294, USA (H. Wiener); Department of Health Behavior, University of Alabama at Birmingham, Ryals Building, Room 241C, 1665 University Boulevard, Birmingham, AL 35294, USA (K. R. Fontaine); Department of Pediatrics, University of Oklahoma Health Sciences, 1200 Children's Avenue Suite 4500, Oklahoma City, OK 73104, USA (D. A. Fields); Epidemiology Consult Division, U.S. Air Force School of Aerospace Medicine, 2510 5th Street, Bldg 840, Wright Patterson Air Force Base, OH 45433, USA (J. D. Voss); Office of Energetics, Nutrition Obesity Research Center, University of Alabama at Birmingham, Ryals Building, Room 140J, 1665 University Boulevard, Birmingham, AL 35294, USA (D. B. Allison).




