Vessel Maps: A Survey of Map-Like Visualizations of the Cardiovascular System
Abstract
Map-like visualizations of patient-specific cardiovascular structures have been applied in numerous medical application contexts. The term map-like alludes to the characteristics these depictions share with cartographic maps: they show the spatial relations of data attributes from a single perspective, they abstract the underlying data to inCrease legibility, and they facilitate tasks centered around overview, navigation, and comparison. A vast landscape of techniques exists to derive such maps from heterogeneous data spaces. Yet, they all target similar purposes within disease diagnostics, treatment, or research and they face coinciding challenges in mapping the spatial component of a treelike structure to a legible layout. In this report, we present a framing to unify these approaches. On the one hand, we provide a classification of the existing literature according to the data spaces such maps can be derived from. On the other hand, we view the approaches in light of the manifold requirements medical practitioners and researchers have in their efforts to combat the ever-growing burden of cardiovascular disease. Based on these two perspectives, we offer recommendations for the design of map-like visualizations of the cardiovascular system.
1. Introduction
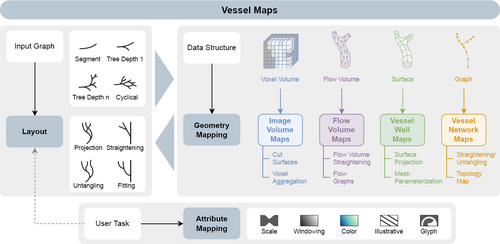
We describe the Creation of a vessel map as a three-step process: the layout of the map must be derived, the geometry or spatiality of the data must be mapped, and the data attributes must be mapped. We differentiate between image volume maps, flow volume maps, vessel wall maps, and vessel network maps depending on the primary data structure the map-like visualization is based on.
Maps of the cardiovascular system have existed for a long time for education and reference purposes. Their function is to simplify complex 3D vascular structures in 2D abstractions to allow efficient identification of principal vessels and branching points and ultimately foster an understanding of blood flow supply areas. The advance of imaging techniques that can non-invasively capture patient-specific vasculature has spawned the Creation of numerous techniques for map-like visualization of cardiovascular structures. The objectives of these vessel maps follow a similar principle: they provide a single uncluttered overview of anatomical features that can be interpreted at a glance. These views can be used to detect and evaluate features by abstracting information and presenting it in a comprehensible layout. Occlusion-free maps of vascular structures can guide medical practitioners to efficiently understand a patient's state, assess possible vessel pathologies, and navigate complex vessel trees. As opposed to other rendering techniques, such as direct volume rendering, map-like depictions generally require more preprocessing of the underlying data but yield representations that drastically reduce the required user interactions and already filter key features. If the map Creation is standardized, it can further enable comparisons in cohort studies and help quantify the effects of treatments, ultimately leading to better and inCreasingly individualized treatments. Due to the prevalence of cardiovascular disease as the number one cause of death worldwide [GBD16], techniques that capture clinically relevant features from angiographic imaging in clear and expressive map-like depictions are of fundamental importance. Creating a vessel map, however, is a twofold challenge. First, in the medical application domain, a broad spectrum of requirements exists that depend on the specific tasks in diagnosis, treatment planning, or research. There is no single depiction of a patient's cardiovascular system that can cover all possible applications. Second, numerous data types can be visualized in a vessel map, necessitating different approaches for Creating map layouts, transferring the geometry of the data to that layout, and visualizing the underlying attributes (cf. Figure 1). To make the challenge of Creating vessel maps more approachable, in this State of the Art Report, we will provide a comprehensive review of techniques to compute patient-specific vessel maps that emerged at the cross-section of visualization, computerized medical imaging, and radiology.
Despite the relevance of the topic and the extensive amount of map-like depictions proposed to visualize cardiovascular structures, no taxonomy or classification of vessel maps has yet been proposed. Most existing surveys on vessel segmentation and visualization do not cover map-like depictions of vessels but focus on 3D techniques [BFC04, LABFL09, PO08]. The recent State of the Art Report on map-like visualization by Hogräfer et al. [HHS20] discusses abstract map Creation in different visualization contexts, however, it does not cover medical data or applications. Only in their survey on flattening-based medical visualization techniques, Kreiser et al. review a subset of the methods proposed to Create 2D overviews of vascular structures under the umbrella of “circulatory system flattenings” [KMM*18]. However, the selected literature is incomplete, as the focus lies on mesh parameterization, missing other techniques for the generation of map-like depictions. Also, no further differentiation of methods is provided. In the following, we will show that a diverse assortment of such methods exists, which are based on heterogeneous data spaces. For instance, the curved planar reformation of an image volume is an entirely different approach than the mesh parameterization of a vessel surface or the radial graph embedding of a centerline. Yet, all techniques intend to facilitate similar user tasks centered around overview, exploration, navigation, and/or comparison. We aim to fill this gap in the literature and provide a consistent classification and complete overview of vessel map techniques that have yet been proposed. Furthermore, we connect the techniques to the domain-specific tasks, from which we ultimately derive suggestions regarding the usefulness and applicability of various vessel map approaches. Vessel maps are also different from map-like depictions of other anatomical structures. They usually need to transfer geometry from the ℝ3 to the ℝ2 space, while simultaneously Creating a readable network layout. The core challenge lies in Creating an optimal layout, mapping the data geometry into the layout, and then encoding the data attributes in the resulting map-like visualization. For each technique, we further filtered relevant attributes, including their algorithmic dependencies (e.g., if a centerline or view direction is required), which type of graphs the technique can handle, whether it is generalizable to different vascular structures and if properties like the vessel length are preserved. In summary, our contributions are:
- A review of domain requirements for vessel maps.
- A classification of the literature on vessel maps according to their mapping technique.
- Recommendations for the Creation of vessel maps, depending on user task and data source for the relevant cardiovascular structure.
Selection Criteria. The literature we chose to include in this report comes from a range of different journals and venues, covering interdisciplinary contributions to the topic. In all selected cases, a map-like visualization of some part of the cardiovascular system is employed to address a medical domain task. The vessel maps are Created from patient-specific data and are designed to facilitate diagnostic, treatment, or research purposes. Primarily, we used the search engines from Google Scholar [Goo22], the IEEE Xplore Digital Library [IEE22], the ACM Digital Library [ACM22], the Vispubdata data set [IHK*17], and the Eurographics Digital Library [Eur22]. We searched for keywords that are a combination of (1) vessel, vascular, or cardiovascular with (2) map, planar visualization, unfolding, untangling, straightening, projection, flattening, parameterization, or reformation.
Outline. We first provide an overview of the medical requirements for vessel maps, followed by the overarching processing pipeline, i.e., how different data spaces are Created. Then, we introduce the taxonomy of vessel maps, structuring different approaches and outlining the design considerations that must be made. Next, the existing literature is categorized by the taxonomy. We use the geometry mapping type (cf. Figure 1) for the top-level categorization of techniques because we aim to provide an overview for readers who know which data they will work with and are looking for related techniques. Finally, we conclude with recommendations on how to Create a vessel map, which are derived from the domain requirements, the taxonomy, and the challenges solved by existing techniques.
2. Vessel Map Requirements
A wide range of medical conditions related to the heart or blood vessels exist. They are grouped as cardiovascular disease (CVD) [MPN12]. With more than 30% of global deaths attributed to CVD, it is the leading cause of fatality [GBD16]. The two most prominent complications from CVD are heart attack, where blood flow to the coronary arteries of the heart deCreases, damaging the heart muscle, and stroke, where blood flow to the brain is restricted, causing brain cell death. Other maladies include venous thrombosis, which can impact lung function, peripheral artery disease, which may necessitate limb amputation, heart valve insufficiency, which impairs overall blood circulation, and many more [MPN12]. An expansive range of symptoms, causes, risk factors, and underlying mechanisms for CVD exist. This leads to the fact that diagnostics, treatment, prevention, and research are often handled by interdisciplinary teams. Within the medical domain, experts from cardiology, hematology, pulmonology, neurology, radiology, vascular surgery, cardiac surgery, and neurosurgery need to cooperate to combat the complexity of CVD. By simplifying the visual output of vascular imaging and inCreasing recognizability and comparability, vessel maps can aid the cross-communication of different experts. A useful vessel map needs to distill the important details relevant to the clinical task and present them effectively. Therefore, it is crucial to determine which features can be targeted and which tasks exist.
CVDs that include visible morphological changes to cardiovascular structures, i.e., vascular malformations that are discernible in imaging data, can be addressed by the use of a vessel map. Three major types of vascular malformation exist: stenosis, aneurysm, and dissection. A stenosis is a localized vessel narrowing, often due to atherosclerotic plaque that builds up on vessel walls. It can cause a stroke if the blood supply to areas of the brain is restricted and heart disease if coronary arteries are affected. An aneurysm is a localized bulging of a vessel, often due to a weak spot on the vessel wall. Aneurysms come in various shapes and sizes but generally inCrease in size over time. They may rupture, causing uncontrolled internal bleeding. A ruptured aneurysm in the brain can also cause a stroke. A dissection is a tear in the wall of a blood vessel, leading to a cavity or pouch of blood that forms within the wall. It may also cause a stroke or heart attack if the blood supply to the brain or heart is reduced as a result of the dissection.
In diagnostics, treatment planning, and treatment evaluation of CVD, multiple tasks exist that clinicians need to perform when analyzing a (potential) vascular malformation. First, patient-specific anatomy needs to be assessed. This visual search task requires clinicians to localize pathologies by spotting irregularities. ConCrete examples include the detection of stenoses, aneurysms, or missing arteries. If any candidates are found, they need to be contextualized to judge their severity, e.g., their spatial location must be known. Next, the distribution of a measured or simulated attribute on the patient's anatomy may need to be assessed. For example, the distribution of atherosclerotic plaque at a stenosis or the wall shear stress on an aneurysm wall can be of interest. At this point, the integration of multiple features is often required, for instance, by combining the morphology, hemodynamics (the properties of the blood flow), and vascular connectivity in the vicinity of the targeted segment. For standardized treatments, many medical guidelines require the classification of cases by measuring predetermined properties, e.g., width, length, volume, shape, or blood flow velocity. An example is the classification of the stenosis degree by measuring its diameter inside versus behind the stenosis [FEB*99]. Lastly, if surgical intervention is deemed necessary, the accessibility of the target region and the fitness of different approaches need to be determined. For instance, the topology of a vascular tree is analyzed before a minimally invasive procedure, during which a surgical instrument needs to be inserted and traverse the inside of the vasculature.
Concurrent to tasks in medical practice, many objectives in CVD research exist that can also benefit from vessel maps. For one, medical researchers are trying to assess correlations of different attributes to determine new and more accurate markers for classifying CVD. Often, recurring patterns are sought in multiple data sets, i.e., cohort studies, to generate new hypotheses. In later-stage clinical trials, usually, the effects of a particular treatment are studied to test these hypotheses and Create a predictor for future cases. Ultimately, the findings of many studies are then condensed in clinical guidelines, for instance, by incorporating a new measurable quantity into the decision-making process for a particular disease treatment. In all of these tasks, visualizations can be effective tools. Map-like visualizations in particular can help to find correlations by providing better overviews that require less interaction. Standardized vessel maps can aid in comparative tasks, make patterns visually discernible, and provide a way to quantify attributes.
From the tasks in medical practice and research, abstract visualization tasks can be derived that map-like depictions can facilitate. We differentiate five categories of abstract tasks:
Overview Identifying features, detecting outliers, exploring attribute distributions, and browsing the topology.
Contextualization Analyzing the spatial and/or topological context of features.
Quantification Measuring attributes on the local coordinate space of the map and classifying features.
Navigation Using the map to navigate other representations of the domain.
Comparison Comparing features, distributions, and/or the topology of multiple domain instances.
3. Data Processing Pipeline
Vessel maps can be Created from divergent data structures, yet they are all based on similar imaging techniques. How these structures are typically derived is shown in Figure 2. The two principal source modalities for non-invasive capturing of a patient's vasculature are computed tomography angiography (CTA) and magnetic resonance angiography (MRA). Both yield volume images of the scanned region where vessels are contrasted against other structures. They are typically not temporally resolved, i.e., they record a static image. Exceptions are specialized techniques, like phase-contrast MRA (PC-MRA) [SAG*14] and real-time MRI [Coh01], which have a temporal dimension. PC-MRA in particular is used to determine not only the occurrence of blood flow but also the flow velocities in large arteries. In clinical routine, cardiovascular structures are also often examined using ultrasound, as it is cheap, non-invasive, and provides direct feedback to the clinician. It is also temporally resolved and allows the measuring of flow velocities using the Doppler effect. Ultrasound generally has a lower resolution and more artifacts compared to CTA or MRA, which is why in diagnostics it is often used in addition to, e.g., a CTA scan of the same region. In routine examinations mostly traditional 2D ultrasound is used but 3D ultrasound is an emerging alternative [HMT14]. Volume images from CTA, MRA, and 3D ultrasound are the basis of most approaches that aim to Create a vessel map. Further imaging modalities that have been applied in some cases are rotational angiography [GCB*08] and digital subtraction angiography [Jea90]. Also, invasive capturing techniques exist, such as intravascular ultrasound [GGGSB11] and intravascular optical coherence tomography [BCG*09], where a probe is inserted into the vasculature via a catheter. In theory, these could also facilitate the Creation of a patient-specific vessel map.
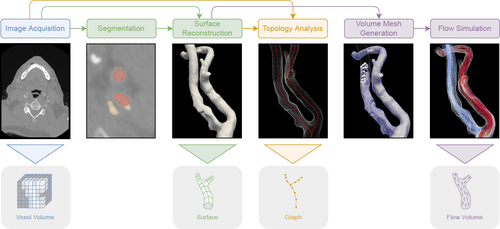
The typical pipeline used to derive the data structures from which vessel maps can be Created. Other possibilities also exist, for example, some modalities allow measuring flow instead of a simulation.
Vessel enhancement. The recorded volume image is often filtered to enhance the contrast of the target structure. A comprehensive overview of vessel enhancement procedures can be found in the survey of Fraz et al. [FRH*12]. Prominent are vesselness filters, originally introduced by Frangi et al. [FNVV98]. A variety of similar and improved filters have been proposed [LMK*21]. Other approaches include Wavelets [SLC*06] and diffusion filtering [KMA97]. In some cases, like PC-MRI processing, artifacts need to be explicitly removed [KBvP*16].
Model extraction. In many clinical and research applications, models are built that describe the bounds of the target structure, for instance, the surface of a vessel tree. The model usually is a triangulated surface mesh or quad mesh [SEEK12]. Model extraction can be split into segmentation, where a target structure is marked in the volume, and surface reconstruction, where the geometric model is Created. Sometimes, multiple models are defined, for example, to differentiate the inner and outer walls of a vessel or to extract regions with atherosclerotic plaque [JN*18]. Due to their simplicity, intensity-based approaches like thresholding and region growing are sometimes used to segment vessels. While they might apply to image data where vessels are delineated, they often do not produce the expected results, as they are not robust against noise and artifacts. Deformable models have also been applied to vascular structures, particularly active contours [LFG*01, MVN06]. They match an initial model to fit the specific image, e.g., based on its gradient. Similarly, graph-based methods, especially graph cuts, have been adapted to vessel tracking [BPS*10,ELD10]. Temporally resolved volumes, such as from PC-MRI or ultrasound, require a segmentation of every time step to adjust for the moving morphology [BPE*15]. For example, Köhler et al. [KPG*15] proposed a modified graph cut to segment the aorta in PC-MRI data. Many model extraction techniques require some form of manual input, such as landmarks or outlined contours. A survey of conventional techniques for vessel lumen segmentation is provided by Lesage et al. [LABFL09]. More recently, the research focus for vessel segmentation has shifted to machine-learning-based methods. Especially convolutional neural networks have proven to be highly successful tools for image analysis. Their advantage lies in the fact that image features are automatically learned, i.e., no specific descriptor needs to be provided. This allows complex automatic segmentations of data with noise, image artifacts, or different types of atherosclerotic plaque, which is often difficult to differentiate from the vessel lumen. Convolutional neural networks have been applied to segment various types of vessels [LK16, MWvdV*16, PHM*16, WXG*16]. They generally require a basis of manually segmented image volumes for training. For further reading, we recommend the surveys of Moccia et al. [MMHM18] and Zhao et al. [ZCHH17]. Extracted surfaces can also be further processed and given additional information, such as relevant landmarks or morphological features. For example, aneurysms can be detected and segmented in models of vessel trees [LMW*19].
Centerline extraction. Many mesh processing and visualization algorithms that work with vascular models require a centerline. The centerline is the geometric vessel skeleton. More generally speaking, it is a graph that defines the tree or network topology of the vascular structure it lies in. It can be reconstructed either from a surface model or directly from the volume image. An overview of skeletal representations for surface meshes is provided by Tagliasacchi [Tag14].
Various approaches to computing the skeleton of voxel volumes, like medical volume images or voxelized surface meshes, have been proposed. A common idea is topological thinning, for instance, by peeling one layer of voxels at a time [GSV96, Pav80, PBJ*98, SSZZ01] or iteratively contracting the volume until a linear graph is retained [WL08]. If the centerline is to be derived from a volume image, these techniques typically require a binarized volume, where the voxels belonging to the target structure are separated [LKC94]. A second widely studied approach is to use distance metrics on the image graph. By connecting neighboring voxels in a graph structure, individual skeleton paths can be defined through the volume [ZT99]. After a start node is selected, the end node can be determined by maximal distance and an ideal path can be found using Dijkstra's algorithm [Dij59]. For the centerline to adhere to the center of the volume, passing through edges closer to the border of the structure can be penalized [BSB*00,BKS01,SBB*00].
If a surface geometry is given, a common strategy for finding the centerline of a vessel tree is to use the medial axis transform of the geometry [B*67]. For a 3D shape, the medial axis tracks the positions of the maximally inscribed spheres. Each sphere is described by three points on the surface. The medial skeleton is then defined by a set of sheets, each described by three points [GK04]. Connecting the centers of the spheres retrieves a curve skeleton – the vessel centerline used in most applications. An advantage of this method is that the minimum radii of the tubular structure are computed as a byproduct. For surfaces made of polygons, the medial axis can be derived by computing the bisectors [CKM04]. This method, however, is computationally complex. Faster strategies usually approach this as a Voronoi diagram problem [OBSC00]. First, the boundary points are sampled, then a 3D Voronoi diagram is computed on them. The medial axis can then be derived by choosing a fitting subset of the diagram, i.e., cells that lie inside the geometry. Antiga et al. [AEIR03] demonstrate this approach with surface models of vessel trees. Other popular approaches for the skeletonization of surface meshes include, similar to the thinning of volumes, a topology-based thinning of the surface [ATC*08] and retrieving the centerline from a clustering of the points composing the object [FW06].
Implementations of vessel centerline algorithms have been included in commonly used medical image analysis toolkits. Examples are the skeletonization plug-in in ImageJ [SRE12], which is based on the method by Lee et al. [LKC94] and the vascular modeling toolkit, aka VMTK [APB*08, ISMA18], which has been implemented as an extension for 3D slicer [PHK05,KPV13]. A comparison of these methods is provided by Wang et al. [WCH*10].
Flow simulation. In an extensive processing step numerical methods can be used to compute a prediction for the blood flow. Overviews of techniques for the generation and visualization of blood flow data can be found in the reviews of Caballero and Laín [CL13], Vilanova et al. [VPvP*14], Köhler et al. [KBvP*16], and Oeltze-Jafra et al. [OJMN*18]. Usually, computational fluid dynamics (CFD) is used to solve the flow field based on boundary conditions on the vessel wall and domain inlets and outlets at the caps of the vessel tree [Lan13]. CFD requires a volumetric mesh that disCretizes the full domain where the simulation should occur. After the simulation, each mesh cell stores information about the predicted flow, which can also be time-resolved. Further quantities, like the wall shear stress or wall normal stress, can be derived from the flow field.
3.1. Data Structures
At this point, data can be encoded in four spatial structures. First, in the cells of a voxel volume, i.e., a regular 3D grid. This can be the original or filtered medical volume image. Data is typically expressed as intensity, i.e., scalar values, which are specific to the imaging modality used. The volume not only covers the cardiovascular structure but also the surrounding context. Usually, there is no temporal resolution, although exceptions exist. Often, the location of a target structure is automatically or semi-automatically marked during preprocessing. Second, in the cells of a flow volume. This is typically an irregular 3D grid that describes the blood flow inside a vessel. It can originate from flow simulation or PC-MRA and is normally confined to the vessel lumen (the volume encased by the inner wall of a vessel, where blood is flowing). A flow volume is often temporally resolved. Common attributes stored in the volume are flow velocity (vector), pressure (scalar), and derivations of the flow field. Third, data can be located on vertices or polygons of a surface geometry. These are usually one or multiple surfaces embedded in ℝ3, like the inner and outer wall of a vessel. Wall surfaces can be temporally resolved, this is typically the case if they are combined with a flow volume. Common attributes stored on vessel wall geometry include wall thickness (scalar), wall shear stress (scalar), wall normal stress (scalar), wall displacement (vector), and the occurrence or thickness of plaque (scalar). Fourth, data can be located on the vertices of a centerline graph, which is also embedded in ℝ3. It is usually not temporally resolved and encodes properties like the vessel radius (scalar), cross-section area (scalar), or branch label.
4. Taxonomy
We introduce the notion of vessel maps as a collective for maplike visualizations of the cardiovascular system. Vessel maps have been proposed for heterogeneous data structures, like volumes, surfaces, or trees, and can be based on a divergent range of algorithmic approaches, for example, untangling, straightening, unfolding, flattening, or reformation. However, they share a common purpose in the simplification of complex cardiovascular structures for visual interpretation, they map attribute distributions and/or connectivity information, and they are designed to aid one or multiple of the tasks described in Section 2. We use the term map-like to allude to the properties of the described visualizations, which are similar to maps in the traditional sense. First, they are 2D depictions of a spatial domain and aim to preserve the locality and the relative positioning of features. Second, they abstract the attributes relevant to the observer to inCrease legibility. Third, they conform to the uses of maps, which include getting an overview of a region, navigating a domain, exploring distributions and connections, and comparing different areas. Following the definition of Hogräfer et al. [HHS20], map-like visualizations exhibit traits of both (cartographic) maps and charts/plots. In this sense, vessel maps are schematizations of cardiovascular structures instead of geospatial data.
Vessel maps are also an interesting case to study from a pure visualization point of view. Their spectrum ranges from visualizations of networks and trees to the depiction of surface fields. Interestingly, many ideas proposed for vessel maps do not fall completely into either category but are situated somewhere in between. This range requires otherwise distinct techniques to be merged, like network and surface visualization. For the Creation of a vessel map, three aspects must be considered:
- What is the layout of the resulting map?
- How is the geometric component of the data mapped to this layout?
- How is the attribute component of the data mapped to this layout?
These steps are also shown in Figure 1. Steps one and two are sometimes solved interdependently [ZHT02b, CES*08, CCR20], sometimes independently [WRRN09, BGP*11, MK16, LKH*19]. Depending on the user task, the branching topology, object geometry, or data attributes can be of interest. It should be kept in mind, however, that preserving a specific property in the mapping process might require sacrificing another.
4.1. Layout Generation
Commonly, a vessel map needs to Create a flat layout from an input graph in ℝ3. Most techniques use constraints to build the layout. Typical constraints include preventing self-intersections and preserving original properties, such as angles, overall shape, or the relative length of segments. As illustrated in Figure 1, the layout directly depends on the input graph of the vascular structure. Also, it indirectly depends on the user task, as it needs to visualize the appropriate region.
In the simplest situation, the region is a single segment, in which case no considerations regarding branching must be made. This is easy to solve, as no actual graph layout must be determined. In practice, a map of a specific vascular segment or surface patch is Created, like an individual aneurysm [GSK*12, MVB*17]. If the region is a tree of depth 1, branch points must be considered but only for a depth of one. We list this as a special case, as sometimes a specific vessel segment is focused but branches exist in the evaluated region [KFW*02, LGZ08, RHR*09]. Often, solving the layout for a tree of depth 1 does not require sophisticated algorithms. If the region is an n-level tree, a variable number of successive sub-branches must be considered. Usually, a generalized solution is used that can be applied to different trees. For the most part, on the macroscopic level, the vascular system is a tree and many layout approaches make use of this property. If the region is a cyclical graph, sub-branches and loops must be considered, which is a harder problem to solve. This must be kept in mind if the examined vasculature can contain loops. This is the case, for instance, for the circle of Willis, a central arterial structure in the cranium.
Depending on which properties the final visualization should have, different 2D layouts are suitable. In simple cases, projection has been used to Create a 2D from a 3D tree structure [KFW*01, TBB*07, NGB*09, BSR*14]. The obvious flaws of this approach are possible self-intersections that may lead to visual ambiguity and/or occlusion of data. Still, simple projection may be viable if, e.g., only a single segment is mapped. Many techniques attempt to Create a readable layout that follows certain rules. A straightening lays out the branches of a tree as straight lines, which can be connected [EMKL21] or disconnected [GWH15]. The advantage of straightening is that the individual segments can be easily visually followed. Often, the arc length of segments is preserved. An untangling removes self-intersections in the layout, while simultaneously preserving attributes like the overall curve or relative positioning of segments [MK16]. Untangled views are closer to the original layout, improving familiarity, but can also Create more complex depictions than other techniques. Some techniques also use a fully pre-determined layout. The input graph is then fitted to align with this blueprint [PSY*20]. With this type of procedure, high comparability between multiple vessel maps can be achieved and it is often used for standardization purposes. However, the original proportions of the input graph will be lost.
4.2. Geometry Mapping
The layout determines where the data should appear in the visualization. How the data is mapped from ℝ3 to ℝ2 is determined by the geometry mapping, see Figure 1. Sometimes, layout and geometry mapping are solved as the same step in an algorithm [MVPL18] but they can also be solved independently [MK16]. Common constraints used for geometry mapping techniques are the prevention of overlaps and the minimization of the area or angle distortions, i.e., the original proportions are attempted to be preserved.
The geometry mapping directly depends on the data structure of the geometry – not on what the data is but where it is. As described in Section 3, the data structure can be a regular 3D grid, which typically is the voxel volume of an angiographic imaging modality. Hence, we group the vessel map visualizations that directly build on this type of data under the term image volume maps. These can either be Created by cutting the volume with a surface and reformatting the cut in a planar layout or by showing voxel values that were aggregated in the vicinity of the vessel. The geometry can also be an irregular grid, which is normally the case for flow volumes, where each cell holds properties of a field that describes the blood flow. Therefore, we call the resulting visualizations flow volume maps. Flow volume maps can be Created by reforming the data space, e.g., by straightening the flow volume, or by deriving a graph layout from the flow features. Often, data is situated not in a volume but on a surface embedded in ℝ3. Focusing the analysis on wall properties makes sense, as CVD generally develops on or inside the walls of the cardiovascular system. If the data shown in the resulting map-like visualization is associated with the vertices or faces of a wall geometry, we call it a vessel wall map. Such maps were Created with projection techniques or surface parameterizations. Lastly, data can be located on the vertices of a centerline graph. If the data is encoded exclusively on this type of graph, the layout step already defines the geometry mapping. As the resulting vessel maps focus on the vascular tree or network, we call them vessel network maps. They can either keep some geometric properties by straightening or untangling the graph structure or be abstract representations that only convey the topology.
4.3. Attribute Mapping
In the final step, a visual encoding for the data attributes needs to be chosen. The attribute mapping is notably distinct from the layout and geometry mapping, as it only defines how the data is shown, not where. We encourage thinking of this step as an individual part of a vessel map visualization. Some data structures have a strong association with certain attribute mappings, e.g., visualizations of image volumes tend to use a grayscale colormap. Defaulting to such a mapping can have benefits regarding recognizability but might also mean that other possibilities are overlooked and remain untested.
The suitability of an attribute mapping must be determined by the user task that it should facilitate. For instance, if the user attempts to find certain features in an attribute range, they should be highlighted by the chosen encoding. For vessel maps, five types of attribute mappings have proven to be useful. First, size encodings, which are often used as a way to show the thickness of a vessel by varying the width of rendered segments. The width can be quickly visually read and is, naturally, an intuitive representation of vascular morphology. Second, windowing encodings that map intensity values to gray values while providing the necessary interaction to explore the entire data range (usually 12 bits). Interactions include changing brightness and contrast. These encodings can be considered a special case of colormaps and are predominantly applied to image volume maps. Third, color encodings are widely utilized to make full use of the properties of colormaps. They are particularly beneficial to show scalar field distributions. Fourth, some approaches exist that use illustrative encodings [MVB*17, MGB*19]. Techniques like hatching can be used to identify certain regions. Fifth, if multiple attributes must be visualized, glyphs can be used as an additional way to encode information [MMNG16, GWE*19a]. Symbols that encode attributes through their shape, size, and color are common in traditional maps, as they can add explorable layers of information to a spatial domain without the need for direct interaction. The advantages of glyphs can just as well be utilized for vessel maps.
Attribute mappings can also be combined to show multiple attributes at once. For example, a size encoding can easily be used in combination with a colormap. Combining attribute mappings to exploit multiple visual channels makes map-like depictions a powerful tool for communicating information efficiently and exploring correlations.
4.4. Classification
In the following, we provide a classification of the literature on vessel maps. We discuss the application domains, which structures are visualized, and why the respective data space is chosen. An overview of the works is shown in Table 1. The primary questions we answer follow the taxonomy:
- What is the input graph? (segment, tree of depth 1 or n, cyclical graph)
- What is the layout of the resulting map? (projection, straightening, untangling, fitting)
- How is the geometric component mapped? (cut surface, voxel aggregation, flow straightening, flow graph, surface projection, mesh parameterization, network straightening/untangling, topology map)
- How is the attribute component mapped? Which encodings are used? (size, windowing, color, illustrative encodings, glyphs)
If applicable, we also answer the following secondary questions:
- Which tasks are facilitated? (overview/exploration, contextualization, quantification, navigation, comparison)
- Which dependencies exist in addition to the data structure? (centerline, view direction, landmarks, manual cut)
- Is the approach generalizable to different structures? If yes, has this been demonstrated?
- Which properties are preserved? (arc length, diameter, surface area, angles)
5. Image Volume Maps
This section covers all techniques that work on the voxel level. Mostly, these are derivations of curved planar reformation (CPR), i.e., techniques that use centerlines to align non-planar cuts and then perform image reformation to display selected vascular structures in volume images within a single 2D depiction. The results are map-like visualizations of the vasculature, which are commonly used to identify and assess calcified plaque and potential vessel stenosis. Typical challenges are diameter preservation, how to incorporate vessel wall features, and how to preserve or display the surrounding context. We differentiate between techniques that display volume cuts [AMRB98, AMB*13, GWH15, HDL*01, KFW*01, KFW*02, KWFG03, KFWG06, KPS14, LR06, LGZ08, RFK*07, SGH03, SČC*04] and techniques that aggregate voxel values in an attempt to display certain features [Cai07, DHS*13, MVB*12,MMV*13,RHR*09].
Achenbach et al. [AMRB98] generated curved planar reformations (CPRs) to study stenotic regions of coronary arteries in electron beam computed tomography (EBCT). They manually defined the cross-sections of each coronary artery in axial slices and use a reference plane (axial, sagittal, or possibly coronal) to Create the reformations. The results show an image for each vessel branch in stretched form, allowing distance measurements. Context visualizations outside the vessel lumen were not presented. This approach can be applied to any tubular structure, since only a curve reflecting the course of the vessel is needed, together with a reconstruction or reference plane.
 area/width,
area/width,  windowing,
windowing,  colormap,
colormap,  illustrative, and
illustrative, and  glyphs. The algorithm dependencies are encoded by:
glyphs. The algorithm dependencies are encoded by:  centerline,
centerline,  view,
view,  landmarks, and
landmarks, and  manual cut.
manual cut.| References | Structure | Input Graph | Layout | Geometry Mapping | Attribute Mapping | Overview | Context | Task Quantif. | Navigat. | Compare | Dependencies | Preservation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image Volume Maps | ||||||||||||
| [AMRB98] | coronary art.* | segment | untangling | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✗ |  |
arc length |
| [KFW*01] | peripheral art.* | tree depth 1 | projection | cut surface |  |
– | – | – | – | – |  |
|
| [HDL*01] | treelike* | tree depth n | untangling | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✗ |  |
arc length, diameter |
| [KFW*02,KFWG06] | ||||||||||||
| projected CPR | peripheral art.* | tree depth n | projection | cut surface |  |
✓ | ✗ | ✗ | ✗ | ✗ |  |
|
| stretched CPR | peripheral art.* | tree depth n | untangling | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✗ | 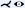 |
arc length |
| straightened CPR | peripheral art.* | segment | straightening | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✓ |  |
arc length, diameter |
| [KWFG03,KFWG06] | ||||||||||||
| helical CPR | peripheral art.* | segment | straightening | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✓ | ✗ | arc length |
| untangled CPR | peripheral art.* | tree depth n | untangling | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✓ |  |
arc length |
| [SGH03] | ||||||||||||
| ruled surface | aorta* | segment | untangling | cut surface | 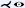 |
✓ | ✗ | ✓ | ✓ | ✗ |  |
arc length |
| free-form surface | aorta* | 1-level-tree | straightening | cut surface |  |
✓ | ✗ | ✓ | ✗ | ✗ | arc length | |
| [SCC*04] | peripheral* | tree depth n | projection | cut surface |  |
✓ | ✓ | ✗ | ✓ | ✗ |  |
|
| [LR06] | treelike* | tree depth n | untangling | cut surface | 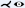 |
✓ | ✗ | ✓ | ✓ | ✗ |  |
arc length |
| [RFK*07] | peripheral art.* | tree depth n | untangling | cut surface | 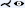 |
– | – | – | – | – |  |
|
| [Cai07] | treelike* | segment | untangling | voxel aggreg. |  |
✓ | ✗ | ✓ | ✓ | ✗ |  |
arc length |
| [LGZ08] | cerebral art.* | segment | untangling | cut surface |  |
✓ | ✗ | ✓ | ✓ | ✓ |  |
arc length, diameter |
| [RHR*09] | mouse aorta* | tree depth 1 | untangling | voxel aggreg. | 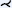 |
✓ | ✗ | ✓ | ✓ | ✓ |  |
arc length, diameter |
| [MVB*12] | treelike* | tree depth n | projection | voxel aggreg. | 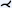 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
|
| [MMV*13] | peripheral art.* | tree depth n | straightening | voxel aggreg. |  |
✓ | ✓ | ✓ | ✓ | ✓ |  |
arc length, diameter |
| [DHS*13] | carotid art.* | segment | straightening | voxel aggreg. | 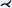 |
✓ | ✓ | ✓ | ✓ | ✓ |  |
arc length, diameter |
| [AMB*13] | treelike* | tree depth n | projection | cut surface | 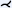 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
|
| [KPS14] | peripheral art.* | tree depth n | any | cut surface | any | – | – | – | – | – |  |
|
| [GWH15] | coronary art.* | tree depth n | straightening | cut surface |  |
✗ | ✓ | ✓ |  |
arc length, diameter | ||
| Flow Volume Maps | ||||||||||||
| [AH11] | aorta* | segment | straightening | flow straight. |  |
✓ | ✗ | ✓ | ✗ | ✓ |  |
arc length |
| [BPEGP21] | aorta* | segment | straightening | flow straight. | 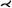 |
✓ | ✗ | ✓ | ✗ | ✓ |  |
(arc length, diameter) |
| [THQ*16] | vessels* | tree depth n | untangling | flow graph | 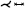 |
✓ | ✗ | ✓ | ✗ | ✗ |  |
|
| [SSK*17] | aorta* | segment | straightening | flow straight. | 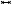 |
✓ | ✗ | ✓ | ✗ | ✓ |  |
(arc length, diameter) |
| [ZTWW21] | flow* | tree depth n | untangling | flow graph |  |
✓ | ✗ | ✗ | ✓ | ✓ |  |
|
| Vessel Wall Maps | ||||||||||||
| [ZHT*02a,ZHT02b] | treelike* | tree depth n | projection | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✗ |  |
angles |
| [ZHT03, ZHT05] | treelike* | tree depth n | projection | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✗ |  |
area |
| [AS03,AS04] | carotid art.* | tree depth 1 | straightening | mesh param. | 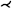 |
✓ | ✗ | ✗ | ✗ | ✓ |  |
|
| [KHB*06] | myocardium | segment | projection | projection | 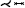 |
✓ | ✗ | ✗ | ✗ | ✗ | ||
| [OKG*06] | myocardium | segment | projection | projection |  |
✓ | ✗ | ✗ | ✗ | ✓ | ||
| [TBB*07] | myocardium | segment | projection | projection |  |
✓ | ✓ | ✗ | ✗ | ✗ | ||
| [CES*08] | carotid art. | tree depth 1 | straightening | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✗ |  |
area |
| [NGB*09] | cerebral art.* | segment | projection | projection | 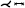 |
✓ | ✓ | ✗ | ✓ | ✗ |  |
|
| [GSK*12] | cerebral art.* | segment | projection | projection |  |
✓ | ✗ | ✗ | ✗ | ✓ | angles | |
| [MKH*12] | left atrium | tree depth 1 | projection | mesh param. |  |
✓ | ✗ | ✓ | ✗ | ✗ | diameter | |
| [CUSF13,CLC13] | carotid art. | tree depth 1 | straightening | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✓ |  |
|
| [BSR*14] | aortic valve* | segment | projection | projection | 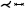 |
✓ | ✓ | ✗ | ✗ | ✓ | ||
| [KMJ*14] | left atrium | tree depth 1 | projection | mesh param. |  |
✓ | ✗ | ✓ | ✗ | ✓ |  |
|
| [SCK*16] | myocardium | segment | projection | projection | 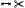 |
✓ | ✗ | ✗ | ✗ | ✓ | ||
| [CCLC17] | carotid art. | tree depth 1 | straightening | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✓ |  |
angles |
| [MVB*17] | cerebral art.* | segment | projection | mesh param. | 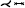 |
✓ | ✓ | ✗ | ✓ | ✗ |  |
angles |
| [PBI*17] | ventricles | segment | projection | mesh param. | 3D mesh | ✓ | ✗ | ✗ | ✗ | ✗ | 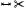 |
angles |
| [WTGZ*17] | left atrium | tree depth 1 | fitting | mesh param. |  |
✓ | ✗ | ✓ | ✗ | ✓ |  |
|
| [MVPL18] | cerebral art.* | segment | projection | mesh param. |  |
✓ | ✓ | ✗ | ✓ | ✗ |  |
angles |
| [MGB*19] | cerebral art.* | segment | projection | mesh param. | 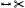 |
✓ | ✓ | ✓ | ✓ | ✗ |  |
angles |
| [EEL*19] | mitral valve | segment | projection | mesh param. | 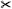 |
✓ | ✗ | ✓ | ✓ | ✓ |  |
arc length, area |
| [LER* 20, CCB* 22] | mitral valve | segment | projection | mesh param. |  |
✓ | ✗ | ✓ | ✗ | ✓ |  |
arc length, area |
| [NGBD*19] | atria | tree depth 1 | fitting | mesh param. |  |
✓ | ✗ | ✓ | ✗ | ✓ | angles | |
| [CCR20] | carotid art. | tree depth 1 | straightening | mesh param. |  |
✓ | ✗ | ✗ | ✗ | ✓ |  |
area |
| [ERM*21] | treelike* | tree depth n | projection | mesh param. | 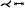 |
✓ | ✗ | ✗ | ✗ | ✗ | area | |
| [MVG*21] | cerebral art.* | segment | projection | mesh param. |  |
✓ | ✓ | ✗ | ✓ | ✗ |  |
area |
| Vessel Network Maps | ||||||||||||
| [WRN06] | aorta* | tree depth n | untangling | untangling | – | ✓ | ✗ | ✗ | ✗ | ✗ | 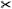 |
arc length |
| [WRRN09] | aorta* | tree depth n | untangling | untangling | 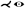 |
✓ | ✗ | ✗ | ✗ | ✗ |  |
arc length, diameter |
| [BGP*11] | coronary art.* | tree depth n | straightening | straightening | 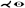 |
✓ | ✗ | ✗ | ✓ | ✗ |  |
arc length |
| [JWY13] | aorta* | tree depth n | untangling | untangling | 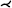 |
✓ | ✗ | ✗ | ✗ | ✗ |  |
arc length, diameter |
| [WJR*13] | aorta* | tree depth n | untangling | untangling | 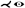 |
✓ | ✗ | ✗ | ✗ | ✗ |  |
arc length, diameter |
| [MK16] | treelike* | tree depth n | untangling | untangling | 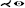 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
arc length |
| [MMNG16] | cerebral art. | cyclical | fitting | topology map | 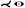 |
✓ | ✓ | ✓ | ✗ | ✗ |  |
|
| [SGBP17] | cerebral art. | cyclical | untangling | untangling | 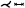 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
arc length, diameter |
| [GWE*19a] | microvessels* | cyclical | straightening | topology map | 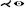 |
✓ | ✓ | ✗ | ✓ | ✓ |  |
|
| [LKH*19] | liver art.* | tree depth n | straightening | topology map | 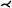 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
|
| [LL20] | liver art.* | tree depth n | straightening | topology map | 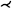 |
✓ | ✓ | ✗ | ✗ | ✗ |  |
|
| [PSY*20] | cerebral art. | cyclical | fitting | topology map |  |
✓ | ✓ | ✗ | ✓ | ✗ |  |
|
| [EMKL21] | carotid art.* | tree depth n | straightening | straightening | 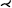 |
✓ | ✓ | ✓ | ✓ | ✓ |  |
arc length, diameter |
Kanitsar et al. [KFW*01] describe a workflow to examine peripheral arteries for stenosis or occlusion. To provide an unobstructed view of the blood vessels in CTA data, the bones must be segmented without holes and masked out. To this end, they use a threshold-based procedure which consists of two steps, the identification of outer cortical bone and the subsequent extension to the softer marrow. In the next step, vessels are tracked between user-defined start and endpoints. The shortest path between the respective two points is calculated using a cost function. Eventually, the obtained vessel centerlines are centered in perpendicular cross-sections using a ray-casting approach. After that, CPRs can be generated and the vessels examined. This workflow is generalizable to arbitrary tubular structures, but some thresholds have to be adjusted accordingly.
Medial axis reformation (MAR) was introduced by He et al. [HDL*01] to visualize the interior of blood vessels. Their approach extracts the medial axis of each vessel branch using a centroid-based skeletonization approach and then improves the centering based on their medialness. These centerlines are then spread segment-wise in image space. The direction of the spread can be controlled by the user. At branching points, the image is split and the process continues for each sub-image. Since each vessel branch is considered a cylinder, it can be projected into image space without any deformation, allowing the user to measure the length and diameter of the branch. This is similar to a stretched CPR as described by Kanitsar et al. [KFW*02]. The technique was applied to coronary, carotid, and iliac arteries imaged by EBCT.
Kanitsar et al. [KFW*02, KFWG06] discuss the properties of projected, stretched, and straightened CPR. The projected CPR offers good spatial orientation, while the straightened CPR does not. The stretched CPR still offers good spatial orientation, because the centerline is stretched only in local areas. Stretching and straightening retain the arc length of the centerline, while straightening also preserves the vessel diameter horizontally. The authors also introduce rotation of the ruling vector, which is referred to as the vector-of-interest in this work. This allows the entire vessel lumen to be inspected from different viewing angles. However, the axis of rotation is fixed, which causes problems when the vessel path is nearly perpendicular to it. To visualize the interior of multiple vessels simultaneously in a single image, the multipath CPR method is presented. Figure 3 illustrates how several CPRs are combined into a single image. To improve accuracy when inspecting small vessels, a thick CPR can be rendered. Here, instead of a thin surface, a small slab is resampled and rendered using averaging, maximum intensity projection (MIP), or minimum intensity projection (MinIP). The presented techniques are demonstrated on a phantom data set and mainly discussed on peripheral CTA data sets, except for a bronchial example. All presented methods are generalizable to any tubular structure but require a tree as input. The generated 2D layout of peripheral vessels is Created by partitioning the image according to the projected branch points.
Although (rotated) CPRs require only a few images to examine the entire vessel lumen, they can still add up to a considerable amount. To reduce the number of images, Kanitsar et al. [KWFG03, KFWG06] proposed two approaches, namely a helical and an untangled CPR. In the former, a sampling helix is used instead of a ruling vector. This allows the entire lumen to be acquired at once and eliminates the need for rotation. However, only a single vessel can be displayed straightened using this method. The other approach, the untangled CPR (see Figure 4), is composed of stretched CPRs of each tree branch without overlaps. For each vessel branch, even if the ruling vector is rotated, a so-called vessel hull (circle sector) is constructed from bottom to top, i.e. starting from the leaves of the tree, in the image space. Then these envelopes are arranged without overlap and the final image is partitioned similarly to the multipath CPR. Results are presented using peripheral CTA data sets, and both methods can be generalized to tree-like tubular structures, where the spiral CPR can visualize only one branch at a time.
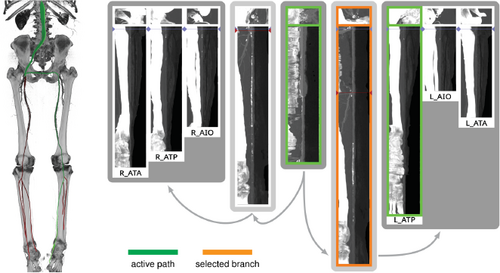
Illustration of the layout composition of multipath CPR for a peripheral CTA data set. A CPR is Created for each vessel segment and combined into the final image. Image adapted from [RFK*07].
Untangled CPR of a peripheral CTA data set showing the entire vessel tree in a single image. Image from [KWFG03].
To improve visual discontinuities when depicting multiple vascular branches in a single image using ruled surfaces as in MAR or CPR and to represent cut surfaces of irregular structures such as the jaw or human pelvis, Saroul et al. [SGH03] used free-form surfaces. First, they extend CPR by defining the orientation of the ruling vector based on the principal direction of the analyzed 3D centerline. The ruled surface is then flattened into image space by resampling the rectangular facets spanned by the vector between two consecutive centerline points and the ruling vector. Flattening this ruled surface produces no angular or metric distortions. They then propose free-form Coons surfaces for analysis of the human aortic arch, including its branches, and other structures such as the jaw. By defining curves along the centerline of a vessel that represent the maximum diameter, the resulting surface interpolates these curves and displays the variation in aortic diameter in a single image. Since Coons surfaces cannot be flattened without distortion, the user can choose a direction along which distances are preserved, as demonstrated on the aortic arch and its branches. The authors also show all teeth of a jaw that was flattened with Coon surfaces in a single image. Specifying free-form surfaces by interpolating user-defined boundary curves does not require centerlines of vascular structures.
To this time, CPR has only represented a cut surface along a curve or tubular structure, without considering alternative visual representations outside the vessel lumen. Straka et al. [SČC*04] presented several ways in which CPR (focus) can be combined with direct volume rendering (DVR) or MIP (context). They differ mainly in the transitions between the focus and context regions and in the way obstructed vessels are represented, e.g., by occlusion lines. Results are presented using peripheral CTA data sets, and the layout of the visualization resembles a multipath CPR. The approach is generalizable to other focus structures and applies not only to vascular structures but to importance-driven rendering in general.
Lee and Rasch [LR06] focused on improving curved sections through generally-oriented vessel trees by aligning the ruling vectors perpendicular to the vessel centerlines. The projected vessel tree is arranged from top to bottom with the largest medialness node at the top. The reason for this decision is that the branch diameter deCreases with inCreasing depth of the tree and the largest node should be at the top. Since the projected y-direction corresponds to the parameterized arc length, the approach resembles a stretched CPR. Results are presented for coronary (CTA) and peripheral (CT) arterial trees.
Roos et al. [RFK*07] evaluated multipath CPR in a clinical prospective study involving 10 patients with peripheral arterial disease. The result showed that multipath CPR produces artifacts when vessels are coincident or nearly collinear with the ruling vector and when multiple vessels positioned behind each other are examined as they overlap in image space. Other than that, it is a viable solution for examining peripheral arteries in a single image but does not replace either single-path CPR or MIP.
Since a single CPR is usually insufficient to assess the entire vessel lumen, several such sections must be examined from different angles (about 20 to 30). Although the effort is considerably reduced compared with the number of sections in the original acquired imaging data set, usually several hundred, this is still a lot. Cai [Cai07] attempted to reduce the number of images to be inspected by enclosing the entire 3D vessel lumen with a so-called biconvex slab rendered with MIP or X-ray. This approach can be viewed as an inverse VesselGlyph [SČC*04] with enhanced contextual representation of the lumen and a thin section through the surrounding anatomy. In this way, the entire lumen of a vessel is represented in a single image. However, a MIP of the biconvex slab shows a stenosis or complete occlusion in case of concentric calcification, because the rays are cast along the viewing direction. This is the reason why CPR needs to be rotated in the first place. Furthermore, this approach presents only a single-path stretched-like CPR on coronary and carotid arteries from CTA data sets.
To obtain centerlines of vascular structures, Lv et al. [LGZ08] used active contours or snakes. Since active contours depend strongly on their initial curve, the authors proposed an improved initial contour determined by casting rays radially from the center to each point on the contour and taking the point with the largest slope. Since this initial contour is close to the true boundary, the snakes quickly converge to the true contour. The midpoints of the resulting contours in the chosen slices are then used to Create a straightened CPR of the vessel branch. Results are presented on several individual vessel branches from a head aneurysm CTA data set.
Multimodal vascular reformation was explored by Ropinski et al. [RHR*09] on positron emission tomography (PET)/CT data of the mouse aortic arch. The aim was to study the development of atherosclerotic lesions at the morphological, functional, and molecular levels. The PET and CT data sets were registered using three artificially inserted ceramic markers. PET captures inflammatory activity, whereas CT captures structure. The vessel centerlines were extracted using a curve skeletonization approach. To compare several different mice or a single mouse over time, a normalization of the aortic arch with its outgoing arteries was introduced. For this purpose, a modified straightened multipath CPR was used. Vessels are flattened outward from the centers using a ray-casting approach to allow comparative assessment. Two options are proposed: the first preserves and displays the diameter of the aorta, while the second flattens the entire aorta into a rectangle. Since this leads to undesirable distortions (especially when normalizing the distances of the aortic arch branches between different individuals) and degradation of spatial orientation, they use multiple linked views to obtain a spatial overview and a comparable detailed view.
Mistelbauer et al. [MVB*12] proposed centerline reformation (CR), which uses wavefronts instead of a ruling vector to render a CPR. Their approach resembles a projected multipath CPR and renders the cut surface through the vessel lumen of arbitrarily oriented vascular structures. To ensure proper visibility of multiple overlapping CPRs in image space, their approach uses a depth buffer and parameterizes the vessel tree according to the length of its branches. Depending on the viewing direction, the lumen that is closer to the viewer and has a minimum distance from the current lumen in the buffer, along the graph (arc length), is chosen. To provide additional depth information, halos [EBRI09] can optionally be added around the lumen visualization and a volume rendering can be displayed as context. Vessel centerlines were extracted from CTA data sets using multiscale vesselness. The results show the vessels of a human head, pulmonary arteries, and a human abdominal aorta. As demonstrated on a phantom data set consisting of differently sized helices, the technique is generalizable and extensible.
To reduce the number of CPR images when examining a vessel lumen, Mistelbauer et al. [MMV*13] use nonlinear ray-casting along concentric circles perpendicular to the centerline of the vessel. Samples along these circular rays are then combined (or aggregated) into a single value using the minimum or maximum. By straightening the centerline of the vessel in the final image, it is divided into left and right sides. Each side can then show either the same aggregation method or two different methods. A combination of MIP and MinIP allows the radiologist to view either calcified or soft plaque in CTA data. Results are presented only for stenoses of the abdominal aorta and peripheral arteries. For the latter, an anatomic layout was proposed because multiple vessels were inspected, see Figure 5. This technique is generalizable to all tubular structures, but the anatomic layout of the multiple straightened curvicircular feature aggregations (CFAs) is case-specific.
Anatomical layout of a peripheral CTA data set (right in 3D) showing several CFA visualizations arranged from the center to the left and right. Image adapted from [Mis13].
At the same time as CFA, Diepenbrock et al. [DHS*13] introduced normalized circular projection (NCP). They acquired PET/CT data to analyze the development of atherosclerotic lesions in mouse carotid arteries. Analogous to CFA, NCP uses a sampling scheme around the centerline of a vessel but starts outside the vessel wall. Within cross-sections perpendicular to the centerline, rays are defined and sampled outward from the centerline point. The vessel wall is estimated in CTA using the maximum gradient along these rays. Once the wall is found, the PET data are sampled. By inflating the vessel wall into a cylinder, PET activity outside the vessel is visualized using NCP with MIP aggregation and in a straightened way. In a multiple linked view application, users can examine the left and right carotid arteries of mice in a standardized and normalized manner.
Previously, CPRs rotation was mainly constrained by the ruling vector, with the main challenge to ensure a continuous and smooth section along the centerline of the vessel and through its surrounding parts. Curved surface reformation (CSR), introduced by Auzinger and Mistelbauer et al. [AMB*13], allows unrestricted rotation of a vessel tree while continuously examining the lumen and surrounding parts of multiple vessels with sufficient visibility. The approach is based on ray-casting, where each ray cuts small strips generated by extruding the small line segments of the sampled vessel branching curves perpendicular to their direction and the viewing direction. A cost function decides which intersection point to use for the final result, favoring points that are closer to the viewer and to the vessel centerline. The resulting images correspond to a projected multipath CPR, but with unrestricted rotation. Vessels of a human head and peripheral vessels, both acquired with CTA, are shown and also presented with maximum intensity difference accumulation (MIDA) [BG09] as context. The technique requires only a graph consisting of curves (vessel branches) and is therefore generalizable.
Kretschmer et al. [KPS14] propose an improvement to most CPR approaches. By filtering the depth image of the cut surface immediately before sampling the data set, small discontinuities are removed. To ensure that the surface still passes through the vessel lumen, the projected pixels of the centerline are marked as fixed and are not considered in the filtering; this could be extended to the entire lumen if diameter information were available. To preserve large discontinuities caused by distant vessel branches along the vascular tree, but to smooth vessels that are close to each other, a bilateral filter is used. The results are demonstrated on a CTA data set.
Gillmann et al. [GWH15] present a visualization for coronary artery analysis, especially for surgical preparation, intervention, and restoration. Coronary artery centerlines are obtained from coronary CT data sets. The layout of their visualization is oriented from left to right and is similar to a treemap and the visualization presented by Borkin et al. [BGP*11]. The individual branches show a CFA with maximum aggregation at the top and average aggregation at the bottom. They use constant arc length sampling along the curved rays or concentric sampling circles. Calculations or intensity values that are above a user-defined isovalue are highlighted in red to draw the user's attention to that region and prompt further analysis.
6. Flow Volume Maps
Maps of flow volumes are a less explored area that is nonetheless distinct from other techniques. Blood flow information can be acquired from PC-MRI, duplex sonography, or simulated with computational fluid dynamics. The results are often visualized with 3D techniques like integral lines, particle animations, volume rendering, or flow profiles of cross-sections. Some visualization techniques have been proposed to Create map-like depictions of complex flow volumes, which are easier to compare and can be quickly assessed. One approach is to straighten vascular structures, including the flow field [AH11, BPEGP21,SSK*17], another is to Create a 2D graph visualization of the flow [THQ*16, ZTWW21]. The challenge here is not only to straighten the vessel structure but also attributes derived from the surface area. Information such as scalar fields on the domain and especially flow data represented as vector information within the surface domain also needs to be transformed consistently. Therefore, it is not sufficient to just straighten the surface; 3D flow information must also be straightened consistently.
Flow volume straightening. Angelelli and Hauser [AH11] present a straightening approach to simplify the aorta with its simulated blood flow. Using volumetric data, they first extract the centerline of the aorta and use it to construct a curvilinear grid, which is then straightened preserving the length of the centerline. The curved grid can also be used to reformat the blood flow into the straightened space, giving a simplified overview of the aorta and blood flow simulation. The blood flow is then represented with streamlines or path lines using a color map. Behrendt et al. [BPEGP21] use a 2.5D representation of the aorta with its blood flow. As in the approach of Angelelli and Hauser [AH11], a centerline is needed to transform the vertices of the surface mesh as well as the points of the pathlines into a straightened space. In addition, the centerline has six landmarks that are used to further simplify the straightened aorta. The parts of the centerline between the landmarks are either stretched or compressed to ensure equal spacing, and the radius is also normalized such that the simplified aorta becomes a cylinder, see Figure 6. During this simplification process, length and radius are intentionally distorted to ensure a consistent model for comparison of different data sets. Seifert et al. [SSK*17] applied a straightening approach to 2D fluorescence reflectance imaging (FRI) data. Using their standardized layout they aim to detect patterns in the development of atherosclerosis. To achieve this, multiple boundary points on the aorta must be defined by the user. Then, the boundary is smoothed and connected to form a polygonal net. In the next step, the centerline is straightened with the polygonal net, which also results in straightened FRI data. To ensure comparability, the image is normalized over the radii of the vessel.

Normalized map of the aorta with flow, Created with the technique of Behrendt et al. [BPEGP21]. From top to bottom: 3D rendering of the domain, straightening, even distribution of segments, radii normalization, flattening along the circumference.
Flow graphs. Another approach to map the flow volume while preserving the perceptual structure of a vessel was proposed by Tao et al. [THQ*16]. The volume of the vessel is divided into blocks, which are then transformed into 2D points. The formation of the 2D vessel structure is formulated as a graph layout problem. Both Euclidean distances and geodesic distances of the volume are integrated to preserve the perceptual structure and to ensure that there is no self-occlusion in the final result. After the 2D map is Created, the user can further explore the underlying blood flow data with heatmaps, graphs, histograms, and color-coded matrices. Brushing-and-linking techniques on the map are used for navigation of the domain. Recently, Zhang et al. [ZTWW21] proposed a simplification of flow data based on a 2D map-like depiction of stream surfaces. Their approach can be applied to a variety of data, including vascular structures with flow fields. To achieve a simplified 2D representation of the flow, the problem is considered as a graph layout optimization based on three energy terms. These energy terms are used to order the simplified flow so that parts of the flow are closer together when they are close in time. This applies to the x- and y- axes and it avoids temporal flipping, i.e., when the temporal ordering changes in the x-direction. The simplification yields a 2D overview of stream surfaces, where color is used to differentiate multiple seeding curves. Additional ellipsoidal glyphs are used to represent velocity or vorticity. A stacked layout of the resulting curves facilitates overview and comparison tasks.
7. Vessel Wall Maps
As vascular pathologies develop on the vessel walls, numerous techniques focus on Creating maps of these walls, on which properties like thickness, plaque occurrence, normal stress, or shear stress can be displayed. There are two principal approaches to generating map-based visualizations of vessel walls: employing mesh parameterizations or projections. Approaches that rely on mesh parameterizations Create one-to-one maps of surface meshes embedded in 3D. Mesh parameterizations are used for mapping different vascular structures comprising: specific structures like aneurysm surfaces [GSK*12, MVB*17, MVPL18, MGB*19, MVG*21], stenosis predilection sites [AS03, AS04, CUS*17, CES*08, CLC13, CUSF13, CCC16, CCLC17, CCR20, ZSC21], or heart valves and cavities [EEL*19, KMJ*14, LER*20, MKH*12, NGBD*19, PBI*17, RPM*19, WTGZ*17] but also arbitrary vessel tree walls [ERM*21, ZHT*02a, ZHT02b, ZHT03, ZHT05]. For techniques based on surface projections, the properties are projected onto a parametric structure like a cylinder, disk, or sphere [BSR*14,KHB*06,NGB*09,OKG*06,SCK*16,TBB*07]. The approach is similar to mesh parameterization, however, the topology is not retained, which means bijectivity cannot be ensured. The advantage of these approaches is that they usually can be computed on the fly for local structures.
All of these techniques result in maps where surface parameters can be assessed without rotation. Some are additionally used for navigation in visualization frameworks and some are specifically standardized maps for anatomical correspondence and statistical evaluations in medical studies. Typical challenges are how to handle branching, how to preserve properties like the area of features, how to standardize layouts, and how to cut vascular structures into topological disks.
7.1. Maps of Cerebral Aneurysms
Several works dealt with the generation of map-based visualizations of cerebral aneurysms. A patient-specific assessment of the rupture risk is important to decide whether treatment, which is also associated with risks, is necessary or whether the aneurysm can continue to be observed. Because estimation of rupture risk is based solely on morphological characteristics, such as the size and shape of the aneurysm, is not reliable, numerous papers are concerned with simulating cerebral blood flow in aneurysms to derive meaningful factors regarding rupture risk. For visual analysis of the simulation data, 3D surface models of the aneurysm and adjacent vessels are usually reconstructed from the clinical image data. On these 3D models, various simulated scalar values, such as wall shear stress (WSS), pressure or wall thickness, are displayed using standard techniques such as color-coding. The goal is to find wall regions where rupture-prone correlations of the scalar fields occur, such as regions with a low wall thickness and high WSS. Due to the time dependence of the scalar fields over a cardiac cycle as well as complex shapes of the aneurysms, the visual analysis of the 3D models is complicated. The user must rotate the 3D model, as well as change the encoding of the currently displayed scalar field, to explore the complete domain. However, since the scalar fields usually change via animation on the surface to reflect the cardiac cycle, it becomes nearly impossible for the user to spot prominent wall regions based on 3D models. The Creation of 2D aneurysm maps solves the rotation problem. In addition, the 2D maps were combined with techniques to explore more than one scalar field at a time to more easily identify conspicuous wall regions. Currently, all aneurysm maps based on the mapping of the vessel wall take a segment as input, since only the aneurysm, without adjacent vessels, is mapped.
Neugebauer et al. [NGB*09] developed the only approach in which the geometry of the aneurysm was mapped using a multiperspective projection. The 3D vessel surface is centered within an invisible cube. Afterward, the perspective projections are used to map the 3D surface to the cube sides. The resulting map consists of five regions representing the flow information of the left, right, top, bottom, and back sides of the vessel surface, giving an overview of the whole 3D surface. Besides the surface mesh, no other dependencies are needed for mapping. However, the map does not preserve any properties such as arc length, diameter, area, or angles of the 3D surface. The map is linked to a 3D view of the aneurysm, where a scalar field can be color-coded. The 3D vascular surface is shown in the center of the illustration surrounded by the map, where a spatial relation between both views is Created. With bidirectional interaction between the two views, the map supports navigation on the 3D surface. In principle, their approach could be applied to aneurysms on arbitrary vessels.
While there is only one projection-based approach to generating an aneurysm map, several works used mesh parametrization techniques for aneurysm mapping. One of the first concepts in this area is the work of Goubergrits et al. [GSK*12], who generated an aneurysm map to analyze statistical WSS distributions. The basic idea is to transfer the aneurysm wall to a unit circle. For this purpose, first, the vertices of the aneurysm surface are moved towards the center of mass of the aneurysm, ensuring that the distance to the center is equal for all vertices. This results in a unit sphere, where an azimuthal equidistant projection is then used for mapping the geometric component, where angle information is preserved. Besides the 3D surface mesh of the aneurysm, no further dependencies such as a centerline are needed for the map generation. To assign the attribute component (the WSS distribution), a simple color-coding based on the rainbow color map was used. With the generated map, an overview is given about the WSS on the aneurysm wall, where different maps can easily be compared due to the uniform shape of the map. However, reasonable results are just produced for convex structures, where the center of mass lies inside the surface. For irregularly shaped aneurysms, where the center of mass is outside the surface, this method results in area distortions in the map, especially for regions farther from the center of the map. Furthermore, this dependence on regular shapes limits the generalizability of the method to other anatomical structures.
Meuschke et al. generated aneurysm maps with different parametrization techniques to support the visual analysis of multiple scalar fields simultaneously [MVB*17, MVPL18, MGB*19, MVG*21]. Since only the aneurysm without adjacent vessels is to be mapped, the aneurysm has to be separated from the healthy vessel part first. Therefore, the user can click on the 3D surface mesh to define landmarks that are automatically connected to a cut line by applying the Dijkstra algorithm that determines the shortest path based on the Euclidean distances. The cut line follows the border of the aneurysm ostium, which is an imaginary surface that separates the aneurysm from the healthy vessel part. To provide anatomical context information, the cut line along the ostium is color-coded on the aneurysm map as well as the 3D surface.
In their first work [MVB*17], they employed the commonly used mesh parameterization least squares conformal maps (LSCM) to generate angle-preserving maps. In addition to the cut line, two points are needed as constraints for the parameterization, which are also set by the user by clicking on the mesh. For anatomical context information, these landmarks are also shown on the resulting map. On the map, two scalar fields can be visualized simultaneously. The first attribute is mapped to a cool-to-warm color scale, while the second attribute is encoded by an image-based hatching scheme. Dark red, strongly cross-hatched regions represent high scalar values. Additionally, a 3D bar chart is used above the map to visually encode a third attribute through the height and color of the bars. The resulting 2D map provides an occlusion-free overview of the aneurysm domain and supports the navigation of the corresponding 3D surface. By clicking on an interesting region in the 2D map, the virtual camera automatically moves to the region on the 3D surface, facilitating the navigation in the 3D space. Regarding, the generalizability, the authors mentioned that their method could also be applied to other aneurysm types, such as aortic aneurysms, but they did not show exemplary results for other structures.
Later Meuschke et al. [MVPL18] used the previous aneurysm map based on LSCM parametrization again to visually explore the interplay between scalar fields defined on the aneurysm wall and scalar fields defined on path lines that represent the internal blood flow. On the aneurysm map, a scalar field is color-coded using a gray-to-red color scale. Moreover, the internal blood flow is grouped by hierarchical clustering, where the user can explore the resulting clusters. The path line points of a selected cluster are projected onto the aneurysm map and are visualized as circles by applying depth-dependent halos. For this projection, for each path line point, the nearest surface point of the aneurysm part is determined using the Euclidean distance. On the resulting contour-based rendering of the path lines, a blue-to-yellow color map is applied to encode a flow-related attribute such as flow velocity. With this, the context and interplay of the wall- and flow-related attributes can be analyzed to further improve the rupture risk assessment. To reduce the manual effort needed for generating aneurysm maps, Meuschke et al. [MGB*19] later used the spectral conformal parameterization (SCP), which is also an angle-preserving approach. In contrast to the LSCM, SCP parameterizes the mesh without constraints. It tries to optimize the boundary of the mesh such that the mapping leads to appropriate results. Again, the map was used to explore two scalar fields simultaneously. For this purpose, the authors introduced a checkerboard visualization to Create a smooth transition between two selected scalar fields, see Figure 7. Both scalar fields are represented by two different color scales and the user has the possibility to switch between both scalar fields with the help of a slider. Moreover, by clicking on the map, the corresponding scalar field values are shown.
Simultaneous analysis of two scalar fields on an aneurysm map using a checkerboard visualization. The continuous value γ provides a smooth transition between both fields. Image from [MGB*19].
To enable a simultaneous exploration of more than two scalar fields, Meuschke et al. [MVG*21] introduced an aneurysm map combined with a glyph-based depiction of the corresponding scalar values, called “Skyline visualization”, see Figure 8. Since the size of conspicuous wall regions on the map should be preserved, the area-preserving parameterization ARAP was chosen. On the resulting map, a 2D regular grid is defined. For each grid cell, a 3D bar is computed, which is separated into floors along its height, where each floor represents a simulated time step. On the side surfaces of the floors, the scalar fields are color-coded. This gives the user an overview of the temporal behavior of the simulated data on the aneurysm wall. In addition, a threshold can be set for each scalar field. If the associated scalar fields within a floor fall below the thresholds, the floor is hidden. Thus, the user can interactively find regions where conspicuous correlations of scalar fields occur. Besides aneurysms, the authors have applied their method to other examples, such as simulated inducer data and iterative smoothed surfaces of organs, to show the generalizability of their approach.
Skyline visualization to visually analyze multiple scalar fields on surfaces simultaneously. On the aneurysm map, 3D bar charts are generated, where the color-coding of the floors encodes different scalar values. Image from [MVG*21].
7.2. Stenosis Predilection Sites
Several works explored the visual analysis of vessel bifurcations, as these highly curved regions favor the initiation and development of atherosclerosis. Atherosclerotic plaque deposits can lead to vessel stenosis or stroke in case the vessel is fully blocked or deposits detach from the vessel wall. Moreover, there are different drug treatments where it is necessary to analyze if plaque deposits are receding. As the assessment of plaque distribution and thickness based on 3D imaging is challenging, much work has been done to Create 2D maps of bifurcating regions, i.e., trees of depth 1. The main applications are the carotid arteries and their bifurcations, where stenoses often develop and have a high risk of causing a stroke.
Antiga et al. [AS03, AS04] introduced an automated mesh parameterization to straighten bifurcations to a 2D parametric plane. For this purpose, first, the centerlines are computed automatically. Based on the centerlines, a reference system is defined at the bifurcation. It consists of four points, which are determined by computing the intersections between the centerline branches and the mesh tubes corresponding to the individual branches. With this, a bijective mapping can be generated to preserve the location of the parameterized surface points relative to the reference system. Using the reference points, the bifurcating vessel is then split into its three constituent vessel branches. Afterward, each branch is parameterized in the longitudinal direction by solving a Laplacian equation over the circumferential direction of the surface-based on the tortuosity of the centerline. Each parameterized branch is mapped onto a rectangular parametric space, where the individual branches are patched together. Due to the bijective mapping on the parametric plane, their algorithm allows a quantitative comparison of anatomically different surface distributions. On the resulting patches, a scalar field is color-coded to observe the results of blood flow simulations, e.g., wall regions with high WSS values which might be an indicator for the generation of atherosclerotic plaque. The authors applied their technique to different bifurcating vessel geometries which shows its robustness and generalizability.
Chiu et al. [CES*08] introduced a map-based representation of carotid arteries to visualize the point-wise change of wall thickness due to plaque deposits. First, the outer vessel wall and vessel lumen were segmented in high-resolution 3D ultrasound images for two points in time, at baseline and a second scanning session. This results in stacked contour-based representations of the lumen and vessel wall which can be transformed into 3D surface meshes. Then, the wall thickness is computed for both time points by determining the point-wise distance between the lumen and outer vessel wall. Afterward, the change in wall thickness must be calculated. For this purpose, the two 3D meshes of the vessel wall are registered to each other using the iterative closest point algorithm. Subsequently, the point-wise change of wall thickness can be computed using the Euclidean distance between the registered walls. To straighten the baseline wall mesh to the 2D domain an arc length parameterization is used that maps the contours in each slice to straight lines. The parameterization was applied to each of the three branches of the bifurcation. For this, three planes are defined to cut open the mesh for mapping. The cut planes are described by the bifurcation apex as well as the centerlines and corresponding tangent vectors of the left and right carotid branches. Since an area-preserving map is needed to assess the change in the amount of plaque within a selected region, the area-preserving method by Zhu [ZHT05] is applied in a post-processing step. On the resulting map, the change of wall thickness is color-coded, where the user can select specific regions on the map to quantitatively assess the change in the amount of plaque. However, the carotid map by Chiu et al. [CES*08] is less suited to compare carotid arteries of different patients, since, the map shape is influenced by the shape of the corresponding 3D vessel wall mesh. To overcome this problem, the authors presented an extension of their carotid map by introducing a standardized carotid map [CUSF13, CLC13]. While the segmentation, wall reconstruction, and thickness computations stay the same, the straightening of the carotid branches changed. To generate a standardized map, the bifurcation apex is mapped to the origin of a Cartesian coordinate system. Moreover, the left and right branches of the carotid artery are mapped to the negative and positive x-axis, where their centerlines are straightened to the y-axis. Thus, the 2D standardized map allows quantitative group-wise comparison between distributions of the thickness changes. Choi et al. [CCLC17,CCR20] extend this line of work and propose an L-shaped continuous template to map the carotid bifurcation as a single 2D patch. They present a conformal mapping approach that retains the local geometry [CCLC17] and an angle-preserving technique [CCR20]. The standardized vessel wall thickness change maps were used in clinical studies to investigate biomarkers that show the effect of different therapies for atherosclerosis [CLC13,CCC16,CUS*17,ZSC21].
7.3. Maps of the Heart
The heart is the center of the cardiovascular system. In the following, we summarize techniques to generate map visualization of different anatomical structures of the heart comprising maps of its wall muscle (see Section 7) as well as its valves and cavities (see Section 7.3.2) together with maps of inserted stents to treat cardiac diseases.
7.3.1. Heart Wall Muscle
Abnormal movement of its wall muscle (myocardium) is an important indicator of many heart diseases. A crucial role falls on the left ventricle, the thickest of the heart's four chambers, as it supplies the whole body with oxygenated blood. With the help of MRI and CT imaging, the complex motion of the left ventricle as well as its perfusion can be analyzed to diagnose cardiac pathologies. To simplify the analysis of cardiac function parameters on the complex left ventricle geometry, several works dealt with the generation of map-based visualizations. All of them used the Cardiac Bull's Eye Plot (BEP) as a basic map design. The BEP is an abstract 2D plot that represents a standardized segmentation of the myocardium into 17 regions. These regions are arranged in a circular pattern, with the apex of the heart being projected into the center of the plot and more distant regions being projected into peripheral plot segments. This corresponds to an anatomical unfolding of the cone-shaped myocardium, where only the myocardial surface is needed as input to generate the BEP. Cardiologists are familiar with this segmentation, therefore, they can immediately understand the information presented and mentally reconstruct the original geometry.
Simultaneous visualization of two perfusion parameters, in rest and stress state, based on the BEP to identify ischemic areas. Image courtesy of Anja Kuß.
Kuehnel et al. [KHB*06] use the BEP to display perfusion data that are relevant for the diagnosis of coronary artery disease, where plaque buildup in the wall of the arteries that supply blood to the heart. The acquisition of perfusion data occurs frequently at rest and under stress, induced by drugs. Within the plot segments, a perfusion parameter is color-coded to provide an overview about myocardial perfusion which simplifies the detection of regions with poor blood supply. Oeltze et al. [OKG*06] extend the BEP-based visualization of myocardial perfusion data. For the simultaneous representation of rest and stress perfusion, the segments of the plot are divided in two, resulting in 34 segments, with 17 each color-encoding rest and stress perfusion, respectively, see Figure 9. The ring-wise subdivision of the segments ensures that adjacent segments in the plot are also adjacent on the heart wall. In this way, it is possible to clearly show the influence of rest and stress on perfusion in the respective area.
To visually analyze regional motion patterns of the myocardium Sheharyar et al. [SCK*16] applied novel glyph based techniques to the BEP. For visual encoding of the myocardial motion, different techniques are provided, i.e., warped BEP segments, pins, and warped lines, where a blue-to-red color scale is used to depict the motion strengths. This supports the detection of abnormal myocardial motion, which is an important indicator for multiple cardiac pathologies. Since the standard BEP does not provide any anatomical information and does not show the amount of scar tissue induced by cardiac diseases, Teermeer et al. [TBB*07] introduced the volumetric BEP (VBEP). While the basic projection of the myocardium is the same as before, in addition, the thickness of the myocardial wall is mapped to the height of the plot segments. The resulting volume shows the amount and position of scar tissue. Furthermore, anatomical information is added to the VBEP by projecting the coronary arteries and displaying two dots that mark the locations where the right ventricle connects to the left ventricle. While all BEP-based visualizations simplify the analysis of complex myocardial data, the depictions do not preserve any properties of the 3D myocardium surface. Moreover, the generalizability is limited due to the underlying standardized segmentation of the myocardium.
7.3.2. Heart Valves and Cavities
Several approaches have been proposed to generate maps of the components of the heart. Eulzer et al. [EEL*19] focused on the mitral valve, which is one of the four heart valves, to flatten its structure and provide an interactive framework for exploring time-dependent data on the resulting map. The motivation is to enhance the clinical assessment of heart valve defects. The surface mesh of the mitral valve is rolled out in the 2D domain to provide a simplified overview with the algorithm described by Lichtenberg et al. [LER*20]. Layering the map-like depictions allows full exploration of the time-dependent nature of these data. For further exploration, different color maps can be used to encode scalar field information, such as the probable closure zone of the heart valve. Later, Casademunt et al. [CCB*22] also employed the method by Lichtenberg et al. [LER*20] to encode additional information, e.g., contact distribution, curvature, and the principal stress, as a colormap on the flattened map.
Karim et al. [KMJ*14] proposed a map of the left atrium, the upper chamber through which blood enters the ventricles of the heart. The left atrium has multiple incoming vessel connections and can thus be seen as a branched structure of depth 1. Their goal was to simplify this structure to study patients with atrial fibrillation, which is an irregular and rapid heart rhythm. The used surface parameterization attempts to find a trade-off between an area-preserving and angle-preserving parameterization to balance distortions of the relative locations and sizes of features. It uses a fixed rectangular layout to enhance comparability. To apply the surface parameterization, an initial manual cut must be defined. The resulting map can then be used to color-code blood flow information, such as delayed enhanced MRI data.
Ma et al. [MKH*12] presented two methods to obtain an overview of cardiac structures. First, a BEP of the left ventricle is presented with the coronary sinus mapped. Second, a technique for parameterization of the left atrium was presented. For this, the orientation of the structure given by the image data is used to generate wrapping contour lines. These lines are unfolded into the 2D domain at uniform intervals, yielding a surface parameterization. A color map is used to encode data recorded with MRI on the map. Similarly, Nuñez-Garcia et al. [NGBD*19] studied the left and right atrium and provided a solution to parameterize these structures in a quasi-conformal manner. To achieve this, boundary conditions must be satisfied. Here, the edges of the structures are mapped onto a 2D disk and holes in the structures that indicate incoming or outgoing vessels are also mapped to predefined contours within the disk. To ensure quasi-conformity, two quadratic programming problems are solved that return the 3D vertex position in 2D to minimize the deviation of the angle. The resulting maps are used to encode wall thickness and delayed enhanced MRI data with a color map.
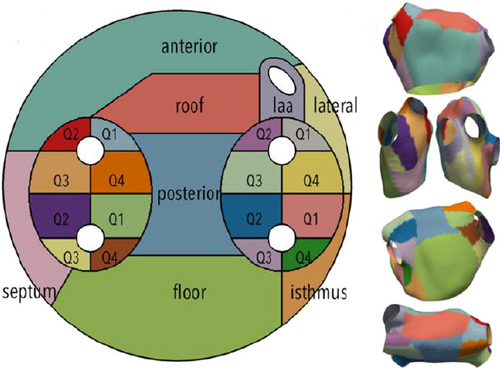
Standardized map of the left atrium with a fixed zone layout. Image from [WTGZ*17] under Creative Commons license [Cre].
Paun et al. [PBI*17] propose a parameterization of the left and right ventricles. In the first step, the boundary surface mesh must be extracted. Then, two landmarks are manually placed on the ridge of the boundary. Finally, the ridge is mapped onto a 2D slice. By using Laplace's equation and the gradient of the Laplace field the 3D anatomy mesh is reconstructed in 2D. The result is a 2D representation with additional detailed anatomy information. Roney et al. [RPM*19] presented a parameterization method that maps the left or right atrium to a unit square. For this, as with the previous approach, the Laplace equation was solved by defining boundary conditions as well as manually placed landmarks. The parameterization can be used to map information with a color map and compare different data sets.
Williams et al, [WTGZ*17] propose a different unfolding technique to visualize the left atrium in an abstract plot. They unfold the atrium with all the structures to a predefined map illustrating the individual parts, see Figure 10. The mapping can be considered an extension of the BEP to the left atrium. It uses a 2D disk and fixed contours within the disk. Then, the left atrium with its incoming branches is identified and mapped onto the 2D slice. The simplified map can be used to illustrate data with color, such as local activation time or delayed enhanced MRI data. This standardized abstract representation is highly suitable for comparison tasks.
Stent projections The aortic valve separates the left ventricle from the trunk of the aorta, i.e., it lies between the heart and the main arterial system. Born et al. [BSR*14] introduced a map-based depiction to investigate side effects occurring after treatment of aortic valve stenosis using transcatheter aortic valve implantation (TAVI). TAVI is a minimally invasive treatment method in which the abnormal valve is displaced toward the aortic wall by an expanded stent containing a prosthetic aortic valve. After a TAVI procedure, paravalvular leakage may occur, which is the backflow of blood between the stent and its surrounding structures into the left ventricle, resulting in volume overload and potential dilatation of this ventricle. Based on numerical simulations, different risk factors were identified for paravalvular leakage such as stent deformation, radial attachment forces, or calcifications. To analyze the influence of these risk factors Born et al. [BSR*14] presented a 2D visualization (stent maps) of the expanded stent. As input the stent mesh including its centerline as well as mesh-based representations of calcifications are needed. Moreover, six anatomical landmarks manually placed in CT images are used to add context information to the resulting stent maps. For generating the stent map, the stent geometry is projected to a curved cylinder around the stent leading to generalized cylindrical coordinates. Based on this cylinder representation the stent can be easily unrolled to 2D. On the stent map, a scalar field is color-coded. Moreover, anatomical landmarks are shown together with a contour rendering of the calcifications and the stent geometry. The stent map provides a comprehensive overview of possible risk factors and allows to contextualize relations between stent placement and thickness of aortic valve calcifications. Due to the generalized cylindrical coordinates, different data sets can be easily compared to identify patterns that are typical for paravalvular leakage. Furthermore, the stent map can be applied to other medical use cases such as treatment planning of other heart valve defects and cerebral aneurysm stenting.
7.4. Arbitrary Vessel Trees
A 2D map-based representation of complex vascular trees with numerous branches supports diagnostic tasks such as the detection of narrowed, dilated, and thrombosed vessel areas as well as the detection of lung nodules (small growths in the lung that can be cancerous). Zhu et al. [ZHT*02a,ZHT02b] introduced a conformal parameterization to project trees of depth n to the 2D domain. As input, the centerline of the vessel tree is needed, which is divided into y-shaped parts consisting of one branch point and three end-points. Between the branch point and the endpoints smooth curves are defined that are used as cut lines to unroll the 3D surface part. By stitching multiple unrolled parts together, the whole vessel tree is mapped. The resulting map provides an overview of the 3D domain where a scalar field can be color-coded on the map. Besides, vascular trees the authors discussed other applications, such as the mapping of bronchial trees. Moreover, they reused their conformal mapping to generate an area-preserving mapping [ZHT03,ZHT05]. For this purpose, they computed a density map that encodes the area changes from 3D to 2D using conformal mapping. Based on this density map, they applied optimal mass transport to minimize the area changes. However, since in both approaches the y-shaped parts are mapped independently of each other, unexpected cuts may result.
Eulzer et al. [ERM*21] introduced a bijective mapping of 3D vascular trees to the 2D domain where the cut and flattening is performed automatically, see Figure 11. No centerline or other inputs are necessary besides the vessel surface itself. First, vessel branches and endpoints are automatically detected. Subsequently, the cutting lines for projecting the mesh to the 2D domain are found automatically. To generate an intuitive mapping, they introduce the notion of natural vessel cuts – the cutting lines remain on one side of the vessel branches, following the longitudinal direction of cylindrical segments. This results in a comprehensible unfolding of the geometry that retains the original branch layout. Instead of a centerline, the graph topology of the cut is used to Create an initial straightened layout in the 2D domain. For mapping the geometry, the area-preserving As-Rigid-As-Possible (ARAP) parameterization technique is used. As the boundary is not fixed, the final layout resembles an untangling of the input tree. Their map provides a good overview of narrowed vessel regions and a scalar field can be color-coded on the map to explore the results of blood flow simulations. The algorithm could be applied to any tree-like structure that can be represented by a surface mesh. Depending on the complexity of the underlying tree, self-intersections may occur in the map, which could be avoided by abandoning area preservation.
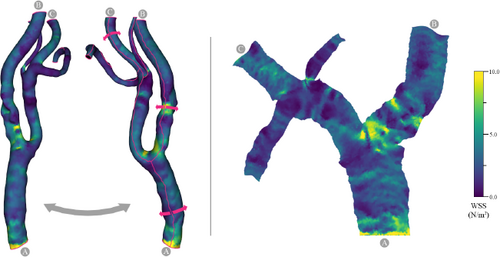
Automatic approach to generate a 2D map-based depiction of an arbitrary 3D vessel tree (left) by applying natural cuts (red lines). The map (right) shows the full surface while retaining its proportions and layout. A: common carotid. B: internal carotid. C: external carotid. Image from [ERM*21].
8. Vessel Network Maps
The visual search for malformations in vascular networks can be understood as a combination of abstract network analysis tasks, like browsing and path following. The underlying idea of vessel network maps is to facilitate such overview tasks, for instance, feature identification and topology browsing. Similarly, they can be applied to analyze the topological context of features and navigate a complex interconnected domain. For tasks involving spatial memory and identification, 2D depictions of data appear to be more effective than 3D represenations [CM02, TSW*07, FCL09, KMK06, KPSL10]. Therefore, vessel network maps transfer the spatial vascular topology into a 2D map-like visualization. Typically, node-link visualizations are used, as they are popular in visualizing networks and have been extensively studied [BETT98, DRSM15, Pur97, WPCM02]. Vessel network maps are based on a graph data structure that describes the connectivity of the cardiovascular region. Usually, this is the vessel centerline derived from image data. Besides the topology, other attributes can be of interest, such as the vessel diameter.
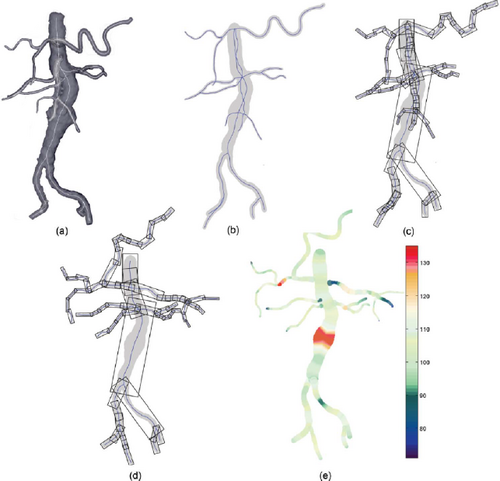
Untangling of the abdominal aorta centerline. (a) Surface rendering of the vessel tree. (b) Flattened centerline with vessel diameter mapping. (c) Bounding box representation. (d) Untangled bounding boxes. (e) Color coding of the width relative to the median width of the segment. Image from [WJR*13].
8.1. Connectivity Maps of Large Arteries
Large vessels, like the aorta, femoral, or carotid arteries, are clearly visible in angiographic imaging modalities. They can be seen as a treelike system of tubes that quickly becomes complex if multiple branches are considered, resulting in intricate 3D structures. Won et al. [WRN06, WRRN09, WJR*13] propose an uncluttered single-image visualization of the abdominal aortic tree. They optimize the 3D geometry of a binary tree of depth n in a 2D layout to resolve overlaps. Their original method [WRN06] built on Kanitsar et al. [KWFG03]. They use the stretched CPR mapping to initialize a 2D layout of the centerline, which may have overlaps of different branches, but already prevents overlaps of individual segments. Then, they relax the spatial configuration of segments but keep the branches connected. They prioritize large branches, such that they inhabit predictable positions and place small branches last. A radial sweep line algorithm is used to iteratively find the available region for the placement of each segment. Later adoptions optimized this procedure [WRRN09,WJR*13]. The relaxation is performed using bounding boxes around each vessel segment, which are rotated to find an optimal configuration (see Figure 12). Each box is denoted by v ∊ V, where V is the index set of the vessel parts. The orientation of a bounding box is given by an angle Θv. An optimal configuration of bounding boxes minimizes their overlap given by Ω(·) and, simultaneously, minimizes the deviation of the layout from the initial configuration, described by the energy Δ(·). The idea is to preserve the relative location of segments and the natural shape of the vessel tree, i.e., an untangled layout is Created. As these are contradicting criteria, a score function is optimized, which is a linear combination of both:
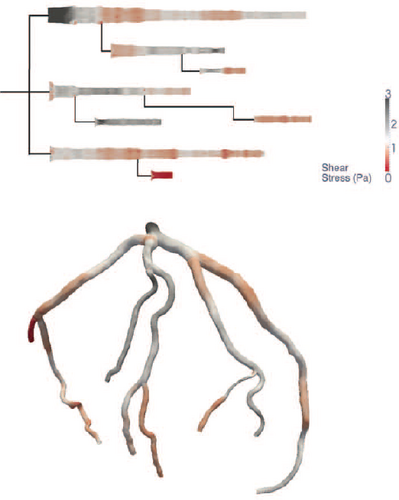
Coronary artery tree visualized as a surface rendering (bottom) and as a map of segments (top). Line width encodes the vessel diameter, the colormap encodes a scalar field (shear stress). Image from [BGP*11].
To optimize this function, Won et al. [WRRN09] first used simulated annealing [KGV83] and later proposed another approach that uses a technique inspired by the protein side-chain placement problem [LW75, WJR*13]. Jeon et al. [JWY13] also extended the procedure to parallel computing architecture. The resulting visualization uses a size and colormap encoding to highlight deviations in vessel width. The overview is thus helpful for identifying possible stenoses and aneurysms. It could, in theory, also be used to compare or navigate domains. As the initial layout is Created by stretched CPR and only rotations of vessel segments occur, the relative arc length of the vessels is preserved but the technique is also view-dependent.
Borkin et al. [BGP*11] propose a diagram representation of coronary artery trees of depth n. They found that users are more efficient and accurate at identifying atherosclerotic lesions (possible stenoses), compared to using a 3D surface depiction. The layout they propose disconnects branches and straightens them parallel to each other, preserving segment length. They map the vessel circumference to the size of the visualized segments. As their center-lines are based on surface models they are also able to add a projection of surface properties into this area, for example, simulated wall shear stress. The resulting field is encoded with a colormap (see Figure 13). They show how the map can be used for overview tasks and navigation by combining a view of a focus domain with a view of the full domain, where the focus region is marked. While they limit the demonstration to coronary artery trees, other vessel trees could plausibly be visualized with the same approach.
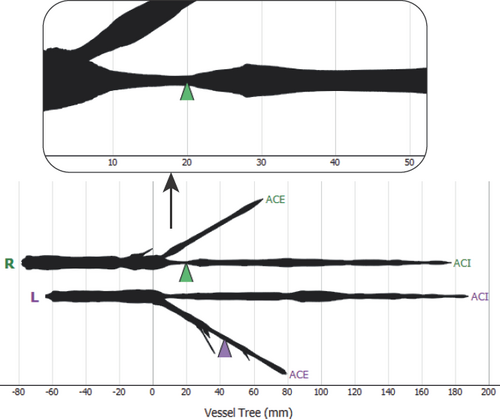
Map of the left (L) and right (R) carotid artery trees with a width encoding. Zooming in allows quantifying the length of a stenosis. The arrow glyphs are used to interactively place probes in a 3D view of the geometry. Image from [EMKL21].
Targeting a general solution, Marino et al. [MK16] propose a planarization of treelike 3D structures. They demonstrate the applicability of the approach to arterial trees of depth n. While they use a surface geometry as input, the Creation of the map-like depiction effectively only requires centerline and width information, which is why we classify the output as a vessel network map. Depending on the 3D view direction, the centerline is projected onto the 2D view plane, which typically leads to overlaps. Separate from this first step, a radial planar layout of the centerline is constructed based on the embedding of phylogenetic trees [BBS05]. Then, the original shape of the tree is recovered by iteratively converging to the angles that are measured in the projection from step one. Again, the final layout is an untangling of the input graph, aiming to achieve visual coherence with the 3D depiction. In the proposed visualization, they map two attributes to the layout: vessel width and segment depth. The width is directly mapped to the width around the centerline geometry and depth cues can be added in form of a grayscale border. The authors also demonstrate how to map a surface into the resulting shape, however, all information visible in the final representation (width, z-axis depth) can be encoded on the centerline alone. Mapping the surface may be useful for future applications, although it should be noted that the surface area is highly distorted in the process, as the vessel width encodes the diameter, not the circumference.
Vessel network maps have also been used as part of multiple coordinated views. The underlying idea is to use the map to first locate points of interest and then navigate to these locations, e.g., by steering a camera in a 3D rendering linked to the map. Eulzer et al. [EMKL21] propose a framework for analyzing carotid stenosis. They employ a map of the vessel tree to find and navigate regions of interest. They straighten the input trees of the left and right carotids and align the two sides such that their principal branches are in parallel. Side branches are connected at a fixed angle. Thus, the layout trades preservation of the original angles for a uniform and symmetric view of the vessel. Similar to other approaches that focus on stenosis analysis, they map the vessel diameter to the line width of the rendering. The result is shown in Figure 14. In their user study, they observed that a linear mapping of the diameter information may not sufficiently highlight stenoses. To remedy this issue, they propose a non-linear scaling around a threshold t, where values above are exaggerated and values below are downsized. A good threshold is the expected approximate vessel width. Radii r in the attribute mapping are then scaled by:
The emphasis factor a ∊ ℝ ≥ 1 sets how strong the scaling should deviate from a linear scale a = 1. As a reference value a = 2 is given. In the final application, the map is used for overview purposes, comparing the left and right trees, and for quantifying stenosis length, which can be directly read on the map. Also, the spatial domain can be navigated with draggable markers on the branches that control probe positions in the 3D data.
Some applications require analysis of a highly branched structure, like the arterial tree of the liver investigated by Lichtenberg et al. [LKH*19]. One target of this approach is to show the proximity of vessels and branch structures for intervention planning to minimize the risk of cutting through vital arteries. The technique visually separates individual subtrees in a straightened compact binary tree layout. A hierarchical or radial layout can be used. In both, overlaps are prevented and the subtrees are delineated. Then, they apply color-coding on the subtrees for branch identification and compute a sCreen space parameterization for pattern mapping [LSHL18]. This parameterization enables an illustrative encoding as an overlay of the map. It shows the proximity of branches to selected structures, for example, vessels close to a tumor or the distance to a simulated surgical needle, which can be utilized for operation path planning. An example application is shown in Figure 15. Later, Lichtenberg and Lawonn [LL20] applied a similar straightening technique and radial embedding of subtrees to generate 2D overview plots. They use an HSV colormap defined in the 2D domain to identify subtrees in a 3D model. Both methods are based on topology analysis of a mesh centerline. The visualizations reduce complex structures to abstract map-like depictions. Original geometric features are lost in exchange for a visual focus on the branch structure.
8.2. Cerebral Connectivity Maps
The cerebral arterial system can be modeled as a graph with weighted edges. These are mostly directed edges, as blood flow is distributed into inCreasingly smaller arteries, ending in capillaries (minuscule vessels through which oxygen and nutrients are exchanged with the surrounding tissue). Compared to other areas of the cardiovascular system, the cerebral arterial network is a special case for three reasons. First, small disturbances in blood distribution can cause stroke and be life-threatening. Second, there are also regulating cyclical arteries, which are undirected graph edges. In our graph model, these hierarchical and non-hierarchical components form a mixed hierarchy. Third, the cerebral network topology is highly relevant to determining which parts of the brain are affected by a vessel pathology and how and if a malformation can be treated. The mechanical accessibility of a pathology is a key factor in clinical risk assessment. Neuroradiologists need to identify stenoses, aneurysms, or missing arteries and then plan a potential intervention, where the ideal path to reach the respective site with surgical instruments needs to be determined, starting from the trunk. The cerebral arterial network can be thought of as consisting of three components. There are four entry points where the two carotid and the two vertebral arteries bring new blood into the system. They are connected in the circle of Willis, which regulates flow between them and acts as a layer of redundancy – a blockage in one artery can often be circumvented. Many anatomical variations of the circle of Willis exist, which necessitates individual assessment. Lastly, the cerebral arteries connect to the circle of Willis and distribute blood further throughout the brain.
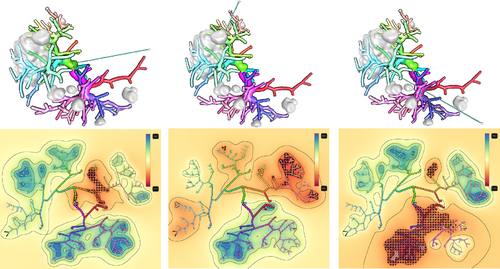
A 3D view (top) and 2D map (bottom) of the arterial tree of a liver. Three possibilities to reach a large tumor structure with a surgical needle are shown. A distance field around the needle is calculated and color-coded on the map. Vessels with a minimal distance of less than 20 mm are at risk of being damaged. They are highlighted with a stippling pattern, which allows for determining an optimal path. Image from [LKH*19].
Miao et al. [MMNG16] propose a standardized description of arteries in the Circle of Willis in the CoWRadar. The CoWRadar is an abstract map-like depiction that allows visual quantification of segment width and connectivity information. They implemented an automatic pipeline to detect the circle of Willis in image data, Create a centerline, derive the vessel graph, and label arteries. The network is fitted to a predetermined layout. The length of segments and vessel intensity in the image data are shown by arc glyphs at fixed locations. The connectivity is visualized with active/inactive line connections on the map. They show how the CoWRadar can be used to quickly identify the presence of vessels, understand the patient-specific network configuration, and quantify the blood perfusion of segments. An example is shown in Figure 16.
Pandey et al. [PSY*20] developed CerebroVis, an abstract 2D network visualization of the cerebral arteries that aims to preserve spatial context. They report an inCreased accuracy in stenosis detection tasks in comparison to conventional 3D visualizations of the same network. The readability of network visualizations is dependent on multiple factors. Node-link depictions should minimize edge-crossings [Pur97], path continuity facilitates visual browsing tasks [KMV15, WPCM02], and symmetry helps comparison [LNS85]. The authors apply these principles to CerebroVis, resulting in an abstract fitting of the topology with spatial constraints, e.g., the left and right sides of the brain are separated, see Figure 17. Furthermore, they run undirected edges horizontally in the final layout, to differentiate them visually from the hierarchical components. This idea was originally proposed by Gutwenger et al. [GJK*03]. Width and color encoding are used to display vessel diameter and an arbitrary additional property, like blood diffusion. CerebroVis can be used to detect points of interest, place them in their topological context, and navigate a 3D rendering of the network by clicking on segments.
The CoWRadar, a standardized connectivity map for the circle of Willis. (a) Maximum intensity projection of the circle of Willis with a centerline and extracted labels. (b) The resulting CoWRadar. The arc glyphs encode the length of segments (outer arc) and the perfusion in the image data (inner arc). Image from [MMNG16].
Projection of a cerebral artery network (left) and an automatically generated network map (right) visualized with the CerebroVis framework [PSY*20]. Line thickness encodes the vessel diameter and color encodes the vessel category.
A further technique that should be mentioned is the animated untangling of the circle of Willis by Saalfeld et al. [SGBP17]. While technically not a 2D map visualization, the geometry is unfolded and acts as a map for annotations. The centerline approximates a planar layout and the depiction can be used from a single perspective, yet the surface geometry remains 3D. The approach is a proof-of-concept, as the unfolding and animation are Created manually, which is unrealistic for time-sensitive clinical applications.
8.3. Maps of Microvasculature Networks
The analysis of microvessels is crucial for research in tissue development, pathophysiology, and treatment [BMM*14, FJ07, PC90]. Tissue degeneration, for example, initiated by diseases, results in subtle differences between networks. Microvasculature consists of complex interconnected vessels across large volumes, which is difficult to visualize [GWE*19b]. Tracing the topology of microvasculature results in a highly cyclical but sparse graph with a large number of redundant edges. Govyadinov et al. [GWE*19a] propose a bi-modal visualization with a graph-based and a geometry-based view of the same microvasculature data. They extract the centerline of microscopy tissue slices with a GPU-based predictor-corrector algorithm [GWE*19b], which results in a graph of the capillary branches. On this graph, they compute a spectra clustering over a user-selected property, like the microvessel length. Then, they show a highly intricate 3D representation of the segmented network, accompanied by a 2D map of clusters and connections between them. They use color to encode the cluster correspondence and arc glyphs to encode the inter- and intra-cluster relationships. The graph view can be used to navigate the volumetric view by brushing and linking. For example, selected regions in a cluster are highlighted in the 3D model. They show how to use the representation to compare microvasculature networks and detect small changes caused by diseases like Alzheimer's.
9. Recommendations for Vessel Map Creation
With the diverse range of existing vessel map techniques, it can be challenging to choose an appropriate method. We propose the following recipe to aid in this process. The outlined steps should be considered as overarching design considerations. They are not guidelines per se, as they are not founded on a well-enough base of perception studies on vessel maps alone. Large-scale quantitative evaluations of vessel maps are practically non-existent. Meaningful evaluation tasks that test the effectiveness of a vessel map require domain experts, often highly specialized physicians or medical researchers, who are hard to come by. Nonetheless, vessel maps have proven successful in terms of adaptation. They are a popular tool for abstracting information about the cardiovascular system, which is unsurprising considering the large body of map-like depictions used to illustrate cardiovascular anatomy in medical education. We base these recommendations on the domain requirements we distilled for vessel maps (Section 2) and recurring patterns found in the discussed literature. Also, the lack of quantitative studies can to some degree be substituted with observations from perception studies that involve similar map-like depictions from other contexts, like geospatial data [KMK06, KPSL10] or node-link visualizations [DRSM15].
Identifying domain tasks. The first and crucial step is to consider what the map is for. Which purpose does it serve? Along the lines of typical visualization design studies [OM20, SMM12], we recommend first clearly identifying and abstracting the user tasks that need to be facilitated. Typical motives, which are pursued by all the discussed vessel map approaches, are overview tasks such as identification of features, exploring distributions, or browsing the topology. The usual incentive is to provide a 2D or abstracted view that is better suited for these tasks than overly detailed 3D renderings of the data. Fitting a spatial domain in one picture may inCrease legibility, leading to higher efficiency and/or accuracy in these tasks. We do, however, encourage thinking beyond these aspects. Other tasks that could be facilitated may be contextualization tasks. Where exactly does a feature occur? What are its spatial relations to the cardiovascular structure? What is the surrounding anatomical context? What is the topological context in the vascular network? Also, some maps allow direct quantification. Can data values be quantified directly on the map? For example, can sizes be measured? The map coordinates may serve this purpose if the geometry mapping preserves the relevant properties. There may also be navigation tasks. Could the map be used to navigate another domain? Does it need to represent all necessary information or could it serve as a secondary depiction, along the lines of focus and context? Examples, where this applies, are typically systems with multiple coordinated views. Keep in mind that maps can help navigation in spatial [EMKL21] and temporal [EEL*19] dimensions. Lastly, aiding comparison is also a common purpose for map-like depictions. May the map be a useful asset to compare multiple instances of a domain? These could be an individual before and after treatment or different patients up to cohorts examined in medical research.
Choosing data type and region complexity. Depending on the domain tasks, the appropriate data type and region of interest must be determined. Even for general mapping approaches, it is advisable to think about which specific tasks – they can be abstract – may be facilitated. The common data structures for vessel maps are described in Section 3.1. Define, where specifically the information relevant for the tasks associated with the map is. For example, the data structure could be a vessel tree surface, but if our main interest for the map is to give a topology overview, it may be much more sensible to Create a map based on data encoded on the centerline. Similar considerations should be made regarding the region's complexity. Knowing if a single segment, a tree, or a network is required to accommodate the tasks, enables choosing an appropriate map layout.
Preservation versus standardization. The question of whether to preserve attributes or provide a more consistent, maybe even standardized map, is a core consideration that should be made before any algorithm is implemented. It is closely related to the question of how vigorously the present information should be simplified for the sake of uniformity and legibility. Preservation can refer to geometric proportions. For mesh parameterization, in particular, techniques are generally grouped by their preservation characteristics. A parameterization method may be area-preserving or angle-preserving (conformal) regarding the mapped mesh structure. But in vascular geometry, more general features may also be preserved, like the arc length of individual segments, the diameter of vessels, or the branching angles. Preservation can also refer to the topology of a vessel tree or network. Preserving the branching topology is required for most overview, navigation, and contextualization tasks.
The primary consideration for preserving attributes is that information crucial to a task is retained. For example, a task might be to assess the distribution of a certain attribute, like plaque occurrence, where the size is important to determine the severity. Sometimes, though, preserving the actual data values might not be the ideal approach to facilitate a task. For instance, the variation in the vessel diameter may be important but too small to be visually discernible [EMKL21]. In very specific instances, it might make sense to explicitly exaggerate values to draw attention to points of interest. This possibility should be handled with care and only applied if the quantification of said values is done outside of the map. Another advantage of attribute preservation lies in the inCreased familiarity that the resulting depictions might have. Users may be familiar with the 3D shape of a particular vessel tree and quickly understand and correspond to a map that preserves, e.g., the overall layout.
The core benefit of uniform maps, on the other hand, is that they are more directly comparable. This applies to visual exploration but also algorithmic evaluation. The advantage particularly holds for approaches that attempt to define a standardized map, where map coordinates are fixed to specific cardiovascular substructures. The goal of standardization in vessel maps is often to develop quantifiable biomarkers [CCC16,CCB*22], where threshold values can support clinical decisions.
Layout, geometry, and attribute mapping. Only after these considerations should the actual vessel map be designed. We propose to think of the process in terms of the taxonomy outlined in Section 4 and view the layout, attribute mapping, and geometry mapping as separate steps. If the region complexity is very low, e.g., for a surface patch or vessel segment without branches, the layout step can usually be solved implicitly. If the underlying data is only of the centerline graph type, the layout and geometry mapping are the same step. Mind that, depending on the input graph, the layout algorithm needs to build on either a hierarchical or mixed hierarchy structure. In most cases, general readability principles from network visualization apply, e.g., regarding edge-crossings [Pur97], path continuity [KMV15], and symmetry [LNS85]. As a rule-of-thumb, untangling techniques lie on the preservation end of the abstraction-level scale, while fitting techniques are more applicable if standardization is required. Often intertwined with the layout step, the geometry of the data needs to be mapped. Here, similar rules apply: choose or develop a technique that fits the necessary preservation characteristics and shows the data required to solve the domain tasks. We also recommend paying attention to the algorithmic dependencies. Requiring landmarks or manual cuts may impose additional pre-processing steps, making the technique less viable for broader applications. Depending on the 3D view direction may defeat the advantage that the map gives a single-image overview. Still, this dependency may be useful in some scenarios. For example, a vessel tree may have a “default” viewing direction, like facing the patient, which may be used to construct the map. Lastly, the data attributes need to be visualized on the map. This should be regarded as an individual step in the map design process, as it is distinct from the geometry mapping. An encoding shared with different (3D) representations of the data may inCrease familiarity and visual coherence. However, relying only on familiar encodings might mean that alternatives are overlooked. Common trends are to visualize vessel diameter with a scale/thickness encoding and to visualize scalar fields with a colormap. Categorical colors are sometimes used, for instance, to distinguish subtrees. The use of glyphs is recommended to encode multiple values or more complex information. Furthermore, we encourage thinking about possible combinations of attribute mappings for simultaneous use of multiple visual information channels.
10. Open Challenges
Looking at Table 1, several conclusions may be drawn and possible starting points for future endeavors emerge. The high number of recent works in the flow, wall, and network maps areas evinces that concurrent investigations into vessel maps are ongoing. While many techniques for mapping vascular structures, ranging in complexity from individual segments to highly branched microvasculature networks, have been investigated, some core challenges remain.
Flow volume maps. Map-like visualizations of blood flow, in particular, are underexplored. The core challenge lies in finding a suitable geometry mapping not only for a 2D embedded structure like the vessel wall but also for the internal 3D flow field. To foster an understanding of qualitative flow information in branched structures, abstractions that transfer flow features into a 2D graph layout appear to be a promising direction [THQ*16,ZTWW21].
Network maps. While several mapping techniques for treelike vascular structures have been proposed, only a few approaches exist that handle cyclical graphs and complex microvasculature [GWE*19a, PSY*20]. Current advances in 3D imaging using, e.g., micro-CT or light-sheet microscopy result in inCreasingly complex vascular data. All arteries eventually terminate in interconnected networks and any inCrease in imaging resolution poses a need for network-based algorithms to explore these data.
Temporally resolved data. A further insufficiently examined application area is temporally resolved data spaces. The cardiovascular system is, after all, a spatio-temporal domain that is highly dependent on the cardiac cycle. The possibility of using vessel maps for, e.g., temporal navigation tasks, has only been adopted in very few works [EEL*19, MVG*21, ZTWW21]. Not only blood flow information is temporally resolved, but parts of the cardiovascular system, namely the heart and larger arteries, are also constantly in pulsating motion. How to reproduce the motion on a map or in which cases this would be beneficial, has not been sufficiently investigated.
Data curation. Furthermore, we would like to draw attention to the general challenge of data curation [GSG*21]. In many areas of medical visualization, the applied techniques require data in very specific formats and of sufficient quality to produce adequate results. Vessel maps are no exception. To inCrease the robustness and comparability of techniques, the availability of standardized data sets must be encouraged.
Clinical adoption. Finally, clinical adoption requires either evidence-based quantifiable biomarkers or strong validations through effectiveness evaluations. Both need objective benchmarks to measure the potential benefits of a new method, which are currently rare.
11. Conclusion
We have presented a literature overview of map-like visualizations of the cardiovascular system. To give a structure to the diverse approaches for the Creation of such vessel maps, we have provided a classification centered around the four principal data types used to generate them: medical volume images, blood flow volume meshes, vessel surface meshes, and centerline graphs. Further, we not only clustered the various algorithmic techniques to transfer these data types to a map layout, but we also examined the resulting visualizations in terms of their applicability. For this purpose, we filtered their visual design properties (layout types, encodings), the domain tasks they facilitate, and the dependencies that must be met to use them. Based on the literature review, we discussed considerations that are repeatedly made in the visual analysis of cardiovascular structures and condensed them to recommendations for the design of vessel maps.
Within the general domain of map-like visualizations, vessel maps are schematizations of cardiovascular structures. They emphasize the display of data over anatomical accuracy. Hogräfer et al. [HHS20] identified various techniques for performing schematizations. The majority of vessel maps naturally use either path-centered techniques, if the network structure is focused, or shape deforming techniques, if the aim is to display surface or volume data. Other types of techniques derived from the schematization of cartographic maps might be worth exploring but many are not applicable. After all, vessel maps represent anatomical structures, which means data is typically not organized around, for example, borders. On a high level, vessel maps do, however, share their advantages and limitations with other map-like visualizations. Their benefits include that they are easier to decode than convoluted 3D renderings and features are filtered from irrelevant anatomical context information. Relevant parts of the data are emphasized, fostering an understanding of important relations. A pitfall to avoid is that misinterpretations become possible due to geometric deformations and data abstractions. Therefore, the purpose of the map must be clear. Often, a certain task is well facilitated by the map but it also needs to be complemented by other techniques to provide an actual benefit. Despite persistent challenges, vessel maps prove to be a valuable component in the toolbox of cardiovascular structure analysis. Through domain simplification and standardization, they enable otherwise impractical or impossible visual and algorithmic assessments and are a significant asset for vascular disease monitoring, treatment planning, and research.
Acknowledgements
This project was partially funded by the BMBF Joint Project 05M20SJA-MLgSA. Open Access funding enabled and organized by Projekt DEAL.




