The Diamond Laplace for Polygonal and Polyhedral Meshes
for Polygonal and Polyhedral Meshes
Abstract
We introduce a construction for discrete gradient operators that can be directly applied to arbitrary polygonal surface as well as polyhedral volume meshes. The main idea is to associate the gradient of functions defined at vertices of the mesh with diamonds: the region spanned by a dual edge together with its corresponding primal element — an edge for surface meshes and a face for volumetric meshes. We call the operator resulting from taking the divergence of the gradient Diamond Laplacian. Additional vertices used for the construction are represented as affine combinations of the original vertices, so that the Laplacian operator maps from values at vertices to values at vertices, as is common in geometry processing applications. The construction is local, exactly the same for all types of meshes, and results in a symmetric negative definite operator with linear precision. We show that the accuracy of the Diamond Laplacian is similar or better compared to other discretizations. The greater versatility and generally good behavior come at the expense of an increase in the number of non-zero coefficients that depends on the degree of the mesh elements.
1. Introduction
Discrete Laplace operators are an important tool in geometry processing, for surface as well as volumetric meshes [SCV14]. In many graphics applications, the mesh is given and not altered throughout interaction and processing. It provides the natural domain for discretizing differential operators. We dare say that, unlike in scientific computing, in graphics and geometry processing we fit the operator to the mesh rather than optimizing the mesh for solving the differential equation. Depending on the application, these meshes may contain different types of elements, such as triangles, quads, and general polygons for surface meshes, or tetrahedra, hexahedra, and general polyhedra for volumetric meshes.
If the mesh happens to be composed entirely of triangles or tetrahedra, the one operator that is used almost exclusively in geometry processing is the cotan Laplacian [PP93, MDSB03, DMSB99, Dzi88]. For surface meshes composed of higher order elements, i.e. polygons, possibly non-planar, there are several generalizations that reduce to the cotan Laplacian for triangle meshes [BHKB20, dGBD20,AW11,HKA15]. For volumetric meshes, besides tetrahedral elements [AHKSH20, Cra19], most other discretizations are based on hexahedra [SDG∗19]. There are only few approaches for more general polyhedral meshes and they typically require numerical integration to obtain the basis functions for each element [WBG07,MKB∗08,KBT17,MRS14].
In this paper we propose a simple and unified construction of gradient, divergence, and Laplace operators for general polygonal and polyhedral meshes. Our main idea, following the Discrete Duality Finite Volume approach (DDFV, Section 4), is to incorporate the primal as well as the (typically non-orthogonal) dual mesh and accommodate the oblique intersection of primal and corresponding dual elements. Specifically, we define discrete gradients, respectively divergences, per diamond: the region spanned by a dual edge and corresponding simplicial primal element. In 2D, the corresponding primal element is an edge; in 3D it is a triangle. If facets have degree higher than three, we insert an additional virtual vertex and in this way triangulate the facet. In all cases, the primal element is incident on two cells, and the dual vertices in these cells define two simplices. In other words, in 2D a diamond is spanned by two triangles; in 3D it is spanned by two tetrahedra.
In the spirit of the original mesh defining the domain for discretization we also want that the Laplace operator maps from values at vertices to values at vertices. We achieve this by combining the DDFV approach with the “sandwiching” of Bunge et al. [BHKB20]. This means all vertices except the primal ones are virtual: They are defined as affine combinations of primal vertices. These affine combinations are encoded as prolongation matrices and multiplied onto the DDFV Laplacian, thereby effectively hiding from the user the involved diamonds and virtual vertices.
The resulting construction is comparatively simple and seamlessly generalizes from arbitrary polygons (Section 5) to arbitrary polyhedra (Section 6). We discuss properties like locality, linear precision, semi-definiteness, the kernel, and the maximum principle in Section 7. The prolongation matrices lead to a decreased sparsity, resulting in increased computation cost. A range of numerical experiments (Section 8) suggests that the effort is well-spend: The accuracy is, in most cases, at least as good and even better than other constructions.
2. Problem Statement
We assume a mesh is given. The particular types of meshes we consider are two-dimensional surface meshes immersed in 3D and volumetric meshes embedded in 3D. Because they are most common, we focus here on the gradient, the divergence, and the Laplacian resulting from taking the divergence of the gradient.
We denote edges by tuples (i, j), triangles by (i, j, k), and tetrahedra by (i, j, k, l), and use ‖(i, j)‖, |(i, j, k)|, and |(i, j, k, l)| to refer to their length, (signed) area, and (signed) volume, respectively. We use the operator ∗ to map between primal and dual entities, such that, e.g., ∗i denotes the dual region of a vertex i and ∗(i, j) denotes the dual edge of the primal edge (i, j).
Given a polygonal or polyhedral mesh with vertices 𝜈, edges ℰ, faces ℱ, cells 𝓒, and diamonds 𝓓, our aim is to generate the following matrices, representing discrete linear approximation of differential operators:
• The gradient G ∊ ℝd·|𝓓| × |𝜈|, where d ∊ 2, 3 is the intrinsic dimension of the mesh and |𝓓| is the number of diamonds to which the operator assigns constant gradients.
- The divergence D ∊ ℝ|𝜈| × d·|𝓓|, which we assume to be constructed as D = GTM⋄. Here, M⋄ ∊ ℝd·|𝓓| × d·|𝓓|“ is a diagonal matrix containing d-times the diamond masses.
- The operator matrix for the Laplacian is then constructed as –DTG = L ∊ ℝ|𝜈| × |𝜈|.
This construction ensures that the discrete operator is symmetric negative semi-definite. These properties are commonly considered desirable. In addition, we ask that the Laplacian operator maps constant vectors to zero and has linear precision, i.e. maps linear functions to themselves. For more information on these and potential additional properties we point the reader to the excellent discussion by Wardetzky et al. [WMKG07].
3. Related Work
The literature on discretizations of differential operators is vast. In computer graphics and geometry processing, discretizations based on the finite element method (FEM) and discrete exterior calculus (DEC) are most frequently used, with the cotan Laplacian for triangle meshes [PP93, MDSB03, DMSB99, Dzi88] and tetrahedral meshes [AHKSH20, Cra19] being the most prominent operator. Since our goal is a Laplacian operator for general polygonal surface meshes or general polyhedral volume meshes, we focus our discussion on operators that are not restricted to standard triangle/tetrahedral or quadrangle/hexahedral meshes.
There have been a couple of approaches for discretizing differential operators on polygonal meshes. These methods have to handle the problem that non-planar polygons do not bound a canonical surface in 3D. Alexa and Wardetzky [AW11] circumvent this problem by considering the projection of the polygon resulting in the largest area, combined with a MFD-based inner product stabilization [BLS05]. A drawback of this discretization is that it requires the suitable choice of a scalar parameter, and that the potentially large number of negative entries in the Laplacian matrix violates the discrete maximum principle [WMKG07].
Herholz et al. [HKA15] extend the definition of desirable properties of discrete Laplacians to polygon meshes, where they characterize polygon tessellations that admit a “perfect” operator with only non-negative weights. Sharp et al. [SSC19] handle potentially non-planar polygons by deriving a version of the “connection” Laplacian, which, in contrast to the standard expression as the divergence of the gradient, is given by the trace of the second covariant derivative. This operator fulfills many of the same properties as the cotan Laplacian and enables the diffusion of vectors from one tangent space to another on curved domains.
De Goes et al. [dGBD20] go beyond the Laplace operator and generalize a whole set of discrete differential operators to general polygonal meshes. They extend the approach of [AW11] by defining a new discrete gradient operator, which can be interpreted as a generalization of mimetic finite differences [BLS05] and the virtual element method [dVBM13]. Using the weak form of the cogradient operator and the divergence theorem, they bypass the need for an interpolation of the non-planar polygon surface. Bunge et al. [BHKB20] adapt the virtual node method [DLN07,TWZZ09] to polygon meshes by refining each face with a virtual vertex to span an implicit triangle fan, on which they apply the standard cotangent Laplacian. These virtual vertices are removed from the differential operators using special prolongation/restriction matrices. We make use of their idea of virtually refining the mesh and also use similar prolongation matrices, but use different, finite-volume-based discrete operators on the virtually refined mesh.
An alternative use of prolongation/restriction matrices was proposed by de Goes et al. [dGDMD16]. Their Subdivision Exterior Calculus (SEC) combines the Laplacian operator introduced by [AW11] with prolongation matrices corresponding to Catmull-Clark or Loop subdivision. Similar to our work, the prolongation results in a larger stencil for the discrete differential operators. However, SEC was designed to work on the geometry of the limit surface of the subdivision process, and hence is not suitable for computing directly on the user-provided polygon mesh.
While there is a certain variety of approaches for polygonal surface meshes, we are not aware of simple discrete differential operators for polyhedral volume meshes. Early works in computer graphics extended conforming FEM frameworks by using generalized barycentric coordinates [HS17] as custom shape functions for polyhedral elements, using either mean value coordinates [WBG07], harmonic coordinates [MKB∗08, SDG∗19], or maximum entropy coordinates [HS08]. This idea, which is also common in the computational mechanics literature [MRS14], has the drawback that both the computation and the numerical integration of these custom shape functions is rather complex and computationally expensive. These methods do therefore not meet our goal of a simple Laplacian operator for polyhedral domains.
We believe that finite volume (FV) discretizations [Dro14], in particular the Discrete Duality Finite Volume (DDFV) method [Her00, DO05, Her09, CH11], offer an interesting alternative to deriving discrete differential operators for geometry processing applications. As our approach is inspired by and extends upon DDFV, we describe this approach in more detail in the next section.
4. Finite Volume Discretizations
Finite Volume (FV) methods are based on the idea to consider the integral of a differential in a small region. There exist a number of identities that allows expressing such integrals of a differential as an integral over only the boundary of the region. For the divergence of a vector-valued function u over a flat two-dimensional region Ω we have
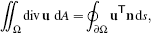 (1)
(1)where n is the outward normal along the boundary ∂Ω. For u = uc with constant vector c and a scalar function u we can exploit the “product rule”
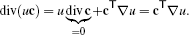 (2)
(2)Plugging this into the divergence theorem above for c = ek (the canonical unit vectors) and combining the results we find the vector-valued identity
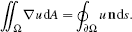 (3)
(3)Applying the divergence theorem to the vector field ∇u we get
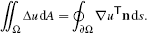 (4)
(4)All identities straightforwardly extend to higher dimensions.
The basic derivation of the Laplace operator with FVs in 2D makes the assumption that the mesh is Delaunay. This means the dual mesh is the Voronoi diagram, such that primal and dual edges are orthogonal. Consider a vertex i with position xi, the dual region associated to it is its Voronoi cell Ωi. The function values of the unknown piecewise linear function u at vertex i are ui = u(xi). For the integrated Laplacian over the region Ωi, the boundary ∂Ωi is piecewise linear and consists of the dual edges ∗(i, j), with j ∊ N(i) denoting the one-ring neighbors of vertex i. If we denote by eij = xj – xi and 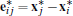 the primal/dual edge vectors, respectively, and exploit that the normal n on the dual edge ∗(i, j) is parallel to eij and that the gradient of the piecewise linear function on the vertices points along this edge, we get
the primal/dual edge vectors, respectively, and exploit that the normal n on the dual edge ∗(i, j) is parallel to eij and that the gradient of the piecewise linear function on the vertices points along this edge, we get
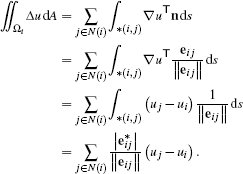 (5)
(5)The last expression directly describes the construction of a linear operator that maps values at vertices {ui} to the integral over the region associated to vertex i of the Laplacian. Note that the (i, j) entry in the matrix L is given by the (signed) length of the dual edge divided by the length of the primal edges. One obtains exactly the same result with the DEC approach [Hir03], which is based on similar arguments. Interestingly, also the Finite Element Method applied to triangles leads to these weights [PP93]. This suggests that the derivation extends to arbitrary triangulations, albeit carefully assigning signed lengths to the dual edges. The resulting negative coefficients for edges without the Delaunay property have undesirable consequences (see, for example, the discussion in [SSC19]). While this is often accepted for applications in graphics, in the FV community it is not considered admissible, which restricts the meshes to be (weighted) Delaunay. From a practical perspective, however, one is often given a mesh and it is costly to generate an orthogonal dual, if one exists [Aur87, Ale20].
Discrete Duality Finite Volume (DDFV)
The FV method that deals with this problem is to give up orthogonality. Rather, the idea is to construct a gradient operator and associate it to the region spanned by a pair of a primal edge (with endpoints x1 and x2) and its corresponding dual edge (with endpoints xl and xr). This region, depicted in Figure 1, is called a diamond.
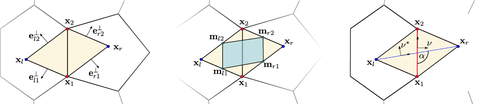
Different formulae and interpretations of the per-diamond gradient in 2D DDFV. Left: The vectors 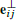 orthogonal to the diamond edges eij needed to compute our gradient for the diamond cell. Center: The midpoints mij of the diamond edges and their enclosed subarea. Fitting an affine function to the function values at these midpoints is another possibility to obtain the 2D derivation of the diamond gradient. Right: Constructing gradients from primal and dual axes v, v∗ and their enclosed angle α.
orthogonal to the diamond edges eij needed to compute our gradient for the diamond cell. Center: The midpoints mij of the diamond edges and their enclosed subarea. Fitting an affine function to the function values at these midpoints is another possibility to obtain the 2D derivation of the diamond gradient. Right: Constructing gradients from primal and dual axes v, v∗ and their enclosed angle α.
Notice that a diamond is always a quadrilateral, regardless of the degree of the faces. The DDFV approach is to associate function values ul and ur to the dual vertices - thereby introducing a second set of degrees of freedom - and to associate a constant gradient with the diamond. As shown in Figure 1, left, we denote by D the diamond built from the four points (x1, x2, xl, xr), by (i, j) ∊ D its edges, and by eij = xj – xi the edge vectors. Making use of Stokes' theorem gives
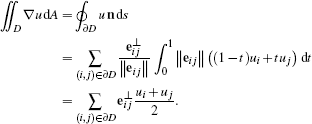 (6)
(6)For the discrete gradient of the diamond we take the mean over the region, so we have to divide the integral by the area |D|, leading to
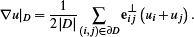 (7)
(7)The literature on DDFV [Her00, DO05, Her09, CH11] provides different derivations for the per-diamond gradient ∇u|D and several interpretations and corresponding formulae:
-
Fitting the gradient to directional derivatives along the primal and dual edges:
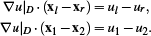 (8)
(8) - Fitting an affine function w(x, y) to the function values uij = ½(ui + uj) at the midpoints mij = ½(xi + xj) of the four diamond edges (i, j) ∊ ∂D, and taking the gradient ∇w of this affine function (see Figure 1, center). Note that fitting an affine function to the four diamond vertices is an over-determined problem, while the midpoint fit is uniquely determined.
-
A formulation based on the primal/dual axes v = (x2 – x1)⊥ / ‖x2 × x1 ‖ and v∗ = (xr – xl)⊥ / ‖xr × xl ‖ as well as their enclosed angle α (Figure 1, right):
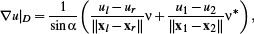 (9)
(9)
Although these formulations are all equivalent, we believe our formulation (6) to be more intuitive when handling boundary cases and when generalizing to polyhedral meshes in Section 6. For boundary edges, the diamond consists of a single triangle (x1, x2, xl) only. The typical DDFV approach is to replace xr by the edge midpoint ½(x1 + x2) and to properly deal with degenerate edges/faces. In contrast, our formulation (7) remains unchanged.
The divergence div u and the Laplacian Δu = div ∇u can be obtained through very similar derivations. The resulting DDFV gradient operator maps from function values at primal and dual vertices to gradients at diamonds, the divergence operator from vectors at diamonds to scalars at primal/dual vertices. The DDFV Laplacian therefore maps functions values at primal/dual vertices to their Laplacians sampled at primal/dual vertices.
5. Diamond Laplace for Surface Meshes
In its standard formulation, the DDFV operators are not directly useful for applications in computer graphics and geometry processing, since they have two main drawbacks: First, by introducing function values at dual vertices it significantly increases the number of degrees of freedom (DoF) to be solved for. For instance, the DoFs are roughly tripled for triangle meshes and roughly doubled for quad meshes. Second, the approach is defined for planar 2D meshes only, but not for two-manifold surface meshes embedded in 3D, which we are mostly interested in.
In this section we address both problems. Replacing the extrinsic per-diamond gradient by a version that is intrinsic w.r.t. the polygonal mesh allows us to generalize the 2D DDFV scheme to embedded surface meshes (Section 5.1). Following Bunge et al. [BHKB20] and representing the dual DoFs as interpolations of the primal DoFs and incorporating this through special prolongation/restriction matrices will remove the dual DoFs and eventually keep only the primal ones.
5.1. Intrinsic Gradient
Compared to mesh faces, diamonds are the better entity to associate gradients with, since for general polygonal meshes higher-degree faces might not be planar and typically cannot be flattened without introducing distortion. Diamonds spanned by a pair of primal vertices x1, x2 and dual vertices xl, xr are not necessarily planar in the 3D embedding, but can be isometrically unfolded into the plane around their primal “hinge” edge (x1, x2). We can therefore represent the diamond in an intrinsic 2D coordinate system, which allows us to then directly apply the gradient construction of (7).
It is convenient to choose the primal edge as the first coordinate axis, i.e.,
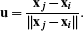 (10)
(10)The second coordinate axis has to be orthogonal to this axis, contained in the planes spanned by the two triangles (x1, x2, xl) and (x2, x1, xr), and consistently oriented w.r.t. u. We achieve this by projecting the edges (1, l) and (1, r) onto the orthogonal complement of the first axis u and normalizing the result:
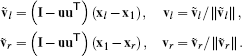 (11)
(11)Notice that both directions vl and vr are consistently oriented, are intrinsically in one plane, and form an orthonormal frame with u. In this frame, the 2D coordinates of the four diamond vertices are
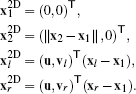 (12)
(12)These 2D coordinates can now be used in the gradient construction of Equation (7), yielding an intrinsic 2D gradient per diamond.
From (7) we can then directly read off the the entries for the diamond's gradient operator matrix GD ∊ ℝ2 × 4 by noticing that the value i depends only on the two diamond edges incident on it. Therefore, the i-th column of GD is
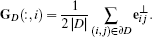 (13)
(13)The matrix Ĝ for the global gradient operator, mapping from function values at primal and dual vertices to gradients at diamonds, is then assembled from all diamond gradient matrices
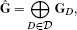 (14)
(14)where ⊕ is the assembly operator that scatters and accumulates the entries of the local matrices into the global matrix.
5.2. Dual Vertices as Affine Combinations
Our approach to remove the dual DoFs from the DDFV formulation is inspired by Bunge et al. [BHKB20], who also introduce dual vertices into primal faces, but represent their position and function values as affine combinations of the positions/values of the face's vertices.
Consider a general polygonal face f with n vertices xi, i ∊ f. We construct the dual face point xf, which takes the role of xl or xr in the gradient construction described above, as an affine combination of the face vertices
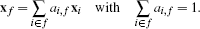 (15)
(15)The dual DoFs, i.e., the function values at dual face vertices xf, are then represented in terms of the primal DoFs by the same affine combination:
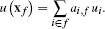 (16)
(16)For a polygonal mesh with |𝜈| vertices and |ℱ| faces, this construction can be packed into an (|𝜈| + |ℱ|) × |𝜈| prolongation matrix P with entries
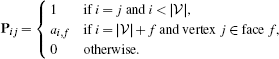 (17)
(17)Combining the gradient matrix (14) and the prolongation matrix (17) yields our gradient operator for polygonal meshes
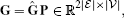 (18)
(18)where |ℰ| denotes the number of edges (and therefore of diamonds) in the mesh. This matrix maps scalar function values ui at primal vertices to 2D intrinsic gradient vectors ∇u|D at diamonds.
While for standard FV methods with orthogonal duals the dual point xf is the circum-center of triangle f, the canonical choice for general polygonal meshes in the DDFV literature [Her00, DO05, Her09,CH11] is the face's barycenter. However, as the barycenter is not necessarily inside a non-convex (planar) face, we instead follow [BHKB20] and compute xf (respectively its affine weights ai,j) by minimizing the sum of squared triangle areas
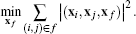 (19)
(19)For a face f with n vertices this minimization requires solving a small n × n linear system (see [BHKB20] for details) and indeed yields more accurate results than other point choices in case of non-convex polygons (see Section 8).
5.3. Divergence and Laplacian
With the intrinsic gradient (18) in place, we can now define the discrete divergence and Laplacian. The DDFV discretization of the divergence operator leads to a matrix 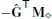 , which we combine with the transposed prolongation (or restriction) matrix to get the diamond divergence matrix
, which we combine with the transposed prolongation (or restriction) matrix to get the diamond divergence matrix
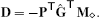 (20)
(20)Here, 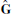 is the gradient matrix of (14) and M⋄ is a 2|ℰ| × 2|ℰ| diagonal matrix with the area |Di| of diamond Di in its entries (2i, 2i) and (2i + 1, 2i + 1). This operator maps intrinsic 2D vectors at diamonds to scalar values at primal vertices.
is the gradient matrix of (14) and M⋄ is a 2|ℰ| × 2|ℰ| diagonal matrix with the area |Di| of diamond Di in its entries (2i, 2i) and (2i + 1, 2i + 1). This operator maps intrinsic 2D vectors at diamonds to scalar values at primal vertices.
The (integrated) diamond Laplace operator is finally defined as the diamond divergence of the diamond gradient, i.e.,
 (21)
(21)and maps from vertices to vertices. The pointwise Laplacian is obtained as M–1 L by multiplying with the inverse of the mass matrix M. This mass matrix is defined as
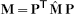 (22)
(22)from the standard DDFV diagonal mass matrix 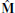
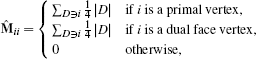 (23)
(23)which assigns to the four (primal and dual) vertices of a diamond one fourth of its area. The “sandwiching” with PT and P distributes the mass from primal and dual vertices to the primal vertices only. Note that the sandwiching leads to a non-diagonal mass matrix M. We avoid lumping this matrix to a diagonal matrix, since numerical results have shown that the initial matrix leads to higher accuracy of our operator. Notice that in above construction, the dual points do not have to be inserted into the mesh explicitly, nor do the matrices  have to be built explicitly. Instead, the matrices G and M can directly be constructed through a diamond-based matrix assembly, which implicitly computes the virtual vertices and their affine weights, similar to the construction of Bunge et al. [BHKB20].
have to be built explicitly. Instead, the matrices G and M can directly be constructed through a diamond-based matrix assembly, which implicitly computes the virtual vertices and their affine weights, similar to the construction of Bunge et al. [BHKB20].
6. Diamond Laplace for Volume Meshes
One particular advantage of our diamond Laplace is that it can be generalized to 3D polyhedral meshes in an intuitive and consistent manner. Given a general polyhedral mesh with vertices 𝜈, edges ℰ, faces ℱ, and cells 𝓒, we will define diamonds 𝓓 from primal and dual vertices. The starting point of our construction is the generalization of the (integrated) gradient of a function u over a diamond. Analogous to the 2D case, given the gradient operator G, we also have a divergence operator D and can then assemble the Laplacian L = DG. Representing the dual vertices as affine combinations of primal vertices will again define the sandwiching operator PT(·)P that removes the dual DoFs. In the following we provide the details of these steps, in particular where they deviate from the case for surface meshes.
6.1. Integrated Gradient
Before we focus on the particular shape and construction of the diamonds, we derive the integral of the gradient (and, by analogy, divergence) for an arbitrary region Ω bounded by a triangulated surface. We assume the function over the triangulated boundary to be linear on the triangles, defined by values ui at vertices i. If the triangles are given as triples of indices (i, j, k) ∊ ∂Ω, we get
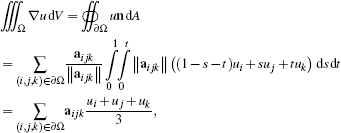 (24)
(24)where
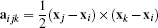 (25)
(25)is the area vector of triangle (i, j, k), i.e., the vector pointing in outward normal direction and with magnitude equal to the area of the triangle (see Figure 3, left). Taking the mean over the region by dividing the integral by the volume |Ω| leads to
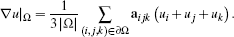 (26)
(26)The local gradient operator for the region Ω, mapping values at the vertices i ∊ ∂Ω to a constant 3D gradient vector, is then built in a column-wise manner as
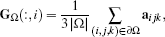 (27)
(27)which is consistent with the 2D version of Equation (13).
6.2. Diamond Rings and Minimal Diamonds
The canonical choice for a diamond in a volumetric mesh would be associated with a dual edge (l, r) with endpoints xl, xr. These two dual vertices, together with the primal vertices x1, x2, …, xn of the face f =∗(l, r) that is dual to (l, r), define a region that is bounded by two triangle fans spanned by xl or xr and two neighboring vertices xi, xi + 1 of the face f. Given that the integrated gradient can be computed easily for this region as shown above, it may be tempting to assign a gradient to each such diamond (as done in [Her09]). Yet, similar to other constructions for non-simplicial meshes [AW11, dGBD20], constructing the gradient, divergence, and Laplacian in this way and then sandwiching the resulting matrices leads to spurious modes, i.e., a Laplacian operator with more than the constant functions in its kernel. This would be a serious drawback, and is a known limitation of the CeVe DDFV method [Her09], as discussed for instance in [ABH13].
Since we are adding a dual vertex to each cell, all vertices in a cell become connected in the operator. Consequently, adding a dual vertex xf to each face f introduces no additional non-zeros in the operator. Based on this virtual face vertex, the diamond is decomposed into a ring of diamonds, where each individual diamond is minimal, i.e., consists of two tetrahedra with tips xl, xr and a base triangle (xi, xi + 1, xf), as shown in Figure 2. Basing the construction in these minimal elements ensures that the kernel of the Laplace operator only contains the constants.
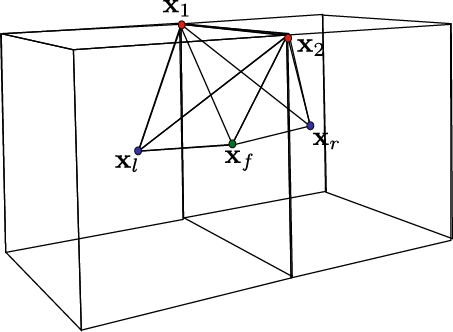
A minimal diamond spanned by two cell points xl, xr, a face point xf, and a primal edge x1, x2.
Incidentally, minimal diamonds are the right analogy to 2D diamonds, in the following sense: Consider a minimal diamond defined by xl, xr and (x1, x2, x3) and the midpoints of the 6 edges emanating from xl and xr (see Figure 3, right):
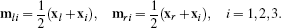 (28)
(28)
For a minimal diamond consisting of two tetrahedra, the gradient can be computed from the area vectors aijk of its faces (left) or by fitting an affine function to edge midpoints mij (right).
We observe that these six midpoints form a parallelotope:
- The two triangles (ml1, ml2, ml3) and (mr1, mr2, mr3) are parallel to the triangle (x1, x2, x3), in fact, translates scaled by a factor of ½.
- The quad ml1, mr1, mr2, ml2 is a planar parallelogram, and likewise for the other two quads. All edges mli – mri connecting corresponding points on opposite sides are copies of the vector xl – xr, scaled by a factor of ½.
This means any two edges of the triangle (x1, x2, x3) together with the vector xl – xr span the linear part of the affine space defined by the six points. Hence, an affine function can uniquely be fitted to these midpoints - analogously to the 2D parallelogram version show in Figure 1, center - and the gradient of this function can be used as the diamond gradient (giving the same result as (27)).
6.3. Dual Vertices as Affine Combinations
There have been several extensions of the DDFV scheme to volumetric meshes, see Hubert and colleagues [CH11, ABHK12] for a good overview. Most 3D DDFV methods define the gradient on minimal diamonds, as proposed above, but require the insertion of additional vertices (and their associated DoFs) per cell, face, and edge, thereby significantly increasing the number of degrees of freedom. Our construction requires virtual vertices per cell and face only, but their DoFs are eventually removed by the sandwiching operator.
Analogous to the surface case, we first insert for each face the point that minimizes the sum of squared triangle areas (see Equation (19)), turning each face into a fan of (virtual) triangles. For a polyhedral cell c, the virtual point xc is then computed to minimize the sum of squared tetrahedron volumes:
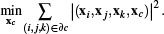 (29)
(29)For a cell c with m vertices (consisting of primal vertices and virtual face vertices), the above minimization requires to solve an m × m linear system for the affine weights defining xc.
This two-step sandwiching procedure results in two prolongation matrices PF and PC for inserting face and cell points, respectively, which are then combined to the prolongation matrix
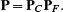 (30)
(30)6.4. Gradient, Divergence, Laplace
The global gradient operator 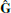 , mapping values at primal vertices and dual face/cell points, is again constructed by assembling per-diamond gradient matrices GD, and is then combined with the prolongation matrix to yield G
, mapping values at primal vertices and dual face/cell points, is again constructed by assembling per-diamond gradient matrices GD, and is then combined with the prolongation matrix to yield G
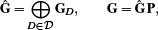 (31)
(31)where ⊕ again is the matrix assembly operator. Following the 2D derivation, the divergence and Laplacian operators for polyhedral meshes become
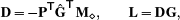 (32)
(32)with a diagonal matrix M⋄ containing diamond volumes. The mass matrix 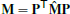 , required for the point-wise Laplacian M–1L, is defined in terms of the diagonal matrix
, required for the point-wise Laplacian M–1L, is defined in terms of the diagonal matrix 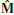 , which distributes the volumes of the (minimal) diamonds D to the primal vertices, face vertices, and cell vertices:
, which distributes the volumes of the (minimal) diamonds D to the primal vertices, face vertices, and cell vertices:
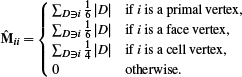 (33)
(33)Analogous to the surface construction, we avoid lumping the mass matrix and instead work with the non-diagonal matrix M.
7. Properties
We analyze the properties of our Diamond Laplacian with respect to the criteria listed in [WMKG07].
Symmetry, Definiteness By construction, the Diamond Laplacian 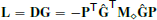 is a real-valued symmetric negative semi-definite matrix, since the diagonal matrix M⋄ (containing diamond areas/volumes) is symmetric positive definite.
is a real-valued symmetric negative semi-definite matrix, since the diagonal matrix M⋄ (containing diamond areas/volumes) is symmetric positive definite.
Linear Precision If the mesh is flat, i.e., a polygon mesh embedded in a plane, respectively a polyhedral mesh embedded in 3D, then we expect that the discrete Laplacian vanishes on linear functions away from the boundary of the domain. The DDFV gradient G of a linear function over a closed region with polygonal or polyhedral boundary reproduces the constant gradient of this function.
The divergence operator 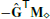 is exact on the resulting constant vector fields, leading to linear precision of the DDFV Laplacian
is exact on the resulting constant vector fields, leading to linear precision of the DDFV Laplacian 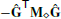 [DO05, Her09, CH11]. The sandwiching PT(·)P preserves this linear precision [BHKB20].
[DO05, Her09, CH11]. The sandwiching PT(·)P preserves this linear precision [BHKB20].
Null-Space The Diamond Laplacian has a one-dimensional kernel containing only the constant functions. It is obvious that constant functions are sufficient for the gradient to vanish, implying that they are in the kernel of the Laplacian. It remains to show that constant values are necessary for the gradient to vanish.
We explain the situation for minimal diamonds in 3D - the case for surface meshes works analogously. The gradient of a minimal diamond can be interpreted as the gradient of the affine function interpolating the values on the edge midpoints mli, mri, i = 1, 2, 3 (Section 6.2). For these values to be identical it is necessary that (i) the values at x1, x2, and x3 are identical and (ii) the values at xl and xr are identical. Because the mesh is connected, it follows that the values at all primal vertices and at all dual vertices need to be identical. Notice that this argument cannot be extended to diamonds with a non-triangular base: If the base is a polygon with more than three vertices already the gradient within this polygon may vanish for non-constant values on the vertices. This problem for diamonds with non-triangular base has also been described in the DDFV literature (cf. [ABH13]).
It remains to explain why the constant values on primal vertices and the constant values on dual vertices are identical. In our setup this follows directly from the fact that values on dual vertices are affine combinations of the values in primal vertices. In other words, while 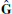 may have a two-dimensional kernel, the kernel of
may have a two-dimensional kernel, the kernel of 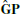 is guaranteed to contain only the constant functions. As long as the diamond mass matrix M⋄ has full rank this implies that also L has the desired kernel.
is guaranteed to contain only the constant functions. As long as the diamond mass matrix M⋄ has full rank this implies that also L has the desired kernel.
Lastly, note that the DDFV literature only considers meshes with boundary, where values on primal and dual vertices are connected through identification on boundary edges. In this case, 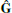 already has the desired kernel [ABH13]. For meshes without boundary this fails. Our sandwiching approach rectifies the situation.
already has the desired kernel [ABH13]. For meshes without boundary this fails. Our sandwiching approach rectifies the situation.
Locality The Diamond Laplacian is local, but less local than related existing schemes, since the diamond gradient couples neighboring cells and the sandwiching couples all primal vertices incident on a cell. For simplicial meshes, the cotan Laplacian of a vertex i depends on all vertices sharing an edge with i. For the polygonal Laplacians [AW11, BHKB20, dGBD20] it depends on all vertices sharing a face with i. For the Diamond Laplacian it depends on the vertices of (i) the cells incident on vertex i and (ii) the cells sharing a face with these cells. This set is larger than the vertices in the edge-based or cell-based one-ring neighborhood, but generally smaller than edge-based two-ring neighborhood. For instance, on a regular triangle mesh the Laplacian of vertex i depends on 12 neighbors, which is in between the 6 and 18 vertices of the one-ring and two-ring neighborhoods, respectively (see inset figure).
Maximum principle The maximum principle for discrete Laplace operators is commonly derived from the sign structure of the operator matrix. If the diagonal elements are all negative and the off-diagonal elements are all positive, then the operator is an M-matrix, implying the maximum principle. The sign of the off-diagonal entries in L depends on the input mesh, and like other Laplacians the Diamond Laplacian, in general, has no maximum principle. A Delaunay triangle mesh guarantees the desired signs for the coefficients of the cotan operator. For Delaunay tetrahedral meshes, the cotan operator has no maximum principle. The DEC construction does provide the maximum principle for Delaunay meshes, but may lack semi-definiteness if the mesh is not Delaunay [AHKSH20]. The Diamond Laplacian, in contrast, has no maximum principle even for Delaunay triangle or tetrahedral meshes.
8. Results
We evaluate the Diamond Laplacian in a variety of geometry processing operations for both volume and surface meshes. We focus our presentation of results on quantitative tests, in particular on comparisons to other constructions for non-simplicial meshes.
8.1. Surface Meshes
On surface meshes, we compare our Diamond Laplacian to the polygon Laplacians of Alexa and Wardetzky [AW11], Bunge et al. [BHKB20], and de Goes et al. [dGBD20]. According to the recommendation of the original authors, we chose the involved hyper-parameters as λ = 2 for [AW11] and λ = 1 for [dGBD20].
Mean Curvature When applied to the coordinate function of the surface mesh, the Laplace operator yields an approximation of the integrated mean curvature vector. We approximate the point-wise mean curvature H at a vertex i as
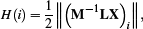
as visualized for a triangle mesh and a general polygon mesh in Figure 4. Quantitative comparisons to other methods are provided in Figure 5, where we compare root-mean-square errors (RSME) on different tessellations of the unit sphere. Since the convergence of point-wise mean curvatures under refinement is not guaranteed and depends on the type of tessellation, we restrict our evaluation to tessellations for which we observe convergence. The Diamond Laplacian generally yields the lowest errors for triangle and quad meshes, and is only bested on hexagon meshes, where it comes second. Note that in contrast to the polygon Laplacians by [AW11, BHKB20,dGBD20], the Diamond Laplacian does not reduce to the cotan Laplacian in case of triangle meshes, but instead provides a more accurate discretization.

Color-coded absolute mean curvature for two different tessellations computed with the Diamond Laplacian (left: hexagon-dominant, right: triangles). The results are visually identical.
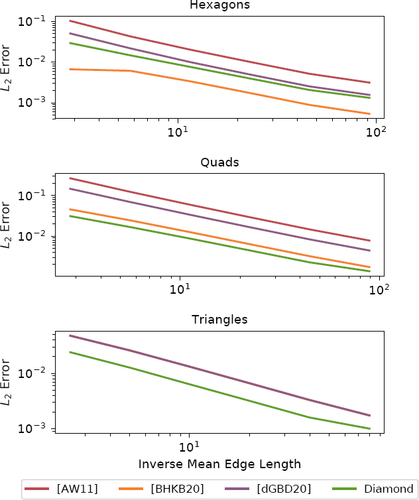
Root-mean-square error of absolute mean curvatures in log-log scale for different tessellations of the unit sphere. The different tessellation types are depicted in Figure 9.
Geodesic in Heat The heat method of Crane et al. [CWW13] approximates geodesic distances from a vertex i to every other vertex. Since the gradient and divergence operators are directly involved in several computation steps, the gradient defined on the diamonds makes the application of this method natural.
An important parameter in the heat method is the time step used for heat diffusion. While Crane et al. [CWW13] suggest the mean edge length squared, a more conservative choice is the square of the maximum edge length [dGDMD16], which we used in our experiments. A qualitative comparison of the distances on different tessellations is shown in Figure 6. The quantitative evaluation displayed in Figure 7 shows the results for different tessellations of the unit sphere (higher-resolution versions of the sphere meshes depicted in Figure 9). The errors are based on the analytical values of the great-circle distance. With few exceptions, the Diamond Laplacian yields the lowest errors. This is a good indicator for the quality of the gradient and divergence operators defined on diamonds compared to other constructions.

Geodesic distances obtained with the Diamond Laplacian, being visually identical despite different tessellations.
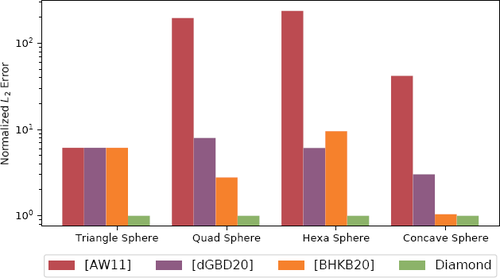
Root-mean-square error of geodesic distances for different tessellations of the unit sphere.
We also evaluated the accuracy of the Diamond operator constructed by placing dual vertices xf at face centroids instead of the minimizer of the squared triangle areas. While the centroid is typically employed in the DDFV literature, its performance on non-convex tessellations (similar to the L-plane and Tetris meshes used in [BHKB20]) yields worse results than the area minimizer, since flipped triangles lead to unfavorable diamond cells, which in turn reduce the overall performance of the operator.
Poisson Problems We also analyze the performance of the Diamond Laplacian for Poisson equations Lu = Mb on different tessellations of the unit square, and compare it to existing approaches. We employ two different Dirichlet boundary conditions b:
-
The Laplacian of Franke's test function [Fra79]
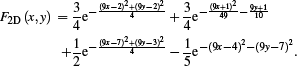
We then measure the deviation of the reconstruction from the true function values.
-
The values of the scaled spherical harmonic function
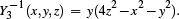
We then measure the deviation of the reconstruction from the input
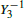 divided by the corresponding eigenvalue λ = 12.
divided by the corresponding eigenvalue λ = 12.
As can be seen in Figures 8 and 9, the Diamond Laplacian has the expected convergence rate and provides lower errors than other discretizations for the majority of test cases. For triangle meshes, the Diamond Laplacian performs favorably for both problems and is more accurate than the cotangent operator, to which the polygon Laplacians of [AW11, BHKB20, dGBD20] reduce.

L2 error in log-log scale of the Poisson system solved for Franke's test function on planar grids with triangles (left), quads (center left), Voronoi cells (center right), and concave faces (right). On triangle meshes, the operators [AW11, BHKB20, dGBD20] reduce to the cotangent Laplacian and hence yield the same results.

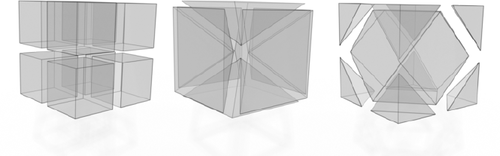
L2 error in log-log scale of the Poisson system solved for the scaled real-valued spherical harmonic function 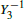 (x, y, z) on differently tessellated unit spheres: Triangles (left), quads (center left), Hexagons (center right), and concave faces (right). On triangle meshes, the operators [AW11, BHKB20, dGBD20] reduce to the cotangent Laplacian and hence yield the same results.
(x, y, z) on differently tessellated unit spheres: Triangles (left), quads (center left), Hexagons (center right), and concave faces (right). On triangle meshes, the operators [AW11, BHKB20, dGBD20] reduce to the cotangent Laplacian and hence yield the same results.
Sparsity and Timings The operator matrix for polygon Laplacians has more non-zero elements than the corresponding adjacency matrix. This reflects that at least the vertices belonging to the same face are connected, since they all influence the (integrated) differential properties of the face. The choice of diamonds as regions for estimating the differentials allows a more accurate estimation of the gradient across (primal) edges. This comes at the expense of introducing additional non-zero entries in the operator matrix that reflect this connection. The reduced sparsity results in higher computational complexity for solving the involved linear systems. Table 1 lists the timings of sparse Cholesky factorization and back-substitution, computed using the supernodal LLT solver of CHOLMOD [CDHR08]. All timings were measured on a standard workstation with a six-core Intel Xeon 3.6 GHz CPU and were taken in single-threaded mode.
| # Vertices | Diamond | [AW11] | [BHKB20] | [dGBD20] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Triangles | 92k | 1198k | 2630 | 59 | 645k | 1491 | 40 | 645k | 1592 | 41 | 645k | 1967 | 41 |
| Quads | 99k | 2064k | 3273 | 68 | 884k | 1659 | 42 | 884k | 1574 | 41 | 884k | 2014 | 42 |
| Hexagons | 82k | 3030k | 3357 | 87 | 1064k | 1796 | 40 | 1064k | 2617 | 42 | 1064k | 2162 | 41 |
| Concave | 130k | 4149k | 5049 | 112 | 1558k | 2391 | 54 | 1558k | 2450 | 55 | 1558k | 2296 | 54 |
8.2. Volume Meshes
Discretizations of the Laplacian for general volume meshes are less common, leading to fewer possibilities for comparison than in the surface case. For tetrahedral meshes, we compare the Diamond Laplacian to the well known volume cotangent Laplacian, from now on called Primal Laplacian, as well as to the Dual Laplacian that was introduced in [AHKSH20].
For comparisons on general polyhedra, we generalize the polygon Laplacian of Bunge et al. [BHKB20] to volumetric meshes. To this end, we insert virtual vertices into faces and cells (minimizing squared areas/volumes as described in Section 6.3), construct gradient, divergence, and Laplacian on the virtually refined tetrahedral mesh using the primal/cotan discretization [Cra19], and employ the sandwiching of Equation (30).
Moreover, we compare to the two major DDFV methods CeVe [Her09] and CeVeFE [CH11]. Both DDFV approaches introduce a significant amount of additional degrees of freedom, with CeVe working on values per vertices and per cells, and CeVeFE with values at vertices, cells, faces, and edges. To compare to our approach, mapping values on vertices to values on vertices, we restrict their results to the per-vertex values and ignore the additional values. This restricts the comparison to the Poisson tests - how to compare eigenmodes remains unclear.
The different types of polyhedral tessellations used in the following evaluation are depicted in Figure 10.
The types of non-simplicial polyhedral meshes used for evaluation in the volumetric case. They will be referred to as Hexahedra (left), Pyramids (center), and Truncated (right).
Poisson Problems As in the surface case, we analyze the convergence behavior for Poisson systems Lu = Mb, with b being the Laplacian of the Franke test function
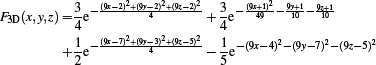
We solve the Poisson system on different tessellations of the 3D unit cube, fixing boundary vertices to the values of F3D. As shown in Figure 11, the Diamond Laplacian has the expected convergence behavior and yields lower errors than other methods.
L2 error in log-log scale of the Poisson system solved for Franke's test function on different tessellations of the unit cube.
Laplacian Eigenmodes When solving the eigenvalue problem of the Laplacian, better known as Helmholtz equation, on a 3-ball B3
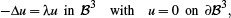
its discrete solution can analytically be expressed in terms of the spherical Bessel functions. Therefore, given a stiffness matrix L and mass matrix M for a polyhedral tessellation of B3, the discrete analogue of the Helmholtz equation can be formulated as the generalized eigenvalue problem Lu = λMu. The plots in Figures 12 and 13 show that the Diamond Laplacian successfully in recovers the desired eigenvalues, rather independent of the tessellation. In particular on non-uniform adaptive tetrahedral meshes (Figure 13) our operator is considerably more accurate than the primal and dual tetrahedral Laplacians.
The 34 smallest eigenvalues of the Laplacian, computed on different polyhedral tessellations of the unit ball. The top row shows the obtained eigenvalues, the bottom row the deviation from the true values. In all cases, our operator is more accurate than [BHKB20].
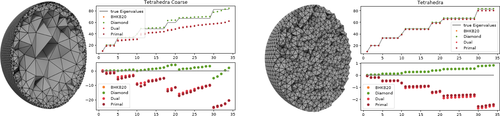
The 34 smallest eigenvalues of the Laplacian, computed on uniform and adaptive tetrahedral tessellations of the unit ball. For tetrahedral meshes the generalization of Bunge et al. [BHKB20] reduces to the Primal cotan operator, therefore yielding the same results. The Diamond Laplacian is not affected by adaptive tessellations and achieves a higher accuracy.
Timings and Sparsity The additional cell and face vertices that we (virtually) insert to construct the minimal diamonds lead to a higher density in the Diamond stiffness matrix compared to both tetrahedral operators presented in [AHKSH20] and the polyhedral generalization of [BHKB20]. Table 2 compares the matrix density for the different Laplace discretizations and the time for solving the resulting Poisson system, again using the supernodal LLT solver of CHOLMOD [CDHR08]. As expected, the Diamond Laplacian is more expensive than the Primal and Dual tetrahedral Laplacians and the polyhedral version of [BHKB20]. Compared to the volumetric DDFV methods, timings are comparable to CeVe [Her09], which however suffers from spurious modes, and it is significantly faster than CeVeFE DDFV [CH11], while at the same time being more accurate than all other methods.
| # Vert. | Diamond | [BHKB20] | CeVeFE | CeVe | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedra | 4.4k | 127k | 378 | 5 | 63k | 122 | 4 | 1664k | 4382 | 95 | 380k | 1017 | 23 |
| Hexahedra | 36k | 2587k | 4487 | 110 | 912k | 1670 | 43 | 1497k | 20813 | 487 | 736k | 4727 | 133 |
| Pyramids | 23k | 1037k | 1255 | 45 | 398k | 880 | 24 | 5021k | 22380 | 479 | 1231k | 4890 | 129 |
| Truncated | 19k | 1988k | 1652 | 44 | 476k | 989 | 22 | 2461k | 5051 | 104 | 580k | 1714 | 41 |
9. Conclusion
We improve on DDFV methods by generalizing the 2D DDFV formulation to surface meshes immersed in 3D (intrinsic gradients) and by providing a formulation for polyhedral meshes (ring of minimal diamonds) that avoids the spurious modes of CeVe [Her09] and is considerably simpler than CeVeFE [CH11]. We combine this with a generalization of the approach of Bunge et al. [BHKB20] from polygon meshes to polyhedral meshes and use the resulting double prolongation to remove the additional degrees of freedom of dual cell and face vertices from the improved DDFV operators. The Diamond Laplacian provides, to the best of our knowledge, the first simple Laplacian for general polyhedral meshes that maps values at vertices to values at vertices while having the appropriate kernel, linear precision, and the desired semi-definiteness. The source code for the polygonal and polyhedral Diamond Laplace is available at https://github.com/mbotsch/polyLaplace.
In extensive numerical evaluations on prototypical geometry processing applications we compare the Diamond Laplacian to seven existing methods from the graphics and DDFV communities as well as to the unpublished generalization of [BHKB20] to polyhedral meshes. In almost all experiments the Diamond Laplacian is superior to all its competitors, otherwise it is placed second. In contrast to existing polygon Laplacians, it does not reduce to the cotan formulation on triangle meshes. It is a viable alternative also for pure simplicial meshes, as it provides more accurate results in particular if the gradient operator is involved.
The price for generality and accuracy is a higher number of non-zero elements, leading to a slight increase in computation time. We believe that this is a useful trade-off in graphics and geometric modeling, where meshes are mostly processed without altering them. We cannot resist to make the obvious remark: Diamonds  are attractive but somewhat expensive.
are attractive but somewhat expensive.
Acknowledgements
The authors are grateful to Hendrik Meyer for his help in rendering the figures, to Fernando de Goes for providing an extensive set of test meshes, and to Philipp Herholz for his help with the volumetric dual Laplacian. Marc Alexa acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy - The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689). Open access funding enabled and organized by Projekt DEAL. [Correction added on 25 November 2021, after first online publication: Projekt Deal funding statement has been added.]