1 INTRODUCTION

One of the major goals in ecology is to understand the environmental drivers behind the spatial distribution of species (Ben-Hur & Kadmon, 2020; Stein et al., 2014). Environmental heterogeneity is hypothesized to be one of the key drivers of variation in species richness and abundance at local and global scales (Ben-Hur & Kadmon, 2020; Stein et al., 2014; Tews et al., 2004). The classical niche model predicts that greater environmental heterogeneity will increase species diversity due to an increase in niche dimensions (Hutchinson, 1957). However, many studies have shown deviations from this prediction (Hortal et al., 2009, 2013), which have been attributed to confounding factors (Ben-Hur & Kadmon, 2020). Further, the recognition that environmental heterogeneity has two components, compositional and spatial (or configurational) heterogeneity, has also helped understand the mechanisms behind the deviations of the classical predictions of the niche model (Ben-Hur & Kadmon, 2020; Fahrig et al., 2011). Compositional heterogeneity is the magnitude of variation in environmental conditions. This component can be expressed using discrete (e.g., number of habitats) or continuous variables (e.g., range of an environmental variable) and has no spatial characteristics (Ben-Hur & Kadmon, 2020). While spatial heterogeneity refers to the spatial pattern of variation in environmental conditions and can be expressed using measures like fractal dimension, spatial autocorrelation, or fragmentation. This last component of heterogeneity has no environmental characteristics (Ben-Hur & Kadmon, 2020). One of the ways in which the environment is spatially heterogeneous is when it is structured in patches and gradients. If these forms of aggregation are not present, the environment is homogeneous or randomly distributed (Fortin & Dale, 2005; Negrete-Yankelevich & Fox, 2015).

Given that plants constitute important habitats for animals, heterogeneity in terrestrial ecosystems has been traditionally associated to the richness of vegetation structures (compositional heterogeneity, e.g., MacArthur & MacArthur, 1961). However, the non-random spatial distribution of vegetation is a source of environmental heterogeneity for animals. Plants are sessile structures/resources that occur irregularly and hierarchically in space, with small patches of resources nested within larger patches (García et al., 2011). For example, fruits aggregated within plants, that are aggregated into forest patches, which in turn are aggregated within landscape units (García et al., 2011). This patchy distribution of plants result in spatial heterogeneity that may determine the richness, abundance, and distribution of animals (García et al., 2011; Gonçalves-Souza et al., 2011; Tews et al., 2004). In addition, the response of animals to the spatial heterogeneity of plants depends on their perceptual scale (Szabó & Meszéna, 2006), that is, the spatial extent in which an animal can perceive habitat distribution (García et al., 2011). Finally, extrinsic mechanisms (such as climatic restrictions, competition or predation) are also important determinants of the spatial match between an interacting plant and animal (García et al., 2011).

Epiphytes are an important habitat for animals in the canopy, because they provide suitable sites for shelter, nesting, and foraging (e.g., for birds and arthropods, Cruz-Angón et al., 2009; Cruz-Angón & Greenberg, 2012). However, epiphytes are heterogeneously distributed in the three-dimensional space of their host trees (Zhao et al., 2015; Zotz, 2007). Current evidence suggests that the spatial distribution of epiphytes within trees of tropical forests is the result of substrate (i.e., branches) and microclimate variation (Johansson, 1974; Ruiz-Cordova et al., 2014; Zhao et al., 2015). For example, vertical variation in humidity, temperature, solar radiation, and accumulation of organic matter, along with changes in substrate type and availability (trunk-branches, Zhao et al., 2015), generate different environmental conditions leading to the occurrence of epiphyte abundance and richness gradients (Benzing, 1990; Johansson, 1974; Kelly et al., 2004; Ruiz-Cordova et al., 2014). Apart from vertical gradients, vascular epiphytes also tend to aggregate in zones of the canopy where substrate is more abundant or in places where the microclimatic conditions favor germination and persistence (García-González et al., 2016; Tremblay & Castro, 2009). Since epiphytes are the main habitat used by different canopy-dwelling animals (Cruz-Angón et al., 2009; Cruz-Angón & Greenberg, 2012), their heterogeneous spatial distribution within trees can be expected to promote a heterogeneous distribution of their associated-fauna. After the colonization of epiphytes, various mechanisms such as environmental filters, competition, predation, or dispersal limitation (Méndez-Castro et al., 2018, 2020) can determine the spatial distribution of animals within the epiphyte habitat of each tree. If these mechanisms do not have a significant role, the spatial distribution of the associated fauna is expected to simply follow that of the epiphytic habitat.

Spiders are among the most common invertebrates associated with epiphytes (Romero et al., 2008; Stuntz, Ziegler, et al., 2002). Whereas epiphytes provide sites for hunting, reproduction, and protection from against predators and adverse climatic conditions (Hénaut et al., 2014, 2018), spiders protect epiphytes from herbivory through predation, and sometimes contribute to their nutrition through excretion (Romero et al., 2008; Romero & Srivastava, 2010; Santos et al., 2002). It is known that the compositional heterogeneity of epiphytes influences spider communities associated with them (Méndez-Castro et al., 2018). For example, epiphyte abundance and number of leaves are positively associated with spider abundance (Gonçalves-Souza et al., 2011), while the different life forms (e.g., orchids, bromeliads, ferns) promote different assemblages of these predators (Stuntz, Ziegler, et al., 2002). There is also evidence that the heterogeneous spatial distribution of epiphytes in their host trees influences spider communities. Gonçalves-Souza et al. (2011) showed a positive association between the vertical stratification of epiphytes and spider richness, whereas Méndez-Castro et al. (2018) reported the opposite pattern. Nevertheless, there are few studies that have evaluated the relationship of these groups in a spatially explicit context (but see Méndez-Castro et al., 2018), and it is still unknown if the distribution in epiphyte-dwelling spiders is driven by the spatial distribution of their host plants or by other processes such as intra-community interactions.

Spiders are rarely randomly distributed within their habitat (Pearce & Zalucki, 2006) because several factors can influence their spatial distribution. For instance, aggregation patterns in ground-dwelling spider communities are believed to be more associated with the distribution of mosses and leaf litter than with the distribution of prey (Sereda et al., 2012). In contrast, other observations suggest that in some cases spiders aggregate in patches with higher prey density (Harwood et al., 2003; Pearce & Zalucki, 2006). Furthermore, abiotic factors such as microclimatic conditions (Ziesche & Roth, 2008) and biotic factors such as limited dispersal (Lubin et al., 1998), philopatry (Hodge & Storfer-Isser, 1997), and competition (Birkhofer et al., 2007, 2010) have also been suggested as important drivers of spider spatial distribution.

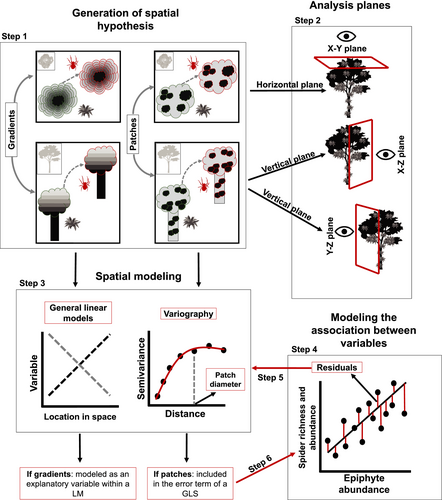
In this study, we used a spatially explicit approach to explore the spatial distribution of spiders associated with vascular epiphytes within trees. We hypothesized that (1) the richness and abundance of epiphyte-dwelling spiders have a positive association with epiphyte abundance; (2) the spiders (richness and abundance) show the same patterns of spatial distribution as the epiphytic habitat (patches and gradients; see Figure 1, step 1); and (3) that their spatial distribution can be accounted for by the spatial heterogeneity of this plant habitat.

2 METHODS

2.2 Data analysis

2.2.1 Study scale and variables

Even though data were collected three-dimensionally in order to model the spatial distribution of epiphytes and their hosted spiders. Positions were analyzed in three two-dimensional planes: a horizontal plane (X-Y), which corresponded to the view of the tree from the top, and two vertical planes (X-Z and Y-Z), which corresponded to South-North and West-East lateral views (Figure 1, step 2). We adopted this strategy because three-dimensional variogram modeling demands large volumes of data to adequately estimate the anisotropy of the models (i.e., changes in autocorrelation with changes in direction, Negrete-Yankelevich & Fox, 2015). Sampling units (Total = 299, T-I = 120, T-II = 83, T-III = 96) corresponded to single individuals or aggregations of epiphytes that shared the same substrate or rhizosphere and were separated from another group or individual (i.e., “mat” sensu Sanford, 1968). Dimensions used to define the spatial scale of the study varied within and between trees. The grain (dimension of the observation unit, mats) varied between approximately 0.01 and 0.08 m in diameter. The extension, defined as the maximum distance between observation units, was of 1377.6 cm for T-I, 1441.8 cm for T-II, and 1198.7 cm for T-III. The strategy of collapsing the three-dimensional distribution of epiphytes into two-dimensional planes resulted in some observation units sharing the same spatial position. Therefore, before performing the spatial analysis, we jittered the units (introduced random micro-changes) with duplicated coordinates with the function jitterDupCoords of the R package geoR (Ribeiro Jr & Diggle, 2018), therefore the interval between some sampling units was a distance close to zero.

For each observation unit, we quantified the richness of the vascular epiphyte groups (bromeliads, orchids, cacti, Piperaceae, ferns, aroids, and others [hemiepiphytes]), biomass (measured as dry weight) and abundance (number of individuals per mat). An epiphyte with an independent root system or several epiphytes of the same taxonomic group sharing the same rhizosphere were considered as one individual. For spiders, we recorded species richness (number of species per mat) and abundance (number of individuals per mat). Given the high correlation between epiphytes' abundance, richness and biomass on each tree (Spearman's correlation, abundance-biomass: r_T-I = 0.69, r_T-II = 0.76, r_T-III = 0.86; abundance-richness: r_T-I = 0.85, r_T-II = 0.85, r_T-III = 0.69), we used only epiphyte abundance as explanatory variable for spider richness and abundance in the analyses. The three variables were transformed to satisfy the assumption of normality required for the variogram (see Table 1 for transformations).

TABLE 1. Summary of linear models and generalized least squares (GLS) models for spider richness and abundance

Tree ID	Response variable	Direction of residual structure	Initial spatial structure		Parameter linear models		Residual patch structure	Omnibus statistic
			Patch	Gradient	E.A	Gradient		R 2	F	ΔAICm
T-I	4√[Richness]	Non-spatial	na	na	0.27***		na	0.51	126.9***	na
		X-Y	246.2		0.27***	2.34 × 10−6**(X2)	np	na	na	na
		X-Z	252.1		0.26***		508.7	na	na	87.7
		Y-Z	219.6		0.26***		529.1	na	na	84.23
	Log10[Abundance]	Non-spatial	na	na	1.22***		na	0.56	157.3***	na
		X-Y	152.07		1.22***		386.1	na	na	96.02
		X-Z	298.1		1.21***		462.01	na	na	98.96
		Y-Z	323.7		1.21***		523.7	na	na	97.09
T-II	Log10[Richness]	Non-spatial	na	na	0.69***		na	0.57	110.8***	na
		X-Y	237.3	X 2	0.69***		np	na	na	na
		Non-spatial	na		0.60***	−2.64 × 10−4**(Z)		0.61	65.57***	na
		X-Z		Z	0.60***	−2.64 × 10−4**(Z)	np	na	na	na
		Y-Z		Z	0.60***	−2.64 × 10−4**(Z)	np	na	na	na
	Log10[Abundance]	Non-spatial	na	na	1.33***		na	0.6	125.8***	na
		X-Y	122.2	X 2	1.33***		np	na	na	na
		Non-spatial	na		1.21***	−3.59 × 10−4**(Z)		0.62	68.41***
		X-Z		Z	1.21***	−3.59 × 10−4**(Z)	np	na	na	na
		Y-Z		Z	1.21***	−3.59 × 10−4**(Z)	np	na	na	na
T-III	3√[Richness]	Non-spatial	na	na	0.52***	−8.53 × 10−7**(X2)	na	0.84	173.9***	na
						−6.51 × 10−7**(Y2)
		X-Y			0.52***	−8.53 × 10−7**(X2)		na	na	na
						−6.51 × 10−7**(Y2)
		X-Z	635.8		0.53***	−8.22 × 10−7**(X2)	np	na	na	na
		Y-Z	332.2		0.52***	−6.27 × 10−7**(Y2)	np	na	na	na
	4√[Abundance]	Non-spatial	na	na	0.64***	−9.67 × 10−7**(X2)	na	0.84	174.4***	na
						−6.69 × 10−7**(Y2)
		X-Y			0.64***	−9.67 × 10−7**(X2)		na	na	na
						−6.69 × 10−7**(Y2)
		X-Z	420.3		0.65***	−9.36 × 10−7**(X2)	np	na	na	na
		Y-Z	230.1		0.64***	−6.42 × 10−7*(Y2)	np	na	na	na

Note

• The significance of the estimated parameters is *p < 0.05, **p < 0.01, ***p < 0.001. Note that the values of the estimated slopes (β) are dependent on the transformations of spider richness and abundance, and therefore not comparable between models with different transformation.
• Abbreviations: E.A, epiphyte abundance; Na, parameter not applying to the estimate; Np, no significant patches in the model residues; R², coefficient of determination of non-spatial linear models; X², concentric gradient in the West–East direction; Z, gradient in height; ΔAICm, change in parsimony between GLS and null models for spatial variation (variable ~1 + Ɛ).

2.2.2 Modeling spatial distribution of vascular epiphytes and spiders within trees

To model the spatial distribution of epiphytes and their hosted spider, we performed a two-stage analysis for each plane (sensu Negrete-Yankelevich & Fox, 2015) (Figure 1, step 3). In the first stage, we modeled gradients (i.e., monotonic changes in some direction) using simple linear models. In the second stage, we modeled aggregation patches (i.e., aggregation zones where the values of a variable are more similar to each other than expected by chance) using variography, as a way to estimate the degree of spatial dependence. To model the gradients, we used the directions (X, Y, or Z) involved in each plane as explanatory variables, including their polynomials in order to consider both unidirectional (e.g., X or X + Y, in the case of the X-Y plane) and concentric (e.g., X² and Y², in the case of the X-Y plane) gradients. We modeled concentric gradients because this is the type of spatial distribution predicted for epiphytes in their host trees (Zhao et al., 2015). Gradient selection was carried out by calculating and comparing the Akaike Information Criterion (ΔAIC) of the five models (i.e., gradient type) generated for each analysis plane (e.g., X, Y, X + Y, X², Y², in the case of the X-Y plane) with a null model (variable = µ + Ɛ). Gradient models with AIC values lower than five units form the null model (sensu Richards, 2015) were selected. When more than one model was selected, the model with the lowest AIC was retained.

Spatial distribution in patches for each direction combination was analyzed with omnidirectional variograms, which are semivariance (inverse of autocorrelation) plots as a function of the separation distance between pairs of observations in each plane. Semivariance was calculated as:

following Matheron (1965).

Where γ(h) is the semivariance of the pairs of observations separated by distance h (lag), W(h) is the total number of pairs of observations separated by h, and y_i is the sample value in each location i. To avoid the bias introduced by semivariance values represented by very few points (which occur with long distances), we only used 60% of the maximum available distance in each plane (sensu Negrete-Yankelevich & Fox, 2015). For planes where spider abundance had unusually high observations, we used the robust estimation (against the effect of outliers) of the semivariance for this variable, proposed by Cressie and Hawkins (1980):

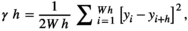
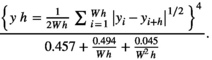
Variograms that reach an asymptote indicate the existence of patches. Thus, the distance at which the asymptote is reached represents the distance at which the spatial autocorrelation ceases to be significantly different from what would be expected by chance, and represents the mean diameter of the aggregation patches (Fortin & Dale, 2005; Negrete-Yankelevich & Fox, 2015). We adjusted theoretical variograms using weighted least squares to determine if there were aggregation patches and estimate their mean size (range), nugget (spatial variance at distances smaller than those sampled, i.e., microscale variance or measuring error), and sill (asymptote reached by spatial variance in the largest sampled distances). The theoretical models considered were:

Spherical

Exponential

Gaussian

Linear

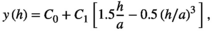
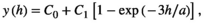
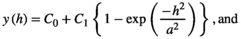
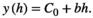
To avoid models where autocorrelation explained a very small portion of the total variation, we only considered variograms with a modeled autocorrelation (C₁) ≥30% of the total semivariance (C₀ + C₁), and we selected the theoretical model with the highest explanatory power (estimated from its determination coefficient [R²]).

2.2.3 Average and spatial relationship of epiphytes and spiders within trees

Once we analyzed the spatial distribution of spiders and epiphytes in each plane (X-Y, X-Z, Y-Z), spatialized linear models (Generalized Least Square- GLS) were used to determine the explanatory power of epiphyte abundance on the variation in spider richness and abundance and their spatial distribution in the trees (Figure 1, step 4). GLS models belong to the mixed model family, but instead of modelling spatial grouping of observations with a random component, they include spatial autocorrelation within the residual structure by estimating a correlation matrix with variogram parameters (range and nugget). To fit and simplify GLS models, we followed the steps described in Negrete-Yankelevich and Fox (2015). Notice that these models were fitted for each plane in all trees, because their spatialized character does not allow fitting different surfaces simultaneously. First, we tested the explanatory power of epiphyte abundance on the average variation (not spatial) of spider richness and abundance using simple linear models. To linearize the relationship between the two groups and improve the predictive power of the models, the same transformations used for variogram modeling were used to fit these linear models (Table 1). However, the observed and predicted values were retrotransformed when plotting, hence the non-linear shapes obtained for the relationships. We used analyses of variance to determine the explanatory power of these models. We then carried out the detection and modeling of the spatial autocorrelation in the model residuals. To verify if epiphyte abundance explained the spatial patterns associated with spider richness and abundance, we performed gradient analyses and constructed variograms with the simple linear model residuals (Figure 1, step 4). If the residuals of these models did not show any autocorrelation but the variables prior to modeling did, this indicated that epiphyte abundance explained the average and spatial variation in richness and abundance of epiphyte-dwelling spiders (Negrete-Yankelevich & Fox, 2015). When residuals had gradients, these were included as independent variables within the final models. In the case of residuals with a patchy spatial distribution, we proceeded to re-fit the GLS models integrating variogram parameters in the residuals (Figure 1, step 6). GLS models were compared in terms of their explanatory power with a null model (variable explained by the general mean) using the ΔAIC. We verified that the residuals of the final model satisfied the assumptions of normality and homogeneity of variance. All spatial and linear modeling was performed in R (R Core Team, 2020) using the packages nlme (Pinheiro et al., 2018) and geoR (Ribeiro Jr & Diggle, 2018).

3 RESULTS

We collected a total of 1182 individual vascular epiphytes, from which we extracted 7479 spiders grouped into 162 morphospecies, 48 genera, and 26 families. Lathys dixiana (Dictynidae) was the species with the largest number of individuals in the study (1041 Ind.), but occurred mostly in T-II (804 Ind.). Modisimus gracilipes (Pholcidae) was the most dominant species in T-I (513 Ind.), while Pippuhana sp1 (Anyphaenidae) was the most abundant morphospecies in T-III (304 Ind.). Bromeliads were the most dominant group of vascular epiphytes in the trees, contributing 72% of the individuals (856 Ind.). The abundance of epiphytes (T-I = 363, T-II = 306, T-III = 513) and spiders (richness: T-I = 94, T-II = 90, T-III = 97; abundance: T-I = 2631, T-II = 2737, T-III = 2111) varied between trees, and the highest epiphyte abundance and spider richness and abundance were found in the tree with the largest DBH and crown diameter (T-III).

3.1 Spatial distribution of epiphytes and spiders within trees

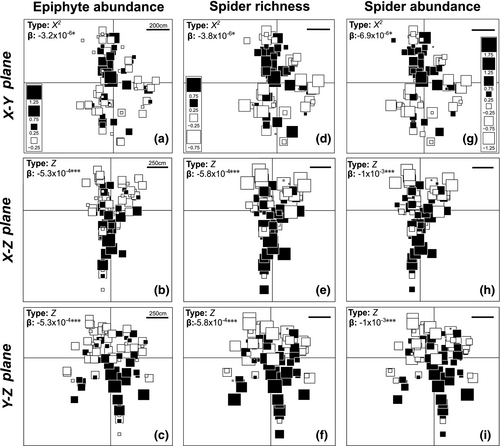
Epiphytes and their hosted spiders showed gradients only in T-II, which were of equal type and direction between the two groups (Figure 2). In the X-Y plane of T-II (Figure 2a,d,g), we detected a concentric gradient (i.e., a decrease from the center toward the edges of the tree), whereas a height gradient was detected in the X-Z and Y-Z planes (i.e., a decrease from the ground toward the canopy) (Figure 2b,e,f). Mean patch diameter (estimated range: 635 cm) was equal between epiphytes and spiders only in T-III (direction X-Z; Figure 3h). For the other trees, spider patches oscillated between 122.2 cm (R² = 0.35) and 323.7 cm (R² = 0.30), and for epiphytes there were patches only in the Y-Z plane of T-II, with a mean diameter of 505.5 cm (R² = 0.70, Figure 3).

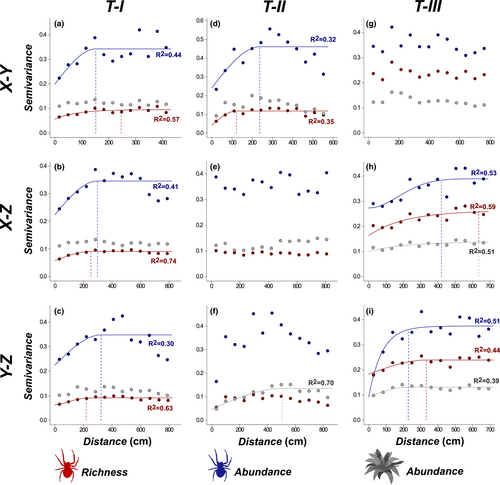
3.2 Average and spatial relationship between spiders and epiphytes

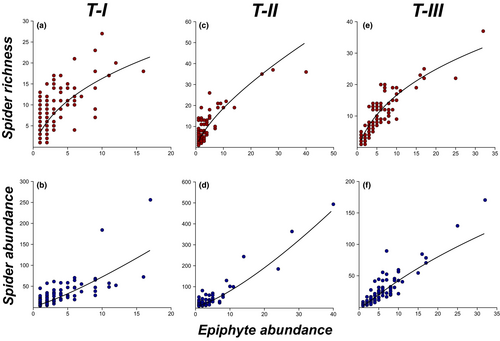
Mean spider richness and abundance increased with epiphyte abundance in mats in all trees (Figure 4). Epiphyte abundance explained the concentric gradients and all patches in the spider community only in one of the analyzed planes (X-Y) of T-II. However, epiphyte abundance did not explain the height gradients exhibited by spiders in this tree (T-II; Table 1). In T-I, the random variation in epiphyte abundance (not related to spatial autocorrelation) explained the aggregation patches of smaller diameter exhibited by spider richness and abundance, because mean patch diameter in the residuals of the linear models increased to approximately twice the diameter of the patches originally detected for these variables (Table 1). In T-III, where epiphyte abundance presented a patchy spatial pattern, models adjusted to spider richness and abundance did not show patches in the spatial autocorrelation of their residuals, but did show concentric gradients (X², Y²) that had not been detected prior to the modeling (Table 1).

4 DISCUSSION

As predicted, our study shows that vascular epiphyte mats within trees and their hosted spiders were spatially distributed in patches and gradients in a Mexican coffee plantation. The spatial distributions of the richness and abundance of the epiphyte-dwelling spiders were partially or totally explained by the spatially autocorrelated variation in vascular epiphyte abundance. In addition, our results suggest that the communities of vascular epiphytes and their hosted spiders were also likely to be spatially heterogenous at scales lower than a mat (our minimum observation unit) and higher than a tree (our maximum study extent), which suggests a possible interaction between both groups at other spatial scales.

As we expected, higher abundance and species richness of spiders was found in epiphyte mats with a higher number of individuals, which agrees with previous studies (Gonçalves-Souza et al., 2011). This relationship, albeit not linear, could be due to mats with high epiphyte abundance representing habitats with a higher compositional heterogeneity (sensu Ben-Hur & Kadmon, 2020), which implies a greater number of niches to be exploited by spider communities, such as roots, vegetative zone (leaves), and flowers (Méndez-Castro et al., 2018; Stuntz, Ziegler, et al., 2002).

The epiphyte mats were not randomly distributed within trees and exhibited patches of variable dimension and gradients of different type and direction. The patches of vascular epiphyte habitat, when observed (e.g., T-III), fully explained the patchy spatial distribution of spider richness and abundance. This finding shows that in addition to the relationship between the compositional heterogeneity of the epiphytic habitat and the spider communities, there is a spatial relationship between these two organisms. That is, the heterogeneous spatial distribution of epiphyte abundance associates with a heterogeneous spatial distribution in the hosted spider communities. In general, habitat spatial heterogeneity is considered to be one of the main ecological drivers shaping invertebrate predator communities including spiders (Malumbres-Olarte et al., 2013; McNett & Rypstra, 2000); however, little is known about the causal mechanisms of this relationship (Langellotto & Denno, 2004). Similar to the present study but at a larger scale (0.16 km²), Sereda et al. (2012) found that the habitat spatial heterogeneity associated with the spatial distribution of mosses and leaf litter on the ground explained the patchy distribution of spider communities. Epiphyte patches, apart from being structurally complex microhabitats (i.e., with high abundance and variety of life forms), may also represent prey aggregation patches (Cruz-Angón & Greenberg, 2012; Richardson, 1999), or zones bearing more stable microclimatic conditions when compared with the fluctuating climate of the surrounding canopy (Freiberg, 2001; Stuntz, Simon, et al., 2002). Future studies should employ an experimental approach that allows identifying the contribution of each factor (e.g., microclimate variation, availability of prey) in the spatial structuring of spider communities in scenarios where the habitat is aggregated in space.

In this study, we found that epiphyte-dwelling spiders can be spatially aggregated when epiphytic habitat were randomly distributed. Given the average relationship between epiphyte abundance and spider richness and abundance, our results suggest that spider patches are not always associated with epiphyte patches, but may be formed around mats with high values of epiphyte abundance in trees. The spatial distribution of animals is known to be the result of biotic interactions and environmental heterogeneity (Ettema & Wardle, 2002). In a spatially randomly or homogeneously distributed habitat (i.e., trees without epiphyte aggregations), spider patches occur, and are probably the result of processes that operate after the colonization of a site (sensu Sereda et al., 2012). For example, Hodge and Storfer-Isser (1997) found that web-building spiders, a dominant guild in the studied tree number one (T-I), prefer sites that have been occupied by conspecifics, and exhibit an aggregated spatial structure. Furthermore, Harwood et al. (2003) showed that spiders with different hunting strategies (e.g., web-building and free-hunting spiders) aggregated in structurally homogeneous habitats according to patches of high prey density. This evidence demonstrates that in equivalent scenarios with different colonization and establishment of populations, such as epiphyte mats within trees, multiple processes can co-occur and act individually or synergistically to cause spiders communities spatial aggregation.

Given that the spatial heterogeneity of epiphyte abundance could explain all patches of spider richness and abundance, but not all gradients, spider gradients could be the result of others ecological processes occurring at a larger scale than the epiphyte habitat within trees. Several studies have reported vertical gradients for the abundance, richness, and composition of arboreal spider communities (Méndez-Castro & Rao, 2014; Pinzon et al., 2011; Quijano-Cuervo et al., 2019; Vanegas et al., 2012). These gradients have been attributed to different factors dependent on the type of ecosystem (Pinzon et al., 2013), such as environmental filters (Oguri et al., 2014; Quijano-Cuervo et al., 2019), variation in the structural complexity between vegetation strata (Oguri et al., 2014), and biotic interactions like competition (Basset et al., 2003; Brown, 1981). For our scenario, the decreasing gradients (from the ground to the canopy) in richness and abundance of epiphytes and spiders are possibly associated with gradients of increasing temperature and decreasing humidity that occur between the vertical layers of tropical forest ecosystems (Freiberg, 1997). On the other hand, error parameters estimated for the variograms (nugget) suggest that, apart from the observed patches, there is additional spatial variation that occurs at a scale lower than an epiphyte mat (our minimum analysis unit). This microscale spatial structure could be a result of the variation in the morphology of vascular epiphytes occurring within mats (Gusmão et al., 2019) or of the differential aggregation of spider guilds in the different microhabitats present within a mat, such as patches of flowers or leaves and aggregations of soil and debris (Yanoviak et al., 2004). These findings open the possibility that the interaction between vascular epiphytes and spiders occurs simultaneously at different dimensions of the spatial scales (e.g., larger than a tree and at the same time smaller than an epiphyte mat), which remains to be investigated.

Even though we selected trees of the same species and with similar structure, the spatial patterns found for epiphytes and their hosted spiders were different among trees. It is possible that the morphology or environmental context of each tree within the ecosystem (e.g., proximity to a canopy gap or to other trees) is determinant for the distribution of epiphytes and the spiders associated with them. Although in previous studies for this system Méndez-Castro et al. (2018) showed that the collection time does not have a significant effect on the mean spider richness, it could be that the differences found here in spider spatial patterns among trees (patch dimensions, presence or absence of gradients, amount of explained spatial variation), may be partly caused by seasonal changes associated to the separation in collection time.

We recognize that the small number of trees studied, due to the level of detail in the three-dimensional mapping of the sampling units, limits the inferential power of our findings. In addition, because the studied system undergoes some management, such as insecticides application, our findings cannot be directly generalized to trees in natural forests. However, our study shows that the spatial heterogeneity of vascular epiphytes within coffee trees (i.e., patch and gradient), and probably other factors such as intra-community interactions, can explain the spatial structure of epiphyte-dwelling spiders. Nevertheless, this spatial dynamic between epiphyte, spiders, and other factors biotic and abiotic, also involves other scales (e.g., within mats and patches of trees), where different processes that operate at those levels could be regulating patterns that emerge at the tree scale.

CONFLICT OF INTEREST

The authors declare no competing interests.

AUTHOR CONTRIBUTIONS

FEM-C and DR conceived the idea to collect the original data; LGQC, FES, SNY conceived the idea for this article and performed statistical analyses; LGQC and SNY wrote the first complete draft; all authors (LGQC, SNY, FEM-C, DR and FES) contributed to subsequent drafts, revisions, review comments, and gave final approval for publication.