Animal Science Journal
Volume 95, Issue 1 e13978
RESEARCH ARTICLE
Full Access

Evaluation of genomic prediction considering non-additive genetic effects on fatty acid traits of Japanese Black cattle

Hidemi Oyama, 

Corresponding Author

Hidemi Oyama

Institute of Livestock and Grassland Science, NARO, Tsukuba, Japan

Correspondence

Hidemi Oyama, Institute of Livestock and Grassland Science, NARO, Tsukuba, Japan.

Email: [email protected]

Search for more papers by this author
Motohide Nishio, 

Motohide Nishio

Institute of Livestock and Grassland Science, NARO, Tsukuba, Japan

Search for more papers by this author
Eri Shibata, 

Eri Shibata

Hiroshima Prefectural Technology Research Institute Livestock Technology Research Center, Shobara, Japan

Search for more papers by this author
Hinaka Takemyo, 

Hinaka Takemyo

Hiroshima Prefectural Technology Research Institute Livestock Technology Research Center, Shobara, Japan

Search for more papers by this author
Kasumi Ichinoseki, 

Kasumi Ichinoseki

National Livestock Breeding Center, Shirakawa, Japan

Search for more papers by this author
Kazuo Ishii, 

Kazuo Ishii

Institute of Livestock and Grassland Science, NARO, Tsukuba, Japan

Search for more papers by this author
First published: 08 July 2024
https://doi.org/10.1111/asj.13978

Abstract

Genomic prediction was conducted using 2494 Japanese Black cattle from Hiroshima Prefecture and both single-nucleotide polymorphism information and phenotype data on monounsaturated fatty acid (MUFA) and oleic acid (C18:1) analyzed with gas chromatography. We compared the prediction accuracy for four models (A, additive genetic effects; AD, as for A with dominance genetic effects; ADR, as for AD with the runs of homozygosity (ROH) effects calculated by ROH-based relationship matrix; and ADF, as for AD with the ROH-based inbreeding coefficient of the linear regression). Bayesian methods were used to estimate variance components. The narrow-sense heritability estimates for MUFA and C18:1 were 0.52–0.53 and 0.57, respectively; the corresponding proportions of dominance genetic variance were 0.04–0.07 and 0.04–0.05, and the proportion of ROH variance was 0.02. The deviance information criterion values showed slight differences among the models, and the models provided similar prediction accuracy.

1 INTRODUCTION

The beef of Japanese Black cattle is known for its excellent palatability, including flavor, sweet aroma, smoothness of fat, and good mouthfeel when heated. These characteristics in meat quality are attributed to the influence of monounsaturated fatty acids (MUFA) (Kobayashi & Shoji, 2006; Sakuma et al., 2012; Westerling & Hedrick, 1979). Furthermore, it has been reported that the proportion of MUFA in the fatty acid composition of Japanese Black cattle is higher than in other beef cattle breeds (Zembayashi et al., 1995). Therefore, breeding improvement of MUFA in Japanese Black cattle is considered crucial for differentiation from other beef cattle breeds.

Genomic prediction using genome-wide single-nucleotide polymorphism (SNP) marker information has been reported in carcass traits in Japanese Black cattle (Onogi et al., 2014), and is now being put to practical use mainly in pre-selection. However, reports on the genomic prediction of fatty acid traits in Japanese Black cattle mostly rely on conventional methods using pedigree information (Inoue et al., 2008, 2011, 2017; Kohama et al., 2021; Nakahashi et al., 2012; Nogi et al., 2011; Yokota et al., 2011; Yoshimura et al., 2018), and there are limited reports using SNP marker information (Nishio, Inoue, Arakawa, et al., 2023).

To date, in genomic prediction of Japanese Black cattle, the primary focus has been on predicting the estimated breeding values of selected candidate cows and utilizing them in breeding programs, leading to ignoring the influence of dominance genetic effects. Varona et al. (2018) reported the advantages of considering the dominance genetic effects in evaluation models, including (i) contributing to improved accuracy of estimated breeding values, (ii) utilization in mating plans among selected candidates, and (iii) enhancing the benefits of dominance genetic effects through appropriate breeding plans for both purebred and crossbred cattle. Therefore, genomic prediction considering dominance genetic effects may contribute to accelerating breeding improvement of Japanese Black cattle.

In recent research, there has been a development allowing for the direct obtaining of “observed” heterozygosity information from an individual's own SNP marker data (Varona et al., 2018). This advancement has led to numerous studies on the dominance genetic effects in genomic prediction. Su et al. (2012) reported that models that included dominance genetic effects improved the unbiasedness of genomic predictions. There are several reports on genomic prediction considering the non-additive genetic effects in Japanese Black cattle for carcass characteristics (Inoue et al., 2021; Onogi et al., 2021) or reproductive performance (Nagai et al., 2022); however, no reports explicitly discuss dominance genetic effects on MUFA.

Furthermore, inbreeding depression contributes to the appearance of potentially detrimental traits and the increase in individuals experiencing reduced fitness due to inbreeding (Doekes et al., 2020; Nishio, Inoue, Ogawa, et al., 2023). Uchida and Yamagishi (1993) reported that the more inbreeding levels increase, the more growth traits decrease for both calves and feeder, and that increased gene homozygosity could be the cause of inbreeding depression. According to Nishio, Inoue, Ogawa, et al. (2023), accurate prediction of inbreeding is essential in designing a breeding program to control the increase in levels of inbreeding and, consequently, deal with the effects of inbreeding depression. Additionally, runs of homozygosity (ROH) is a measure of inbreeding, considered to capture differences in region-specific inbreeding depression better than the homozygosity of individual SNPs (Doekes et al., 2020). In some studies, ROH-based inbreeding coefficients have been reported to capture inbreeding depression in particular (Keller et al., 2011; Nishio, Inoue, Ogawa, et al., 2023). Nishio, Inoue, Arakawa, et al. (2023) reported that the ROH-based inbreeding coefficient is a good estimator for qualifying inbreeding level, and genomic inbreeding measures seemed to capture more phenotypic differences than pedigree-based measures. Furthermore, to accurately estimate dominance genetic effects, it is necessary to incorporate inbreeding as a covariate (Xiang et al., 2016). Models that simultaneously consider ROH effects, calculated as a genomic relationship matrix, and the dominance genetic effects have shown improved fitness compared to models considering only additive genetic effects (Doekes et al., 2020). Therefore, incorporating both the dominance genetic and ROH effects into a model for fatty acid composition in Japanese Black cattle may lead to improved predictive accuracy compared to considering only dominance genetic effects.

The objective of this study was to determine whether genomic prediction accuracy can be improved when considering the dominance genetic and ROH effects for MUFA and oleic acid (C18:1) in fatty acid composition for Japanese Black cattle.

2 MATERIALS AND METHODS

2.1 Animal resources and dataset

All samples used in this study were obtained from carcasses processed at slaughterhouses; therefore, approval from the Animal Care and Use Committee was considered unnecessary. Phenotypic records for the percentages of MUFA and C18:1 were collected from 2494 Japanese Black cattle raised in Hiroshima Prefecture, with measurements conducted using gas chromatography. Fat samples were taken from the longissimus thoracis muscle located between the sixth and seventh ribs. Methyl esterification of fatty acids followed O'Keefe et al. (1968). For gas chromatography analysis, a capillary column was used. Additionally, calibration curves that described the methyl ester standards for myristic, myristoleic, palmitic, palmitoleic, stearic, oleic, and linoleic acids were used for measurement of overall MUFA composition. Descriptive statistics for fatty acid composition (%) are presented in Table 1.

TABLE 1. Descriptive statistics (%).
Trait or effect Mean SD Minimum Maximum
MUFA 57.0 3.6 46.6 67.7
C18:1 50.4 3.5 39.8 61.1
F ROH $$ {F}_{ROH} $$ 7.4 4.1 0.1 27.1
  • Abbreviations: MUFA, monounsaturated fatty acids; C18:1, oleic acid; F ROH $$ {F}_{ROH} $$ , inbreeding coefficient based on ROH; N = 2494; ROH, runs of homozygosity; SD, standard deviation.

All animals with phenotypic records underwent genotyping using the GeneSeek Genomic Profiler: GGP BovineLD v40, which included 30,105 SNPs (Illumina, San Diego, CA, USA). Subsequently, imputation to the BovineSNP50 BeadChip (Illumina) was carried out using the Beagle v4.0 software (Browning & Browning, 2007). The reference population for imputation consisted of the BovineSNP50 BeadChip genotypes of 651 Japanese Black cattle, and the details of this reference population are outlined in Watanabe (2016). Quality control criteria were applied and excluding the data under the thresholds. The thresholds set as follows: call rate for each animal < 0.95, minor allele frequency < 0.01, and Hardy–Weinberg equilibrium p < 0.001. After SNP editing, the final dataset included 2494 genotyped animals and 34,481 SNP markers.

2.2 Identification of ROH

We conducted an estimation of ROH utilizing the inbreeding coefficient based on ROH and the ROH-based relationship matrix. The inbreeding coefficient based on ROH was defined as the total length of ROH divided by the overall length of the autosomal genome covered by SNPs (Nishio, Inoue, Ogawa, et al., 2023). However, even individuals with the same inbreeding coefficient based on ROH do not necessarily share the exact same ROH region. Doekes et al. (2020) reported that the ROH-based relationship matrix indicates whether the animals are inbred at the same genomic positions. Therefore, we aimed to assess which of the two ROH definitions more effectively captures the phenomenon of inbreeding depression.

The ROH calculation was performed using the R package detectRUNS, employing a sliding window approach. We defined ROH according to the criteria outlined by Nishio, Inoue, Ogawa, et al. (2023), which has already been investigated the appropriate criteria in Japanese Black Cattle: (1) the minimum number of consecutive homozygous SNPs included in the ROH (L) was 60, (2) the minimum region length constituting the ROH was 1 Mbp, (3) the minimum SNP density in a genome window was 1 SNP every 100 kbp, (4) the maximum allowed distance between consecutive SNPs was 1 Mbp, (5) the number of heterozygous SNPs allowed in the ROH was 1, (6) the scanning window size was 15 SNPs, and (7) the scanning window threshold was 0.05.

2.3 Statistical models

In this study, we computed variance components, assessed prediction accuracy, and evaluated all SNP effects using the BGLR package (Pérez & de los Campos, 2014) in the R language with a Bayesian Gaussian-scaled inverse chi-square model. The Markov chain Monte Carlo (MCMC) was run for 100,000 cycles with a 50,000 burn-in period and a thinning interval of 10. For each trait, we employed four models: incorporating only additive genetic effects (A), incorporating both additive and dominance genetic effects (AD), incorporating additive and dominance genetic effects with the ROH effects calculated by ROH-based relationship matrix (ADR), and incorporating additive and dominance genetic effects with the linear regression of ROH-based inbreeding coefficient (ADF). The formulation for Model A follows:
y = Xb + Zu + e , $$ \mathbf{y}=\mathbf{Xb}+\mathbf{Zu}+\mathbf{e}, $$
where y $$ \mathbf{y} $$ is the vector of observed phenotypes; b $$ \mathbf{b} $$ is the vector of fixed effects including slaughter year (seven levels: 2013–2019), sex (two levels: steer and female), slaughterhouse (two levels), and linear and quadratic covariates of the slaughter age of month for all traits; X $$ \mathbf{X} $$ and Z $$ \mathbf{Z} $$ are the known incident matrices relating fixed and random additive genetic effects to observations, respectively; u $$ \mathbf{u} $$ is the vector of random additive genetic effects, assumed to be distributed as u ~ N 0 G σ A 2 $$ \mathbf{u}\sim N\left(\mathbf{0},\mathbf{G}{\sigma}_A^2\right) $$ , where σ A 2 $$ {\sigma}_A^2 $$ is the additive genetic variance and G $$ \mathbf{G} $$ is the genomic relationship matrix; and e $$ \mathbf{e} $$ is the vector of random residuals, assumed to be distributed as e ~ N 0 I σ E 2 $$ \mathbf{e}\sim N\left(\mathbf{0},\mathbf{I}{\sigma}_E^2\right) $$ , where σ E 2 $$ {\sigma}_E^2 $$ is the resisual variance and I $$ \mathbf{I} $$ is the identity matrix. The formulation for Model AD follows:
y = Xb + Zu + Hv + e , $$ \mathbf{y}=\mathbf{Xb}+\mathbf{Zu}+\mathbf{Hv}+\mathbf{e}, $$
where H $$ \mathbf{H} $$ is the known incident matrix relating random dominance genetic effects to observationsand v $$ \mathbf{v} $$ is the vector of random dominance genetic effects, assumed to be distributed as v ~ N 0 D σ D 2 $$ \mathbf{v}\sim N\left(\mathbf{0},\mathbf{D}{\sigma}_D^2\right) $$ , where σ D 2 $$ {\sigma}_D^2 $$ is the dominance genetic variance and D $$ \mathbf{D} $$ is the genomic relationship matrix. The formulation for Model ADR follows:
y = Xb + Zu + Hv + Jw + e , $$ \mathbf{y}=\mathbf{Xb}+\mathbf{Zu}+\mathbf{Hv}+\mathbf{Jw}+\mathbf{e}, $$
where J $$ \mathbf{J} $$ is the known incident matrix relating random ROH effects to observations and w $$ \mathbf{w} $$ is the vector of random ROH effects, assumed to be distributed as w ~ N 0 R σ ROH 2 $$ \mathbf{w}\sim N\left(\mathbf{0},\mathbf{R}{\sigma}_{ROH}^2\right) $$ , where σ ROH 2 $$ {\sigma}_{ROH}^2 $$ is the ROH variance and R $$ \mathbf{R} $$ is the ROH-based relationship matrix. The formulation for Model ADF follows:
y = Xb + Zu + Hv + β F ROH + e , $$ \mathbf{y}=\mathbf{Xb}+\mathbf{Zu}+\mathbf{Hv}+\beta {\boldsymbol{F}}_{\boldsymbol{ROH}}+\mathbf{e}, $$
where F ROH $$ {\boldsymbol{F}}_{\boldsymbol{ROH}} $$ is the vector of the inbreeding coefficient based on ROH and β $$ \beta $$ is the coefficient of the linear regression on F ROH $$ {\boldsymbol{F}}_{\boldsymbol{ROH}} $$ .
The additive genetic relationship matrix ( G $$ \mathbf{G} $$ ) was calculated according to VanRaden (2008):
G = A ′ A ∑ j = 1 n m 2 p j q j , $$ \mathbf{G}=\frac{{\mathbf{A}}^{\prime}\mathbf{A}}{\sum_{j=1}^{n_m}2{p}_j{q}_j}, $$
where A $$ \mathbf{A} $$ is a centered genotype incident matrix for individuals i = 1 , 2 , ⋯ , n and n is number of animals $$ \left(i=1,2,\cdots, n\ \mathrm{and}\ n\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{animals}\right) $$ of SNP additive codes j = 1 , 2 , ⋯ , n m and n m is number of markers $$ \left(j=1,2,\cdots, {n}_m\ \mathrm{and}\ {n}_m\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{markers}\right) $$ . The SNP genotype codes were 0 − 2 p j $$ 0-2{p}_j $$ , 1 − 2 p j $$ 1-2{p}_j $$ , and 2 − 2 p j $$ 2-2{p}_j $$ for genotypes A 1 A 1 $$ {A}_1{A}_1 $$ , A 1 A 2 $$ {A}_1{A}_2 $$ or A 2 A 1 $$ {A}_2{A}_1 $$ , and A 2 A 2 $$ {A}_2{A}_2 $$ , respectively; where p j $$ {p}_j $$ and q j $$ {q}_j $$ are the allele frequencies of A 1 $$ {A}_1 $$ and A 2 $$ {A}_2 $$ at locus p j = 1 − q j $$ \left({p}_j=1-{q}_j\right) $$ , respectively.
The dominance genetic relationship matrix ( D $$ \mathbf{D} $$ ) was calculated according to Vitezica et al. (2013) and Nishio and Satoh (2014):
D = S ′ S ∑ j = 1 n m 2 p j q j 2 , $$ \mathbf{D}=\frac{{\mathbf{S}}^{\prime}\mathbf{S}}{\sum_{j=1}^{n_m}{\left(2{p}_j{q}_j\right)}^2}, $$
where S $$ \mathbf{S} $$ is a centered genotype incident matrix for individuals i = 1 , 2 , ⋯ , n and n is number of animals $$ \left(i=1,2,\cdots, n\ \mathrm{and}\ n\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{animals}\right) $$ of SNP additive codes j = 1 , 2 , ⋯ , n m and n m is number of markers $$ \left(j=1,2,\cdots, {n}_m\ \mathrm{and}\ {n}_m\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{markers}\right) $$ . The SNP genotype codes were − 2 p j 2 $$ -2{p}_j^2 $$ , 2 p j q j $$ 2{p}_j{q}_j $$ , and − 2 q j 2 $$ -2{q}_j^2 $$ for genotypes A 1 A 1 $$ {A}_1{A}_1 $$ , A 1 A 2 $$ {A}_1{A}_2 $$ or A 2 A 1 $$ {A}_2{A}_1 $$ , and A 2 A 2 $$ {A}_2{A}_2 $$ , respectively.
The ROH-based relationship matrix ( R $$ \mathbf{R} $$ ) was calculated according to Doekes et al. (2020):
R = M ′ M ∑ j = 1 n m 2 p j * q j * , $$ \mathbf{R}=\frac{{\mathbf{M}}^{\prime}\mathbf{M}}{\sum_{j=1}^{n_m}2{p}_j^{\ast }{q}_j^{\ast }}, $$
where M $$ \mathbf{M} $$ is a centered genotype incident matrix for individuals i = 1 , 2 , ⋯ , n and n is number of animals $$ \left(i=1,2,\cdots, n\ \mathrm{and}\ n\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{animals}\right) $$ of SNP additive codes j = 1 , 2 , ⋯ , n m and n m is number of markers $$ \left(j=1,2,\cdots, {n}_m\ \mathrm{and}\ {n}_m\ \mathrm{is}\ \mathrm{number}\ \mathrm{of}\ \mathrm{markers}\right) $$ . The SNP genotype codes were 1 − p i * $$ 1-{p}_i^{\ast } $$ and 0 − q i * $$ 0-{q}_i^{\ast } $$ for being in a ROH or not, respectively, where p j * $$ {p}_j^{\ast } $$ and q j * $$ {q}_j^{\ast } $$ are the frequency of SNP j $$ j $$ being in a ROH or not, respectively.

The verification of predictive accuracy across models was performed using a sevenfold cross-validation. This process involves dividing the available dataset into seven equally sized subsets. The model is then trained on six of these subsets, and its performance evaluated on the remaining one. This process is repeated seven times, with each subset taking a turn as the test set. The evaluation metrics obtained from each iteration are collected, and the final performance assessment derived by calculating the average of these metrics.

To compare the magnitude and association of each SNP effect, we determined all SNP effects through back-solving according to Doekes et al. (2020). The formulation for each SNP effect follows:

α ̂ = A ′ G − 1 u ̂ ∑ j = 1 n m 2 p j q j $$ \hat{\boldsymbol{\alpha}}=\frac{{\mathbf{A}}^{\prime }{\boldsymbol{G}}^{-\mathbf{1}}\hat{\boldsymbol{u}}}{\sum_{j=1}^{n_m}2{p}_j{q}_j} $$ , δ ̂ = S ′ D − 1 v ̂ ∑ j = 1 n m 2 p j q j 2 $$ \hat{\boldsymbol{\delta}}=\frac{{\mathbf{S}}^{\prime }{\mathbf{D}}^{-\mathbf{1}}\hat{\mathbf{v}}}{\sum_{j=1}^{n_m}{\left(2{p}_j{q}_j\right)}^2} $$ , ω ̂ = M ′ R − 1 w ̂ ∑ j = 1 n m 2 p j * q j * . $$ \hat{\boldsymbol{\omega}}=\frac{{\mathbf{M}}^{\prime }{\boldsymbol{R}}^{-\mathbf{1}}\hat{\boldsymbol{w}}}{\sum_{j=1}^{n_m}2{p}_j^{\ast }{q}_j^{\ast .}} $$ where α ̂ $$ \hat{\boldsymbol{\alpha}} $$ , δ ̂ $$ \hat{\boldsymbol{\delta}} $$ , and ω ̂ $$ \hat{\boldsymbol{\omega}} $$ are the additive, dominance, and ROH SNP effects, respectively, and u ̂ $$ \hat{\mathbf{u}} $$ , v ̂ $$ \hat{\mathbf{v}} $$ , and w ̂ $$ \hat{\boldsymbol{w}} $$ are the estimated genomic breeding values, dominance, and ROH deviations, respectively. We employed the correlation coefficient between each estimate (genomic breeding values, dominance, and ROH deviations) and corrected phenotype value y ̂ $$ \hat{\mathbf{y}} $$ as predictive accuracy. The formula for each model follows:
y ̂ = y − X b ̂ $$ \hat{\mathrm{y}}=\mathrm{y}-\mathrm{X}\hat{\mathrm{b}} $$
where b ̂ $$ \hat{\mathbf{b}} $$ is the vector of fixed effects including slaughter year, sex, slaughterhouse, and linear and quadratic covariates of the slaughter age of month for all traits.

3 RESULTS AND DISCUSSION

3.1 Variance component estimate

Descriptive statistics and estimated genetic parameters for MUFA and C18:1 collected using gas chromatography are given in Tables 1 and 2, respectively. Means for MUFA and C18:1 were 57.0 ± 3.6% and 50.4 ± 3.5%, respectively, and were comparable to previous reports in Japanese Black cattle. The narrow-sense heritability estimates for MUFA and C18:1 were 0.52 ± 0.04 to 0.53 ± 0.04 and 0.57 ± 0.03, respectively. These estimates were slightly lower compared to previous studies in Japanese Black cattle (Inoue et al., 2011, 2017; Kohama et al., 2021; Onogi et al., 2015), but comparable to those of Nishio, Inoue, Arakawa, et al. (2023), likely because we utilized a subset of data used by Nishio, Inoue, Arakawa, et al. (2023). Regarding this, Nishio, Inoue, Arakawa, et al. (2023) discussed differences in narrow-sense heritability compared to previous studies.

TABLE 2. Estimated genetic parameters per model.
Trait Model σ A 2 $$ {\sigma}_A^2 $$ σ D 2 $$ {\sigma}_D^2 $$ σ ROH 2 $$ {\sigma}_{ROH}^2 $$ σ R 2 $$ {\sigma}_R^2 $$ σ P 2 $$ {\sigma}_P^2 $$ h A 2 $$ {h}_A^2 $$ σ D 2 / σ P 2 $$ {\sigma}_D^2/{\sigma}_P^2 $$ σ ROH 2 / σ P 2 $$ {\sigma}_{ROH}^2/{\sigma}_P^2 $$ DIC
MUFA A 7.84 - - 6.99 14.83 0.53 - - 12,193
(1.01) (0.22) (0.97) (0.04)
AD 7.83 0.97 - 6.07 14.87 0.52 0.07 - 12,127
(0.99) (0.23) (0.30) (0.96) (0.04) (0.02)
ADR 7.83 0.67 0.35 6.15 14.99 0.52 0.04 0.02 12,138
(1.02) (0.22) (0.09) (0.28) (0.97) (0.04) (0.04) (0.01)
ADF 7.83 0.82 - 6.19 14.84 0.53 0.06 - 12,130
(1.04) (0.25) (0.31) (1.00) (0.04) (0.02)
C18:1 A 8.43 - - 6.21 14.64 0.57 - - 11,921
(1.01) (0.20) (0.97) (0.03)
AD 8.38 0.79 - 5.45 14.63 0.57 0.05 - 11,850
(0.99) (0.25) (0.29) (0.97) (0.03) (0.02)
ADR 8.46 0.65 0.29 5.44 14.83 0.57 0.04 0.02 11,869
(1.01) (0.21) (0.07) (0.27) (0.98) (0.03) (0.01) (0.00)
ADF 8.34 0.70 - 5.53 14.58 0.57 0.05 - 11,856
(1.03) (0.21) (0.27) (1.00) (0.03) (0.02)
  • Upper row, posterior mean; bottom row, posterior standard deviation; σ A 2 $$ {\sigma}_A^2 $$ , additive genetic variance; σ D 2 $$ {\sigma}_D^2 $$ , dominance genetic variance; σ ROH 2 $$ {\sigma}_{ROH}^2 $$ , ROH variance; σ R 2 $$ {\sigma}_R^2 $$ , residual variance; σ P 2 $$ {\sigma}_P^2 $$ , phenotypic variance; h A 2 $$ {h}_A^2 $$ , narrow-sense heritability; σ D 2 / σ P 2 $$ {\sigma}_D^2/{\sigma}_P^2 $$ , ratio of σ D 2 $$ {\sigma}_D^2 $$ to σ P 2 $$ {\sigma}_P^2 $$ ; σ ROH 2 / σ P 2 $$ {\sigma}_{ROH}^2/{\sigma}_P^2 $$ , ratio of σ ROH 2 $$ {\sigma}_{ROH}^2 $$ to σ P 2 $$ {\sigma}_P^2 $$ . Abbreviations: MUFA, monounsaturated fatty acids; C18:1, oleic acid; ROH, runs of homozygosity; DIC, deviance information criterion.

Additionally, the estimated additive genetic variance and the narrow-sense heritability showed no differences among models, indicating that addition of dominance genetic and ROH effects to the traditional Model A had no effect. In Model AD, the estimated dominance genetic variance for MUFA and C18:1 was 0.97 ± 0.23 and 0.79 ± 0.25, respectively. It seems that the part of residual variance in Model A was transferred to the dominance genetic variance in Model AD. Additionally, the proportion of the dominance genetic variance relative to phenotypic variance for MUFA and C18:1 was 0.07 ± 0.02 and 0.05 ± 0.02, respectively. This suggested that the dominance genetic variance did not have a negligible effect in Japanese Black cattle for MUFA and C18:1. However, in Models ADR and ADF, the proportions of dominance genetic variance relative to phenotypic variance were lower at 0.04 ± 0.04 and 0.06 ± 0.02 for MUFA, respectively, and correspondingly 0.04 ± 0.01 and 0.05 ± 0.02 for C18:1, compared to Model AD. Models ADR and ADF showed a tendency for estimated dominance genetic variance to be separated into variance associated with ROH variance.

Previous studies reported orthogonality between additive genetic and dominance genetic effects (Doekes et al., 2020; Vitezica et al., 2013), and collinearity between dominance genetic effects and inbreeding depression has also been noted (Doekes et al., 2020; Garcia-Baccino et al., 2020). Therefore, we calculated the correlation coefficients for the off-diagonal elements between each genomic relationship matrix (Table 3). The correlation coefficients for the off-diagonal elements of between G $$ \mathbf{G} $$ and D $$ \mathbf{D} $$ , between G $$ \mathbf{G} $$ and R $$ \mathbf{R} $$ , and between D $$ \mathbf{D} $$ and R $$ \mathbf{R} $$ were 0.06, 0.13, and 0.37, respectively. The results showed a similarity to those of Doekes et al. (2020) (between G $$ \mathbf{G} $$ and D $$ \mathbf{D} $$ , 0.03; between G $$ \mathbf{G} $$ and R $$ \mathbf{R} $$ , 0.18; and between D $$ \mathbf{D} $$ and R $$ \mathbf{R} $$ , 0.44). Garcia-Baccino et al. (2020) reported that populations in Hardy–Weinberg equilibrium exhibit no correlation (0.05) between G $$ \mathbf{G} $$ and D $$ \mathbf{D} $$ . The above suggests collinearity between the dominance genetic and ROH effects in Japanese Black cattle, and also regarding traits associated with fatty acid composition.

TABLE 3. Correlation coefficient of off-diagonal elements between each genomic relationship matrix.
G-D G-R D-R
Correlation coefficient 0.06 0.13 0.37
  • Abbreviations: G, additive genetic relationship matrix; D, dominance genetic relationship matrix; R, ROH-based relationship matrix; G-D, correlation of off-diagonal elements between G and D; G-R, correlation of off-diagonal elements between G and R; D-R, correlation of off-diagonal elements between D and R; ROH, runs of homozygosity.

In classical quantitative genetics theory, inbreeding depression is primarily assumed to be due to the directional dominance genetic effects (Varona et al., 2018). Directional dominance genetic effects indicate larger positive compared to negative dominance genetic effects. In this study, the ROH effect may capture similar SNP effects as dominance genetic effects. Therefore, further investigation is necessary using more data. The ROH variance in Model ADR and its contribution to the phenotypic variance was 0.35 ± 0.09 and 0.02 ± 0.01 for MUFA, respectively, and correspondingly 0.29 ± 0.07 and 0.02 ± 0.00 for C18:1, with minimal impact. Additionally, no significant differences were observed in F ROH $$ {\boldsymbol{F}}_{\boldsymbol{ROH}} $$ in Model ADF. Nishio, Inoue, Ogawa, et al. (2023) reported the average inbreeding coefficient based on ROH ranged from 11.2 ± 7.0% to 25.0 ± 7.0% in another population of the breed. Therefore, our result might be attributed to the relatively low inbreeding coefficient based on ROH, averaging 7.4 ± 4.1% in the population of this study, indicating a low level of inbreeding. Furthermore, comparing the goodness of fit of each model using the deviance information criterion (DIC) indicated that Model AD (MUFA, 12,127; C18:1, 11,850) was the most favorable, but with only slight differences among the models (ranges: MUFA, 12,127–12,193; C18:1, 11,850–11,921). Hence, there was no significant disparity in stability of the models.

3.2 Prediction accuracy

The genomic prediction accuracies for MUFA and C18:1 derived from sevenfold cross-validation for each model were as follows: genomic estimated breeding value (GEBV) 0.49 ± 0.03 to 0.50 ± 0.03 and 0.61 ± 0.02, respectively, dominance deviation 0.06 ± 0.03 to 0.08 ± 0.03 and 0.05 ± 0.03 to 0.07 ± 0.03, ROH deviation 0.09 ± 0.06 and 0.05 ± 0.04, and the genetic value (GEBV + dominance deviation) 0.50 ± 0.03 and 0.61 ± 0.02 to 0.62 ± 0.02 (Table 4). There were no significant differences in prediction accuracies among the models. This suggests that considering dominance genetic and ROH effects did not improve prediction accuracy compared to traditional methods, likely because the variance of these effects may be small. If these effects have a larger impact in the future as inbreeding level increases, a model such as Model ADR may be better.

TABLE 4. Predictive accuracy of genomic evaluation in each model.
Traits Model Mean correlation coefficient
GEBV Dominance deviation ROH deviation Genetic value
MUFA A 0.50 - - -
(0.03)
AD 0.50 0.06 - 0.50
(0.03) (0.03) (0.03)
ADR 0.50 0.08 0.09 0.50
(0.03) (0.03) (0.06) (0.03)
ADF 0.49 0.06 - 0.50
(0.03) (0.03) (0.03)
C18:1 A 0.61 - - -
(0.02)
AD 0.61 0.05 - 0.62
(0.02) (0.03) (0.02)
ADR 0.61 0.07 0.05 0.62
(0.02) (0.03) (0.04) (0.02)
ADF 0.61 0.04 - 0.61
(0.02) (0.03) (0.02)
  • Upper row, posterior mean; bottom row, posterior standard deviation. Abbreviations: MUFA, monounsaturated fatty acids; C18:1, oleic acid; GEBV, genomic estimated breeding value; Genetic value, GEBV + dominance deviation; ROH, runs of homozygosity.

In our study, the prediction accuracy of GEBV was slight better than the findings of Nishio, Inoue, Arakawa, et al. (2023) (MUFA, 0.352–0.461; C18:1, 0.394–0.503), likely because we used data from only one prefecture, while Nishio, Inoue, Arakawa, et al. (2023) used data from multiple prefectures. The Japanese Black cattle populations in each prefecture exhibit unique genetic characteristics. This is because, historically, the closed breeding system in Japanese Black cattle has brought a subpopulation structure by each prefecture (Zoda et al., 2022). Particularly, the population of Japanese Black cattle in Hiroshima Prefecture is involved in the breeding and maintenance of bulls originating from the strain “Iwata,” designated as a rare strain by the Ministry of Agriculture, Forestry and Fisheries. Rare strains in Japanese Black cattle are important for the genetic diversity of the population because of a high probability of genetic loss not being carefully managed (Ministry of Agriculture, Forestry and Fisheries (MAFF), 2019). Furthermore, animals that are close in genetic distance to the reference population also had higher values of the reliability based on genomic information (Pszczola et al., 2012). Therefore, in Japanese Black cattle, using data from only one prefecture may have contributed to prediction accuracy rather than data from some prefectures.

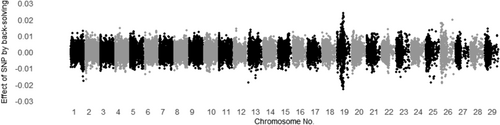
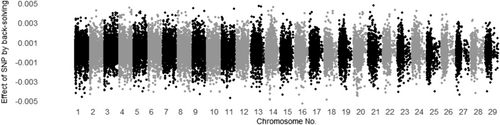
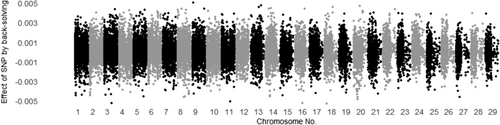
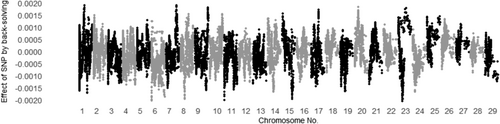
3.3 Evaluating all SNP effects by back-solving

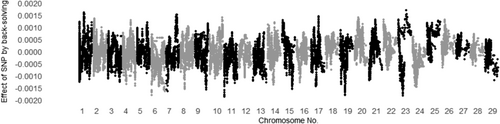
The SNP effects for MUFA and C18:1 calculated by back-solving from Model ADR are shown in Figures 1 and 2 for additive genetic effects, Figures 3 and 4 for dominance genetic effects, and Figures 5 and 6 for ROH effects, respectively. It has been reported that two polymorphisms, related to the FASN and SCD genes, influence the proportions of C18:1 and MUFA, respectively, and are significantly associated with fatty acid composition in Japanese Black cattle (Abe et al., 2009; Hayakawa et al., 2015; Taniguchi et al., 2004). As expected, Figures 1 and 2 show that the additive effects of the SNPs on chromosome 19 (FASN) contributed to phenotype of MUFA and C18:1, and on chromosome 26 (SCD) has only affected in phenotype of MUFA. This study is the first to investigate the dominant genetic and ROH effects on fatty acid traits in Japanese Black cattle. As mentioned above, the correlation coefficient of the off-diagonal elements of dominant genetic and ROH effects was 0.37, whereas the absolute values of the dominance genetic and ROH effects for both traits had minimal impact, with magnitudes close to 0.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
The additive effects of SNPs of monounsaturated fatty acids. SNPs, single-nucleotide polymorphisms.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
The additive effects of SNPs of oleic acid. SNPs, single-nucleotide polymorphisms.
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The dominance effects of SNPs of monounsaturated fatty acids. SNPs, single-nucleotide polymorphisms.
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
The dominance effects of SNPs of oleic acid. SNPs, single-nucleotide polymorphisms.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
The ROH effects of SNPs of monounsaturated fatty acids. SNPs, single-nucleotide polymorphisms; ROH, runs of homozygosity.
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
The ROH effects of SNPs of oleic acid. SNPs, single-nucleotide polymorphisms; ROH, runs of homozygosity.

We investigated genetic ability and prediction accuracy when considering the dominance genetic and ROH effects for MUFA and C18:1 in fatty acid composition for Japanese Black cattle in genomic prediction. The variance component estimate and prediction accuracy were similar for all models. However, the dominance genetic effects could not be ignored because of the proportion of the dominance genetic variance relative to phenotypic variance. Further research is needed to investigate the collinearity between the dominance genetic and ROH effects for MUFA and C18:1 in fatty acid composition for Japanese Black cattle.

ACKNOWLEDGMENTS

This work was supported by a research project for technologies to strengthen the international competitiveness of Japan's agriculture and food industry.

    CONFLICT OF INTEREST STATEMENT

    The authors declare no conflicts of interest for this article.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.