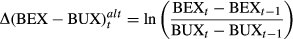Partial moment volatility indices
Abstract
Forward-looking partial moment volatility indices are developed using state-pricing, called the bear index (BEX) and bull index (BUX). Using S&P 500 index (SPX) option prices, we find that BEX and BUX provide superior forecasts for the lower and upper partial moments of future market realised volatility, respectively. We examine the relation between SPX returns and changes in BEX and BUX at the daily level. Results are consistent with the volatility feedback hypothesis. Further, we show that BEX may be more suitable as the ‘investor fear gauge’ than VIX.
1 Introduction
Volatility forecasts are of central importance to investors in managing their portfolio risk and timing the market.1 In particular, VIX has been available as a proxy for market risk since 1993 (Whaley, 1993). However, VIX is deficient in that it accounts for deviations on either side of the mean and cannot indicate the asymmetry of outcomes in terms of upside potential versus downside threat.
Investors with long positions in equities are more sensitive to downside losses than upside gains. Risk is frequently associated with failure to deliver the target return in the investment contexts (Fishburn, 1977), and variance is less suitable to measure the risk in this case. Prospect theory states that in equilibrium, investors who place greater weight on downside losses should demand greater compensation (Kahneman and Tversky, 1979; Gul, 1991). Psychological studies also question variance as a measure of investor perception of risk (Mao, 1970; Unser, 2000; and Veld and Veld-Merkoulova, 2008).
Previous studies have shown that US stock market returns are not symmetric (Campbell et al., 1997). Skewed distributions provide a better fit of market returns, allowing different volatilities below and above the mean (Estrada, 2008). Negative skewness in S&P 500 returns is also reflected in the implied volatility of option post-1987 (Bates, 2000). This suggests that lower partial moment (LPM) volatility may better capture potential downside threats and therefore be a better proxy for equity risk than the VIX itself.
To address these shortcomings with the VIX, we construct forward-looking indexes for LPM and upper partial moment (UPM) volatility, denoted the bear index (BEX) and bull index (BUX), respectively. BEX is a downside measure capturing returns below a threshold, while BUX captures upside above a threshold. BEX and BUX are constructed using a state prices calculated from Black-Scholes analytic second derivatives, providing superior forecasts for partial moment volatility than VIX.
The concept of state-pricing originates from the general equilibrium model of security markets in Arrow and Debreu (1954). For each future state, the price of any asset is calculated as the state price weighted sum of its future pay-offs across states s = {1,…, S} (Duffie, 2001). This result is similar to the result proposed in Harrison and Kreps (1979) and Harrison and Pliska (1981).
We examine contemporaneous relations between S&P 500 index returns and changes in BEX, BUX and VIX. Our results provide insight into the negative correlation between volatility and expected return. Moreover, we show that BEX may be more suitable as the ‘investor fear gauge’ than VIX.
The remainder of this study is organised as follows. Section 2 reviews the literature on the partial moment framework and how our research fits in. Section 3 describes the data and the methodology used to construct BEX and BUX. Section 4 presents the hypotheses, studies the performance of BEX and BUX as partial moment volatility forecasts and investigates the contemporaneous changes in daily market returns. Section 5 concludes.
2 Literature review on partial moment framework
Variance has been challenged as a measure of risk on theoretical and empirical grounds (Mao, 1970b and Fishburn (1977)). The mean-variance model is central to the Sharpe-Lintner Capital Asset Pricing model (Sharpe, 1964; Lintner, 1965). However, it has limited generality (Bawa, 1975 and Fishburn, 1977), relying on a quadratic utility function or normally distributed asset return process (Borch, 1969; Feldstein, 1969).2
Markowitz (1959) recognises the failure of mean-variance analysis to capture asymmetry of returns. He advocates semivariance as a risk measure, equivalent to partial moment variance where the threshold is set at the mean return. This measure is defined as, S = E(min(0, R – h)2), where R is the return and h can be chosen as the mean return E(R). h represents the safety-first disaster level return that the investor tries to avoid (Roy, 1952). Markowitz shows that if the utility function is quadratic up to h but linear above h, then the expected utility maximiser ranks portfolios according to the mean-semivariance criteria. He presents mean-semivariance as an alternative, being less complicated than fitting higher-moment parameters in the model.
Semivariance is a special class of downside risk measure within the LPM framework, Bawa (1975, 1978) and Fishburn (1977) show that more general utility assumptions can be provided by downside risk measures.
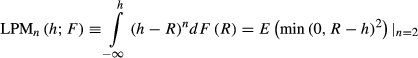 (1)
(1)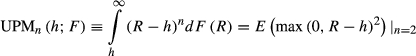 (2)
(2)Given that we are not performing risk-return analysis, the case where n = 2 corresponds to semivariance.4 LPM volatility is defined as the square root of LPM degree 2, and UPM volatility the square root of UPM degree 2.
Popular candidates for h include: (i) 0 for the avoidance of losses; (ii) Rf for the avoidance of returns below the risk-free rate; and (iii) mean return rate E(R) for comparison with the original mean-variance analysis. Psychological studies evidence no clear determination of the LPM threshold (Mao, 1970b; Unser, 2000; Veld and Veld-Merkoulova, 2008). We follow the industry standard for zero mean assumption in 30-day realised variance of market returns (see e.g. Carr and Wu (2006)) and set the threshold h to be 0.
Previous literature has focused on developing both theoretical and empirical grounds in the LPM framework. There is mixed evidence in support of LPM asset models over benchmarks such as the CAPM (Jahankhani, 1976; Bawa et al., 1981; Harlow and Rao, 1989; and Anthonisz, 2012). One difficulty is that semivariance is less tractable mathematically, and there is no one-to-one correspondence in the co-semivariance among individual securities and the market portfolio.5
Holthausen (1981) is among the first to use both UPMs and LPMs as measures for investor preferences. More recently, Andersen and Bondarenko (2010) use Chicago Mercantile Exchange (CME) American-style option prices of the S&P 500 futures to estimate the risk-neutral densities and examine the market price of upside and downside variance. They define the Down-Up Ratio as the ratio of variance on the downside versus upside. They use the Positive Convolution Approximation method of Bondarenko (2003) to estimate the risk-neutral densities each day, assuming a fixed maturity of 21 trading days.6
Numerous studies have examined realised semivariance. Ang et al. (2006) show that the cross section of equity returns contains a premium for bearing downside risk. Using past price movements, they explore the determinants of downside risk. Barndorff-Nielsen et al. (2010) obtain realised semivariance based on high frequency downward movements in asset prices.
Our work differs from realised semivariance research and contributes to prediction of the ex ante semivariance from traded index option prices. Our innovation is to extend the well-established analysis on VIX (volatility) to its LPM counterpart BEX (LPM volatility) and UPM counterpart BUX (UPM volatility).
In this study, we do not attempt to build a testable asset pricing model in the partial moments framework. Rather, we propose the BEX and BUX as estimates for the 30-day ex ante LPM and UPM volatility of market returns. Our downside/upside risk measures are similar in spirit to Andersen and Bondarenko (2010), but fundamentally different in that they are based on state-pricing theory, rely on different option series and can be extended to forecast partial skewness and kurtosis.
3 BEX and BUX
In this section, we describe the data and methodology used to construct BEX and BUX. We first identify the pay-off structure for BEX and BUX securities, and then estimate the state prices.
3.1 Data collection
Historical prices of SPX call and put options were based on closing quotes of SPX from 4 January 1996 to 30 August 2013 obtained from OptionMetrics. Data include the highest closing bid and ask quotes for each SPX option, and Black-Scholes implied volatilities based on the average of best bid and ask. Using the standard approach of the Chicago Board Options exchange (CBOE) with the option price approximated by the average of best bid and ask.
US one-month and three-month Treasury-bill yields were used as risk-free interest rates, after adjusting for dividend yields. Treasury-bill and dividend yields are obtained from the Federal Reserve Bulletin and Option Metrics, respectively. For SPX option with the maturity shorter (longer) than either of the two Treasury-bill maturities, the risk-free rate is approximated by the dividend-adjusted one-month (three-month) yield.
Daily quotes of VIX are obtained from both OptionMetrics and CBOE VIX Historical Price Data7 to ensure the completeness of the data.
Common data filters are applied. SPX options with maturities less than 7 and greater than 81 days are excluded, to avoid any market microstructure impacts, liquidity issues and price effects near contract expiration (Figlewski, 2010). Options with bid prices below $0.05 are eliminated, along with any put (call) options with strike prices lower (higher) than that of the first two consecutive puts (calls) with zero bid prices. At- and out-of-the-money options are also excluded, along with options with Black-Scholes implied volatilities below 0 or above 1.
3.2 Methodology
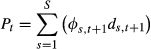 (3)
(3)summing over all possible states {1,…, S}. Pt is the price of some asset at time t, Φs,t + 1 is the state price, and ds,t + 1 is the pay-off of this asset at state s and time t + 1. BEX2 is calculated with a similar process to the theoretical derivation of VIX, by replicating the fair value of future variance, with BEX its squared-root. BUX can be obtained similarly.
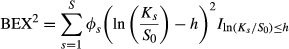 (4)
(4)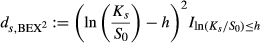 (5)
(5)As discussed in the previous section, we assume an industry standard zero mean assumption for short-term SPX returns. We also consider the nonzero mean counterparts, where Treasury-bill yields and the realised mean return of SPX over the most recent thirty trading days are adopted. Results are qualitatively the same.
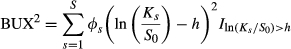 (6)
(6)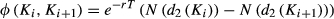 (7)
(7)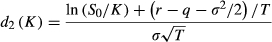 (8)
(8)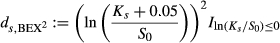 (9)
(9)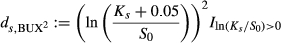 (10)
(10)Summing all products of the state pay-off and the state price, we obtain the BEX2 and BUX2. BEX and BUX are obtained by taking the square root of these measures.
3.3 Description of indices
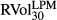 and
and 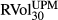 . Logarithmic returns are defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013. All entries are represented in percentage volatility points. As we have set h = 0 in BEX and BUX, we use the zero mean assumption in realised LPM and UPM variance calculation for a direct comparison. Two ex post LPM and UPM realised volatility estimates are estimated, as shown in equations 11 and 12, respectively.
. Logarithmic returns are defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013. All entries are represented in percentage volatility points. As we have set h = 0 in BEX and BUX, we use the zero mean assumption in realised LPM and UPM variance calculation for a direct comparison. Two ex post LPM and UPM realised volatility estimates are estimated, as shown in equations 11 and 12, respectively.
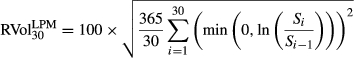 (11)
(11)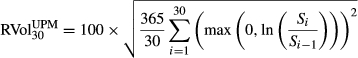 (12)
(12)| Moments | BEX | BUX | VIX |
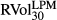
|
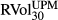
|
ΔBEX | ΔBUX | ΔVIX |
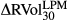
|
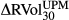
|
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 15.51 | 12.34 | 21.74 | 12.51 | 12.79 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Median | 14.61 | 11.62 | 20.31 | 10.66 | 10.94 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Maximum | 60.16 | 47.85 | 80.86 | 68.20 | 60.27 | 0.53 | 0.47 | 0.50 | 0.94 | 0.83 |
| Minimum | 6.68 | 5.32 | 9.89 | 1.23 | 3.43 | −0.51 | −0.55 | −0.35 | −1.05 | −0.71 |
| Std. Dev. | 6.23 | 4.96 | 8.48 | 8.30 | 7.05 | 0.07 | 0.07 | 0.06 | 0.11 | 0.09 |
| Skewness | 1.94 | 1.94 | 1.94 | 2.57 | 2.59 | 0.43 | 0.43 | 0.59 | −0.25 | 0.55 |
| Kurtosis | 9.64 | 9.64 | 9.63 | 13.24 | 13.30 | 6.71 | 7.11 | 6.78 | 23.29 | 16.20 |
-
This table reports the sample mean, median, maximum, minimum, standard deviation, skewness and kurtosis on the levels and logarithmic returns of the lower partial moment (LPM) volatility index BEX, the upper partial moment (UPM) volatility index BUX, the CBOE volatility index VIX, the 30-day LPM and UPM realised volatilities with calendar days convention
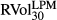 and
and 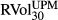 , respectively. The logarithmic return is defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013. All entries are represented in percentage volatility points.
, respectively. The logarithmic return is defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013. All entries are represented in percentage volatility points.
In Table 1, the sample means of BEX and BUX are 15.51 and 12.34, respectively. As expected, the sample means, medians, maximums and standard deviations of BEX and BUX are smaller than those of VIX, as the measures only describe a portion of the return distribution
The sample mean of BUX is similar to 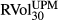 at 12.79, although the standard deviation of BUX is smaller than the realised counterpart. In comparison, the sample mean of BEX is much higher than
at 12.79, although the standard deviation of BUX is smaller than the realised counterpart. In comparison, the sample mean of BEX is much higher than 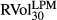 , with a difference of 3. This suggests index options traders are more risk averse and pay a premium for extreme losses or ‘Black swan’ events, consistent with the findings in Bates (1991) and Rubinstein (1994).10
, with a difference of 3. This suggests index options traders are more risk averse and pay a premium for extreme losses or ‘Black swan’ events, consistent with the findings in Bates (1991) and Rubinstein (1994).10
For logarithmic daily changes, all sample means are approximately zero. Standard deviations, absolute maximums and minimums of ∆BEX, ∆BUX and ∆VIX are all smaller than their ex post realised counterparts. This suggests that while risk-neutral moments over-estimate the ex post measures on average, they appear less volatile in daily changes and do not capture them in extreme market conditions.
Table 2 reports the cross-correlations between BEX, BUX, VIX and 30-day forward LPM and UPM realised SPX return volatilities. Although based on different methodologies, BEX, BUX and VIX are highly positively correlated in both levels and logarithmic daily changes, and all three correlate with ex post realised measures. However, these correlations become negligible in the daily changes.
| Correlation | BEX | BUX | VIX |

|
|
ΔBEX | ΔBUX | ΔVIX |
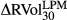
|
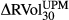
|
|---|---|---|---|---|---|---|---|---|---|---|
| BEX | 1.00 | 0.99 | 0.99 | 0.64 | 0.82 | |||||
| BUX | 0.99 | 1.00 | 0.99 | 0.64 | 0.82 | |||||
| VIX | 0.99 | 0.99 | 1.00 | 0.63 | 0.81 | |||||
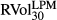
|
0.64 | 0.64 | 0.63 | 1.00 | 0.80 | |||||
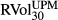
|
0.82 | 0.82 | 0.81 | 0.80 | 1.00 | |||||
| ΔBEX | 1.00 | 0.99 | 0.90 | −0.37 | 0.31 | |||||
| ΔBUX | 0.99 | 1.00 | 0.90 | −0.38 | 0.31 | |||||
| ΔVIX | 0.90 | 0.90 | 1.00 | −0.39 | 0.32 | |||||
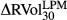
|
−0.37 | −0.38 | −0.39 | 1.00 | −0.15 | |||||
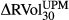
|
0.31 | 0.31 | 0.32 | −0.15 | 1.00 |
-
This table reports cross-correlations on the levels and logarithmic returns of the lower partial moment (LPM) volatility index BEX, the upper partial moment (UPM) volatility index BUX, the CBOE volatility index VIX, the 30-day LPM and UPM realised volatilities with calendar days convention
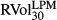 and
and 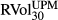 , respectively. The logarithmic return is defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013.
, respectively. The logarithmic return is defined as, for example, ∆BEXt = ln(BEXt/BEXt−1). Each series has 4445 daily observations from 4 January 1996 to 30 August 2013.
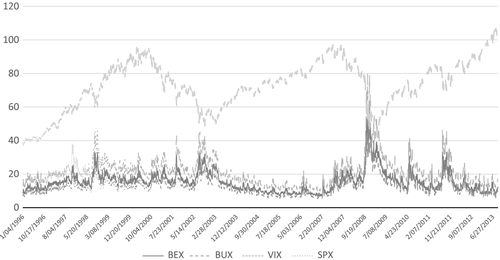
Figure 1 shows daily closing levels of BEX, BUX, VIX and the scaled S&P 500 index from 6 January 1996 to 30 August 2013. It is clear that BEX and BUX follow VIX, especially during the GFC. BEX is invariably higher than BUX. The difference between BEX and BUX appears to increase when the market is moving downwards particularly around the mid-2003 and post-GFC, and becomes almost negligible when the market is moving upwards.
4 Hypotheses and results
In this section, we test whether BEX and BUX provide better predictions than VIX. We then study whether contemporaneous changes in daily S&P 500 market returns can be better explained by daily changes of BEX and BUX versus that of VIX. Finally, we test whether BEX is a better estimate as ‘investor fear gauge’ than the VIX itself.
4.1 Forecasting partial moment volatilities
The VIX is a measure of ex ante 30-day expected volatility of the S&P 500 index (CBOE, 2009). VIX does not, however, describe the proportion of upside potential versus downside threat. To solve this problem, we construct BEX (BUX) as a predictor of the ex ante 30-day expected LPM (UPM) volatility and expect they provide a better forecast in the corresponding partial moment volatility than VIX.
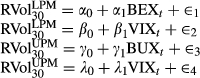 (13)
(13)Hypotheses are tested using these regressions. First, if BEX and VIX contain some information about future realised LPM volatility, then the slope coefficients should be nonzero. Second, if BEX and VIX are unbiased forecasts of future realised LPM volatility, one should expect an intercept of zero and slope coefficients not significantly different from 1. We report the ordinary least-squares estimates in Table 3. The covariance matrix is computed according to Newey and West (1994) to correct for any potential serial correlations in the error terms.
| Panel A |
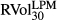
|
Coefficient | Std. error | t-Statistics | Prob. | Adj. R2 | Wald test |
|---|---|---|---|---|---|---|---|
| BEX | 0.852 | 0.069 | 12.300 | 0.0000 | 0.0132 | ||
| Intercept | −0.726 | 0.965 | −0.752 | 0.452 | 40.9% | ||
| VIX | 0.621 | 0.050 | 12.519 | 0.0000 | 0.0000 | ||
| Intercept | −1.011 | 0.973 | −1.039 | 0.299 | 40.2% |
| Panel B |
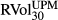
|
||||||
|---|---|---|---|---|---|---|---|
| BUX | 1.164 | 0.066 | 17.527 | 0.0000 | 0.0281 | ||
| Intercept | −1.596 | 0.725 | −2.199 | 0.0279 | 67.1% | ||
| VIX | 0.673 | 0.038 | 17.650 | 0.0000 | 0.0000 | ||
| Intercept | −1.859 | 0.733 | −2.538 | 0.011 | 65.6% |
-
This table presents regression results of the lower partial moment (LPM) volatility index BEX, the upper partial moment (UPM) volatility index BUX and the CBOE volatility index VIX against the 30-day LPM and UPM realised volatilities with calendar days convention
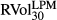 and
and 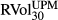 , respectively. There are 4445 daily observations from 4 January 1996 to 30 August 2013 in each series. The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regressions equations are presented in equation 13. All volatility estimates calculate the realised volatility using monthly logarithmic returns. The last column on the right reports the F-statistics in the Wald Test, which is to test whether the slope coefficient is significantly different from 1. The lower the number, the higher the chance of being significantly different from 1.
, respectively. There are 4445 daily observations from 4 January 1996 to 30 August 2013 in each series. The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regressions equations are presented in equation 13. All volatility estimates calculate the realised volatility using monthly logarithmic returns. The last column on the right reports the F-statistics in the Wald Test, which is to test whether the slope coefficient is significantly different from 1. The lower the number, the higher the chance of being significantly different from 1.
Panel A reports the regression results of BEX and VIX against 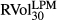 . The estimate of intercept α0 is −0.726 and is not statistically significantly against a null of α0 = 0 at the 5 percent level. Similarly, for VIX, the estimate of β0 is −1.011 and also not statistically significantly different from 0.
. The estimate of intercept α0 is −0.726 and is not statistically significantly against a null of α0 = 0 at the 5 percent level. Similarly, for VIX, the estimate of β0 is −1.011 and also not statistically significantly different from 0.
For the slope coefficients, the estimate of α1 is 0.852 and is statistically significant against a null of α1 = 0. This indicates that BEX contains information about future realised LPM volatility. In comparison, the estimate of β1 from the regression of 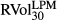 and VIX is 0.621 with a standard error of 0.05. This is statistically significant against a null of β1 = 0. We also run the Wald test, rejecting the null hypothesis at the 5 percent level for BEX and at all levels for VIX. The slope coefficient of VIX is more likely to be statistically different from 1 than that of BEX. The adjusted R2 of BEX model is 40.9 percent, being 0.7 percent higher than the VIX model. We conclude that BEX is a better predictor of future realised LPM volatility.
and VIX is 0.621 with a standard error of 0.05. This is statistically significant against a null of β1 = 0. We also run the Wald test, rejecting the null hypothesis at the 5 percent level for BEX and at all levels for VIX. The slope coefficient of VIX is more likely to be statistically different from 1 than that of BEX. The adjusted R2 of BEX model is 40.9 percent, being 0.7 percent higher than the VIX model. We conclude that BEX is a better predictor of future realised LPM volatility.
We also test hypotheses related to BUX and VIX. First, if BUX and VIX contain some information about future realised UPM volatility, then slope coefficients in equation 13 should be nonzero. If BUX and VIX are unbiased forecasts of future realised UPM volatility, one should expect an intercept of zero and slope not significantly different from 1.
Panel B reports the regression results of BUX and VIX against 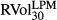 . The estimate of intercept γ0 is −1.596 which is statistically significant against a null of γ0 = 0 at the 5 percent level. Similarly, the estimate of λ0 is −1.859 and also statistically significantly different from 0. Both BUX and VIX provide biased forecasts, but this should not be problematic if the magnitude of the bias is constant.
. The estimate of intercept γ0 is −1.596 which is statistically significant against a null of γ0 = 0 at the 5 percent level. Similarly, the estimate of λ0 is −1.859 and also statistically significantly different from 0. Both BUX and VIX provide biased forecasts, but this should not be problematic if the magnitude of the bias is constant.
For the slope coefficients, the estimate of γ1 is 1.164, being statistically significant against a null of γ1 = 0. In comparison, the estimate of λ1 from the regression of LPM and VIX is 0.673 with a standard error of 0.038. Again, the Wald test statistics show that we reject the null hypothesis at the 5 percent level.
Table 3 also shows that while BEX overestimates UPM volatility, BUX does the opposite, implying that SPX option traders tend to underestimate upside potential and overestimate the downside threats. This is consistent with findings in Bakshi et al. (2003) that the market is risk-neutrally left-skewed. The adjusted R2 of the BUX model is 67.1 percent, being 1.5 percent higher than the VIX model. We conclude that BUX is a less unbiased forecast with greater predictive power for future realised UPM volatility.
4.2 Explaining contemporaneous changes in daily market returns
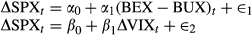 (14)
(14)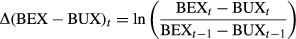
To examine relationships among BEX, BUX and market returns, we need to include both BEX and BUX as explanatory variables. To overcome the problem with multicollinearity between BEX and BUX, we create a variable that takes the difference of BEX and BUX on each trading day. It is well documented that empirical returns are asymmetric (Bates, 1991 and Rubinstein, 1994). Subtracting BEXt by BUXt describes how much more deviation is expected in the downside than the upside from the options market. A positive ∆(BEX − BUX)t shows that the difference between the downside and upside risk becomes larger with BEXt − BUXt > BEXt−1 − BUXt−1, meaning more downside losses versus upside gains. This definition allows us to extract the risky component of volatility.
Two hypotheses can be tested using regressions in equation 14. First, if there is a negative relation between returns and changes of volatility, the slope coefficient β1 should be negative, consistent with results in the literature. Second, given that ∆(BEX − BUX)t measures variation between the difference in downside and upside volatilities, we expect a negative relation with the market return, with α1 < 0.
Table 4 reports ordinary least-squares results. The covariance matrix is computed according to Newey and West (1994) to correct for potential serial correlations in errors.
| Panel A | ΔSPXt | Coefficient | Std. error | t-Statistics | Prob. | Adj. R2 |
|---|---|---|---|---|---|---|
| Δ(BEX – BUX)t | −0.132 | 0.005 | −24.607 | 0.0000 | ||
| Intercept | 0.0002 | 0.0001 | 1.890 | 0.0588 | 52.3% |
| Panel B | ΔSPXt | |||||
|---|---|---|---|---|---|---|
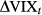
|
−0.154 | 0.006 | −26.837 | 0.0000 | ||
| Intercept | 0.0002 | 0.0001 | 1.912 | 0.056 | 56.4% |
-
This table presents the regression results of the daily logarithmic change of the lower partial moment (LPM) volatility index BEX and the upper partial moment (UPM) volatility index BUX against the daily logarithmic return of S&P 500 index. The daily changes are defined as, ΔSPXt = ln (SPXt – SPXt−1) and
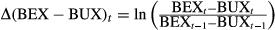 . There are 4445 daily observations from 5 January 1996 to 30 August 2013 in each series. The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regression equations are presented in equation 14.
. There are 4445 daily observations from 5 January 1996 to 30 August 2013 in each series. The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regression equations are presented in equation 14.
Panel A reports the results for ∆(BEX − BUX)t against ∆SPXt. The estimate of α0 is 0.0002 and is not significantly different from 0 at all levels. The estimate of α1 is −0.132 with a standard error of 0.005, and we cannot reject a null of α1 < 0 at any level. Similar results can be found in the bottom panel for ∆VIXt with intercept not significantly different from 0 and slope −0.154 with a standard error 0.006.
Although both slope coefficients are negative, more insight is provided by the first regression. While the negative β1 from the second regression is consistent with prior literature evidencing a negative relation between changes in volatility and market returns, the negative α1 emphasises that the negative relation between risk and return comes from the downside. The volatility feedback effect states that an anticipated increase in volatility leads to an immediate price drop. By extracting the risky component of volatility, we show that when downside volatility exceeds upside volatility, this excess contributes to the decline in returns.
4.3 Investor fear gauge: BEX or VIX
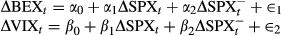 (15)
(15)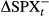 describes the rate of change of SPX conditional on whether it is a negative return,
describes the rate of change of SPX conditional on whether it is a negative return, 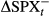 = min(0, ∆SPXt).
= min(0, ∆SPXt).Three hypotheses are tested. First, if the rate of change in BEX and VIX is related to daily market returns, then the slope coefficients α1 and β1 should be negative. Second, coefficients α2 and β2 should also be negative to reflect an asymmetric response to market declines. Third, if this relationship is unbiased, then intercepts should be zero.
Table 5 reports ordinary least-squares results with the covariance matrix computed according to Newey and West (1994) with a lag truncation of 8.
| Panel A | ΔBEXt | Coefficient | Std. error | t-Statistics | Prob. | Adj. R2 |
|---|---|---|---|---|---|---|
| ΔSPXt | −3.541 | 0.161 | −22.041 | 0.000 | ||
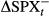
|
−0.811 | 0.263 | −3.087 | 0.002 | ||
| Intercept | −0.003 | 0.001 | −2.412 | 0.016 | 52.6% |
| Panel B |
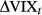
|
|||||
|---|---|---|---|---|---|---|
| ΔSPXt | −3.187 | 0.146 | −21.785 | 0.000 | ||
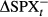
|
−0.885 | 0.249 | −3.554 | 0.000 | ||
| Intercept | −0.003 | 0.001 | −3.040 | 0.0002 | 56.9% |
-
This table presents the regression results of the daily logarithmic change of the lower partial moment (LPM) volatility index BEX and the volatility index VIX against the daily logarithmic return and conditional return of S&P 500 index. The daily change is estimated as ∆SPXt = ln(SPXt/SPXt−1). The conditional rate of change of S&P 500 index, depending on whether it is a negative return, is estimated as
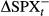 = min(0, ∆SPXt). The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regression equations are presented in equation 15.
= min(0, ∆SPXt). The heteroskedasticity-consistent standard errors and covariance matrix are computed according to Newey and West (1994) with the lag truncation of 8. Regression equations are presented in equation 15.
Panel A presents results for BEX, with α1 estimated at −3.541 with a standard error of 0.161. This is statistically significant against a null of α1 = 0 at all levels. The estimate of α2 is −0.811 with a standard error of 0.263 and is also statistically significant against a null of α2 = 0 at all levels. The intercept is −0.003 with a standard error of 0.001, being statistically significant against a null of α0 = 0 at the 5 percent level. This reflects not only the inverse relationship between movements in BEX and movements in the SPX market, but also the asymmetry.
The bottom panel B presents the result of VIX, confirming Whaley (2009). However, the p-value for intercept term β0 is also statistically significant against a null of 0. That is, the relationship between these contemporaneous changes tends to be biased.
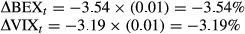
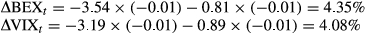
That is, when there is a drop in the market, a larger response is found in BEX than VIX. BEX rises by an extra 27 basis points for every 100 basis points drop in SPX. We conclude that BEX may be more qualified as the barometer of investors’ fear for downside threats than VIX.
5 Conclusion
Volatility has been long referred to as a proxy for equity market risk. However, volatility takes account of deviations from the mean on both sides, and forward volatility indices such as VIX do not differentiate between upside potential and downside threat. Alternative measures of risk have been proposed, including semivariance (Markowitz, 1959) and LPM measures by Bawa (1975) and Bawa and Lindenberg (1977).
This study uses the state-preference pricing approach with Black-Scholes analytic second derivatives as state prices. We develop a forward-looking LPM volatility index BEX as a proxy for S&P 500 market downturns in the next 30 days, and an UPM counterpart BUX as a proxy for upturns. We first show that BEX and BUX are less data dependent and easier to compute. Even though BEX and BUX are constructed using a different methodologies and principles to VIX, they are highly correlated in terms of both levels and logarithmic daily changes. More importantly, we find that BEX and BUX are better forecasts for the LPM and UPM of market volatility than VIX, respectively.
We then examine the contemporaneous relation between the SPX returns and changes in BEX, BUX and VIX. The negative relation between changes of volatility and market returns is well documented. By breaking volatility into upside and downside components, our results provide more insight. To overcome the problem of multicollinearity, we create a variable to describe how much more deviation is expected in the downside than the upside. By extracting the downside component from volatility, we are able to show that when the downside volatility is greater than the upside counterpart, this excess downside contributes to a decline in returns.
Last, we examine whether BEX is a better ‘investor fear gauge’ than VIX. Whaley (2009) documents that VIX responds more to negative changes in S&P 500 index returns than positive changes, justifying it as the investors’ fear gauge. By regressing daily logarithmic changes of BEX against daily changes of S&P 500 index conditional on whether returns are negative, we find that BEX responds more than VIX when there is a market drop. We conclude that BEX might be more qualified as the ‘investor fear gauge’ than VIX.
The BEX and BUX indices have obvious applications for participants looking to time the market, including long-term investors and short-term traders and speculators. Moreover, the BEX proves to be a more valuable downside measure than the VIX and can be applied to measure downside volatility exposures and hedge using swaps or derivatives. There is significant potential for application of these methods to value complex contingent claims in other asset markets, including other global equity markets, debt markets, energy markets and markets for renewable energy credits.
Notes
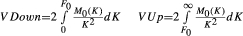
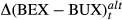 .implies that BEXt – BEXt−1 > BUXt – BUXt−1, given that the natural logarithm function is strictly increasing. The problem with this approach is that the function is undefined if either the numerator or the denominator in the logarithm function becomes negative. In contrast, we do not have this problem with ∆(BEX − BUX)t because BEX is always greater than BUX in our sample, as illustrated in Figure 1.
.implies that BEXt – BEXt−1 > BUXt – BUXt−1, given that the natural logarithm function is strictly increasing. The problem with this approach is that the function is undefined if either the numerator or the denominator in the logarithm function becomes negative. In contrast, we do not have this problem with ∆(BEX − BUX)t because BEX is always greater than BUX in our sample, as illustrated in Figure 1.