Association between Big 4 auditor choice and cost of equity capital for multiple-segment firms
Abstract
Prior studies document a negative association between Big 4 auditor choice and the implied cost of equity capital, suggesting that Big 4 auditors mitigate information asymmetry (IA) between shareholders and managers. This study extends this line of research and reports that the negative association is more pronounced in multiple-segment firms, where IA is more severe than in single-segment firms. We also find that the association between Big 4 auditor choice and the cost of equity capital becomes more negative as the number of segments increases. Taken together, our findings suggest that the role of Big 4 auditors in reducing the cost of equity capital becomes more significant when greater IA exists.
1. Introduction
This study examines whether the negative association between high-quality auditor choice and the implied cost of equity capital is more pronounced in multiple-segment firms than in single-segment firms. Prior studies document that Big 4 auditors provide higher quality auditing services than non-Big 4 auditors and that such high-quality service enables firms to decrease information asymmetry (IA) between shareholders and managers (e.g. Francis et al., 1999; Willenborg, 1999).1 In contrast, Lawrence et al. (2011) argue that the difference in audit quality documented in prior studies is mainly due to client characteristics that endogenously determine auditor choice; thus, they call for future research to further disentangle client characteristics from audit quality effects.
To respond to their call and to add on inconclusive prior literature, we examine whether or not the strong monitoring role of Big 4 auditors mitigates the diversification discount documented in prior studies. Lang and Stulz (1994), Berger and Ofek (1995) and Gomes and Livdan (2004) all report that multiple-segment firms are valued at a discount compared with single-segment firms. They describe this phenomenon as a ‘diversification discount’ or ‘negative excess value’. More specifically, previous studies show that diversified firms have higher expected returns, suggesting that the cost of equity capital is higher for the multiple-segment firms than for single-segment firms (Bens and Monahan, 2004; Demirkan et al., 2012). Investors in diversified firms require a premium, because they expect lower cash flow from inefficient resource allocation, such as over- or underinvestment, cross-subsidization among segments (Martin and Sayrak, 2003), self-interested suboptimal behaviours of managers (Morck et al., 1990; Denis et al., 1997) or mergers of already inefficient firms (Graham et al., 2002). Another line of research deals with information problems associated with the diversification discount, which suggests that information asymmetries can lead to higher expected returns for diversified firms (Krishnaswami and Subramaniam, 1999; Gilson et al., 2001). In addition, investors' ability to monitor the value-destroying activities of managers is limited due to the complexity of diversified firms. This exacerbates the IA problem between managers and shareholders in such firms (Denis et al., 1997; Bens and Monahan, 2004). Thus, investors value multiple-segments firms at a discount to compensate for the higher risk related to increased IA (Bens and Monahan, 2004; Demirkan et al., 2012). Hence, the cost of capital for multiple-segment firms becomes higher than that for single-segment firms.2
Big 4 auditors decrease the cost of equity capital by providing a high-quality audit service, which enables them to perform a stronger monitoring role than the non-Big 4 auditors (e.g. Fan and Wong, 2005). As a result, investors trust the financial information audited by Big 4 auditors, which is reflected in their decision-making (i.e. information role of audits). Consequently, Khurana and Raman (2004) and Chen et al. (2011) report a lower cost of equity capital for Big 4 clients compared with the clients of non-Big 4 firms. Therefore, we expect that the cost of equity capital is lower for both single-segment and multiple-segment firms audited by Big 4 auditors. Moreover, we expect that the association between Big 4 auditor choice and the decrease in the cost of equity capital is more pronounced in multiple-segment firms than in single-segment ones, because high-quality audits play a more important role in the presence of greater IA (Pittman and Fortin, 2004; Ahmed et al.,2008 Chen et al., 2011).
To empirically examine this prediction, we use 21,177 firm-year observations from 1987 to 2010, of which 12,460 firm-year observations come from single-segment firms and the remaining 8717 firm-year observations are from multiple-segment firms. The cost of equity capital is measured by the average value of four different implied cost of capital estimates based on Gebhardt et al. (2001), Claus and Thomas (2001), Gode and Mohanram (2003) and Easton (2004). We find that the negative association between Big 4 auditor choice and the cost of equity capital is more pronounced among multiple-segment firms. When we control other factors that may influence the cost of equity capital, Big 4 clients exhibit lower equity cost in multiple-segment firms only, but not in single-segment firms. Further tests reveal that the negative association between Big 4 and the cost of equity in multiple-segment firms is mainly driven by firms with more than four segments. When we employ Heckman's (1979) method, an instrumental variable approach or propensity score matching techniques (Lawrence et al., 2011), we find that the documented results are not sensitive to potential endogenous auditor choices.
This study contributes to firms, practitioners, regulators and academics in various ways. First, we confirm the beneficial effects of high-quality audits regarding the decrease in the cost of capital for the multiple-segment firms.3 Second, the findings in this study imply that investors respond more to the higher quality information audited by Big 4 auditors when IA is more severe. Thus, the present study complements the findings reported in prior studies regarding the stronger monitoring role of Big 4 audits (Fan and Wong, 2005; Choi and Wong, 2007), especially in situations where high IA exists (Pittman and Fortin, 2004; Chen et al., 2011). We also extend these findings to settings related to the diversification discount. Third, findings in this study are of interest to regulators and auditors. Maintaining proper audit quality is a great concern for regulators and auditors. Thus, this study suggests that auditors, especially small ones, should exert greater efforts when auditing multiple-segment firms to enhance audit quality. Both regulators and investors also need to be more vigilant of such firms. Finally, our findings provide academics with insights into the dynamics of multiple-segment firms, in terms of the effect of IA on the cost of equity capital and the influence of auditor choice on the effect. This study can serve as a starting point for academics, allowing them to explore the effect of multiple-segments in various accounting-related contexts that, in turn, complements the findings of Demirkan et al. (2012).4
2. Theory and hypotheses development
Prior studies document various valuation implications of firm diversifications. First, managers may channel the resources of one segment to others experiencing financial difficulties (Stulz, 1990; Lamont, 1997; Rajan et al., 2000; Ozbas and Scharfstein, 2010). They do so not to maximize firm value, but to build a managerial empire as this enables them to control more resources and increase their private wealth or perquisite consumption (Meyer et al., 1992; Denis et al., 1997; Rajan et al., 2000; Aggarwal and Samwick, 2003). Second, Graham et al. (2002) document that diversified firms engage in nonvalue maximizing merger and acquisition activities, which result in decreased expected future cash flow. Similarly, Morck et al. (1990) suggest that the maximization of the self-interest of managers is the main reason for the poor investment decisions of diversified firms. Third, Lamont and Polk (2001) document that diversified firms have a higher expected future return, which accounts for about half of the diversification discount, while the other half is attributable to future cash flow. Recently, Mitton and Vorkink (2010) document that the higher expected returns in diversified firms are attributable to smaller skewness exposure, which offers less upside potential to investors. Finally, there is evidence on the inherent inefficiency of diversified firms (Maksimovic and Phillips, 2002).
Due to these suboptimal behaviours, the quality of accounting information in multiple-segment firms could be lower than that of single-segment firms. Consistent with this argument, Demirkan et al. (2012) find that the magnitude of discretionary accruals is higher in multiple-segment firms than in single-segment ones. Diversified firms are more likely to have greater agency problems between the top and divisional managers; thus, they tend to compensate the divisional managers based on observable performance. In contrast, single-segment firms are more directly monitored; thus, they are more likely to be compensated based on the level of managers' efforts.5 These differences lead to different incentives of managers to engage in earnings management in order to camouflage the observable level of performance, which results in lower quality financial information for multiple-segment firms (Demirkan et al., 2012). Based on prior evidence that high earnings lower the cost of capital (Bhattacharya et al., 2003; Francis et al., 2004), Demirkan et al. (2012) argue that investors and creditors require higher costs of capital for the same level of discretionary accruals in multiple-segment firms than in single-segment firms.6
One way to restore the credibility of accounting information is to hire auditors who can provide high-quality auditing service (Fan and Wong, 2005; Choi and Wong, 2007).7 Teoh and Wong (1993) find that investors respond more to the earnings news presented by Big 4 clients than by non-Big 4 clients. Willenborg (1999) finds that underpricing for IPO firms is less severe for Big 4 clients. Krishnan (2003a) also reports that market return reflects the discretionary accruals of the Big 4 clients more than those of non-Big 4 auditors. Similarly, Pittman and Fortin (2004) and Khurana and Raman (2004) find that the costs of debt and equity capital are lower for Big 4 clients.8 Kim et al. (2011) document that the cost of debt capital is lower for privately held firms that voluntarily hire auditors, especially when they are Big 4 clients. In summary, earlier findings suggest that Big 4 audits increase information quality and enhance the credibility of financial statements. As a result, IA between firms and shareholders is lower in Big 4 clients, thus resulting in lower costs of raised equity capital.9
However, none of these studies investigate the effect of high-quality audit services on the diversification discount. If the audits provided by Big 4 auditors can reduce IA via a more rigorous monitoring process, diversification discounts should decrease in Big 4 clients. In contrast, we expect single-segment firms to experience a less significant decrease in the cost of equity capital regardless of auditor choice, because they have relatively less IA than multiple-segment firms. If investors can easily obtain transparent information relevant to the value of the firm, which is the case for the single-segment firms in our context, then audit quality differences can have a relatively less impact on the cost of equity capital. As a result, we expect that the decrease in the cost of equity capital due to higher audit quality is more salient among multiple-segment firms than in single-segment ones. We propose the following hypothesis based on the discussions above:
- H1: The magnitude of the decrease in the cost of equity capital for Big 4 clients is greater for multiple-segment firms than that for single-segment firms.
Consistent with our hypothesis, Brown and Hillegeist (2007) find that the negative association between disclosure quality and IA is stronger when the latter is more severe. This implies that in the presence of high IA, enhanced disclosure leads to reduced IA. In an auditing-related setting, Pittman and Fortin (2004) report that the choices of Big 4 auditors decrease the cost of debt capital as firms get older. In their study using Chinese firms, Chen et al. (2011) document the positive association between the cost of equity capital and the magnitude of earnings management. They also revealed that designating a large auditor decreases this association. The findings of Pittman and Fortin (2004) and Chen et al. (2011) imply that the role of Big 4 auditors becomes more important when greater IA exists. Choi and Wong (2007) also argue that the signalling role of Big 4 audits is more prominent when no other mechanism exists to guarantee the quality of financial reports. Similarly, Ahmed et al. (2008) report that the role of a high-quality audit is more important when corporate governance is weaker. In summary, prior studies conclude that Big 4 audits can be more effective when greater IA exists. This leads us to examine whether the effect of Big 4 audits on the cost of equity is more pronounced in multiple-segment firms.
3. Methodology
The research design and empirical evidence are provided in this section to answer the research question.
3.1. Empirical proxies for the implied cost of equity capital
Based on prior studies, we estimate the implied cost of equity capital using four methods developed by Gebhardt et al. (2001), Claus and Thomas (2001), Gode and Mohanram (2003) and Easton (2004), respectively. First, we estimate the implied cost of equity by deriving the discount rate that satisfies each of the four valuation models. The alternative estimates from different valuation methods are highly correlated with each other and similar within a reasonable range. Thus, by taking the average of these four estimates, we obtain a comprehensive measure of the cost of equity, which is denoted by CoE. This average estimate is used as the measure of the implied cost of equity throughout the article, because the averaging process mitigates the potential measurement errors associated with individual estimates.10
3.2. Empirical specification
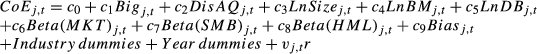 (1)
(1)Equation 1 is separately estimated for single-segment and multiple-segment firms. We expect the mean effect of Big to be negative (c1 < 0), because a higher audit quality reduces the cost of equity capital in the United States (Khurana and Raman, 2004). Such impact is expected to be more pronounced in multiple-segment firms where investors are likely to face greater IA than in single-segment firms.
In addition, we include several variables to control other factors that are likely to affect the cost of equity capital. Poor accounting quality (DiscAQ) is expected to be positively related to the cost of equity, which yields a positive sign for c2 (Francis et al., 2005; Demirkan et al., 2012). Based on existing literature (e.g. Gode and Mohanram, 2003; Dhaliwal et al., 2007), we expect that the cost of equity is negatively related to firm size (LnSize) and positively related to book-to-market ratio (LnBM), financial leverage (LnDB) and market risk premia. To adjust risk premia, we include Beta(MKT), Beta(SMB) and Beta(HML). Finally, optimism in forecasts of analysts produces an upwardly biased cost of capital estimates (Easton and Sommers, 2007). Thus, we control forecast bias to reduce potential measurement errors in the cost of equity proxies. The formal variable definitions used for the regression analysesb are reported in Table 1.
| Variable | Description |
|---|---|
| Regression variables | |
| CoE | The average value of four cost of equity estimates based on Gode and Mohanram (2003), Easton (2004), Claus and Thomas (2001) and Gebhardt et al. (2001) |
| Multi | Equals 1 if a firm operates at least two business segments, and 0 otherwise |
| #Seg | The number of business segments |
| Big | Equals 1 if a firm is audited by one of the Big 4 audit firms, and 0 otherwise |
| Specialist | Equals 1 if a firm is audited by an industry specialist auditor, and 0 otherwise. We classify an auditor as an industry specialist when he earns the greatest market share in terms of audit fee in each 2-digit SIC industry |
| DiscAQ | Discretionary accrual quality as defined by Francis et al. (2005) |
| LnSize | The natural logarithm of total assets |
| LnBM | The natural logarithm of book-to-market ratio |
| LnDB | The natural logarithm of total debt-to-equity ratio |
| Beta(MKT) | Estimates of market premium from the three-factor model by Fama and French (1996) are calculated for more than 36 months until the end month of the fiscal year |
| Beta(SMB) | Estimates of size premium from the three-factor model by Fama and French (1996) are calculated for more than 36 months until the end month of the fiscal year |
| Beta(HML) | Estimates of book-to-market premium from the three-factor model by Fama and French (1996) are calculated for more than 36 months until the end month of the fiscal year |
| Bias | Actual EPS minus the mean analyst forecast, deflated by stock price at the end of the fiscal year |
| Partitioning variables | |
| Size | The natural logarithm of total assets |
| Age | The number of years between the event year and the first year when a stock appears in CRSP |
| Volatility | The standard deviation of daily returns for the fiscal year |
| Volume | The average daily turnover in percentage over the fiscal year, where daily turnover is the ratio of the number of shares traded each day to the number of outstanding shares at the end of the day |
| Following | The number of analysts following a firm |
| Dispersion | Forecast dispersion of analysts measured when the number of analysts following a firm is more than two |
4. Empirical results
4.1. Sample selection and descriptive statistics
Our sample selection process begins with all the firms listed on NYSE, AMEX or NASDAQ for any year from 1987 through 2010. Financial statement data, stock price and monthly return data, as well as analyst earnings and long-term growth forecasts data are extracted from Compustat, CRSP and I/B/E/S, respectively. Multiple-segment firms are those that report at least two segments operating in four-digit SIC codes obtained from the Compustat NAIC file.12 Similar to Berger and Ofek (1995), Lamont and Polk (2001) and Bens and Monahan (2004), we eliminate firm-years with the following characteristics: firm-years that lack at least one segment on the Compustat Industry Segment database, firm-years with one or more segments in the financial services industry (SIC 6000–6999) or in regulated industries (SIC 4900–4999), firm-years with less than $20 million total sales and firm-years in which the absolute value of the difference between the aggregate segment sales and the total reported sales exceeds 1 per cent of the total reported sales. Finally, we ensure that all observations have no missing variables, ultimately yielding 21,177 firm-year observations. Observations that fall within the top and bottom 1 per cent of the major research variables included in Equation 1 are winsorized to avoid potential outlier influence.
Table 2 presents descriptive statistics of the key variables. Panel A of Table 2 shows the mean and median of the implied cost of equity measure (CoE variable), which are 13.4 per cent and 10.5 per cent, respectively.13 The number of multiple-segment firms is 8717, which covers 41.2 per cent of the entire sample, as evidenced by the mean value of the Multi variable. On average, about two segments operate within a firm (#Seg variable). Notably, about 92.1 per cent of the sample observations are Big 4 clients (Big).14 With respect to the fundamental determinants of the cost of equity, the sample mean values are 6.324 for LnSize, −0.792 for LnBM and −0.151 for LnDB.15 The mean values of the three-factor loadings [Beta(MKT), Beta(SMB) and Beta(HML)] also fall within reasonable ranges. The mean value of Bias is −0.193, which is consistent with the optimistic bias of analysts in their earnings forecasts.
| Variable | Mean | SD | 5% | Q1. | Median | Q3. | 95% |
|---|---|---|---|---|---|---|---|
| (Panel A) Summary statistics (N = 21,177) | |||||||
| CoE | 0.134 | 0.092 | 0.051 | 0.079 | 0.105 | 0.151 | 0.337 |
| Multi | 0.412 | 0.492 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 |
| #Seg | 1.903 | 1.344 | 1.000 | 1.000 | 1.000 | 3.000 | 5.000 |
| Big | 0.921 | 0.270 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DiscAQ | 0.000 | 0.021 | −0.029 | −0.013 | −0.003 | 0.009 | 0.041 |
| LnSize | 6.324 | 1.696 | 3.743 | 5.080 | 6.161 | 7.429 | 9.517 |
| LnBM | −0.792 | 0.681 | −1.985 | −1.212 | −0.756 | −0.336 | 0.290 |
| LnDB | −0.151 | 0.911 | −1.740 | −0.753 | −0.094 | 0.459 | 1.290 |
| Beta(MKT) | 1.081 | 0.650 | 0.069 | 0.673 | 1.028 | 1.439 | 2.290 |
| Beta(SMB) | 0.752 | 0.937 | −0.620 | 0.119 | 0.637 | 1.275 | 2.514 |
| Beta(HML) | 0.031 | 1.115 | −1.956 | −0.617 | 0.094 | 0.734 | 1.805 |
| Bias | −0.193 | 0.388 | −0.894 | −0.208 | −0.054 | −0.001 | 0.022 |
| (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | (j) | (k) | Bias | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Panel B) Pearson correlation matrix | |||||||||||
| (a) CoE | 0.076 | 0.120 | −0.044 | 0.034 | −0.044 | 0.220 | 0.102 | 0.071 | 0.062 | 0.144 | −0.195 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| (b) Multi | 0.803 | 0.053 | 0.002 | 0.263 | 0.041 | 0.179 | −0.014 | −0.105 | 0.125 | 0.083 | |
| 0.00 | 0.00 | 0.76 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | ||
| (c) #Segment | 0.067 | 0.012 | 0.333 | 0.015 | 0.197 | −0.012 | −0.147 | 0.121 | 0.082 | ||
| 0.00 | 0.08 | 0.00 | 0.03 | 0.00 | 0.09 | 0.00 | 0.00 | 0.00 | |||
| (d) Big | −0.024 | 0.202 | −0.053 | 0.136 | −0.003 | −0.074 | −0.016 | 0.102 | |||
| 0.00 | 0.00 | 0.00 | 0.00 | 0.68 | 0.00 | 0.02 | 0.00 | ||||
| (e) DiscAQ | 0.003 | −0.101 | −0.004 | 0.037 | 0.033 | −0.045 | −0.034 | ||||
| 0.68 | 0.00 | 0.54 | 0.00 | 0.00 | 0.00 | 0.00 | |||||
| (f) LnSize | −0.129 | 0.355 | 0.020 | −0.368 | 0.035 | 0.232 | |||||
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||||
| (g) lnBM | 0.000 | 0.022 | 0.139 | 0.147 | −0.198 | ||||||
| 0.99 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||
| (h) LnDB | −0.028 | −0.094 | 0.177 | 0.080 | |||||||
| 0.00 | 0.00 | 0.00 | 0.00 | ||||||||
| (i) Beta(MKT) | 0.010 | 0.142 | −0.075 | ||||||||
| 0.13 | 0.00 | 0.00 | |||||||||
| (j) Beta(SMB) | 0.135 | −0.164 | |||||||||
| 0.00 | 0.00 | ||||||||||
| (k) Beta(HML) | 0.047 | ||||||||||
| 0.00 | |||||||||||
Panel B of Table 2 reports the Pearson correlations between the key variables. Both the multiple-segment indicator (Multi) and the number of segments (#Seg) are positively associated with CoE. This means that the cost of raised equity capital is higher in multiple-segment firms than in single-segment ones. Consistent with Khurana and Raman (2004), Big is negatively associated with CoE, which suggests that higher audit quality mitigates IA within a firm, thereby reducing the cost of equity capital. DiscAQ is positively associated with CoE. This result is consistent with Francis et al. (2005) who suggest that market participants impose a higher cost of capital on firms with poor accruals quality. CoE is negatively associated with firm size (LnSize), but positively associated with book-to-market ratio (LnBM), financial leverage (LnDB) and market risk premia [Beta(MKT), Beta(SMB) and Beta(HML)]. Correlations between control variables are not high. The largest correlation is between LnSize and Beta(SMB) at −0.368. Thus, it is unlikely that multicollinearity can significantly affect the empirical findings in the multivariate analyses.
4.2. Univariate analyses
Table 3 presents the average values of the implied cost of capital (CoE) by the number of segments. The sample firms are partitioned into four groups: single-segment firms, firms with two or three segments, firms with four or five segments and firms with six or more segments. Column (3) shows that the proportion of Big 4 clients increases with the number of segments, whereas Column (4) shows that the cost of equity capital monotonically increases with the number of segments. For example, the average implied cost of equity capital for single-segment firms is 13.2 per cent, whereas it increases to 17.2 per cent for firms with at least six segments. This trend is observed in both Big 4 clients [Column (6)] and non-Big 4 clients [Column (5)]. Furthermore, the mean values of the cost of equity capital are consistently greater for non-Big clients, as reported in Khurana and Raman (2004). In addition, the difference in the cost of equity capital between Big 4 and non-Big 4 clients [Column (7)] increases with the number of segments. The difference is −0.012 in single-segment firms but increases to −0.134 in firms with six or more segments. A difference of −0.134 for firms with six or more segments implies that the cost of equity capital for non-Big 4 clients is 13.4 per cent higher than that of Big 4 clients. This highlights the dramatic effect of Big 4 audits; it also implies that the informative role of audit quality becomes more important as IA increases. The above analyses, however, are not conclusive given that other factors potentially influencing the cost of capital are not controlled. This control seems more critical for multiple-segment firms, because of the huge difference in the cost of capital between Big 4 and non-Big 4 clients. Results of multivariate analyses are reported in the next section.
| (1) #Seg | (2) Sample size | (3) Big 4 (%) | (4) Full sample | Big 4 versus non-Big 4 | ||
|---|---|---|---|---|---|---|
| (5) Non-Big 4 | (6) Big 4 | (7) Diff. [(6)–(5)] | ||||
| Total | 21,177 | 0.921 | 0.134 | 0.148 | 0.133 | −0.015*** |
| Least | ||||||
| 1 | 12,460 | 0.909 | 0.132 | 0.139 | 0.127 | −0.012*** |
| 2–3 | 5859 | 0.928 | 0.139 | 0.151 | 0.133 | −0.018*** |
| 4–5 | 2391 | 0.955 | 0.166 | 0.218 | 0.155 | −0.063*** |
| Most | ||||||
| 6 | 467 | 0.979 | 0.172 | 0.305 | 0.171 | −0.134* |
| Diff. (most to least) | 0.070*** | 0.040*** | 0.166*** | 0.044*** | −0.122*** | |
- * and *** represent statistical significances at the 10% and 1% levels, respectively. See Table 1 for variable definitions.
4.3. Regression analyses
Multivariate regression analyses are performed to ensure that the results are not driven by other firm characteristics. The report t-statistics are estimated based on robust standard errors adjusted for clustering by each firm. For every regression result reported below, t-statistics are based on robust standard errors adjusted for clustering by each firm.
Equation 1 is applied separately for each firm group in consideration of the underlying factors that may have caused the reported differences between single- and multiple-segment firms. In Panel A of Table 4, the Big coefficient for the single-segment firms is not statistically different from zero, whereas it is significantly negative for multiple-segment firms. This implies that the earlier findings of Khurana and Raman (2004) may be driven by multiple-segment firms. The coefficient for the multiple-segment group is −0.009, which indicates that Big 4 clients enjoy an approximately 0.9 per cent lower implied cost of equity capital compared with non-Big 4 clients. The difference between the two coefficients (−0.010) is significant at the 5 per cent level as reported in the rightmost column of Panel A. This finding is consistent with the notion that the informative role of big auditors is greater under greater information asymmetry. Consistent with Francis et al. (2005), the coefficients on DiscAQ are significantly positive in both groups, although this difference is not significant. Other coefficients on control variables also exhibit expected signs even though some coefficients are not statistically significant.
| Parameter | Single segment (Multi = 0) | Multiple segments (Multi = 1) | Diff (multi-single) | ||
|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | ||
| (Panel A) Regression results for single-segment versus multiple-segment firms | |||||
| Intercept | 0.175*** | 24.59 | 0.148*** | 11.96 | −0.027*** |
| Big | 0.001 | 0.36 | −0.009** | −2.15 | −0.010** |
| DiscAQ | 0.123*** | 3.79 | 0.033 | 0.65 | −0.090** |
| LnSize | −0.007*** | −13.22 | −0.003*** | −3.94 | 0.004*** |
| LnBM | 0.030*** | 28.15 | 0.031*** | 19.94 | 0.001 |
| LnDB | 0.017*** | 19.82 | 0.019*** | 14.66 | 0.002 |
| Beta(MKT) | 0.004*** | 3.82 | 0.004*** | 2.49 | 0.000 |
| Beta(SMB) | 0.002*** | 2.75 | 0.005*** | 4.82 | 0.004** |
| Beta(HML) | 0.001 | 1.22 | 0.001* | 1.39 | 0.001* |
| Bias | −0.025*** | −12.80 | −0.029*** | −9.01 | −0.004 |
| Industry/year | Yes | Yes | |||
| No. observations | 12,460 | 8,717 | |||
| Adj. R2 | 0.371 | 0.402 | |||
| Parameter | (1) #Seg = 1 | (2) #Seg = 2 or 3 | (3) #Seg = 4 or 5 | (4) #Seg ≥ 6 | ||||
|---|---|---|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | Estimate | t-stat. | Estimate | t-stat. | |
| (Panel B) Regression results by the number of segments | ||||||||
| Intercept | 0.175*** | 24.59 | 0.126*** | 12.68 | 0.206*** | 5.29 | 0.123* | 1.56 |
| Big | 0.001 | 0.36 | −0.003 | −0.73 | −0.024** | −2.04 | −0.101** | −1.67 |
| DiscAQ | 0.123*** | 3.79 | 0.018 | 0.33 | 0.114 | 1.08 | −0.170 | −0.45 |
| LnSize | −0.007*** | −13.22 | −0.004*** | −4.69 | −0.001 | −0.94 | 0.003 | 0.63 |
| LnBM | 0.030*** | 28.15 | 0.028*** | 16.02 | 0.038*** | 11.36 | 0.035*** | 3.73 |
| LnDB | 0.017*** | 19.82 | 0.018*** | 12.93 | 0.023*** | 7.33 | 0.023** | 2.29 |
| Beta(MKT) | 0.004*** | 3.82 | 0.005*** | 2.62 | 0.004 | 0.97 | −0.006 | −0.39 |
| Beta(SMB) | 0.002*** | 2.75 | 0.006*** | 5.29 | 0.003 | 1.07 | 0.011 | 1.04 |
| Beta(HML) | 0.001 | 1.22 | 0.002** | 1.66 | 0.000 | −0.12 | −0.007 | −0.74 |
| Bias | −0.025*** | −12.80 | −0.028*** | −8.01 | −0.031*** | −4.22 | −0.028 | −0.62 |
| Industry/year | Yes | Yes | Yes | Yes | ||||
| No. observ-ations | 12,460 | 5,859 | 2,391 | 467 | ||||
| Adj. R2 | 0.371 | 0.382 | 0.415 | 0.415 | ||||
- *, ** and *** represent statistical significances at the 10%, 5% and 1% levels, respectively (one-tailed). The t-statistics are computed using robust standard errors that are adjusted for clustering by each firm. See Table 1 for variable definitions.
The full sample in Panel B of Table 4 is divided into four subsamples based on the number of segments. Regression analyses are performed in each subsample. Column (1) shows the results for single-segment firms, which are consistent with the results in Panel A. Panel B clearly demonstrates a monotonic increase in Big coefficients with the number of segments. The coefficients on Big are -0.003 in firms with two or three segments [Column (2)], −0.024 in firms with four or five segments [Column (3)] and −0.101 in firms with the most segments [Column (4)]. Interestingly, only the coefficients on Big in Columns (3) and (4) are statistically significant, suggesting that the findings in Panel A are driven by firms with at least four segments. Thus, the findings in Panel B corroborate those in Panel A, providing strong evidence of the negative association between Big 4 auditor choice and the cost of capital in multiple-segment firms.16
The above argument focuses on the role of auditors in mitigating IA in multiple-segment firms. However, it can be argued that the findings may be driven by operational complexity rather than IA in multiple-segment firms. One way to reaffirm the information-based explanation for the previously reported findings is to examine whether or not the effect of auditors in multiple-segment firms varies with other proxies for information asymmetry. If the role of Big 4 firms in decreasing the cost of equity capital for multiple-segment firms is more significant when the direct measure of IA is relatively high (i.e. when IA is more severe), the results support our main findings. On the other hand, if our previous findings are only driven by the operational complexity inherent in multiple-segment firms, the monitoring role of Big 4 firms in multiple-segment firms should be observed regardless of the degree of IA measured by other proxies.
We employ six measures of firm-level IA in addition to our original measure (i.e. the number of segments). The six measures represent the level of IA from different and more direct perspectives than the number of segments. Based on prior studies, we classify smaller firms, young firms, those followed by fewer analysts, as well as those with higher trading volatility, with lower liquidity and with higher forecast dispersion as firms with higher IA.17 The median values of each variable are used to divide the sample into high- versus low-IA groups. The relation of the six variables to information symmetry is summarized in Panel A of Table 5.
| Size | Age | Volatility | Volume | Following | Dispersion | |
|---|---|---|---|---|---|---|
| (Panel A) Firm characteristics associated with information asymmetry | ||||||
| High IA | Small | Young | High | Low | Low | High |
| Low IA | Large | Old | Low | High | High | Low |
| Firm characteristics | IA | #Seg | Big * #Seg | N | Adj. R2 | ||
|---|---|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | ||||
| (Panel B) Regression results by the degree of information asymmetry | |||||||
| Size | High | 0.005 | 1.57 | −0.006* | −1.71 | 10,588 | 0.314 |
| Low | 0.007 | 1.48 | −0.007 | −1.37 | 10,589 | 0.472 | |
| Age | High | 0.008** | 2.16 | −0.006* | −1.71 | 10,631 | 0.389 |
| Low | 0.004 | 0.98 | −0.003 | −0.80 | 10,546 | 0.387 | |
| Volatility | High | 0.008** | 2.39 | −0.009** | −2.61 | 10,495 | 0.342 |
| Low | 0.001 | 0.34 | −0.005 | −1.00 | 10,494 | 0.448 | |
| Volume | High | 0.008* | 1.85 | −0.006 | −1.52 | 10,494 | 0.365 |
| Low | 0.004 | 1.26 | −0.004 | −1.23 | 10,495 | 0.421 | |
| Following | High | 0.007** | 1.96 | −0.006* | −1.68 | 10,396 | 0.314 |
| Low | 0.002 | 0.86 | −0.002 | −0.89 | 10,781 | 0.376 | |
| Dispersion | High | 0.008** | 2.28 | −0.008** | −2.17 | 8,495 | 0.476 |
| Low | 0.001 | 0.43 | −0.001 | −0.28 | 8,501 | 0.331 | |
- * and ** and&!ast;&!ast;&!ast; represent statistical significances at the 10%, 5% and 1% levels, respectively (one-tailed). The t-statistics are computed using robust standard errors that are adjusted for clustering by each firm. See Table 1 for other variable definitions.
Panel B of Table 5 reports the regression results using Equation 2, where the interaction variables of Big and #Seg (Big*#Seg) are added into Equation 1. The number of observations used in these analyses varies across partitioning variables, because not all of the IA-related variables are available for all of the sample observations and all the available observations are used for each analysis. Regression analyses are performed separately for firms with high IA and low IA. The coefficients on the two variables of interest (i.e. #Seg and Big*#Seg) are only used for simplicity. For illustration purposes, we use bold characters to represent the results of subsamples with high IA and normal characters to represent subsamples with low IA.
Interestingly, a similar pattern is observed in all partitioning IA variables. Most of the coefficients on Big*#Seg are significant and negative when IA is more severe. For example, when a firm is relatively young and IA is high, the coefficient on Big*#Seg is −0.006, which is significant at the 10 per cent level (t = −1.71). On the other hand, when IA is less severe in low-IA groups, their coefficients are all negative but generally insignificant. For example, when a firm is relatively old and IA is low, the coefficient on Big*#Seg is −0.003, which is insignificant at any conventional level (t = −0.80).
In summary, the negative association between the choice of high-quality auditors and the cost of capital is more pronounced among firms with greater information asymmetry. In contrast, we fail to find significant results in most cases for firms with low information asymmetry. These results indicate that the greater influence of audit quality in multiple-segment firms is related to the information role of the audit. Moreover, these findings do not support the claims of a number of finance articles that the diversification discount is caused by factors other than agency problem (e.g. Lang and Stulz, 1994).
4.4. Tests on the potential endogeneity of auditor choice
Fan and Wong (2005) and Choi and Wong (2007) report that firms with greater agency problems tend to hire high-quality auditors to mitigate investors' concerns. They also observe that this tendency is more pronounced in firms with a higher demand for equity capital, implying that such firms demand high-quality auditors to decrease their equity capital costs. Therefore, controlling for auditor choice decision is critical to the extent that the results of Table 4 could be driven by the intentions of multiple-segment firms to lower their costs of raising equity capital by hiring high-quality auditors.18
In Table 6, we perform an additional test to address potential endogeneity concerns in relation to auditor choice. First, we utilize the instrumental variable approach and report first-stage results in Panel A. Based on prior studies including Chaney et al. (2004) and Behn et al. (2008), we adopt the probit model to estimate the probability of selecting a Big 4 auditor and include several firm characteristics. The determinant variables include firm size (Size, natural logarithm of total assets), asset turnover (Aturn, sales divided by total assets), financial leverage (Lev, long-term debt divided by average total assets), current ratio (Curr, current assets divided by total assets), quick ratio (Quick, current assets minus inventory divided by current liabilities), return-on-assets ratio (ROA, net income divided by average total assets), loss indicator (Loss, having a value of 1 if a firm incurred a loss, and 0 otherwise), an indicator for long-term debt issuance (ISSUE, having a value of 1 if a firm issued more than 20 per cent of existing long-term debt for the past 2 years) and year- and industry-indicator variables. The model fits reasonably well as pseudo R2 reaches 0.163.
| Estimate | p-Value | |
|---|---|---|
| (Panel A) First-stage regression | ||
| Intercept | −3.996*** | 0.00 |
| Size | 0.818*** | 0.00 |
| Aturn | 0.257*** | 0.00 |
| Lev | 0.918*** | 0.00 |
| Curr | 0.402* | 0.07 |
| Quick | −0.006 | 0.72 |
| ROA | 0.487 | 0.47 |
| ROA*Loss | −1.590* | 0.05 |
| Loss | 0.012 | 0.90 |
| Issue | −0.306*** | 0.00 |
| Accruals | −1.520*** | 0.00 |
| Year | Yes | |
| Industry | Yes | |
| No. observations | 17,488 | |
| Pseudo R2 | 0.163 | |
| Parameter | Single segment (Multi = 0) | Multiple segments (Multi = 1) | Diff (multi-single) | ||
|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | ||
| (Panel B) Instrumental variable approach | |||||
| Intercept | 0.161*** | 9.11 | 0.195*** | 18.34 | 0.034* |
| Fitted value of Big | −0.026* | −1.42 | −0.040*** | −3.34 | −0.014** |
| DiscAQ | −0.011 | −0.20 | 0.109*** | 2.97 | 0.120 |
| LnSize | −0.002*** | −2.33 | −0.004*** | −5.61 | −0.002* |
| LnBM | 0.031*** | 18.31 | 0.030*** | 26.22 | −0.001 |
| LnDB | 0.019*** | 13.78 | 0.017*** | 17.95 | −0.002 |
| Beta(MKT) | 0.004** | 2.06 | 0.004*** | 3.62 | 0.000 |
| Beta(SMB) | 0.006*** | 4.58 | 0.002*** | 2.65 | −0.004 |
| Beta(HML) | 0.001 | 0.82 | 0.001** | 1.98 | 0.000*** |
| Bias | −0.026*** | −7.43 | −0.025*** | −11.61 | 0.001 |
| Year | Yes | Yes | |||
| Industry | Yes | Yes | |||
| No. observations | 10,221 | 7,267 | |||
| Adj. R2 | 0.370 | 0.400 | |||
| Parameter | Single segment (Multi = 0) | Multiple segments (Multi = 1) | Diff (multi-single) | ||
|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | ||
| (Panel C) Heckman's approach | |||||
| Intercept | 0.153*** | 9.10 | 0.184*** | 18.13 | 0.031* |
| Big | −0.015 | −0.92 | −0.022** | −1.99 | −0.006* |
| DiscAQ | −0.011 | −0.20 | 0.111*** | 3.03 | 0.122 |
| LnSize | −0.002*** | −2.80 | −0.005*** | −6.88 | −0.002* |
| LnBM | 0.031*** | 18.19 | 0.030*** | 26.13 | 0.000 |
| LnDB | 0.019*** | 13.65 | 0.017*** | 17.76 | −0.002 |
| Beta(MKT) | 0.004** | 1.97 | 0.004*** | 3.54 | 0.000 |
| Beta(SMB) | 0.006*** | 4.54 | 0.002*** | 2.49 | −0.004 |
| Beta(HML) | 0.001 | 0.84 | 0.001** | 2.09 | 0.000 |
| Bias | −0.027*** | −7.53 | −0.026*** | −11.76 | 0.001*** |
| IMR | 0.003 | 0.35 | 0.013** | 2.18 | 0.010** |
| Year | Yes | Yes | |||
| Industry | Yes | Yes | |||
| No. observations | 10,221 | 7,267 | |||
| Adj. R2 | 0.369 | 0.400 | |||
- *, ** and *** represent statistical significances at the 10%, 5% and 1% levels, respectively (two-tailed for Panel A and one-tailed for Panels B and C). The t-statistics are computed using robust standard errors that are adjusted for clustering by each firm. ROA, return-on-assets.
In Panel B of Table 6, we present the results of using the instrumental variables (IV) approach by incorporating the fitted value of the Big 4 auditor indicator from the first stage of regression. In Panel C, we adopt the Heckman's 2-stage least squares approach by calculating the inverse Mills ratio (IMR) for the Big 4 auditor choice. As shown in Panels B and C (Table 6), the results corroborate our previous findings that the association between audit quality and cost of equity is stronger in multiple-segment firms than in single-segment firms even after controlling the potential endogeneity of auditor choice. The IMR coefficient is also only statistically significant in the multiple-segment group.
Although these approaches are common in accounting literature, we are cautious in drawing clear inferences from these tests. For the IV approach, tests of instrument power reflect the relevance of our specification. The overidentification test using the Hansen's J statistic marginally fails to reject the null with p-value of 0.1053, whereas the underidentification test of Kleibergen and Paap (2006) that uses the rk LM statistic rejects the null with p-value of 0.0091. In addition, the p-value (<0.01) of the endogeneity test shows that the selection of Big 4 auditors is endogenous. In other words, no correlation exists between the explanatory variable and the error terms in the failure of OLS. Therefore, the IV application, which collectively supports the validity of our approach, is necessary.19 However, if the instrument is only weakly correlated with the endogenous regressor, instrumental variable estimates are more likely to be biased and produce an incorrect statistical inference than simple OLS estimates (Larcker and Rusticus, 2010). The weak identification test of Kleibergen and Paap (2006) with a yield of 3.855 for the Wald F statistic, which does not exceed the heuristic threshold value of 10 by Staiger and Stock (1997) for weak instruments, indicates the relative weakness of selected instruments. Moreover, for the Heckman approach, identifying a valid exogenous variable is vital, but we are unable to perfectly identify the exogenous variable in our selection model. These caveats to our specifications necessitate additional specification, which will be discussed in the next section.
4.5. Controlling for client characteristics
Propensity score matching has several advantages over IV methods as a solution to the endogeneity problem (Core, 2010). First, it does not require the identification of reliable instrument variables that can be very challenging in many empirical settings. Second, it is robust to misspecification of the functional form because it is not subject to parametric assumptions of IV methods (Armstrong et al., 2010). Thus, we believe that the propensity score matching technique supplements the weak instrument problem discussed in Table 6. Another reason for the use of propensity score matching is that it matches observations based on the probability of selecting a Big 4 auditor. For example, if significant size differences are present between the clients of Big 4 and of non-Big 4 auditors in each segment grouping, our previous results may simply capture the size effect on the cost of equity. Lawrence et al. (2011) also argue that differences between Big 4 and non-Big 4 auditors are a reflection of their clients' characteristics.
To address these concerns, we estimate the propensity of selecting Big 4 auditors from the auditor choice model in Table 6 and then match a non-Big 4 client with a Big 4 client with the closest predicted value.20 Based on the method by Lawrence et al. (2011), we match the pairs with replacements, which yields 2788 matched pairs. Panel A in Table 7 presents the mean values of the variables for both full and propensity score-matched samples. Before matching, all variables except Beta(HML) exhibit significant differences between Big 4 and non-Big 4 clients. However, after matching, differences of most variables become statistically insignificant, implying effective propensity score matching.
| Full sample | Propensity-matched sample | |||||
|---|---|---|---|---|---|---|
| Non-Big 4 | Big 4 | Diff. | Non-Big 4 | Big 4 | Diff. | |
| (Panel A) Mean values of variables for full and propensity score-matched samples | ||||||
| CoE | 0.148 | 0.133 | −0.015*** | 0.138 | 0.125 | −0.012 |
| DiscAQ | 0.002 | 0.000 | −0.002*** | 0.003 | −0.003 | −0.006* |
| LnSize | 5.156 | 6.424 | 1.269*** | 5.219 | 5.522 | 0.303 |
| LnBM | −0.668 | −0.803 | −0.135*** | −0.638 | −0.749 | −0.111 |
| LnDB | −0.574 | −0.114 | 0.460*** | −0.615 | −0.409 | 0.206 |
| Beta(MKT) | 1.087 | 1.080 | −0.007 | 1.189 | 0.983 | −0.205* |
| Beta(SMB) | 0.990 | 0.732 | −0.258*** | 0.879 | 0.914 | 0.035 |
| Beta(HML) | 0.091 | 0.026 | −0.065** | 0.159 | 0.093 | −0.066 |
| Bias | −0.329 | −0.182 | 0.147*** | −0.241 | −0.192 | 0.049 |
| No. observations | 1,672 | 19,505 | 1,394 | 1,394 | ||
| Parameter | Single segment (Multi = 0) | Multiple segments (Multi = 1) | Diff (multi-single) | ||
|---|---|---|---|---|---|
| Estimate | t-stat. | Estimate | t-stat. | ||
| (Panel B) Regression results for single-segment versus multiple-segment firms | |||||
| Intercept | 0.188*** | 9.89 | 0.109*** | 4.66 | −0.079 |
| Big | 0.003 | 0.92 | −0.013** | −1.99 | −0.016*** |
| DiscAQ | 0.232*** | 2.72 | −0.013 | −0.09 | −0.245 |
| LnSize | −0.010*** | −5.99 | −0.004* | −1.62 | 0.005* |
| LnBM | 0.025*** | 8.50 | 0.033*** | 6.38 | 0.008 |
| LnDB | 0.017*** | 7.52 | 0.016*** | 4.20 | −0.001** |
| Beta(MKT) | 0.005** | 2.04 | 0.005 | 1.14 | 0.000 |
| Beta(SMB) | 0.001 | 0.93 | 0.009*** | 2.85 | 0.007 |
| Beta(HML) | 0.000 | 0.18 | −0.001 | −0.32 | −0.001 |
| Bias | −0.030*** | −7.70 | −0.018*** | −2.71 | 0.012 |
| Year | Yes | Yes | |||
| Industry | Yes | Yes | |||
| No. observations | 1,878 | 910 | |||
| Adj. R2 | 0.358 | 0.345 | |||
- *, ** and *** represent statistical significances at the 10%, 5% and 1% levels, respectively (one-tailed). The t-statistics are computed using robust standard errors that are adjusted for clustering by each firm. See Table 1 for variable definitions.
In Panel B of Table 7, we confirm our previous results using the matched sample. For single-segment firms, the proportion of Big audit clients is 50.18 per cent, while that of multiple-segment firms is 49.67 per cent, suggesting effective control of the potentially endogenous relation between auditor and diversification choice. Even after propensity score matching, a significant difference is still found in the Big coefficients between single-segment and multiple-segment firms. Consistent with the result in Table 4, the negative association between Big and CoE is higher in multiple-segment firms for the matched sample. In sum, the greater impact of a number of auditors in mitigating IA for multiple-segment firms is robust in several treatments that address endogeneity concerns.
4.6. Alternative measures of audit quality
In this section, we discuss sensitivity analyses using alternative measures of audit quality. First, we consider auditor tenure as a proxy for audit quality, because understanding client-specific knowledge, such as operations, accounting system and internal control structure, is crucial for auditors to enhance audit quality. Despite earlier debates on how the tenure of the auditor affects auditor independence, recent studies conclude that auditor tenure allows auditors to rely less on managerial estimates and become more independent of management (e.g. Johnson et al., 2002; Myers et al., 2003; Mansi et al., 2004; Ghosh and Moon, 2005).21 Thus, we include Tenure instead of Big as an alternate for audit quality in Equation 1. We count auditor tenure from 1978, while the first year observation is counted as 1 by construction. We define Tenure as an indicator variable with a value of 1 if auditor tenure is 10 years or more, and 0 otherwise.22 We use 10 years to define Tenure, because the sample mean (median) of auditor tenure is 10.10 (9.00) years. We also restrict the sample to Big 4 clients (N = 19,505) to draw clearer inferences on auditor tenure as a proxy of audit quality. We then replace Big with Tenure in Equation 1.
This specification resolves a few potential statistical problems inherent in Equations 1 and 2. As reported in Table 2, only 8 per cent of our samples are non-Big 4 clients, and this proportion decreases as the number of segments increases. Thus, firms in this study are rarely audited by non-Big 4 auditors due to the lengthy requirements in sample selection criteria that allow most large firms to be included in the data set. This small percentage may cause a lack of statistical vigour in Big 4 versus non-Big 4 tests, although our earlier findings remain robust. Nevertheless, to address potential problems in relation to the small proportion of non-Big 4 clients, we employ empirical analyses using only the Tenure variable for Big 4 clients. Untabulated results reveal that the Tenure coefficient for multiple-segment firms is significantly negative, although it is not statistically different from that of single-segment firms. The coefficient on Tenure in single-segment firms is −0.003 (t = −1.41), while that of multiple-segment firms is −0.003 (t = −2.39). This result corroborates our earlier findings that are documented in Panel B, Table 4.23
Thus far, the discussion relies on the relationship between auditor tenure and audit quality based on extensive empirical evidence. However, other evidences also suggest that long auditor tenure does not have a negative impact on audit quality (e.g., Geiger and Raghunandan, 2002). Thus, we choose auditor industry expertise as another alternative proxy for audit quality. Prior studies report that auditor expertise plays an important role in audit quality (e.g. Balsam et al., 2003; Krishnan, 2003b). We follow these studies and examine whether the choice of an industry expert auditor decreases the cost of equity capital, unlike in single- and multiple-segment firms that are audited by Big 4 auditors. Then, we determine auditor expertise by considering the individual market shares of different auditor industries in a specific year. We construct an indicator variable (Specialist) that is equal to 1 if the firm is audited by an industry specialist that reports the highest market share in terms of audit fees in each 2-digit SIC industry. We then replace the Big variable in Equation 1 with Specialist. Accordingly, we restrict our sample to firms that are audited by one of the Big 4 auditors with audit fee data. The resulting sample consists of 5642 firm-year observations.24 Untabulated results suggest that the Specialist coefficient is significantly negative when we use the entire sample. If we divide our sample into single- and multiple-segment firms, only the Specialist coefficient for multiple-segment firms (−0.015, t = −2.00) is significantly negative. Such coefficient is also significantly higher than that of single-segment firms (p-value of the difference = 0.02), which is consistent with the results reported in Table 4.25
5. Conclusion
This study examines whether the role of Big 4 auditors in decreasing the cost of equity capital is more pronounced in multiple-segment firms than in single-segment firms. Prior studies document that multiple-segment firms are valued at a more discounted price than single-segment firms are, and describe the finding as a ‘diversification discount’ or ‘negative excess value’. A diversification discount implies that the cost of equity capital is higher for multiple-segment firms than for single-segment firms. This phenomenon occurs due to higher IA between managers and shareholders in multiple-segment firms. Thus, investors discount the value of multiple-segment firms to compensate for the increased agency risk.
We use 21,177 firm-year observations from 1987 to 2010 to empirically test this prediction. We use the implied cost of equity capital measures to proxy for the cost of equity capital. The empirical results support our prediction that the association between the Big 4 auditor choice and the decrease in cost of equity capital is more pronounced among multiple-segment firms. As the number of segments increases, the association becomes stronger.
Although the findings in this study clearly reveal the significant effect of Big 4 audits on the cost of capital, the scope of this research still has limitations. First, a firm's diversified decision may possibly be endogenous. We do not formally incorporate this issue; rather, we perform subsample analyses classified by the degree of diversifications (i.e. number of segments) to show the significant effect of high-quality audits in each subsample. Second, although we attempt to solve the endogenous auditor choice issue, some unknown factors, such as governance mechanism, may simultaneously influence both auditor choice and the cost of capital. Third, the measure of implied cost of equity capital in this study can be correlated with unknown factors that, in turn, may also be correlated with auditor choice. Third, this study does not directly observe the effort of auditors (e.g. audit hours), but uses the choice of Big 4 auditors as a proxy for audit quality. Fourth, although our theory highlights the role of IA as a determinant of the cost of capital differential, IA may possibly not be priced in the market (Hughes et al., 2007; Lambert et al., 2007). Instead, the quality of accounting information can directly and indirectly influence the cost of capital (Lambert et al., 2007). We leave these caveats for future research.
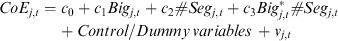 (2)
(2)



