Flood Risk Information, Actual Floods and Property Values: A Quasi-Experimental Analysis
Abstract
Hedonic property price analysis tells us that property prices can be affected by natural hazards such as floods. This paper examines the impact of flood-related variables (among other factors) on property values, and examines the effect of the release of flood risk map information on property values by comparing the impact with the effect of an actual flood incidence. An examination of the temporal variation of flood impacts on property values is also made. The study is the first of its kind where the impact of the release of flood risk map information to the public is compared with an actual flood incident. In this study, we adopt a spatial quasi-experimental analysis using the release of flood risk maps by Brisbane City Council in Queensland, Australia, in 2009 and the actual floods of 2011. The results suggest that property buyers are more responsive to the actual incidence of floods than to the disclosure of information to the public on the risk of floods.
1 Introduction
The global frequency and severity of natural disasters have shown an increase over the past several decades. As a result, common natural disasters such as floods, bushfires, cyclones and earthquakes have had an increasingly severe impact on both properties and lives (Gentle et al., 2001). Among them, floods are one of the most common. Australia has also experienced highly variable extremes in weather conditions and a rise in the frequency of natural disasters. Of these, the Brisbane floods of 2011 were one of the worst natural disasters in Australia's recent history in terms of economic damage. In the wake of such major disasters, relevant authorities and independent researchers have reported on the causes and damage inflicted, but have generally considered only direct tangible costs (see Queensland Government, 2011). In particular, although the losses to private property have been estimated, there is little consideration given to the change in property values due to flooding. This paper, therefore, focuses on the impact of such natural disasters on property market behaviour using the 2011 Brisbane floods as a case study.
The property market is an important indicator of an economy's health involving a wide range of stakeholders, which include real estate agents, banks, insurance companies, policymakers and the public. Moreover, the maintenance of property values is a key element in the sustainability of local communities (Lamond, 2008). Property price changes affect the expected lifetime wealth of home owners and the collateral values of homes (Miller et al., 2011). This suggests that it would be in the interest of governments to invest in appropriate infrastructure and policies to minimise the adverse impacts of natural hazards such as floods on the property market.
Numerous studies have looked at the behaviour of the property market, particularly in relation to natural disasters. For example, the impact of flooding and flood plains on property markets has been investigated by Samarasinghe and Sharp (2010), Bin and Landry (2013), Petrolia et al. (2013), Rambaldi et al. (2013) and Eves and Wilkinson (2014), a number of which have investigated the impact of floods on property values. Importantly, a meta-analysis of flood risks in the USA has shown that there is a difference between ex-ante and ex-post analysis (Daniel et al., 2009). However, none of the research has investigated the impact of floods on property values after a flood event (such as the 2011 floods) in the Brisbane City Council (BCC) region.
Although the hedonic pricing (HP) theory has been extensively used for investigating the impact of floods on property prices, most studies have ignored inherent deficiencies in traditional HP theory. In this paper, quasi-experimental and spatial econometric techniques are employed to avoid methodological issues and to distinguish specific objectives. For example, adoption of a quasi-experimental hedonic method is useful to take into account endogeneity and omitted variable biases (see Parmeter & Pope, 2013).
This study was motivated by the 2011 Brisbane floods. Prior to this event, the BCC mapped flood risk areas and made them available to the public in October 2009 – a decision which may have influenced property market behaviour. However, existing studies are limited by considering only either the actual flood incidence or availability of flood risk information. This study will be the first to analyse the effect on the property market of flood risk map information being made public and to compare this with the effect on the property market of the actual flood incidence. This is tested using the difference-in-differences (DID) method, which takes account of different time variables and treatment effects. Prior to this, we examine the impact of flood-related variables (among other factors) on property values. Furthermore, we examine the temporal variation of flood impacts on property values. This is because several studies show that any negative effect on property values following a natural event disappears with time (see Lamond, 2008; Bin & Landry, 2013).
2 Literature Review
The demand for property depends on certain characteristics, primarily structural, environmental and neighbourhood, with property prices being a function of those characteristics. A review of the role of such structural characteristics in determining property prices is found in Sirmans et al.'s (2005) study. Several studies have shown their importance in influencing property values (see Acharya & Bennett, 2001). Thus neighbourhood amenities such as parks, green spaces, water bodies, reservoirs, and open spaces have been found to be important determinants of property prices. Previous studies have shown that residential properties closer to open spaces and recreational facilities have higher values than similar properties farther away (see Acharya & Bennett, 2001). In addition to physical factors such as water bodies and parks, pollution and environmental quality are also important considerations for people when deciding on residential location (see Gayer, 2000; Kim et al., 2003).
Other researchers have studied the effect of natural disasters and climate change on property markets (see Schlenker et al., 2005; Michael, 2007; Butsic et al., 2011). Butsic et al. (2011), for example, applied the HP model to simulate the impact of climate change on real estate prices in Canada and showed a negative impact on housing prices. Numerous studies have focused on investigating the impact of flooding and flood risks on property values, indicating that flood risk tends to discount property values (see Bin & Landry, 2013). However, the findings vary due to the use of different methodologies and the nature of impacts (Lamond, 2008), and discounted property values vary according to the country and location.
Previous studies of flood risk on properties cover a range of issues, including climate change predictions, analysing past flood events, existence of flood risk maps and following actual flood events. Such studies have evaluated the impact of flood risks on the property market rather than focusing on an actual flood event (see Samarasinghe & Sharp, 2010; Rambaldi et al., 2013). Other studies have been conducted immediately following a major flood incident (Bin & Landry, 2013; Eves & Wilkinson, 2014). A recent qualitative analysis of price behaviour of the Brisbane property market has suggested that floods create negative effects on the average listing price (Eves & Wilkinson, 2014). Another important study (Page et al., 2014) investigated the risk-seeking behaviour of flood-affected households following the 2011 Brisbane floods, and concluded that households in flood-affected areas were 50 per cent more likely to take risks than their neighbours who were unaffected. The data for this study were collected from 220 individual home owners two months after the floods.
Hedonic pricing price analysis is a widely used method which indirectly estimates flood risks, a methodology which is continuously being developed to address econometric questions. Importantly, many HP studies have indicated that, where cross-sectional data are used, the value of a property in one location may also be affected by the property values in its neighbouring area – a phenomenon described as spatial autocorrelation (see Anselin, 1988, 2010).
Some studies have adopted before-and-after analyses to examine the effect of floods on property values (see Bin & Polasky, 2004). More precisely, these analyses have compared one group over two time periods. Before-and-after analysis does not control for changes of market behaviour between the two time periods, although it is an effective tool for measuring other unobserved variables. Bin and Landry (2013) examined the effects of hurricanes Fran and Floyd in North Carolina, USA, within a DID framework. However, this study did not consider the impact of floods on demographic submarkets.
Previous studies have confirmed that following a flood event, there is a significant negative effect on the value of properties at risk. But as many studies have suggested, flood risk tends to disappear over time (see McCluskey & Rausser, 2003; Bin & Landry, 2013). Thus, particularly when flooding is infrequent, the actual flood impact is most pronounced during the event and immediately after. However, many factors such as suburb characteristics also need to be taken into consideration. The following section presents a methodology designed to isolate the impact of floods and the disclosure of flood risk information on property values – a linkage which has not been tested before in the literature. This section then continues with the analysis of the temporal distribution.
3 Methods and Data Collection
As mentioned in the introduction, this study examines the impact of flood risk variables on property values, analyses the effect on the property market of release of flood risk information to the public and compares it with the effect on the property market of the actual flood incidence. It also examines the temporal variation of flood impacts on property values. Below we discuss the methodological approaches and data used in the study.
3.1 Hedonic Property Price Approach
In HP models, the price of a commodity can be attributed to a vector of characteristics which may include property characteristics, environmental and socio-economic factors. Given that the market is in equilibrium, the marginal price of a housing attribute is equal to the marginal willingness to pay for a change in the attribute. The hedonic theory provides a methodology for identifying the structure of prices of each property attribute.
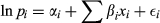 (1)
(1)The next challenge is to analyse and compare the impact of two incidences (the release of flood maps and actual flood event) simultaneously within a DID framework. In this analysis, data on property transactions were collected first before flood risk information was made available (from between 2006 and September 2009; i.e., before October 2009) until the flood incidence (October 2009 to January 2011) and secondly post-floods (January 2011 to March 2013).
3.2 Quasi-Experimental Approach
The release of flood prone area maps for the BCC suburbs in October 2009 and the actual floods in 2011 provide an interesting experiment to assess the impact of flood risks on property markets compared to only examining the effect of either one of these events. For this purpose, the DID framework was employed. According to Woodridge (2007), this method can be applied to both repeated cross-sectional data and panel data. Our study has demonstrated the applicability of this approach for both random as well as natural experiments (see Bin & Landry, 2013; Gawande et al., 2013; Parmeter & Pope, 2013).
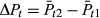 (2)
(2)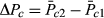 (3)
(3)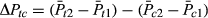 (4)
(4)3.3 Study Area and Data
As a case study, BCC suburbs were selected for empirical investigation. According to Bureau of Transport Economics (2011) estimates, Queensland experiences the second most frequent natural disasters of any Australian state. Brisbane, the capital city of Queensland, is prone to floods as a result of overflow from the Brisbane river and cyclones. In the years following the 1974 floods, the peak water level recorded in Brisbane was in January 2011, at 4.46 metres. Before this flood, the BCC mapped flood risk areas, making them available to the public in October 2009. Although property buyers may not have any experience of the 1974 floods, the release of flood risk maps in October 2009 may reduce information asymmetry, which is assumed will be reflected in the property market. The release of flood maps and the 2011 floods were used as a basis for our case study. A study area, including heterogeneous suburban income groups within the BCC region, was selected using a stratified random sampling procedure. Property transaction data for selected suburbs within the BCC region were collected for the period 2006–2013, and the supplementary secondary data, published by different sources, were collected using Geographical Information System (GIS) techniques. The data collection procedure is summarised in Figure 1.
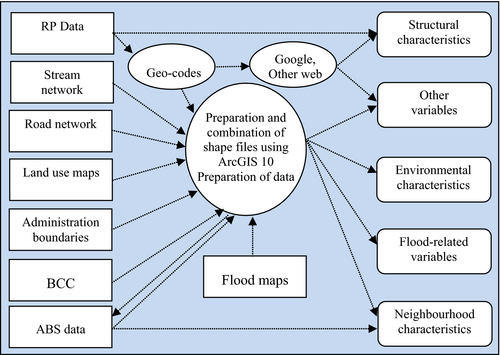
For this study all the relevant property data were available from RP Data Information Service (www.rpdata.com).1 This database provided a comprehensive overview of Australian property sales history and attributes, transactions and other information, including transaction data for multiple and single dwellings, and commercial and vacant properties. Researchers have often used market transaction price as a dependent variable in HP analysis. However, there was no single recognised comprehensive database with which to estimate the HP function. In this case further information available from different sources in different formats (i.e., maps) was merged using ArcGIS. Selected variables and descriptive statistics are shown in the Appendix.
The property market consists of a number of structural variables, surrounding amenities, environmental characteristics and social factors. These attributes include number of bedrooms, number of bathrooms, garage spaces, lot size, type of construction material (wooden or brick), carpeting or not, and existence of a pool. Neighbourhood characteristics of a house include median weekly income, travelling distance to the nearest school, travelling distance to the nearest shopping centre, and distance to amenities (i.e. distance to park). All these characteristics have an influence on property values.
The focus of this study is, however, on flood-related variables and their impact on property values, analysing the impact on property values of the release of flood risk information to the public, comparing it with the effect on property values of the actual flood incidence, and examining the temporal variation of flood impacts.
3.4 Empirical Estimation
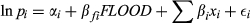 (5)
(5)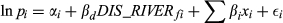 (6)
(6)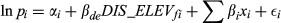 (7)
(7)| OLS estimation | ML estimation | |||||||
|---|---|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 1 | Group 2 | |||||
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| CONSTANT | 11.701328*** | 11.68829*** | 11.7087*** | 11.67813*** | 7.959063*** | 7.923163*** | 9.577748*** | 9.316872*** |
| BEDRM | 0.0274607** | 0.026216** | 0.038291** | 0.039109** | 0.026583* | 0.025387** | 0.041165** | 0.042119** |
| BATHRM | 0.0451245*** | 0.045375*** | 0.108704*** | 0.107054*** | 0.041307*** | 0.041634*** | 0.103538*** | 0.101106*** |
| GARAGE | 0.0552711*** | 0.054394*** | 0.017109 | 0.016837 | 0.054131*** | 0.05331*** | 0.018963 | 0.019058 |
| AREA | 0.0002302*** | 0.000229*** | 0.000485*** | 0.000493*** | 0.000222*** | 0.000221*** | 0.00047*** | 0.000477*** |
| HOUSETYPE | 0.0143539** | 0.015474** | 0.005277 | 0.005848 | 0.01339** | 0.014326** | 0.005024 | 0.005845 |
| FLOOR_CARP | 0.045492** | 0.046148** | −0.02102 | −0.01936 | 0.037792** | 0.03827** | −0.0216 | −0.01929 |
| FLOOR_TILE | 0.0003183 | −0.00263 | 0.042293 | 0.04471 | −0.0052 | −0.00814 | 0.043673 | 0.046645 |
| FLOOR_WOOD | 0.0652864*** | 0.065564*** | 0.005018 | 0.005683 | 0.057759*** | 0.057795*** | 0.009459 | 0.010952 |
| ROOF_TILE | 0.0120244 | 0.013189 | −0.00991 | −0.00608 | 0.005845 | 0.006617 | −0.01414 | −0.01024 |
| ROOF_ASBES | 0.0212661 | 0.024845 | 0.01748 | 0.013895 | 0.014104 | 0.017271 | 0.018705 | 0.015376 |
| WALL_BRICK | −0.0210556 | −0.02323 | −0.02678 | −0.03264 | −0.01594 | −0.01795 | −0.02603 | −0.03289 |
| WALL_WOOD | 0.0212269 | 0.022266 | −0.00658 | −0.00479 | 0.01515 | 0.015821 | −0.0025 | −0.00125 |
| POOL | 0.0546497** | 0.05555** | 0.142154*** | 0.144515*** | 0.050192** | 0.051316** | 0.135236*** | 0.136784*** |
| GARDEN | 0.0570809*** | 0.060746*** | 0.071464*** | 0.072951** | 0.054932*** | 0.058189*** | 0.073143** | 0.074851*** |
| STORIES | 0.0650049 | 0.0652*** | 0.098362*** | 0.105767*** | 0.067397*** | 0.067501*** | 0.096244*** | 0.10372*** |
| RIVERVIEW | −0.1145237 | −0.12135 | 0.322308*** | 0.343242*** | −0.14387 | −0.1498 | 0.298448*** | 0.318181*** |
| INCOME | 0.0000773** | 7.34E-05** | 3.75E-05 | 3.32E-05 | 4.45E-05 | 4.02E-05 | 0.000026 | 1.89E-05 |
| PARKDIS | −0.0000146 | −1.7E-06 | −8.1E-05 | −0.00021** | −2.2E-05 | −8.9E-06 | −0.00013 | −0.00027** |
| HIGHWAY | 0.0000819*** | 0.000086*** | −0.00014*** | −0.00019*** | 0.000055*** | 0.000059*** | −9.7E-05*** | −0.00015*** |
| FLOOD | −0.0626698** | −0.07155** | −0.05916** | −0.06885** | ||||
| DISSHOP | 0.0000944*** | 8.71E-05*** | 4.79E-05 | −2.3E-07 | 7.43E-05*** | 6.71E-05*** | 0.000027 | −2.4E-05 |
| RAILWAY | −0.000093*** | −0.0001*** | 0.000251*** | 0.000484*** | −6.8E-05*** | −7.5E-05*** | 0.000212** | 0.000458*** |
| DISCBD | 0.0000199 | 2.06E-05 | 0.000151** | 0.000152** | 1.71E-05 | 1.86E-05 | 0.000125** | 0.000118** |
| DIS_ELEV | 1.89E-07 | 1.78E-05*** | 1.37E-07 | 1.89E-05*** | ||||
| D_2006 | 0.0678472** | 0.067146* | −0.11235** | −0.11696** | 0.065377** | 0.065063** | −0.11634** | −0.12146** |
| D_2007 | 0.2339419*** | 0.232405*** | 0.094414* | 0.093579* | 0.227376*** | 0.226137*** | 0.085767 | 0.084006 |
| D_2008 | 0.2753989*** | 0.273881*** | 0.089733 | 0.084176 | 0.271701*** | 0.270431*** | 0.086296 | 0.079724 |
| D_2009 | 0.2385291*** | 0.235701*** | 0.086793 | 0.083688 | 0.231178*** | 0.22877*** | 0.082407 | 0.077962 |
| D_2010 | 0.2064737*** | 0.201132*** | 0.073006 | 0.072126 | 0.201254*** | 0.196656*** | 0.070368 | 0.068749 |
| D_2011 | 0.0896609** | 0.086931** | −0.0913 | −0.09461 | 0.091909** | 0.089758** | −0.09419 | −0.09822* |
| D_2012 | 0.0806578** | 0.078817** | −0.05943 | −0.06361 | 0.081836** | 0.080249** | −0.06309 | −0.06824 |
| R 2 | 0.4608 | 0.4578 | 0.68 | 0.68 | ||||
| Adj. R2 | 0.449 | 0.4459 | 0.67 | 0.67 | ||||
| n | 1,399 | 1,399 | 946 | 946 | ||||
| rho | 0.300053*** | 0.301386*** | 0.171414*** | 0.19189*** | ||||
| Log-likelihood | 298.902 | 295.0711 | 116.6622 | 112.3683 | ||||
| Wald test | 51.206*** | 51.452*** | 10.142 | 12.805 | ||||
Note
- ***, ** and * denote that coefficients are significant at 1%, 5% and 10% levels, respectively.
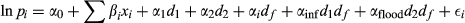 (8)
(8)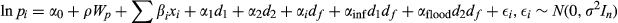 (9)
(9)| OLS estimation | ML estimation | |||||||
|---|---|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 1 | Group 2 | |||||
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| CONSTANT | 12.15933*** | 12.1886*** | 11.65049*** | 11.7921*** | 8.170768*** | 8.195209*** | 9.298884*** | 9.305311*** |
| BEDRM | 0.028467** | 0.029949** | 0.039653** | 0.038511** | 0.02742** | 0.027745** | 0.042948** | 0.041861*** |
| BATHRM | 0.052969*** | 0.050809*** | 0.109633*** | 0.107662*** | 0.048855*** | 0.048198*** | 0.103881*** | 0.101298*** |
| GARAGE | 0.05489*** | 0.055411*** | 0.010351 | 0.01122 | 0.053481*** | 0.053746*** | 0.012322 | 0.014597 |
| AREA | 0.000239*** | 0.000241*** | 0.000479*** | 0.000491*** | 0.00023*** | 0.000231*** | 0.000463*** | 0.000475*** |
| HOUSETYPE | 0.021338** | 0.021551** | 0.001985 | 0.0039 | 0.020122*** | 0.020149*** | 0.00165 | 0.003876 |
| FLOOR_CARP | 0.05412*** | 0.054669*** | −0.01393 | −0.00813 | 0.044963*** | 0.045397*** | −0.01485 | −0.00839 |
| FLOOR_TILE | 0.019814 | 0.019977 | 0.077428 | 0.080524 | 0.012689 | 0.013679 | 0.078802 | 0.082343 |
| FLOOR_WOOD | 0.071662*** | 0.071245*** | 0.001372 | 0.003777 | 0.062775*** | 0.062914*** | 0.006049 | 0.009065 |
| ROOF_TILE | −0.01119 | −0.00976 | −0.00926 | −0.00475 | −0.01669 | −0.01649 | −0.01385 | −0.00912 |
| ROOF_ASBES | 0.011 | 0.0135901 | 0.030523 | 0.029694 | 0.004001 | 0.003522 | 0.032054 | 0.031265 |
| WALL_BRICK | −0.07255*** | −0.07231*** | −0.04282 | −0.05282 | −0.06599*** | −0.06558*** | −0.04094 | −0.05204 |
| WALL_WOOD | −0.01923 | −0.017232 | −0.01825 | −0.02592 | −0.02464 | −0.02435 | −0.01299 | −0.02135 |
| POOL | 0.046564** | 0.046092** | 0.147046*** | 0.147711*** | 0.041853** | 0.040747** | 0.139487*** | 0.139709*** |
| GARDEN | 0.062282*** | 0.062071*** | 0.077649*** | 0.07692*** | 0.060053*** | 0.05998*** | 0.079771*** | 0.079027*** |
| STORIES | 0.064739*** | 0.065711*** | 0.100373*** | 0.104659*** | 0.067457*** | 0.06801*** | 0.09777*** | 0.102317*** |
| RIVERVIEW | −0.1811 | −0.18181 | 0.331865*** | 0.34863*** | −0.20996* | −0.21008* | 0.305676*** | 0.322543*** |
| INCOME | 4.35E−05 | 0.000045 | 3.37E-05 | 2.93E-05 | 1.09E-05 | 1.29E-05 | 2.17E-05 | 6.25E-06 |
| PARKDIS | −3E-06 | −6.8E-06 | −6.1E-05 | −0.00016* | −1.2E-05 | −1.7E-05 | −0.00011 | −0.00022** |
| HIGHWAY | 7.21E-05*** | 7.13E-05*** | −0.00013*** | −0.00016*** | 4.43E-05*** | 4.34E-05** | −8.6E-05*** | −0.00012*** |
| FLOOD | 0.015731 | 0.011544 | 0.017288 | 0.014305 | ||||
| DISSHOP | 7.16E-05*** | 0.000072*** | 5.48E-05 | 0.0000394 | 5.18E-05** | 5.34E-05** | 3.21E-05 | 0.000014 |
| RAILWAY | −8.3E-05*** | −8.1E-05*** | 0.000264*** | 0.000453*** | −5.7E-05*** | −5.6E-05*** | 0.000221** | 0.000427*** |
| DISCBD | 2.69E-07 | −2.37E-06 | 0.000161** | 0.000136** | −1.6E-06 | −3.7E-06 | 0.00013** | 0.0001* |
| DIS_ELEV | 1.04E-07 | 1.31E-05** | 5.6E-08 | 1.45E-05** | ||||
| D 1 | −0.01445 | −0.00644 | −0.04388 | −0.0223 | −0.01584 | −0.00146 | −0.04131 | −0.01638 |
| D 2 | −0.19779*** | −0.2519*** | −0.18701*** | −0.1880*** | −0.18894*** | −0.18907*** | −0.19128*** | −0.19257*** |
| R 2 | 0.3834 | 0.3875 | 0.6692 | 0.6716 | ||||
| Adj. R2 | 0.3722 | 0.3764 | 0.6602 | 0.6627 | ||||
| n | 1,399 | 1,399 | 946 | 946 | ||||
| rho | 0.318157*** | 0.31758*** | 0.189323*** | 0.201703*** | ||||
| Log-likelihood | 206.0023 | 205.8612 | 134.6597 | 130.3533 | ||||
| Wald test | 50.314 | 50.068 | 12.13 | 13.825 | ||||
Note
- ***, ** and * denote that coefficients are significant at 1%, 5% and 10% levels, respectively.
3.5 Temporal Variation of Flood Risk
In this section we capture the temporal variation of flood risk. It was hypothesised that the disclosure of flood risk map information and the actual flood-incidence-induced effect on the property market disappeared with time or varied inversely with elapsed time (see Lamond, 2008; Bin & Landry, 2013). In order to test this hypothesis, the spatial HP model was extended to incorporate the elapsed time variable (see Hansen et al., 2006; Bin & Landry, 2013).
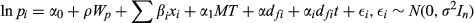 (10)
(10)| OLS estimation | ML estimation | |||
|---|---|---|---|---|
| Group 1 | Group 2 | Group 1 | Group 2 | |
| CONSTANT | 11.85259*** | 11.67174*** | 9.6964*** | 10.54767*** |
| BEDRM | 0.037972** | 0.0213289 | 0.03642** | 0.021991 |
| BATHRM | 0.072928** | 0.132123*** | 0.071922*** | 0.133088*** |
| GARAGE | 0.05946*** | 0.0283755 | 0.057972*** | 0.029293 |
| AREA | 0.000138*** | 0.000539*** | 0.000138*** | 0.000538*** |
| HOUSETYPE | 0.0338124** | 0.03361** | 0.033288** | 0.032713** |
| FLOOR_CARP | −0.02145 | −0.015277 | −0.025233 | −0.01195 |
| FLOOR_TILE | −0.08355* | −0.03751 | −0.08481* | −0.04078 |
| FLOOR_WOOD | 0.02753 | 0.00498 | 0.0260779 | 0.006601 |
| ROOF_TILE | 0.03031 | 0.026397 | 0.030716 | 0.030372 |
| ROOF_ASBES | −0.00113 | 0.03796 | −0.003362 | 0.045079 |
| WALL_BRICK | 0.00492 | 0.0096 | 0.0066 | 0.008813 |
| WALL_WOOD | 0.03785 | 0.0351 | 0.038469 | 0.037328 |
| POOL | 0.04489 | 0.10881** | 0.04251 | 0.104478** |
| GARDEN | 0.077567** | 0.11951** | 0.07663*** | 0.11675** |
| STORIES | 0.043288 | 0.12744** | 0.049887 | 0.128276** |
| RIVERVIEW | 0.152028 | 0.22393** | 0.15047 | 0.215611** |
| INCOME | 0.00017** | 5.71E-05 | 0.000152** | 0.000054 |
| PARKDIS | −0.00011** | −0.00029** | −0.000118** | −0.00031** |
| HIGHWAY | 2.05E-05 | −0.00017** | 1.49E-05 | −0.00015** |
| FLOOD | −0.17237*** | −0.15051** | −0.1657*** | −0.14185*** |
| DISSHOP | 7.27E-05 | −6.56E-05 | 6.86E-05* | −6.5E-05 |
| RAILWAY | −9.46E-05** | 0.000385** | −7.43E-05* | 0.000373** |
| DISCBD | 1.27E-05 | 0.000106 | 4.22E-05 | 8.77E-05 |
| DIS_ELEV | 5.88E-06 | 1.97E-05** | 6.24E-07 | 2.04E-05** |
| MT | −0.003029** | 0.0020667 | −0.00285** | 0.002006 |
| R 2 | 0.5575 | 0.7552 | ||
| Adj. R2 | 0.5203 | 0.7283 | ||
| n | 323 | 254 | 323 | 254 |
| rho | 0.1759*** | 0.092842*** | ||
Note
- ***, ** and * denote that coefficients are significant at 1%, 5% and 10% levels, respectively.
4 Results
For this analysis pooled cross-sectional data relevant to the selected flood-affected suburbs within the BCC region were used. Data cleaning was conducted and some were discarded due to missing attributes and outliers. It is noted that the application of the spatial technique discussed in Section III is not possible for a large dataset (e.g., Neill et al., 2007). Moreover, the observations need to be close enough to create a spatial impact. Thus, if some variables are dispersed, a weight matrix cannot be estimated. On the other hand, the dataset should be large enough to incorporate sufficient determinants to minimise the effect of outliers. Hence, selected suburbs were grouped after examining suburb characteristics and dispersion.
For example, Chelmer and Graceville are two adjacent suburbs and show similar characteristics. According to the census and statistics data (2011), both suburbs belonged to the high-income category (average weekly household median income was $A2,216 in 2011). These two suburbs were therefore merged into a one cluster (group 2) to obtain a reasonable number of transaction records for the study period. The first group, comprising of Oxley and Durack, which are also in close geographical proximity, showed an average median income of $1,329 and were therefore classified as low-income suburbs in line with Australian Bureau of Statistics census data (2011). The second group is close to the river, while the first group is much farther (the mean distances to the river are 3,259 m and 513 m for group 1 and group 2, respectively). A correlation matrix was used to examine the presence of multicollinearity – an econometric problem which may occur in using HP analysis.
Overall, the real price of property varied between $371,500 and $8 million. The differences in the mean value of property were observed across different groups. The high correlation (0.66) between house price and income is a good approximation for dividing submarkets based on house prices. The descriptive statistics of structural characteristics such as number of bedrooms (BEDRM), number of bathrooms (BATHRM) and number of garage spaces (GARAGE) are presented in the Appendix. These data indicate that the distribution of these variables is more or less similar for both groups. However, the variables of interest in this study, namely the dummy variable for flood affected area (FLOOD) and interaction of elevation and distance to the river (DIS_ELEV) did show differences between the groups.
4.1 OLS and ML Estimation
The HP price regression parameters for OLS and ML estimations for groups 1 and 2 which are based on Equations 5 and 7 are presented in Table 1. As mentioned previously, estimations are undertaken first using OLS (columns 2–5). This is followed by ML estimation (columns 6–9). In model 1, the flood affected area was specified using flood maps, while in model 2 the flood risk was specified two dimensionally as a product of distance to the river and elevation (DIS_ELEV). If properties are close to the river but are located at a higher elevation, then they are likely to have higher amenity values rather than flood risk. In such a situation, the distance to the river is not an appropriate indicator to capture the flood risk.
All coefficients for property attributes, environmental characteristics and flood-related variables were found to have the expected signs, and most coefficients were statistically significant (see Table 1). For example, the estimated coefficients for the number of bedrooms, number of bathrooms and land area show positive and significant effects on property values.
The OLS estimates (columns 2–5) remain unbiased; however, many studies have observed spatial interactions in the property market (e.g., Hayunga & Pace, 2010; Osland, 2010; Samarasinghe & Sharp, 2010; Bin & Landry, 2013). Hence, estimated coefficients are not likely to be efficient if the market is spatially interacted. The spatial interaction, which is determined by the estimated spatial weight matrix, can be due to unobserved characteristics that may be shared between close properties. The significant Moran's I statistics provided evidence for the presence of such spatial interaction. Robust LM lag statistics were significant and hence spatial lag models were estimated. An ML estimation was executed to incorporate the spatial effect. Table 1 (columns 6–9) show the results of the ML estimation of the HP price function. The results are similar to the OLS estimation, but the coefficient values are different. As observed with the presence of the spatial effect, the ML estimation is more robust than the OLS estimation. The estimation of two models under each cluster of properties was similar to the OLS estimation, but incorporated the spatial lag effect.
As expected, the number of bedrooms (BEDRM), number of bathrooms (BATHRM), number of garage space (GARAGE) and land area (AREA) positively affected property values. According to the estimations, each additional bedroom increased a property's price by 3 per cent for the first group. Other important structural factors describing a property are construction materials (for the roof, walls and floors). However, these structural dummy variables are not always significant, possibly due to differences in quality rather than the material. The data also indicate that two- or three-storey houses are more valuable than single-storey houses.
The dummy variable for having a swimming pool (POOL) – an attractive attribute for property values – positively affected property values and had statistically significant coefficients. The dummy variables used to control for the year of sale showed mixed results. In most cases, year dummies are positive, with some being significant, particularly in the case of low-income categories where property prices increased, whereas in the high-income category property prices were prone to fluctuation.
The impact of floods on property values showed a significant drop in property prices when the property was in the flood zone (see the model 1 variable named FLOOD, Table 1). If the property was in the flood zone, the average property price decreased by 6 per cent in group 1 and 7 per cent in group 2. Group 1 and 2 were different in terms of the median household income. This finding is consistent with Gayer (2000) who found that the risk varied with the neighbourhood income. Next, flood risk as a function of the product of distance to the river and elevation was tested. It was found to have a significant and positive effect on property values (see the model 2 variable named DIS_ELEV, Table 1). This interaction term was more robust than using two variables separately, namely distance to river and elevation.
4.2 Spatial Quasi-Experimental Analysis
In this section, a quasi-experimental design was employed to overcome the problem of isolating the effect of actual floods and release of flood risk map information on property values. This is because the flood-affected variable (FLOOD) and the interaction variable (distance × elevation, DIS_ELEV) in Table 1 did not isolate the impact on property values of the October 2009 release of flood risk maps or the actual floods in 2011. To overcome this shortcoming one possibility is to use before-and-after analysis which compares pre- and post-incident effects (e.g., Bin & Polasky, 2004). However, the changes in property market behaviour over two time periods, such as changes in the macroeconomic situation, migration, and interest rates, are not captured in the before-and-after analysis. A means to overcome this problem is to control the variability with non-affected properties. For comparison purposes, DID models were estimated with ML and without the spatial effect (OLS). Estimated coefficients were found to be more or less similar (see Table 2). OLS estimates are found to be high and significant, and adjusted R2 ranges from 0.37 to 0.66. The two treatments for the release of flood maps in 2009 and the Brisbane floods in 2011 were examined in this study. This is shown in Table 2 for groups 1 and 2. The average treatment effects are shown in the coefficients of D1 (impact of release of flood maps) and D2 (impact of the 2011 floods).
In a quasi-experimental technique, DID distinguishes the impact of floods and release of flood risk map information on property values. The first DID coefficients (D1) of estimated models do not provide significant results, although they show the expected negative signs. The second (D2) is significant at the 1 per cent level. These results indicate that the average value of properties in the flood affected zones decreased after the 2011 flood event. In comparison to the actual flood event, the impact of the release of flood risk map information was found to be minimal. The release of flood maps decreased property values by 1–4 per cent whereas the impact of actual flood incidence was 18–19 per cent. These results are consistent with the findings of Siegrist and Gutscher (2008) who interviewed people in flood-affected and non-affected areas within flood-prone areas and found that people who did not experience floods undervalued the risk. However, some studies have found a significant effect from the release of public information on property values (see Samarasinghe & Sharp, 2010).
4.3 Temporal Variation of Flood Risk
Based on the existing literature (see Lamond, 2008; Bin & Landry, 2013), we assume that the negative effect on property values resulting from the 2009 release of flood risk maps and the 2011 flood is likely to disappear over time. Reasons for this include residents forgetting unpleasant experiences over time, appropriate flood mitigation mechanisms being undertaken and the development of additional amenities. Moreover, there are indications that property values tend to bounce back due to rehabilitation efforts undertaken after the floods. An examination of the history of the occurrence of floods would highlight the fact that the frequency of extreme floods statistically happens (on average) once in a lifetime. The hypothesis was tested using data following the flood incident. Since only a few years have lapsed since the flood (at the time of data collection), monthly sales were counted for the analysis.
The results of Equation 10 are reported in Table 3 for groups 1 and 2. Both OLS and ML estimates are reported. The variable of interest (MT) is negative and significant at the 5 per cent level for group 1 and is positive but statistically non-significant for group 2. The results for group 1 (low-income suburbs) show that property values are still in decline, while for the group 2 (high-income suburbs) the sign is in a recovery trend.
According to data from the census and statistic survey (2011), group 1 falls into the low-income category with many households in the low income category, whereas group 2 is in the high-income category based on the ranking of median income. The results suggest that property prices in the poorer suburbs are declining. However, the study's brief time frame becomes an important qualification to these results. According to Lamond (2008) property prices recover after 3 years, while Bin and Landry (2013) found that it takes about 5–7 years for total recovery.
5 Conclusions
This paper has examined the impact on property values of flood-affected and flood risk variables among other factors. The impact of floods on property values is shown to produce a significant drop in property prices in cases where the property was in the flood zone (see Table 1). For such properties the average property price decreased by 6 per cent in group 1 (low-income suburbs) and 7 per cent in group 2 (high-income suburbs). This analysis is followed by examining the impact of releasing flood risk map information and the effect of actual floods on property values. Application of the conventional HP function was not appropriate for comparing two consecutive events such as the release of flood risk maps (i.e., information on a potential disaster) and the actual flood incidence (i.e., disaster event). Therefore, in this study two treatments – release of flood risk map information and actual flood incidence – were compared using a quasi-experimental technique using DID estimation. More robust estimation was achieved by comparing the two incidents with a suitable control group. Previous studies have not distinguished between the effects of these incidences.
The results show that the average value of properties in the flood zones decreased after the 2011 flood event. In comparison to the actual flood event, the impact of the release of flood risk map information is found to be minimal. The release of flood maps decreased property values by 1–4 per cent (see Table 2). The release of flood risk maps undoubtedly reduced the level of information asymmetry among buyers, but was not expected to have a larger impact than the impact of the actual floods, which reduced property values by 18–19 per cent. There are good reasons why there is discounting of the possibility of properties in flood zones being affected in another flood. For example, the history of the occurrence of floods highlights the fact that extreme floods happen (on average) once in a lifetime. As well, after the 1974 floods in Brisbane, the Wivenhoe dam was built below the Somerset dam to prevent another repeat of the major floods (Atfield & Moore, 2011). Atfield and Moore (2011) quote Professor Trevor Grigg, who authored a report on the flood mitigation advantages of Wivenhoe Dam after the 1974 floods, as saying: ‘A lot of people believed we were protected by these dams but of course we never were.’ Furthermore, there is evidence in the academic literature to show that people who did not experience floods undervalued the risk (see Siegrist & Gutscher, 2008). It is also to be expected that properties located closer to a water body have both amenity as well as disamenity values. The results from Table 2 confirmed that the release of flood risk information in October 2009 was largely discounted. Apart from the reasons provided above, it is also possible that amenity values to households resulting from living close to a water body outweigh the potential disamenities. As well, there is the probability that ‘some consumers appear to not have a good understanding of their level of risk or of their insurance policy’ (Productivity Commission, 2014, p. 414). With respect to underinsurance, the Productivity Commission (2014, p. 414) states: ‘While a significant proportion of households appear to be underinsured, it is not known how many are making a fully informed choice and how many are underinsured due to market distortions (especially information asymmetry) or cognitive barriers.’
We also estimated the temporal variation of flood impacts on property values. Our hypothesis, based on past studies (see Lamond, 2008; Bin & Landry, 2013), was that property values tend to bounce back due to factors such as rehabilitation efforts undertaken after the floods (see Table 3). The regression results showed that in low-income suburbs property values are still in decline, while for high-income suburbs the sign is positive, although not statistically significant. In other words, the results indicate that property values in rich suburbs recover faster than those in poorer suburbs.
This research also highlights the importance of suburb characteristics for property values and the speed of recovery of property values after a flood event. These findings are important to guide post-disaster funding, such as response, relief assistance to households, recovery and mitigation undertaken by the state and local governments.
This study also provides additional information needed to create better price signals for effective risk management, as called for by the Productivity Commission (2014). As the Commission states: ‘For insurers to price premiums according to the risk the policyholder faces, they need information on natural disaster risk’ (p. 427). The Commission further states: ‘For insurers to efficiently price insurance products, good information is required for all these component elements of risk’ (p. 427). While, ‘historically, insurers have had limited information with which to price risk’ (p. 427), progress has been made with better information being made available. Nevertheless there is still room for improvement in areas such as ‘insurers’ knowledge about individual property characteristics’ (p. 428), distance to river and elevation of property and other suburb characteristics and amenity values.
In addition, this study provides further information that could assist insurers to price premiums based on the risk households face such as property, geographical as well as suburb characteristics. In short, the study identifies some of the main characteristics of ‘high-risk households’. As the Productivity Commission (2014, p. 414) states: ‘Governments should not address affordability concerns by providing subsidies, especially to high-risk households. Subsidies reduce the effectiveness of insurance in communicating and managing risk.’ The study results also provide an opportunity for insurers to narrow down risks beyond postcode levels in formulating insurance premiums where risks can be more accurately determined. This could avoid flat insurance premiums where ‘both high- and low risk policyholders are paying the same premium, [and] low-risk policyholders are likely to be cross-subsidising high-risk policyholders’ (p. 427). A lack of insufficient information ‘can also lead to insurers pricing defensively and charging higher premiums to all policyholders’ (p. 427).
Finally, there is the more general point that the availability of reliable information is a key precondition for competitive markets, given that investors need this information to make appropriate investment decisions. Awareness of the behaviour of property values is equally important for banks and other financial institutes in order to implement appropriate mortgage payments.
Notes
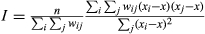 , where x is the mean of the x and the wij are the elements of the weight matrix.
, where x is the mean of the x and the wij are the elements of the weight matrix.
Appendix A
Description of Variables
| Constant | Description |
|---|---|
| N_PRICE | House sale price |
| R_PRICE | House sale price adjusted to 2013 Q1 price |
| BEDRM | Number of bedrooms |
| BATHRM | Number of bathrooms |
| GARAGE | Number of garage spaces |
| AREA | Total floor area in square metres |
| HOUSETYPE | A number for the decade that the property was built (proxy variable for the age of the house) |
| FLOOR_CARP | Dummy variable for floor construction material: 1 if carpet, 0 otherwise |
| FLOOR_TILE | Dummy variable for floor construction material: 1 if tile, 0 otherwise |
| FLOOR_WOOD | Dummy variable for floor construction material: 1 if wood, 0 otherwise (omitted category is mixed) |
| ROOF_TILE | Dummy variable for roof construction material: 1 if tile, 0 otherwise |
| ROOF_ASBES | Dummy variable for roof construction material: 1 if asbestos, 0 otherwise (omitted category is galvanised) |
| WALL_BRICK | Dummy variable for wall construction material: 1 if brick, 0 otherwise |
| WALL_WOOD | Dummy variable for wall construction material: 1 if wood, 0 otherwise (omitted category is mixed) |
| POOL | Dummy variable: 1 if a swimming pool is available, 0 otherwise |
| GARDEN | Dummy variable for well-maintained garden: 1 if yes, 0 otherwise |
| STORIES | Number of storeys |
| ELEV | Elevation |
| RIVERVIEW | Dummy variable: 1 if property is on the waterfront, 0 otherwise |
| INCOME | Median household income in the mesh block |
| PARKDIS | Distance in metres to the closest park |
| HIGHWAY | Direct distance in metres to the highway |
| FLOOD | Dummy variable for flood-affected property: 1 if the property is flood-affected in 2011, 0 otherwise |
| DIS_RIVER | Direct distance in metres to the Brisbane river or water stream |
| DISSHOP | Distance in metres to the closest shopping centre |
| RAILWAY | Direct distance in metres to the railway track |
| DISCBD | Distance in metres to the Central Business District |
| DIS_ELEV | DIS_RIVER and ELEV interaction |
| MT | Elapsed time in months after 2011 floods |
| D_2006 | Dummy variable for the year of sale: 1 if sale occurs in 2006, 0 otherwise |
| D_2007 | Dummy variable for the year of sale: 1 if sale occurs in 2007, 0 otherwise |
| D_2008 | Dummy variable for the year of sale: 1 if sale occurs in 2008, 0 otherwise |
| D_2009 | Dummy variable for the year of sale: 1 if sale occurs in 2009, 0 otherwise |
| D_2010 | Dummy variable for the year of sale: 1 if sale occurs in 2010, 0 otherwise |
| D_2011 | Dummy variable for the year of sale: 1 if sale occurs in 2011, 0 otherwise |
| D_2012 | Dummy variable for the year of sale: 1 if sale occurs in 2012, 0 otherwise (omitted category is 2013) |
| n | Number of observations |
Descriptive Statistics
| Variable | Group 1 | Group 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min | Max | Mean | SD | Min | Max | |
| N_PRICE | 371,500.10 | 109,708.30 | 115,000.00 | 1,260,000.00 | 811,142.50 | 535,159.30 | 104,000.00 | 5,160,000.00 |
| R_PRICE | 447,631.60 | 128,267.50 | 152,459.00 | 1,567,934.00 | 962,409.40 | 640,991.40 | 116,365.20 | 6,893,080.00 |
| BEDRM | 3.38 | 0.71 | 1.00 | 6.00 | 3.56 | 0.84 | 2.00 | 7.00 |
| BATHRM | 1.55 | 0.60 | 0.00 | 4.00 | 1.99 | 0.83 | 1.00 | 5.00 |
| GARAGE | 1.56 | 0.76 | 0.00 | 6.00 | 1.63 | 0.83 | 0.00 | 4.00 |
| AREA | 655.25 | 315.44 | 119.00 | 5,640.00 | 640.46 | 326.00 | 300.00 | 4,530.00 |
| STORIES | 1.18 | 0.39 | 1.00 | 2.00 | 1.35 | 0.48 | 0.00 | 3.00 |
| RIVERVIEW | 0.00 | 0.05 | 0.00 | 1.00 | 0.08 | 0.27 | 0.00 | 1.00 |
| ELEV | 24.76 | 10.29 | 7.03 | 66.55 | 15.23 | 3.97 | 7.38 | 25.49 |
| INCOME | 1,329.18 | 260.76 | 614.00 | 1,898.00 | 2,216.31 | 437.24 | 1,536.38 | 3,291.13 |
| PARKDIS | 703.17 | 377.52 | 60.00 | 1,900.00 | 440.95 | 205.62 | 10.00 | 900.00 |
| HIGHWAY | 1,756.76 | 1,005.58 | 50.00 | 4,100.00 | 2,302.06 | 749.86 | 750.00 | 3,800.00 |
| FLOOD | 0.10 | 0.30 | 0.00 | 1.00 | 0.39 | 0.49 | 0.00 | 1.00 |
| DIS_RIVER | 3,258.76 | 1,849.20 | 400.00 | 6,700.00 | 512.90 | 228.83 | 100.00 | 1,000.00 |
| DISSHOP | 1,940.46 | 631.69 | 500.00 | 3,220.00 | 1,465.58 | 355.43 | 760.00 | 2,160.00 |
| RAILWAY | 2,041.83 | 1,610.59 | 10.00 | 4,620.00 | 470.20 | 250.47 | 10.00 | 1,070.00 |
| DISCBD | 12,181.13 | 1,501.59 | 10,100.00 | 15,000.00 | 6,984.04 | 337.26 | 6,300.00 | 7,800.00 |




