The Impacts of Different Farm Programs on Cash Rents
This paper was presented at the ASSA winter meetings (Washington D.C., January 2003). Papers in these sessions are not subjected to the journal's standard refereeing process.
Farmland is the main asset of the U.S. agricultural sector's balance sheet, accounting for an average of 68% of U.S. agricultural assets between 1960 and 2001. This is important for at least three reasons. First, the sector's solvency is intimately linked to the value of farmland. Second, the opportunity cost of farmland represents a major production expense from the perspective of individual farmers. Finally, related to the opportunity cost of farmland, farmland values have a significant effect on the estimation of productivity and competitiveness measures across regions.
The significance of farmland values for the agricultural sector's economic performance has made factors determining farmland values a frequent subject of research. Studies of farmland values have typically emphasized expected returns, interest rates, and government payments to farmers, among other factors. In a recent comparison of rates of return between farm and nonfarm businesses, Hopkins and Morehart show that nonfarm businesses generate much higher sales from their assets than farm businesses do. They suggest that farmland may be responsible for this perceived inefficiency, through the capitalization of payments from government programs into farmland prices. The capitalization of farm program payments into land values has often been discussed in the literature (e.g., Just and Miranowski, Tweeten and Martin, Herdt and Cochrane, Melichar). However, these studies were limited in the way returns to farmland were measured. For example, returns to farmland were estimated as the residual return remaining after paying for all other factors. Additionally, some studies include farm payments as explanatory variables of land prices or returns, without providing a theoretical foundation to include them in the analysis and to interpret the results in economic terms.
The present study is unique in several ways. First, unlike previous related research, the focus is on the impact of government payments on cash rental rates, which are representative of the observed price of land as an input in the production process (Alston). Second, a theoretical model is developed to investigate the effect of government payments on cash rental rates. Third, government payments are disaggregated into four distinct categories: (1) deficiency payments (DEF), (2) payments associated with the market loss assistance program (MLA), (3) production flexibility contract (PFC) payments, and (4) conservation reserve program (CRP) payments. This disaggregation of government payments allows us to test whether they exert different impacts on cash rental rates. Finally, because of the geographic nature of the data used for the empirical analysis, the econometric estimation specifically allows for spatial autocorrelation.
Theoretical Model
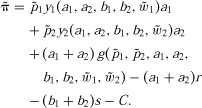 (1)
(1)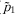 and
and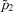 ) and environmental conditions during the growing season (e.g., weather and the like) (
) and environmental conditions during the growing season (e.g., weather and the like) (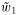 and
and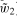 ), and may be correlated with each other. Yields per acre [y1(·) and y2(·)] are determined by the acres planted (a1 and a2) and the levels of other variable inputs (b1 and b2), and are random because they are affected by the environmental conditions. Government payments per acre [g(·)] may also be random because they may depend on crop prices and environmental conditions, in addition to planted acres and input levels. Finally, r denotes the rental rate per acre, s is the per unit cost of other variable inputs, and C represents fixed costs.
), and may be correlated with each other. Yields per acre [y1(·) and y2(·)] are determined by the acres planted (a1 and a2) and the levels of other variable inputs (b1 and b2), and are random because they are affected by the environmental conditions. Government payments per acre [g(·)] may also be random because they may depend on crop prices and environmental conditions, in addition to planted acres and input levels. Finally, r denotes the rental rate per acre, s is the per unit cost of other variable inputs, and C represents fixed costs.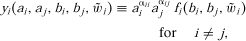 (2)
(2)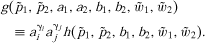 (3)
(3)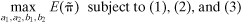 (4)
(4)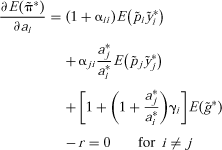 (5)
(5) , and asterisks are used to denote optimal levels of the decision variables.
, and asterisks are used to denote optimal levels of the decision variables.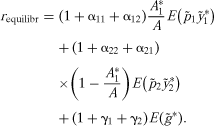 (6)
(6)Estimation Methods
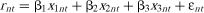 (7)
(7)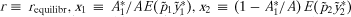 , and
, and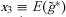 . The ε term is a zero-mean regression error uncorrelated with x1, x2, and x3. Note that a testable restriction of (7) is that the intercept should equal zero. In the context of (7), the effect of government payments on land rents can be obtained as the estimate of coefficient β3.
. The ε term is a zero-mean regression error uncorrelated with x1, x2, and x3. Note that a testable restriction of (7) is that the intercept should equal zero. In the context of (7), the effect of government payments on land rents can be obtained as the estimate of coefficient β3.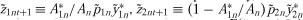 , and
, and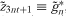 , so that
, so that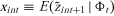 . That is, E(· | φt) denotes the expectation operator conditional on information at time t. Because it is always possible to write
. That is, E(· | φt) denotes the expectation operator conditional on information at time t. Because it is always possible to write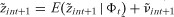 provided
provided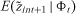 does exist,3 it follows that
does exist,3 it follows that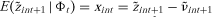 . Therefore, xint = zint+1 − νint+1, where zint+1 and νint+1 (without tildes) denote actual realizations of
. Therefore, xint = zint+1 − νint+1, where zint+1 and νint+1 (without tildes) denote actual realizations of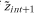 and
and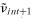 , respectively. Since zint+1 is observable, in principle, the advocated solution consists of estimating regression (8) instead of (7):
, respectively. Since zint+1 is observable, in principle, the advocated solution consists of estimating regression (8) instead of (7):
 (8)
(8)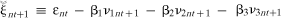 .
.Compared with (7), the key feature of (8) is that the residual is correlated with the regressors (because zint+1 measures xint+1 with error). This causes ordinary least squares estimates of βs in (8) to be biased. To control for this problem, we use the generalized method of moments (GMM) with lagged realizations (zint) as instruments. Since lagged realizations are in the information set available at the time of decision making, they are uncorrelated with the difference between the conditional expectation and the actual realization (i.e., zint and
is correlated with the regressors (because zint+1 measures xint+1 with error). This causes ordinary least squares estimates of βs in (8) to be biased. To control for this problem, we use the generalized method of moments (GMM) with lagged realizations (zint) as instruments. Since lagged realizations are in the information set available at the time of decision making, they are uncorrelated with the difference between the conditional expectation and the actual realization (i.e., zint and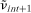 are uncorrelated because
are uncorrelated because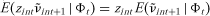 ).
).
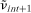 in the time dimension is zero
in the time dimension is zero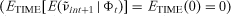 , so that its sample counterpart tends to zero as the time series becomes infinitely long:
, so that its sample counterpart tends to zero as the time series becomes infinitely long:
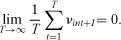 (9)
(9)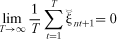 (10)
(10)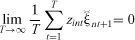 (11)
(11)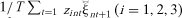 to estimate the three coefficients β1, β2, and β3. Condition (10) shows that the intercept in (8) should equal zero.
to estimate the three coefficients β1, β2, and β3. Condition (10) shows that the intercept in (8) should equal zero.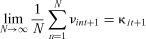 (12)
(12)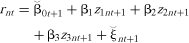 (13)
(13)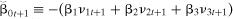 ≡−(β1ν1 t+1 + β2ν2t+1 + β3ν3t+1) and
≡−(β1ν1 t+1 + β2ν2t+1 + β3ν3t+1) and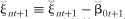 .4 The cross-sectional counterparts of (10) and (11) are (14) and (15), respectively,
.4 The cross-sectional counterparts of (10) and (11) are (14) and (15), respectively,
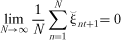 (14)
(14)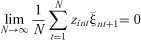 (15)
(15)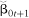 , β1, β2, and β3 are estimated from the four sample counterparts of (14) and (15).
, β1, β2, and β3 are estimated from the four sample counterparts of (14) and (15).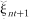 are correlated across counties, but also that residuals of neighboring counties are more correlated than residuals of counties far apart from each other.5 For this reason, it is important to allow for spatial error dependence as well. Succinctly, defining the (N × 1) cross-sectional vectors rt ≡ [r1t, …, rNt]′, rit+1 ≡ [zi1t+1, …, ziNt+1]′, and
are correlated across counties, but also that residuals of neighboring counties are more correlated than residuals of counties far apart from each other.5 For this reason, it is important to allow for spatial error dependence as well. Succinctly, defining the (N × 1) cross-sectional vectors rt ≡ [r1t, …, rNt]′, rit+1 ≡ [zi1t+1, …, ziNt+1]′, and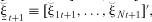 , autoregressive spatial error dependence means that (Anselin and Bera):
, autoregressive spatial error dependence means that (Anselin and Bera):
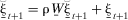 (16)
(16)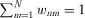 (Anselin and Bera).
(Anselin and Bera).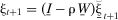 , where I̱ is the (N × N) identity matrix, it follows from (13) that the uncorrelated error vector ξ̱t+1 can be expressed as
, where I̱ is the (N × N) identity matrix, it follows from (13) that the uncorrelated error vector ξ̱t+1 can be expressed as
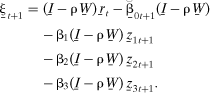 (17)
(17)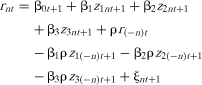 (18)
(18)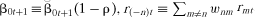 , and zi(−n)t+1 ≡ ∑m≠nwnmzimt+1.
, and zi(−n)t+1 ≡ ∑m≠nwnmzimt+1.From the earlier discussion about (8), residual ξnt+1 in (18) is correlated with both zint+1 and zi(−n)t+1 because they measure, respectively, xint+1 and xi(−n)t+1 with error. Residual ξnt+1 is also correlated with r(−n)t becausernt and r(−n)t are simultaneously determined.6 This means that the desired coefficient β3 in (7) can be estimated from cross-sectional data by applying GMM to (18) and using as instruments the lagged values of the regressors (and a constant). If panel data are available, (18) can be estimated in the form of a system of equations, each of them corresponding to each cross-section available, restricting all coefficients other than the intercept to being the same across equations.
Data
The model was estimated using county-level annual panel data for the state of Iowa. Lack of county-level price and/or cash-rental information prevented us from fitting the model with data from other states. Data were obtained from various sources. Cash rental rates were the average typical cash rental rates per acre of cropland reported in publication FM 1851 of the Iowa State University Cooperative Extension Service. Prices received by farmers for corn and soybeans data were downloaded from the Iowa Agricultural Statistics Service's website. Corn and soybean yields were calculated by dividing county output by the respective planted areas. Output and area planted data were furnished by the National Agricultural Statistics Service of the U.S. Department of Agriculture (USDA).
County-level government payments were obtained from the Farm Service Agency of the USDA. The database contained forty different categories of government payments. Because of the substantially different nature of many of such payments, for estimation purposes they were aggregated into four broad types rather than pooling all of them into a single series. In this manner, differential effects across types of government payments may be uncovered while maintaining a parsimonious model. The four types of government payments are deficiency payments and payments associated with price support programs (zDEF), market loss assistance payments for corn and soybeans (zMLA), production flexibility contract payments (zPFC), and payments corresponding to the conservation reserve and related programs (zCRP). The composition of each type of government payment is shown in table 1.
|
Payments zDEF, zMLA, and zPFC were converted to a per acre basis by dividing the total county-level payments by the respective county-level sum of the areas planted with corn and soybeans. By contrast, to express zCRP payments on a per acre basis, total county-level CRP payments were divided by the corresponding county-level CRP acreages (Farm Service Agency, USDA). The reason for this is that CRP acres cannot be planted with corn or soybeans.
During the period 1996–2000, the ninety-three Iowa counties under study received a total of $6.54 billion in farm program payments, comprising $1.80 billion in DEF payments, $1.35 billion in MLA payments, $2.56 billion in PFC payments, and $0.71 billion in CRP payments. That is, the categories included in the analysis accounted for 98.2% of the total farm program payments. The remaining 1.8% comprised the miscellaneous programs described in table 1.
The period used for estimation was 1996–2000, because government payments were greatly affected by the Federal Agricultural Improvement and Reform Act of 1996, and no price data for 2001 were available. The estimated model involved equations analogous to (18) only for years 1997 through 2000, because the 1996 equation could not be estimated, as lagged values were used as instruments. Summary statistics for the basic variables are shown in table 2. The distance matrix was constructed using the distances between the centroids for every pair of counties in Iowa. Distances were obtained from the Economic Research Service of the USDA.
| Variables | Mean | Standard Deviation | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Cash rents (rn) | 117.90 | 13.27 | 73.00 | 158.17 | −0.51 | 0.94 |
| Acreage-weighted corn revenues (zCORN,n) | 154.95 | 37.75 | 65.88 | 335.35 | 0.97 | 1.78 |
| Acreage-weighted soybean revenues (zBEAN,n) | 110.92 | 25.91 | 36.84 | 175.33 | 0.06 | −0.32 |
| Government payments: | ||||||
| Deficiency (zDEF,n) | 15.79 | 20.75 | − 8.30 | 57.25 | 0.40 | −1.53 |
| Market loss assistance (zMLA,n) | 20.23 | 6.87 | 8.70 | 34.18 | −0.11 | −1.10 |
| Production flexibility contracts (zPFC,n) | 23.25 | 5.11 | 14.24 | 42.64 | 0.88 | 0.74 |
| Conservation reserve program (zCRP,n) | 104.22 | 26.96 | 53.15 | 222.68 | 1.20 | 2.08 |
- Note: Data correspond to years 1996 through 2000 in 93 Iowa counties, for a total of 465 observations on each variable other than market loss assistance payments (zMLA,n). Market loss assistance payments started in 1998, so they involve only years 1998 through 2000, for a total of 279 observations. Six of the 99 Iowa counties (Appanoose, Clarke, Lucas, Monroe, Wayne, and Worth counties) were not included in the dataset because of missing observations on cash rental rates.
Results and Discussion
The model was estimated by means of the econometric program TSPTM version 4.4, using the GMM command under the default options. The instruments used for each equation were the values of the corresponding explanatory variables lagged one year. The fact that the market loss assistance program started in 1998 was problematic for the estimation of the 1998 equation. The reason for this is that zMLA,n,1997 = zMLA,(−n),1997 = 0, and therefore, they provide very poor instruments for zMLA,n,1998 and zMLA,(−n),1998, respectively. For this reason, two alternative specifications were estimated. In the MLA98-N (MLA98-Y) specification, the 1998 equation excluded (included) zMLA,n,1998 and zMLA,(−n),1998 as explanatory variables.
The results are summarized in tables 3 through 5. Table 3 shows the results obtained by performing an iterative search over the power factor used to compute the spatial weights (δ) so as to maximize the model's p-value (as implied by the test of overidentifying restrictions). The results in table 3 are very consistent across the MLA98-N and MLA98-Y specifications. More important, the tests of overidentifying restrictions have very high p-values, providing support for the advocated model. The pseudo-R2s imply that the model can explain between 51% and 71% of the variability in cash rental rates.
| Coefficients | MLA98-N | MLA98-Y |
|---|---|---|
| Acreage-weighted corn revenues (βCORN) | 0.384*** (0.054)a | 0.373*** (0.056) |
| Acreage-weighted soybean revenues (βBEAN) | 0.350*** (0.062) | 0.300*** (0.066) |
| Government payments: | ||
| Deficiency (βDEF) | −0.23** (0.11) | −0.24** (0.11) |
| Market loss assistance (βMLA) | 0.84*** (0.25) | 0.90*** (0.32) |
| Production flexibility contracts (βPFC) | 0.86** (0.34) | 0.71* (0.38) |
| Conservation reserve program (βCRP) | 0.048 (0.041) | 0.049 (0.040) |
| Annual intercepts: β1997 | −0.8 (1.4) | −0.22 (0.99) |
| β1998 | 0.52 (0.87) | 0.61 (0.92) |
| β1999 | 0.25 (0.72) | 0.74 (0.99) |
| β2000 | 0.09 (0.68) | 0.6 (1.1) |
| Spatial autoregression (ρ) | 0.960*** (0.064) | 0.952*** (0.062) |
| Power factor for spatial weights (δ) | 4.72 | 4.64 |
| Test of overidentifying restrictions | χ241 = 25.53 [0.972]b | χ241 = 26.55 [0.961] |
| Pseudo-R2:c 1997 equation | 0.716 | 0.716 |
| 1998 equation | 0.534 | 0.520 |
| 1999 equation | 0.514 | 0.523 |
| 2000 equation | 0.634 | 0.637 |
- a Numbers between parentheses next to coefficient estimates denote the respective standard deviations.
- b Numbers between brackets next to test statistics denote the corresponding p-values.
- c Pseudo-R2 for equation i ≡ 1 − Var(ei)/Var(yi), where Var(ei) is the variance of the residuals from equation i and Var(yi) is the variance of the dependent variable in equation i. *** (**, *) Significantly different from zero at the 1% (5%, 10%) level of significance, based on the two-tailed t-statistic.
As expected, acreage-weighted corn and soybean revenues are found to have a positive and significant impact on cash rental rates. The coefficients on the alternative types of government payments suggest that cash rental rates are affected very differently according to the type of payment. The coefficients corresponding to the MLA payments (βMLA) and the PFC payments (βPFC) are both positive and significant in an economic as well as a statistical sense. The point estimates of βMLA and βPFC suggest that cash rental rates increase by about 85 cents for each dollar paid per acre under the MLA and PFC programs. The coefficient associated with CRP payments (βCRP) is positive but economically and statistically insignificant. The most surprising result is the negative and statistically significant estimated effect of DEF payments. The point estimate of βDEF is considerably smaller in absolute terms than any of the other statistically significant farm payment coefficients, but its negative value is difficult to rationalize.
The point estimates of the spatial autoregression coefficient are close to one and highly significant. This confirms the existence of important spatial dependencies in the data. Given the large and significant spatial autoregression coefficients found, it is of interest to see how different the estimated model would be if spatial dependency were neglected. To this end, specifications MLA98-N and MLA98-Y were estimated under the restriction ρ = 0. Since this constraint eliminates variables r(−n) and z(−n) from the basic estimation model (18), their lagged values were also omitted from the set of instrumental variables.
Results from the GMM estimation with ρ= 0 are shown in table 4. Compared with the models that allow for spatial correlation, the models with ρ = 0 have much smaller p-values. Indeed, both the MLA98-N and MLA98-Y specifications with ρ = 0 are rejected at the 5% significance level, indicating that misspecification problems are likely to be present. Another hint of the poorer fit of the models with ρ= 0, compared with the models allowing for spatial correlation, is that the former exhibit notoriously smaller pseudo-R2s.
| Coefficients | MLA98-N | MLA98-Y |
|---|---|---|
| Acreage-weighted corn revenues (βCORN) | 0.109** (0.055)a | 0.092 (0.057) |
| Acreage-weighted soybean revenues (βBEAN) | 0.273*** (0.046) | 0.227*** (0.044) |
| Government payments: | ||
| Deficiency (βDEF) | −0.12 (0.18) | −0.07 (0.17) |
| Market loss assistance (βMLA) | 0.53*** (0.17) | 0.27 (0.20) |
| Production flexibility contracts (βPFC) | 1.34*** (0.27) | 1.30*** (0.30) |
| Conservation reserve program (βCRP) | 0.139*** (0.026) | 0.144*** (0.026) |
| Annual intercepts: β1997 | 16 (12) | 26** (12) |
| β1998 | 30.4*** (9.9) | 35*** (10) |
| β1999 | 28*** (10) | 39*** (10) |
| β2000 | 28*** (11) | 40*** (11) |
| Test of overidentifying restrictions | χ216 = 28.45 [0.028]b | χ216 = 29.93 [0.018] |
| Pseudo-R2:c 1997 equation | 0.481 | 0.465 |
| 1998 equation | 0.424 | 0.401 |
| 1999 equation | 0.480 | 0.490 |
| 2000 equation | 0.400 | 0.424 |
- a Numbers between parentheses next to coefficient estimates denote the respective standard deviations.
- b Numbers between brackets next to test statistics denote the corresponding p-values.
- c Pseudo-R2 for equation i ≡ 1 – Var(ei)/Var(yi), where Var(ei) is the variance of the residuals from equation i and Var(yi) is the variance of the dependent variable in equation i. *** (**, *) Significantly different from zero at the 1% (5%, 10%) level of significance, based on the two-tailed t-statistic.
Several of the coefficient estimates in table 4 are quite different from the coefficients in table 3. Setting ρ= 0 leads to much larger intercepts.7 More important, the point estimates of the acreage-weighted corn revenue coefficient (βCORN) under ρ= 0 are about one-fourth the size of the respective estimates obtained when ρ is unrestricted. Further, the estimate of βCORN in the MLA98-Y specification is not significant under ρ= 0. Similarly, neglecting spatial autocorrelation yields smaller estimates of βMLA (which is not significant in the case of the MLA98-Y specification). Also, the βDEF estimates under ρ = 0 are considerably smaller in absolute magnitude and are not significant. In contrast, the restriction ρ = 0 results in appreciably larger estimates for βPFC and, especially, βCRP. Unlike the scenario allowing for spatial autocorrelation, CRP payments are statistically significant under ρ = 0.
In summary, a comparison of the results in table 4 with the results in table 3 provides strong indications of misspecification problems with the specifications that ignore spatial autocorrelation. Such a comparison highlights the need to account for spatial autocorrelation to avoid faulty inferences regarding the effect of government payments on cash rental rates.
For completeness, the model without disaggregating among the various types of farm program payments was also estimated. Results for a specification using the aggregate farm program payments variable zGOV≡zDEF + zMLA + zPFC + zCRP are shown in table 5. The power factor for spatial weights that yielded the largest p-value was δ = 3.45. The model's p-value is large and the pseudo-R2s are similar to the pseudo-R2s corresponding to the specifications with disaggregated farm payments. The estimates of βCORN and βBEAN in table 5 are comparable to their counterparts in table 3. More important, the effect of government payments on cash rental rates (βGOV) is found to be statistically significant but economically small, with one additional dollar per acre in government payments increasing cash rental rates by only 13 cents per acre.
| Coefficients | |
|---|---|
| Acreage-weighted corn revenues (βCORN) | 0.448*** (0.068)a |
| Acreage-weighted soybean revenues (βBEAN) | 0.293*** (0.069) |
| Government payments (βGOV) | 0.131*** (0.047) |
| Annual intercepts: β1997 | 1.0 (2.5) |
| β1998 | −0.6 (2.2) |
| β1999 | −0.8 (2.1) |
| β2000 | −1.1 (2.1) |
| Spatial autoregression (ρ) | 1.144*** (0.088) |
| Power factor for spatial weights (δ) | 3.45 |
| Test of overidentifying restrictions | δ224 = 19.42 [0.729]b |
| Pseudo-R2:c | |
| 1997 equation | 0.736 |
| 1998 equation | 0.556 |
| 1999 equation | 0.582 |
| 2000 equation | 0.639 |
- a Numbers between parentheses next to coefficient estimates denote the respective standard deviations.
- b Numbers between brackets next to test statistics denote the corresponding p-values.
- c Pseudo-R2 for equation i ≡ 1 − Var(ei)/Var(yi), where Var(ei) is the variance of the residuals from equation i and Var(yi) is the variance of the dependent variable in equation i. *** (**, *)Significantly different from zero at the 1% (5%, 10%) level of significance, based on the two-tailed t-statistic.
An issue with the model reported in table 5 is that the point estimate of the spatial autoregression coefficient (ρ) is considerably greater than one. Although such an estimate is computationally feasible, it does not seem reasonable and cannot be interpreted in terms of the advocated model. The point estimate of ρ greater than one is also the reason why the intercepts in table 5 bear opposite signs with respect to the intercepts in table 3. This is true because the intercept in equation (18) is a function of (1 − ρ).
Concluding Remarks
Farmland values are intrinsically associated with the economics of the farm sector. Also, government programs have played a major role in U.S. agriculture since the 1920s (Kohls and Uhl, p. 369). This explains why there exists a large body of research addressing the effect of government programs on land values. The present study departs from the previous literature in that it focuses on the impacts of government program payments on cash rental rates. Another innovation is that the econometric analysis allows for different impacts across farm programs. In addition, econometric methods are used to account for potential spatial dependencies in the data.
County-level annual observations for Iowa from 1996 through 2000 were used to measure the impacts of the main types of farm program payments on cash rental rates. The data were found to exhibit strong geographic dependency. Accounting for spatial autocorrelation in the econometric analysis was shown to be crucial to avoid misleading inferences.
Results reveal important differences in the effects of alternative farm programs on cash rental rates. Cash rental rates were found to increase by almost one dollar per acre for each additional dollar per acre paid for market loss assistance and production flexibility contracts, whereas conservation reserve program payments appear to exert no effect on cash rental rates. A counterintuitive finding that warrants further examination is the negative impact of deficiency payments on cash rental rates.
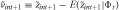 .
.



