Tracing the Effects of Agricultural Commodity Prices and Food Costs
Abstract
We estimate a system of product and input-demand equations for food-processing industries to trace the links among farm commodity prices, food-processing costs, and food prices. Disembodied technical change, which likely reflects increasing consumer demand for convenience and product variety, has sharply reduced agricultural materials demand relative to most other food-processing inputs. This implies weakening impacts of farm price shocks on food prices. But improving quality and falling relative prices for agricultural inputs, in combination with increasing factor substitution, has counteracted these forces to encourage greater usage of agricultural inputs in food processing, and limit these trends.
Food prices today often appear less responsive to farm price shocks than in the past, a development sometimes attributed to failures in market institutions. However, powerful long-run technological and social changes, leading to adaptations in production processes and food consumption patterns, have also altered the demand for primary agricultural materials by changing the structure of food-processing industries. The social shifts surrounding the expanded role of women in the labor force represent one striking example of such changes. The fraction of married women in the labor force—less than one-third in 1960—rose sharply through the next three decades before stabilizing at around 61% in the 1990s. Such demographic shifts increased the demand for food products requiring less home preparation time, which, in combination with enhanced technology, has led to more in-plant processing of agricultural materials, and likely a growing share of nonagricultural inputs in food-processing costs.1
This inference is supported by Goodwin and Brester, who found an increased share of value-added, and a correspondingly reduced share for agricultural materials, in U.S. food-processing costs in the 1980s. A declining factor share should lead to a weaker linkage between farm prices and food prices. But other well-known factors also drive processors' production choices. The business environment, including market structure and the regulatory framework, has undergone important changes since the 1970s. Energy and labor prices have risen sharply compared to prices for agricultural commodities. Tax changes have had impacts on relative input prices by affecting the prices of capital inputs. Less well-documented technical changes, associated with capital equipment and the quality of agricultural materials, could also have had effects on the demand for agricultural products. These developments could also affect the linkages between farm and food prices.
In this study, we measure and evaluate these patterns for U.S. food-processing industries. We use a cost-function representation of input substitution resulting from technological shifts and price changes among capital, labor, energy, and three materials aggregates—agricultural, food, and “other” materials. This framework allows us to assess the roles of changes in food product demand, input prices, and food-processing technology on food processors' costs, input demands, and output prices, with a particular focus on the use of agricultural inputs. Our framework also facilitates consideration of technological factors affecting costs and factor demands, such as the quasi-fixed nature of capital, scale economies, technical change associated with either time trends (disembodied) or capital composition (embodied in capital), and agricultural innovations or market power embodied in input prices for agricultural commodities.
We find that the share of agricultural materials in processor costs fell during 1972–92, along with the sensitivity of food prices to farm prices. We also find that the direct effect of disembodied technical change in food processing has been agricultural materials-saving, likely induced by changes in product demand. But technological change eased substitution among factor inputs during the period, particularly in the 1980s, leading to a more price-elastic agricultural demand and lower relative farm prices, and muting the effects of direct technical change on agricultural demand. Moreover, we find that improved quality of agricultural materials meant that effective prices for those inputs fell even faster—relative to other input prices—than measured prices, inducing more substitution toward agricultural materials, and further limiting the effects of changes in consumption patterns.
The Model
Our framework assumes that food processors choose inputs to minimize costs, given input prices and output levels faced in supply- and demand-side markets. The cost model is specified in terms of true economic or “effective” prices, to recognize that effective prices for some inputs may not be equivalent to their measured counterparts, due to imperfect markets or measurement associated with quasi-fixities, deviations from perfect competition, or innovation and quality changes. The resulting cost model is also augmented to characterize profit-maximizing output prices and quantities, through an equality of the associated marginal cost and marginal revenue.
More formally, the technology and cost-minimizing behavior underlying the observed production structure can be represented by a total cost specification of the form TC = TC(Y, p, r), where Y is (food) output, p is a vector of variable input prices, and r is a vector of exogenous technological determinants. The TC–Y relationship, summarized by the elasticity of total cost with respect to output, εTC,Y=∂lnTC/∂lnY, represents the shape of the minimized long-run cost curve, given observed factor prices and the existing technological base. Changes in components of the p and r vectors affect this cost relationship, and thus implied overall costs and input demands. Measures of these cost structure patterns may thus be derived in terms of first and second-order elasticities with respect to these arguments of the cost function.
Internal or external adjustment costs may, however, sever the equivalence of the observed price of input xk, pk, and its true economic return or shadow value, p*k, and thus the duality underlying the cost function. In this case, observed costs exceed minimum possible long-run production costs. Other discrepancies between the observed and effective or shadow price, observationally equivalent to adjustment costs, may stem from other input market imperfections such as imperfect competition in factor markets, or unmarketed (or unmeasured) characteristics.
One way to deal with such implicit costs is to include xk instead of pk as an argument in the (variable) cost function, and thus represent the shadow value wedge as ∂TC/∂xk = pk − p*k ≠ 0.2 Alternatively, the true economic, shadow, or effective price of input xk, p*k = pk+λk, may be directly incorporated into the cost function, where λk represents the wedge between pk and p*k. This approach is particularly appealing if the cross- or interaction-terms from a model incorporating xk as an argument seem uninformative, but an imperfect market gap, λk, seems to exist (λk statistically deviates from zero).3 If instead p*k appears well approximated by pk, or λk ≈ 0, one can assume that rigidities or other input market imperfections are not binding constraints on, or determinants of, measured cost structure patterns.
For our application, after preliminary investigation of estimation patterns, we adopted an effective price framework as that most consistent with our data. The total cost function for producing output in the U.S. food-processing sector then becomes TC = TC(Y, pv, p*x, r), where pv represents the vector of observed variable input prices for factors that satisfy standard requirements for Shephard's lemma to be valid, and p*x is a vector of effective prices that deviate from observed prices by the additive factors λx.4 We found evidence of deviations between observed and effective or shadow prices for capital (K) and agricultural materials (MO), but support for an assumption of no such deviations for labor (L), energy (E), and two materials inputs (food, MF; and other, MO), with prices pL, pE, pMF, and pMO. Demand decisions for these inputs are accordingly represented by vj = ∂TC/∂pj.
The effective price of capital may be defined as p*K = pK + λK, with the wedge λk potentially attributable to capital rigidities (adjustment costs) or unmeasured taxation or quality impacts. We tested various forms for λK to establish their empirical justification in terms of significance of the parameters, robustness of the overall results, and plausibility of resulting elasticities. The specification chosen is an augmented version of an additive shift factor embodying technical change trends; λK = λK1 + λKtt + λK2t2, where t is a trend term and t2 a dummy variable reflecting post-1980 structural change. This is essentially a simple hedonic model recognizing differences in the level and trend of quality-adjusted prices not fully captured in measured pK, which might be expected to arise from internal or external adjustment costs.
Similarly, we defined the effective agricultural materials price as p*MA = pMA + λMA, with λMA = λMA1 + λMAtt + λMA2t2. The existence of such a gap between pMA and p*MA is plausible on several grounds. For example, if the processing industries perceive some market power over agricultural prices, the (higher) marginal price, not the observed average price, will drive agricultural input demand (λMA > 0). Alternatively, or in combination, technical change embodied in higher quality agricultural products could imply lower effective prices of agricultural materials compared to their measured values (λMA < 0). With p*MA as an argument in the cost function, the sign and thus interpretation of λMA may be established empirically.5
The variables in the r vector, reflecting the industry's technological base, include a time trend t representing disembodied technical change, and an intercept dummy shift t2 capturing structural shifts in the 1980s as compared to the 1970s (t2 = 1 for 1982, 1987, and 1992). A capital equipment to structures ratio, (EQ/ST = ES), is also used to represent technology embodied in the capital stock. The resulting model allows both for technical change embodied in K and MA, through the inclusion of t and t2 in the effective price specification, and for disembodied technical change, through the time terms in the r vector.
Our model accommodates output supply and pricing decisions by also permitting output price to differ from marginal cost. This extension of the cost function framework imposes a standard profit-maximizing condition underlying output choice (equality of marginal cost, MC, and marginal revenue, MR), implicitly assuming that downward-sloping firm demand curves drive any measured gaps between output price and marginal revenue. This is implemented through the optimization equation MR = pY + ∂pY/∂Y × Y = ∂TC/∂Y = MC, so ∂pY/∂Y × Y reflects the wedge between MR and MC. We found ∂pY/∂Y to be well approximated by a parameter, λY, which is consistent with a linear demand curve. So the effective output price is p*Y + λYY, and the resulting optimization equation becomes p*Y= MC, or pY = −λYY + MC. Alternative treatments tried, with λY specified as a function of other exogenous variables, including t and t2, caused no substantive impact on the resulting estimated patterns.6
Based on the resulting model, consisting of the total cost function TC = TC(p*MA, p*K, pL, pMF, pE, pMO, Y, ES, t, t2) and associated input-demand and output-supply (pricing) optimization equations, we can quantify and evaluate a variety of issues raised above. In particular, we can assess the impact of agricultural prices on food prices, and identify the means by which the relationship changed through time. We can also determine the paths by which various factors drove processing costs during the time period under consideration.
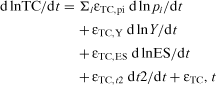 (1)
(1)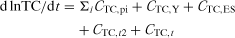 (2)
(2)Each term underlying (2) has a specific interpretation as a cost driver. For example, the scale elasticity εTC,Y captures the extent of scale economies. The contribution of such economies to observed cost changes, CTC,Y, depends on both the elasticity, εTC,Y, and the actual output (scale of production) change, d lnY/dt. Similarly, the cost-contribution of an input-price change depends both on the cost elasticity with respect to the price, and on the actual price change.
The other contributions represent shifts in the cost function from external technological and economic forces. Cost impacts of observed adaptations toward enhanced capital equipment, or embodied technical change, are measured by CTC,ES, and CTC,t (εTC,t) is typically interpreted as disembodied technical change that results in a downward shift of the cost relationship over time, while CTC,t2 captures a structural shift in the 1980s, as suggested by Goodwin and Brester.
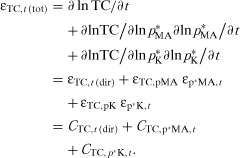 (3)
(3)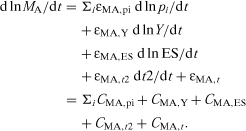 (4)
(4)The elasticities in (4), such as εMA,pi = ∂lnMA/∂lnpi, quantify the shape of and shifts in the MA demand curve for changes in pMA and other arguments of the function, and the contribution measures, CMA, reflect the actual contributions given observed changes in these determinants. In particular, εMA,pi indicates the responsiveness of agricultural demand to its own price for i = MA, and substitutability between input vi and MA for other inputs. Similarly, the MA-specific impacts of changes in the scale of production or technological factors are captured by the analogously defined εMA,Y and εMA,rn elasticities.
For example, if εMA,Y > 1 product demand expansions imply disproportionate increases in agricultural product demand, and scale increases are MA-using. If εMA,Y > εTC,Y expansions are also relatively MA-using, or biased. If εMA,rn < 0 for rn = t2, the demand for agricultural commodities was more limited, given other economic and technological factors, in the 1980s than in the 1970s. This suggests a structural shift toward lower MA-intensity of production (possibly induced by output demand composition changes). εMA,t indicates the force of disembodied technical change, or trend, on MA demand. And if εMA,t deviates from the overall cost change εTC,t, this is often referred to as a technical change bias.
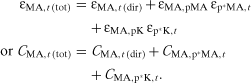 (5)
(5)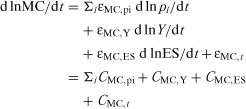 (6)
(6)In particular, we can consider how pMA changes affect marginal as compared to average cost, and thus εTC,Y = MC/AC, using the εMC,pMA and εTC,pMA elasticities. Also, based on our output-pricing expression pY = −λYY + MC, we can construct a decomposition of pY analogous to those presented above, with the difference from that for MC = p*Y depending on λY. This may be used to evaluate how pMA changes impact pY as compared to MC, which provides some information on the pass-through of agricultural materials prices to food prices, and on the implications for markup behavior (pY/MC).
The Data
For the empirical implementation of our model, we required data on prices and quantities of output and inputs for industries in the U.S. food-processing sector. Our base data were taken from the four-digit manufacturing NBER (National Bureau of Economic Research) productivity database, which is often used as a foundation for production structure studies, such as Griliches and Lichtenberg; Bartlesman, Caballero, and Lyons; and Fixler and Siegel.
We also, however, needed to distinguish cost shares for three materials aggregates—agricultural materials, food materials (shipped among food-processing establishments), and other materials. We used Census of Manufactures data to calculate the share of each materials aggregate in the industry value of shipments for which cost information is available, and adjusted the published data in two ways.9 First, we subtracted re-sales (purchased materials that are not processed before being resold, which are important in some industries) from the value of shipments, to better capture manufacturing output. Second, some small establishments do not separately report individual materials purchases, but instead report all materials in an “n.s.k.” (not separately classified) category. We allocated n.s.k. shipments to agricultural, food, and other materials categories in proportions equivalent to those reported by the larger institutions.
Materials input-price series were constructed primarily from commodity producer price indexes (PPIs) from the Bureau of Labor Statistics. In cases where an industry consumed several specific agricultural or food materials, an aggregated materials price index was constructed from the constituent materials indexes, with each price index weighted by its expenditure share in the Census aggregate. In the few cases where PPI indexes were not available, we constructed indexes from average price series maintained by USDA's National Agricultural Statistics Service. The resulting data panel covers five-year intervals from 1972 through 1992, for 34 consistently defined four-digit SIC industries in the U.S. food-processing sector (SIC 20).
Empirical Implementation
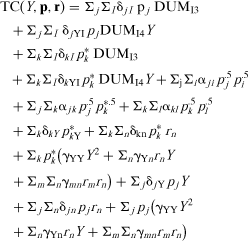 (7)
(7)The final estimating model is comprised of a system of demand equations for the inputs (L, K, E, MA, MF, MO), and a pricing equation for output. As alluded to above, the input-demand equations are constructed according to Shephard's lemma; vj(·) = ∂TC(·)/∂pj (j = L, E, MF, MO) and xk(·) = ∂TC(·)/∂p*k (k = MA, K), where p*k = pk + λk, and λk = λk1 + λktt + λk2t2. Also, for the output-pricing equation pY = −λYY + ∂TC/∂Y, derived from equating MR and MC, λY was differentiated across industries to incorporate fixed effects into this relationship; λY = ∑IλYIDI4.
Estimation was carried out by seemingly unrelated (SUR) regression, with the potential for heteroskedasticity accommodated by techniques in TSP that allow standard errors to be computed from a heteroskedastic-consistent matrix (Robust-White). An alternative approach to heteroskedasticity adjustment—to reconstruct the equations as input/output instead of input demand equations—was also tried in empirical estimation, but did not improve the estimates.
Although instrumental variables (IV) procedures such as three-stage least squares are often used in the literature on which this study is based, to accommodate potential endogeneity or measurement errors in the data, we did not rely on them for a variety of reasons. First, IV techniques frequently require an arbitrary specification of instruments, which can be problematic. In addition, models of this form are typically estimated with time series data, and often use lagged values of the observed arguments of the function as instruments. But this is not conceptually or empirically appealing for our application due to the short time series, as well as the five-year gaps between data points. Preliminary investigation was carried out to determine the sensitivity of the results to some IV specifications, but the results from these specifications were individually more volatile (less robust) and not as plausible as those from a basic SUR model. Because on balance the emerging story from the results was consistent with SUR estimates, we thus relied on SUR techniques for the final estimation.
Results
Appendix table A.1 displays the estimated parameters for our model (dummy terms are not included in the table since there are too many to be illuminating, but they are primarily statistically significant). The overall explanatory power of the model is indicated by the high R2's for the estimating equations provided in appendix table A.2, including the total cost equation, which was not estimated but was fitted to determine the implied R2. Many parameter estimates that are not individually statistically significant are jointly significant, such as the ES parameters mentioned above.12 And the story emerging from the final model was robust to a variety of alternative specifications tried to evaluate sensitivity.13
Parameter estimates were used to construct the elasticity and contribution measures overviewed above, which were averaged across the whole sample, and separately for 1972–82 and 1982–92, to distinguish temporal patterns. The elasticity estimates were constructed by computing the indicators for each data point and then averaging across the sample under consideration. Statistical significance of these measures (since they involve combinations of parameters) was imputed by evaluating the elasticity estimates for the averaged data; values significantly different from zero at the 5% level are indicated by an asterisk.14 In most cases, the significance implications were not data-dependent, although for some estimates the data point at which the measure was evaluated contributed to evidence of significance.
Total Cost Drivers
Consider first the elasticity and contribution measures presented in table 1 for total costs. The cost elasticity most directly associated with agricultural materials use, εTC,pMA, reflects the cost share of agricultural materials. The estimated average value, 0.25, indicates that rising pMA has a substantive positive impact on production costs, and thus strongly affects food-processing output and price. Note, however, that the overall contribution of agricultural prices to total cost increases, 1.4% per year over 1972–92, is much smaller than that for capital.
| lnΔ | εTC, i | C TC, i | |
|---|---|---|---|
| Input prices | |||
| Agricultural materials | 0.0547 | 0.2497* | 0.0137 |
| Food materials | 0.0403 | 0.1031* | 0.0042 |
| Other materials | 0.0653 | 0.1293* | 0.0084 |
| Labor | 0.0908 | 0.0836* | 0.0076 |
| Capital | 0.0680 | 0.4213* | 0.0287 |
| Energy | 0.1186 | 0.0130* | 0.0015 |
| Output | 0.0218 | 0.8677* | 0.0191 |
| Technical change | |||
| Equipment and structures | 0.0200 | −0.0176 | −0.0008 |
| t | −0.0354* | 0.0004 | |
| t2 | 0.0187* | −0.0141 | |
| Sum | 0.0824 |
- Note: The first column (lnΔ) capture annual average log differences, or growth rates, in the explanatory variables. Contributions (C) are elasticities times growth. All estimates are derived from parameters reported in appendix table 2. Asterisks denote 95% statistical significance.
The εTC,Y estimate of 0.868 implies significantly increasing returns to scale, a result largely driven by a very small capital-output elasticity. Scale expansions instead seem agricultural materials-using, although this conclusion is closely linked to the inclusion of t in the λK and λMA specifications. When t is not included as an argument in these specifications, output increases instead appear MA-saving (εMA,Y is significantly smaller than 1), and the εK,Y and εTC,Y estimates are much closer to 1, more closely approximating constant returns to scale overall.
Table 2 reports elasticity and contribution measures for two periods— 1972–82 and 1982–92. Note that the share of agricultural materials in total costs fell noticeably over time, from 0.273 to 0.226. The declining elasticity, combined with factor price inflation of less than 1% per year, meant that agricultural materials had virtually no contribution to the observed total cost increases of 4.17% per year in food processing in 1982–92. By contrast, the growing cost share of capital, along with factor price increases, led to a continued impact on increased processing costs. Moreover, the scale elasticity changed little between the 1970s and 1980s; continued modest demand growth therefore led to dampened effects on total costs.
| lnΔ | εTC, i | C TC, i | lnΔ | εTC, i | C TC, i> | |
|---|---|---|---|---|---|---|
| Input prices | 1972–82 | 1982–92 | ||||
| Agricultural materials | 0.1021 | 0.2734* | 0.0279 | 0.0080 | 0.2263* | 0.0018 |
| Food materials | 0.0687 | 0.1096* | 0.0075 | 0.0123 | 0.0967* | 0.0012 |
| Other materials | 0.1048 | 0.1382* | 0.0145 | 0.0264 | 0.1206* | 0.0032 |
| Labor | 0.1334 | 0.0951* | 0.0127 | 0.0489 | 0.0723* | 0.0035 |
| Capital | 0.1076 | 0.3715* | 0.0400 | 0.0291 | 0.4703* | 0.0137 |
| Energy | 0.2410 | 0.0122* | 0.0030 | −0.0019 | 0.0138* | 0.0000 |
| Output | 0.0266 | 0.8677* | 0.0191 | 0.0170 | 0.8871* | 0.0150 |
| Technical change | ||||||
| Equipment and structures | 0.0244 | −0.0189 | −0.0238 | 0.0156 | −0.0592 | −0.0009 |
| t | 0.0020* | 0.0004 | 0.0388* | 0.0077 | ||
| t2 | −0.2530* | −0.0123 | −0.5203* | 0.0000 | ||
| Sum | 0.0890 | 0.0417 | ||||
- Note: See table 1.
Patterns of Agricultural Materials Demand
The drivers of agricultural materials (MA) demand may also be examined using the measures reported in table 3, as specified in equation (4). The own price elasticity, εMA,pMA = −1.138, implies that MA demand is fairly elastic. Own price increases (holding other factors constant) lead to disproportionately lower MA demand. Based on observed pMA trends, own prices thus provided a negative contribution of CMA,pMA = −0.062 (6.2% per year) to the overall observed increase in MA use of 0.038 (or 3.8% per year); other factors outweighed the negative own-demand effect.15
| lnΔ | εMA, i | C MA, i | |
|---|---|---|---|
| Input prices | |||
| Agricultural materials | 0.0547 | −1.1375* | −0.0622 |
| Food materials | 0.0403 | 0.0868 | 0.0035 |
| Other materials | 0.0653 | 0.2399* | 0.0157 |
| Labor | 0.0908 | 0.1306 | 0.0119 |
| Capital | 0.0680 | 0.6490* | 0.0441 |
| Energy | 0.1186 | 0.0312* | 0.0037 |
| Output | 0.0218 | 1.0946* | 0.0238 |
| Technical change | |||
| Equipment and structures | 0.0200 | 0.7159 | 0.0143 |
| t | −0.0390* | −0.0078 | |
| t2 | −0.4248* | −0.0207 | |
| Sum | 0.0439 |
- Note: See table 1.
All other inputs are substitutable with MA, as is apparent from their positive price elasticities, and the observed increases in these input prices over the sample period thus imply positive shift effects on MA demand that in sum more than compensate for the own price effect. In particular, MA seems somewhat substitutable with both MF and MO, but the contributions of pMF and pMO changes (0.0035 and 0.016, respectively) are not substantial since the price changes have been small. Labor and energy prices rose more, but their contributions to MA use (0.012 and 0.004, respectively) were limited by smaller substitution elasticities.
The contribution of increased capital prices to agricultural materials demand is much greater than the price effects associated with other inputs (CMA,pK = 0.044). If weighted by p*K, which rose more rapidly than pK, the contribution is even greater, at 0.056. Output growth also had a more than proportional effect on MA demand; the elasticity of 1.095, evaluated at observed demand growth levels, implies an output demand contribution (CMA,Y) of 0.024.16
Table 4 reports a temporal decomposition of agricultural demand, similarly to that in table 2 for costs. Note that the own price elasticity of demand for agricultural materials became considerably greater as time passed—from –0.97 in 1972–82 to −1.30 in 1982–92 (which, with a standard error of 0.05, is a statistically significant difference). In turn, all cross-price elasticities increased in the later from the former period, and the pattern suggests technical change that allows for easier substitution among inputs. The measures in table 4 also show that output expansion became more intensive in the use of agricultural materials in the 1980s, as the εMA,Y elasticity increased to 1.143 from 1.045. But as output growth slowed, the contribution of output growth to agricultural demand growth also slowed.
| lnΔ | εMA, i | C MA, i | lnΔ | εMA, i | C MA, i | |
|---|---|---|---|---|---|---|
| Input prices | 1972–82 | 1982–92 | ||||
| Agricultural materials | 0.1021 | −0.9731* | −0.0994 | 0.0080 | −1.2992* | −0.0104 |
| Food materials | 0.0687 | 0.0791 | 0.0054 | 0.0123 | 0.0943 | 0.0012 |
| Other materials | 0.1048 | 0.2094* | 0.0219 | 0.0264 | 0.2699* | 0.0071 |
| Labor | 0.1334 | 0.1082 | 0.0144 | 0.0489 | 0.1527 | 0.0075 |
| Capital | 0.1076 | 0.5484* | 0.0590 | 0.0291 | 0.7479* | 0.0217 |
| Energy | 0.2410 | 0.0281* | 0.0068 | −0.0019 | 0.0343* | −0.0001 |
| Output | 0.0266 | 1.0452* | 0.0278 | 0.0170 | 1.1433* | 0.0194 |
| Technical change | ||||||
| Equipment and structures | 0.0244 | 0.7008 | 0.0171 | 0.0156 | 0.7307 | 0.0114 |
| t | −0.1174* | −0.0235 | 0.0381* | 0.0076 | ||
| t2 | −0.0608* | −0.0060 | −0.7828* | 0.0000 | ||
| Sum | 0.0302 | 0.0573 | ||||
- Note: See table 1.
Technical Change and Agricultural Materials Use
Our model allows for three sources of technical change. It directly captures effects embodied in new investment in equipment and structures through ES. Equations (2) for total cost, and (5) for agricultural materials demand, capture the other sources. That is, the direct effects of disembodied technical change are reflected by a time trend that shifts the cost function. And technical change operating through effective prices for labor and capital is accommodated by allowing the gaps between the effective and observed prices to vary over time. In addition, the shift terms and decompositions represent time differences in the impacts of technical change.
First, our inclusion of ES as a cost-determinant in addition to the standard time trend t, to capture technical change embedded in new equipment and structures, seemed important in preliminary empirical investigation for explaining cost- and input-demand patterns. The ES parameters, interpreted as the impact of technical change embodied in the capital stock, tended to be significant and plausible. When t2 was also included to represent the potential impact of structural changes in the 1980s, the t2 parameters became statistically significant but the ES parameters lost significance. The ES parameters remained jointly statistically significant, however, so they were retained in the final specification. Both variables thus seem to reflect changes in the 1980s—perhaps toward greater capital- or high-tech-intensity of production. And escalation of the ES ratio seems to have had a positive (but statistically insignificant) impact on agricultural materials demand; CMA,ES = 0.011.
Second, we may consider the direct and indirect effects of disembodied technical change on MA demand, as summarized in table 5. The overall impact is represented by the contribution CMA,t(tot), which is −0.008 on average. The trend in this contribution is also substantively and statistically relevant; the εMA,t (tot) estimates are significantly different from zero for most individual observations, and the trend was augmented post-1980 (CMA,t2(tot) = −0.021). Aggregated over time, the estimates suggest a 17% decline in agricultural demand, holding food demand constant, over the full period.
The direct impacts exhibit a much greater magnitude than the total or overall measures, however, since large proportions of the direct effects are counteracted by effective price trends that may be interpreted as embodied technical change or adjustment costs. These patterns can be seen from the decompositions of direct and indirect impacts in table 5, that arise from the inclusion of t-terms in the p*MA and p*k (λMA and λK) specifications, as in equation (5).
| C MA, t (tot) = | C MA, t (dir) + | C MA, p*MA, t + | C MA, p*K, t | |
|---|---|---|---|---|
| Agricultural materials | ||||
| Full sample, t | −0.0078* | −0.0525* | 0.0284* | 0.0166* |
| 1972–82, t | −0.0235* | −0.0632* | 0.0222* | 0.0174* |
| 1982–92, t | 0.0076* | −0.0420* | 0.0353* | 0.0147* |
| Full sample, t2 | −0.0207* | −0.0126* | −0.0041* | −0.0039* |
| 1972–82, t2 | −0.0006* | −0.0126* | −0.0054* | −0.0060* |
| Total cost | ||||
| Full sample, t | 0.0004* | −0.0042* | −0.0062* | 0.0108* |
| 1972–82, t | −0.0071* | −0.0126* | −0.0062* | 0.0118* |
| 1982–92, t | 0.0078* | 0.0041* | −0.0061* | 0.0092* |
| Full sample, t2 | −0.0141* | −0.0123* | 0.0009* | −0.0025* |
| 1972–82, t2 | −0.0052* | −0.0026* | 0.0011* | −0.0036* |
- Note: The total contribution (CMA, t (tot)) is the sum of the three direct and indirect terms. Asterisks denote 95% statistical significance.
In particular, the direct effect, CMA,t(dir), captures the temporal shift in the MA demand curve, holding output and factor prices fixed. This effect is quite large; agricultural demand not accounted for by other factors falls by 5.25% per year, with a greater decrease in the 1972–82 than the 1982–92 period. The direct disembodied effects on costs are much more modest −0.42% per year—with a larger rate of decline in the 1970s. This is very consistent with most other studies of food-processing productivity, including Heien; Gopinath, Roe, and Shane; and Morrison; as well as with more general studies of productivity patterns across industries, such as Jorgenson and Stiroh.
These large direct effects are offset by two indirect effects, operating through changes in effective agricultural materials and capital prices. The effective price p*MA rose by only 3.6% per year as compared to the pMA growth of 5.5% per year. This lower growth in p*MA could derive from various factors—including augmented quality that is not captured in the measured values—but is inconsistent with increases in market (monopsony) power.17 Thus, it appears that λMA may reflect technical change or productivity embodied in agricultural materials, representing the impact of technical innovation in agricultural markets transferred to the next level of the food chain-food processing.18
By contrast, effective capital prices grew faster than their measured values. Factors driving this trend could include substantive and rising adjustment costs (perhaps from larger scale and more high-tech production resulting in greater production rigidities), environmental or safety standards, or taxes, that are not effectively captured in the measured user cost of capital. These trends in capital costs motivate a substitution effect toward primary agricultural products.
Because the full trend impact on agricultural materials demand is the sum of terms involving the direct- and indirect-t-effects exhibited through the trend in p*k, and the trend component of p*MA is negative (εp*MA,t = −0.125), for our scenario εMA,pMA < 0. However, the indirect p*MA effect on MA use is positive—as is the p*K effect because K is a substitute but p*K is rising (εp*K,t = 0.128). Thus each of these components partially counteracts the large direct t-impact of –0.0525. This evidence is consistent with the embodied technical change interpretation of the t-impacts on effective prices implied by our comparison of p*MA and p*K to pMA and pK changes. Declines in effective relative to measured pMA, and the reverse for pK, each augment MA use.
Note also that the input-specific measure CMA,t(dir) = −0.0525 is much larger than the associated overall (total cost) input declines captured by CTC,t(dir) = −0.004. And that the totalMA effect, CMA,t(tot), is negative whereas that for TC, CTC,t(tot), is positive, indicating that “technical change” has been both relatively and absolutely MA-input-saving. Over time there has been a technical change bias toward reducing agricultural materials use more than other inputs for a given level of output.
Finally, the effective price p*MA actually trends down after 1980, so the full contribution of own price changes to agricultural demand is positive—a tendency that is particularly worth highlighting because measured agricultural prices continued to fall after our sample period. It also appears that although agricultural demand growth in the 1980s exceeded that in the 1970s, the individual input-price contributions of output and input prices to that growth were generally smaller. In fact, a large proportion of agricultural demand expansion seems to have arisen from technical effects. In particular, the indirect p*MA effect has increased over time to the point where CMA,t(tot) is positive post-1980, although the direct impact, CMA,t(dir), reported in table 2, remains negative (but smaller) in the later time period.
Effects of Agricultural Price Changes on Marginal Costs, Average Costs, and Food Prices
We may also consider the pass-through of agricultural prices, using the estimates presented in table 6 for the elasticity and contribution measures relating to marginal cost and food prices. Input-price effects for materials and labor inputs are slightly larger for marginal than for total (and thus average, given Y) cost, implying a depressing impact on scale economies (MC increases more than AC with higher input prices, so their ratio rises). The reverse is true, however, for the pK and pE elasticities, supporting the notion that capital is subject to adjustment costs and “lumpiness” that are driving forces for returns to scale. This observation is also consistent with the virtually nonexistent MC impacts of changing output.
| lnΔ | εMC, i | C MC, i | εPY, i | C PY, i | |
|---|---|---|---|---|---|
| Input prices | |||||
| Agricultural materials | 0.0547 | 0.2533 | 0.0139 | 0.2725 | 0.0149 |
| Food materials | 0.0403 | 0.2080 | 0.0084 | 0.2131 | 0.0086 |
| Other materials | 0.0653 | 0.1938 | 0.0127 | 0.2078 | 0.0136 |
| Labor | 0.0908 | 0.1611 | 0.0146 | 0.1732 | 0.0157 |
| Capital | 0.0680 | 0.1773 | 0.0121 | 0.1887 | 0.0128 |
| Energy | 0.1186 | 0.0065 | 0.0008 | 0.0086 | 0.0010 |
| Output | 0.0218 | −0.0157 | −0.0003 | −.0776 | −0.0017 |
| Technical change | |||||
| Equipment and structures | 0.0200 | 0.0328 | 0.0007 | 0.0340 | 0.0007 |
| t | 0.0100 | −0.0139 | −0.0028 | −0.0149 | −0.0030 |
| t2 | −0.0042 | −0.0002 | −0.0042 | −0.0002 | |
| Sum | 0.0634 | 0.0654 |
- Note: See table 1. Here, each contribution (C) is the product of the growth rate in the first column and the relevant elasticity.
Table 7 reports elasticities for food prices, marginal processor costs, and total (average) processor costs for a 1% change in agricultural prices. First, comparisons of food prices and marginal costs provide insights about markups and their determinants. A 1% increase in agricultural prices increases food prices by proportionately more than average costs, and marginal more than average costs—0.272, compared to 0.253, and 0.250, respectively. In turn, rising agricultural prices drive slightly higher markups (pY/MC). The elasticity measures also changed substantively over time. In particular, the food price elasticity fell sharply, from 0.308 in 1972–82 to 0.237 in the later period, and moved closer to the cost elasticities.
| Full Sample | 1972–82 | 1982–92 | |
|---|---|---|---|
| Percentage change | |||
| Total cost | 0.250* | 0.273* | 0.226* |
| Marginal cost | 0.253* | 0.287* | 0.220* |
| Output price | 0.272* | 0.308* | 0.237* |
| Ag input quantity | −1.137* | −0.973* | −1.299* |
- Note: See table 1.
Conclusions
Our analysis investigates an often-raised and widely discussed trend that has generated significant concern about agricultural markets. Steady changes toward more highly processed food products have been observed for many years, and the connections among those trends and fundamental changes in household demographics and lifestyle choices have been extensively documented. It is easy to see the key implications of such developments for agriculture; descriptive data alone would show that the share of agricultural materials inputs in food-processing shipments fell over time, in amounts close to the values presented in table 2. By inference, the linkage between agricultural and food prices should also have weakened in accordance with the trend change in factor shares.
A more detailed analysis of these patterns can be developed, however, by characterizing a more complete model of the network of factors driving demand for agricultural commodities in food processing. In this study, such an approach has yielded insights about several less widely understood—particularly quantitatively—factors affecting the demand for agricultural products.
First, in line with earlier findings by Goodwin and Brester, we find that processors' demand for agricultural commodities is price sensitive, and has become more elastic over time. Along with falling relative prices for agricultural inputs, this has led to substitution toward agricultural inputs, and away from labor and capital. Second, we find that the demand for agricultural materials is slightly scale intensive; increases in industry demand for food products lead to more than proportionate increases in agricultural input demand. Thus, modest continuing food industry growth has led to a slight intensification of agricultural demand growth. And third, we find that some forms of technical change have intensified agricultural input demand. Effective agricultural prices have dropped relative to observed prices, a trend that is likely driven by quality improvements in agricultural commodities and in the marketing system, and in our model leads to more substitution toward agricultural materials. Moreover, effective capital prices have risen relative to observed, possibly due to growing adjustment costs, or tax, regulatory, or environmental wedges, which reinforces substitution toward agricultural inputs.
Conversely, the direct impact of technical change (t) has been large and negative, and only partly counteracted by the positive technological impacts embodied in the effective MA and K prices. The implied drop in primary agricultural product demand has also been stronger than the overall cost diminution effect, which implies a relative MA-input-saving bias. The 1982–92 (t2) structural change impact also suggests that this trend is intensifying, and is being further exacerbated by diminishing effective price (p*MA and p*K) changes.
In sum, the effect of changes in consumer preferences on agricultural input demand appears to have been much greater than descriptive statistics suggest, since the descriptive measures co-mingle all of the above forces. Overall, the measured share of primary agricultural materials in total costs has been dropping, so the contribution of MA price increases to cost changes has fallen over time. As a result, the link between MA demand and food prices has clearly weakened, and this trend is likely to continue into the future.
Appendix
| Parameter | Estimate | t-statistic | Parameter | Estimate | t-statistic |
|---|---|---|---|---|---|
| λMA1 | 0.0951 | 1.53 | δMAT | −0.1887 | −2.54 |
| λMA2 | 0.0712 | 1.56 | δMAT2 | 0.4743 | 2.62 |
| λMAt | −0.0906 | −5.31 | δMAES | 0.1488 | 0.66 |
| λK1 | −0.1089 | −1.24 | αL | 0.1524 | 0.62 |
| λK2 | −0.2256 | −3.74 | δLY | 0.0822 | 11.24 |
| λKt | 0.1536 | 4.79 | αLMF | −0.1789 | −2.11 |
| αE | −0.0522 | −1.11 | αLMO | 0.4867 | 2.72 |
| δEY | 0.0147 | 2.23 | δLK | −0.1017 | −0.53 |
| αLE | −0.0228 | −0.82 | δLT | −0.1230 | −4.63 |
| αEMA | 0.0226 | 1.86 | δLT2 | 0.3691 | 4.59 |
| αEMF | −0.0002 | −0.02 | δLES | −0.1718 | −1.89 |
| αEMO | −0.0581 | −1.19 | αMF | −0.6892 | −2.29 |
| δEK | 0.1208 | 2.35 | δMFD | 0.1298 | 0.72 |
| δET | −0.0791 | −4.80 | δMFY | 0.0889 | 9.85 |
| δET2 | 0.4020 | 6.39 | αMFMO | −0.0537 | −0.44 |
| δEES | 0.0294 | 0.70 | δMFK | 0.2563 | 1.93 |
| γYT | −0.0006 | −3.87 | δMFT | −0.0896 | −2.42 |
| γYT2 | 0.0001 | 0.33 | δMFT2 | 0.4720 | 4.85 |
| γYES | 0.0018 | 1.21 | δMFES | −0.1769 | −1.30 |
| γTES | −0.0028 | −0.96 | αMO | −0.4973 | −1.17 |
| γT2ES | 0.0018 | −0.24 | δMOY | 0.0471 | 5.90 |
| γTT2 | −0.0748 | −6.59 | δMOK | 0.0249 | 0.06 |
| γYY | −0.0002 | −1.37 | δMOT | −0.1108 | −2.95 |
| γTT | 0.0305 | 7.32 | δMOT2 | 0.4105 | 4.12 |
| γESES | 0.0118 | 0.84 | δMOES | −0.4599 | −3.88 |
| αMA | 0.5887 | 1.12 | αK | −1.4212 | −2.64 |
| δMAY | 0.7710 | 56.13 | δKY | 0.1643 | 19.01 |
| αLMA | 0.0824 | 0.98 | δKT | −0.0373 | −0.86 |
| αMAMF | 0.0574 | 0.39 | δKT2 | 0.4104 | 3.45 |
| αMAMO | 0.0137 | 0.11 | δKES | 0.3393 | 2.56 |
| δMAK | 0.3775 | 2.84 | λY | −0.0008 | −0.54 |
| Equation | R2 |
|---|---|
| TC | 0.976 |
| M A | 0.993 |
| M F | 0.946 |
| M O | 0.954 |
| L | 0.946 |
| E | 0.948 |
| K | 0.979 |
| P Y | 0.976 |




