Estimating Recreational User Counts
This research was funded by Connecticut Sea Grant and the Rhode Island Agricultural Experiment Station No. 3968. The authors would like to acknowledge the assistance of the Preservation Society of Newport County. Opinions belong solely to the authors and do not imply endorsement by the funding agencies or the Preservation Society of Newport County.
Abstract
This article outlines a methodology for estimating the number of individual visitors to a set of recreational sites, as well as counts of specific visitor groups. The model is designed for sets of sites characterized by: (a) unrestricted recreation from a wide and partially unknown geographic market; (b) individuals who may visit more than one site; (c) accurate visitation (gate) counts from each site. The model provides consistent estimates of the total number of individual visitors, based on information embedded in site-level count and survey data. Monte Carlo analysis and an empirical application illustrate the properties of visitor count estimates.
Multiple-site recreation demand and welfare analyses typically estimate the number of trips to a particular site or set of sites. However, the number of individual visitors is often unknown. Although visitation estimates for each site may be available, the fact that individuals may visit more than one site per season or per trip, and may visit a site on more than one occasion, prevents summation of single-site attendance estimates into an aggregate estimate of the total number of visiting individuals. Hence, while the total number of site visits may be known, researchers do not know the total number of visiting individuals. The problem becomes more difficult when it is necessary to count several different types of recreational visitors (e.g., catch-and-release versus catch-and-keep anglers; day-trippers versus overnight visitors), each of whom may realize different benefits from a recreational experience, and may reveal different behavior and visitation rates.
Despite assumptions to the contrary, estimating visitor numbers is rarely a trivial matter (Smith). While the lack of accurate visitor counts over multiple sites may be of little interest in some cases, in others it may provide a significant barrier to estimation of aggregate benefits or economic impacts. For example, in the absence of accurate visitor or user counts, recreation demand models that estimate benefits per visitor may require ad hoc assumptions to estimate aggregate welfare impacts (e.g., Johnston et al., Garrod and Willis, pp. 289–310).1 Even if welfare estimates may be legitimately estimated per average trip—and hence total benefits may be estimated as per trip surplus multiplied by the number of trips—policy makers may still wish to know how many different individuals realize these benefits, or are otherwise influenced by a particular policy. Moreover, as shown by Morey, interpretation of per-trip benefit measures is less straightforward than is typically assumed. Analogous cases appear in the tourism literature: ad hoc efforts are often used to estimate visitor numbers, allowing aggregate economic impacts or expenditures to be calculated (e.g., Crompton, Lee, and Shuster; Fesenmaier et al.).
Although estimates of recreational visitor numbers are often obtained using inappropriate or ad hoc methods (Smith), there are special cases in which the number of visitors is either known or may be estimated as a simple extension of the model. For example, if all visitors live in an identifiable geographic region, random surveys may allow one to estimate visitor numbers during any time period through simple multiplication of estimated participation rates by the population of potential users. Identification of the geographical extent of the market, however, is often a controversial issue (Cameron, Shaw, and Ragland); many recreation studies define markets based on data availability rather than on the true origin of recreational visitors. Such problems can be avoided if all visitors are from an identifiable pool, such as fishing license holders (e.g., Feather, Hellerstein, and Tomasi; Herriges, Kling, and Phaneuf). Similarly, if individuals visit only one site per season, and site visitor numbers are known, then simple summation will yield an estimate of total recreational users.
The above-mentioned instances, however, are special cases. In the general case, the geographic origin of visitors is unknown, preventing researchers from simply multiplying participation rates by a known population size. In other instances, research goals or constraints may require an on-site survey, rather than random state- or nationwide sampling (e.g., McKean, Johnson, and Walsh; Johnston et al.). In such cases, one generally lacks information concerning the total number of individual users of a particular set of sites (for an exception, see Cooper).
This article outlines a methodology for estimating the number of individual visitors to a predefined set of sites, typically in a single geographic region. Unlike special-case methods of estimating recreational visitor numbers, the model does not require that researchers specify the extent of the geographic market from which visitors originate. The model is designed for a set of multiple sites characterized by: (a) unrestricted recreation from a wide and at least partially unknown geographic market; (b) individuals who typically visit more than one site; (c) the availability of accurate visitation (i.e., gate) counts from each site. The third assumption concerns information regarding the number of visits, not the number of individual visitors. We assume that all recreational users of interest visit at least one of the sampled set of sites, but no single site attracts all users (Tyrrell and Johnston).
Where such conditions hold, the presented model provides statistically consistent estimates of the total number of recreational visitors to the sampled sites, based on efficient use of information embedded in site-level count and survey data. That is, the presented model provides a straightforward means to answer a simple, yet fundamental question: How many individuals of different groups, in total, visited a known set of recreational sites, during a specified season? The model is based on the idea that triangulation of evidence from site visitation and participation rates can resolve the user count problem. In estimating the total number of regional recreational users, the methodology also provides consistent estimates of visitation for specified visitor sub-groups.
Determining Recreational User Counts from Observable Data
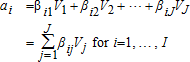 (1)
(1)Implicit in (1) is a particular time dimension, say a month, year, or weekend. Hence, Vj is the total number of visitors of type j to any of the I sites, over the time period chosen for analysis. For example, if a1 represents total seasonal visits to a particular fishing site among all angler types, and β11 represents the visitation rate of catch-and-release anglers, then V1 would represent the unobserved number of catch-and-release anglers visiting any sampled site within the region. Similarly, if β12 represents the visitation rate of catch-and-keep anglers, V2 would represent the unobserved number of catch-and-keep anglers visiting any sampled site within the region.
It is important to note that, unlike the notation found in typical econometric models, the goal here is to produce consistent estimates of Vj, given data concerning ai and βij. Hence, in this model the βij do not represent parameters to be estimated, but are rather true visitation rates that may be observed, albeit with unavoidable errors, from sample data, such as random on-site surveys of site visitors. As the visitation rate is only observable through some type of empirical sampling or surveying, it is composed of two components, the “true” visitation rate for the activity under consideration (βij) and a stochastic error (ɛij). Hence one must distinguish between the true, fixed βij and the observable, stochastic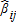 , where the observed proportion
, where the observed proportion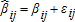 . It is assumed that the visitor survey or other data collection is conducted appropriately, and that the estimates of βij are unbiased such that the expected value of ɛij is zero (i.e., E(ɛij) = 0).
. It is assumed that the visitor survey or other data collection is conducted appropriately, and that the estimates of βij are unbiased such that the expected value of ɛij is zero (i.e., E(ɛij) = 0).
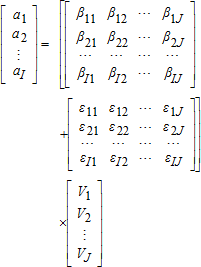 (2)
(2)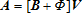 (3)
(3)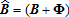 is observable.
is observable.The goal is to estimate V—representing the total numbers of the j different recreational user types visiting one or more of the I sites—using matrix equation (2). Note that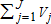 represents the total visitor count for all sites combined, over the length of time chosen for analysis. As each Vj is unobservable,
represents the total visitor count for all sites combined, over the length of time chosen for analysis. As each Vj is unobservable,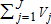 may not be estimated through simple summation of observable user counts.
may not be estimated through simple summation of observable user counts.
If I ≥ J, and |B′B| ≠ 0, it is possible to estimate each Vj (and hence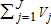 ) from (2). That is, there must be more sites than user types, and B′B must be non-singular. In the special case that I = J, a unique algebraic solution to the problem exists, obtained by inverting B and multiplying the inverted matrix by both sides of (2). The more common, relevant, and desirable case, however, is the case in which I > J. The advantage of the I > J case is the additional information provided by a greater number of observed sites. Since in this case there are more sites than user types, there is more than enough information to solve the problem, preventing a single, simple algebraic solution. The remainder of this article is devoted to estimation of the number of regional recreational users in each of the J types, for the case in which I > J.
) from (2). That is, there must be more sites than user types, and B′B must be non-singular. In the special case that I = J, a unique algebraic solution to the problem exists, obtained by inverting B and multiplying the inverted matrix by both sides of (2). The more common, relevant, and desirable case, however, is the case in which I > J. The advantage of the I > J case is the additional information provided by a greater number of observed sites. Since in this case there are more sites than user types, there is more than enough information to solve the problem, preventing a single, simple algebraic solution. The remainder of this article is devoted to estimation of the number of regional recreational users in each of the J types, for the case in which I > J.
Estimators for V when I > J
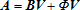 (4)
(4)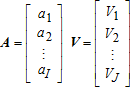
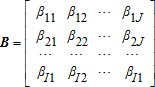

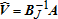 (5)
(5)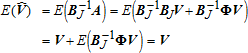 (6)
(6)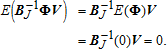 (7)
(7)A Unique Estimator When I > J
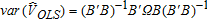 (8)
(8)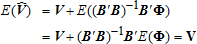 (9)
(9)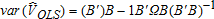 (10)
(10)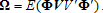 (11)
(11)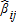 . The small sample properties of these are unknown, but they are asymptotically more efficient. That is, given that the
. The small sample properties of these are unknown, but they are asymptotically more efficient. That is, given that the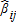 are observed through survey methods, one also has an estimate of the variances of the
are observed through survey methods, one also has an estimate of the variances of the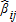 ; this information is embedded in Ω. Incorporating this information into the estimator improves asymptotic efficiency.
; this information is embedded in Ω. Incorporating this information into the estimator improves asymptotic efficiency.Asymptotically More Efficient Estimators
The Generalized Least Squares Estimator
Let us assume that E(ɛ2ij) = σ2ij, E(ɛijɛi′j) = σii′j and E(ɛijɛij′) = E(ɛijɛi′j′) = 0 where i ≠ i′ and j ≠ j′. The first two of these assumptions are standard in that they describe stochastic errors with constant variances and constant covariances between activities for each single type of visitor. The third assumption implies that there are no covariances of participation rate estimates at one site across J visitor types (errors in observations across visitor types are independent). It is important to note that we are not assuming that there is no competition for sites or that the rate of participation by one type at a site will be independent of the rate of participation of another group. These dependencies are captured in the estimated β's.
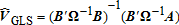 (12)
(12)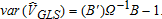 (13)
(13)As V and Ω are unobserved, the true GLS models cannot be estimated (Judge et al.). However, a consistent feasible estimator can be constructed and estimated iteratively, based on an initial consistent estimate of V. A number of consistent initial estimates are available. One example is the simple OLS estimator derived above (8). This initial estimate of V is unbiased, and therefore consistent. The consistent initial estimate of V guarantees a consistent estimate of the variance-covariance matrix (i.e.,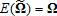 ) for the Feasible GLS estimator (Greene, Judge et al.). Based on this initial estimate
) for the Feasible GLS estimator (Greene, Judge et al.). Based on this initial estimate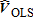 and the corresponding variance-covariance matrix, the Feasible GLS (FGLS) estimator is estimated iteratively, with each prior estimate of V and Ω providing initial estimates for the subsequent iteration. Generally, iterations of this type converge quickly to a constant solution for the number of visitors of each type. The Feasible GLS solution is consistent and asymptotically more efficient than the initial estimate of V, as it incorporates information from the variance-covariance matrix in each successive iteration.
and the corresponding variance-covariance matrix, the Feasible GLS (FGLS) estimator is estimated iteratively, with each prior estimate of V and Ω providing initial estimates for the subsequent iteration. Generally, iterations of this type converge quickly to a constant solution for the number of visitors of each type. The Feasible GLS solution is consistent and asymptotically more efficient than the initial estimate of V, as it incorporates information from the variance-covariance matrix in each successive iteration.
The Weighted Least Squares Estimator
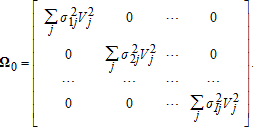 (14)
(14)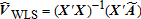 (15)
(15)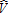 is a J × 1 vector of the numbers of visitors of each type,
is a J × 1 vector of the numbers of visitors of each type,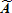 is an I × 1 vector of weighted total visitor counts at each of the major attractions aiρi, and X is an I × J matrix of weighted estimated visitation rates βijρi. In these definitions,
is an I × 1 vector of weighted total visitor counts at each of the major attractions aiρi, and X is an I × J matrix of weighted estimated visitation rates βijρi. In these definitions,
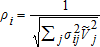 (16)
(16)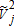 is the square of a consistent estimate of the number of visitors of the jth type. As above mentioned, the estimator is solved iteratively, with the initial
is the square of a consistent estimate of the number of visitors of the jth type. As above mentioned, the estimator is solved iteratively, with the initial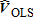 providing the initial consistent estimate. As implied by 12-13 above, the WLS estimator is a special case of the GLS estimator.
providing the initial consistent estimate. As implied by 12-13 above, the WLS estimator is a special case of the GLS estimator.The Maximum Likelihood Estimator
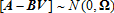 (17)
(17)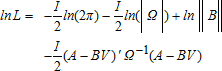 (18)
(18)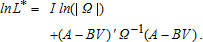 (19)
(19)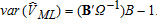 (20)
(20)Monte Carlo Simulation
While small sample properties may be calculated for the OLS estimator, the feasible GLS, weighted least squares, and ML estimators have unknown small sample properties. Although the OLS estimator is unbiased it may not be as efficient as alternative estimators. The feasible GLS, weighted least squares, and ML estimators are consistent, but may not perform well in small samples. This is an important consideration, as the sample size for all estimators is equal to the number of recreational sites in the sample, and is therefore likely to be relatively small. Accordingly, it is unclear a priori which estimator will provide the most appealing estimates.
To explore the performance of the alternative estimators, we present a Monte Carlo analysis of the four potential estimators (OLS, FGLS, WLS, and ML). The estimators are applied to four different recreation participation scenarios, denoted cases I–IV. Each scenario assumes two types of visitors and three recreational sites, yet is based on different assumed visitation behavior (and thus patterns of visits across sites). One thousand draws, each containing 100 observations are generated for each case. (This is equivalent to surveying 100 individuals (site users) to determine their site visitation behavior.)
The four scenarios are described in table 1. We refer to the two types of visitors as “catch-and-keep anglers” (j = K) and “catch-and-release anglers” (j = R), respectively. The 100 observations for each type are selected randomly from the illustrated distribution of participation rates (table 1). For this analysis, we make the simplifying assumption that total site counts add to exactly the number of site visitors (i.e., an angler will visit each site a maximum of one time per season). This implies that participation rates add to 1.00 and allows interpretation of participation rates as visitation probabilities. For example, in case II there is a 80% probability that a catch-and-keep angler will visit site 3 only, and a 10% chance that he will visit both sites 2 and 3 (table 1). Thus, the total probability of visiting site 3 on a trip is 90% and the total probability that he will visit site 2 is 10%. This may also be interpreted as an average catch-and-keep angler making 0.9 visits to site 3 during the season. Although this assumption simplifies modeling and discussion, it is not required, and has negligible implications for simulation results.
| Case I | Case II | Case III | Case IV | |||||
|---|---|---|---|---|---|---|---|---|
Catch-and-Keep |
Catch-and-Release |
Catch-and-Keep |
Catch-and-Release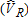 |
Catch-and-Keep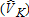 |
Catch-and-Release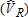 |
Catch-and-Keep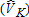 |
Catch-and-Release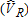 |
|
| Probabilities | ||||||||
| P(1) | 0.4 | 0.1 | 0.0 | 0.8 | 0.3 | 0.2 | 0.05 | 0.85 |
| P(2) | 0.1 | 0.05 | 0.0 | 0.0 | 0.4 | 0.6 | 0.1 | 0.1 |
| P(3) | 0.1 | 0.1 | 0.8 | 0.0 | 0.3 | 0.2 | 0.85 | 0.05 |
| P(1,2) | 0.05 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| P(1,3) | 0.05 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| P(2,3) | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| P(1,2,3) | 0.0 | 0.05 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Participation rates | ||||||||
| B1 | ||||||||
| P(1) + P(1,2) + P(1,3) + P(1,2,3) | 0.5 | 0.35 | 0.0 | 0.9 | 0.3 | 0.2 | 0.05 | 0.85 |
| B2 | ||||||||
| P(2) + P(1,2) + P(2,3) + P(1,2,3) | 0.25 | 0.3 | 0.1 | 0.1 | 0.4 | 0.6 | 0.1 | 0.1 |
| B3 | ||||||||
| P(3) + P(1,3) + P(2,3) + P(1,2,3) | 0.25 | 0.35 | 0.9 | 0.0 | 0.3 | 0.2 | 0.85 | 0.05 |
| ∑P(·) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| True visitor numbers and site visits | ||||||||
| VK | 500 | 500 | 500 | 500 | ||||
| VR | 1000 | 1000 | 1000 | 1000 | ||||
| a 1 (true visits to site 1) | 600 | 900 | 350 | 875 | ||||
| a 2 (true visits to site 2) | 425 | 150 | 800 | 150 | ||||
| a3 (true visits to site 3) | 475 | 450 | 350 | 475 | ||||
| Correlations | ||||||||
| Corr(BH, BB) | 0.50 | −0.66 | 1.00 | −0.59 | ||||
| Corr(VH, VB) | −0.97 | −0.00 | 1.00 | −1.00 | ||||
The four scenarios were chosen to characterize different degrees of correlation among Bj and Vj for j = {K, R}. The last two rows of table 1 characterize these correlations. Corr(BK, BR) measures the correlation between participation rates of catch-and-release and catch-and-keep anglers across sites. Corr(VK, VR) measures the correlation between population estimates of the two groups (Vj) from the GLS (most efficient unbiased) estimator using the true underlying participation rates.
As noted above, the comparison of estimators is based on their average performance over 1,000 simulated data sets drawn for each of the four scenarios. The simulated datasets were designed to mimic data that might be obtained through on-site surveys, combined with site-specific visitation estimates. For each scenario defined in table 1, a simulated dataset was generated through 100 repetitions of seven successive draws from a binomial distribution (i.e., a random number between 0 and 1), with each draw corresponding to one of the seven visitation probabilities from table 1 (i.e., P(1), P(2),…, P(1,2,3)). If the random draw exceeded the associated probability, a ‘0’ was entered for that observation; otherwise a ‘1’ was entered. These entries represent yes-or-no responses to survey questions regarding visits to various sites or groups of sites. Again, to simplify the analysis we assume a maximum of one visit per site, per season. These visitation probabilities are used to calculate sample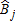 from the true Bj shown in table 1.
from the true Bj shown in table 1.
For each scenario the true probabilities (participation rates) are multiplied by the true numbers of visiting catch-and-keep and catch-and-release anglers, then aggregated as appropriate to generate ai, or total visits per site (table 1). In actual analyses this number would be generated from gate counts, ticket sales, or similar data sources at each site.2 For this analysis, we assume true values of VR = 1,000 catch-and-release anglers and VK = 500 catch-and-keep anglers; this is the total true angler (or visitor) population used to calculate simulated sample ai. These are also the true values for VR and VK against which estimates are compared.
Estimated solutions for the FGLS and WLS estimators were calculated and found to converge to the fourth significant digit after three iterations. The log-likelihood function for the ML estimator was maximized using the generalized reduced gradient (GRG2) non-linear optimization algorithm (Lasdon et al.). The alternative estimators were tested in a large number of simulations, of which cases I–IV were selected to illustrate the estimators' performance under a wide range of conditions.
Results for the four estimators are summarized in tables 2 and 3. Results are characterized for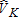 (total catch-and-keep anglers),
(total catch-and-keep anglers),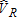 (total catch-and-release anglers), and
(total catch-and-release anglers), and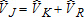 Table 2 illustrates mean bias and variance of each estimator across the 1,000 samples. Table 3 illustrates mean squared error (MSE) and the ratio of sample-estimated variance to true variance.
Table 2 illustrates mean bias and variance of each estimator across the 1,000 samples. Table 3 illustrates mean squared error (MSE) and the ratio of sample-estimated variance to true variance.
| Case I | Case II | Case III | Case IV | |||||
|---|---|---|---|---|---|---|---|---|
Catch-and-Keep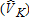 |
Catch-and-Release |
Catch-and-Keep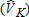 |
Catch-and-Release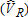 |
Catch-and-Keep |
Catch-and-Release |
Catch-and-Keep |
Catch-and-Release |
|
| True number of visitors | 500 | 1000 | 500 | 1000 | 500 | 1000 | 500 | 1000 |
| Bias of estimators (percent bias in parentheses) | ||||||||
| OLS: Individual visitors | 6.3 (1.26) | −5.4 (0.54) | −0.5 (0.1) | −0.7 (0.07) | −4.9 (0.98) | 4.0 (0.4) | −0.6 (0.12) | −1.0 (0.1) |
| Total visitors | 0.9 (0.06) | −1.2 (0.08) | −0.9 (0.06) | −1.6 (0.11) | ||||
| WLS: Individual visitors | 4.9 (0.98) | −0.6 (0.06) | 0.0 (0.00) | 0.2 (0.02) | 9.7 (1.94) | −7.2 (0.72) | 0.3 (0.06) | −0.3 (0.03) |
| Total visitors | 4.3 (0.29) | 0.2 (0.01) | 2.5 (0.17) | −0.1 (0.01) | ||||
| GLS: Individual visitors | 4.1 (0.82) | 0.0 (0.00) | 0.0 (0.00) | 0.1 (0.01) | 9.3 (1.86) | −6.9 (0.69) | 0.1 (0.02) | −0.1 (0.01) |
| Total visitors | 4.2 (0.28) | 0.1 (0.01) | 2.4 (0.07) | 0.0 (0.00) | ||||
| ML: Individual visitors | 125.9 (25.18) | −166.1 (16.61) | −1.8 (0.36) | −4.8 (0.48) | 57.8 (11.56) | −85.4 (8.54) | −2.8 (0.56) | −10.6 (1.06) |
| Total visitors | −40.2 (2.68) | −6.6 (0.44) | −27.6 (1.84) | −13.4 (0.89) | ||||
| Variance of estimators | ||||||||
| BLUE: Individual visitors | 95,878 | 105,445 | 277 | 1102 | – | – | 683 | 683 |
| Total visitors | 6979 | 1375 | – | 0 | ||||
| OLS: Individual visitors | 121,860 | 132,602 | 279 | 1142 | 66,581 | 54,629 | 1141 | 1855 |
| Total visitors | 9480 | 1445 | 7759 | 2523 | ||||
| WLS: Individual visitors | 122,932 | 133,790 | 277 | 1141 | 65,655 | 53,949 | 1145 | 1857 |
| Total visitors | 9592 | 1426 | 7712 | 2522 | ||||
| GLS: Individual visitors | 121,704 | 132,364 | 278 | 1143 | 65,853 | 54,114 | 1158 | 1852 |
| Total visitors | 9620 | 1425 | 7736 | 2529 | ||||
| ML: Individual visitors | 21,065 | 22,005 | 256 | 1032 | 19,585 | 15,694 | 1096 | 1581 |
| Total visitors | 6675 | 1294 | 5855 | 2326 | ||||
- Note: Bias and variance are measured in visitor numbers; values in parentheses represent bias as a percentage of the true value.
| Case I | Case II | Case III | Case IV | |||||
|---|---|---|---|---|---|---|---|---|
Catch-and-Keep |
Catch-and-Release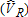 |
Catch-and-Keep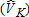 |
Catch-and-Release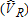 |
Catch-and-Keep |
Catch-and-Release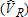 |
Catch-and-Keep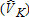 |
Catch-and-Release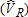 |
|
| MSE of Estimators | ||||||||
| OLS: Individual visitors | 121,900 | 132,632 | 279 | 1142 | 66,605 | 54,646 | 1141 | 1856 |
| Total visitors | 9481 | 1446 | 7760 | 2525 | ||||
| WLS: Individual visitors | 122,957 | 133,790 | 277 | 1142 | 65,748 | 54,001 | 1145 | 1857 |
| Total visitors | 9610 | 1426 | 7719 | 2522 | ||||
| GLS: Individual visitors | 132,365 | 132,365 | 278 | 1143 | 65,940 | 54,161 | 1158 | 1852 |
| Total visitors | 9638 | 1426 | 7742 | 2529 | ||||
| ML: Individual visitors | 36,926 | 49,592 | 259 | 1055 | 22,920 | 22,985 | 1104 | 1694 |
| Total visitors | 8287 | 1338 | 6619 | 2506 | ||||
| Ratio of sample-estimated variance to true variance of estimators | ||||||||
| OLS: Individual visitors | 2.03 | 2.10 | 1.05 | 0.99 | 1.27 | 1.32 | 1.00 | 1.05 |
| Total visitors | 1.35 | 0.99 | 1.22 | 1.07 | ||||
| WLS: Individual visitors | 2.06 | 2.13 | 1.02 | 0.99 | 1.27 | 1.31 | 1.00 | 1.05 |
| Total visitors | 1.34 | 0.99 | 1.21 | 1.07 | ||||
| GLS: Individual visitors | 2.00 | 2.07 | 1.02 | 0.98 | 1.27 | 1.31 | 0.98 | 1.04 |
| Total visitors | 1.33 | 0.98 | 1.21 | 1.06 | ||||
| ML: Individual visitors | 5.29 | 5.53 | 1.10 | 1.08 | 3.19 | 3.40 | 1.02 | 1.19 |
| Total visitors | 1.31 | 1.07 | 1.35 | 1.13 | ||||
Estimator Bias
Table 2 illustrates bias of the four estimators for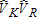 , and
, and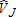 , for each of the four scenarios. Despite theoretical differences among the three least squares estimators (OLS, FGLS, WLS), measures of bias are similar. The least squares estimators, on average, generate estimates with negligible bias, with no clear distinction between the degree of bias associated with each estimator. In contrast, the ML estimator is markedly biased, particularly in cases I and III. The direction of bias varies across estimators, scenarios, and visitor types; no pattern is discernable. All estimators have relatively smaller biases in cases II and IV, characterized by a concentration of each type of visitor on specific sites, and a strong negative correlation between participation rates as measured by corr(BK, BR). Larger biases are found in cases I and III where corr(BK, BR) > 0. This distinction is particularly notable for the ML estimator, although the bias of this estimator exceeds that of all other estimators, in all cases.
, for each of the four scenarios. Despite theoretical differences among the three least squares estimators (OLS, FGLS, WLS), measures of bias are similar. The least squares estimators, on average, generate estimates with negligible bias, with no clear distinction between the degree of bias associated with each estimator. In contrast, the ML estimator is markedly biased, particularly in cases I and III. The direction of bias varies across estimators, scenarios, and visitor types; no pattern is discernable. All estimators have relatively smaller biases in cases II and IV, characterized by a concentration of each type of visitor on specific sites, and a strong negative correlation between participation rates as measured by corr(BK, BR). Larger biases are found in cases I and III where corr(BK, BR) > 0. This distinction is particularly notable for the ML estimator, although the bias of this estimator exceeds that of all other estimators, in all cases.
Estimator Variance and Mean Squared Error (MSE)
Table 2 illustrates the variance associated with estimates of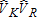 , and
, and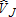 . Aside from the variances of the four tested estimators, table 2 also illustrates the variance of a best linear unbiased estimator (BLUE); this consists of a GLS estimator incorporating actual Ω. The BLUE estimator is shown for comparison only; in actual (i.e., non-simulated) circumstances Ω is unobservable. (The BLUE variance estimate cannot be calculated for case III because of a singularity of the omega matrix.)
. Aside from the variances of the four tested estimators, table 2 also illustrates the variance of a best linear unbiased estimator (BLUE); this consists of a GLS estimator incorporating actual Ω. The BLUE estimator is shown for comparison only; in actual (i.e., non-simulated) circumstances Ω is unobservable. (The BLUE variance estimate cannot be calculated for case III because of a singularity of the omega matrix.)
Despite the substantial bias associated with the ML estimator, it generates the smallest variance of all estimators; this is particularly striking in cases I and III where correlation between participation rate patterns is positive. As a result, and despite its larger bias, the ML estimator has the smallest MSE in all cases (table 3). The variances and MSE of the least squares estimators (OLS, WLS, FGLS) are in all cases larger than that of the ML estimator, but approach the simulated BLUE estimate in cases I and II. This mirrors the similar performance with regard to bias discussed above. This combination of results suggests that the ability of WLS and FGLS to incorporate additional information concerning the variances and covariances of the data does not lead to a significant improvement in estimator performance over the simpler OLS estimator, at least for the illustrated cases.
Sample-Estimated versus Actual Variances
The sample-estimated variances (calculated for each draw) for each of the estimators were calculated for each of the samples (i.e., 1,000 draws). The ratio of the mean of these sample-estimated variances to the actual variances (calculated over all 1,000 draws) are given in table 3. The desirable ratio is 1.0; values above 1.0 would indicate overestimates of variance and conservative estimates of confidence intervals. All estimators have ratios near 1.0 for cases II and IV. For case III, the least squares estimates have ratios of about 1.3 while the ML estimator has ratios of approximately 3.0. For case I the individual least squares estimators have ratios of approximately 2.0 and the ML estimator has ratios of greater than 5.0, while all estimators of total visitors numbers have ratios of about 1.3. As a result, all estimators would provide conservative estimators of confidence intervals.
Results suggest that the least squares, sample-based estimates of variance provide relatively accurate, if somewhat conservative, estimates of variance for visitor estimates. Sample-based variance estimates are poorest (i.e., relatively largest) in case I, characterized a strong positive correlation between participation rates of catch-and-release and catch-and-keep anglers across sites (corr(BK, BR) > 0) and a strong negative correlation between population estimates of the two groups (corr(VK, VR) < 0). While this is true of all estimators, the ratio of sample-estimated to actual variance is least robust for the ML estimator, with a ratio of greater than 5.0 in case I and 3.0 in case III.
Frequency Distributions of Visitor Estimates
Figures 1–3 provide another depiction of estimator performance. These figures show the frequency distributions of visitor estimates from the 1,000 samples for case I. Figures are not included for cases II–IV. The frequency distribution of estimates for case III resembles that for case I. Cases II and IV result in estimates highly concentrated around the true values, with little difference among frequency distributions for any of the alternative estimators.
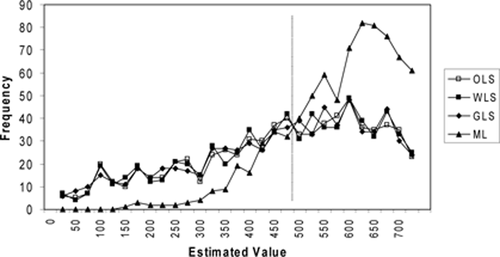
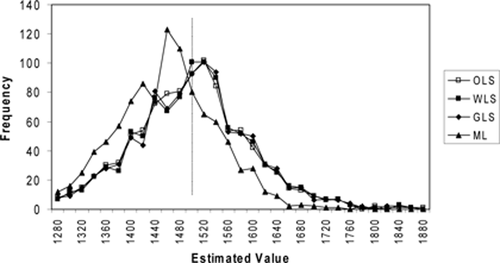
Estimate distribution for catch-and-keep anglers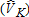 , case I (distribution left-truncated at 25 and right-truncated at 725)
, case I (distribution left-truncated at 25 and right-truncated at 725)
Estimate distribution for catch-and-release anglers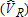 , case I (distribution left-truncated at 640 and right-truncated at 1,800)
, case I (distribution left-truncated at 640 and right-truncated at 1,800)
Estimate distribution for total anglers , case I
, case I
Figure 1 shows the case I distribution of estimates for the number of catch-and-keep anglers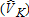 , where true VK = 500. The ML estimate has a concentration of estimates in the 500–700 range with few estimates below 400. This concentration above the true value of 500 is reflected in the average bias reported for the ML estimates. The least squares estimates are spread more thinly across the entire figure with a substantial number of estimates below zero. The least squares estimates also show a relatively high concentration of estimates in the 500–700 range, but these overestimates are almost entirely balanced by the large number of low estimates, leading to the relatively low mean bias illustrated in table 2. The least squares estimators generate markedly similar frequency distributions. However, there is a substantial difference between the least squares distribution and that of the ML estimate of
, where true VK = 500. The ML estimate has a concentration of estimates in the 500–700 range with few estimates below 400. This concentration above the true value of 500 is reflected in the average bias reported for the ML estimates. The least squares estimates are spread more thinly across the entire figure with a substantial number of estimates below zero. The least squares estimates also show a relatively high concentration of estimates in the 500–700 range, but these overestimates are almost entirely balanced by the large number of low estimates, leading to the relatively low mean bias illustrated in table 2. The least squares estimators generate markedly similar frequency distributions. However, there is a substantial difference between the least squares distribution and that of the ML estimate of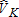 .
.
Figure 2 shows the complementary distributions of estimates of catch-and-release anglers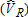 for the same case I samples where true VR = 1,000. The ML estimates are concentrated in the range 650 to 1,000 while the least squares estimates are again spread more evenly across a wider range of values. The ML concentration below the true value of 1,000 is reflected in the average negative bias of ML estimates. Despite the relatively wide distribution of the least squares estimates, there is minimal mean bias in any of these estimators. Figure 3 shows the distribution of estimates for
for the same case I samples where true VR = 1,000. The ML estimates are concentrated in the range 650 to 1,000 while the least squares estimates are again spread more evenly across a wider range of values. The ML concentration below the true value of 1,000 is reflected in the average negative bias of ML estimates. Despite the relatively wide distribution of the least squares estimates, there is minimal mean bias in any of these estimators. Figure 3 shows the distribution of estimates for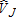 , the sum of
, the sum of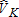 and
and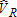 . The distribution of
. The distribution of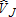 more closely resembles a normal distribution. In contrast to the distributions of
more closely resembles a normal distribution. In contrast to the distributions of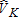 and
and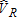 , the
, the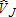 (i.e., total visitor) distribution shows smaller tails, and a greater concentration of estimates around the true value; this is true for all estimators. The peak for the least squares estimators occurs just above the true value of 1,500, while the peak for the ML estimator occurs just below this value. As mentioned above, there is little difference between any of the least squares estimates, but a notable distinction between the ML estimator and the least squares estimators.
(i.e., total visitor) distribution shows smaller tails, and a greater concentration of estimates around the true value; this is true for all estimators. The peak for the least squares estimators occurs just above the true value of 1,500, while the peak for the ML estimator occurs just below this value. As mentioned above, there is little difference between any of the least squares estimates, but a notable distinction between the ML estimator and the least squares estimators.
Interpreting Monte Carlo Results: Recommendations for Estimator Choice
Although tables 1–4 illustrate only four potential patterns of site visitation, the general performance of estimators is similar over a wide range of potential patterns, including many not illustrated here. Monte Carlo results illustrate that, despite its theoretical inefficiency, the OLS estimator may perform as well as alternative least squares estimators that account for non-spherical disturbances (e.g., FGLS, WLS). Given its computational simplicity and average qualities no worse than alternative least squares estimators, OLS may provide the best practical means to estimate visitor numbers. The three least squares estimators produce nearly identical results in the four cases estimated. OLS produces virtually the same average bias, variance, and sample-estimated variance as the alternative least squares approaches. It is of course possible that the added efficiency of feasible GLS and WLS might result in improved estimator performance given large numbers of sites and visitor types. However, for a small number of simulated sites, OLS performance appears to match that of the more efficient estimators.
| Property | Visitation Ratea (Overnight Visitors) | Visitation Ratea (Day trippers) |
|---|---|---|
| The Breakers | 0.829 | 0.679 |
| The Breakers Stable | 0.138 | 0.085 |
| Green Animals Gardens | 0.079 | 0.079 |
| Marble House | 0.443 | 0.315 |
| Chateau sur Mer | 0.256 | 0.155 |
| The Elms | 0.409 | 0.308 |
| Kingscote | 0.104 | 0.091 |
| Rosecliff | 0.451 | 0.277 |
- a The visitation rate is defined as the percentage of sampled visitors who visited a particular property. For example, 82.9% of overnight visitors reported visiting The Breakers.
Comparison of the ML estimator performance with that of the least squares estimators provides less conclusive results. The ML estimator has a smaller variance and MSE than any of the least squares estimators. However, it also shows the potential for significant bias, and potentially poor performance of sample-estimated variance. As a result, the ML estimator will, on average, produce biased results, but—given it's much smaller variance—may be less likely to provide a result that is clearly noncredible (e.g., a negative estimate). Hence, the choice between OLS and ML must be based on the researcher's willingness to accept estimator bias in return for a reduced variance and MSE. However, considering both its simplicity and performance, OLS may offer the best practical solution to the visitor count problem. Alternatively, researchers may wish to contrast results of both OLS and ML models; once data are available the additional labor required to estimate both models is trivial.
Although least squares estimators offer perhaps the simplest and most straightforward approaches to visitor count estimation, other estimation methods may be useful, particularly given the characteristics of the data. For example, maximum entropy estimators might offer an alternative means to estimate visitor numbers, particularly given the superior performance of these estimators in small sample datasets (Golan, Judge, and Miller). The authors are presently assessing the potential of maximum entropy visitor count estimators. Development of such alternative approaches is left for future analysis.
An Empirical Illustration
The visitor count model was applied to estimate the number of visitors to the principal Preservation Society of Newport County (PSNC) properties (mansion houses in Newport, Rhode Island), over the weekend of 7–8 September 2002. Data were drawn from surveys of visitors together with official gate counts from each site. Eight houses were incorporated in the analysis, including The Breakers, Breakers Stable, Marble House, The Elms, Chateau Sur Mer, Green Animals Topiary Garden, Kingscote, and Rosecliff. The Preservation Society maintains gate counts for each house, and also approximates the total number of visitors to all houses combined through a count of total ticket sales. Although this approximation over-counts visitors who purchase individual tickets at multiple houses (as opposed to purchasing a single multiple-house ticket), and does not distinguish visits by different groups (e.g., overnight visitors, day trippers), it does provide an approximate benchmark from which estimated visitor counts may be compared. Hence, the PSNC data provides an opportunity to both test and illustrate the proposed methodology.
Visitor surveys were conducted in proportion to the total gate count at each site, with an approximately equal number of visitors sampled during each day. Sampling was spread over the entire business day (i.e., the time that each house was open to the public). A total of 1162 complete and useable surveys were collected, with per-house samples ranging from 526 at the Breakers to 33 at Kingscote. The survey asked respondents to indicate (check off from a list) “which of the following mansions are you visiting today?” Answers provide data regarding individual sites visited by each respondent, and allow average visitation probabilities to be calculated for each site. Of the 1,162 visitors sampled, 781 reported visiting more than one PSNC property, preventing a simple summation of gate counts to estimate total visitor numbers. Respondents were also asked to indicate whether they were (a) Rhode Island residents and/or (b) staying overnight in Newport; allowing Newport day-trippers to be distinguished from non-resident overnight visitors. Visitation rates for each property and group are given by table 4.
Using visitor survey data and gate counts for each property, visitor counts for PSNC properties were estimated using the least squares and ML variants of the visitor count model. Results are reported in table 5. Compared to the PSNC ticket sales approximation of visitor numbers (3,922) for the same weekend, all least squares methods provide reasonable estimates (i.e., 3,642–3,764). The ML estimate (1,160), by comparison, appears unreasonably low. The difference between least squares estimates and the ticket sales approximation may be due to visitors who purchased multiple individual tickets at different houses (and were hence over-counted by the ticket sales approximation), rather than the standard and less expensive option of purchasing multiple-house tickets at a single booth. In this case, the least squares estimates might provide a more accurate illustration of actual visitor numbers, whereas the ticket sales approximation would provide upwardly biased results.
| OLS (Std. Error) | GLS (Std. Error) | WLS (Std. Error) | ML (Std. Error) | |
|---|---|---|---|---|
| Overnight visitors | 697 | 897 | 560 | 546 |
| (11367) | (9655) | (10034) | (2819) | |
| Day trippers/residents | 3067 | 2745 | 3143 | 614 |
| (14638) | (12278) | (13290) | (3562) | |
| Total visitors | 3764 | 3642 | 3702 | 1160 |
| (3563) | (2900) | (3547) | (826) |
The relatively poor performance of the ML estimator is likely due to the characteristics of available data. The estimated residual variance component of the likelihood function (A − BV)′Ω−1(A − BV) is close to zero for all the least squares estimators, yet is much larger for the ML estimator. It appears that the ML estimator sacrifices minimization of (A − BV)′Ω−1(A − BV) in order to obtain a smaller estimated value for I ln (|Ω|), the remaining component of the likelihood function. The ML estimator's difficulty in minimizing I ln (|Ω|), and hence the larger value of (A − BV)′Ω−1(A − BV), may be related to a violation of multivariate normality in the errors of site attendance equations.
The relatively large standard errors associated with estimates of overnight visitors and day trippers (table 5) is likely due to the highly correlated visitation patterns of the two groups; there is a 98.5% correlation between the visitation patterns of overnight visitors and those of residents/day trippers. This correlation reduces estimator efficiency, particularly with regard to estimates of the number of visitors in distinct groups. We expect that—on average—a greater divergence among the behavior of different visitor groups (i.e., less correlation) would reduce standard errors associated with estimates of visitor counts, particularly for specific visitor groups.
As found in the Monte Carlo analysis, the empirical application of the visitor count estimators suggests that the least squares estimators provide more accurate estimates of total visitor counts, despite the reduced variance of the ML estimator. However, unlike the reported Monte Carlo results, the empirical application illustrates a case in which the least squares estimators clearly outperform the ML estimator. Indeed, the ML estimator provides a visitor count estimate that appears to be less than half of the suspected true value, based on the best alternative approximation available (the PSNC ticket count).
Conclusions
The accuracy of visitor count estimates can have important implications for estimation of aggregate welfare estimates or other impacts of regional recreation. Without accurate visitor counts, even the most accurate estimates of per-visitor benefits cannot be extrapolated into meaningful aggregate benefit estimates. Errors in visitor counts will typically carry through to unknown and potentially substantial biases in aggregate estimates. The proposed recreational visitor count methods provide means to estimate visitor numbers in regions where direct counts of all visitors are intractable.
Data requirements for the proposed visitor count estimators are not trivial, but are in most cases obtainable. They include a sample of recreational sites of interest for which accurate visitation data may be obtained, and representative survey data including all visitor types. Visitor counts for particular sites may already be available for many recreational sites; for others it may be necessary to conduct on-site counts or compile existing attendance records, ticket sales or other data to obtain this information. Survey data need only cover a representative sample of visitors at each site; it is not necessary to obtain survey data for every visitor. The surveys must request at least two types of information: (a) information allowing researchers to distinguish among the different types of visitors, and (b) information regarding visitation to all sites.
The primary advantage of the proposed method is the ability to estimate total visitor numbers across multiple sites, where conditions prohibit a direct and accurate count. The alternatives often include estimates of visitor numbers based on ad hoc assumptions, attendance at a single site, or simple summation of attendance at a collection of sites (Smith). None of these alternatives will, in general, provide accurate results. In contrast, the presented methodology provides unbiased or at least consistent and asymptotically efficient estimates of regional visitors. Such estimates may be combined with the results of recreational demand models to provide more accurate estimates of the aggregate welfare implications of recreational activities.




