Multiple Reflections on Huygens' Principle
ABSTRACT
According to Huygens' principle, all points on a wave front act as secondary sources emitting spherical waves and the envelope of these spherical waves forms a new wave front. In the mathematical formulation of Huygens' principle, the waves emitted by the secondary sources are represented by Green's functions. In many present-day applications of Huygens' principle, these Green's functions are replaced by their time-reversed versions, thus forming a basis for backpropagation, imaging, inversion, seismic interferometry, etc. However, when the input wave field is available only on a single open boundary, this approach has its limitations. In particular, it does not properly account for multiply reflected waves. This is remedied by a modified form of Huygens' principle, in which the Green's functions are replaced by focusing functions. The modified Huygens' principle forms a basis for imaging, inverse scattering, monitoring of induced sources, etc., thereby properly taking multiply reflected waves into account.
1 Introduction
Dutch mathematician, physicist and astronomer Christiaan Huygens (1629–1695) described light as a longitudinal mechanical wave, propagating through an ether medium. Even though, centuries later, Maxwell proposed light as a transverse electromagnetic wave and Einstein showed that it does not need an ether to support its propagation, the early wave theoretical approach of Huygens appeared very effective in the analysis of the propagation and reflection of light. In his book Traité de la Lumière (Treatise on Light, published in 1690), he explains that around each undulating particle of the matter through which a wave propagates, a spherical wave is formed of which this particle is the centre. The common tangent (or envelope) of these spherical waves forms a new wave front. This is, in a nutshell, Huygens' principle, and it applies to light as well as to other wave phenomena. For an extensive discussion of the work of Huygens and his important role in bridging ancient and modern science, see Moser and Robinson (2024).
In the early nineteenth century, French physicist Augustin-Jean Fresnel (1788–1827) added the theory of interference to Huygens' principle. With this extension, the new wave front along the envelope of aforementioned spherical waves can be explained as the result of constructive interference of these spherical waves. In the following, when we speak of ‘Huygens’ principle', we mean the original theory of Huygens, extended with the theory of interference.
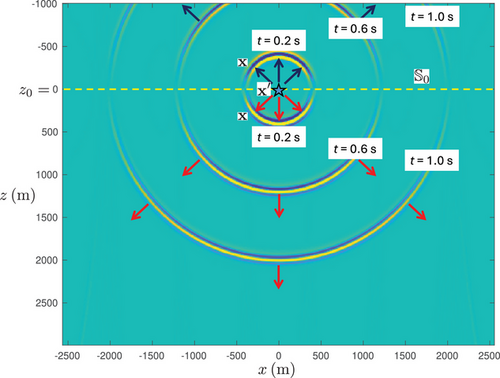
Figure 1 is an illustration of Huygens' principle, applied to acoustic waves. A point source, indicated by the red star, emits a circular wave which propagates through a medium with a constant propagation velocity (the example is in two dimensions; hence, instead of spherical waves, we have circular waves). At a certain time, this wave reaches a screen with a small opening (Figure 1a). The wave field in this opening acts as a secondary source, which emits a circular wave into the half-space above the screen. Figure 1b shows a similar setup, but this time the screen has many small openings, which all act as secondary sources, emitting circular waves at the time the original wave reaches these openings. Hence, the field above the screen consists of a superposition of circular waves. The envelope of these superposed waves approximately forms a circular wave, resembling the wave that would be radiated by the original point source into the upper half-space in the absence of the screen. In Figure 1c, the screen contains one large opening. All points in this opening act as secondary sources (indicated by the dense distribution of blue stars), and the superposition of the circular waves above the screen has indeed converged to the circular wave radiated by the original source.
Huygens' principle has found many applications in optics, acoustics and other fields in which wave propagation and scattering play a role. In this paper, we restrict ourselves to applications in acoustics and geophysics, in particular for wave field extrapolation. Traditionally, the waves emitted by the secondary sources in Huygens' principle are represented by Green's functions. In Section 2, we review applications of Huygens' principle in forward and inverse wave field extrapolation through homogeneous and inhomogeneous media. It appears that with the traditional Huygens' principle, internal multiply reflected waves are not correctly handled in inverse extrapolation through an inhomogeneous medium. In Section 3, we first introduce focusing functions for homogeneous and inhomogeneous media. Next, we discuss a modified version of Huygens' principle, in which the Green's functions are replaced by these focusing functions. We discuss applications of this modified Huygens' principle in forward and inverse wave field extrapolation through an inhomogeneous medium and in the retrieval of the homogeneous Green's function of an inhomogeneous medium. We show that internal multiply reflected waves are correctly handled in these applications.
The style of the main text is informal, with an emphasis on explanations of the different forms of Huygens' principle, using simple mathematics. More detailed derivations can be found in the Appendices.
2 Traditional Huygens' Principle, Using Green's Functions
2.1 Forward Wave Field Extrapolation Through a Homogeneous Medium
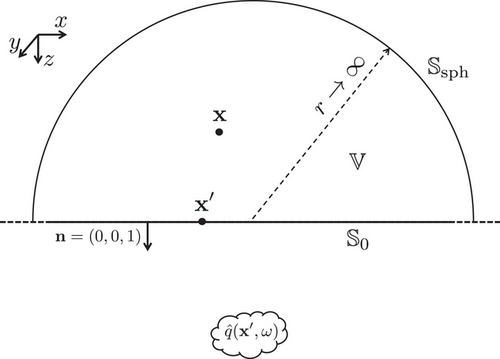
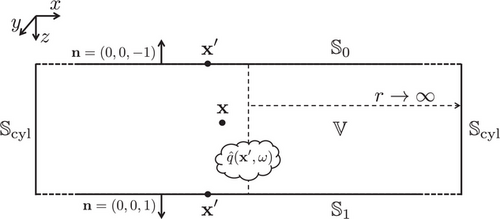
We discuss some mathematics behind Huygens' principle, as illustrated in Figure 1, and use this as a starting point for the discussion of forward wave field extrapolation. We define a Cartesian coordinate system, with the -axis pointing downward and the coordinate vector denoting position in this system. For the three-dimensional (3D) situation, this vector is defined as ; whereas most of the theory in this paper holds for three dimensions, the examples are in two dimensions, in which case the coordinate vector is defined as . Time is denoted by .
Huygens' wave-theoretical description of light was not immediately accepted. One of the reasons was that it does not explain why the secondary sources radiate only forward: if each point in a wave field acts as a secondary source, one would expect it to radiate in all directions (like the dipole source of the Green's function in Figure 2). Consequently, the envelope of the superposed waves of all secondary sources on a plane would consist of two contributions: one propagating forward, in the direction of the original wave, and one propagating backward, against the direction of the original wave. In the time of Huygens, it was not clear why the secondary sources do not give rise to this backward propagating wave. This was seen as a serious drawback of Huygens' wave-theoretical approach. Newton's competing theory (light consisting of particles moving along straight lines) did not have this drawback, but it had other shortcomings, such as not explaining diffraction and interference. All in all, Huygens' wave theory has withstood the test of time.
To understand why the secondary sources generate only the forward propagating wave, consider the Kirchhoff–Helmholtz integral in Equation (B8). This integral contains monopole and dipole Green's functions, driven by the particle velocity and acoustic pressure, respectively, at the horizontal boundary . Equation (B8) states that the combination of secondary monopole and dipole responses yields the forward propagating wave in the half-space above , whereas their contributions cancel in the half-space below . Moreover, for the homogeneous medium configuration of Figure 1, the secondary monopoles and dipoles give equal contributions to the wave field above , so one of the terms can be omitted and the other term doubled, yielding Equation (6) and explaining the factor 2 in this equation. Whereas Equation (B8) holds for at either side of , Equation (6) is only valid for above .
Huygens' principle was developed in the pre-Industrial age. At the time, it was merely meant to explain the physics of wave propagation. Technological developments in the 20th century enabled many other interesting applications of Huygens' principle. For example, in Equation (6), the wave field at can be replaced by electric signals that are fed to a dense array of piezoelectric transducers which emit ultrasound. Equation (6) then describes the synthesized wave field emitted by the array into the half-space above . On the other hand, digitized measurements of an acoustic or seismic wave field at can be fed to a computer and Equation (6) can be evaluated numerically to compute the wave field at any position in the half-space above . The latter application is wave field extrapolation (Berkhout 1985). In practice, the convolution along the time coordinate is often replaced by a multiplication in the frequency domain (see Equation B9), but for clarity we keep our expressions in the time domain because this appeals better to the physics of Huygens' principle.
2.2 Inverse Wave Field Extrapolation Through a Homogeneous Medium
Equations (11) and (12) are the basic expressions for inverse wave field extrapolation through a homogeneous lossless medium, as applied in acoustic and seismic imaging methods. They can be implemented in the space-time domain, as in Kirchhoff migration (Schneider 1978; Tygel et al. 2000) and reverse-time migration (Whitmore 1983; McMechan 1983), in the space-frequency domain, as in seismic inversion (Cohen et al. 1986) and seismic migration (Berkhout 1985), or in the wavenumber–frequency domain, as in migration with the phase-shift method (Gazdag 1978).
2.3 Inverse Wave Field Extrapolation Through an Inhomogeneous Medium
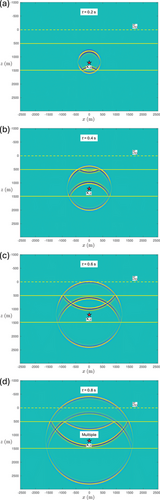
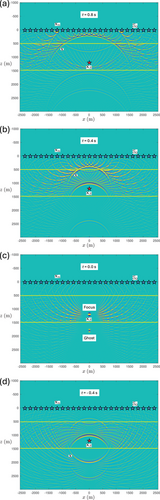
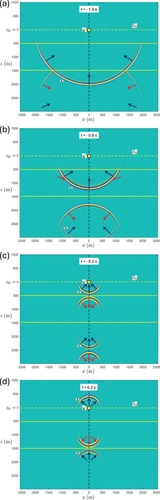
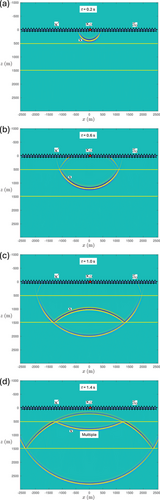
We discuss Huygens' principle for backpropagation through an inhomogeneous lossless medium. To show the essence, we consider for simplicity the horizontally layered medium of Figure 4, with interfaces (indicated by the yellow solid lines) at m and m. The propagation velocity is taken constant throughout at 2000 m/s. The mass density in the half-spaces m and m equals 1000 kg/m and in the layer m it equals 4000 kg/m . We place again a monopole source at m (indicated by the red star), between the two interfaces. The source function is again a Ricker wavelet with a central frequency of 20 Hz. We use a recursive ‘layer-code’ method (Kennett 1983) to model the response to this source. This response, , is shown in Figure 4a–d for s, s, s and s (note that the amplitudes along the wave fronts are again tapered at large propagation angles). The interfaces at m and m partially reflect and partially transmit the waves. Figure 4d shows the first multiply reflected wave.
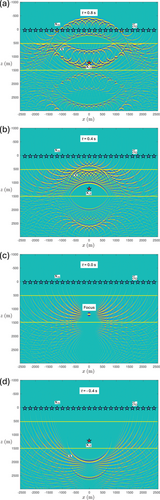
For the same layered medium, the dipole Green's function , for a dipole at on , is shown in Figure 5. Snapshots of this Green's function for s and s are shown in Figure 5a, whereas Figure 5b shows a snapshot for s, including the first multiply reflected event. Figure 5c is a cross section of along a vertical line through the dipole source, as a function of depth and time . The vertical dashed lines in this figure at s, s and s correspond to the vertical dashed lines in the snapshots in Figure 5a,b. The vertical solid line in Figure 5c at s indicates the causality condition, which states that is non-zero only after the source at (hence, right of this line). Figure 5d is a ray diagram of this dipole Green's function.
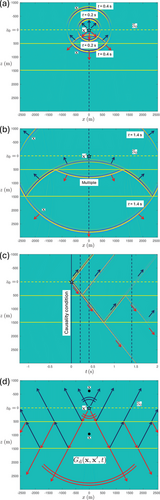
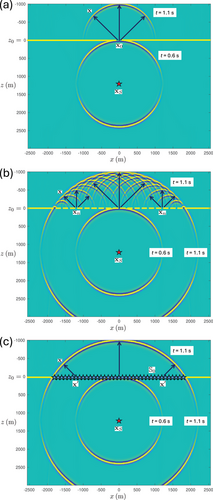
We use the time-reversal of the dipole Green's function of Figure 5 to backpropagate the acoustic pressure wave field of Figure 4 from to any point below . First, we use the discretized form of Huygens' principle, as formulated by Equation (9), with , m and . The results for s and s are shown in Figure 6a and 6b. Compare these figures with Figure 4d and 4b, which show the desired field at the same time instants. It appears that the envelopes of the superposed waves in Figure 6a,b resemble parts of the desired field, but significant parts are missing (in particular, the downgoing field in the lower half-space), the amplitudes of the reflected waves are too low, and circular ghost events appear in the lower half-space. Figure 6c shows for s. Apart from the focus on the position of the original point source, a ghost focus is formed below the second interface. Figure 6d shows for s. Clearly, does not vanish for negative times. The situation is more complex than in Figure 3, which is the result of applying Equation (9) in a homogeneous medium. In particular, reflected waves are not correctly backpropagated by the time-reversed dipole Green's function of the layered medium, despite the fact that primary and multiply reflected waves are included in this Green's function (see Figure 5).
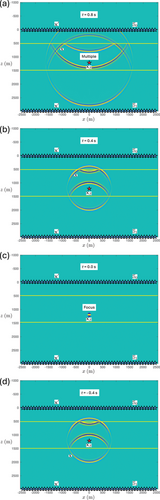
In most practical situations, measurements are available only at a single boundary, say , meaning that the second integral in Equation (14) cannot be evaluated. Hence, we are left with the integral along , as formulated by Equation (10), with defined in the inhomogeneous medium. Similar to a homogeneous medium, we can reformulate this again into Equation (11), which then describes approximate inverse extrapolation of upgoing waves from through an inhomogeneous medium, to below and above the source in the lower half-space. As we have seen above, this approximation does not properly handle multiply reflected waves, so it only accounts for primary waves. Moreover, even for these primary waves, amplitude errors occur, which are proportional to amplitudes of multiply reflected waves (see Wapenaar et al. 1989 for a detailed analysis). Despite these approximations, Equation (11), with the dipole Green's function defined in the inhomogeneous medium, forms the basis for many acoustic and seismic imaging schemes, including reverse time migration, time-reversed acoustics, etc. The approximations are acceptable as long as the contrasts in the medium are sufficiently small so that internal multiply reflected waves can be ignored. For situations in which internal multiply reflected waves cannot be ignored, other approaches are needed. One of these approaches is the replacement of the dipole Green's functions by focusing functions. This modification of Huygens' principle is the subject of the next section.
3 Modified Huygens' Principle, Using Focusing Functions
3.1 Introducing the Focusing Function
Huygens' principle, formalized by Kirchhoff, Rayleigh and others, accurately explains the physics of wave propagation. As we have seen, it can also be used for forward extrapolation of a wave field measured on a plane into a source-free half-space. This is formulated by Equation (6) and illustrated for a homogeneous upper half-space in Figure 1. When the upper half-space is inhomogeneous, Equation (6) still holds when the dipole Green's function is replaced by that of the inhomogeneous upper half-space (and the wave field at by its upgoing part). Hence, for these situations, there is no need to modify the mathematical formulation of Huygens' principle.
For inverse wave field extrapolation (i.e., extrapolation of a wave field measured on a plane into the half-space containing the source(s) of this wave field), the dipole Green's function is commonly replaced by its time-reversed version (see Equation 10). This is illustrated for a homogeneous lower half-space in Figure 3 and for an inhomogeneous lower half-space (using the time-reversed dipole Green's function of this inhomogeneous half-space) in Figure 6. In the latter case, inverse wave field extrapolation yields reasonable results for the primary waves but it breaks down for multiply reflected waves, even though these are included in the Green's functions.
Huygens' principle was meant to explain the physics of wave propagation, so the fact that it has limitations for inverse wave field extrapolation is not a shortcoming of this principle in itself. Nevertheless, it is worthwhile to modify Huygens' principle for inverse wave field extrapolation, in such a way that it accounts for multiply reflected waves. To address this, in this section, we replace the dipole Green's functions by focusing functions and, hence, the dipole sources by focal points. In previous work on the Marchenko method, we introduced two types of focusing functions: , which has a focal point inside the inhomogeneous medium, and , with its focal point at the boundary between the inhomogeneous lower half-space and the homogeneous upper half-space (Wapenaar et al. 2014). Since the dipole Green's functions in Huygens' principle have their sources at the boundary , we choose for focusing functions with their focal points at . Hence, the focusing function we discuss below is akin to the focusing function . However, it is normalized in a different way. Moreover, whereas is defined in a truncated version of the actual medium, the focusing function is defined in the actual medium and it is not decomposed into downgoing and upgoing components inside the medium. Before we discuss this focusing function in an inhomogeneous medium, we start with discussing the focusing function in a homogeneous medium.
3.2 Focusing Function in a Homogeneous Medium
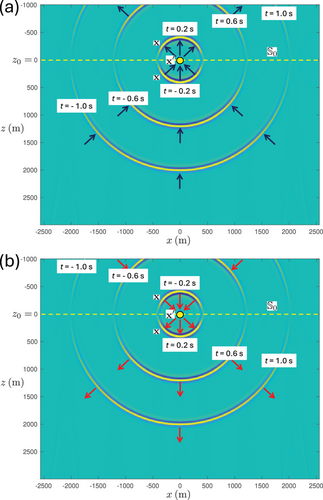
We define the focusing function for a homogeneous lossless medium as an upward propagating wave field, of which the wave fronts are half-spheres (in three dimensions) or half-circles (in two dimensions) centred at on (at depth ) (see Figure 8a for the 2D situation). At negative times, the focusing function propagates (as a function of and ) upward through the lower half-space towards , at it focuses at on , and at positive times it propagates upward through the upper half-space away from . The time-reversed focusing function , illustrated in Figure 8b for the 2D situation, propagates at negative times downward through the upper half-space towards , at it focuses at on , and at positive times it propagates downward through the lower half-space away from .
By introducing the focusing function and its time-reversal, we achieved that the four equations for forward and inverse extrapolation of upgoing and downgoing waves through a homogeneous medium (Equations 7-11 and 12) are now captured by the two Equations (21) and (22). These equations formulate modified versions of Huygens' principle for a homogeneous medium. Figures 1 and 3 can be seen as examples of Equation (21) for above and below , respectively. For a homogeneous medium, there are no further advantages of using the focusing functions instead of the dipole Green's functions. This changes considerably for an inhomogeneous medium.
3.3 Focusing Function in an Inhomogeneous Medium
We consider a medium which is inhomogeneous below the boundary (at depth ), with propagation velocity and mass density . At and above this boundary, we assume that the medium is homogeneous, with propagation velocity and mass density . For this configuration, we define the focusing function , with again denoting a focal point at (hence, ). Throughout space, obeys the source-free acoustic wave equation, with the condition that at it obeys the focusing condition, formulated by Equation (20), and that at and above it propagates upward. Hence, at and above this focusing function is the same as that for a homogeneous medium, discussed in the previous section; below , it is of course different. Assuming the medium is lossless throughout space, the time-reversed focusing function obeys the same source-free wave equation as . At and above , this time-reversed focusing function propagates downward.
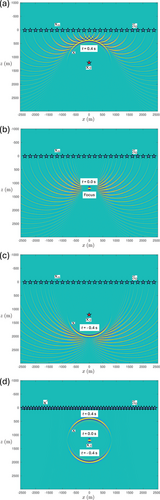
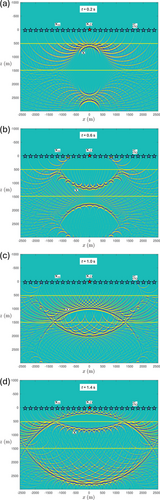
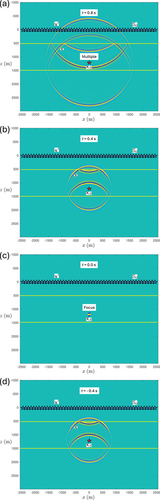
We illustrate for the same layered medium as used for previous examples. Figure 9a–d shows snapshots at times s, s, s and s, respectively. Figure 10a,b shows cross sections of , and of its time-reversed version , along a vertical line through the focal point, as a function of depth and time . The vertical dashed lines in Figure 10a at s, s, s and s correspond to the vertical dashed lines in the snapshots in Figure 9a–d. Figure 10c,d shows ray diagrams of and . From these figures, we observe that the focusing function starts with upgoing waves in the half-space below the deepest interface, which are tuned in such a way that, after interaction at the interfaces, a single upgoing wave converges to the focal point (Figures 9c and 10c), focuses at and and continues as a single upgoing wave, diverging from the focal point (Figures 9d and 10c).
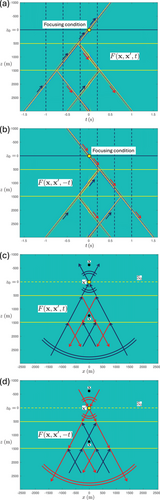
Note the different character of the focusing function in Figures 9 and 10 in comparison with the dipole Green's function in Figure 5. Whereas the dipole Green's function obeys a causality condition related to the source at , indicated by the vertical solid line in Figure 5c, the focusing function obeys a focusing condition at , indicated by the horizontal solid lines in Figure 10a,b. Conversely, the focusing function is not causal (it exists at negative and positive times; see Figure 10a), whereas the dipole Green's function does not focus at (it contains multiple upgoing events at ; see Figure 5c,d).
3.4 Modified Huygens' Principle for an Inhomogeneous Medium
We now discuss how the focusing functions and can replace the dipole Green's functions and in Huygens' principle for an inhomogeneous medium. Recall that we assume that the medium at and above the boundary is homogeneous, with propagation velocity and mass density . This means that in the upper half-space we can handle downgoing and upgoing waves independently of each other. On the other hand, the medium below is inhomogeneous with propagation velocity and mass density . Although in inhomogeneous media, decomposition into downgoing and upgoing waves is often possible locally, in the following analysis we will not make use of this, so in the lower half-space we will consider the total wave field. For the moment, we will assume that the entire medium (at, above and below ) is source-free for the wave field . Hence, obeys the wave equation (with defined in Equation (A2)) in the entire medium. The focusing functions and obey the same source-free wave equation.
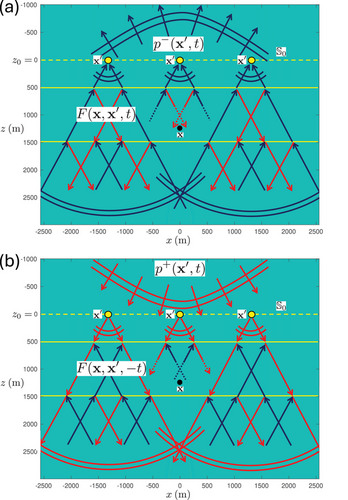
Equation (23) formulates the modified Huygens' principle for an inhomogeneous medium. The two terms on the right-hand side are illustrated with ray diagrams in Figure 11 for below . First, consider Figure 11b. A downgoing wave field is incident from above to the inhomogeneous lower half-space. For each on , it is convolved with the time-reversed focusing function . The integral over all on , as formulated in the second term on the right-hand side of Equation (23), extrapolates the field from into the lower half-space. Since the focusing function implicitly consists of a superposition of downgoing and upgoing waves in the lower half-space (the red and blue rays in Figure 11b), the result of this integral is not the forward extrapolated downgoing field in the lower half-space (unlike in the homogeneous medium situation, as formulated by Equation 22). Next, we consider Figure 11a. Here, the upgoing field is convolved with the focusing function for all on . The integral over all on (the first term on the right-hand side of Equation 23) extrapolates the field from into the lower half-space. For similar reasons as above, this is not the inverse extrapolated upgoing field in the lower half-space. However, the superposition of the two integrals, as formulated by Equation (23), yields the total wave field in the lower half-space, including all internal multiply reflected waves. In comparison with Equation (14), where the two integrals are taken over two different boundaries, in Equation (23) the two integrals are taken over one and the same boundary. Hence, this makes Equation (23) very useful for practical situations in which a medium is often accessible from one side only, such as in the seismic reflection method. The focusing function can be retrieved from the reflection response, acquired at the same boundary, using the Marchenko method for 1D, 2D or 3D inhomogeneous media (Broggini and Snieder 2012; Wapenaar et al. 2014; Slob et al. 2014; Van der Neut et al. 2015; Meles et al. 2015). In most papers on the Marchenko method, it is assumed that the wave field and focusing functions inside the medium can be decomposed into downgoing and upgoing components. This decomposition is avoided in Equation (23), which opens the way to handle refracted and evanescent waves (Wapenaar et al. 2021; Diekmann and Vasconcelos 2021). A further discussion of the Marchenko method is beyond the scope of this paper. In the next sections, we indicate applications of Equation (23), assuming the focusing function is known (either from numerical modelling or from applying the Marchenko method to the reflection response).
3.5 Simultaneous Forward and Inverse Wave Field Extrapolation Through an Inhomogeneous Medium
Extrapolation of reflection data with focusing functions finds applications in acoustic and seismic imaging schemes, accounting for internal multiply reflected waves (Ravasi et al. 2016; Jia et al. 2018; Staring and Wapenaar 2020; Brackenhoff et al. 2022). In those applications, the focusing functions are obtained with the Marchenko method from numerically modelled or field reflection responses of 2D and 3D inhomogeneous media. The focal points of those focusing functions are inside the medium, but, as long as evanescent waves can be neglected, they are straightforwardly related to focusing functions with their focal points at (Wapenaar et al. 2014).
3.6 Retrieval of the Homogeneous Green's Function in an Inhomogeneous Medium
Retrieval of the homogeneous Green's function from wave field observations at a single boundary finds applications in holographic imaging and inverse scattering (Wapenaar et al. 2016; Diekmann and Vasconcelos 2021) and in monitoring of induced acoustic (Van der Neut et al. 2017) and seismic sources (Brackenhoff et al. 2019). In those applications, the focusing functions are obtained with the Marchenko method from numerically modelled or field reflection responses of 2D inhomogeneous media.
4 Conclusions
Huygens' principle stands as a milestone in the history of wave theory. Originally formulated to explain the propagation of light, it has found many applications in optics, acoustics, geophysics, etc. Central in the mathematical formulation of Huygens' principle, due to 19th century physicists Fresnel, Kirchhoff, Helmholtz, Rayleigh and others, is the Green's function, which formalizes the responses to the secondary sources in Huygens' principle. Many of the present-day applications of Huygens' principle use time-reversed Green's functions. These time-reversed Green's functions are acausal and as such do not describe physical responses to secondary sources. However, they play a fundamental role in algorithms for backpropagation, imaging, inversion, seismic interferometry, etc.
We have demonstrated with numerical examples that the traditional Huygens' principle with time-reversed Green's functions has limitations when the medium is inhomogeneous. In particular, when measurements are available only at a single boundary, internal multiply reflected waves are incorrectly handled. To remedy this, Huygens' principle has been modified by replacing the Green's functions by focusing functions. For a homogeneous medium, this replacement does not make much difference but for an inhomogeneous medium the improvement is considerable. Using the modified Huygens' principle with focusing functions, the limitations of the traditional Huygens' principle with time-reversed Green's functions are evaded. This has been demonstrated with numerical examples for a simple horizontally layered medium, but note that the modified principle holds for an arbitrary inhomogeneous medium. The only assumption is that evanescent waves can be ignored at the boundary. No assumptions are made about up-down decomposition inside the inhomogeneous lower half-space.
Similar to the time-reversed Green's functions in Huygens' principle, the focusing functions in the modified Huygens' principle do not describe physical responses to secondary sources. However, they play an important role in novel algorithms for acoustic and seismic imaging and inverse scattering, for monitoring of induced acoustic and seismic sources, etc. In all these cases, the focusing functions can be obtained from the reflection response with the Marchenko method, taking internal multiply reflected waves properly into account.
Appendix A: Monopole and Dipole Green's Functions
A.1 Monopole Green's Function
A.2 Homogeneous Green's Function
A.3 Dipole Green's Function
Appendix B: Forward Wave Field Extrapolation
Appendix C: Inverse Wave Field Extrapolation
Appendix D: Extrapolation With Focusing Functions
Open Research
Data Availability Statement
Animations associated with the figures in this paper are available and can be accessed via the following URL https://gitlab.com/geophysicsdelft/OpenSource in the directory …/huygens




