Homotopy scattering series for seismic forward modelling with variable density and velocity
ABSTRACT
We have derived a convergent scattering series solution for the frequency-domain wave equation in acoustic media with variable density and velocity. The convergent scattering series solution is based on the homotopy analysis of a vectorial integral equation of the Lippmann–Schwinger type. By using the Green's function and partial integration, we have derived the vectorial integral equation of the Lippmann–Schwinger type that involves the pressure gradient field as well as the pressure field from the wave equation. The vectorial Lippmann–Schwinger equation can in principle be solved via matrix inversion, but the computational cost of matrix inversion scales like , where is the number of grid blocks. The computational cost can be significantly reduced if one solves the vectorial Lippmann–Schwinger equation iteratively. A simple iterative solution is the Born series, but it is only convergent when the scattering potential is sufficiently small. In this study, we have used the so-called homotopy analysis method to derive an iterative solution for the vectorial Lippmann–Schwinger equation which can be made convergent even in strongly scattering media. The computational cost of our convergent scattering series scales as . Our algorithm, which is based on the homotopy analysis method, involves a convergence control operator that we select using hierarchical matrices. We use a three-layer model and a resampled version of the SEG/EAGE salt model to show the performance of the developed convergent scattering series.
INTRODUCTION
The integral equation method is one of the most valuable methods in seismic forward modelling and inversion (Aki and Richards, 1980; Van Den Berg and Kleinman, 1997; Carcione et al., 2002; Abubakar et al., 2003; Innanen, 2009; Jakobsen, 2012; Jakobsen and Ursin, 2015; Malovichko et al., 2018; Huang et al., 2020). It considers the total wavefield in the actual medium as a superposition of a background wavefield and a scattering wavefield. The background wavefield and the scattering wavefield are found from the integral representations in terms of the Green's function and the actual and virtual source. The virtual source is caused by the contrast between the actual medium and the background medium. If the contrast part is compact enough, the computation will be accelerated. Although the integral equation system matrix is relatively small due to the compact contrast part, it is still a full matrix. If we implement it through matrix inversion, it will cause a relatively high memory demand and computational burden (Jakobsen and Wu, 2018), especially when the model is a large-scale model. This fact leads researchers to use iterative methods based on scattering series solutions instead of direct matrix inversion for solving the integral equation. One of the most well-known series solutions in the geophysical community is the Born series solution (Morse and Feshbach, 1954). However, the conventional Born series is only guaranteed to converge when the contrast or the scattering potential of the model is relatively small (Jakobsen and Ursin, 2015; Osnabrugge et al., 2016). Therefore, a lot of effort has been devoted to solving the divergence problem of the Born series in the presence of strong contrasts. Zhdanov and Fang (1997) have generalized the Born series by using the higher order quasi-linear approximations to ensure the modified series converge to the true solution. Osnabrugge et al. (2016) have modified the Born series to converge for high scattering potentials by introducing a pre-conditioner and an auxiliary parameter to localize the energy of the Green's function. Jakobsen and Wu (2016) have replaced the Born series with a convergent renormalized scattering series by utilizing the leading De Wolf approximation. By using the modified volume integral equation proposed by Bonnet and others (2017), Abhishek et al. (2020) have developed a modified Born series, that is unconditionally convergent, for the forward and inverse scattering problem.
All the methods mentioned above assume that the density is constant. But in fact density plays an important role in the amplitude of the wavefield. If we only consider the velocity in wavefield forward modelling when density varies in reality, the synthetic seismic wavefield will not match the observed wavefield well, which may cause serious artefacts in the full waveform inversion (Virieux and Operto, 2009). Many forward modelling methods, most of them for the ultrasound imaging, have been developed with variable density (Kwon and Jeong, 1998; Lavarello and Oelze, 2009; Mojabi and LoVetri, 2015; Rao et al., 2020). In recent years, some studies about integral equation methods for seismic forward modelling with variable density have been considered in several publications (Yang et al., 2016; Yao et al., 2016; Sun et al., 2017; Jiménez et al., 2018; Luo and Wu, 2018; Farshad and Chauris, 2020). Although these studies have been developed, there is still an important need to develop more accurate and efficient methods for seismic forward modelling with variable density. Therefore, in this study, we present a new integral equation scheme applicable in the case of variable density and velocity.
Unlike other seismic forward modelling methods that include density and velocity, we have derived two coupled integral equations and combined them into a vectorial Lippmann–Schwinger (LS) equation. Because there are already many methods for solving the LS equation (Jakobsen and Ursin, 2015; Jakobsen and Wu, 2016; Eftekhar et al., 2018; Huang et al., 2020; Eikrem et al., 2020), we may use those methods to solve the vectorial LS equation. This is our main motivation to extend the previous methods to the variable velocity and density case. Because of the introduction of the density term, the scattering potential involving two parameters in the vectorial LS equation becomes complicated. It is necessary to further develop a convergent scattering series solution for the vectorial LS equation due to the strong scattering potential. In this study, we use the homotopy analysis method developed by Liao (1997, 2003), and Liao and Tan (2007) to solve the vectorial LS equation. There have been many successful applications of the homotopy techniques in geophysics. Keller and Perozzi (1983) introduced continuation in their methods for fast seismic ray tracing. Hanyga and Pajchel (1995) further explored homotopy methods in complicated models. Allgower and Georg (1990) give an introduction to numerical homotopy methods. Huang and Greenhalgh (2018) used the modern homotopy analysis method (Liao, 2003) to solve anisotropic eikonal equation for traveltime approximations. Jakobsen et al. (2020) have proposed a convergent scattering series solution of the scalar LS equation through the homotopy analysis method. Jakobsen et al. (2020) have compared convergence performance of different scattering series derived from homotopy continuation method and renormalization group. Previously, Jakobsen et al. (2020) have concluded that the scattering series solution is guaranteed to converge in fixed density case by introducing a suitable convergence control operator. In the present study, we modify the homotopy analysis method in Jakobsen et al. (2020) to solve the vectorial LS equation. Due to the strong scattering potential in the vectorial LS equation, the simple convergence control operator given in Jakobsen et al. (2020) cannot ensure that the scattering series converges. So we introduced another convergence control operator developed by Eikrem et al. (2020) based on the matrix low rank approximation (Halko et al., 2011) and the hierarchical matrix (Börm et al., 2003). In Eikrem et al. (2020), they mainly focus on the convergence control operator for the scalar LS equation. In this study, we developed a new convergence control operator for the vectorial LS equation based on Eikrem et al. (2020) by constructing hierarchical matrices for different blocks of the full matrix. In principle, if we choose the parameters related to the convergence control operator properly, the homotopy scattering series will converge.
This paper is structured as follows. First we transform the wave equation for acoustic medium into the vectorial integral equation of the LS type. Then we discuss the reference solution from matrix inversion as well as the conventional Born series solution. Next we give a description of the homotopy analysis method and derive the convergent homotopy series solution. Finally we use numerical examples to demonstrate the performance of the proposed method, compare it with the conventional Born series and give the concluding remarks. The formulation of two-dimensional and three-dimensional acoustic Green's functions and their spatial derivatives are given in Appendices A and B.
THEORY
The vectorial Lippmann–Schwinger equation
Matrix representation of the vectorial LS equation
The Born series iteration
Homotopy analysis method for the vectorial LS equation
The main difference between the Born series (19) and the homotopy series (27) is the introduction of the convergence control operator , which makes the homotopy scattering series more flexible in convergence than the conventional Born series.
The construction of by hierarchical matrices
In order to find a suitable , we adopt the method based on matrix low-rank approximation and hierarchical matrix proposed by Eikrem et al. (2020). The key idea of this method is to find an to make the spectral radius as close to 0 as possible, so as to ensure that the homotopy scattering series converges. When we set in equation (25), we obtain . It can be seen that if approximates , then and . Next we will use the hierarchical matrices to approximate and find the approximation of its inverse.
NUMERICAL EXAMPLES
| The three-layer model | The resampled SEG/EAGE salt model | |||||
|---|---|---|---|---|---|---|
| Frequency | 5 Hz | 20 Hz | 40 Hz | 5 Hz | 20 Hz | 40 Hz |
| Level | 4 | 4 | 3 | 4 | 3 | 3 |
| Rank 1 | 10 | 20 | 60 | 10 | 60 | 120 |
| Rank 2 | 5 | 10 | 30 | 5 | 30 | 120 |
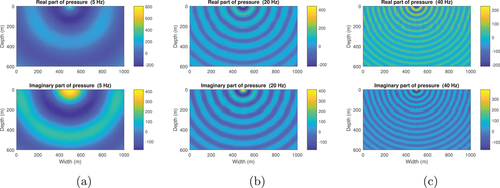
- 1. The wavefields from the homotopy series matches well with the reference wavefields at all frequencies;
- 2. The Born series only converges at very low frequencies;
- 3. The homotopy series still converges when the Born series diverges;

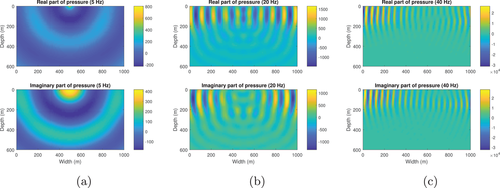
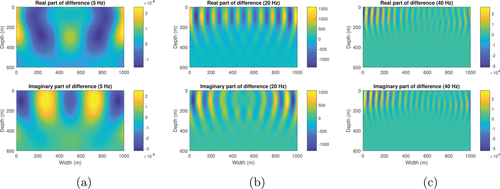
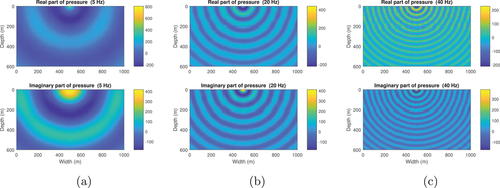
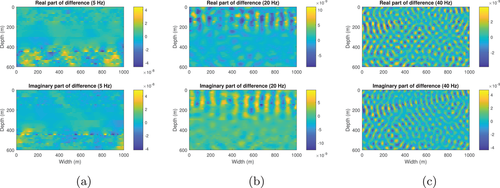
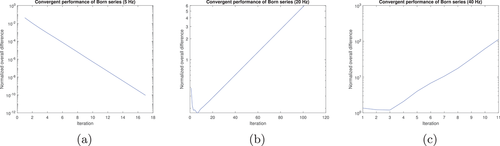
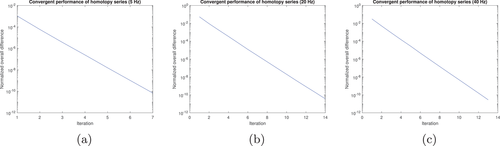
Next we calculate the wavefield in the resampled SEG/EAGE salt model (Fig. 11). The density of this model (Fig. 11b, upper) apart from the salt dome portion is obtained from velocity (Fig. 11a, upper) by Gardner's relation: (Gardner et al., 1974). The density of the salt dome portion is set equal to the density of halite, which is 2160 kg/m (Mavko et al., 2009). The size of this model is 1390 m wide and 740 m deep. The grid size of each discrete point is 10 m 10 m. The number of grid blocks is . Figure 12 shows the reference wavefield obtained via matrix inversion at different frequencies. Figures 13 and 15 show the wavefield at different frequencies via the Born series and the homotopy series. Figure 14 and 16 show the differences for Born and homotopy series at different frequencies. Figures 17 and 18 present the convergence performance of the Born series and the homotopy series. Clearly, we see that the wavefield from homotopy series is similar to the reference wavefield and the normalized overall difference becomes very small after up to 45 iterations while the wavefield produced using the Born series is totally different from the reference wavefield, and the normalized overall difference diverges in all frequencies.
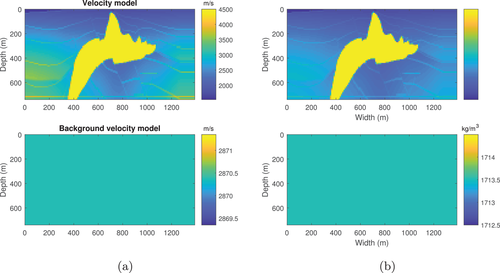
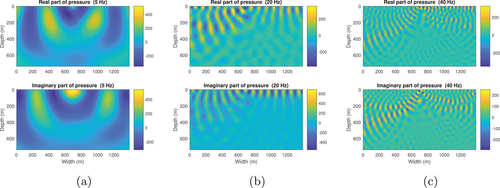
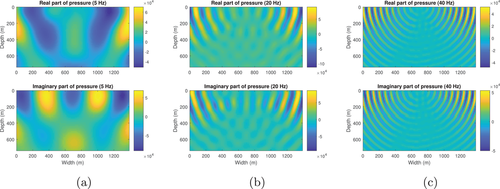
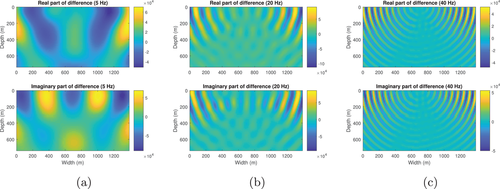
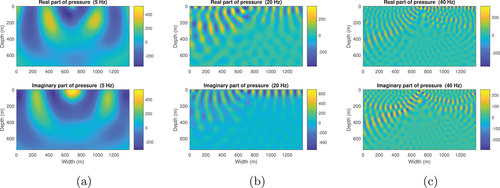
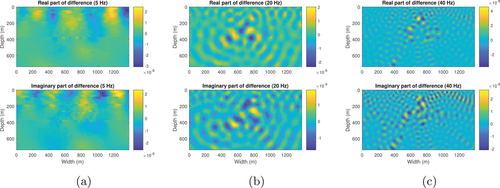
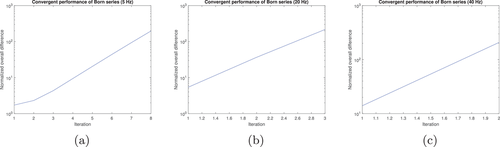
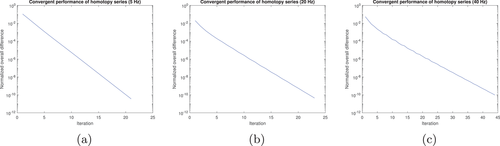
Table 2 shows the computational time of different method for different models and frequencies. From Table 2, we see: (1) Matrix inversion is the most time-consuming method; (2) In the case of convergence, Born series is the least time-consuming; (3) Born series only converges at low frequencies in low contrast model; That is because even if the contrast of density or the bulk modulus is very small, putting them together will make the entire contrast arise; (4) Homotopy series not only guarantees convergence in all cases, it also takes much less time than matrix inversion; (5) The larger the model, the more time homotopy series saves compared to matrix inversion. All experiments are performed on an computer with an Intel i7-7700, a 3.6 GHz CPU and a 64 GB RAM.
| The three-layer model | The resampled SEG/EAGE salt model | |||||
|---|---|---|---|---|---|---|
| Frequency | 5 Hz | 20 Hz | 40 Hz | 5 Hz | 20 Hz | 40 Hz |
| Matrix inversion | 111 s | 117 s | 111 s | 589 s | 675 s | 606 s |
| Born series | 8 s | diverge | diverge | diverge | diverge | diverge |
| Homotopy series | 23 s | 30 s | 43 s | 77 s | 145 s | 227 s |
CONCLUSIONS
We have derived a vectorial integral equation of the Lippmann-Schwinger (LS) type for seismic forward modelling in acoustic medium with variable velocity and density. This vectorial LS equation is derived from two coupled integral equations. In order to solve it efficiently, we have introduced the homotopy analysis method. The homotopy series is obtained after solving the vectorial LS equation with the homotopy analysis method. It is more flexible than the conventional Born series due to the introduction of the convergence control operator . We have analysed that if approximates , the homotopy series will converge. Based on this, we constructed the convergence control operator by using low-rank matrix approximation and hierarchical matrices.
On the basis of the numerical experiments, we have compared the performance of homotopy series with conventional Born series and matrix inversion. Compared with the conventional Born series, the corresponding homotopy series assures convergence in high contrast media and for high frequencies. Compared with matrix inversion, the homotopy series reduces the scale of computational cost from to , where is the number of grid blocks. Numerical examples also show that the larger the model, the more computational time is reduced. This makes our approach suitable for the application of realistic large problems.
This paper mainly focuses on providing a new perspective for seismic forward modelling with variable density and velocity. In future work, an investigation of the optimal form of the hierarchical matrices for constructing convergence control operators as well as the use of Fast Fourier Transform in the construction of the hierarchical matrices (Eikrem et al., 2020) should be included. Also, it might be interesting to use the vectorial LS equation and its homotopy series solution for simultaneous inversion of velocity and density.
ACKNOWLEDGEMENTS
The authors acknowledge the China Scholarship Council for the financial support for Kui Xiang study in Norway. Eikrem, Nævdal and Jakobsen would like to acknowledge the Research Council of Norway (RCN) for the Petromaks II project 267769 (Bayesian inversion of 4D seismic waveform data for quantitative integration with production data) and the National IOR Centre of Norway and its industrial partners, ConocoPhillips Skandinavia AS, Aker BP ASA, Vår Energi AS, Equinor ASA, Neptune Energy Norge AS, Lundin Norway AS, Halliburton AS, Schlumberger Norge AS and Wintershall DEA for support. We are also very grateful to the reviewers and editors for their effort and patience in reviewing this manuscript.
APPENDIX
3D GREEN'S FUNCTION AND ITS SPATIAL DERIVATIVES
2D GREEN'S FUNCTION AND ITS SPATIAL DERIVATIVES
Open Research
DATA AVAILABILITY STATEMENT
The data that support this study are available from the corresponding author on reasonable request.




