Influence of subsurface injection on time-lapse seismic: laboratory studies at seismic and ultrasonic frequencies
ABSTRACT
Seismic monitoring of reservoir and overburden performance during subsurface CO2 storage plays a key role in ensuring efficiency and safety. Proper interpretation of monitoring data requires knowledge about the rock physical phenomena occurring in the subsurface formations. This work focuses on rock stiffness and elastic velocity changes of a shale overburden formation caused by both reservoir inflation induced stress changes and leakage of CO2 into the overburden. In laboratory experiments, Pierre shale I core plugs were loaded along the stress path representative for the in situ stress changes experienced by caprock during reservoir inflation. Tests were carried out in a triaxial compaction cell combining three measurement techniques and permitting for determination of (i) ultrasonic velocities, (ii) quasistatic rock deformations, and (iii) dynamic elastic stiffness at seismic frequencies within a single test, which allowed to quantify effects of seismic dispersion. In addition, fluid substitution effects connected with possible CO2 leakage into the caprock formation were modelled by the modified anisotropic Gassmann model. Results of this work indicate that (i) stress sensitivity of Pierre shale I is frequency dependent; (ii) reservoir inflation leads to the increase of the overburden Young's modulus and Poisson's ratio; (iii) in situ stress changes mostly affect the P-wave velocities; (iv) small leakage of the CO2 into the overburden may lead to the velocity changes, which are comparable with one associated with geomechanical influence; (v) non-elastic effects increase stress sensitivity of an acoustic waves; (iv) and both geomechanical and fluid substitution effects would create significant time shifts, which should be detectable by time-lapse seismic.
1 INTRODUCTION
In order to ensure safety, efficiency, and optimization of field operations, proper monitoring technique, as well as correct interpretation of monitoring data, is needed. During injection of fluid into a reservoir (e.g., CO2 for storage or enhanced oil recovery), time-lapse seismic (4D) is a proven technology used for monitoring purposes. Most of the monitoring surveys and associated laboratory investigations concentrate on time shifts connected with saturation, pore pressure, and stress changes in the reservoir (e.g., Landrø et al. 2003; Meadows 2008; Lumley 2010). However, it has been recognized that true shifts caused by stress and strain changes in the overburden can also give valuable information about deformations of both reservoir and caprock (e.g., Kenter et al. 2004; Hatchell and Bourne 2005; Barkved and Kristiansen 2005). Field case studies performed by Duffaut and Landrø (2007) have shown that the 4D time shifts observed in a real case are hard to describe by a single dominant factor and that proper interpretation of surveys requires consideration of many possible aspects. It is therefore important to understand how temperature, in situ stress conditions, and fluid distribution/substitution influence the elastic velocities of both reservoir and overburden formations. Holt and Stenebråten (2013) performed a series of ultrasonic tests in which artificially manufactured rock samples, representative for some types of a storage rock and a caprock, were exposed to stress changes characteristic of reservoir and overburden in situ conditions during reservoir depletion and inflation. Their work indicated significant velocity changes in both formations, as well as possible yield of the overburden caused by associated stress changes. Holt and Stenebråten (2013) also showed that the effects of fluid substitution (in a reservoir) and stress/strain changes on the velocities may have comparable magnitudes and would be hard to distinguish during seismic data interpretation. However, as pointed out by the authors, the use of synthetic analogues can be challenged. Further, dispersion is observed in several fluid-saturated rocks (e.g., Winkler and Nur 1979; Johnston and Christensen 1995; Wang 2002; Batzle et al. 2005; Duranti, Ewy and Hofmann 2005; Batzle, Han and Hofmann 2006; Mikhaltsevitch, Lebedev and Gurevich 2014; Pimienta, Fortin and Gueguen 2015), which may cause different stress sensitivity at seismic frequencies compared with ultrasonic frequencies (Mavko and Vanorio 2010). Therefore, further examination of the problem is required.
In this work, we report on laboratory experiments in which Pierre shale I, mimicking caprock, was exposed to a generic stress path that might be representative of overburden in situ conditions during injection into a reservoir beneath it. The experiments were performed in a set-up allowing for combined measurements of quasistatic rock deformations, ultrasonic velocities, and dynamic elastic stiffness at seismic frequencies, with applied pore pressure and deviatoric stresses. The primary objective of this paper is to contribute to the understanding of elastic velocity changes in the overburden formation under reservoir inflation. However, parallel-performed multi-frequency tests, combined with static experiments, allow to identify the influence of the seismic dispersion on stress sensitivity, as well as permits to recognize possible factors behind differences between static and dynamic properties of rocks. After a short description of the used material and the applied laboratory techniques, we present experimental results focusing on the stress sensitivity of (i) dynamic and static rock mechanical parameters (Young's modulus and Poisson's ratio) and (ii) seismic and ultrasonic P-wave and S-wave velocities. We also model possible fluid substitution effects (within the overburden) with the use of the modified anisotropic Gassmann model, accounting for adsorption and capillary-pressure effects observed in shales (Szewczyk, Bauer and Holt 2018b).
2 MATERIALS AND METHODS
2.1 Pierre shale
Laboratory tests were conducted on a Pierre shale I core plug with a diameter of 1 in. and a length of 2 in. Pierre shale I used in this work is an outcrop shale from North Dakota; it exhibits transverse isotropy (TI) (e.g., Islam and Skalle 2013) and is considered as an analogue for some overburden formations. Tested core plugs were drilled from outcrop material preserved in oil at 0o angle of inclination with respect to the symmetry axis. X-ray diffraction (XRD) data show that the studied batch contains about 48 wt% clays, 44 wt% silicates (27 wt% quartz), and around 6 wt% of carbonates. Due to the short sample consolidation time (strain measurements shows that, while exposing the core plugs to brine under stress, the strains stabilize within ̴ 53 hours), as-received material is considered as nearly fully saturated. The porosity of the tested sample was not determined directly; however, based on the measured bulk density of as-received material and mineral density of its composites (taken from XRD test), we have estimated a porosity of 16% ± 1%. This result is in good agreement with data reported in the literature ( ̴ 10%–25% porosity) (e.g., Schultz et al. 1980; Olgaard, Nuesch and Urai 1995; Holt et al. 2015).
2.2 Experimental set-up
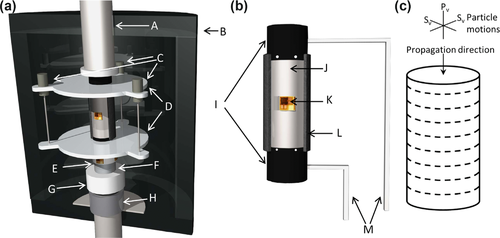
The experiments were carried out in a low frequency apparatus at the Formation Physics Laboratory of SINTEF Petroleum Research. The apparatus combines three measuring techniques that allow for determination of ultrasonic velocities, quasistatic rock deformations, and dynamic elastic stiffness at seismic frequencies under deviatoric stresses, within a single test. Design of the apparatus, together with an in-house-developed strain gauge fitting/sample mounting procedure, allows for sealing of the core plugs within ̴ 1 hour after removing them from preservation oil, thus most likely providing maintenance of their initial state. A schematic illustration of the experimental set-up is shown in Fig. 1.
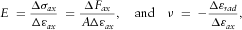 (1)
(1)
2.3 Experimental conditions
According to the linear elastic nucleus of strain model introduced by Geertsma (1973), for an isotropic homogenous sub-surface, the mean stress remains constant in the overburden during reservoir depletion or inflation (constant mean stress (CMS) loading). This implies that the overburden above the centre of the reservoir will experience a decrease in horizontal stress and increase in vertical stress, as a response to injection into a reservoir. At the edge of the storage site, the response is opposite, i.e., an increase in horizontal stress and a decrease in vertical stress. In order to simulate those effects, we have performed an experiment in which a Pierre shale core plug was loaded according to the idealized stress path characteristic for caprock above the centre of a reservoir (Fig. 2(i)). First, the sample was loaded hydrostatically to a 5 MPa confining pressure. Next, confining pressure, axial stress, and pore pressure were increased simultaneously to 19.5 MPa, 21 MPa, and 2 MPa, respectively. Subsequently, after sample has stabilized (which took around 53 hours), a CMS loading cycle was performed to simulate the effect of reservoir inflation. Here, the axial stress was increased by to 5 MPa, and the confining pressure was reduced by 2.5 MPa to keep the mean stress constant. It is known that properties measured during first loading differ from those obtained during subsequent loading cycles (e.g., Walsh 1965). For this reason, a second CMS cycle was performed. After each loading/unloading step, we have allowed the sample to stabilize before conducting low-frequency and ultrasonic measurements (the stabilization time was varying between 4 to 10 hours). After the second CMS loading cycle, the axial stress was gradually reduced to 19 MPa while holding the confining pressure constant at 17 MPa (triaxial unloading). This phase of the experiment was used to determine quasistatic properties of Pierre shale. Finally, to assure that the experiments were not executed close to the material failure, the axial load was increased with simultaneous reduction of the confining pressure until the stress state of 31 MPa axial load and 14.5 MPa confining pressure were reached (not shown in Fig. 2(i)). During this step, the shale did not fail. For all loading/unloading stages, the applied loading rate was equal to 5 MPa/h for all stresses and pressures, which corresponds to axial strain rates between  and
and 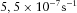 . All segments of the experiments were conducted under drained conditions (assured by a metal mesh wrapped around the sample and covering about 60%–70% of the sample's lateral surface), with 3.5% NaCl brine as a pore fluid, and at constant pore pressure of 2 MPa. It should be noted, that at the time scale of typical 4D seismic surveys, shale formations in the field are usually considered undrained, which implies pore pressure change. However, during CMS loading, the pore pressure change is usually small, and for the Pierre shale, we can roughly estimate the pore pressure change to be between 10% and 25% of the axial stress change (Skempton 1954; Holt et al. 2015).
. All segments of the experiments were conducted under drained conditions (assured by a metal mesh wrapped around the sample and covering about 60%–70% of the sample's lateral surface), with 3.5% NaCl brine as a pore fluid, and at constant pore pressure of 2 MPa. It should be noted, that at the time scale of typical 4D seismic surveys, shale formations in the field are usually considered undrained, which implies pore pressure change. However, during CMS loading, the pore pressure change is usually small, and for the Pierre shale, we can roughly estimate the pore pressure change to be between 10% and 25% of the axial stress change (Skempton 1954; Holt et al. 2015).
2.4 Conversion between properties measured at seismic and ultrasonic frequencies
 , and the strain tensor,
, and the strain tensor,  , of any elastic material (Hooke's law), as follows:
, of any elastic material (Hooke's law), as follows:
 (2)
(2) (3)
(3) .
.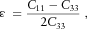 (4)
(4)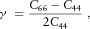 (5)
(5)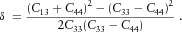 (6)
(6)- a)
For properties acquired at ultrasonic frequencies:
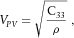 (7)
(7)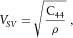 (8)
(8)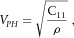 (9)
(9)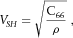 (10)
(10)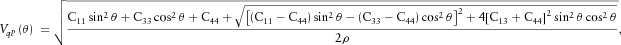 (11)
(11)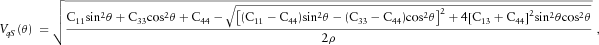 (12)
(12) and
and  represent phase velocities of “quasi P-waves” and “quasi S-waves” with wave-fronts normals oriented at angle θ with respect to the symmetry axis. Subscript V denotes the direction of the symmetry axis, whereas subscript H denotes any direction within the symmetry plane.
represent phase velocities of “quasi P-waves” and “quasi S-waves” with wave-fronts normals oriented at angle θ with respect to the symmetry axis. Subscript V denotes the direction of the symmetry axis, whereas subscript H denotes any direction within the symmetry plane.
- b)
For properties acquired at seismic frequencies:
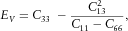 (13)
(13)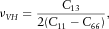 (14)
(14)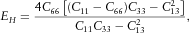 (15)
(15)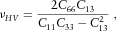 (16)
(16)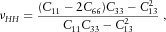 (17)
(17)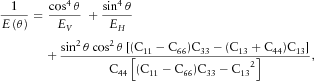 (18)
(18) (19)
(19)In the following, values of Thomsen parameters representative for our specimen at seismic frequencies were assumed to be identical with the one obtained from Pierre shale field measurements at 950-ft depth performed by White, Martineau-Nicoletis and Monash (1983): 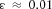 ,
, 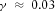 ,
, 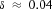 . At ultrasonic frequencies, Thomsen's parameters were previously measured on samples cut from the same batch of material by Holt et al. (2015):
. At ultrasonic frequencies, Thomsen's parameters were previously measured on samples cut from the same batch of material by Holt et al. (2015): 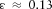 ,
, 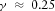 ,
,  . Possible errors associated with this approach will be discussed later.
. Possible errors associated with this approach will be discussed later.
3 EXPERIMENTAL RESULTS
3.1 Rock mechanical properties
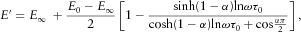 (20)
(20)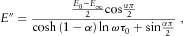 (21)
(21) are high and low frequency moduli, τ0is the relaxation time,
are high and low frequency moduli, τ0is the relaxation time,  and
and 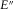 stand for real and imaginary part of complex modulus, ω is angular frequency, and α is a parameter controlling the width of the relaxation time distribution. Open symbols at ultrasonic frequencies represent isotropic conversion from velocities to rock mechanical parameters and were added to illustrate the effect of anisotropy and the error associated with neglecting material anisotropy.
stand for real and imaginary part of complex modulus, ω is angular frequency, and α is a parameter controlling the width of the relaxation time distribution. Open symbols at ultrasonic frequencies represent isotropic conversion from velocities to rock mechanical parameters and were added to illustrate the effect of anisotropy and the error associated with neglecting material anisotropy.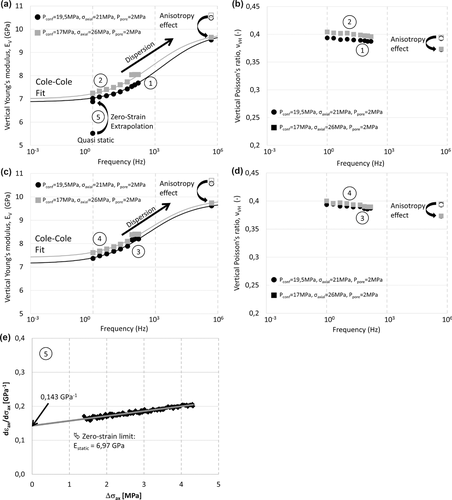
| Reference stress | 1st CMS loading | Reference stress (repetition) | 2nd CMS loading | |||||
|---|---|---|---|---|---|---|---|---|
| Seismic (1 Hz) | ultrasonic | Seismic (1 Hz) | ultrasonic | Seismic (1 Hz) | ultrasonic | Seismic (1 Hz) | ultrasonic | |
| Vertical Young's modulus, EV (GPa) | 7.03 | 9.54 | 7.25 | 9.65 | 7.34 | 9.62 | 7.62 | 9.74 |
| EV dispersion | 36% | 33% | 31% | 28% | ||||
Vertical Poisson's ratio,  (-) (-) |
0.394 | 0.373 | 0.404 | 0.373 | 0.394 | 0.373 | 0.4 | 0.373 |
| Vertical P-wave velocity, VPV (m/s) | 2443 | 2981 | 2578 | 3014 | 2496 | 2999 | 2599 | 3028 |
| VPV dispersion | 22.0% | 16.9% | 20.2% | 16.5% | ||||
| Vertical S-wave velocity, VSV (m/s) | 1087 | 1254 | 1105 | 1260 | 1114 | 1258 | 1132 | 1265 |
| VSV dispersion | 15.4% | 14.0% | 12.9% | 11.8% | ||||
| VPV/ VSV (-) | 2.248 | 2.377 | 2.333 | 2.392 | 2.241 | 2.384 | 2.296 | 2.394 |
Stress-sensitivity factor,  (MPa−1) (MPa−1) |
− | − | 11.5·10−3 | 2.4·10−3 | − | − | 8.4·10−3 | 2·10−3 |
Strain-sensitivity factor,  (-) (-) |
− | − | 23 | 4.5 | − | − | 25 | 6 |
Figure 3 (a) and (b) shows data obtained during initial CMS loading (indicated with numbers 1 and 2 in Fig. 2(i)). Rather large seismic dispersion (about 36%) is observed for vertical Young's modulus at the reference stress state. In case of shales, large dispersion of Young's moduli is not unusual and, in some cases, it may exceed 50% (e.g. Suarez-Rivera et al. 2001; Duranti et al., 2005, Szewczyk et al. 2016), which indicates the importance of accounting for dispersion effects during seismic data interpretation. Simulated reservoir inflation leads to the stiffening of the sample in both frequency regimes. Note, however, that the responses are different at seismic and ultrasonic frequencies. While at 1 Hz Young's modulus increases by around 0.2 GPa, the change at ultrasonic frequency is about two times smaller (see Table 1). Frequency-dependent stress sensitivity of Young's modulus results, during loading, in a decrease of dispersion. Different stress sensitivities at seismic and ultrasonic frequencies were observed before in relatively dry Pierre shale (Holt et al. 2016) and Mancos shale subjected to isotropic loading (Szewczyk, Bauer and Holt 2018a).
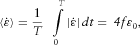 (22)
(22) .
.The result of applying this method is shown in Fig. 3(e). The compliance, dεax/dσax, is plotted as a function of unloading stress, Δσax, and extrapolated towards zero stress leading to the zero-strain limit of Young's modulus Ezero-strain = [dεax/dσax(Δσax = 0)]−1 = 6.9 GPa. This zero-strain-extrapolated Young's modulus agrees well with the dynamic Young's modulus measured at 1 Hz. Since the strain rate used during triaxial unloading phase of our experiment ( ) roughly corresponds to that of a 1 Hz elastic wave in our test (
) roughly corresponds to that of a 1 Hz elastic wave in our test (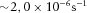 ), this result suggests that, indeed, the difference between static and dynamic Young's modulus at a given frequency originates from both strain effect and dispersion effects (Holt et al. 2015). It also confirms that, in some cases, dynamic stiffness can be obtained from quasistatic measurements.
), this result suggests that, indeed, the difference between static and dynamic Young's modulus at a given frequency originates from both strain effect and dispersion effects (Holt et al. 2015). It also confirms that, in some cases, dynamic stiffness can be obtained from quasistatic measurements.
The vertical Poisson's ratio ( ) shown in Fig. 3(b) does not exhibit large stress sensitivity. For seismic frequencies, it changes by around 0.01 under CMS loading. At ultrasonic frequencies,
) shown in Fig. 3(b) does not exhibit large stress sensitivity. For seismic frequencies, it changes by around 0.01 under CMS loading. At ultrasonic frequencies,  of Pierre shale exhibits even smaller stress sensitivity. Measured values are slightly lower than for seismic frequencies and stable at both stress states. Usually, an increase in Poisson's ratio from seismic to ultrasonic frequencies is observed (e.g., Hofmann 2006). It should be noted, however, that the values of Thomsen parameters used for anisotropic corrections were obtained during tests performed at different stresses, which may introduce error (see Discussion section).
of Pierre shale exhibits even smaller stress sensitivity. Measured values are slightly lower than for seismic frequencies and stable at both stress states. Usually, an increase in Poisson's ratio from seismic to ultrasonic frequencies is observed (e.g., Hofmann 2006). It should be noted, however, that the values of Thomsen parameters used for anisotropic corrections were obtained during tests performed at different stresses, which may introduce error (see Discussion section).
Figure 3 (c) and (d) shows data obtained during second CMS loading (indicated with numbers 3 and 4 in Fig. 2(i)). The values of Young's modulus at seismic and ultrasonic frequencies are systematically higher than during the first CMS cycle (see Table 1), which is expected to be seen due to the sample over-consolidation. Note that during second CMS loading cycle, at both seismic and ultrasonic frequencies, increase of the vertical Young's modulus is similar to the case of the first loading cycle. This indicates that the measured stress sensitivity of Pierre shale (in absolute values) during CMS loading is not affected by material consolidation. Changes in vertical Poisson's ratio are also similar to the one obtained during the first loading cycle (see Table 1). After first CMS unloading, the acquired values did not show any considerable change. Slightly smaller increase of Poisson's ratio was observed after the second CMS loading; however, differences are within the experimental errors.
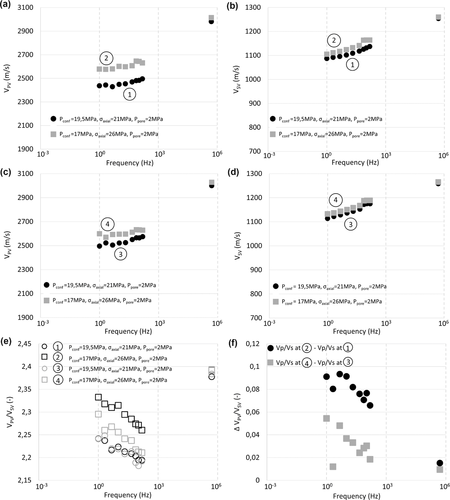
3.2 Wave velocities
Vertical P-wave and S-wave velocities obtained during both loading cycles are shown in Fig. 4 and summarized in Table 1. Ultrasonic velocities were measured directly, whereas seismic velocities were calculated from the measured Young's moduli and Poisson's ratios, assuming stress-independent Thomsen parameters (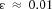 ,
, 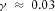 ,
,  ; White et al. 1983).
; White et al. 1983).
 (23)
(23) (24)
(24) being the axial strain and
being the axial strain and  being the axial stress. Both stress sensitivity and strain sensitivity factors are about five times higher at seismic frequencies compared with ultrasonic frequencies. The S-wave velocity exhibits smaller stress sensitivity than a P-wave. At the reference stress, vertical S-wave velocities exhibit around 15% dispersion. Again, CMS loading caused different increase of S-wave velocities at seismic and ultrasonic frequencies. As a consequence, dispersion decreased slightly. Different stress sensitivity of P-wave and S-wave results in a distinct VP/VS evolution at various frequencies (see Fig. 4(e)). In the seismic regime, the VP/VS changes are about five to six times larger than at ultrasonic frequencies (see Fig. 4(f)). Note that unloading in the first CMS cycle reduces the VP/VS ratio almost to its original values despite rather large irreversible changes in VP and VS. At seismic frequencies, the CMS unloading to the reference stress, induces a reduction of VPV and VSV. The measured velocities are, however, higher than those measured at the reference stress before the first CMS cycle. At ultrasonic frequencies, we also observe a small increase in absolute values of P-wave and S-wave velocities after CMS unloading, but the effect is about four to five times smaller than for seismic frequencies (see Table 1). During the second CMS cycle, S-wave velocities show a stress sensitivity comparable to the one measured during the first loading cycle, for both seismic and ultrasonic frequencies. As a consequence, dispersion does not change significantly. Also, P-wave velocity measurements roughly reproduce values obtained after the first CMS loading. During the second CMS loading, we again observe rather large stress sensitivity at seismic frequencies and a much smaller sensitivity at ultrasonic frequencies, leading to reduced dispersion. The average velocity change with stress (
being the axial stress. Both stress sensitivity and strain sensitivity factors are about five times higher at seismic frequencies compared with ultrasonic frequencies. The S-wave velocity exhibits smaller stress sensitivity than a P-wave. At the reference stress, vertical S-wave velocities exhibit around 15% dispersion. Again, CMS loading caused different increase of S-wave velocities at seismic and ultrasonic frequencies. As a consequence, dispersion decreased slightly. Different stress sensitivity of P-wave and S-wave results in a distinct VP/VS evolution at various frequencies (see Fig. 4(e)). In the seismic regime, the VP/VS changes are about five to six times larger than at ultrasonic frequencies (see Fig. 4(f)). Note that unloading in the first CMS cycle reduces the VP/VS ratio almost to its original values despite rather large irreversible changes in VP and VS. At seismic frequencies, the CMS unloading to the reference stress, induces a reduction of VPV and VSV. The measured velocities are, however, higher than those measured at the reference stress before the first CMS cycle. At ultrasonic frequencies, we also observe a small increase in absolute values of P-wave and S-wave velocities after CMS unloading, but the effect is about four to five times smaller than for seismic frequencies (see Table 1). During the second CMS cycle, S-wave velocities show a stress sensitivity comparable to the one measured during the first loading cycle, for both seismic and ultrasonic frequencies. As a consequence, dispersion does not change significantly. Also, P-wave velocity measurements roughly reproduce values obtained after the first CMS loading. During the second CMS loading, we again observe rather large stress sensitivity at seismic frequencies and a much smaller sensitivity at ultrasonic frequencies, leading to reduced dispersion. The average velocity change with stress ( ) during second loading decreased with respect to those of the first loading cycle for both frequency ranges. The strain sensitivity factors, on the other hand, slightly increased when compared with the previous loading. Finally, the VP/VS changes during second loading cycle are comparable with the one obtained during initial loading, and their absolute values are reproduced with an accuracy of ±0.05.
) during second loading decreased with respect to those of the first loading cycle for both frequency ranges. The strain sensitivity factors, on the other hand, slightly increased when compared with the previous loading. Finally, the VP/VS changes during second loading cycle are comparable with the one obtained during initial loading, and their absolute values are reproduced with an accuracy of ±0.05.4 DISCUSSION
4.1 Effect of frequency-dependent stress sensitivity
Presented experimental studies aim to demonstrate how the stress changes caused by an injection into a reservoir influence the mechanical properties of overburden shales for monitoring purposes. It has been observed that velocities and stiffness of shales exhibit significant seismic dispersion, and available rock physics models are not always capable of capturing the observed phenomena (Müller, Gurevich and Lebedev 2010). Therefore, the applicability of ultrasonic laboratory tests to seismic field measurements is questionable. For a better understanding of dispersion effects, we have performed experiments at seismic and ultrasonic frequencies. The obtained results indicate that also stress sensitivity of velocities in clay-rich materials strongly depend on frequency. In situations where pore-pressure changes in a reservoir influence a thick zone above the reservoir, the effect of dispersive stress sensitivity on the interpretation of 4D seismic data would be significant. Numerical simulations (Kenter et al. 2004) indicate that, in case of a 100-m thick reservoir, the influence of a pore-pressure change may affect a zone up to 1,000 m above the injection site. In such case, based on measurements performed during first CMS loading, the modelled change in P-wave two-way travel time would differ by a factor of five depending on whether stress sensitivities obtained from seismic or ultrasonic measurements are taken into account. Data acquired during the second CMS cycle exhibits smaller difference between seismic and ultrasonic stress sensitivities; however, the changes in travel time would still differ by a factor of ̴ 4.
4.2 Representativeness of laboratory tests for in situ studies
Presented experiments were conducted on Pierre shale core plugs drilled from outcrop material. Even though Pierre shale is considered as an analogue for overburden rocks, such materials are obviously not fully representative for in situ situations. Coring the samples and associated stress release could influence their mechanical properties (Holt, Brignoli and Kenter 2000) and make measured responses to differ from in situ behaviour. Also, in contrast to the present experiments, in a real case, there is usually a stiffness contrast between reservoir and overburden, which results in overburden stress paths that differ from a CMS loading. It is known that velocities are not only stress dependent but also stress path dependent. We have recently showed (Holt et al. 2016) that velocities in shales near in situ stresses are characterized by nearly monotonous (linear) dependence on stress path. In a real field case, inhomogeneities in rock elastic properties, rock plasticity, and the real geometry of reservoir and overburden formations should be taken into account, and the appropriate stress path should be determined by numerical modelling.
Finally, Thomsen's parameters that were used to convert between velocities and rock mechanical parameters were not measured directly during our experiments, which obviously introduces an additional error. To this end, it should be noted that (i) properties of Pierre shale I, including Thomsen's parameters differ depending on the shale origin (e.g., Schultz et al. 1980) and that (ii) Thomsen's parameters are dispersive and may be affected, among others, by stress applied to the sample, loading path, saturation, and stress history. Ultrasonic Thomsen's parameters used in this paper were obtained with core plugs drilled from the same batch of material as used in the present work (Holt et al. 2015). However, measurements performed by Holt et al. (2015) were conducted at slightly higher stresses (25 MPa confining pressure, 30 MPa axial stress, and about 12 MPa pore pressure) than those used in our experiments, which could lead to a change of the Thomsen's parameter value. Thomsen's parameters at seismic frequencies were taken from Pierre shale field measurements performed by White et al. (1983) at 950-ft depth. White et al. (1983) do not give direct information about saturation, mechanical parameters, in situ stresses, or density of their shale. However, suggested by White et al. (1983), density of 2.25 g/cm3 is smaller than the density of Pierre shale used in the present study (2.39 g/cm3). Based on the velocity data published by White et al. (1983), the vertical Poisson's ratio, νVH, of the field shale was 0.397, which is in good agreement with our measurements. Taking into account the large saturation sensitivity of Poisson's ratio in shales (e.g., Vales et al. 2004; Szewczyk, Bauer and Holt 2018b), it is reasonable to assume that the field shale was fully saturated, as the sample used in the present study. Also, based on the velocity data, the dynamic vertical Young's modulus, EV, of the Pierre field shale was 5.3 GPa, about 1.7 GPa smaller than EV of our sample. Young's modulus in Pierre shale, however, strongly increases with increasing stress experienced by the material (e.g., Szewczyk et al. 2018a). Bearing in mind that under normal pressure conditions, effective stress used in our experiment corresponds to a depth of about 1,000 m, which is significantly deeper than the shale formation studied by White et al. (1983), the discrepancy between Young's modulus values can be attributed to the difference in stress. In addition, taking into account that the Thomsen's parameters are stress dependent, the fact that Thomsen's parameters obtained by White et al. (1983) correspond to a lower stress could mean that they are not fully representativeness for our case. Qualitatively, the dependence of Thomsen's parameters on stress and stress path can be deduced from Szewczyk et al. (2018a,b) and Holt et al. (2016). The sensitivity of conversion between seismic and ultrasonic parameters measured in this work to the value of Thomsen's parameters ε, γ, and δ is illustrated in Fig. 5.
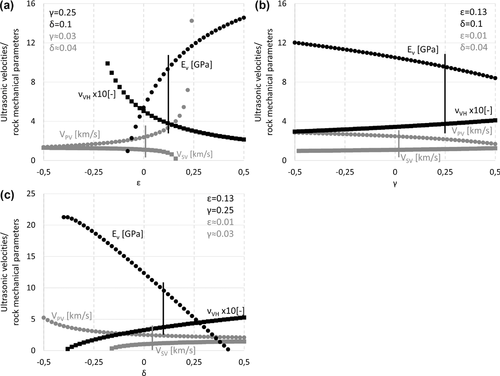
Figure 5 shows that the conversion from ultrasonically measured vertical velocities to rock mechanical parameters is more sensitive to Thomsen's parameters than conversion from low frequency laboratory measurements of E and ν to velocities. The converted data are particularly sensitive to ε and δ. In the vicinity of the values used in this work, while converting from velocities to mechanical parameters, 0.02 variation in ε value causes around 5% difference in the vertical Young's modulus, EV, and about 4% difference in the vertical Poisson's ratio,  . Similar variation of the δ parameter creates around 6% difference in EV and about 2% difference in
. Similar variation of the δ parameter creates around 6% difference in EV and about 2% difference in  . The influence of the variations of the γ parameter is below 1% for both Young's modulus and Poisson's ratio. While converting from rock mechanical parameters to velocities, the effects of similar variation of Thomsen's parameters are on average two to three times smaller.
. The influence of the variations of the γ parameter is below 1% for both Young's modulus and Poisson's ratio. While converting from rock mechanical parameters to velocities, the effects of similar variation of Thomsen's parameters are on average two to three times smaller.
4.3 Possible leakage from reservoir
Pierre shale used in our experiment was tested in fully brine-saturated conditions. In the field case, there could be some gas partially saturating the caprock (e.g., due to a leakage from the reservoir). In case of CO2 storage, leakage from the storage site is a concern, and suitable and reliable monitoring methods are required. Here, we present possible effects of CO2 leakage on 4D seismic attributes.
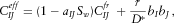 (25)
(25)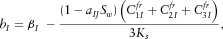 (26)
(26) (27)
(27) (28)
(28)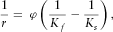 (29)
(29)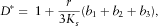 (30)
(30) stands for the bulk modulus of pore fluid and solid phase, respectively; φ indicates the porosity;
stands for the bulk modulus of pore fluid and solid phase, respectively; φ indicates the porosity; 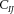 represent the independent coefficient of stiffness elastic tensor;
represent the independent coefficient of stiffness elastic tensor;  is the wetting phase saturation; and
is the wetting phase saturation; and  is the fitting parameter accounting for the fluid-phase driven frame weakening through adsorption effects, which, in general, may be different for each of the independent
is the fitting parameter accounting for the fluid-phase driven frame weakening through adsorption effects, which, in general, may be different for each of the independent 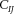 ’s. The capillary pressure effects at a microscopic scale and at low frequency limit, on the other hand, may be accounted for by calculating the effective fluid modulus through Brie's mixing law (e.g., Santos, Corberó and Douglas 1990; Papageorgiou, Amalokwu and Chapman 2016), despite the typical patchy saturation interpretation of this mixing law. The Brie's empirical equation (Brie et al. 1995) is as follows:
’s. The capillary pressure effects at a microscopic scale and at low frequency limit, on the other hand, may be accounted for by calculating the effective fluid modulus through Brie's mixing law (e.g., Santos, Corberó and Douglas 1990; Papageorgiou, Amalokwu and Chapman 2016), despite the typical patchy saturation interpretation of this mixing law. The Brie's empirical equation (Brie et al. 1995) is as follows:
 (31)
(31) stands for non-wetting phase saturation,
stands for non-wetting phase saturation, 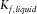 and
and  are bulk moduli of wetting and non-wetting phases, respectively, and e is an adjustable parameter, which, in case of high values, would move the effective fluid modulus towards Reuss average and, in case of low values, towards Voigt average. The use of the Gassmann model requires anisotropic frame properties. In the present work, the frame properties were estimated in such a way that the modified Gassmann model reproduces values measured for full brine saturation. The effective bulk moduli of solid phase (
are bulk moduli of wetting and non-wetting phases, respectively, and e is an adjustable parameter, which, in case of high values, would move the effective fluid modulus towards Reuss average and, in case of low values, towards Voigt average. The use of the Gassmann model requires anisotropic frame properties. In the present work, the frame properties were estimated in such a way that the modified Gassmann model reproduces values measured for full brine saturation. The effective bulk moduli of solid phase ( ), Brie's adjustable parameter (
), Brie's adjustable parameter ( ), and parameter
), and parameter  accounting for frame weakening (
accounting for frame weakening ( between 0.42 and 0.45) of Pierre shale were taken from Szewczyk et al. 2018b). We have considered a two-phase fluid system filling up the pore space (brine and CO2). The bulk modulus and the density of the brine were
between 0.42 and 0.45) of Pierre shale were taken from Szewczyk et al. 2018b). We have considered a two-phase fluid system filling up the pore space (brine and CO2). The bulk modulus and the density of the brine were 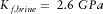 and
and  , respectively, (e.g., Batzle and Wang 1992), whereas bulk modulus and density of CO2 were
, respectively, (e.g., Batzle and Wang 1992), whereas bulk modulus and density of CO2 were  and
and  (e.g., Burke 2011). Being aware that CO2 properties are affected by pressure and temperature, we decided to keep them constant, since bulk modulus and density of CO2 are low compared with those of brine; thus, accounting for pressure and temperature dependence would have only a small impact on the final results.
(e.g., Burke 2011). Being aware that CO2 properties are affected by pressure and temperature, we decided to keep them constant, since bulk modulus and density of CO2 are low compared with those of brine; thus, accounting for pressure and temperature dependence would have only a small impact on the final results.Figure 6(a) shows vertical P-wave velocities as a function of CO2 saturation calculated based on seismic (1 Hz) measurements performed at all examined stress states.
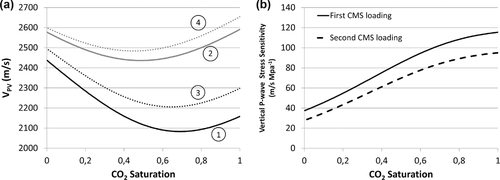
The modelled effect of gas saturation (in relative terms) is quite similar during the first and second CMS cycles. The modelling of the fluid substitution indicates that small leakages of the CO2 into the overburden formation would create noticeable travel time shifts, under the assumption that the overburden formation was initially fully brine saturated. Ten percent CO2 saturation in the overburden due to possible leakage could create up to 3% P-wave velocity change. Obviously, the possibility of detecting such events during 4D surveys depends on the related changes of the two-way travel times and, thus, on the length of CO2 penetration into the shale formation. Assuming good quality data, current 4D detection limit for changes of the two-way travel time is below 1 ms (e.g., Landrø and Amundsen 2017). Using vertical P-wave velocities from our 1 Hz data (about 2,500 m/s) and assuming 3% velocity change due to the CO2 leakage, this threshold would be reached after the CO2 has propagated for about 40 m into the overburden formation, which is quite likely in the case of the over-pressured reservoirs (e.g., during CO2 injection for storage or enhanced recovery). The fluid substitution effects are visible up to about 50%–60% gas saturation. Afterwards, the changes of the velocities are mainly controlled by the adsorption effects present in shales and leading to the weakening of anisotropic frame moduli (those effects may have magnitude comparable with the fluid substitution effects). This can be seen by the drop of seismic velocities while going from fully gas-saturated shale up to about 30%–40% fluid saturation and increase of the velocities afterwards (similar behaviour was observed experimentally in Szewczyk et al. 2018). Another interesting observation is that the CMS loading seems to decrease the range in which fluid substitution effects are dominant (compare black and grey curves in Fig. 6(a). Note also that the P-wave velocity changes associated with fluid substitution may be of comparable magnitude as one associated with a stress change: based on seismic data obtained at reference stress, ten percent CO2 saturation would lead to a velocity change comparable to that obtained by about 1.9 MPa shear stress change during CMS loading.
Velocity changes associated with fluid substitution are clearly stress dependent (additional load decreases fluid phase sensitivity). Moreover, fluid substitution effects depend on the material hysteresis. This is further shown in Fig. 6(b) where the shear stress sensitivity of vertical P-wave velocities (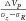 ) is plotted as a function of CO2 saturation. In absolute values, during initial CMS loading, the seismic stress sensitivity reduces from 115 m/s MPa−1 to 38 m/s MPa−1 when going from full CO2 saturation to full brine saturation. For the second CMS cycle, the seismic stress sensitivity of the P-wave velocity decreases from 95 m/s MPa−1 to 28 m/s MPa−1. Note, however, that in the relative values, the stress sensitivity at seismic frequencies is about three times higher in case of full CO2 saturation than in case of full brine saturation regardless of the loading cycle (during first CMS loading stress sensitivity reduces by ̴ 67%, whereas during second CMS loading, it reduced by ̴ 70%).
) is plotted as a function of CO2 saturation. In absolute values, during initial CMS loading, the seismic stress sensitivity reduces from 115 m/s MPa−1 to 38 m/s MPa−1 when going from full CO2 saturation to full brine saturation. For the second CMS cycle, the seismic stress sensitivity of the P-wave velocity decreases from 95 m/s MPa−1 to 28 m/s MPa−1. Note, however, that in the relative values, the stress sensitivity at seismic frequencies is about three times higher in case of full CO2 saturation than in case of full brine saturation regardless of the loading cycle (during first CMS loading stress sensitivity reduces by ̴ 67%, whereas during second CMS loading, it reduced by ̴ 70%).
5 CONCLUSIONS
Pierre shale I (mimicking caprock) was subjected to laboratory tests evaluating expected mechanical and acoustic responses of the overburden formation to fluid injection into a reservoir beneath it (e.g., for CO2 storage or enhanced recovery). Outcrop core plugs were tested in drained condition, with 3.5% NaCl brine as a pore fluid and under constant pore pressure. The experiments were carried out in set-up allowing for quasistatic rock deformation measurements, ultrasonic velocity determination, and quantification of the sample responses at seismic frequencies. In addition, possible fluid substitution effects were simulated with the use of modified anisotropic Gassmann model.
Our experiments at seismic and ultrasonic ranges reveal big frequency dependence of elastic moduli and wave velocities, thus demonstrating significance of low frequency laboratory studies. The observed stress sensitivity of the shale was higher at seismic frequencies, indicating importance of accounting for the dispersion effects during seismic data interpretation based on ultrasonic laboratory measurements. Injection into the reservoir increases overburden in Young's modulus and acoustic P-wave and S-wave velocities and would create significant travel time reduction. Repeated constant mean stress loading reveals that elimination of the non-elastic effects decrease the stress sensitivity, increase the acoustic velocities, and stiffer the sample. The observed phenomena are in qualitative agreement with field observations; however, care needs to be taken while generalizing those results due to limitations of applied procedures and possible differences in material properties. Nevertheless, the experiments point out possible mechanisms that should be accounted for during geomechanical or 4D seismic modelling of injection scenarios. Simple poroelastic modelling of the fluid substitution (based on the modified Gassmann model) demonstrates that relatively small leakages of the CO2 into the overburden rock may lead to velocity changes, which are comparable with those induced by stress modifications. Both the geomechanical and the fluid substitution effects would create significant time shifts, which could be detected with 4D seismic. Presented quasistatic measurements indicates, as claimed by others, that the differences between static and dynamic moduli are due to both strain amplitude and dispersion effects and that correct experimental procedure allows, in some cases, to obtain dynamic stiffness from quasistatic measurements.
ACKNOWLEDGEMENTS
This publication has been produced with support from the BIGCCS Centre, performed under the Norwegian research program Centres for Environment-Friendly Energy Research (FME). The authors acknowledge the following partners for their contributions: ConocoPhillips, Gassco, Shell, Statoil, TOTAL, ENGIE, and the Research Council of Norway (193816/S60). The authors would also like to acknowledge financial support from The Research Council of Norway, BP Norge, Dong, Engie, Maersk, and Total through the Knowledge-building project for industry “Shale Rock Physics: Improved seismic monitoring for increased recovery” at SINTEF Petroleum Research (234074/E30). The authors thank Serhii Lozovyi for his help during the laboratory experiments.




