A new mathematical model of asymmetric hydraulic fracture growth
ABSTRACT
Hydraulic fractures generated by fluid injection in rock formations are often mapped by seismic monitoring. In many cases, the microseismicity is asymmetric relative to the injection well, which has been interpreted by stress gradient along the direction of the hydraulic fracture. We present a mathematical model of asymmetric hydrofracture growth based on relations between the solid-phase stress and the fracture hydraulics. For single fracture and single injection point, the model has three parameters, hydraulic conductivities of the fracture wings, and normalised stress gradient and predicts the positions of the fracture tips as functions of time. The model is applied to a set of microseismic event locations that occurred during and after an injection process. Two different methods are suggested that make it possible to delineate the fracture tips from the set of microseismic events. This makes it possible to determine the model parameters and to check the agreement between the model prediction and the measured data. The comparison of the measured and modelled growth of fracture wings supports both the assumption of the non-zero stress gradient and the existence of the post-injection unilateral growth.
1 INTRODUCTION
Hydraulic stimulation is a standard procedure for increasing the permeability of rock formation in hydrocarbon and geothermal reservoirs. During injection, a borehole section is sealed off from the fluid pressure above and below and is pressurised for several minutes until the initiation of tensile fracture, which happens when the injection pressure exceeds the minimum compressive stress. The tensile fracture propagates from the injection point in two opposite directions along the direction of the maximum confining stress component σ1; see the work of Economides and Nolte (2003). The fracture opening is accompanied by brittle fracturing, which radiates elastic energy. Location of the associated microseismic events enables us to determine the geometry of the stimulated rock volume and its growth characteristics (House 1987; Cornet and Julien 1989). Details of seismicity patterns can be nowadays recognised, thanks to the high relative precision of location methods using downhole sensors (e.g., Oye, Chavarria and Malin 2004; Rutledge, Phillips and Mayerhofer 2004; Fischer et al. 2008) or surface seismic arrays (e.g., Chambers et al. 2010; Duncan and Eisner 2010). The fracturing-induced seismicity is usually related to the opening of the fracture tip and shear stress released on surrounding fractures that are favorably oriented for slip; see Evans et al. (1999) and Rutledge and Phillips (2003). It is thus assumed that the seismicity maps the fracture extent. The shape of the fracture and its growth depends on stress orientation in rock mass, rock stiffness and existence of pre-existing cracks, injection rate, and loss of the injected fluid through the fracture walls.
Different hydromechanical fracture models have been developed to explain the geometry of the fracture. The model of Perkins and Kern (1961), which assumes an elliptical shape of the vertical cross section of the fracture, was later extended by Nordgren (1972) to account for leak off and storage and is known as the PKN model. Similar models aim to estimate the fracture width as a function of injection pressure, flow rate, and fracture length. Accompanying seismicity is usually explained by pore pressure perturbations affecting the normal stress on pre-existing cracks surrounding the propagating hydraulic fracture (e.g., Shapiro, Huenges and Borm 1997; Shapiro 2000; Shapiro, Dinske and Rothert 2006).
In some cases, the observations of the induced microseismicity indicate an asymmetric growth of the hydraulic fracture with respect to the injection well (e.g., Kochnev et al. 2007; Fischer et al. 2008). The asymmetric pattern of induced seismicity cannot be always explained by the unequal sensitivity of the seismic monitoring network. Also, local heterogeneities preventing the fracture growth in one direction are usually limited to a single sedimentary layer rather than span vertically over several layers. If the hydrofracture in different layers exhibits the same direction of asymmetry, and hypocentres show a similar migration pattern during different experiments within different sedimentary layers, this anomaly can be explained by lateral change in stress as was suggested in the study by Fischer, Hainzl and Dahm (2009). A more detailed model of asymmetric hydraulic fracture was further developed by Dahm, Hainzl and Fischer (2010). It considers stress gradients and quantifies the bidirectional and further unidirectional post-injection growth. The introduced analytical equations allow for calculating the Coulomb stress change in the neighborhood of the fracture.
The main disadvantage of the presented models is their inability to determine the fracture length as a function of time. In this paper, we revisit the problem of the creation of asymmetric fracture and its growth, as presented by Fischer et al. (2009). We apply the same assumptions concerning the solid-phase stress distribution and the fracture opening condition. The assumption concerning the length and volume of the fracture's leading part is newly formulated. Actually, this was tacitly assumed by Fischer et al. (2009), too. Following the assumptions, our model is based on a balance law and involves the opening condition and a flow equation. We do not put into relation the lengths of the fracture wings and do not derive the governing equation from this relation, since the approach does not make it possible to derive the dependence of the length of the fracture wing on time.
Instead, we base the model on a balance law expressed in the form of an ordinary differential equation. The solution to this equation gives the lengths of the fracture wings as functions of time. Consequently, this allows for determining the relative stress gradient and conductivities of the two fracture wings. Finally, we apply our model to the microseismic dataset from West Texas, which was also utilised by Fischer et al. (2009) and Dahm et al. (2010), and present the obtained results.
2 FRACTURE AND ITS GROWTH
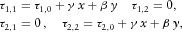 (1)
(1) , are components of the stress tensor in horizontal plane. We assume that β and γ are constants and
, are components of the stress tensor in horizontal plane. We assume that β and γ are constants and  ; otherwise; the orientation of the axes can be changed. The fracture is initiated by pumping fluid into a vertical borehole situated at
; otherwise; the orientation of the axes can be changed. The fracture is initiated by pumping fluid into a vertical borehole situated at  ; its development is affected by the anisotropy and heterogeneity of the horizontal stress (Fig. 1).
; its development is affected by the anisotropy and heterogeneity of the horizontal stress (Fig. 1).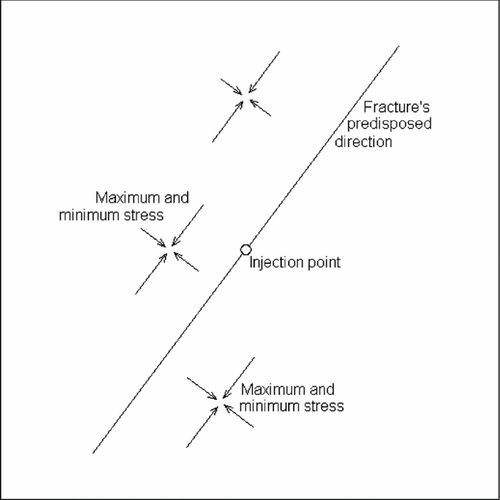
We do not investigate the distribution of the fluid flow within the fracture. Because of non-changing pressure conditions, the fracture does not change its aperture at the point of injection and at its tip. Consequently, we simplify the problem by working with mean values: constant resistance (conductivity) of the fracture and constant aperture.
- (i) The fracture is considered as a vertical plane situated in a horizontal geological layer; its detailed geometry is not studied. A linear law of the Hagen–Poiseuille type is supposed to govern the fluid flow in fracture.
- (ii) The roughness of the fracture and the fluid-phase viscosity dominate, and the aperture differences along the open fracture can be neglected when determining the fracture's resistance–the fracture conductivity is constant.
- (iii) The process of opening and the detailed shape of the fracture's leading part will not be studied. It is only supposed that there exists a similarity from the viewpoint of length and volume between any two states of the fracture during its development.
- (iv) The microseismic events reflect the growth of fluid pressure in the fracture and, in particular, the position of the fracture front.
 . Now, the problem is one-dimensional with space coordinate x normal to the minimum compressive stress τ2, 2 (along the direction of the maximum compressive stress τ1, 1). According to the assumption, the minimum compressive stress along the fracture is as follows:
. Now, the problem is one-dimensional with space coordinate x normal to the minimum compressive stress τ2, 2 (along the direction of the maximum compressive stress τ1, 1). According to the assumption, the minimum compressive stress along the fracture is as follows:
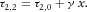 (2)
(2)The flow of fluid in the borehole opens the rock layer at the injection point in the direction of the y-axis (direction of the minimum stress) and splits the opening into two components associated with the positive and the negative direction of axis x.
 the x-coordinate of a fracture tip at time t. The driving pressure is now the difference between the fluid pressure within the fracture and the normal stress τ2, 2 acting from outside upon the fracture's walls. We do not study the process of solid-phase deformation produced by stress τ, the liquid-phase pressure p, and the dynamic effects of groundwater flow (see e.g., Biot 1941; Mls 1999). We just assume that the fracture opens under conditions of sufficiently high value of liquid-phase pressure. More precisely, it will be supposed that a positive value
the x-coordinate of a fracture tip at time t. The driving pressure is now the difference between the fluid pressure within the fracture and the normal stress τ2, 2 acting from outside upon the fracture's walls. We do not study the process of solid-phase deformation produced by stress τ, the liquid-phase pressure p, and the dynamic effects of groundwater flow (see e.g., Biot 1941; Mls 1999). We just assume that the fracture opens under conditions of sufficiently high value of liquid-phase pressure. More precisely, it will be supposed that a positive value  of the driving pressure opens the fracture and enables its growth along the x-axis. Hence, the fluid pressure at the tip of the fracture that increases its length is equal to the sum of the normal stress τ2, 2 and the driving pressure
of the driving pressure opens the fracture and enables its growth along the x-axis. Hence, the fluid pressure at the tip of the fracture that increases its length is equal to the sum of the normal stress τ2, 2 and the driving pressure  as follows:
as follows:
 (3)
(3)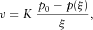 (4)
(4)The studied process is non-stationary and particularly due to the growth of the fracture; the momentum of liquid in the fracture changes. The changes of the liquid-phase momentum can be taken into account by applying the Cattaneo principle and involving the relaxation time into equation 4; see the work of Cattaneo (1958), and for groundwater flow, see the work of Mls and Herrmann (2011). In this paper, we assume that the inertial forces are negligible and do not modify equation 4.
As it cannot be supposed that the fracture at its tip opens immediately to the final or mean size of its aperture, the aperture of the fracture's leading part remains unknown. To be able to determine the rate of the fracture's growth, another kind of similarity assumption will be introduced. During the fracture's development, the relation between its length and volume remains unchanged. The fracture develops in such a way that the volume of the leading part is preserved. More precisely, there exists a positive length λ0 such that for any two subsequent times t1 and t2 and any length  , the volume of the opening between
, the volume of the opening between  and
and  is equal to the volume of the opening between
is equal to the volume of the opening between  and
and  .
.
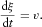 (5)
(5)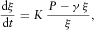 (6)
(6) is a given constant. In virtue of the problem formulation, the fracture is initiated by imposing pressure p0 at point
is a given constant. In virtue of the problem formulation, the fracture is initiated by imposing pressure p0 at point  and time
and time  . Hence, the following initial condition has to be prescribed:
. Hence, the following initial condition has to be prescribed:
 (7)
(7)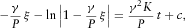 (8)
(8) and hence with positive value of the argument as follows:
and hence with positive value of the argument as follows:
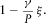 (9)
(9)We understand this equation as a definition of a function  ,
,  that defines the position ξ of the fracture tip at time t. Here and in the sequel, we denote by
that defines the position ξ of the fracture tip at time t. Here and in the sequel, we denote by  the half-open interval, open at a and closed at b. In order to study the uniqueness of the function ξ and to find its values
the half-open interval, open at a and closed at b. In order to study the uniqueness of the function ξ and to find its values  , we consider equation 10 as a non-linear equation with unknown value ξ.
, we consider equation 10 as a non-linear equation with unknown value ξ.
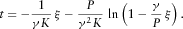 (11)
(11) decreases in the interval
decreases in the interval  from ∞ to 0 at
from ∞ to 0 at  and increases in
and increases in  from 0 to ∞. In view of this, there are exactly two solutions,
from 0 to ∞. In view of this, there are exactly two solutions,  and
and  , of the problem in equations 6 and 7, both defined for
, of the problem in equations 6 and 7, both defined for  . The function ξ1 decreases from 0 to
. The function ξ1 decreases from 0 to  as time increases from 0 to ∞. The function ξ2 starts in 0 at time
as time increases from 0 to ∞. The function ξ2 starts in 0 at time  and approaches
and approaches  as time increases to ∞. This means that the fracture develops along the x-axis in both the positive and negative directions. The length of the fracture in the direction of decreasing stress τ2, 2 is unlimited, whereas in the opposite direction, it is limited by the distance, as follows:
as time increases to ∞. This means that the fracture develops along the x-axis in both the positive and negative directions. The length of the fracture in the direction of decreasing stress τ2, 2 is unlimited, whereas in the opposite direction, it is limited by the distance, as follows:
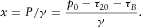 (12)
(12) (13)
(13)
 , equation 11: the inverse function to the time dependence of the fracture tip position.
, equation 11: the inverse function to the time dependence of the fracture tip position.  MPa,
MPa, 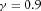 kPa/m,
kPa/m,  m3 N−1 s−1. The vertical dashed line at
m3 N−1 s−1. The vertical dashed line at 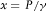 depicts the asymptote of the function.
depicts the asymptote of the function.3 DATA AND PREPROCRESSING
The same set of data as in the work of Fischer et al. (2009) was utilised in order to test the presented model, i.e., earthquake source observations recorded during a hydrofracturing process carried out at the Canyon Sands gas field in West Texas.A hydraulic stimulation of tight sand formation was applied in a depth interval from 1600 to 1800 m that was vertically divided into four stages numbered 1 to 4 (Fischer et al. 2008; see Fig. 3). Note the highly asymmetric fracture, in particular, in the depth layers of stages 3 and 4.
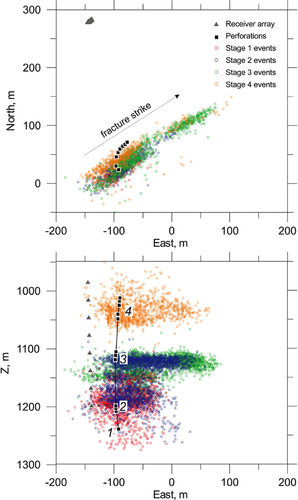
The horizontal distributions of microseismic events in space and time registered at stages 2, 3, and 4 have been utilised in this paper. The clouds of their locations are elongated in a direction that will be denoted by x (see below). Moreover, it is apparent that, in this direction, the centroid of the cloud is shifted from the position of the injection well. A possible interpretation is that the speed of propagation of one of the wings is higher than that of the other.
In order to compare the measured data with predictions obtained by the presented model, we transform the original horizontal space coordinates  into horizontal coordinates
into horizontal coordinates  , which are chosen so that their origin lies at the point of injection and that the x-axis is oriented in the direction of the shorter wing.
, which are chosen so that their origin lies at the point of injection and that the x-axis is oriented in the direction of the shorter wing.
 the x-coordinate of the event appearing in the chosen stage at time
the x-coordinate of the event appearing in the chosen stage at time  . Let us assume that the following set of couples:
. Let us assume that the following set of couples:
 (14)
(14)
Analysing the data of x-coordinates versus time, we can see that the microseismic events are not connected with the fracture tips exclusively; they continue to appear along the whole range that has already been marked. On the other hand, the length of this range increases with time so that it can be assumed that the events appearing at its bounds mark the positions of the fracture tips.
The first step of the data treatment was to separate those events of the whole set that can be considered as indicating the positions of the fracture tips at corresponding time instants. Two possible ways, A and B, of such a separation have been suggested and presented as follows:
A. The analysed time period is divided into equidistant time intervals with starting time ϑ0, time step d, and a half-width h. We denote 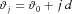 , and for each time interval
, and for each time interval  , the minimum
, the minimum 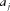 and maximum
and maximum  of the event x-coordinate are determined,
of the event x-coordinate are determined,  , where M is sufficiently large to cover the considered set of events.
, where M is sufficiently large to cover the considered set of events.
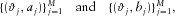 (15)
(15) (16)
(16)In the sequel, the sequences will be presented and utilised without the outliers and after the renumbering of the remaining members. The resulting number of members of the  sequence is denoted by N1, whereas N2 denotes the resulting number of members of the
sequence is denoted by N1, whereas N2 denotes the resulting number of members of the 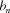 sequence.
sequence.
An example of such sequences, based on the microseismic events of the second stage for  and
and  s (50% overlap), is shown in Fig. 5. It should be noted that these sets are not subsets of the set in equation 14.
s (50% overlap), is shown in Fig. 5. It should be noted that these sets are not subsets of the set in equation 14.

 and
and  obtained for stage 2.
obtained for stage 2. (17)
(17)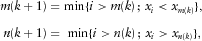 (18)
(18)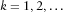 until the sets on the right-hand side are empty. We denote by M1 and M2 the last obtained indexes. The resulting sequences of times and locations are then, as follows:
until the sets on the right-hand side are empty. We denote by M1 and M2 the last obtained indexes. The resulting sequences of times and locations are then, as follows:
 (19)
(19)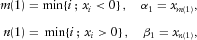 (20)
(20)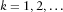 ,
,
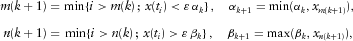 (21)
(21) is the relaxation factor. Similarly, as previously, we obtain the following two subsequences:
is the relaxation factor. Similarly, as previously, we obtain the following two subsequences:
 (22)
(22) and
and  .
.  switches off the relaxation and gives the sequences in equation 19, whereas
switches off the relaxation and gives the sequences in equation 19, whereas  is over-relaxation, which gives the complete sequence in equation 14. Sequences
is over-relaxation, which gives the complete sequence in equation 14. Sequences  and
and  defined in equation 19 are monotonous, whereas those defined in equation 22, generally, are not. Figure 6 shows the sequences in equation 22 obtained for the second stage and
defined in equation 19 are monotonous, whereas those defined in equation 22, generally, are not. Figure 6 shows the sequences in equation 22 obtained for the second stage and  . Unlike the sets of couples in equation 15, the sets in equation 22 are always subsets of the set in equation 14.
. Unlike the sets of couples in equation 15, the sets in equation 22 are always subsets of the set in equation 14.
 and
and  obtained for stage 2 and
obtained for stage 2 and  .
.4 PARAMETER DETERMINATION
As the sequences in equations 15 and 22 are supposed to indicate the positions of the fracture tips, they can be utilised to determine unknown parameters in equation 10. The form of equation 10 does not make it possible to distinguish between parameters P and γ. From the viewpoint of parameter determination, the solution in equation 10 is a two-parameter function with parameters 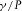 and
and  or
or 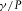 and
and  . Hence, P and γ cannot be both determined unless an additional information is involved. According to their nature and our assumptions, parameters P and γ are defined for a stage and the fraction
. Hence, P and γ cannot be both determined unless an additional information is involved. According to their nature and our assumptions, parameters P and γ are defined for a stage and the fraction 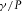 has a unique value for both wings of the fracture. On the other hand, parameter K is a characteristic of a fracture wing, and since the wings differ in the length and the solid-phase stress τ22, they can differ in parameter K. In view of this, the optimisation will be done for three parameters at each stage:
has a unique value for both wings of the fracture. On the other hand, parameter K is a characteristic of a fracture wing, and since the wings differ in the length and the solid-phase stress τ22, they can differ in parameter K. In view of this, the optimisation will be done for three parameters at each stage:  ,
,  , and
, and 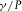 , where
, where  and
and  are the conductivities of the positive
are the conductivities of the positive  and the negative
and the negative  fracture wings, respectively.
fracture wings, respectively.
To determine the parameters, we make use of the least-squares method applied to the differences between the measured and calculated values of function ξ. Either of the datasets in equations 15 and 22 can be utilised as the measured data.
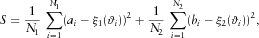 (23)
(23)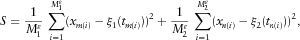 (24)
(24)The final determination of values  , and
, and 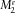 that terminate the applied data sequences was done with respect to the length of the period of pumping into the borehole. For stages 2, 3, and 4, the periods were 1290, 1580, and 1740 s, respectively, i.e., those couples
that terminate the applied data sequences was done with respect to the length of the period of pumping into the borehole. For stages 2, 3, and 4, the periods were 1290, 1580, and 1740 s, respectively, i.e., those couples  were excluded, where
were excluded, where  exceeded the corresponding bound. In Fig. 7 and in the following figures depicting the obtained results, the periods are shown by solid parts of resulting curves.
exceeded the corresponding bound. In Fig. 7 and in the following figures depicting the obtained results, the periods are shown by solid parts of resulting curves.

There is an important feature of the minimising problem that we meet when determining the parameters  ,
,  , and
, and 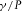 . The sum S given by either equation 23 or 24 can change very little with a significant change of the parameters. It is minimised along curves in
. The sum S given by either equation 23 or 24 can change very little with a significant change of the parameters. It is minimised along curves in  rather than at points in
rather than at points in  , and this holds for all the three stages. The relative difference of values of the sum S can be less than 1%, whereas the relative difference of the parameters
, and this holds for all the three stages. The relative difference of values of the sum S can be less than 1%, whereas the relative difference of the parameters 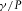 is over 50%. If we take into account the fact that the set of microseismic events chosen for the optimisation can hardly be determined uniquely, we have to consider the problem of the optimisation of parameters
is over 50%. If we take into account the fact that the set of microseismic events chosen for the optimisation can hardly be determined uniquely, we have to consider the problem of the optimisation of parameters 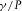 ,
,  , and
, and  ill posed. On the other hand, with the parameter
ill posed. On the other hand, with the parameter 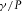 being given, the sums in equations 23 and 24, as functions of two parameters
being given, the sums in equations 23 and 24, as functions of two parameters  and
and  , take sharp minimum values. In view of this, the parameter
, take sharp minimum values. In view of this, the parameter 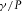 was chosen uniquely for each stage as a point lying between the values that minimised the sum S for the stage and both Methods A and B.
was chosen uniquely for each stage as a point lying between the values that minimised the sum S for the stage and both Methods A and B.
Table 1 presents the parameters 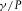 ,
,  , and
, and  that minimised the sum in equation 23 by making use of the dataset in equation 15 of stages 2, 3, and 4. The development in time of the fracture (functions ξ1 and ξ2) in the fourth stage based on the obtained parameters is depicted in Fig. 7.
that minimised the sum in equation 23 by making use of the dataset in equation 15 of stages 2, 3, and 4. The development in time of the fracture (functions ξ1 and ξ2) in the fourth stage based on the obtained parameters is depicted in Fig. 7.
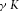 of fracture wings obtained using method A; data in equation 15
of fracture wings obtained using method A; data in equation 15| Method | 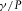 |
 |
 |
|---|---|---|---|
| A | m−1 | m s−1 | m s−1 |
| Stage 2 |  |
 |
 |
| Stage 3 |  |
 |
 |
| Stage 4 |  |
 |
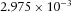 |
The parameters 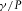 ,
,  , and
, and  obtained again for stages 2, 3, and 4 by using the data in equation 22 and minimising the sum in equation 24 are presented in Table 2.
obtained again for stages 2, 3, and 4 by using the data in equation 22 and minimising the sum in equation 24 are presented in Table 2.
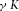 of fracture wings obtained using the data in equation 22
of fracture wings obtained using the data in equation 22| Method | 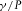 |
 |
 |
|---|---|---|---|
| B | m−1 | m s−1 | m s−1 |
| Stage 2 |  |
 |
 |
| Stage 3 |  |
 |
 |
| Stage 4 |  |
 |
 |
The results obtained for the same stage by minimising the sum in equation 24 are shown in Fig. 8. The same way of depiction is used in Figs. 9 and 10 that show the corresponding results for stages 2 and 3 obtained by optimizing both kinds of datasets in equations 15 and 22.

 and
and  consist of the set of microseismic events locations in equation 22. The functions
consist of the set of microseismic events locations in equation 22. The functions  and
and  in these figures consist of two parts showing the theoretical development of the fracture during the period of pumping (solid line) and how would the fracture develop providing the pumping continues (dashed line).
in these figures consist of two parts showing the theoretical development of the fracture during the period of pumping (solid line) and how would the fracture develop providing the pumping continues (dashed line).
 and
and  , and the set of microseismic events locations.
, and the set of microseismic events locations.
 and
and  and the set of microseismic events locations
and the set of microseismic events locations5 DISCUSSION
When solving a direct problem, the model requires five parameters; see equation 6. Three of them, 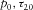 , and γ, are measurable; the remaining two are difficult to measure. On the other hand, when solving the inverse problem related to the presented data, the model has two parameters for each fracture wing; one of these parameters is common for both wings of the fracture. This results from the inner structure of the model. As it was shown above, the parameters are grouped and the new ones are
, and γ, are measurable; the remaining two are difficult to measure. On the other hand, when solving the inverse problem related to the presented data, the model has two parameters for each fracture wing; one of these parameters is common for both wings of the fracture. This results from the inner structure of the model. As it was shown above, the parameters are grouped and the new ones are 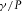 and
and  ; see the first paragraph of Section 4. Consequently, not all the parameters initially involved in the model can be determined from the applied set of data. We were able to determine the grouped parameters, although with a certain range of inaccuracy for the first one. To be able to determine the fracture conductivity K, it is necessary to get the value of parameter γ from another source.
; see the first paragraph of Section 4. Consequently, not all the parameters initially involved in the model can be determined from the applied set of data. We were able to determine the grouped parameters, although with a certain range of inaccuracy for the first one. To be able to determine the fracture conductivity K, it is necessary to get the value of parameter γ from another source.
The data utilised in this paper were also utilised by Fischer et al. (2009) in order to test their model. Their suggestions of values of 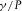 , which they denote as large, exceed those obtained in this study by factors ranging from 1.3 to 80 for individual stages. The large range of this ratio reflects the above-mentioned ill-posed problem of determining the gradient. The systematic character of this difference, however, appears to reflect other systematic effects. The following one is likely to play a role.
, which they denote as large, exceed those obtained in this study by factors ranging from 1.3 to 80 for individual stages. The large range of this ratio reflects the above-mentioned ill-posed problem of determining the gradient. The systematic character of this difference, however, appears to reflect other systematic effects. The following one is likely to play a role.
When solving the inverse problem for a fracture, our model includes three parameters: besides the stress gradient term 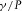 , we search for two fracture conductivity terms—a single one for each fracture wing. As expected, the longer fracture wings, growing to negative coordinates, show higher conductivities; an approximate factor of two has been found for all the cases (see Tables 1 and 2). Since the wider fracture wing takes more injected water, which enables the wing to grow faster, a positive feedback acts between the length of the fracture and its aperture until the length of the longer wing sufficiently lowers its hydraulic gradient.It was found that increasing the chosen value of the stress gradient γ results in a decrease of the obtained ratio
, we search for two fracture conductivity terms—a single one for each fracture wing. As expected, the longer fracture wings, growing to negative coordinates, show higher conductivities; an approximate factor of two has been found for all the cases (see Tables 1 and 2). Since the wider fracture wing takes more injected water, which enables the wing to grow faster, a positive feedback acts between the length of the fracture and its aperture until the length of the longer wing sufficiently lowers its hydraulic gradient.It was found that increasing the chosen value of the stress gradient γ results in a decrease of the obtained ratio 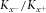 . It can be expected that imposing a unique value
. It can be expected that imposing a unique value  results in an overvaluation of the gradient γ. As a result, the model by Fischer et al. (2009) overestimates the stress gradient, since it does not include these difference between the wings.
results in an overvaluation of the gradient γ. As a result, the model by Fischer et al. (2009) overestimates the stress gradient, since it does not include these difference between the wings.
We admitted different values of the parameter 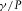 for individual stages. This was not necessary because of the low sensitivity of the sums in equations 23 and 24 to this parameter. Moreover, it can be expected that the gradient γ does not change significantly between the stages. Our reason for doing so was inherent in the parameter P, which may have different values in different stages.
for individual stages. This was not necessary because of the low sensitivity of the sums in equations 23 and 24 to this parameter. Moreover, it can be expected that the gradient γ does not change significantly between the stages. Our reason for doing so was inherent in the parameter P, which may have different values in different stages.
The available measured data are not sufficient to give information on the apertures of the fractures. Suppose we get over the problem of the described ill posedness above and obtain the couple of parameters  ,
,  , e.g., as presented in Table 1 and Table 2. We face two other problems: it is not possible to separate the parameter K without getting further information, and it is not possible to understand our value of fracture conductivity K as equal to that of Hagen–Poiseuille formula. Whereas the latter has been derived under the assumption of smooth parallel walls of the fracture, real fractures, which we follow in our study, are quite different.
, e.g., as presented in Table 1 and Table 2. We face two other problems: it is not possible to separate the parameter K without getting further information, and it is not possible to understand our value of fracture conductivity K as equal to that of Hagen–Poiseuille formula. Whereas the latter has been derived under the assumption of smooth parallel walls of the fracture, real fractures, which we follow in our study, are quite different.
Several authors (e.g., Pyrak-Nolte, Cook and Nolte 1988; Hakami et al. 1995; Hakami and Larsson 1996) published results of asperity and aperture measurements on real fractures. Their results show that the asperity exceeds the aperture size by one or two orders. Although the applied injection lowers this rate, the real aperture may be seriously underestimated when neglecting asperity and tortuosity.
The presented model assumes impervious walls of the fracture. In a real medium, there is always some flow through the porous matrix, i.e., some leakage from the fracture. This leakage is negligible initially, but its effect increases with increasing length of the fracture. It slows down the fracture's growth compared with its theoretical size and can be expected that the wings reach such lengths that the leakage from the fractures into the neighboring porous medium comes in equilibrium with the discharge pumped in. Any further increase of the fracture length can be only enabled by adding up to the discharge at the point of injection. Figures 4–7 show that the pumping periods considered in this study did not reach the size sufficient to observe the effect.
The discussed comparison of the theoretical results with the observed data shows another important phenomenon. We observe a rather surprising development of the fracture after finishing the injection. Whereas all the shorter (positive) fracture wings cease their growing, all the longer (negative) fracture wings continue their growth, even in such a rate that the model predicts for continuous injection. A similar observation was given by Fischer et al. (2008, 2009) and was interpreted in detail by Dahm et al. (2010) as the post-injection unilateral growth. Here, we note that the result obtained by our model is an independent evidence for the existence of the post-injection unilateral growth produced by pressure energy accumulated in water in the fracture and by the stress gradient γ along the fracture.
6 CONCLUSION
A mathematical model of asymmetric hydraulic fracture growth has been developed. The output of the model is the time dependence of lengths of two fracture wings that propagate from the injection point in opposite directions along a line normal to the direction of the minimum horizontal stress.
One of the input parameters, the minimum stress gradient in the direction of the fracture, was involved in order to explain the asymmetry that exhibits the utilised data.
The model was applied to a set of microseismic source observations recorded during a hydrofracturing process, and as shown above, the obtained results are in very good agreement with the measured data.
The observed data show that the longer wings of the fractures continued their growth after finishing the injection. When simulating the continuous injection by making use of parameters obtained for the period of injection, it was found that the simulated growth agrees precisely with the measured data. This agreement significantly supports the assumption of the existence of non-zero stress gradient.
The model with the utilised data does not give the aperture of the studied fracture. The problem requires either additional measurements or a more detailed study of relations between the aperture of the fracture and its conductivity. Another interesting theme of a further study might be the modelling of the post-injection unilateral growth of hydraulic fractures and particularly the size of its possible extent.



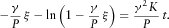
 and
and  and the set of microseismic events locations in equation
and the set of microseismic events locations in equation 
