Offset-variable density improves acoustic full-waveform inversion: a shallow marine case study
ABSTRACT
We have previously applied three-dimensional acoustic, anisotropic, full-waveform inversion to a shallow-water, wide-angle, ocean-bottom-cable dataset to obtain a high-resolution velocity model. This velocity model produced an improved match between synthetic and field data, better flattening of common-image gathers, a closer fit to well logs, and an improvement in the pre-stack depth-migrated image. Nevertheless, close examination reveals that there is a systematic mismatch between the observed and predicted data from this full-waveform inversion model, with the predicted data being consistently delayed in time. We demonstrate that this mismatch cannot be produced by systematic errors in the starting model, by errors in the assumed source wavelet, by incomplete convergence, or by the use of an insufficiently fine finite-difference mesh. Throughout these tests, the mismatch is remarkably robust with the significant exception that we do not see an analogous mismatch when inverting synthetic acoustic data. We suspect therefore that the mismatch arises because of inadequacies in the physics that are used during inversion. For ocean-bottom-cable data in shallow water at low frequency, apparent observed arrival times, in wide-angle turning-ray data, result from the characteristics of the detailed interference pattern between primary refractions, surface ghosts, and a large suite of wide-angle multiple reflected and/or multiple refracted arrivals. In these circumstances, the dynamics of individual arrivals can strongly influence the apparent arrival times of the resultant compound waveforms. In acoustic full-waveform inversion, we do not normally know the density of the seabed, and we do not properly account for finite shear velocity, finite attenuation, and fine-scale anisotropy variation, all of which can influence the relative amplitudes of different interfering arrivals, which in their turn influence the apparent kinematics. Here, we demonstrate that the introduction of a non-physical offset-variable water density during acoustic full-waveform inversion of this ocean-bottom-cable field dataset can compensate efficiently and heuristically for these inaccuracies. This approach improves the travel-time match and consequently increases both the accuracy and resolution of the final velocity model that is obtained using purely acoustic full-waveform inversion at minimal additional cost.
INTRODUCTION
Full-waveform inversion (FWI) is a technique that seeks to find a high-resolution subsurface model that is capable of matching individual seismic waveforms of a raw field dataset. In current commercial practice, an acoustic approximation to the wave equation is almost always used; the kinematic effects of anisotropy are properly included, but an independent density model is not used; and the full dynamic effects of elasticity, attenuation, and fine-scale variations in anisotropy are ignored (Plessix and Perkins 2010; Sirgue et al. 2010; Vigh, Kapoor, and Li 2011; Kapoor et al. 2013; Morgan et al. 2013; Warner et al. 2013).
Warner et al. (2013) showed that the anisotropic acoustic wave equation is sufficient for 3D FWI to generate a P-wave velocity model for depth migration, provided that trace-to-trace amplitude variations are normalized. This approach leads to a good match to the kinematics of the field data and a reasonable match to the amplitude spectra of each individual trace, and it produces a significant and verifiable improvement in the resultant velocity model. To match amplitude variations accurately however requires accurate knowledge of short-wavelength density and anisotropy variations and of attenuation and shear-wave properties (Warner et al. 2012). Elastic FWI has been applied to 3D field data (Guasch et al. 2012; Vigh, Jiao, and Watts 2012; Lu et al. 2013), but problems with crosstalk between the solution spaces, uncertainties about density, attenuation and elastic anisotropy, together with the increased computational cost, means that elastic FWI is not yet widely used in a commercial setting.
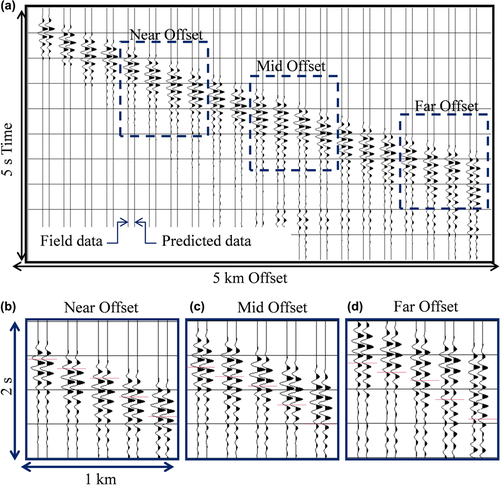
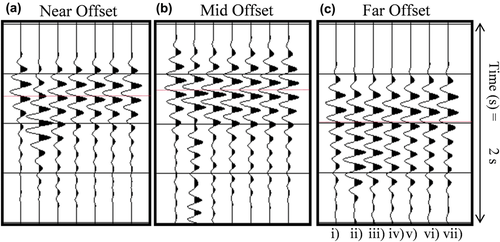
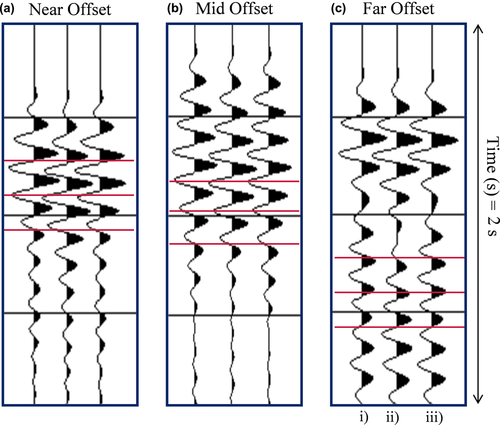
Acoustic, anisotropic FWI has been successfully applied to a 3D full azimuth ocean-bottom-cable dataset in the North Sea (Ratcliffe et al. 2011; Nangoo et al. 2012; Warner et al. 2013). FWI produced measurable improvements in the resolution of the velocity model and fidelity of the pre-stack depth-migrated image, as well as a better match to the sonic logs and a reduction in misfit between the predicted and field data. Surprisingly, however, individual peaks and troughs in the predicted data generated by the final FWI model arrive consistently late by up to 12 ms (Fig. 1). Although this mismatch is small, it should be easily resolved and removed by FWI, and we do not encounter such mismatches during the inversion of synthetic test examples. There are many potential effects in FWI that can produce systematic error in the resultant velocity model, but there are rather few of these than can produce a systematic mismatch in arrival times since FWI is specifically configured to vary the model to remove such a data mismatch.
We considered the range of possible reasons why such a mismatch might occur and ran a comprehensive suite of tests to investigate the importance of each of these. We explored inaccuracies in the timing and shape of the source wavelet, incomplete convergence resulting from too few iterations, systematic bias in the starting velocity model, and the effect of inaccurate wavefield simulation through the use of an insufficiently fine finite-difference mesh for forward modelling. In all cases, we were unable to explain, or to remove, the mismatch using such mechanisms. For example, biasing the starting velocity model to either high or low velocity leads always to a final model in which the predicted data arrive late. Shifting the source timing or changing the assumed source wavelet to remove the apparent timing mismatch, then rerunning the inversion, always restored the original mismatch. Changing the mesh size at which we invert does not change the mismatch. Using synthetic data generated on one mesh with data inverted on another does not reproduce the effect that we see in the field data. The robustness of this result leads us to conclude that the problem is most likely caused by the approximations inherent in our acoustic forward modelling, particularly when it is applied at and close to the seabed.
In an acoustic code, several effects are unaccounted for, including anelastic attenuation and elasticity. Attenuation in the shallow part of the model may be significant, for example, in changing the phase spectrum of the wavelet and creating apparent delays to the data. The implicit representation of the seabed at 75 m in a velocity model that is computed on a 50 m mesh can also introduce inaccuracies into the modelled wavefield. In addition, we use a Gardner relationship for density (Gardner et al. 1974), which is unlikely to be correct in detail, particularly in the shallowest portion of the model. Together, these effects will all tend to lead to an incorrect impedance contrast at the seabed and to incorrect variations of amplitudes with reflection angle. This in turn changes the strength of the sea-bottom multiples and strongly affects the character and coda of the wavefield (Silverton et al. 2014). This means that the approximate representation of the sea-bottom in the velocity model can produce physical effects that can cause an apparent travel-time mismatch. Here we explore an inexpensive and efficient way of dealing with such travel-time mismatch heuristically through using a non-physical offset-variable value for the density of sea water.
The density of sea water can be considered a free parameter if we use FWI to match the kinematics of seismic data. In the approach adopted here and that by Warner et al. (2013), the inversion is steered principally to match the phase spectra of each trace and, secondarily, the amplitude variation along a trace. The trace-to-trace amplitude variation, however, is not modelled. This means that we can make non-physical changes to the water density as this will affect only amplitudes and will not directly alter travel times; changing water density as a function of source–receiver offset can also be used to influence how the amplitudes of sea-bottom multiples vary with offset. While changes in density do not directly influence the kinematics of the data, changes in sea-bottom density do nonetheless affect apparent arrival times of low-frequency events in the wavefield, which result from the interference pattern between the refractions and sea-bottom multiples. That is, density changes can and do affect the positions in time of the individual troughs and peaks in composite waveforms, which act to drive FWI.
Here, we investigate the effects of changing sea water density, to test whether we can reproduce better the sea-bottom reflectivity and address the apparent travel-time mismatch without introducing other undesirable consequences. Mulder and Plessix (2008) used a similar approach when inverting a synthetic elastic dataset with an acoustic FWI code to obtain models of velocity and density. They used a variable density and found it helped address the differences in amplitude and phase between elastic and acoustic data, and led to an improvement in the recovery of velocity at the expense of density (Mulder and Plessix 2008). Here, the adopted approach has been to generate a suite of synthetics using different densities for sea water and then establish which best matches the shallow marine field data at different source–receiver offsets. We show that an offset-variable density in the water layer leads to an improved match between the field and predicted data. Using this scheme, we also find that we are able to obtain an even-higher-resolution recovered velocity model, and that this model leads to an improvement in the migrated seismic image.
PREVIOUS RESEARCH
The field dataset used for our study is from a field in the Norwegian North Sea, where there are two fractured, hydrocarbon-charged reservoirs at about 3 km depth within a broad anticline of the Cretaceous chalk. The presence of gas at depths of approximately 1 km–2 km in the overlying clastic section inhibits P-wave reflection imaging and results in a seismically obscured reservoir section (Granli et al. 1999). A high-density, full-azimuth, 3D, four-component, ocean-bottom-cable survey was acquired to help improve the images of the reservoir beneath the gas cloud. The dataset comprises three swaths of eight parallel cables, each 6 km in length, with 96,000 sources and 5,760 receivers (Warner et al. 2013). The receiver cable separation was 300 m, and receivers were spaced every 25 m along the cable in the inline direction. Airgun sources were fired using a flip-flop shooting pattern that was orthogonal to the cables, with a 75-m cross-line and 25-m inline separation. These data have good azimuthal coverage for offsets of up to 7 km, and reduced coverage to a maximum offset of 11 km. The early arriving data at each receiver are dominated by wide-angle turning rays and sea-bottom multiples (due to the shallow water depth of 75 m) and post-critical reflections at larger offsets. The presence of strong refractions, as well as the large offsets and good azimuthal coverage, make this dataset particularly favourable for full-waveform inversion (FWI).
3D acoustic, anisotropic FWI was undertaken with the aim of improving the imaging beneath the seismically obscured region, thereby allowing for better interpretation of the underlying chalk reservoirs (Ratcliffe et al. 2011; Nangoo et al. 2012; Warner et al. 2013). We used an anisotropic starting model that was generated for pre-stack depth-migration (PSDM) by the original processing contractor. The gas cloud region lies close to the centre of the survey; there are four wells within the survey area that either penetrate the gas cloud or are located on its periphery. Data preprocessing included a top mute ahead of the first arrivals, deletion of bad traces, low-pass filtering of the data to the required frequency range for FWI, and a bottom mute that was designed primarily to remove Scholte waves (Warner et al. 2013). FWI was then performed for a frequency range of 3.0 Hz–6.5 Hz incrementing linearly for six frequency bands to recover a high-resolution velocity model. This FWI velocity model better matches the well logs, improves the flattening of common image gathers, and improves the PSDM image. Thus, acoustic 3D FWI improved the velocity characterization of the thin, shallow gas-charged layers, as well as the imaging beneath the seismic obscured area.
Although the data misfit improved substantially during FWI, a close examination of the observed and predicted synthetics (Fig. 1) and phase plots revealed an approximate systematic mismatch of up to 12 ms, equivalent to about 30° of phase at the frequencies used here (Shah et al. 2012; Warner et al. 2013; Silverton et al. 2014). In addition, this delay gradually increases with time for individual arrivals (Fig. 1). We thus ran a suite of tests to verify whether we could gain a better understanding of this unexplained mismatch and remove the misfit.
TESTS TO IMPROVE MISMATCH
In view of the unexplained mismatch, we ran a suite of tests to verify whether we could remove the misfit by making adjustments to the source, increasing the number of iterations, or perturbing the starting velocity model.
Varying the source wavelet
The accuracy of the source wavelet is important for full-waveform inversion (FWI) particularly at the lowest frequencies (Lua et al. 2007; Warner et al. 2012). During our original inversion, we initially attempted to use the wavelet supplied by the acquisition contractor. This however leads to a poor match between the observed and predicted first arrivals at short offsets at the lowest frequencies (Warner et al. 2013). This is unsurprising since the simulations used to generate these wavelets are of only short duration, are designed to produce a good match at higher frequencies only, and do not attempt to model the bubble correctly; consequently, they provide only a poor representation of the true source at the very low frequencies used to begin FWI. Consequently, we instead obtained the source wavelet from the direct arrivals recorded on short-offset ocean-bottom hydrophones. From these, we removed the source ghost and the first and second seafloor multiples, correctly taking into account the finite offset and the effects of divergence, and applying a low-pass Ormsby filter rolling off from 5.0 Hz to 7.5 Hz (Warner et al. 2010). The ghost and sea-bottom multiples are regenerated when we forward model the wavefield during FWI through the use of a free-surface boundary condition. This approach provides an extremely accurate match to the field data at short offset prior to inversion. If we then follow this with direct source inversion in an attempt to improve the match further, minimal additional changes to the source wavelet occur, and critically, such an inverted wavelet does not contain any systematic time shift that would serve to compensate the effect that we are here seeking to explain.
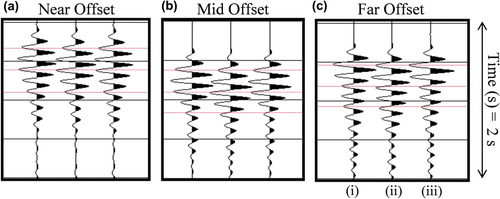
Since the predicted data arrive late, a potential cause is that the source is delayed at the frequencies used for the inversion. To investigate this, we advanced the source wavelet in time and repeated the inversion. If the apparent time delay were a function of source timing errors, then this test would tend to remove, or at the very least tend to change, the apparent time delay. We found however that the final inverted model was almost indistinguishable from that originally recovered, and critically, the delay in the predicted data remained (Fig. 2). We conclude from this, and a suite of similar tests on source timing and source inversion, that errors in the source cannot explain the mismatch—such errors may produce errors in the velocity model, but they cannot prevent FWI from bringing the observed and predicted data into close temporal alignment.
Increasing the number of iterations
FWI is a local optimization scheme whereby we minimize the misfit function so that the difference between the observed and predicted data gradually reduces towards zero. Thus, it is possible that the inversion has not yet converged to the global minimum model and that we might continue to reduce the travel-time mismatch if we continue to iterate. Hence, we doubled the number of iterations in each frequency band, thereby yielding a final model after 216 iterations for the inversion. When we do this, we see no further improvement in the travel-time mismatch, and the delay remained (Fig. 3). We also obtain substantially the same result when we reinvert from this final model, restarting from low to high frequency.
Perturbing the velocity model
A poor initial starting model may result in incomplete global convergence, with the inversion converging to a local minimum. As the predicted data were systematically late, we perturbed the final velocity model, increasing the velocity model everywhere by 1%, such that the predicted data were initially systematically early in time with respect to the field data. If the observed mismatch is caused by a systematic error in the starting model, then perturbing the velocity model in this fashion and then rerunning the inversion should lead to either a better final travel-time fit or a mismatch of the opposite sense – such that the predicted data would then be systematically early instead of late. However, we found, as with all our tests, that the model velocities were reduced by FWI to their original lower values, and that the final predicted data were returned to their original delayed state (Fig. 3).
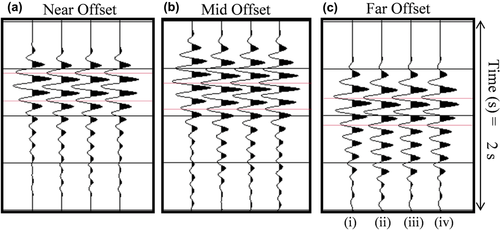
This result is particularly revealing. It demonstrates that the best fitting model is indeed the one that produces data that appear to be systematically late since forcing the predicted data initially to be early still leads to a final outcome that is late. We believe that the final FWI recovered model by both strategies results in a data match, whereby convergence is complete. Whether we increase the number of iterations or perturb the model, we found that the end results are the same in both velocity and residual – the delay in the predicted data remains.
Changing the finite-difference grid spacing
In this study, we used a finite-difference scheme for the forward modelling that employed a 50 m mesh size. In this survey, the water depth is about 75 m. In finite-difference modelling schemes, the water bottom is not defined explicitly in the model. Rather, it is defined implicitly, in this case with the velocity at 50 m being that of water and the velocity at 100 m being that of the sub-seabed. Given the coarse mesh and shallow water, it is possible that the travel-time mismatch could be caused by an inaccurate representation of the sea-bottom boundary. We investigated this by using a range of different mesh sizes, from 50 m to 15 m, generating predicted data for each one, and comparing their accuracy. We found that, regardless of the mesh size, the timing of the predicted data remained unchanged—an example of this with a 20 m mesh size is shown in Fig. 4.
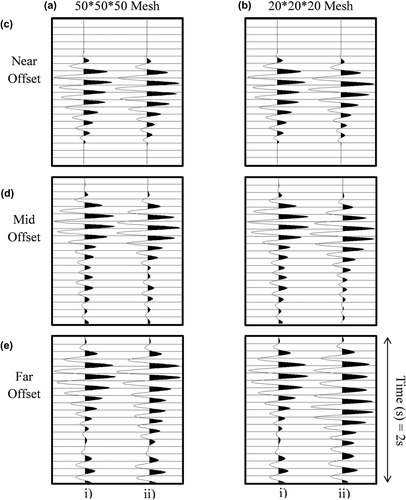
We note also, that even if a modelling scheme or representation of a sharp boundary is inaccurate, this will lead FWI to change the velocity model to improve the data fit. This means that the resultant velocity model recovered by the inversion may be wrong, but the resultant synthetic data will still provide a good match to the observed data—it is this match that drives FWI, and it is this mismatch that FWI always seeks to minimize. FWI will minimize the data mismatch whether or not it is caused by the velocity model, by numerical inadequacies in the model scheme, or by inadequacies in the source wavelet. The fact that the apparent timing mismatch is robust throughout all these tests carries the message that something more subtle is happening here.
Test conclusions
The obvious potential simple explanations for the temporal mismatch that we observe are not correct. Further, we do not observe analogous systematic delays in the predicted data when inverting data from synthetic velocity examples, whether or not the original data were generated with a different source or on a different mesh size. As such, we presume that the mismatch is likely to be due to physical effects that are not properly accounted for when inverting field data. One possibility is that this mismatch is attributable to the shallow portion of the model and particularly to the multiple-generating properties of the seabed.
The seabed is a significant boundary because there is a large difference in acoustic impedance between water and rock, and P-wave reflectivity and transmission amplitudes are strongly affected by conversions to transmitted S-waves and by an unknown density contrast at the seabed. Without being able to populate models of near-surface density, attenuation, anisotropy, and elastic properties, the seabed reflectivity, and particularly its variation with angle and frequency, cannot be properly modeled, and we do not have the data required to invert for these properties convincingly. Thus, the mismatch observed may indeed be caused by an inadequate representation of the shallow part of the model.
In an acoustic inversion, FWI will attempt to match the travel times of the early arriving wavefield (a function of the water velocity and depth, and sub-seafloor velocity) and the water-bottom multiples (a function of the water velocity, water depth, and impedance contrast at the seabed). In an attempt to improve the match between the observed and predicted data, we explored the possibility of using non-physical values for water density since density is the simplest parameter that we can freely change to alter amplitudes without introducing kinematic errors.
USE OF A NON-PHYSICAL WATER DENSITY
We performed a heuristic investigation, to determine the effect of different water densities on the arriving wavefield. Data were generated using the original, recovered full-waveform inversion (FWI) velocity model (after 108 iterations) but with a variety of non-physical densities in the water layer. The use of non-physical water densities changes the apparent travel times (Fig. 5) because the early arriving wavefield is in reality an interference pattern between refracted and sea-bottom multiple arrivals. Changing the density of the water layer alters the relative strength of the water-bottom multiples and thus changes the positions of individual peaks and troughs within the extended wave train. This in turn changes apparent arrival times. The predicted and field data can be compared to determine which densities provide the best match. Figure 5 shows that, at short offsets, a better match is produced using a water density of about 500 kg·m−3, whereas at longer offsets, a better apparent travel-time match is obtained using a density of about 250 kg·m−3. A quantitative representation of this is shown in Fig. 6.
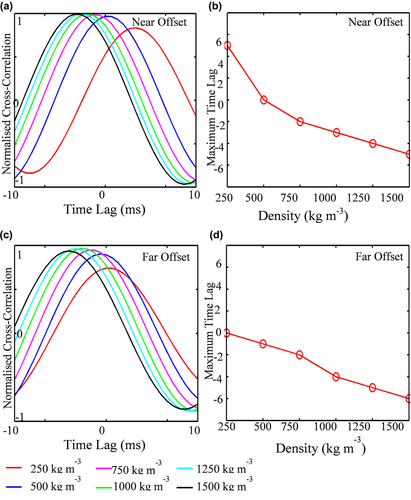
The normalized cross-correlation between the field and forward-model synthetics for different water densities show time lags ranging between 5 ms and 12 ms (Fig. 6a, c). Furthermore, the relationship between density and maximum correlation lag (Fig. 6b, d) emphasizes that at a density of ∼500 kg m−3 for near offsets and ∼250 kg m−3 for far offsets, there is a near-perfect match between the two datasets corresponding to a time lag of zero. This suggests that an offset-variable model of water density should be able to remove the systematic mismatch obtained in our original inversions.
Implementation
Our inversions are computed source by source, i.e., the wavefield is calculated for one source at a time. Consequently, it is feasible to simulate an offset-dependent density in the water layer during the forward calculation; the water-density model for every source position is different, and this density is a function of distance from the source. The specific values for density were fixed by the non-physical density tests (Figs. 5 and 6); at zero offset, the density was set to 500 kg·m−3, and this was reduced to 250 kg·m−3 at the largest offsets. The zero-offset density is initially kept constant and then, at a specified offset, is decreased linearly until it reaches the far-offset density at a specified distance from the source. A variation of offset-dependent water density with shot location has not been applied here, given the consistency of the shot records across the dataset, and that we are using offset principally of a proxy for incident angle at the seabed. In more complicated sections, it might be beneficial to allow offset-dependent water density to vary with shot location in datasets where the near surface is less laterally homogeneous.
This change in water density with increasing offset appears to be able to reproduce the change in amplitudes of the sea-bottom multiples for different seabed reflection angles that occur in the field data but that do not occur in pure acoustic modelling. When the model velocity values are above that of water velocity, the density model is populated in the normal way, following Gardner's law (Gardner, Gardner, and Gregory 1974), proven to be a sufficient approximation regardless of the geological environment, in many FWI applications (Borisov et al. 2014). Using this scheme, we ran the inversion again using the original parameterization and inversion strategies.
RESULTS
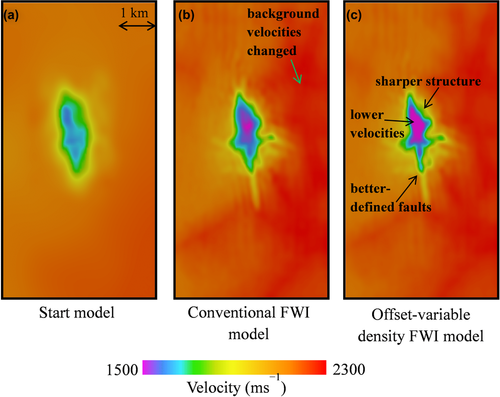
Figures 7 and 8 show horizontal and vertical slices through the starting velocity model, original velocity model recovered using FWI (from Warner et al. 2013), and the new velocity model recovered using FWI with an offset-variable density scheme. In these slices, we can see that the new velocity model is sharper, has stronger negative velocity anomalies within the gas cloud, and appears to resolve better the faults leading away from the gas cloud. The vertical pseudo-wells through the original and offset-variable FWI models as compared with the well log profile for this field confirms that the offset-variable density scheme does in fact improve the model resolution and fidelity (Fig. 9).

Synthetics were generated to investigate whether the velocity model generated using the offset-variable density scheme had addressed the systematic travel-time mismatch. Figure 10 shows a comparison between the synthetics generated by both the original and offset-variable FWI models and the field data. The systematic mismatch evident with the synthetic obtained using original FWI is less evident in the offset-variable FWI synthetic. The wave train remains similar in amplitude and phase, and the delay is now absent. The visible improvement in the match between the field and predicted data (Fig. 10) is confirmed by a reduction in the objective function.
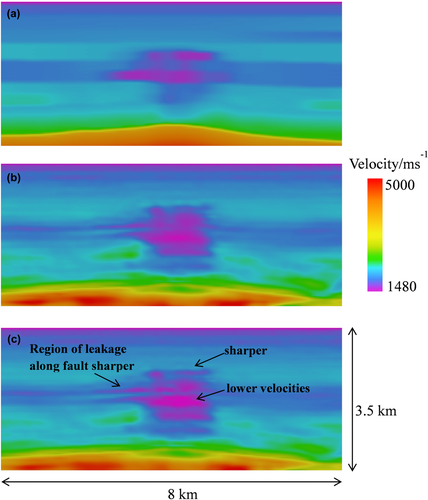
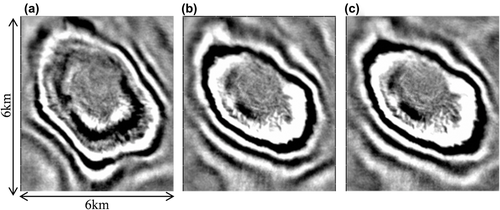
To test further whether the model recovered using an offset-variable density is a better representation of subsurface velocity, the velocity model was used to migrate the reflection data using reverse time migration (RTM) (Fig. 11).

The input data to the migration include the original 3D contractor's model of anisotropy, the source wavelet used in FWI, and the FWI recovered model processed to remove edge effects that were introduced during FWI. The processing of the FWI model entailed ramping the FWI velocity model smoothly back into the starting model around the periphery of the model. This processing resulted in small qualitative differences in the migrations using the original and newly recovered FWI models. A defined density was not used in the migration and processes such as smoothing to remove a minor shallow acquisition footprint were also not undertaken. The migrations were performed on a 50 m mesh, as was the case for the FWI.
It is apparent that the reflectors in this migration show better continuity; directly above the broad anticline faults and horizons are clearer and simpler. With a delayed compactional diagenesis and the onset of hydrocarbon production at the reservoir, leading to an unexpected degree of subsidence, we expect the anticlinal structure to be symmetric. We found that the rim of the anticlinal structure is subtly smoother due to the offset-variable density approach; therefore, we believe that the RTM image with this scheme yields a much more geologically plausible result (Fig. 12).
CONCLUSIONS
For the inversions of the shallow marine field dataset shown here, the predicted data from our original recovered full-waveform inversion (FWI) velocity models were delayed with respect to the field data, and the delay was more apparent at later arrival times. Here, we have shown that the delay was not caused by using an incorrect source, incomplete convergence, or the use of a poor starting velocity model. The mismatch may be a common occurrence when using acoustic FWI codes, together with imprecise density and attenuation models, to invert field data that have previously gone unnoticed because the delay is quite small. The delay may be more pronounced in the dataset used here as a result of the shallow water and presence of strong water-bottom multiples. We are unclear as to the precise cause of the apparent delay, given that there are several effects that are not properly accounted for (fine-scale anisotropy, anelastic attenuation, and elasticity) and that the wavefield will not be accurately modelled if the density and/or velocity contrast at the seabed are incorrect or are incorrectly captured on a coarse mesh. In this study, sea water density values were chosen empirically, based upon the observed match between predicted and field data for selected gathers. However in principle, it would be straightforward to invert for the optimal density variation with offset during conventional acoustic FWI.
We have demonstrated that using non-physical water densities can improve the match between the predicted and field data and that this leads to an improvement in resolution in the recovered velocity model, with the shallow gas anomaly and associated fault structures better defined, leading to higher fidelity of the final RTM image. This suggests that inaccuracies in modelling the wavefield at the seabed, which are caused by a variety of phenomena, can be addressed and at least partially compensated through the use of a non-physical, offset-variable density in the water layer. This is a simple, efficient, and effective scheme that improves the performance of acoustic FWI when applied to 3D field data.
ACKNOWLEDGEMENTS
The authors would like to thank the PL044 partnership: ConocoPhillips Skandinavia AS, Total E&P Norge AS, ENI Norge AS, Statoil Petroleum AS for their kind permission to use their data and publish this work. Imperial College London wishes to thank the sponsors of the FULLWAVE consortia. CGG is thanked for providing the RTM images. The 3D ProMAX/SeisSpace package, supplied by Halliburton under a university software grant, was used to preprocess and analyze the data within Imperial College.




