An Efficient Nonmarket Institution under Imperfect Markets: Labor Sharing for Tropical Forest Clearing
The authors gratefully acknowledge the people of our two study villages for their kind collaboration that made this project possible. Rinda Mozombite, Limber Barbarán, and Carlos Rengifo Upiachihua provided valuable assistance in the field. This article benefited significantly from the insightful comments and suggestions of Clément Imbert, Daiji Kawaguchi, Takashi Kurosaki, and conference and seminar participants on an earlier version of this work presented at NEUDC (2011, Yale) and Hitotsubashi University. We thank Edward Taylor, the co-editor, and two anonymous referees for their most helpful comments and suggestions. Funding support was provided by the Social Science and Humanities Research Council of Canada, The Fonds Quebeçois pour la Formation de Chercheurs et l'Aide à la Recherche (FCAR), McGill University, University of Toronto, and the Japan Society for the Promotion of Science.
Abstract
This article examines the substitutability, productivity, efficiency, and evolution of an important agrarian nonmarket institution—labor sharing. Analysis of field-level data on forest clearing through time among Amazonian shifting cultivators reveals that (a) family, hired, and cooperative labor are perfect substitutes, and hired and cooperative labor are equally productive, and both are more productive than family labor; (b) the combination of labor market and labor sharing makes productivity-adjusted total labor use unconstrained by household and network endowments (i.e., efficient labor allocation); and (c) as labor composition is constrained by network endowments and liquidity, credit policies alter both labor composition and labor network formation.
In rural developing areas where market institutions are missing or imperfect, how informal, nonmarket institutions serve as market substitutes for better resource allocation is a central question. In peasant agriculture, credit market imperfections often preclude poor farmers with limited working capital from hiring sufficient labor, although they need extra-family labor to accomplish certain tasks such as weeding, harvesting, and field opening. Peasant farmers have long resorted to labor-sharing arrangements, which are given various names depending on locales and contexts, such as cooperative labor, reciprocal labor, collective labor, communal labor, exchange labor, festive labor, work group, and work party (Eras- mus 1956; Moore 1975). Distinct from hired labor for which buyers pay market wages, the cost of cooperative labor reflects the opportunity cost of labor to be reciprocated and the costs of drink/food to be offered to the laborers. Ethnographic studies have shown that labor-sharing institutions remain common around the world and persist alongside rural labor markets (e.g., Chibnik and de Jong 1989; Donaldson 2011; Downey 2010; Geschiere 1995; Guillet 1980; Sajor 2000; Şaul 1983; Worby 1995). Although development economists have extensively studied agrarian contracts such as share cropping (e.g., Bardhan 1989), agricultural labor sharing has not been given comparable treatment (for exceptions, see Kevane 1994; Gilligan 2004); this is in contrast with extensive economic analyses of reciprocal nonmarket institutions such as risk sharing (Coate and Ravallion 1993; Ligon, Thomas, and Worrall 2002) and credit arrangements (Besley, Coate, and Loury 1993).
Reciprocal labor-sharing arrangements with limited commitment can be considered analogous to informal risk sharing (Coate and Ravallion 1993; Ligon, Thomas, and Worrall 2002). Incentive and/or enforcement problems associated with securing cooperative labor for one's farm over time may be mitigated through reputational mechanisms (Ernst, Gächter, and Kirchsteiger 1997), social norms (Bandiera, Barankay, and Rasul 2010), mutual monitoring, peer pressure (Kandel and Lazear 1992; Mas and Moretti 2009), and high returns to teamwork (Hamilton, Nickerson, and Owan 2003), as found in other work settings; these and other factors may even make cooperative labor more productive than family labor. Similarly, if wage labor contracts are not based on an anonymous spot market but on personalized, repeated interaction, reputational mechanisms for future employment may mitigate incentive problems in hired labor even without reciprocity (i.e., analogous to a permanent labor contract in contrast with a casual labor contract; Dutta, Ray, and Sengupta 1989); this is especially so when employment opportunities are limited in poor communities.
Using original field-level data on forest clearing through time among shifting cultivators in the Peruvian Amazon, where land is claimed by clearing and held in usufruct (i.e., land market is missing) and credit is scarce, this article examines the substitutability, productivity, efficiency, and institutional evolution of cooperative labor sharing. Specifically, we pursue three lines of enquiry as follows.
First, are family, hired, and cooperative labor perfect substitutes, and are they as productive as one another? The extant literature shows mixed empirical findings on substitutability and productivity of hired and family labor for agriculture, although not explicitly for field opening (e.g., Bardhan 1973; Brown and Salkin 1974; Deolalikar and Vijvergerg 1983; Deolalikar and Vijvergerg 1987; Desai and Mazumdar 1970; Frisvold 1994; Pitt and Rosenzweig 1986). Although no previous works examine the substitutability of labor sharing, interhousehold labor reciprocation may facilitate labor substitution, and the simplicity of forest clearing task may make them perfect substitutes. Put differently, if perfect substitutability of labor inputs is possible, we expect that this would be so for forest clearing among shifting cultivators; as such, this article serves as a benchmark case for the study of rural labor substitution. To our knowledge, the only extant study on the productivity of agricultural labor sharing was conducted by Gilligan (2004), who finds that Indonesian exchange labor is more productive than family and hired labor by estimating Cobb–Douglas production function (with unitary elasticities of substitution). We estimate two-level constant-elasticity-of-substitution (CES) production functions for forest clearing with family, hired, and cooperative labor as separate inputs, controlling for household fixed effects; our results show infinite elasticities of substitution (i.e., perfect substitutes), equal productivity of hired and cooperative labor, and their higher productivity compared with family labor. We offer evidence that extra-family laborers are younger and more highly motivated and thus more productive than family laborers.
Second, does the combination of labor market and sharing enable efficient labor allocation, despite market imperfections? When markets are perfect, household consumption (labor supply) and production (labor demand) decisions are separated (Singh, Squire, and Strauss 1986; Taylor and Adelman 2003). The well-established test for this separability hypothesis is to see whether total labor use follows market wages, unconstrained by household demographic characteristics (Benjamin 1992); inseparability makes labor demand dependent on the household shadow wage determined by supply factors. Whereas extant empirical results on separability are mixed (e.g., Benjamin 1992; Kevane 1996; López 1986; Pitt and Rosenzweig 1986), agricultural household models have not yet been extended to incorporate nonmarket labor institutions. Although extending a theory of agricultural household model with labor sharing is beyond the scope of this article, we augment the separability test: a null hypothesis is that labor demand is unconstrained not only by household demographic characteristics but also by network characteristics, given that labor-sharing arrangements are organized by household networks (as risk-sharing arrangements are; e.g., Fafchamps and Gubert 2007; Fafchamps and Lund 2003).1 We develop an empirical model that does not involve potential identification problems associated with network formation by using kinship as exogenous determinants of labor-sharing networks. Importantly, both the conventional and augmented separability tests assume perfect substitutability of labor inputs; distinct from most extant works, we first test this critical assumption. Even if the perfect substitutability holds, productivity differences of labor inputs, if any, need to be considered in the separability tests; in contrast with most previous studies, we first estimate the productivity difference and use productivity-adjusted total labor use. Our results do not strongly reject separability, suggesting that forest clearing is labor efficient and responsive to market prices (see de Janvry, Fafchamps, and Sadoulet 1991).
Third, how do market and nonmarket institutions for labor allocation coevolve in response to economic policies? We use credit policies, which were introduced in one of our sample villages, as a “natural experiment” to address this question. Kranton (1996) demonstrates theoretically that market and nonmarket reciprocal institutions interact with each other through mutually imposed external costs—search costs in an anonymous market and enforcement costs in personalized reciprocal exchanges—and that the persistence of one institution over the other depends on the initial distribution of participants in these two institutions. Although both market and nonmarket institutions are personalized in our context (and in many other rural developing areas), the key implications of Kranton's (1996) work still hold; as credit relaxes liquidity constraints and labor market exchange expands, it becomes difficult to recruit cooperative labor (i.e., external cost). We conjecture that households not only reallocate hired and cooperative labor (i.e., substitution, or quantity adjustment) but also alter the formation of labor-sharing networks for stronger reciprocity (i.e., network tightening, or quality adjustment; Downey (2010) finds similar flexibility in labor-sharing networks among Amerindians in Belize). Although formal testing is infeasible with our data, our analyses reveal supportive evidence for both.
This article begins with a description of the study area and the data. We then report descriptive statistics of land holdings and forest clearing labor. After developing econometric specifications to test the hypotheses discussed herein, we report our estimation results. The last section presents a summary of the main results and a conclusion.
Study Area and Data
This study is based on household survey data gathered in 2001 from traditional mestizo peasant (ribereño) households in two communities located on the Marañón River, one of the primary Andean tributaries of the Amazon River in Peru, about one-day's travel by river boat to Iquitos.2 Each year the river rises and falls over a range of 8–10 meters, demarking the seasons—higher water versus low water. One village is located on the lowland, which is susceptible to flooding, and the other is on the nonflooding upland where residents also have access to land in the lowland. Although all households in the lowland village were sampled (n=35), in the larger upland village households were randomly sampled in each of three strata defined by land holding size (n=41).3
Local credit opportunities changed over time as follows. In the 1970s, credit for jute on lowland was available in both villages; from 1986 through 1990, under Alan Garcia's populist regime, a new agrarian reform program, PRESA (Programa de Reactivación Agropecuaria y Seguridad Alimentaria), was implemented, and the region experienced a credit boom targeted through the National Agrarian Bank toward upland crops (only in the upland village) (Coomes 1996);4 in the early 1990s, credit virtually disappeared under Alberto Fujimori's regime, followed by private credit expansion for lowland rice production in the late 1990s.
Forests are de facto open access within community territory. Once cleared, land is held by usufruct (i.e., without title), privately used, and transferred principally along family lines; land markets are absent. Forest clearing is a highly laborious task, undertaken by men using only machetes and axes (no chainsaws). Only during the PRESA period, did titling constitute an alternate way of claiming upland, but not lowland. We collected field-level data on land type, size, the year and mode of acquisition (claimed, transferred, or titled), and forest clearing labor (if cleared) in a retrospective manner for each field held at the time of survey (2001) and also for each field acquired at the time of household formation in the current village but not held in 2001. For each field, we focused on first clearing because only the initial clearing determines land accumulation and also because labor inputs for subsequent clearing depend on fallowing practices—more labor is needed for clearing of larger trees found in older fallows. This necessitated the collection of retrospective data. Although respondents were readily able to recall their forest clearing practices,5 recall bias merits particular attention. The database does not contain information about forest clearing for fields transferred from others (i.e., when they were originally claimed) or fields acquired (cleared or not) after household formation and not held in 2001 (i.e., transferred to others). We discuss how first-difference/fixed-effects specifications control for potential attrition bias; note that because our field-level data are recorded for different years for each household (in most cases), they yield an unbalanced household panel over time.
All live births, deaths, arrivals, and departures of household members from each household in the sample since household inception in the two study villages were also recorded, allowing us to reconstruct the evolution of household demographic composition through time. Although the data do not capture entire households that migrated out, those were few. Households were formed from 1949 through 2001—54%, 11%, and 35% of households were formed before, during, and after the PRESA period, respectively. The population size of sample households in the lowland and upland villages, respectively, increased from 38 and 35 people in 1970 to 126 and 132 people in 1985 and to 218 and 251 people in 2001. We also collected information about the fixed kin-group affiliation of each household (not individuals) that made forest clearing decisions. By combining household demographic data with household kin-group affiliation, we constructed the demographic composition of each kin group through time. Our augmented separability test discussed herein combines these demographic panel data with labor panel for each field, thus allowing us to control for unobserved household fixed effects. These demographic variables, however, underestimate true historical kin-group size because of attrition due to migration (albeit very uncommon)6 and sampling (not census) in the upland village; we discuss how first-difference/fixed-effects specifications can control for systematic measurement errors.
Our analysis is based on 74 households with complete information on forest clearing. In field data at the time of forest clearing, there was no significant difference in demographic characteristics at the household and kin-group levels between the two villages (see table A1); this is also true in household-level data in 2001 (results not shown).
Land and Labor
Land Holdings and Portfolio
At the time of interviews in 2001, on average, a household in the lowland village held 6.2 fields with 6.3 hectares and in the upland village, 4.6 fields with 9.5 hectares (see table 1). In addition to upland, four distinct types of lowland exist depending on land form and elevation relative to flood levels: (a) high levee, which is flooded only by high floods in some years; (b) low levee, which is flooded each year; and (c) mudflat and (d) sandbar, which appear only for a limited time during the low-water season. Lowland alluvial soils are significantly more fertile than upland soils. Land portfolios are quite distinct between the two villages: upland is available only in the upland village (upland portfolio size is typically larger than other lands because of fallowing); fertile high levee and mudflat are scarce (especially in the lowland village and the upland village, respectively); low levee holdings are almost uniform (locally abundant); and sandbar is an uncommon land type. A typical household agricultural portfolio includes food crops on low levee along with a combination of cash crops (especially rice) on fertile mudflat and/or food/tree crops on secure upland and relatively secure/fertile high levee.7
| All Fields | Share of Cleared Fields | |||||
|---|---|---|---|---|---|---|
| Total No. Fields | Holds at Least One Field (0/1) | Mean No. Fields | Mean Area (ha) | Fields | Area | |
| A. Lowland village (n=34) | ||||||
| All land | 212 | 1.00 | 6.24 (2.72) | 6.25 (3.65) | 58% | 56% |
| Upland | 0 | 0.00 | 0.00 | 0.00 | ||
| High levee | 11 | 0.32 | 0.32 (0.47) | 0.14 (0.25) | 73% | 70% |
| Low levee | 123 | 1.00 | 3.62 (2.24) | 3.74 (2.61) | 73% | 68% |
| Mudflat | 61 | 0.94 | 1.79 (0.98) | 1.78 (1.45) | 30% | 39% |
| Sandbar | 9 | 0.24 | 0.26 (0.51) | 0.27 (0.65) | 11% | 3% |
| B. Upland village (n=40) | ||||||
| All land | 182 | 1.00 | 4.55 (2.55) | 9.49 (15.6) | 70% | 36% |
| Upland | 58 | 0.68 | 1.45 (1.43) | 4.91 (12.9) | 83% | 30% |
| High levee | 24 | 0.33 | 0.60 (1.17) | 0.78 (2.10) | 88% | 95% |
| Low levee | 76 | 0.83 | 1.90 (1.41) | 2.89 (4.52) | 67% | 37% |
| Mudflat | 16 | 0.33 | 0.40 (0.63) | 0.39 (0.89) | 38% | 34% |
| Sandbar | 5 | 0.10 | 0.13 (0.40) | 0.11 (0.50) | 20% | 2% |
- a Note: Standard deviations are in parentheses.
Current land holdings consist of cleared and noncleared land, which includes transferred land, upland fields titled under PRESA, and claimed mudflats/sandbars (typically mudflats/sandbars without woody vegetation do not require clearing). In the upland village, 80% and 67% of upland and low levee fields, respectively, have been cleared, but they account for only 30% and 37% of the total area of land claimed on upland and low levees, respectively; as such, noncleared fields are much larger than cleared fields, and this is especially so for titled upland. In contrast, about 70% of high/low levee fields in the lowland village and most high levee fields in the upland village, in both number and area, are cleared ones.
Forest Clearing
Our analyses on forest clearing focus on cleared upland/high levee/low levee fields with complete labor use data (n=258). In the lowland village (n=120), low levee is dominant in terms of the number and area of fields cleared; in the upland village (n=138), upland and low levee are the main land types, followed by high levee (see panel A of table 2). The mean size of cleared field is about 1 hectare in both villages, regardless of land types; total labor use for clearing per hectare is also similar across land types in each village (26–31 labor days) (panel B).
| Lowland Village | Upland Village | ||||||
|---|---|---|---|---|---|---|---|
| High Levee/Low Levee | High Levee | Low Levee | Upland/High Levee/Low Levee | Upland | High Levee | Low Levee | |
| A. Cleared fields | |||||||
| No. fields | 120 | 7 | 113 | 138 | 55 | 17 | 66 |
| 1949–1985 | 37 | 3 | 34 | 45 | 11 | 12 | 22 |
| 1986–1990 | 15 | 1 | 14 | 19 | 6 | 0 | 13 |
| 1991–2001 | 68 | 3 | 65 | 74 | 38 | 5 | 31 |
| Mean area (ha) | 1.03 | 0.80 | 1.04 | 0.99 | 1.14 | 1.02 | 0.87 |
| (0.79) | (0.41) | (0.81) | (0.90) | (0.86) | (1.13) | (0.87) | |
| B. Forest clearing labor in 1949–2001 | |||||||
| Employment (0/1): | |||||||
| Family labor | 0.68 | 0.57 | 0.68 | 0.62 | 0.56 | 0.59 | 0.68 |
| Hired labor | 0.16 | 0.14 | 0.16 | 0.12 | 0.09 | 0.29 | 0.11 |
| Cooperative labor | 0.54 | 0.43 | 0.55 | 0.50 | 0.55 | 0.29 | 0.52 |
| Minga | 0.20 | 0.29 | 0.19 | 0.40 | 0.45 | 0.24 | 0.39 |
| Mañaneo | 0.35 | 0.14 | 0.36 | 0.07 | 0.09 | 0.06 | 0.06 |
| Labor composition (proportion): | |||||||
| Family labor only | 0.36 | 0.43 | 0.35 | 0.39 | 0.36 | 0.41 | 0.41 |
| Hired labor only | 0.06 | 0.14 | 0.05 | 0.07 | 0.09 | 0.18 | 0.03 |
| Cooperative labor only | 0.25 | 0.29 | 0.25 | 0.30 | 0.35 | 0.24 | 0.27 |
| Family and hired labor | 0.04 | 0.00 | 0.04 | 0.04 | 0.00 | 0.12 | 0.05 |
| Hired and cooperative labor | 0.02 | 0.00 | 0.02 | 0.01 | 0.00 | 0.00 | 0.02 |
| Cooperative and family labor | 0.23 | 0.14 | 0.24 | 0.19 | 0.20 | 0.06 | 0.21 |
| Family, hired, and cooperative labor | 0.04 | 0.00 | 0.04 | 0.01 | 0.00 | 0.00 | 0.02 |
| Mean amount (labor-day): | |||||||
| Total | 27.5 | 21.0 | 27.9 | 30.4 | 35.4 | 30.7 | 26.1 |
| (20.8) | (12.6) | (21.2) | (27.9) | (32.9) | (28.3) | (22.5) | |
| Per hectare | 26.7 | 26.4 | 26.7 | 30.6 | 31.0 | 30.1 | 30.2 |
| Family labor | 15.3 | 4.9 | 15.9 | 11.5 | 11.7 | 9.6 | 11.7 |
| (20.5) | (5.9) | (20.9) | (15.6) | (17.6) | (14.9) | (14.2) | |
| Hired labor | 3.0 | 4.3 | 2.9 | 7.5 | 9.7 | 13.5 | 4.1 |
| (9.9) | (11.3) | (9.9) | (28.3) | (34.3) | (32.2) | (20.7) | |
| Cooperative labor | 9.2 | 11.8 | 9.0 | 11.4 | 13.9 | 7.6 | 10.3 |
| (12.8) | (16.8) | (12.6) | (16.1) | (19.1) | (13.3) | (13.7) | |
| Minga | 5.9 | 10.0 | 5.6 | 10.0 | 12.6 | 7.2 | 8.5 |
| Mañaneo | 3.3 | 1.8 | 3.4 | 0.4 | 0.5 | 0.4 | 0.3 |
| C. Forest clearing labor in 1949–1985 | |||||||
| Family labor (0/1) | 0.49 | 0.53 | 0.53 | 0.55 | 0.42 | 0.59 | |
| Hired labor (0/1) | 0.16 | 0.15 | 0.20 | 0.18 | 0.33 | 0.14 | |
| Cooperative labor (0/1) | 0.68 | 0.68 | 0.49 | 0.45 | 0.33 | 0.59 | |
| Minga (0/1) | 0.54 | 0.53 | 0.44 | 0.45 | 0.33 | 0.50 | |
| Mañaneo (0/1) | 0.14 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Mean amount of family labor (labor-day) | 12.0 | 13.0 | 9.5 | 7.6 | 6.1 | 12.3 | |
| Mean amount of hired labor (labor-day) | 4.6 | 4.1 | 13.0 | 10.5 | 18.8 | 11.1 | |
| Mean amount of cooperative labor (labor-day) | 17.9 | 17.4 | 12.7 | 14.7 | 10.2 | 13.0 | |
| D. Forest clearing labor in 1986–2001 | |||||||
| Family labor (0/1) | 0.76 | 0.75 | 0.67 | 0.57 | 1.00 | 0.73 | |
| Hired labor (0/1) | 0.16 | 0.16 | 0.09 | 0.07 | 0.20 | 0.09 | |
| Cooperative labor (0/1) | 0.48 | 0.49 | 0.51 | 0.57 | 0.20 | 0.48 | |
| Minga (0/1) | 0.05 | 0.05 | 0.38 | 0.45 | 0.00 | 0.34 | |
| Mañaneo (0/1) | 0.45 | 0.46 | 0.11 | 0.11 | 0.20 | 0.09 | |
| Mean amount of family labor (labor-day) | 16.8 | 17.2 | 12.4 | 12.8 | 18.2 | 11.4 | |
| Mean amount of hired labor (labor-day) | 2.2 | 2.3 | 4.8 | 9.5 | 0.6 | 0.6 | |
| Mean amount of cooperative labor (labor-day) | 5.3 | 5.4 | 10.8 | 13.7 | 1.3 | 9.0 | |
- a Note: The sample consists of cleared fields held in 2001 and fields cleared at the time of household formation and not held in (2001) “Panels C and D do not report data for high levee in the lowland village due to the small number of observations”, Standard deviations are in parentheses.
In addition to family labor and hired labor (based on fixed-wage contract), households commonly host cooperative labor events, whereby they recruit people in the same village to clear forest for a day or less and offer drink (usually a fermented drink made from manioc) and occasionally food to the guests in exchange. Distinct from exchange labor or a work group in which reciprocity among group members is explicit, attendance is voluntary and thus reciprocity is implicit. It is not uncommon for someone to decline an invitation or fail to show up and for others to attend, even if they were not formally invited.8 This type of cooperative labor is well suited for forest clearing because it involves massive laborious work to be done quickly (a cleared field needs to be burned soon before convective storms wash away the nutrient-rich ash and weeds invade the plot), it can be done irregularly (although low levee is cleared and burned during the low water season when both the soil and vegetation are dry enough to work, upland and noninundated high levee can be cleared and burned throughout the year), and the task is so simple that work quality may not be a major concern (Chibnik and de Jong 1989). Cooperative labor events in the sample are categorized into two major types: minga, which involves a full day of work (7 hours) with two meals as well as generous drink, and mañaneo, which entails a half-day of work (3 hours in the morning) with drink but no meal (Brisson 2003).9
In each village, family and cooperative labor were much more commonly deployed for clearing than hired labor (approximately 67% and 50% of fields versus more than 10% of fields), and the mean amounts of family and cooperative labor used were much larger than that of hired labor. Of the two types of cooperative labor events, mañaneo was more common in the lowland village, and minga was more common in the upland village. At the same time, hired labor played a major role in the upland village: it was commonly used (29% of fields) and in large amounts (44% of labor days) to clear high levee; hired labor was uncommon to clear upland (9% of fields) but used in large amount (27% of labor days versus 16% of labor days to clear low levee). The most common among the seven possible combinations of three labor inputs were family labor alone (36%–40% of fields), cooperative labor alone (25%–29% of fields), and family with cooperative labor (19%–23% of fields). Importantly, cooperative labor and hired labor are almost mutually exclusive (i.e., households typically deployed either cooperative or hired labor, not both, when they needed extra-family labor).
Evolution of Forest Clearing
Fields were cleared from 1949 through 2001—32%, 13%, and 55% of fields were cleared before, during, and after the PRESA period (panel A of table 2). Recently cleared fields are more common than younger households, in proportion, because many old cleared fields have been transferred to others. Whereas 69% of low levee fields were cleared during and after the PRESA period, in the upland village only six upland fields and no high levee fields were cleared during PRESA, and 69% of upland fields and 30% of high levee fields were cleared after PRESA. This is because during PRESA land titling was more commonly used to claim upland than clearing; it is also possible that upland fields cleared at that time were transferred to others and thus are not captured in our data.
Panels C and D in table 2 compare forest clearing labor before and after the PRESA intervention, where postintervention (1986–2001) includes the PRESA period, with a relatively small number of fields (using fields cleared only after 1990 does not significantly alter the comparison). Before PRESA, the use and mean amount of each labor type—family, hired, and cooperative labor—were very similar across land types and villages, suggesting the absence of a structural difference (the only exception is high levee in the upland village, as discussed previously). In contrast, significant changes in labor composition followed the intervention only in the upland village in two ways. First, in the upland village, although hired labor became less common across land types and its mean amount for high/low levee clearing decreased, the mean amount of hired labor for upland clearing augmented among fields with hired labor employed; in contrast, hired labor in the lowland village changed little. Second, although cooperative labor became less commonly used to clear high/low levee in both villages, cooperative labor to clear upland persisted. These results offer descriptive evidence that the credit intervention led to distinct use of two forms of extra-family labor to clear upland (but not high/low levee): some households augmented hired labor, probably because of the relaxed liquidity constraints, whereas others continued to rely on cooperative labor. Lack of data on household wealth and individual loan history prevents us from capturing liquidity constraints, however.
By the 1990s, in the lowland village, minga was replaced by mañaneo, and in the upland village, mañaneo emerged across land types; family labor became more common and its mean amount mostly augmented across land types in both villages. These results suggest that cooperative labor decreased in scale as a common trend and, correspondingly, family labor became more significant as a substitute.
Econometric Specification
Substitutability and Productivity
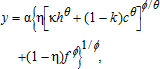 (1)
(1)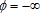 implies perfect complementarity). In equation (1), although the elasticities of substitution between hired and family labor and between cooperative and family labor are the same, the elasticity of substitution between hired and cooperative labor can be different from them. In the case where θ=ϕ, equation (1) becomes a CES production function
implies perfect complementarity). In equation (1), although the elasticities of substitution between hired and family labor and between cooperative and family labor are the same, the elasticity of substitution between hired and cooperative labor can be different from them. In the case where θ=ϕ, equation (1) becomes a CES production function
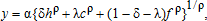 (2)
(2)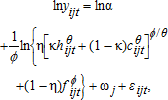 (3)
(3)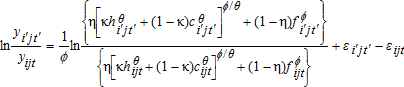 (4)
(4)Hypothesis 1 (perfect substitutability): θ=ϕ=1 and ρ=1.
In the two-level CES production function (1), κ measures the productivity of hired labor relative to cooperative labor and η measures the productivity of nested extra-family labor relative to family labor. In the CES production function (2), δ and λ measure the productivity of hired and cooperative labor, respectively, relative to family labor. With perfect substitutability (ρ=1), equation (2) becomes the linear production function with a constant marginal product of each input; that is, productivity-adjusted total labor use—weighted sum of each input (l=δh+λc+(1−δ+λ)f)—determines output (note that perfect substitutability does not necessarily mean equal productivity).
We first consider upland/high levee/low levee together, ignoring across-type heterogeneity, and then low levee only because other land types are too uncommon for this disaggregate analysis. Although within-type heterogeneity is still uncontrolled for, it should be much smaller than across-type heterogeneity. The first-difference specification controls for potential attrition bias in our field data, unless household past land transfers are systematically related with the productivity of forest clearing, not field, within the same land type and such correlations significantly change over time. The first-difference specification also controls for potential systematic recall errors at the household level (e.g., respondents may recall old clearing practices by referring to recent ones). To check the robustness of our results to recall bias, we repeated the analysis dropping fields cleared before 1980 (19% of fields; 84% of the remaining fields are post-PRESA fields), which are more likely to contain larger recall errors, finding very similar results.
Separability
We conjecture that the combination of labor market and labor sharing enables efficient labor allocation. On one hand, even if the labor market is constrained by liquidity, households can efficiently use total labor because cooperative labor can be substituted for hired labor; alternatively, even if labor sharing is constrained by network endowments (households with stronger networks can better mobilize cooperative labor), hired labor can be substituted for cooperative labor. Such flexible adjustments in labor composition are possible, especially when hired and cooperative labor are perfect substitutes and equally productive. Theoretically, the household can set the unit cost of cooperative labor (i.e., the opportunity cost of reciprocated labor evaluated at its shadow wage and the costs of drink/food to be offered) at the level of market wage by adjusting reciprocation and the type of labor sharing (minga versus mañaneo) as well as quantities and quality of drink/food.10
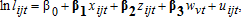 (5)
(5)Hypothesis 2 (augmented separability): Productivity-adjusted total labor use for forest clearing is not affected by household and network endowments (i.e., β1=β2=0).
If network endowments positively (and negatively) affect cooperative (and hired) labor, the nonrejection of hypothesis 2 means that network endowments constrain labor composition but not demand. Again, lack of historical wealth and credit data limits our ability to capture liquidity constraints, which presumably affect hired and cooperative labor in opposite manners.11
A key empirical question is how we can capture network characteristics. Characteristics of labor-sharing networks are not exogenous as determinants of labor demand (and composition) because networks are endogenously formed by households. We employ a reduced-form approach by using exogenous determinants of labor-sharing networks to avoid such identification problems. Although historical labor network data are lacking, Abizaid et al. (2013) conducted social network analyses on cooperative labor for all agricultural tasks (mostly forest clearing, plus weeding and harvesting) in 2001 in the lowland village with data from a complete census and estimated the determinants of network formation using the dyadic regression framework (Fafchamps and Gubert 2007). Two major findings stemming from that work are relevant here. First, cooperative labor networks are formed by kin-group affiliation and female kin relationship, within and outside kin group. That is, cooperative male labor is organized by female networks, not by male networks. Second, kin-group structure (connections/relationships of households in the group), not size (number of households in the group), matters in the within-group networks.12 Based on these results, we focus on kin networks, using the following three specifications.
First, we focus on within-group networks using kin-group dummies (fixed effects), which fully control for their characteristics: specifically, we employ OLS using seven dummies for major kin groups (four in the lowland village; three in the upland village) with minor kin groups/no kin-group affiliation as a base. Within-group networks are not sufficient for cooperative labor; the number of male working adults (aged 15–64 years) in the same kin group (excluding own male adults), including both major and minor groups, is much smaller than the number of workers per event on average (5.1 versus 22.3 in the lowland village; 5.2 versus 16.2 in the upland village). Thus, households must also rely on across-group networks, which are wider than within-group networks.
Second, we capture across-group networks while controlling for within-group network size. Specifically, we use number of male working adults in the same kin group (excluding own endowment) to capture within-group network size and number of female working adults in the same kin group (excluding own) to capture across-group networks and the characteristics other than size of within-group networks, both of which are formed by female connections (both major and minor kin groups are considered). Our working assumption is that the more female adults in the kin group, the more female relatives in the village/group and thus the better connections; in particular, in mestizo peasants' patrilineal society, marriage across kin groups strongly forms across-group networks. We employ the fixed-effects specification, fully controlling for time-invariant group factors such as social capital and fixed components of all networks (within- and across-group), as well as unobserved household fixed effects. As discussed above, distinct from the OLS specification, the fixed-effects model controls for potential attrition bias and potential household-level systematic measurement errors in our field data. As discussed, these two variables underestimate true kin-group size. Whether such measurement errors cause bias after controlling for group fixed effects depends on whether changes in such errors are systematically correlated with changes in group size and household demographic factors.
Third, we use the share of male/female working adults in the same kin group within the village. They do not cause bias, unless household attrition patterns, because of migration and sampling, change in distinct manners across kin groups. In any case, qualitatively the same results of the level and share variables suggest the robustness of the estimation results. We also repeated the analysis dropping old fields, which contain larger attrition and recall errors, and found very similar results.
Household demographic factors other than labor endowments measured by number of male/female working adults include number of children (almost no households had elderly members at the time of forest clearing), household age in the village (which can affect labor-sharing network), age of household head (lifecycle), and two dummies for male and female heads' birth in the village (which also can affect network) (descriptive statistics of these variables are shown in table A1). In the fixed-effects specification, the last two dummies vanish, and effects of household age and age of household head cannot be distinguished.13
Although the market wage in the pre-/postintervention period in each village is fully controlled for by the village-period dummies,14 lack of historical wage data precludes us from controlling for within-period (yearly) variations. Whether omitted variable bias in the estimated effects of household/network endowments is significant depends on whether an unobserved change in wage is systematically correlated with a change in migration patterns. In our sample, because local wage labor employment plays a minimal role in households' livelihoods, the local wage is unlikely to be strongly related to migration, and out-migration itself is uncommon; thus, unobserved product and input prices in the region are also unlikely to cause significant bias. In other locales where labor markets are well developed and migration is common, this potential omitted variable bias becomes a major concern; if standard household panel data are available, local wage can be fully controlled for by village-year dummies.
Evolution
Our conjecture is that after the credit intervention, households in the treatment (upland) village altered not only labor composition across land types (quantity adjustment) but also the formation of labor-sharing networks (quality adjustment). In particular, as the recruitment pool for cooperative labor shrank, households relied more on tighter within-group networks with a higher degree of reciprocity, whereas in the control (lowland) village, such network tightening did not occur and households continued to rely on both within- and across-group networks. The small number of pre- and postintervention fields in each village does not allow us to test this hypothesized network evolution; however, we do find supportive evidence for it in the effects of network endowments on labor composition: network endowments affect the two forms of extra-family labor in opposite manners, and cooperative labor networks in the treatment (upland) village are tighter than those in the control (lowland) village.
Hypothesis 3 (network formation): In the treatment village, the greater within-group, but not across-group, network endowments, the more (and the less) cooperative (and hired) labor. In the control village, the greater within- and across-group network endowments, the more (and less) cooperative (and hired) labor.
We estimate equation (5) for hired and cooperative labor separately; we do so for both employment ( , where 1(•) is an indicator function that takes 1 if the argument holds and 0 otherwise and
, where 1(•) is an indicator function that takes 1 if the argument holds and 0 otherwise and 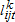 is type k labor input) and log of amount (
is type k labor input) and log of amount (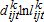 ).
).
Estimation Results
Substitutability and Productivity
Estimation results of forest clearing functions are reported in table 3, where standard errors are clustered by household.15 Results for upland/high levee/low levee and low levee are very similar, suggesting that forest clearing technology is not significantly different across land types—a finding consistent with first-hand field observation. NLLS and first-difference NLLS estimation results are also similar to one another in each specification, indicating that unobserved household fixed effects are unlikely to cause significant bias.
| Upland/High Levee/Low Levee | Low Levee | |||||||
|---|---|---|---|---|---|---|---|---|
| NLLS (n=258) | First-Difference NLLS (n=184) | NLLS (n=179) | First-Difference NLLS (n=114) | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| A. Two-level CES | ||||||||
| θ | 1.155** | 1.000a | 1.346* | 1.000a | 1.374* | 1.000a | 1.574 | 1.000a |
| (0.526) | (0.683) | (0.713) | (1.031) | |||||
| ϕ | 0.857*** | 0.907*** | 1.035*** | 1.000a | 1.063*** | 1.000a | 1.055*** | 1.000a |
| (0.162) | (0.145) | (0.248) | (0.290) | (0.342) | ||||
| κ | 0.493*** | 0.491*** | 0.395*** | 0.419*** | 0.526*** | 0.511*** | 0.583** | 0.541*** |
| (0.054) | (0.046) | (0.110) | (0.100) | (0.055) | (0.040) | (0.231) | (0.108) | |
| η | 0.745*** | 0.759*** | 0.771*** | 0.790*** | 0.808*** | 0.818*** | 0.824*** | 0.840*** |
| (0.062) | (0.052) | (0.069) | (0.030) | (0.080) | (0.023) | (0.085) | (0.033) | |
| Constraints | No | θ,ϕ≤1 | No | θ,ϕ≤1 | No | θ,ϕ≤1 | No | θ,ϕ≤1 |
| R squared | 0.163 | 0.163 | 0.303 | 0.302 | 0.220 | 0.218 | 0.410 | 0.407 |
| F (p value): | ||||||||
| θ=1 | 0.769 | 0.614 | 0.601 | 0.581 | ||||
| ϕ=1 | 0.381 | 0.552 | 0.888 | 0.830 | 0.879 | |||
| κ=1/2 | 0.892 | 0.851 | 0.346 | 0.420 | 0.638 | 0.781 | 0.720 | 0.703 |
| η=1/2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| B. CES | ||||||||
| ρ | 0.886*** | 0.930*** | 1.060*** | 1.000a | 1.106*** | 1.000a | 1.121*** | 1.000a |
| (0.159) | (0.137) | (0.236) | (0.280) | (0.329) | ||||
| δ | 0.381*** | 0.381*** | 0.329*** | 0.331*** | 0.429*** | 0.418*** | 0.469*** | 0.455*** |
| (0.039) | (0.039) | (0.093) | (0.087) | (0.046) | (0.036) | (0.121) | (0.104) | |
| λ | 0.397*** | 0.397*** | 0.468*** | 0.459*** | 0.405*** | 0.400*** | 0.389*** | 0.386*** |
| (0.034) | (0.034) | (0.084) | (0.070) | (0.042) | (0.034) | (0.093) | (0.080) | |
| Constraints | No | ρ≤1 | No | ρ≤1 | No | ρ≤1 | No | ρ≤1 |
| R squared | 0.162 | 0.162 | 0.303 | 0.302 | 0.219 | 0.218 | 0.408 | 0.407 |
| F (p value): | ||||||||
| ρ=1 | 0.474 | 0.474 | 0.801 | 0.707 | 0.715 | |||
| δ=λ | 0.805 | 0.895 | 0.420 | 0.411 | 0.734 | 0.781 | 0.701 | 0.706 |
| δ=μ | 0.016 | 0.016 | 0.298 | 0.277 | 0.004 | 0.000 | 0.056 | 0.031 |
| λ=μ | 0.003 | 0.003 | 0.010 | 0.000 | 0.004 | 0.000 | 0.019 | 0.001 |
| δ=λ=2μ | 0.815 | 0.815 | 0.715 | 0.696 | 0.772 | 0.711 | 0.638 | 0.349 |
| C. Linear | ||||||||
| δ | 0.389*** | 0.662*** | 0.331*** | 0.675*** | 0.418*** | 0.689*** | 0.455*** | 0.710*** |
| (0.042) | (0.032) | (0.087) | (0.033) | (0.036) | (0.034) | (0.104) | (0.033) | |
| λ | 0.406*** | 0.459*** | 0.400*** | 0.386*** | ||||
| (0.036) | (0.070) | (0.034) | (0.080) | |||||
| Constraints | No | λ=δ | No | λ=δ | No | λ=δ | No | λ=δ |
| R squared | 0.161 | 0.160 | 0.302 | 0.294 | 0.218 | 0.218 | 0.407 | 0.405 |
| F (p value): | ||||||||
| δ=λ | 0.821 | 0.411 | 0.781 | 0.706 | ||||
| δ=μ | 0.003 | 0.277 | 0.000 | 0.031 | ||||
| λ=μ | 0.000 | 0.000 | 0.000 | 0.001 | ||||
| δ=λ=2μ | 0.960 | 0.696 | 0.711 | 0.349 | ||||
| δ=1/2 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| δ=2/3 | 0.885 | 0.811 | 0.512 | 0.200 | ||||
- a Note: Dependent variables are log size of field cleared (m2) for NLLS and its first difference for first-difference NLLS. Standard errors clustered by household are in parentheses. Other controls not shown here are a dummy for 1986–2001 and its interaction with a dummy for upland village; a dummy for upland village and constant are also included for NLLS. A single asterisk indicates 10% significance, a double asterisk indicates 5% significance, and a triple asterisk indicates 1% significance.
- a Boundary value.
In the unconstrained models for the two-level CES production function (panel A) and the CES production function (panel B), respectively, all estimated θ and ϕ, but one for θ taking .91, and all estimated ρ, but one taking .93, are slightly larger than unity (up to 1.6), and none of them are statistically different from unity (a null hypothesis that θ=ϕ is not rejected at all); in the constrained models, all results corresponding to estimates greater than unity take the boundary value 1. These results strongly support the perfect substitutability of family, hired, and cooperative labor (hypothesis 1), which is necessary for the separability test.
In each specification, estimation results for κ and η (panel A in table 3) and for δ and λ (panel B in table 3) are very similar to each other between the unconstrained and constrained models. Although estimated κ is not statistically different from 1/2, estimated η is significantly greater than 1/2 in all cases. Estimated δ and λ are not statistically different from each other, although they are significantly greater than 1−δ−λ(=μ) in almost all cases. Further, the null hypothesis that hired and cooperative labor are twice as productive as family labor (i.e., δ=λ=2μ) is not rejected. These results suggest that hired and cooperative labor are equally productive and they are more productive than family labor (we discuss a possible reason and interpretation later).16
When the linear production function with perfect substitutability is used, very similar results for productivity comparison across labor types are obtained (columns 1, 3, 5, and 7 of panel C in table 3). Hence, the separability test would need to capture the productivity difference between extra-family and family labor but not between hired and cooperative labor. Indeed, combining hired and cooperative labor (unweighted sum) as extra-family labor in the linear production function with two inputs (i.e., δ=λ) yields results strongly consistent with those with three inputs: estimated δ are significantly greater than 1/2 and are not statistically different from 2/3 (columns 2, 3, 6, and 8 of panel C in table 3).
Separability
Estimation results of labor demand equations are reported in table 4, where standard errors are clustered by household: OLS with kin group dummies in panel A and fixed-effects models with the size and share of male/female working adults in the kin group in panels B and C, respectively (only household labor endowments and network variables are shown; the results of household labor endowments not reported in panel C for brevity are almost the same as those in panel B). In addition to upland/high levee/low levee and low levee in both villages, we analyze upland/high levee in the upland village separately. In each panel in table 4, columns 1, 3, and 5 show results for productivity-unadjusted total labor and columns 2, 4, and 6 are for productivity-adjusted total labor in family labor unit—family labor plus hired/cooperative labor weighted by two (results are robust to other weights near two).
| Upland/High Levee/Low Levee in Lowland & Upland Villages (n=258) | Low Levee in Lowland & Upland Villages (n=179) | Upland/High Levee in Upland Village (n=72) | ||||
|---|---|---|---|---|---|---|
| Productivity | Unadjusted | Adjusted | Unadjusted | Adjusted | Unadjusted | Adjusted |
| (1) | (2) | (3) | (4) | (5) | (6) | |
| A. OLS with kin-group dummies | ||||||
| Kin group in lowland village (0/1) | ||||||
| Group 1 | −0.072 | −0.094 | −0.198 | −0.293 | ||
| (0.222) | (0.201) | (0.243) | (0.217) | |||
| Group 2 | 0.261 | 0.227 | 0.323 | 0.313 | ||
| (0.256) | (0.250) | (0.294) | (0.248) | |||
| Group 3 | −0.167 | −0.144 | −0.219 | −0.218 | ||
| (0.195) | (0.212) | (0.189) | (0.185) | |||
| Group 4 | 0.357* | 0.277 | 0.420* | 0.325 | ||
| (0.214) | (0.211) | (0.218) | (0.199) | |||
| Kin group in upland village (0/1) | ||||||
| Group 5 | −0.056 | 0.019 | −0.098 | 0.061 | −0.088 | −0.037 |
| (0.243) | (0.235) | (0.351) | (0.348) | (0.348) | (0.370) | |
| Group 6 | −0.157 | −0.236 | −0.163 | −0.206 | −0.348 | −0.483 |
| (0.236) | (0.292) | (0.278) | (0.327) | (0.383) | (0.398) | |
| Group 7 | 0.238 | 0.233 | 0.520 | 0.632 | −0.142 | −0.284 |
| (0.227) | (0.250) | (0.365) | (0.407) | (0.332) | (0.348) | |
| F for kin groups (p-value) | ||||||
| Lowland village | 0.068 | 0.154 | 0.010 | 0.000 | ||
| Upland village | 0.524 | 0.537 | 0.262 | 0.170 | 0.823 | 0.599 |
| R squared | 0.127 | 0.170 | 0.189 | 0.251 | 0.191 | 0.299 |
| B. Fixed-effects models with no. of male/female adults (15–64 years) in kin group | ||||||
| Male adults in | −0.011 | −0.009 | −0.074 | −0.039 | −0.360 | −0.418 |
| household | (0.089) | (0.106) | (0.100) | (0.113) | (0.282) | (0.326) |
| Female adults in | 0.112 | 0.126 | 0.021 | 0.150 | 0.376 | 0.384 |
| household | (0.129) | (0.141) | (0.208) | (0.191) | (0.270) | (0.253) |
| Male adults in | 0.018 | 0.018 | 0.048 | 0.035 | −0.102 | −0.101 |
| kin group | (0.040) | (0.043) | (0.049) | (0.054) | (0.078) | (0.079) |
| Female adults in | −0.057 | −0.042 | −0.085 | −0.071 | 0.115 | 0.098 |
| kin group | (0.055) | (0.052) | (0.064) | (0.057) | (0.113) | (0.105) |
| R squared | 0.029 | 0.034 | 0.086 | 0.093 | 0.128 | 0.143 |
| C. Fixed-effects models with share of male/female adults (15–64 years) in kin group | ||||||
| Male adults in kin | −1.32 | −1.32 | −0.64 | −1.03 | −2.28 | −2.77 |
| group | (1.59) | (1.77) | (1.34) | (1.38) | (4.82) | (4.54) |
| Female adults in | −1.13 | −1.11 | −3.32* | −3.62** | 4.95 | 5.70 |
| kin group | (1.36) | (1.52) | (1.94) | (1.79) | (3.23) | (3.39) |
- a Note: Dependent variables are log amount of productivity-unadjusted/-adjusted total labor (labor-day). Standard errors clustered by household are in parentheses. Other controls not shown here are number of male/female children (<15 years), age of household head, a dummy for 1986–2001, and constant. The interaction of a dummy for 1986–2001 and a dummy for upland village is also included in columns 1–4 of panels A–C; household age and male/female head born in the vilage are also included in panel A; a dummy for upland village is also included in columns 1–4 of panel A; and, male/female adults (15–64 years) in household are also included in panel C. All labor endowments in panels B and C are measured at the time of forest clearing. A single asterisk indicates 10% significance, a double asterisk indicates 5% significance, and a triple asterisk indicates 1% significance.
First, neither household labor endowments nor other household demographic factors (not shown in table 4) are statistically significant across fixed-effects models; some OLS estimates are statistically significant (results not shown), suggesting some bias caused by unobserved household fixed effects. Second, kin group dummies and network endowments are statistically nonsignificant for upland/high levee/low levee in both villages and upland/high levee in the upland village. Third, in contrast, for low levee, kin group dummies in the lowland village, but not upland village, are jointly, but not individually, statistically significant (especially for productivity-adjusted labor), and the share, but not size, of female adults in the kin group is also statistically significant. Thus, the augmented separability (hypothesis 2) is not strongly rejected in either village.
Evolution
Estimation results of labor composition (employment and amount) are reported in table 5 (OLS with kin group dummies) and table 6 (fixed-effects models with network endowments interacted with village dummies)—low levee in both villages in panel A and upland/high levee in the upland village in panel B; in table 6, only household labor endowments and network variables are shown. The following findings are consistent with hypothesis 3. First, within-group network endowments, captured by kin group dummies, largely positively (and negatively) affect cooperative (and hired) labor to clear low levee in the lowland village but not in the upland village and also upland/high levee in the upland village (note that such systematic patterns are absent for labor demand, as in table 4). Although none of the estimated coefficients are statistically significant, many of them are considerable in magnitude, and some results are jointly significant at a 15% significance level. Second, across-group network endowments, captured by female adult size/share, in the lowland village positively (and negatively) affect cooperative (and hired) labor to clear low levee. In contrast, across-group network endowments in the upland village alter neither upland/high levee nor low levee clearing in a significant manner. Results are similar when fields cleared after 1980 are dropped, indicating that network formation is likely to be distinct across the two villages in the postintervention period.
| Employment (0/1) | Log Amount (Labor-Day) | |||
|---|---|---|---|---|
| Hired | Cooperative | Hired | Cooperative | |
| (1) | (2) | (3) | (4) | |
| A. Low levee in lowland & upland villages (n=179) | ||||
| Kin group in lowland village (0/1) | ||||
| Group 1 | 0.013 | −0.139 | 0.002 | −0.455 |
| (0.114) | (0.119) | (0.327) | (0.312) | |
| Group 2 | −0.131 | 0.075 | −0.481 | 0.631 |
| (0.110) | (0.220) | (0.297) | (0.568) | |
| Group 3 | −0.100 | 0.110 | −0.350 | 0.289 |
| (0.121) | (0.155) | (0.313) | (0.411) | |
| Group 4 | −0.079 | 0.165 | −0.198 | 0.440 |
| (0.133) | (0.125) | (0.346) | (0.346) | |
| Kin group in upland village (0/1) | ||||
| Group 5 | −0.048 | 0.158 | 0.118 | 0.148 |
| (0.077) | (0.222) | (0.167) | (0.672) | |
| Group 6 | 0.082 | −0.125 | 0.436* | −0.508 |
| (0.100) | (0.177) | (0.250) | (0.562) | |
| Group 7 | 0.241 | −0.085 | 0.841 | −0.181 |
| (0.163) | (0.220) | (0.672) | (0.702) | |
| F for kin groups (p-value) | ||||
| Lowland village | 0.481 | 0.147 | 0.302 | 0.022 |
| Upland village | 0.122 | 0.688 | 0.225 | 0.711 |
| R squared | 0.174 | 0.081 | 0.148 | 0.138 |
| B. Upland & high levee in upland village (n=72) | ||||
| Kin group in upland village (0/1) | ||||
| Group 5 | −0.245 | 0.327 | −0.869 | 0.710 |
| (0.151) | (0.199) | (0.634) | (0.598) | |
| Group 6 | −0.118 | 0.069 | −0.422 | −0.338 |
| (0.159) | (0.268) | (0.661) | (0.676) | |
| Group 7 | −0.320 | 0.125 | −1.310 | 0.422 |
| (0.193) | (0.307) | (0.810) | (0.936) | |
| F for kin groups (p-value) | 0.138 | 0.284 | 0.251 | 0.248 |
| R squared | 0.253 | 0.399 | 0.284 | 0.439 |
- a Note: Standard errors clustered by household are in parentheses. Other controls not shown here are number of male/female children (<15 years), household age, age of household head, male/female head born in the village, a dummy for 1986–2001, and constant. A dummy for upland village and its iteraction with a dummy for 1986–2001 are also included in panel A. A single asterisk indicates 10% significance, a double asterisk indicates 5% significance, and a triple asterisk indicates 1% significance.
| Employment (0/1) | Log Amount (Labor-Day) | |||
|---|---|---|---|---|
| Hired | Cooperative | Hired | Cooperative | |
| (1) | (2) | (3) | (4) | |
| A1. Low levee in lowland & upland villages (n=179)—No. male/female adults in kin group | ||||
| Male adults (15–64 years) in household | 0.043 | 0.062 | −0.127 | 0.192 |
| (0.046) | (0.088) | (0.134) | (0.238) | |
| Female adults (15–64 years) in household | 0.197 | 0.095 | 0.703* | 0.100 |
| (0.134) | (0.201) | (0.407) | (0.562) | |
| Male adults in kin group of lowland village | 0.004 | −0.041 | 0.069 | −0.081 |
| (0.030) | (0.039) | (0.091) | (0.100) | |
| Male adults in kin group of upland village | −0.055 | −0.037 | −0.149** | −0.027 |
| (0.034) | (0.063) | (0.069) | (0.192) | |
| Female adults in kin group of lowland village | −0.039 | 0.109* | −0.212 | 0.224 |
| (0.041) | (0.055) | (0.136) | (0.141) | |
| Female adults in kin group of upland village | −0.004 | 0.096 | −0.011 | 0.169 |
| (0.033) | (0.082) | (0.084) | (0.247) | |
| R squared | 0.185 | 0.098 | 0.147 | 0.100 |
| A2. Low levee in lowland & upland villages (n=179)—share of male/female adults in kin group | ||||
| Male adults in kin group of lowland village | 0.17 | −1.20 | 1.09 | −4.62 |
| (0.85) | (1.49) | (2.34) | (4.54) | |
| Male adults in kin group of upland village | −1.85 | 0.64 | −4.59 | 3.03 |
| (2.50) | (2.46) | (3.90) | (6.93) | |
| Female adults in kin group of lowland village | −2.78* | 2.81* | −11.43** | 5.92 |
| (1.43) | (1.61) | (4.47) | (4.77) | |
| Female adults in kin group of upland village | −0.53 | 5.14 | −0.30 | 9.28 |
| (1.75) | (3.36) | (3.87) | (8.69) | |
| R squared | 0.217 | 0.095 | 0.228 | 0.101 |
| B1. Upland & high levee in upland village (n=72)—No. male/female adults in kin group | ||||
| Male adults in household | −0.167 | 0.079 | −0.697 | 0.197 |
| (0.109) | (0.070) | (0.488) | (0.201) | |
| Female adults in household | 0.082 | −0.083 | 0.396 | 0.150 |
| (0.095) | (0.091) | (0.423) | (0.261) | |
| Male adults in kin group | 0.003 | −0.042** | 0.031 | −0.162** |
| (0.019) | (0.017) | (0.073) | (0.062) | |
| Female adults in kin group | 0.001 | 0.018 | 0.017 | 0.053 |
| (0.024) | (0.027) | (0.101) | (0.085) | |
| R squared | 0.084 | 0.415 | 0.120 | 0.427 |
| B2. Upland & high levee in upland village (n=72)—share of male/female adults in kin group | ||||
| Male adults in kin group | −1.01 | 0.94 | −6.63 | 0.92 |
| (1.36) | (1.73) | (5.94) | (4.00) | |
| Female adults in kin group | 1.05 | −0.15 | 6.18 | 1.10 |
| (1.24) | (1.07) | (5.21) | (2.40) | |
| R squared | 0.099 | 0.393 | 0.159 | 0.389 |
- a Note: Standard errors clustered by household are in parentheses. Other controls not shown here are number of male/female children (<15 years), age of household head, a dummy for 1986–2001, and constant. The interaction of a dummy for 1986—2001 and a dummy for upland village is also included in panel A. All labor endowments are measured at the time of forest clearing. A single asterisk indicates 10% significance, a double asterisk indicates 5% significance, and a triple asterisk indicates 1% significance.
On the other hand, within-group network size, measured by male adult size/share, has a very limited influence across land types/villages, confirming that network size is not a key factor for labor sharing (Abizaid et al. 2013); household male labor endowments do not alter labor composition either.17
Why Is Extra-Family Labor More Productive Than Family Labor?
We conjecture that extra-family laborers are younger and thus more productive in forest clearing than family laborers for two reasons. First, young male adults are generally stronger and have greater physical endurance than older adults, making them better suited for highly laborious forest clearing. As male working adults in the household become older over the lifecycle, the household must rely increasingly on extra-family labor (especially after adult children leave). The second reason is reputational: young male adults may well work harder on the fields of others than on their own to enhance future prospects for wage employment and to secure access to cooperative labor as a means for land accumulation. If our conjecture holds, households differentially and flexibly use family and extra-family labor, which are perfect substitutes but are not equally productive, over the lifecycle of working adults; then, labor-sharing arrangements for forest clearing can be reciprocated over a long period of time, even across generations. Although a lack of complete data on labor offered to others precludes us from measuring the degree or pattern of reciprocity, Abizaid et al. (2013) show supportive evidence on the pivotal roles of composite households—those comprised of parents and the families of adult children—in labor sharing in 2001.18
In the absence of individual-level data on forest clearing labor, we indirectly test our conjecture by repeating the analyses of labor composition using young male/female adults (aged 15–29 years) and older male/female working adults (aged 30–64 years) in the household/kin group separately (this division is based on the distribution of adults through time; many adults were relatively young at the time of clearing). Although aggregate male labor endowments in the household/kin group do not alter labor composition, if young male adults are more productive, especially as extra-family laborers, disaggregated male labor endowments can influence the use of extra-family labor as follows. On one hand, although physical advantages of own young male labor decrease the use of both hired and cooperative labor (because of lower demand), its reputation effects positively influence holding cooperative labor events (for reputation building) and thus decrease hired labor. As such, the combination of significant and nonsignificant net effects on hired and cooperative labor, respectively, would give some evidence for both physical and reputation effects of own labor. On the other hand, both physical and reputation effects of young male labor in the group would augment cooperative labor (although these two effects cannot be distinguished). The effects of older male labor are opposite to those of young male labor, and when young and older working adults are combined, the effects vanish as they counteract each other.
Hypothesis 4 (adult-lifecycle effects): The more young (older) male labor endowments in the household, the less (more) hired labor; cooperative labor is not affected. The more young (older) male labor endowments in the kin group, the more (less) cooperative labor.
That adult-lifecycle effects influence both hired and cooperative labor gives indirect evidence that they alter the productivity of two forms of extra-family labor in the same way (i.e., equal productivity).
Fixed-effects estimation results are reported in table 7. To maintain the degrees of freedom, within-group labor endowments are not interacted with village dummies, as in the labor demand equations in table 4. Results with disaggregated male/female adult size in the kin group are shown; those with the share of disaggregated male/female adults are similar. The following findings are consistent with hypothesis 4. First, household adult lifecycle affects hired labor but not cooperative labor: households with a larger number of own older male working adults are more likely to hire labor (especially to clear low levee), and households with fewer young male adults hire a larger amount of labor. Second, group lifecycle affects cooperative labor but not hired labor: households with a greater number of older male adults in the kin group use less cooperative labor.19
| Employment (0/1) | Log Amount (Labor-Day) | |||
|---|---|---|---|---|
| Hired | Cooperative | Hired | Cooperative | |
| (1) | (2) | (3) | (4) | |
| A. Upland/high levee/low levee in lowland & upland villages (n=258)—No. male/female adults in kin group | ||||
| Young male adults (15–29 years) in household | −0.005 | 0.065 | −0.241** | 0.247 |
| (0.041) | (0.079) | (0.118) | (0.221) | |
| Older male adults (30–64 years) in household | 0.080 | −0.034 | 0.036 | 0.144 |
| (0.080) | (0.089) | (0.229) | (0.276) | |
| Young male adults in kin group | 0.008 | 0.002 | 0.034 | 0.016 |
| (0.024) | (0.035) | (0.073) | (0.102) | |
| Older male adults in kin group | −0.020 | −0.097** | 0.007 | −0.229* |
| (0.032) | (0.045) | (0.076) | (0.128) | |
| R squared | 0.095 | 0.077 | 0.088 | 0.078 |
| B. Low levee in lowland & upland villages (n=179)—No. male/female adults in kin group | ||||
| Young male adults in household | 0.031 | 0.078 | −0.199 | 0.253 |
| (0.042) | (0.093) | (0.121) | (0.243) | |
| Older male adults in household | 0.174* | −0.101 | 0.196 | 0.058 |
| (0.100) | (0.109) | (0.261) | (0.360) | |
| Young male adults in kin group | −0.014 | −0.014 | −0.060 | 0.029 |
| (0.026) | (0.049) | (0.082) | (0.133) | |
| Older male adults in kin group | −0.050 | −0.069 | 0.017 | −0.237 |
| (0.047) | (0.065) | (0.111) | (0.192) | |
| R squared | 0.203 | 0.115 | 0.154 | 0.108 |
- a Note: Standard errors clustered by household are in parentheses. Other controls not shown here are number of young/older female adults in household, number of young/older female adults in kin group, number of male/female children (<15 years), age of household head, a dummy for 1986–2001, its interaction with a dummy for upland village, and constant. All labor endowments are measured at the time of forest clearing. A single asterisk indicates 10% significance, a double asterisk indicates 5% significance, and a triple asterisk indicates 1% significance.
Conclusions
-
Family, hired, and cooperative labor are perfect substitutes. Although hired and cooperative labor are as productive as one another, their productivity is higher than that of family labor, probably because extra-family laborers are younger and more highly motivated during agricultural work events—for future employment and land accumulation—than family laborers.
-
Labor allocation is efficient because the combination of labor market and labor sharing makes productivity-adjusted total labor use unconstrained by household and network endowments. Labor reciprocation allows cooperative labor to be substituted for hired labor under credit constraints.
-
Labor composition, however, is constrained by network endowments and liquidity; hence, credit policies alter not only labor composition but also labor network formation—network tightening for stronger reciprocity.
These findings suggest four key implications for research and policy. First, nonmarket labor-sharing institutions can serve as market substitutes for efficient labor allocation. Because interhousehold labor reciprocation facilitates labor substitution, the perfect substitutability of labor inputs may hold for more complicated tasks than forest clearing studied in our benchmark case. Reputational mechanisms in personalized exchange can make extra-family labor even more productive than family labor. Future empirical analyses on the substitutability, productivity, and efficiency of agricultural labor must explicitly consider labor sharing, where present, and potential productivity differences across various forms of labor, and the results of past analyses that overlook this informal labor institution and the heterogeneity in labor quality are perhaps now open to question. More attention is needed to better understand the economics of agricultural labor sharing (cooperative labor) and its potential role in and implications for rural development. For example, labor sharing may be complementary to other social networks among peasants, such as ones for technology adoption, and may significantly influence local public goods provisioning in community-based development (World Bank 2002).
Second, although, in general, as economic development relaxes market constraints, market exchange tends to expand and nonmarket exchange contracts (North 1990), labor-sharing institutions among poor farmers can and do persist. This is not only because of labor-sharing institutions' efficiency and productivity comparable with market exchange but also because of their flexibility in network formation. The coevolution of market and nonmarket institutions is a broad theme that is critical in studying development process for better policymaking. Exploring labor-sharing institutions along this line is promising and important because of their continued prevalence, significance, and dynamism in rural areas of the developing world, as documented in many ethnographic studies.
Third, efficient forest clearing among shifting cultivators does not necessarily lead to efficient allocation of land under missing/imperfect land markets. This occurs because land accumulation is determined not only by the application of labor but also by interhousehold land transfers (e.g., gifting, inheritance), another network-based nonmarket institution, which over time reallocates cleared lands. Better understanding forest-clearing decisions and consequences—land accumulation and distribution and broad environmental outcomes, such as secondary forest regrowth, ecosystem service provisioning, and biodiversity loss—to inform policymaking for conservation and development in tropical forests requires the examination of the interaction between labor transfer (sharing) and land transfer.
Finally, our empirical models can be broadly applied to other agrarian contexts and problems where data on production output, labor inputs (and other inputs, if any), and demographics are available. The two-level CES production function is a powerful tool in testing for perfect substitutability as well as productivity. The augmented separability test based on network endowments, not networks themselves, neither requires network data nor involves potential identification problems associated with network formation (although one needs to consider the determinants of network formation itself, such as kinship). Field-level data allow researchers to control for household fixed effects even for a relatively small sample of households. Clearly, data capturing rich variations in institutions across regions/villages before and after policy interventions, which we lacked, are needed to further advancing our understanding of the evolution of agrarian institutions.
Appendix
| Lowland Village | Upland Village | |
|---|---|---|
| Labor endowments (15–64 years) | ||
| No. male adults in household | 1.6 (1.1) | 1.3 (0.7) |
| No. female adults in household | 1.3 (0.9) | 1.3 (0.7) |
| No. male adults in kin group | 5.1 (4.5) | 5.2 (5.1) |
| No. female adults in kin group | 4.3 (3.9) | 4.8 (4.6) |
| Within-village share of male adults in kin group | 0.11 (0.08) | 0.13 (0.11) |
| Within-village share of female adults in kin group | 0.12 (0.09) | 0.13 (0.10) |
| Other household demographic characteristics | ||
| No. male children (<15 years) | 1.2 (1.3) | 1.1 (1.0) |
| No. female children (<15 years) | 1.1 (1.3) | 1.2 (1.1) |
| No. male elderly (65 yrs or above) | 0.03 (0.18) | 0.03 (0.17) |
| No. female elderly (65 years or older) | 0.00 (0.00) | 0.01 (0.12) |
| Household age | 9.9 (12.6) | 8.3 (10.9) |
| Age of household head | 35.0 (12.9) | 33.4 (11.8) |
| No. observations | 120 | 138 |
- a Note: Standard deviations are in parentheses.




