Foreclosures and Invasive Insect Spread: The Case of Asian Citrus Psyllid
Support from the Specialty Crop Research Initiative (NIFA-USDA, grant no. 2010-01182) is gratefully acknowledged. All conclusions remain the authors and do not represent official positions of the USDA.
Abstract
Human economic activity is considered to be an important factor in exacerbating the speed of invasive species spread, but may also play an important role in preventing it. In this study, we investigate the role of home foreclosure in the spread of Asian Citrus Psyllid (ACP, Diaphorina citri Kuwayama) throughout residential areas of Southern California. We find that foreclosures are indeed a significant factor in explaining ACP spread, even after controlling for other human and environmental effects. Our results suggest that human economic activity may be more important in controlling the spread of invasive species than previously realized, and that the external costs of the foreclosure problem may also be underestimated.
Understanding the movement of invasive species in a host environment is critical to detection, management, and eradication. Statistical models of insect spread typically include measures of the time and distance from introduction, biologic suitability of the host environment, and perhaps a control activity such as spraying or the introduction of natural predators.1 Only recently, however, has the role of human economic activity been recognized as exacerbating the speed of invasive species spread (Bossenbroek, Kraft, and Nekola 2001; Sharov et al. 2002; Gilbert et al. 2004; Muirhead et al. 2006). Most insects have the ability to move only short distances on their own over short periods of time, so long-distance dispersion is typically thought to result from human transport. Because human-monitoring is an important tool for detecting and eradicating invasive species in urban areas, abandoned homes provide a potentially critical pathway for uninterrupted spread (USDA-APHIS 2012). In fact, home ownership provides an example of how property owners' self interest can help mitigate the spread of invasive species. In this study, we investigate the role of home foreclosure in the spread of Asian Citrus Psyllid (ACP, Diaphorina citri Kuwayama) insects throughout residential areas of Southern California.
The ACP is perhaps the pest most feared by citrus growers. As a vector for the bacteria that causes citrus greening disease, or huanglongbing (HLB), it can devastate citrus over an entire region. Huanglongbing causes citrus yields to fall, drastically reduces fruit quality, can ultimately kill the tree itself, and has no known cure once a tree is infected (Halbert and Manjunath 2004). In 2009, California citrus represented nearly $1.8 billion in direct cash receipts, $3.0 billion in total economic activity, and some 26,000 jobs in direct and related activities (USDA-ERS 2012; Richards 2009). Therefore, the potential economic damage caused by widespread ACP movement is indeed significant, but the human role in mediating ACP spread, and perhaps facilitating greater damage, is not well understood.
Invasive insect species follow a three-stage process when invading a new environment: introduction, establishment, and spread (Liebhold and Tobin 2008). Once an invasive population is established, optimal management programs require a careful parameterization of its spread (Epanchin-Niell and Wilen 2012). There are essentially four types of biological models that describe the spread of invasive species: (a) reaction-diffusion models (Skellam 1951); (b) integro-difference equation models (Kawasaki and Shigesada 2007; Kot, Lewis, and Van den Drissche 1996; Neubert and Parker 2004); (c) gravity models (Bossenbroek, Kraft, and Nekola 2001); and (d) stratified diffusion models (Shigesada, Kawasaki, and Takeda 1995; Havel, Shurin, and Jones 2002; Gilbert et al. 2004; Muirhead et al. 2006). Reaction-diffusion models tend to explain localized spread well, but imply continuous rates of expansion, asymptotically constant speeds of wave travel, and Gaussian dispersion from the origin that is not necessarily descriptive of most invasive insect populations. Empirical observation tends to find that spread is rather leptokurtic, exhibiting fat tails rather than Gaussian spread (Hastings et al. 2005; Liebhold and Tobin 2008). Integro-difference equations are more appropriate for explaining populations that tend to spread in non-continuous waves, but do not explain seemingly random, long-term dispersal. Stratified diffusion and gravity models, on the other hand, are well-suited to explain both local spread and long-term diffusion while permitting empirical tests of mechanisms that facilitate both. A stratified diffusion model assumes that insects “… disperse by two independent dispersal processes occurring at different spatial scales…,” (Gilbert et al. 2004), one over short distances within the range of natural movement, and one over longer distances, generally at ranges that can only be explained by aided transport. In this paper, we estimate the spread of ACPs throughout Southern California using a stratified diffusion model in which we introduce measures of home-foreclosure activity as an explicit argument in the rate of invasive insect spread.
Mass foreclosures impose a number of externalities, some expected and some not. The effect of foreclosures on neighboring home prices is relatively well-understood, as is the effect on local tax receipts (Immergluck and Smith 2006a; Schuetz, Been, and Ellen 2008; Lin, Rosenblatt, and Yao 2009). Less obvious, but nonetheless apparent, are the effects of foreclosures on the rate of violent crime (Immergluck and Smith 2006b) and the psychological and physiological health of those going through a foreclosure (Pollack and Lynch 2009). When a homeowner abandons a foreclosure, not only does the community lose a monitor with a vested interest in maintaining the health of his or her trees, but gains an owner with the indifference of scale (the bank) and often loses access to trap and (if required) spray to control the invasive insect. Moreover, lower home values reduce existing homeowners' incentive to manage their own trees. To the extent that foreclosed homes are rented by banks, renters are likely to have less of an interest in monitoring and reporting insects on trees that they do not own.
Further, the potential economic damage of widespread movement of HLB-infected ACP has drawn the California Department of Agriculture (CDFA) into partnership with not only the USDA, but state-level citrus grower organizations (California Citrus Mutual) and research organizations (California Citrus Research Board) in the hopes that combining resources will make their joint efforts more effective. Detection and treatment by the CDFA, however, is more difficult, if not impossible, without access to foreclosed homes. One of the key strategies used by the CDFA to control the spread of ACPs is a detection hotline. The existence of unoccupied homes represents a weakness in this strategy, as reporting requires monitoring. With a high concentration of foreclosures in an urban neighborhood, the result is thus a virtually uninterrupted path by which ACPs can migrate through residential areas on their way to other, perhaps commercial, orchards.
Controlling the spread of an invasive species is sufficiently complex that removing one pathway does not necessarily solve the problem. In fact, some find that it is not the absence but the presence of human economic activity that facilitates spread (Gilbert et al. 2004). Transporting infested citrus, failing to clean trucks or farm implements, or sharing implements are but three ways that a higher population density can increase the probability of infestation. This observation emphasizes both the need to control for other types of activity in identifying the foreclosure effect, as well as the more general insight that eliminating one externality may, in fact, create others.
We contribute to the literature on invasive species management by documenting an important class of human-insect interactions that has previously been ignored: the effect of home abandonment (or orchard abandonment of any type) on the rate at which invasives are allowed to spread. Our findings suggest a very simple implication, namely that homeowners with a vested economic interest in maintaining the health of their citrus can serve as an effective, decentralized means of controlling spread. Our case differs from others in the literature because visitors to public recreation areas or campgrounds have no property rights over the trees or lakes they unwittingly infect. Because homeowners have property rights over host trees, controlling spread through residential areas is a fundamentally different issue than spread through public lands. We also contribute to the literature on spread modeling by introducing an econometric model of ACP diffusion that not only includes gravity-type measures of population density, but explicit measures of economic activity that are thought to provide a catalytic effect to insect movement.
The paper is structured as follows. In the first section we provide a brief narrative on the entomological and policy background underlying the ACP problem. We also describe our data collection process and summarize the ACP sightings data in the first section. In the second section we develop an empirical model of ACP spread and diffusion that represents a synthesis of existing gravity and stratified diffusion models. Our estimation results are presented in the third section, along with a discussion of their implications for policy and future model efforts. The final section concludes.
Asian Citrus Psyllid: Background
Invasive insect species represent a significant economic risk to both the financial viability of specialty crop producers and to the sustainability of U.S. agriculture more generally. With the rapid growth of international trade in agricultural commodities of all types, agricultural systems in the United States are under constant threat that new species will be introduced, spread, and thrive in an environment lacking natural predators. Indeed, Pimentel, Zuniga, and Morrison (2005) claim that insects alone are responsible for losses amounting to 13% of total U.S. crop production, valued at $33.0 billion. According to these authors, 40% of all insects can be regarded as invasive. Therefore, including the indirect costs associated with control, the total damage attributable to invasive insect species in the United States is $13.5 billion in 2001 dollars. The ACP problem is but one example of how invasive insect damage manifests in one specific industry.
Asian Citrus Psyllids represent a catastrophic threat if allowed to spread unchecked when the pathogens that cause HLB are also present (Halbert and Manjunath 2004). The ACP is an invasive insect species that has been identified in Mexico, Central America, South America, sub-tropical Asia, Afghanistan, Mauritius, Saudi Arabia, and Reunion (Grafton-Cardwell et al. 2006), and has been present in Florida since 1998 (Halbert 1998). Now established throughout Florida, ACPs were accidentally introduced to the Rio Grande Valley in Texas in 2001, and were first found in San Diego County, California, in August 2008. Asian Citrus Psyllids have since been sighted in Imperial County in October 2008 and Orange and Los Angeles counties in August 2009. As of October 2009, the California Cooperative Asian Citrus Psyllid Project (CCACPP) reported positive tests for ACPs at 614 sites out of a total of 107,650 surveyed. Administrative efforts to stop the spread of ACPs included a wide-area quarantine placed on citrus movements from parts of San Diego, Riverside, and Imperial counties, and all of Los Angeles and Orange counties in September 2009, while the USDA announced a $5.8 million program to help prevent the spread of ACPs in California in October 2008. From the first sighting in 2008 until early 2012, there had not been a positive test for HLB in Southern California. However, in late March 2012, CDFA officials reported the first positive test in a hybrid-lemon tree in a residential neighborhood, confirming the importance of orchards in residential landscapes to the likelihood of devastating damage resulting from ACP spread (Nelson 2012).
Asian Citrus Psyllids damage citrus directly by feeding on the leaf and depositing a large amount of honeydew, leading to the formation of molds (Manjunath 2004). During feeding, ACPs also deposit a toxin that stunts the leaf and causes extreme malformation (Michaud 2004). Adults cluster to feed and mate on leaf bud sites, which impairs their growth and further reduces fruit yield. On their own, however, these issues are relatively minor. More significantly, ACPs vector the bacterium that causes HLB, which is often referred to as “…one of the most devastating diseases to citrus in the world…” (Grafton-Cardwell et al. 2006). Huanglongbing causes a number of physiological problems to the tree and to the fruit itself. Trees infected with HLB are smaller, have fewer leaves, bloom off-season, and will drop both leaves and fruit (Halbert and Manjunath 2004; Grafton-Cardwell et al. 2006). Moreover, fruit from HLB-infected trees are small, lopsided, and hard with immature seeds and, perhaps not surprisingly, green. Most trees infected with HLB survive only 5–8 years and typically fail to produce any valuable fruit over their lifetimes. Although CDFA officials detected ACPs in San Diego and Imperial counties, and found a positive test for HLB in March of 2012, they have yet to find widespread evidence of HLB in California citrus. In fact, HLB was not detected in Florida until 2005, despite the presence of ACPs for almost ten years (Meyer, Hoy, and Singh 2007). Because many species closely related to citrus can serve as viable hosts, there are a number of avenues for the spread of ACPs throughout California.2
Data Description
The primary insect-count data for this study were gathered under the auspices of the CDFA between October 2008 and March 2011. Both yellow panel traps and visual inspection were used to establish counts of nymph, adult, and dead ACPs at site locations determined by CDFA entomologists. Although visual inspection is not necessarily confined to the same location as the traps, they are reported as such in the CDFA sightings data. That is, each visual sighting is associated with a specific latitude and longitude coordinate in a manner similar to the trap sightings, so we pool all sightings data and assume they are generated by the same process. Only positive sightings are reported, so developing a probabilistic indicator of presence or absence of ACPs is not possible. In the empirical model below, we take the truncated nature of the CDFA sightings data into account. Latitude and longitude measures for each trap are used to establish the location of each sighting. Because of the relatively long distances between sightings, and the fact that the earth is not flat, Euclidean distance is not an acceptable method of calculating the distance from the first sighting in October 2008 and each subsequent sighting. For any appreciable distance there will be a significant error associated with using Euclidean distance to measure travel distance for insects, so we use the great circle distance between each sighting and the origin.3 Table 1 provides a summary of the CDFA sightings data, as well as the hypothesized mediating variables described below.
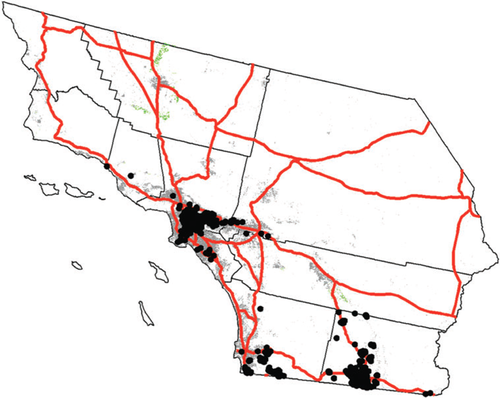
ACP sightings, Southern California, 2008–2011
| Variable | Units | Mean | Std. Dev. | Minimum | Maximum |
|---|---|---|---|---|---|
| Total ACP | # | 7.28 | 19.92 | 0.00 | 386.00 |
| Distance from Major Highway | km | 7.23 | 1.37 | -1.70 | 10.23 |
| Foreclosures | #/'000 ha | 0.08 | 0.06 | 0.00 | 0.38 |
| Housing Density | #/'000 ha | 3.16 | 2.49 | 0.00 | 18.39 |
| Cooling Degree Days | °F/day | 0.26 | 0.66 | 0.00 | 4.77 |
| Wind Speed | Mph | 1.54 | 0.82 | 0.20 | 4.50 |
| Wind Direction | binary | 0.45 | 0.50 | 0.00 | 1.00 |
| Treatment | binary | 0.00 | 0.05 | 0.00 | 1.00 |
| Population | '000/ZIP | 0.49 | 0.23 | 0.00 | 1.09 |
| Fall | binary | 0.48 | 0.50 | 0.00 | 1.00 |
| Winter | binary | 0.27 | 0.44 | 0.00 | 1.00 |
| Spring | binary | 0.09 | 0.29 | 0.00 | 1.00 |
| Los Angeles Quarantine | binary | 0.93 | 0.25 | 0.00 | 1.00 |
| San Diego Quarantine | binary | 0.93 | 0.26 | 0.00 | 1.00 |
| Ventura Quarantine | binary | 0.27 | 0.44 | 0.00 | 1.00 |
| Renters | % | 5.94 | 1.48 | 1.21 | 10.00 |
| Poverty | % | 0.25 | 0.08 | 0.00 | 1.00 |
| Distance from First Sighting | Miles | 226.63 | 101.14 | 0.00 | 402.20 |
| Days from First Sighting | Days | 577.01 | 208.71 | 0.00 | 895.00 |
The geographic distribution of sightings is remarkable for the concentration of ACPs in urban areas (figure 1). While invasive species are typically regarded as an agricultural problem, ACPs are clearly non-discriminatory in moving through residential citrus. In fact, it is the stylized fact that ACPs move through residential citrus that provides the core hypothesis for this research, namely that human-mediated movement represents a critical driver in the spread of any invasive species.
We combine the insect-count data with five measures of human and physical environments that may be relevant to insect spread. First, highway transport is often cited as a means by which invasives are able to move distances much longer than the limits of self-transport (Godfrey and Grafton Cardwell 2006; Burnett et al. 2008; Halbert et al. 2010). We combined the CDFA data with a public highway layer available in ARCGis 10.0 in order to calculate the distance of each sighting from the transportation network.
Second, stratified-diffusion models commonly assume that insect transport is mediated by human activity, so we include housing density as a potential determinant of spread (Gilbert et al. 2004; Muirhead et al. 2006). We associated each sighting with a housing density value by assigning each sighting in the nearest ZIP code, then obtaining ZIP-code level housing and population data from the U.S. Census Bureau, and merging the two. Housing density is then calculated as the number of residential housing units per thousand hectares. Ownership status is also likely to be an important measure of the occupant's incentive to maintain the value of the property and, thereby, monitor and control ACP spread. For this reason, we also include housing tenure (rentals as a proportion of total occupied housing) on a ZIP code basis from the Census Bureau. Because population density may also be important in its own right (as a proxy measure of the level of economic activity) regardless of housing density (Gilbert et al. 2004), we include ZIP code level population as well. Low income households may also lack either the ability to monitor infested trees, or lack the resources to treat those that are identified as infected. Therefore, we include a measure of the proportion of households earning below the federal poverty line in each ZIP code, as well as from the Census Bureau.
Third, we merged ZIP code level foreclosure data obtained from RealtyTrac, Inc. RealtyTrac follows foreclosure activity on a monthly, ZIP code basis. Because foreclosure is a lengthy process, however, there are many different ways to track foreclosure activity. Our data include five measures, each represented as counts at a ZIP code geography level: (a) Notice of Default (NOD) is filed by a trustee after a homeowner has defaulted on a mortgage, and represents the initial step in the pre-foreclosure process; (b) Lis Penden (LIS) is a notification of pending lawsuit and is the first judicial step in the pre-foreclosure process as it is filed by lawyers and not the trustee; (c) Notice of Trustee's Sale (NTS) is a notice announcing a public auction; (d) Notice (Judgment) of Foreclosure Sale (NFS) is a formal order, signed by a judge, that instructs the trustee to publish a “Notice of Sale” and to sell the property at public auction; and (e) Real Estate Owned (REO) indicates that the property has been conveyed back to the lender and represents the final step in the foreclosure process. The total of all five measures represents an indicator of how many homes in a given geographic area there are at any stage of the pre-foreclosure and foreclosure processes.4 Table 1 provides a summary of the foreclosure data.
Fourth, insect growth and spread are critically dependent upon weather conditions (Halbert and Manjunath 2004). Asian Citrus Psyllid reproduction has been shown to reach optimal levels at approximately 65° F (Halbert et al. 2010), so we include a measure of cooling degree days (CDD)—cumulative degrees above 65° F in the previous 30 days—to capture the temperature effect on reproduction.5 Long-distance ACP spread is commonly thought to be either wind-aided or human-aided, because ACPs are notoriously poor flyers.6 Further, the first ACP sighting in California was in San Diego County, so virtually all of the citrus lies further to the northeast, directly in the path of the prevailing winds. Therefore, we also include average windspeed and wind direction to measure wind-aided spread. We measure wind direction by including a binary variable for observations where the fastest two-minute wind (a metric provided by our data source) was from the southwest.7 Both of these variables are from the National Climatic Data Center of the U.S. Department of Commerce (NCDC - DOC).
Fifth, seasonal variation is important to both ACP spread and detection because ACPs feed on leaf flush (Grafton-Cardwell 2012) that is more likely to appear in both spring and fall. Although greater opportunities for feeding would suggest more movement and spread, insect traps of the type used by CDFA are more effective when trees are not flushing.8
CDFA control activities may effect the observed rate of spread in a number of ways. Following a positive sighting at a trap site, the surrounding area is typically treated with insecticide to ensure that any further spread is controlled. Therefore, we include an indicator of whether a site was treated in the past as an explanatory variable for the number of ACPs on the current inspection. Similarly, California Department of Agriculture officials enforced citrus quarantines on counties, or portions of counties, following positive sightings. During our sample period, quarantines were extended to Orange County on August 28, 2009, to Los Angeles County on September 2, 2009, to Northern San Diego County on November 18, 2009, and to Ventura, Southern Santa Barbara, and West Riverside counties on December 31, 2010. Quarantines are likely to negatively impact the probability of a positive sighting because long-distance spread is generally thought to result from the physical movement of either fruit or nursery material from one area to another, among the other factors described here (Grafton-Cardwell 2012).
Empirical Model of ACP Spread
We test for the effect of foreclosures on the rate of ACP spread within the context of a bio-economic model of invasive dispersal. We specify a stratified diffusion model, which combines a reaction-diffusion model of local ACP spread and a long-range dispersal component. In this sense, stratified diffusion models are a synthesis of theory-based and purely empirical models, since they are meant to explain movement that derives from biological factors, environmental factors, and human-mediated influences. Further, because stratified diffusion models nest a reaction-diffusion model and an empirical model of long-term dispersal, they are inherently more general.
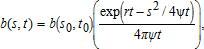 (1)
(1)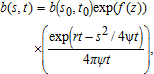 (2)
(2)The elements of z include each of the environmental variables described above: distance to the nearest highway; cumulative CDD over the past 30 days; windspeed; wind direction (binary indicator for southwest wind); household density (number of households per hectare); total population in the ZIP code area; rental properties as a percentage of total housing; the proportion of households earning below the federal poverty level; a summary measure of the total rate of foreclosures (per hectare) in the surrounding ZIP code; season indicator variables; binary indicators for whether a particular site had been treated with insecticide in the past; and dummy variables indicating whether or not a county was under quarantine at the time of the sighting.9 Therefore, the dispersal kernel is written as: 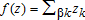 where the zk are elements of z and βk is the effect of the kth element on the contribution to long-term dispersal. Temporal and spatial distances to all other sightings are calculated based on the initial date and latitude/longitude coordinate. Temporal distance is calculated as the number of days after t=0, while distance is calculated using the great-circle algorithm described above.10
where the zk are elements of z and βk is the effect of the kth element on the contribution to long-term dispersal. Temporal and spatial distances to all other sightings are calculated based on the initial date and latitude/longitude coordinate. Temporal distance is calculated as the number of days after t=0, while distance is calculated using the great-circle algorithm described above.10
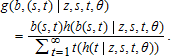 (3)
(3)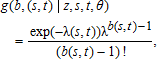 (4)
(4)We estimate the non-linear stratified diffusion model in (4) using maximum likelihood. The full non-linear stratified-diffusion model (model 3) is compared against alternative specifications in order to examine the robustness of our findings. Namely, we test our maintained model (model 3) against a pure reaction-diffusion model that accounts for local movement only, ignoring long-range dispersal (model 1), and a linear stratified-diffusion version (model 2) that measures spread and growth as direct functions of distance and time, respectively, without the structure of the Skellam (1951) model. We also estimate a version of the model in which we assume, incorrectly, that the dependent variable is not truncated (model 4). We report all estimation results, and the findings of our robustness tests, in the following section.
Results and Discussion
We begin our presentation of the results with a set of specification tests that compare a diffusion-only model of ACP spread (model 1) to a stratified-diffusion model that accounts long-range dispersal, but is linear in time and distance (model 2), and to a model that includes the non-linear Skellam (1951) diffusion term (model 3). All three of these models account for the T-ES nature of our data. We then compare the parameter estimates from model 3 to one that does not account for the T-ES nature of our data, in order to demonstrate the extent of bias involved. Once a preferred model is selected, we then interpret the estimated spread and growth parameters both in terms of our hypotheses regarding the likely mediators for ACP spread, and the implications for current management and eradication plans.
We present the estimates from models 1–3 in table 2 below, and for model 4 in table 3. We compare the first three specifications using three criteria: (a) likelihood-ratio (LR) tests, (b) root-mean-square error (RMSE) in-sample, (c) Akaike information criterion (AIC), and (d) the significance and plausibility of individual parameters. In each model, the dependent variable is the same, so LR tests are an appropriate model selection method. We first compare model 1 to model 2 using the LR criteria. For this comparison, the calculated LR chi-square test statistic value is 17,960.76, and the critical chi-square value with 18 degrees of freedom is 26.27, so we easily reject the null hypothesis that the two models are equivalent (p-value = 0.00) and prefer model 2. We also compare model 1 to model 3 using the LR criteria, which yields a chi-square test statistic of 14,240.02, again favoring model 3 over model 1 (p-value = 0.00). Comparing the two stratified-diffusion models, the LR chi-square test statistic with two degrees of freedom (two parameter restrictions are required to render the non-linear and linear models the same) is 5.99, and the chi-square statistic is 3,720.74 (p-value = 0.00), so we favor model 2 over model 3. According to the AIC, we prefer model 2, as the information-loss is minimized in the linear stratified-diffusion model. If these were the only evaluation criterion, we would reject the theory of insect diffusion developed by Skellam (1951) in favor of a linear stratified-diffusion model.
| Model 1 | Model 2 | Model 3 | ||||
|---|---|---|---|---|---|---|
| Variable | Estimate | t-ratio | Estimate | t-ratio | Estimate | t-ratio |
| Distance from Major Highway | N.A. | N.A. | 0.0478* | 81.0339 | 0.0786* | 124.6984 |
| Foreclosures | N.A. | N.A. | −0.1668* | −5.2224 | 2.9022* | 94.0742 |
| Housing Density | N.A. | N.A. | 0.0255* | 33.0649 | −0.0026* | −3.4533 |
| Cooling Degree Days | N.A. | N.A. | −0.3266* | −78.6867 | −0.3922* | −96.3612 |
| Wind Speed | N.A. | N.A. | −0.0846* | −46.7403 | −0.1120* | −61.5165 |
| Wind Direction | N.A. | N.A. | 0.4469* | 213.8469 | 0.5778* | 279.1208 |
| Treatment? | N.A. | N.A. | −0.4981* | −6.9885 | −0.2925* | −4.6145 |
| Population | N.A. | N.A. | 0.0609* | 11.8023 | 0.3527* | 69.8495 |
| Fall | N.A. | N.A. | 0.0332* | 11.9568 | 0.3457* | 120.4495 |
| Winter | N.A. | N.A. | −0.8037* | −202.4358 | −0.5919* | −147.9675 |
| Spring | N.A. | N.A. | −0.5592* | −82.1072 | −0.7559* | −108.7683 |
| Los Angeles Quarantine | N.A. | N.A. | −2.2441* | −15.2173 | −1.5823* | −10.8459 |
| San Diego Quarantine | N.A. | N.A. | 1.3051* | 8.8517 | 1.1525* | 7.9186 |
| Ventura Quarantine | N.A. | N.A. | −0.1895* | −49.4700 | −0.6189* | −160.3446 |
| Renters | N.A. | N.A. | −0.0702* | −45.0256 | 0.1897* | 131.7639 |
| Poverty | N.A. | N.A. | 0.3335* | 14.6963 | −0.7171* | −32.9995 |
| Distance from First Sighting | 2.7905* | 640.0183 | 0.8158* | 197.0531 | 4.0256* | 310.6142 |
| Days from First Sighting | 0.5850* | 76.6940 | 1.3485* | 112.5593 | 19.7311* | 44.9128 |
| LLF | 28,127.03 | 37,107.41 | 35,247.04 | |||
| AIC | −9.905 | −13.602 | −12.407 | |||
| Chi-Square | 7,609.64 | 16,590.02 | 12,869.26 | |||
| RMSE | 0.2659 | 0.3323 | 0.2616 | |||
- a Notes: A single asterisk indicates significance at a 5% level. Model 2 is a stratified diffusion model in which all covariates affect observed population linearly, while these combine with the Skellam model in model 3. Spread and growth are marginal effects of time (per day) and distance (per mile). Chi-square compares the log-likelihood function value of the estimated model to a null model (model in which all coefficients are restricted to zero, constant only).All variables are scaled for estimation, and LLF is the log-likelihood function value.
| Variable | Estimate | t-ratio |
|---|---|---|
| Distance from Major Highway | 0.0617* | 19.6433 |
| Foreclosures | −0.1000 | −0.7014 |
| Housing Density | 0.0158* | 5.0000 |
| Cooling Degree Days | −0.1948* | −14.0165 |
| Wind Speed | −0.0598* | −7.6314 |
| Wind Direction | 0.4076* | 26.1643 |
| Treatment? | −0.3176* | −2.2122 |
| Population | 0.1085* | 3.3992 |
| Fall | 0.1186* | 6.4510 |
| Winter | −0.5984* | −27.8858 |
| Spring | −0.3867* | −14.3823 |
| Los Angeles Quarantine | −1.2924* | −7.8402 |
| San Diego Quarantine | 0.5669* | 3.4907 |
| Ventura Quarantine | −0.2585* | −11.1953 |
| Renters | −0.0333* | −4.6601 |
| Poverty | 0.2926* | 3.1553 |
| Distance from First Sighting | 1.5504* | 21.5241 |
| Days from First Sighting | 0.5850* | 45.6706 |
| LLF | −51,193.75 | |
| AIC | 18.053 | |
| Chi-Square | 11,845.39 |
- a Note: A single asterisk indicates significance at a 5% level. Chi-square compares the log-likelihood function value of the estimated model to a null model (model in which all coefficients are restricted to zero, constant only).
Predictive ability, however, yields a different ranking. According to predictive ability (as measured by RMSE), model 3 predicts substantially better than model 2 (0.2596<0.3323), while model 3 predicts only marginally better than model 1 (0.2616<0.2659). Based on this comparison, model 3 appears to explain the data as well as a model that does not account for long-range dispersal (model 1), and better than an atheoretic (model 2) alternative.
According to our third criteria, the significance and plausibility of individual parameter estimates, we prefer model 3. The first reason is because the parameters describing long-distance dispersal in model 3 are all statistically significant, the individual parameter estimates of model 1 are likely to be biased due to the likely omitted-variables bias in the local-diffusion-only model. Therefore, we compare the estimates in model 2 with those in model 3. The second reason for our preference is that, because of their primacy to the stratified-diffusion model, we focus on the temporal-growth and spatial-spread effects implied by each model. Both the spatial and temporal parameters estimated using models 2 and 3 are statistically significant, so significance does not provide a useful basis for comparison.12 Therefore, we calculate the marginal effect (at the mean of the data) implied by each model and compare it to our prior expectations based on the theory of insect diffusion developed in the entomology literature (Liebhold and Tobin 2008). Namely, if the population in any given area exceeds a certain minimum threshold, then we expect the growth rate of the population to be positive. Further, all else being constant, if the same population is spread over a wider distance, we expect the marginal effect of distance from the origin to be negative, as insects have more difficulty finding mates the greater the dispersion. Calculating the marginal temporal effect in models 2 and 3, we find very similar values: 25.39 insects per day for model 3 and 26.68 insects per day for model 2. However, the marginal spatial effect for model 2 is 16.19 insects per mile, while the marginal spatial effect for model 3 is −10.40. Because greater spread should reduce insect numbers on the margin, plausibility favors model 3. The implausibility of the marginal, local diffusion effects implied by the linear stratified-diffusion model (model 2) also highlights the importance of separating the dispersal kernel from factors that influence localized spread. Consequently, we prefer model 3 for interpretation and hypothesis-testing purposes.
Before interpreting the parameters of model 3, we show estimates from the non-truncated model of ACP spread. In this model, we account for both long-distance dispersal and local diffusion, but make no attempt to correct for the fact that our data are not randomly generated. Our purpose in making this comparison is simply to show the extent of bias in the non-truncated specification. From the estimates in table 3, it is clear that the goodness-of-fit according to the AIC is significantly worse for the non-truncated model (model 4) relative to the preferred T-ES model (model 3) (18.305>−12.407), but fit is of little consequence when the parameters of interest are inconsistently estimated. To that point, the key parameters describing the rates of spatial diffusion and temporal growth in model 4 are far lower than in the preferred T-ES model (1.5504<4.2056, and 0.5850<19.7311, respectively). If our T-ES estimates are truly unbiased, then the extent of bias introduced by not accounting for truncation is indeed substantial.
Regarding model 3, each of the variables described above has a statistically significant effect on the number of ACPs observed at each trap site. Distance from a major highway has a positive effect on the number of observed ACPs at each sighting. While our prior expectations for this variable were that it would have a negative effect on ACP counts, this effect is estimated holding everything else constant. That is, for a given level of housing density and population, the further away from a major highway, the more ACPs there are likely to be. This makes sense, as these other measures capture the “transportation corridor” effect, while the remaining influence likely stems from the fact that most large orchards are far from major highways.
Among environment-related variables, CDD (higher values indicating more warm days) and wind speed have negative effects on ACP counts, while wind direction has a positive effect. Because every increment in CDD is one degree above optimal breeding temperature, this negative effect is to be expected (Halbert et al. 2004). The wind direction effect is also consistent with our priors, as it assumes a value of 1 when the wind blows from the southwest. Given that ACPs do not fly very far during their lifetimes, wind-aided transport is likely to be an important factor in long-term dispersal: if the prevailing winds in the previous 30 days were from the southwest, the number of ACPs rise significantly. However, the negative wind speed effect means that stronger winds are associated with fewer ACPs at each trap site, perhaps suggesting that traps (and visual inspections) are less effective when the wind has been strong enough to blow ACPs out of the area (Catling et al. 1972). Finally, the literature suggests that ACPs feed more actively during spring and fall (Grafton-Cardwell 2012). This effect could go either way, as more active feeding may mean that insects are moving around more, are more abundant and are therefore easier to trap, or that they are focused on feeding and are less susceptible to being trapped. We find that ACP counts fall in the spring and rise in autumn, so we cannot conclude definitively one way or the other.
Due to the potential damage inflicted by the uncontrolled spread of ACPs, both federal and state officials have developed a number of strategies aimed at not only controlling spread, but eradicating the ACP population. One strategy is that each site is treated with insecticide following a positive ACP sighting. As expected, the treatment binary variable has a significant negative effect on subsequent ACP counts. Another strategy was that the USDA mandated a series of quarantines on citrus movement on a county or sub-county basis in response to evidence that ACPs had become established in a particular region. Our findings show that the quarantines imposed in Los Angeles and Ventura counties (including south Santa Barbara and west Riverside) had the expected negative effects on ACP movement, while the San Diego quarantine had a positive effect. Either this quarantine was singularly ineffective, or this binary variable is associated with a period of rapid ACP spread that is not captured by any of our other variables.
We now examine our primary hypothesis, that home foreclosures increase the number of ACPs observed at each trap site. As expected, foreclosures were found to be a significant factor in the spread of ACPs across Southern California. Controlling for housing density, population, and the proportion of renters in the area surrounding a trap, we find that the number of foreclosures in a ZIP code is associated with a relatively large (2.9) and significant (t-ratio = 97.074) rise in the expected number of ACPs. This finding is robust to various measures of foreclosure, or whether we define foreclosures on a per hectare or per household basis. Accelerating the spread of invasive species is an important externality not commonly associated with the foreclosure crisis. It is easily explained, however, as backyards that are not monitored for ACPs, either because the owner is not attentive, or has lost his or her home to bankruptcy and the home is not occupied, are more likely to serve as ACP hosts. Housing density has a negative influence when we control for total population, the proportion of renters, and the number of foreclosures in the surrounding area. While housing density, as a measure of the level of economic activity, may be expected to have a positive effect in a traditional gravity model, we control for this effect by including population in the NLSD model. What remains is the possibility that more multi-family or small-yard housing units are simply associated with fewer opportunities to grow citrus.13 As expected, population and the proportion of renters have strong, positive effects on ACP counts.
Controlling for long-distance dispersal, we find plausible estimates for the rates of geographic spread, and of temporal growth. Localized spread, in the absence of human- or weather-aided transport, occurs at a rate of about four-tenths of a mile per year. Because ACPs do not fly long distances, this estimate is reasonable. Population growth occurs at a rate of 0.025 insects per day, which may seem to be low but is reasonable given that the sightings data used here are actually density estimates, as there is no way to obtain an accurate measure of total populations through random-trapping.
For policy purposes, it is necessary to translate our estimates into measures of economic benefit and cost. Our counterfactual is to assume that policymakers have the ability to stop foreclosures entirely. If they could, the benefit to doing so, at least in terms of the problem at hand, would be removing a significant number of ACPs from the environment. The marginal value of reducing the number of ACPs through non-chemical methods is assumed to be the avoided cost of additional treatments. The pesticides that have proven most effective are standard neocontinoids and pyrethroids, at a cost per acre of some $746.99 (in 2013 dollars) based on the application of pyrethroids, Movento, Delegate and imidacloprid in the fall and spring.14 Based on the estimates reported above, each treatment is responsible for removing 0.29 ACPs, all else being constant, per trap site. Removing foreclosures, on the other hand, has a marginal effect of removing approximately 2.9 ACPs, or the equivalent of 10 treatments, or $7,469.90, assuming each treatment covers one acre surrounding the trap site. Aggregating over all sites provides the total value of eliminating the foreclosure effect of $19.84 million, based on 2,656 unique trap sites in our data. Although this estimate is based on a number of assumptions, it is based on reasonable and conservative estimates of the total savings by eliminating this source of externality. From a policy perspective, this is the benefit that should be added to the other, numerous benefits of resolving the foreclosure crisis, and compared to the cost of doing so. Accounting for these other benefits, and the ultimate cost of helping homeowners, is beyond the scope of this paper, but would seem to be a reasonable exercise for an agency with more macro-policy responsibilities.
The implications of our findings are important on a number of levels. The first implication is that we identify and quantify an important external effect of the foreclosure crisis that has been previously overlooked. While it is well-understood that urban blight imposes significant management costs on municipalities, our findings highlight additional costs to the environment and to agricultural production. Once regarded as an urban problem, foreclosures represent a clear pathway through which the built environment imposes an unintended cost on food production. More generally, if foreclosures aid the spread of ACPs, then they are likely to have the same effect on the spread of other invasive species, controlling for other measures of economic activity as we do. When state officials were negotiating with the major mortgage lenders in settlement of the lawsuit regarding unfair lending and foreclosure practices, we would hope that externalities like the one we identify were taken into account (Dennis and Horwitz 2012). Because it is more than likely they were not, we would hope that any part of the settlement that goes to public coffers would be directed at remedying externalities such as the one found here.
Another implication of our findings is that if humans mediate spread, then humans must also serve as important agents of control and prevention. Because they have a vested interest in preventing spread, homeowners are perhaps best situated to monitor, report, and manage ACP dispersal throughout densely-populated urban areas.
Our findings are relevant to industry-sponsored information and monitoring activities, as well as government-led control and eradication programs. Although the California Citrus Mutual (CCM), the Citrus Research Board (CRB), and the California Department of Food and Agriculture (CDFA) have initiated aggressive information campaigns targeting non-commercial citrus growers, our findings suggest that they may need to expand the range of potential grove-monitors to include mortgage lenders, city managers, and even commercial real estate management companies that may have citrus on unoccupied properties. Designing incentives that encourage these groups to participate may be problematic.15 Fines for non-resident owners would be effective, but would certainly be resisted. One would hope that local governments—whether municipalities, counties, or even homeowners' associations—have the same broader, social objectives as state officials, but that is not likely the case. Witholding services would be an option. Detection and eradication are inherently capital- and labor-intensive processes, but our findings provide justification for intensifying trapping activities on a household-level scale in order to be effective. Deciding on the amount of resources to allocate to monitoring invasive species in an economically efficient way requires careful consideration of the marginal costs and benefits involved. Although we quantify the benefit to removing a few ACPs by reducing the foreclosure effect, ultimately the public benefit from solving the problem entirely may include preventing the loss of the California citrus industry. If this is the case, then the cost of micro-level monitoring and eradication may be justified.
Suggesting that these other agents be held responsible for monitoring and controlling the problem, however, begs the question of how precisely they would be incentivized to comply. Many municipalities adopted a simple solution during the foreclosure crisis. Namely, in many of the most blighted areas, municipal governments enacted bylaws and regulations intended to make lenders legally responsible for a full range of maintenance issues on bank-owned properties. We envision a program similar to that used in Oakland, CA, in which banks are fined for not complying with maintenance ordinances (Drummond 2012). We would recommend that such ordinances include a clause that covers invasive species, as well as trash and other more visible signs of neglect.
Conclusion
Human economic activity is an important mediating factor in the spread of invasive species. International trade, recreational activities, commercial transport, or smuggling are commonly cited as the primary means by which invasive plants or animals move from an infested area to one that is not. Our understanding of the range and importance of these activities, however, is not well-developed.
In this study, we estimate a stratified-diffusion model of ACP spread throughout Southern California from 2008-2011. Localized spread is modeled as a Skellam (1951) reaction-diffusion model in which spatial-temporal growth depends on a non-linear function of time and distance from the first sighting, while long-distance ACP spread is modeled as depending on a host of environmental factors (temperature, windspeed, and wind direction) and economic factors (distance from a highway, population, treatment, quarantine, proportion of renters, and housing density). Because citrus trees in abandoned backyards represent an ideal, unmonitored host environment for ACPs, we include measures of foreclosure activity in the dispersal kernel of the stratified-diffusion model. We find that all factors hypothesized to be important in long-distance dispersal are statistically significant.
We also find that the number of foreclosed homes is an important mediating factor for the spread of an invasive species. Our finding is a unique and important outcome on a number of levels. While the difficulties foreclosed homes create for citizen-based monitoring and eradication programs are somewhat obvious, our finding adds one more negative externality associated with the mortgage crisis that began in 2007. Invasive species spread like crime and blight through neglected urban environments, creating one more reason to return foreclosed properties to some form of responsible ownership. Perhaps more important to ongoing control efforts, if humans mediate spread, they can also help manage it. Because homeowners have an incentive to maintain the value of their homes, our findings suggest that they serve as an effective, if decentralized, means of managing the spread of invasives throughout residential areas.
Nevertheless, human-aided transport is a well-understood means by which insects move over long distances, so removing one externality may in fact also restore another. More generally, we show that establishing property rights over host environments can be an effective means of incentivizing individual agents so that market control of an invasive species can be part of a viable solution, but not necessarily the entire solution.
Our findings also allow us to parameterize local and long-distance ACP spread. Future research, therefore, may use the estimates shown here in the design of spatial-temporal optimal control programs. Only by explicitly calculating the marginal benefits and costs of ACP eradication and control will it be possible to determine whether invasive species control is an important factor in the restoration of property rights to foreclosed properties.
One weakness of this study is the nature of the CDFA sightings data. Obtaining trap data on invasive species is always problematic, as researchers necessarily select trap sites using heuristics and personal judgement. Data from a controlled experiment may capture the underlying biology more accurately, but would not be able to measure the underlying human-environmental interactions that we focus on here.
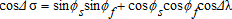 , where Δσ and Δλ are the differences between the latitude and longitude coordinates, respectively. Third, we solve for Δσ by taking the arccos of the result. This gives the geodesic distance in radians. Finally, we multiply by 6,372.8, which is the radius of the earth in miles, to arrive at distance measure.
, where Δσ and Δλ are the differences between the latitude and longitude coordinates, respectively. Third, we solve for Δσ by taking the arccos of the result. This gives the geodesic distance in radians. Finally, we multiply by 6,372.8, which is the radius of the earth in miles, to arrive at distance measure.



