Modeling Conjunctive Water Use as a Reciprocal Externality
Technical and financial support were provided by the U.S. Bureau of Reclamation Pacific Northwest Regional Office, Snake River Area Office, and Science and Technology Program. Funding for Taylor was provided, in part, by the Idaho Agricultural Experiment Station and the USDA-NIFA.
Abstract
A reciprocal externality is created in the conjunctive use of hydrologically connected surface and ground water. Hydrologic and economic modeling are integrated to conduct basin-wide cost benefit analysis to address the market failure of reciprocal conjunctive use externalities. An n-node partial equilibrium model was formulated in which economic equilibrium was defined by a system of complementary slackness equations. The general model was applied to a three-node example of a ground water pumper that enjoys the positive externality of canal seepage while inflicting a negative externality of pumping-induced seepage upon a canal water user. Exogenous demand, supply, and canal conveyance variables were parameterized using site-specific functional forms and data. The example was solved using mixed complementary programming for the endogenous equilibrium water prices which in turn were used to calculate consumer and producer surplus in the respective surface and ground water markets. A Pigouvian tax/subsidy policy was contrasted against two real-world policies; eliminating the externality through conservation infrastructure and aquifer recharge. The Pigouvian tax/subsidy aligns prices to erase the wedge between social and private costs. The reciprocal externality produces feedback between the surface and ground water markets that reinforces or cancels the tax/subsidy effect. The recharge payment prices canal seepage via a payment from pumper to canal user that matches the decrease in total pumping cost attributable to the seepage resulting from canal diversion. The Pigouvian tax/subsidy yielded the highest social welfare, followed by the aquifer recharge payment. Conserving water by lining the leaky canal decreased social welfare.
Introduction
Exploding municipal, energy, agricultural and environmental water demands are colliding with limited or diminishing supplies. Policies and projects that increase water supplies are either cost prohibitive or environmentally unacceptable. Agriculture, being the least valued and largest water user1 is the principal target of the imperative to reallocate and use water more efficiently.
The conventional water planning approaches of supply or demand management fail to adequately evaluate water project or water allocation efficiency. The supply management approach first forecasts a perfectly inelastic water requirement, and then calculates the prices necessary to recover costs (Howitt and Lund 1999). The demand management approach ignores water supply elasticity and focuses on reducing water demand through regulation, conservation, or infrastructure. By ignoring the elasticity of the opposing supply or demand blade of Marshall's scissors, both approaches disregard the value of water. Furthermore, conventional analyses are too often conducted piecemeal, for a specific water project or irrigation district, detached from the basin-wide hydrology. Ground water and surface water are an integrated hydrologic system. Thus, managing surface and subsurface water resources efficiently requires conjunctive water accounting and modeling tools capable of simulating the interactions between surface water storage or conveyances (rivers, canals, and drains) and ground water recharge from those sources.
Aquifers created or sustained by irrigation activities extend over vast areas in every western state. In the aquifers of California's Central Valley, virtually all recharge is gained from “infiltration of irrigation water” (Alley et al. 2002). Aquifers in Idaho's Eastern Snake River Plain (Cosgrove, Contor, and Johnson 2006), and Lower Boise Valley, Nebraska's North Platte, Colorado's South Platte (Howe 2002) and Washington's Columbia River Basin are also sustained largely by seepage from canals, off-stream reservoirs, or on-farm infiltration. Shakir et al. (2011) raised alarm of the impact of canal water shortages on the conjunctive ground water in the Punjab. Schmidt et al. (2013) estimated that 55% of diversions in the Lower Boise River Basin recharge the shallow aquifer or discharge to drains.
Externalities occur when the economic activities of one entity affect those of another, and pecuniary remuneration is wanting (Mishan 1971; Baumol and Oates 1988). Meade (1952) illustrated a positive reciprocal production externality using the classic example of bees providing nectar for honey and pollination for apples. In contrast to Meade's positive/positive reciprocal externality, conjunctive (joined or connected) surface water and ground water use is capable of producing a positive/negative reciprocal externality. For example, ground water pumpers near a canal enjoy the positive externality of canal seepage while inflicting a negative externality of pumping-induced seepage upon the canal user. The wells that extract tepid water from these hydrologically connected canals have been aptly labeled “warm water wells.”2
Water management decisions are often made without regard to existing surface/subsurface hydrologic connections, or to the benefits/costs to other water users in the basin (Booker et al. 2012; Evans 2010). In many western states, ground water and surface water conjunctive property rights are poorly defined or non-existent and lack compensation mechanisms to sustain or curtail conjunctive use, which promulgates externalities (e.g., Strawn 2004; Evans 2010; Blomquist et al. 2001). The resulting conjunctive use externalities cause a divergence between private and social benefit or cost, with price institutions failing to sustain desirable activities or curtail undesirable activities (Bator 1958). Omitting conjunctive use externalities also compromises basin-wide cost-benefit analysis (CBA) as required for federal water project planning (Council on Environmental Quality 2013).
The objective of this study is to demonstrate a generalized integrated hydrologic and economic modeling methodology for conducting basin-wide CBA that recognizes conjunctive use externalities. The tasks required to achieve that goal are as follows: (a) create a functional model of conjunctive surface and ground water hydrologic interactions as conjunctive use externalities; (b) formulate a spatial partial equilibrium model in which economic equilibrium is defined by a system of complementary slackness equations; and (c) perform CBA of alternative water policies aimed at addressing the market failures and inefficient water use resulting from conjunctive use externalities.
Literature Review and Methods
Within the taxonomy of hydro-economic models, conjunctive use of surface water and ground water is a distinct category of research (Harou et al. 2009). At the foundation was Burt's (1964) research which treated conjunctive ground water and surface water use as substitutes in determining optimal inventory of reservoir storage for aquifer recharge to meet given water demands. Following Burt, Milligan and Clyde (1970) used a linear program to evaluate the least cost alternative to recharge a conjunctive aquifer. O'Mara and Duloy (1984) also used linear programming to address the tax/subsidy for efficient conjunctive use between rivers, canals and pumping. Beginning with Noel et al. (1980) optimal control eclipsed linear programming. Noel et al. (1980) used optimal control to determine the pumping tax for optimal spatial and temporal allocation of ground water and surface water. Tsur (1990, 1991) and Tsur and Graham-Tomasi (1991) extended Burt's optimal control framework with uncertain surface water supplies. Azaiez (2002) developed a multi-staged decision model to optimize conjunctive use of ground water and surface water with artificial recharge. Burness and Martin (1988) determined the optimal recharge rate to restore a hydrologically connected and perennially losing tributary aquifer to a steady-state condition. Pongkijvorasin and Roumasset (2007) expanded the static framework optimal control model of Chakravorty and Umetsu (2003) to optimize canal water use and ground water pumping from an aquifer recharged by canal seepage and on-farm return flows. In summary, the conjunctive use research has largely focused on the optimal ground water and surface water use and optimal aquifer recharge. Despite explicit labeling of conjunctive hydrologic connection as an externality, research have not treated the externality as interrelated supply functions and thus been unable to address the market failures with CBA.
Researchers have taken either network simulation and optimization approach to integrating hydrologic with economic models (Harou et al. 2009). Beginning with Maass et al. (1962), hydrologic systems have been modeled as networks of water storage, with demand and supply nodes linked by the conveyance structures of rivers, canals, and pipelines. The network simulation approach conjoins a hydrologic network model, for example a river-reservoir prior appropriations water allocation model (Labadie 1994) with a system-wide agricultural optimization model (Hamilton et al. 1999 and Houck et al. 2007). While network simulation models have the necessary basin spatial dimension, these models are limited to “what if” questions and cannot maximize social welfare to address market failures of conjunctive use externalities, or conduct CBA of water projects and policies.
The partial equilibrium optimization model was introduced in the water literature by Flinn and Guise (1970), who adopted the Takayama and Judge (1964) interregional trade model. Howe and Easter (1971) used the trading model concept to evaluate large-scale inter-basin water transfers. Cummings (1974) introduced supply cost into a linear program to measure nonlinear benefits with piecewise linearization. Vaux and Howitt (1984) formulated the first regional water-trading model linking water demand and supply sectors to demonstrate the cost-effectiveness of reallocating water from existing uses, as opposed to developing new supplies. To compare the benefits of intrastate versus interstate water transfers, Booker and Young (1994) included salinity and hydropower to the water-trading framework. Further extensions used sequential and dynamic aspects to analyze climate or drought impacts on interregional water allocation (Booker 1995; Booker and Ward 1999).
Partial Equilibrium Model
Following Takayama and Judge (1964), partial equilibrium models have been cast as an optimization problem, where a quasi-welfare or net social function is maximized subject to constraints, and equilibrium is assumed to be the optimal point that maximizes this objective function. In the early 1970's numerical optimization techniques were well known but mixed complementary programming (MCP) was under development Takayama and Judge (1971). The non-linear optimization MCP approach used by Takayama and Judge (1964) is underpinned by the Karush-Kuhn-Tucker (KKT) conditions (Kjeldsen 2000). The KKT theorem demonstrates that a constrained optimization problem, in certain circumstances, can be transformed into a nonlinear complementary problem. The set of complementary slackness equations or KKT conditions are the first-order nonlinear complementary problem conditions for the constrained optimization problem that can be solved using MCP (Ferris and Munson 1999). With the advent of GAMS (Brooke et al. 1988) and accompanying solvers, the equilibrium equations can be formulated and directly solved as complementary slackness equations in a mixed complementary problem. The Takayama and Judge restriction of linear supply and demand functions can be relax to include convex functions. The alternative would be to formulate an objective function optimization problem and assume that the KKT conditions coincide with the equilibrium conditions.
A partial equilibrium model is defined for a single commodity exchanged between nodes, where I=set of supply nodes, J=set of demand nodes, and IJ⊂I⊗J=set of allowable arcs between nodes. A supplier produces a commodity at node i and ships a quantity Xi,j to node j along arc i,j. A supplier at node i can ship to the same node i, thus I∩J is not necessarily empty. The exogenous variables are the demand functions Pj(q) ∀j∈J, supply or marginal cost functions Pi(q) ∀i∈I, and transportation cost function ti,j ∀(i,j)∈IJ. The endogenous variables are: qj=quantities demanded ∀j∈J, qi=quantities supplied ∀i∈I, Xi,j=quantities shipped from node i to node j∀(i,j)∈IJ, ρj=market demand price ∀j∈J, and ρi=market supply price ∀i∈I. Per the notation of Takayama and Judge (1964) a variable superscript is a node index, not an exponent.
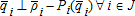 (1a)
(1a)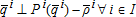 (2a)
(2a)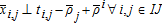 (3a)
(3a)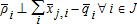 (4a)
(4a)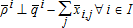 (5a)
(5a)Partial Equilibrium with Conjunctive Use Externalities
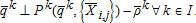 (2b)
(2b)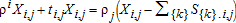 . The transportation cost is the seepage along the kth arc (canal) between nodes i and j: S{k},i,j(Xi,j,{qk}), where Xi,j is the diversion at the head of the canal and qk{k}⊆I is the total pumping that induces canal seepage from kth canal arc. Taking the derivative of both sides of the equation with respect to Xi,j results in the price linkage equation:
. The transportation cost is the seepage along the kth arc (canal) between nodes i and j: S{k},i,j(Xi,j,{qk}), where Xi,j is the diversion at the head of the canal and qk{k}⊆I is the total pumping that induces canal seepage from kth canal arc. Taking the derivative of both sides of the equation with respect to Xi,j results in the price linkage equation: 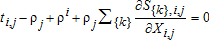 , and 3a becomes:
, and 3a becomes:
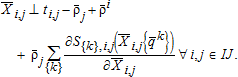 (3b)
(3b)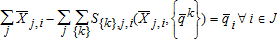 . With the reciprocal externality, the excess demand for canal water is eliminated by:
. With the reciprocal externality, the excess demand for canal water is eliminated by:
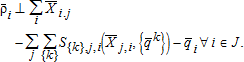 (4b)
(4b)A reciprocal conjunctive use externality is illustrated with an example of a leaky canal that recharges an aquifer used by a ground water pumper (figure 1). Three nodes define three respective markets. node 1 is a canal company at the head of the canal with an exogenous marginal cost, P1(q1). Node 1 then supplies water through a leaky canal to node 2 (a farm at the canal terminus) that has an exogenous demand, P2(q2). Node 2 lacks an exogenous supply function but faces an effective supply of canal water from node 1, minus the canal seepage. The conveyance arc between nodes 1 and 2 is the leaky canal. The exogenous seepage function S{3},1,2, analogous to transportation shrinkage of canal water conveyed from the canal head (node 1) to canal end (node 2), determines the recharge of the aquifer used by node 3. The farm at node 3 is supplied by an aquifer that is in part recharged by canal seepage, and has a demand for pumped water, P3(q3). The sole water source for node 2 is the canal, where the water source for node 3 is seepage from the canal (both passive and induced), and aquifer recharge from sources other than the canal. The marginal cost function for ground water at node 3 equals the pecuniary marginal costs (P3(q3)) and the externality of seepage gifted by node 2, S{3},1,2. The indices for the example are thus, i={1,3}, j={2,3} and ij={(1,2),(3,3)}.
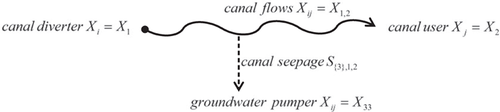
Schematic of 3 node example
Economic equilibrium is defined by the system of complementary slackness equations (1, 3b, and 4b). Endogenous equilibrium prices 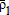 ,
, 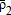 , and
, and 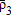 and quantities
and quantities 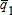 ,
, 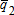 , and
, and 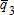 , can be determined by solving the complementary slackness equations using MCP or by maximizing a social welfare objective function (e.g., Booker and Young 1994; Booker and Ward 1999). In our example, complementary slackness conditions were programmed in GAMS and solved using the PATH solver (Ferris and Munson 1999). Equilibrium prices and quantities are then limits on the respective consumer and producer surplus integrals.
, can be determined by solving the complementary slackness equations using MCP or by maximizing a social welfare objective function (e.g., Booker and Young 1994; Booker and Ward 1999). In our example, complementary slackness conditions were programmed in GAMS and solved using the PATH solver (Ferris and Munson 1999). Equilibrium prices and quantities are then limits on the respective consumer and producer surplus integrals.
Exogenous Functions
The two exogenous demand functions (node 2 demand at the end of the canal and node 3 demand at the well head); two exogenous marginal cost functions (node 1 supply at the head of the canal and node 3 supply of ground water at the well head), and an exogenous transportation cost of canal seepage are outlined below and detailed with data in the appendix.
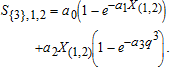
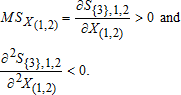
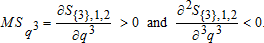
Thus, MSq3 is downward sloping; with increased pumping (ceteris paribus the canal head condition) the water table declines, the aquifer becomes disconnected from the canal (over a greater length of the canal), and the pumper is less able to induce seepage. Thus, as MSq3→0, seepage is increasingly passive.
The locational price equilibrium (equation 3a) is determined by equating the sum of supply price and transportation cost (effective supply) with demand price. The effective cost of supply at node 2 (P2) is the cost of water supplied at the head of the canal, plus the marginal cost of seepage; P2=P1+ρ2MSX1,2 where the exogenous marginal cost for node 1 at the head of the canal (in our example, P1=k1) and ρ2 is the price at node 2. In our example, the total charge at the head of the canal equals k1X1 where k1 is a constant O&M charge, thus P1=k1. Therefore, P2 is the sum of an exogenous levy at the canal head, plus the externality of MSX1,2, which is determined in part by the amount of pumping (q3) of node 3. The quantity of water delivered to node 2 at the end of the canal is the quantity at the head of the canal net of canal seepage. Downward sloping seepage costs are added to a fixed levy, resulting in an effective supply cost at node 2, which declines as diversion increases.
The marginal cost of ground water to node 3 at the well head is: P3=k2+k3lift where k2 is a fixed pumping cost, k3 is the power cost per foot of pumping lift, and pumping lift is lift=b0⋅e(b1q3−b2X1,2). Thus, P3 is a function of the exogenous pumping cost parameters, plus the canal seepage externality, as determined by the actions of node 2. As pumping increases, the water table drops and becomes disconnected from the canal. Thus, as MSq3 goes to zero, seepage becomes increasingly passive. Simultaneously, the drop in the water table causes the marginal cost of pumping to escalate.
The two exogenous irrigation demand functions correspond spatially to the respective supply functions, the well head, and head gate at the end of the canal for nodes 3 and 2, respectively. Demand is short-run, exhibiting decreasing marginal returns to the variable input of water and with crop mix, acreage, and irrigation technology fixed. The general functional of the demand is 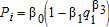 (Contor et al. 2008) where β0, β1, and β2 are case-specific parameters, reflecting crop yield, evapotranspiration, irrigation efficiency, and commodity prices (see the appendix).
(Contor et al. 2008) where β0, β1, and β2 are case-specific parameters, reflecting crop yield, evapotranspiration, irrigation efficiency, and commodity prices (see the appendix).
Results and Analysis
Externalities result in undesirable market behavior when market institutions fail to sustain desirable activities or reduce undesirable activities (Bator 1958). A production externality creates a Pigouvian wedge between private and social supply with positive externalities being under-produced and negative externalities over-produced. Using the three node example, three scenarios illustrate the application of partial equilibrium modeling with reciprocal conjunctive use externalities. A Pigouvian tax/subsidy scenario internalizes the reciprocal externalities to contrast with two real-world scenarios that mitigate the conjunctive use externality: (a) eliminating the externality with water conservation infrastructure; and (b) payment for aquifer recharge. Equilibrium prices, quantities, and surpluses for each scenario are reported in table 1. Results for the Pigouvian tax/subsidy and aquifer recharge payment in the canal and ground water markets are displayed in figures 2a and 2b, and figures 3a and 3b, respectively. The numeric CBA results for the recharge payment in table 1 are illustrated graphically in figures 4 and 5 (Griffin 1998).
Pigouvian tax/subsidy scenario in the surface water market
Pigouvian tax/subsidy scenario in the ground water market
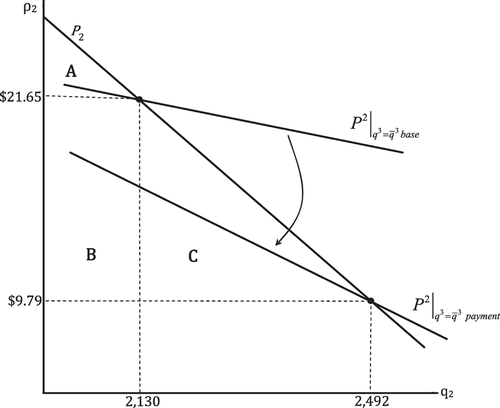
Aquifer recharge payment scenario in the surface water market
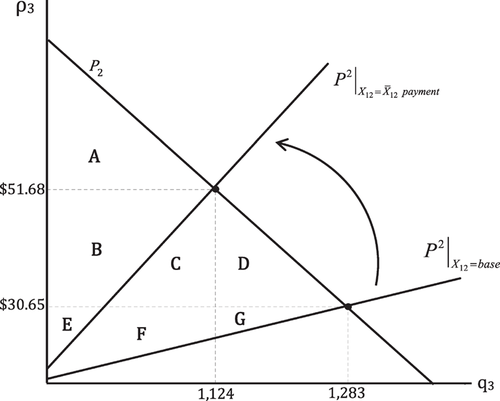
Aquifer recharge payment scenario in the ground water market
| Variable | Scenario | ||||
|---|---|---|---|---|---|
| Description | Equalities | Baseline | Pigouvian tax/subsidy | Seepage Elimination | Recharge Payment |
| Consumer surplus node 2 | $90,900 | $121,986 | $105,709 | $118,253 | |
| Consumer surplus node 3 | $64,242 | $70,625 | $3,346 | $38,737 | |
| Producer surplus node 1 | $0 | $0 | $0 | $0 | |
| Producer surplus node 3 | $8,946 | $5,555 | $1,184 | $34,214 | |
| Total surplus | $164,087 | $198,166 | $110,239 | $191,204 | |
Supply price node 1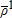 |
$15.00 | $15.00 | $15.00 | $15.00 | |
Demand price node 2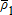 |
$21.65 | $8.31 | $15.00 | $9.79 | |
Demand quantity node 2 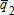 |
2,130 | 2,542 | 2,327 | 2,492 | |
Demand price node 3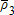 |
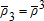 |
$30.65 | $25.72 | $95.24 | $51.68 |
Supply price node 3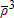 |
|||||
Demand quantity node 3 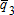 |
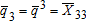 |
1,283 | 1,306 | 408 | 1,124 |
Supply quantity node 3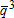 |
|||||
Shipped quantity node3 to node 3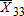 |
|||||
Supply quantity node 1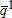 |
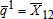 |
3,097 | 3,692 | 2,327 | 3,604 |
Quantity shipped node 1 to node 2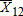 |
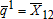 |
3,097 | 3,692 | 2,327 | 3,604 |
| Canal seepage node 1 to node 2 | 967 | 1,150 | 0 | 1,112 | |
| Payment per pumped quantity | n/a | n/a | n/a | $8.17 | |
| Payment per canal quantity | n/a | n/a | n/a | $26.48 | |
| Total payment | n/a | n/a | n/a | $29,445 | |
| Pigiouvian tax α | $0.45 | ||||
| Pigouvian subsidy β | $9.23 | ||||
- a Note: Absent constraints, the demand/ supply quantity node 3 will equal quantity shipped node 3 to node 3, and the supply quantity node 1 will equal quantity shipped node 3 to node 3. Also absence a constraint, node 3 demands and supply price are equal.
Baseline
The baseline is the “without” scenario, as required by the with-versus-without CBA. In the baseline, the aquifer is connected to the leaky canal for some portion of the canal length. The ground water pumper receives a positive externality of reduced pumping lift from canal seepage, and pumping inflicts a negative externality upon canal users by inducing additional seepage. The rudimentary water budget for the baseline is evident in the equilibrium prices and quantities. In the surface water market, node 1 supplies 3,097AF priced at $15/AF, of which 2,130AF reaches node 2, who is willing-to-pay $21.65/AF for the water delivered at the canal end. node 2 makes a payment to node 1 in the amount of $46,455 ($15 × 3097), which includes $14,505 ($15 × (3097-2130)) for water not received, that is, canal seepage. In the ground water market, node 3 pumps 1,283AF (286AF of induce seepage plus 681AF of passive seepage, plus 316AF from sources other than seepage) for which he pays $30.65/AF in pumping costs.4 The node 3 pumper thus makes a payment to the node 3 supplier (i.e., the power company) in the amount of $39,325 ($30.65×1283). Baseline surplus totals $164,087, that is, a $90,900 node 2 consumer surplus, a $64,242 node 3 consumer surplus, and an $8,946 node 3 producer surplus. The horizontal supply function of node 1 yields no producer surplus.
Pigouvian Tax/Subsidy
In a competitive equilibrium, the welfare of two agents depends only on consequences of their own choices. An externality creates an asymmetry between social and private prices, while an internalization forces both agents to account for the consequences of their actions on the other's welfare by aligning prices. Absent this internalization (i.e., the base case), the canal water user responds only to the pecuniary supply cost of the canal company and the shrinkage cost of seepage. The reduction in costs that the pumper receives from canal seepage is ignored. Similarly, the pumper is signaled only by the pecuniary cost of pumping, ignoring the cost to the canal diverter of pumping-induced seepage. A Pigouvian tax/subsidy internalizes the externality by aligning marginal supply prices of canal diverters and ground water pumpers. The price alignment signals to decrease production of the negative externality (pumping induced seepage) and increase production of the positive externality (canal diversions that create seepage).
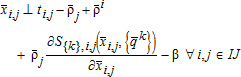 (3c)
(3c)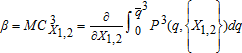 is the Pigouvian subsidy to the canal diverter, defined as the node 3 marginal cost of pumping with respect to canal diversion. Equation 3c states, that at equilibrium, if the quantity of water diverted in the canal is greater than zero, the sum of supply price, and seepage cost plus the Pigouvian subsidy equals the demand price.
is the Pigouvian subsidy to the canal diverter, defined as the node 3 marginal cost of pumping with respect to canal diversion. Equation 3c states, that at equilibrium, if the quantity of water diverted in the canal is greater than zero, the sum of supply price, and seepage cost plus the Pigouvian subsidy equals the demand price.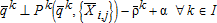 (2c)
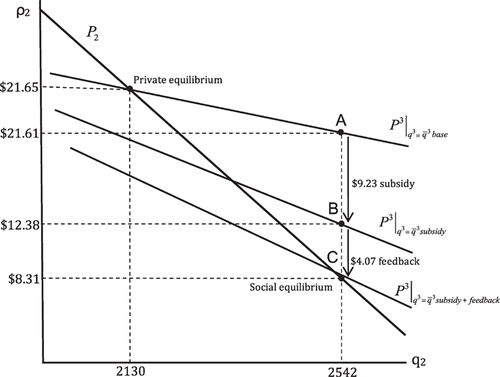
(2c)In the surface water market, the Pigouvian subsidy shifts the effective supply down from the baseline effective supply 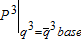 to the effective supply with subsidy, plus the feedback
to the effective supply with subsidy, plus the feedback 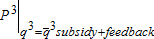 (figure 2). At the social equilibrium, node 1 supplies 3,692AF to node 2 (an increase of 595AF over the base case) for which node 2 is willing to pay $8.31/AF. The Pigouvian subsidy (β) for canal diversion is $9.23/AF. Node 2 pays node 1 $55,383 ($15×3,692), which includes a payment for seepage of $17,250 (1,150×$15). The canal effective supply function, given the baseline quantity of pumping
(figure 2). At the social equilibrium, node 1 supplies 3,692AF to node 2 (an increase of 595AF over the base case) for which node 2 is willing to pay $8.31/AF. The Pigouvian subsidy (β) for canal diversion is $9.23/AF. Node 2 pays node 1 $55,383 ($15×3,692), which includes a payment for seepage of $17,250 (1,150×$15). The canal effective supply function, given the baseline quantity of pumping 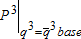 , solved for the equilibrium rate of diversion (2,542 AF), is priced at $21.61/AF (point A, figure 2).5 The total Pigouvian wedge between social and private cost in the surface water market is therefore $13.30 (point A to C or $21.61 - $8.31, figure 2). Of the total wedge, $9.23 is attributed to the canal subsidy (A to B, figure 2), and $4.07 is attributed to the feedback of the pumping tax (B to C, figure 2). The feedback results from the pumping tax, which reduces pumping and thereby reduces the negative externality of induced canal seepage.
, solved for the equilibrium rate of diversion (2,542 AF), is priced at $21.61/AF (point A, figure 2).5 The total Pigouvian wedge between social and private cost in the surface water market is therefore $13.30 (point A to C or $21.61 - $8.31, figure 2). Of the total wedge, $9.23 is attributed to the canal subsidy (A to B, figure 2), and $4.07 is attributed to the feedback of the pumping tax (B to C, figure 2). The feedback results from the pumping tax, which reduces pumping and thereby reduces the negative externality of induced canal seepage.
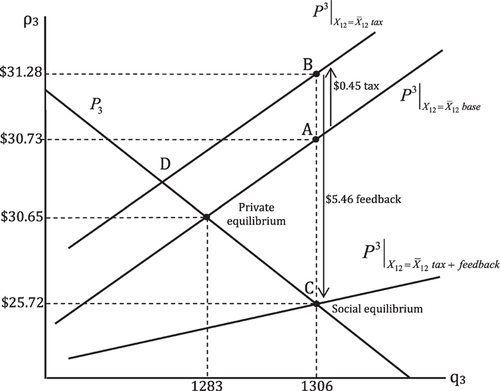
In the ground water market, the Pigouvian tax and the feedback of the subsidy in the surface water market shifts down the marginal cost function from the baseline 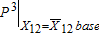 to the marginal cost with the tax and feedback
to the marginal cost with the tax and feedback 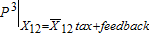 (figure 3). The combined effect of tax and the feedback causes the equilibrium price of ground water to fall from $30.65/AF at the private equilibrium to $25.72/AF at the social equilibrium, and pumping to increase from the private equilibrium (1,283) to the social equilibrium (1,306). Imposition of the tax alone, without the feedback from the surface water market, shifts up the base marginal cost
(figure 3). The combined effect of tax and the feedback causes the equilibrium price of ground water to fall from $30.65/AF at the private equilibrium to $25.72/AF at the social equilibrium, and pumping to increase from the private equilibrium (1,283) to the social equilibrium (1,306). Imposition of the tax alone, without the feedback from the surface water market, shifts up the base marginal cost  to the marginal cost with the tax
to the marginal cost with the tax 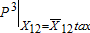 , which raises pumping price and decreases pumping (D, figure 3). At equilibrium, the Pigouvian tax (α) on pumping is $0.45/AF (A to B, figure 3). The base marginal cost of pumping
, which raises pumping price and decreases pumping (D, figure 3). At equilibrium, the Pigouvian tax (α) on pumping is $0.45/AF (A to B, figure 3). The base marginal cost of pumping 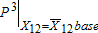 evaluated at the equilibrium pumping quantity 1,306 AF is $30.73 (point C, figure 3).6 The total feedback of the tax is thus $5.46 ($31.28 - $25.72 or B to C in figure 3). The Pigouvian wedge between social and private marginal cost in the ground water market of $5.01 is the feedback net of the pumping tax ($30.73 - $25.72 or A - C in figure 3). The feedback results from the canal subsidy, which encourages canal diversions and thereby increases the positive externality of canal seepage.
evaluated at the equilibrium pumping quantity 1,306 AF is $30.73 (point C, figure 3).6 The total feedback of the tax is thus $5.46 ($31.28 - $25.72 or B to C in figure 3). The Pigouvian wedge between social and private marginal cost in the ground water market of $5.01 is the feedback net of the pumping tax ($30.73 - $25.72 or A - C in figure 3). The feedback results from the canal subsidy, which encourages canal diversions and thereby increases the positive externality of canal seepage.
Internalization with a tax/subsidy increases the welfare of both ground water pumper and canal diverter. In the with-versus-without CBA comparison, total irrigator surplus increased by 21% over the baseline. In the ground water market, consumer surplus increased by 10% ($64,242 to $70,625), and in the surface water market consumer surplus increased by 34% ($90,900 to $121,986). The reciprocal tax and subsidy (α and β) can be increased or decreased without being offset by greater social cost or reduced social benefit. The Pigouvian tax/subsidy is predicated upon exogenous cash flows, that is, collected tax revenues are received and subsidies are funded by an external agent. A tax paid to the injured party (canal user) or a subsidy paid by the beneficiary (pumper) distorts the tax/subsidy incentive (Baumol and Oates 1988).
Correcting the market failure through omniscient regulation of the reciprocal externality requires upper and lower bounds on pumping and canal diversions, respectively. Regulating induced seepage damage alone (e.g., a binding constraint on pumping) will simply reproduce the equilibrium quantities and welfare of the baseline scenario. Prior appropriations regulations enacted to protect senior canal or river rights from the damage of induced seepage are usually enforced as setbacks or outright bans. For example, Oregon (Oregon Water Resources Department 2010) mandates a quarter-mile set back from the river for wells in a riparian aquifer. Absent damage to the senior water users, prior appropriations regulation cannot compel canal users to “waste water” for aquifer recharge (Fereday et al. 2006). Thus, regulations preventing the damage of pumping-induced seepage also deprives ground water users from the benefit of passive seepage.
Eliminating Seepage
Canal lining is promoted as a conservation panacea that maintains agricultural production, while liberating water for environmental or municipal use (Rodgers 2008; Hanak et al. 2010). Indeed, millions of dollars have been expended to subsidize agricultural water conservation by either reducing on-farm infiltration or improving conveyance efficiency. However, correct CBA for water conservation infrastructure requires accounting for all costs and benefits, including recipients of the seepage externality.
When the canal is lined and the externality is eliminated and the cost of seepage is no longer imposed upon the canal diverter. The quantity supplied by node 1 (2,327AF) equals the quantity demanded at node 2, making the node 1 supply price ($15) equal to the node 2 demand price. Canal diverter demand increases 196AF (2,327 - 2,130). Absent canal seepage, aquifer levels decline, pumping costs increase from $30.65 to $95.24/AF, and pumping declines by 875AF (1,283-408). Further, surface water market consumer surplus increases by 16% ($90,900 to $105,709), but is offset by decreased consumer and producer surplus in the ground water market by 64%. Total surplus, the CBA of with-versus-without comparison, declined 67% ($110,239 to $164,087). In the example, construction costs are ignored and the sole beneficiary of canal lining is the short run increase in irrigation intensity of the existing crop mix and acreage of the canal water user.
Aquifer Recharge Payment
As illustrated in previous research, aquifer recharge is an accepted policy in conjunctive use management (Blomquist et al. 2001). In contrast to the external Pigouvian tax/subsidy flows, aquifer recharge payments are internal, that is, the junior appropriator pays to receive the benefit or compensate for damages to the senior. As is the case with most conjunctive use situations, the pumper has an adjudicated right that is junior to the canal diverter whose seepage created the aquifer. Thus, in our example, the junior pumpers compensate the senior canal users for canal flows to recharge the aquifer.
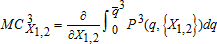 . The total value of canal seepage to ground water pumpers is
. The total value of canal seepage to ground water pumpers is 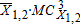 , and the payment rate for canal diversion per acre-foot of ground water pumping is
, and the payment rate for canal diversion per acre-foot of ground water pumping is 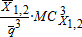 . Ground water pumpers maximize their benefits by paying the canal diverter this amount for each acre-foot of water diverted down the canal. In turn, this payment is inserted into the canal water and ground water price linkage equations, (3b) and (1). Equation 3d states that at equilibrium, if canal diversion is greater than zero, the sum of supply price, transportation, and seepage costs, minus the payment from ground water pumpers equals the canal diverter's marginal demand price:
. Ground water pumpers maximize their benefits by paying the canal diverter this amount for each acre-foot of water diverted down the canal. In turn, this payment is inserted into the canal water and ground water price linkage equations, (3b) and (1). Equation 3d states that at equilibrium, if canal diversion is greater than zero, the sum of supply price, transportation, and seepage costs, minus the payment from ground water pumpers equals the canal diverter's marginal demand price:
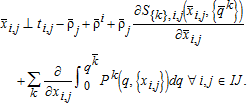 (3d)
(3d)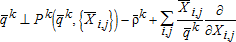 (2d)
(2d)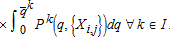 (1)
(1)In the ground water market, the transfer payment raises the marginal cost of pumping, thereby shifting up the pumpers' marginal cost function from the baseline, P2|X12=base to the payment marginal cost, P2|X12=recharge (figure 5). The transfer payment from node 3 to node 2 increases node 3 marginal cost by $21.04/AF ($51.68 - $30.65) relative to the base case scenario. As a consequence, ground water pumping decreases by 159AF (1,283 - 1124) relative to the base case.
In the surface water market, the transfer payment lowers the effective supply of deliveries at the end of the canal from the baseline canal effective supply 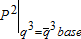 to the effective supply with the payment
to the effective supply with the payment 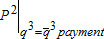 (figure 4). In the surface water market, the transfer payment reduces node 2 marginal cost by $11.86 ($21.65-$9.79) from the base case. As a result, the quantity of water shipped from node 1 to node 2 increases by 507AF (3604 - 3097) and node 2 increases demand by 362AF (2492 - 2130). The increase in diversion increases seepage by 145AF (1112 - 967). The node 3 ground water pumper pays the node 2 canal diverter $8.17/AF for canal water diverted at node 1, which translates into a payment of $26.21/AF of ground water pumped. The total payment made by node 3 is $29,445 ($26.48×1,112), which matches the total receipts received by node 2 of $29,445 ($8.17×3,604), that is, the decrease in total pumping costs attributable to the seepage resulting from canal diversion.
(figure 4). In the surface water market, the transfer payment reduces node 2 marginal cost by $11.86 ($21.65-$9.79) from the base case. As a result, the quantity of water shipped from node 1 to node 2 increases by 507AF (3604 - 3097) and node 2 increases demand by 362AF (2492 - 2130). The increase in diversion increases seepage by 145AF (1112 - 967). The node 3 ground water pumper pays the node 2 canal diverter $8.17/AF for canal water diverted at node 1, which translates into a payment of $26.21/AF of ground water pumped. The total payment made by node 3 is $29,445 ($26.48×1,112), which matches the total receipts received by node 2 of $29,445 ($8.17×3,604), that is, the decrease in total pumping costs attributable to the seepage resulting from canal diversion.
In the surface water market, node 2 consumer surplus increased by 30% ($90,900 to $118,253); (A+B+C) – A in figure 4). In the ground water market, node 3 consumer surplus decreased by 40% ($64,242 to $38,737); (A+B+C+D) – A in figure 5). Node 3 producer surplus increases 282%, from $8,946 (E+F+G in figure 5) to $34,214 (B+E in figure 5). The increase in node 3 producer surplus is attributable to the payment made to node 2. The ground water pumper is better off paying for relatively cheap electricity than paying the canal diverter for relatively costly seepage water. The managed recharge alternative lifts net social welfare above the baseline by 17% ($164,087 to $191,204). Even after making payments for canal seepage, the ground water pumpers' surplus is not exhausted. The surplus of node 2 canal diverters damaged by the negative externality of pumping induced seepage increases with receipt of payment from ground water pumpers. Although the managed recharge scenario does not penalize pumping induced seepage, the social benefit from this scenario exceeds the baseline.
In contrast to the Pigouvian remedy, which corrects both sides of the reciprocal externality, the recharge payment sustains only the positive externality of seepage. The seniority of the canal user establishes that the pumper pay for previously free seepage. In lieu of a law that forces the canal to waste water, the recharge payment provides the incentive to sustain the positive externality of seepage to the aquifer.
Summary and Conclusions
Aquifers created or sustained by surface water are a global phenomenon. Previous conjunctive use research failed to treat conjunctive surface and ground water use as an externality of un-priced and interrelated supply functions. These reciprocal conjunctive use externalities result in failures in the surface water and ground water markets; the positive externality of passive seepage is under-produced and the negative externality of induced seepage is over-produced. The conventional supply and demand planning approaches were rejected in favor of a partial equilibrium method that incorporates supply and demand functions to accurately value water. The reciprocal externality created by conjunctive use is an exogenous supply function allowing correct CBA. An n-dimension generalized partial equilibrium model of conjunctive ground water and surface water use was formulated. Using MCP, a three node example was parameterized with site-specific data and was solved for equilibrium water prices and quantities in the respective surface water and ground water markets. The three exogenous variables are: (a) crop demand, (b) marginal costs for pumping and canal, and (c) the transportation arc or seepage function. The crop demand functional forms are generalizable for any various crops and irrigation technologies, and scalable to any acreage or crop mix. The marginal cost functions are readily available and can be fitted with the appropriate functional form (e.g., increasing block rate). The seepage functional form used in this example may not be generalizable to more complex conjunctive hydrologic connections (e.g., gaining versus losing reaches of a river). A basin water budget, which accompanies ground water models, provides an external check on baseline scenario results.
CBA was performed on three conjunctive management policies: tax/subsidy, conservation, and payment for aquifer recharge. Of the three policy scenarios, internalizing the externalities via a tax/subsidy generated the greatest social benefit. The Pigouvian tax/subsidy completes both the surface and ground water markets and trade is unimpeded, thus ensuring, by definition, the gains in efficiency from trade (Randall 1983). Conservation failed the CBA—the foregone benefit of canal seepage to the pumpers by eliminating the externality outweighs the increase in canal benefit. In the recharge scenario, canal seepage is priced via a payment from pumper to canal water user that matches the decrease in total pumping cost attributable to the seepage resulting from canal diversion. In our example, total surplus of the recharge policy was 97% of the Pigouvian scenario. With the recharge payment, the equilibrium quantities in all three markets were only slightly less than the Pigouvian scenario. However, the price of water at node 3, driven higher by the recharge payment, almost doubled.
The Pigouvian tax/subsidy corrects the market failure in surface water and ground water markets, by aligning prices to erase the wedge between social and private costs. The reciprocal externality produces feedback between the surface and ground water markets that reinforces or cancels the tax/subsidy effect. In the ground water market, the subsidy to increase canal diversion increases the seepage available for pumping, which more than offsets the tax-induced reduction in pumping. Pumping quantity at the social equilibrium increased over the private equilibrium, despite taxing the negative externality of pumping. The feedback effect improves the welfare of the recipient, for example, the tax discourages the negative externality of pumping to the benefit of the canal user, and the subsidy encourages canal diversions to the benefit of the pumper. The magnitude of the feedback is determined by the relative magnitude and elasticity of exogenous supply, demand, and transportation variables.
Market failures arise from poorly assigned and/or enforced property rights. Existing water governance often fails to acknowledge conjunctive hydrologic connections, let alone manage conjunctive use as a reciprocal externality. The Prior Appropriation Doctrine defines and protects property rights, but does not maximize social welfare or correct externalities. Water law fails to address either side of the reciprocal externality; junior ground water users are not forced to pay for the seepage they now freely enjoy, nor is there a mechanism to compensate senior canal users for the damage of pumping induced seepage. Absent damage to the senior water users, prior appropriations regulation cannot compel canal users to “waste water” for aquifer recharge (Fereday et al. 2006). Further, water law confiscates the property right for seepage from the canal user; the loss of physical control of water, whether through surface returns or percolation to aquifers returns water to the public domain to be appropriated for beneficial use.
Cheung's (1973) rejoinder to Meade's bee example pointed out that the market failure of a reciprocal externality can be corrected, without government intervention, by payments from apple to bee farmers. Reciprocal conjunctive use externalities have not been similarly resolved. As water supplies shrink and demands grow symptoms of market failure conflict, lawsuits and water calls, etc., will proliferate. Continued reliance upon regulating conjunctive use externalities will increase inefficient water use that a water-scarce society can ill afford. A functional model of reciprocal conjunctive use externalities is a first step in the investigation of conjunctive water management policy alternatives.
Appendix
Hydrologic response data used to estimate the seepage function was generated using analytic element modeling methods (Strack 1989; Haitjema 1995). Analytic element models represent each hydrologic feature (e.g., canal or well) by one or more analytic functions. A head-specified or flow-specified boundary condition is assigned to each element, and the model calculates the steady-state hydrologic response. For head-specified canals the response is the canal seepage rate, for flow-specified wells the response is the aquifer head condition at the well radius, from which pumping lift can be derived. Steady-state canal seepage and pumping lift response data are generated and fitted to canal seepage and pumping lift response functions for a range of canal diversion and pumping rates as the canal transitions between direct water table contact and a perched condition. Non-linear least squares was used to estimate the site-specific parameters for the steady-state canal seepage function: S{3},1,2=15000(1−e−1.5E−5X(1,2))+0.1X(1,2)(1−e−0.002q3) (Schmidt et al. 2013). Seepage is thus determined by canal diversion and pumping with all other hydrologic influences represented by a far-field hydrologic boundary condition. The steady-state seepage function is likewise compatible with the comparative statics of a partial equilibrium model.
Node 1 marginal cost of canal water is: P1=$15. Node 3 marginal cost of ground water at the well collar is: P3=9.50+0.08⋅ lift where lift=1000⋅e(0.00017q3−0.0005X1,2).
The marginal benefit functions for node 2 and node 3 are: 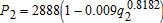 and
and 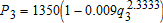 . The marginal benefit functions were calibrated for 825 acres of alfalfa at node 2 with 45 % efficiency and an application rate of 3.5 AF/acre, and for 600 acres of alfalfa at node 3 with 70 % irrigation efficiency and an application rate of 2.25AF/acre. The differences in efficiency reflect surface versus sprinkler application.
. The marginal benefit functions were calibrated for 825 acres of alfalfa at node 2 with 45 % efficiency and an application rate of 3.5 AF/acre, and for 600 acres of alfalfa at node 3 with 70 % irrigation efficiency and an application rate of 2.25AF/acre. The differences in efficiency reflect surface versus sprinkler application.




