Using Mixed Logit in Land Use Models: Can Expectation-Maximization (EM) Algorithms Facilitate Estimation?
Roger Claassen ([email protected]) and Daniel Hellerstein ([email protected]) are Senior Economists at the Economic Research Service, United States Department of Agriculture. Seung Gyu Kim ([email protected]) is an Assistant Professor at Kyungpook National University. The views expressed are those of the authors and cannot be attributed to ERS or USDA.
This article was presented in an invited paper session at the 2012 AAEA annual meeting in Seattle, WA. The articles in these sessions are not subjected to the journal's standard refereeing process.
The loss of native grassland habitat in the Northern Plains of the United States is prompting concern about the effect of farm programs on rangeland-to-cropland conversion. Native grassland, that is, rangeland that has never been tilled, is breeding habitat for many species of migratory birds and further loss could reduce bird populations and related benefits (e.g. hunting).
Farm programs that are coupled to current production (e.g. crop insurance) could be increasing average crop revenue, encouraging producers to increase cropland acreage. In the Northern Plains, additional cropland could come from hayland, pasture, rangeland, or the Conservation Reserve Program (CRP) as contracts expire. To the extent that farmers add cropland by reducing hay, pasture, or CRP acreage, rather than rangeland, the effect of farm programs on native grassland loss could be relatively modest.
Recent studies of agricultural land use employ conditional logit (CL) models, for example Gardner, Hardie, and Parks (2010), or nested logit (NL) models, for example Lubowski, Plantinga, and Stavins (2008). Some have also estimated multiple models based on initial land use (Lubowski, Plantinga, and Stavins 2008; Rashford, Walker, and Bastain 2010). The CL model is analytically tractable but requires highly restrictive assumptions regarding the independence of irrelevant alternatives (IIA). Under IIA, farmers respond to an increase in crop profits by drawing land proportionally from each alternative land use to increase cropland area. That is, cross-elasticities are constrained to be the same across land use alternatives. Because Northern Plains rangeland area exceeds that of pasture, hay, or CRP, a CL model will always predict that the largest share of additional cropland comes from rangeland. Nested logit models can be used to relax IIA, but still place significant restrictions on choice probabilities.
In theory, a mixed logit model can capture any pattern of response to economic or policy change. In reality, mixed logit likelihood functions can be time-consuming and difficult to maximize using conventional methods, even when only a small number of parameters are random. Models often fail to converge, or converge to a local, rather than a global, maximum (Knittel and Metaxoglou 2008). Expectation-Maximization (EM) algorithms (Train 2009) dramatically reduce solution time while allowing a relatively large number of random parameters. These features facilitate robust estimation, allowing us to (1) specify a single model without assuming IIA and (2) use empirical parameter distributions, rather than more restrictive parametric distributions typical of mixed logit.
Mixed Logit, Empirical Distributions, and EM Algorithms
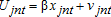
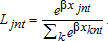

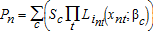
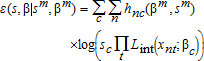
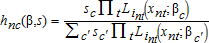
Starting values are calculated by randomly dividing the sample into C parts. The initial class probabilities, 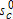 , are equal to 1/C. Starting values for each set of class-specific parameters,
, are equal to 1/C. Starting values for each set of class-specific parameters, 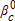 .
.
The class probabilities (sc), parameter vectors (βc), and the parcel- and class-specific weights (hnc) are updated sequentially until they converge (do not change with several updates). The class probabilities are updated using the parcel- and class-specific weights: 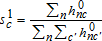 . Each of C class-specific parameter vectors are updated using a conditional logit model estimated from all of the data (not a subset as in the starting value estimation) weighted with the parcel- and class-specific weights (
. Each of C class-specific parameter vectors are updated using a conditional logit model estimated from all of the data (not a subset as in the starting value estimation) weighted with the parcel- and class-specific weights (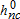 ), yielding
), yielding 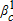 . Finally, the parcel- and class-specific weights are updated for use in the next iteration:
. Finally, the parcel- and class-specific weights are updated for use in the next iteration: 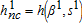 .
.
Data
The 2007 National Resources Inventory (NRI) includes annual land use observations for 1997-2007 for a nationally representative set of 110,771 “core” points. We use core points that: (1) are located in the intersection of the Northern Great Plains with Nebraska, South Dakota, North Dakota, and Montana; (2) remained in cultivated crops, range, hay, pasture, or CRP throughout 1997-2007; (3) are designated as point one within a primary sampling unit (PSU); and (4) were not under an ongoing CRP contract. Land in expiring CRP contracts is included because farmers are free to reapply for CRP (re-enrollment is not guaranteed) or change land use. To reduce optimization time, we randomly selected one-third of the counties in our study region, resulting in a dataset containing 88 counties, 999 NRI points, and 10,243 choice events over 11 years.
Expected crop revenue includes market revenue, marketing loan gains, crop insurance, and disaster assistance for corn, soybeans, and wheat. Expected crop prices are averages for a post-harvest futures contract for a single month just prior to planting, less the expected basis. Expected corn prices, for example, are based on the average of daily closing prices in February for the December Chicago Board of Trade (CBOT) contract. The expected basis is the 5-year average difference between the harvest month futures price (October for corn) for a post-harvest futures contract (December for corn) and the harvest month cash price (October for corn). Expected yields are 5-year averages of National Agricultural Statistics Service (NASS) county estimates, excluding high and low years. Overall crop revenue is the average of crop-specific revenue weighted using acreage shares based on a 3-year rolling average of NASS county crop acreage estimates.
To model the effect of farm programs, we create empirical distributions of crop prices, yields, and revenue based on the deviation of expected prices and yields from realized prices and yields, respectively, using data for the 22 most recent years (see Cooper 2010). Realized prices are the average of daily closing prices during harvest for a post-harvest futures contract, less the expected basis. The realized price for corn, for example, is based on the average closing price in October for the Chicago Board of Trade (CBOT) December corn contract. Realized yields are NASS county estimates. Because aggregation can average out some of the farm-level yield variation, yield deviations are inflated following Coble, Dismukes, and Thomas (2007).
Marketing loan benefits are estimated by calculating expected revenue when the lower end of the price distribution is truncated at the crop loan rate. Net crop insurance indemnities are calculated by truncating yield (for yield insurance) or revenue (for revenue insurance) distributions (see Claassen et al. 2011, for details). Based on typical provisions of ad hoc disaster assistance programs between 1997 and 2007, we assume that losses of 35% or more (on a crop-by-crop basis) will be indemnified at 50% of market value.
NASS data on hay prices and yields are used to represent hay and pasture revenue. Expected prices are based on a 3-year moving average of state-level season average prices. Expected yields are a 5-year moving average of county yield estimates with the high and low years removed. Rangeland revenue per cow-calf animal unit for the Northern Plains, obtained from ERS cost and return data, is converted to per acre revenue using stocking rates derived from NRCS forage yield data and technical documents. Expected revenue is trend revenue from regressing revenue on lagged revenue and time.
CRP eligibility is based on general signup criteria and includes cropland that is highly erodible or located in a national and state priority area, including the Prairie Pothole Region. (which includes parts of Iowa, Minnesota, Montana, Nebraska, North Dakota, South Dakota, and several Canadian provinces) For eligible land, CRP revenue is represented by the county average Soil Rental Rate (SRR), obtained from the Farm Service Agency. For ineligible land, CRP revenue is set equal to zero.
Production costs for cropland and range are based on ERS cost and return data. Production costs for hay and pasture are based on hay cost estimates developed by Claassen et al. (2011). Land productivity is represented by the National Commodity Crop Productivity Indicator (NCCPI), which is calculated for soil and climate conditions at each NRI point. The irrigation indicator is also based on NRI data.
Model Estimation
To estimate model parameters, we used the “lclogit” module in STATA. Although EM algorithms solve quickly (in minutes rather than hours), the likelihood function is highly non-linear and may terminate without converging or may converge to a local rather than a global maximum. Knittel and Metaxoglou (2008) studied these issues in a random coefficients model. Using a large number of starting values, they found that: (1) optimizations frequently failed to converge; (2) models converged to many local maxima; and (3) the best objective function value was not achieved frequently and was considerably different from function values achieved for a majority of the converged optimizations.
For the model reported in the next section, 400 starting values were generated by randomly selecting 400 seed values to generate random variables used to divide the sample into C groups. The optimization converged for 114 starting values (28.5%), reaching 94 different log-likelihood values. The reported model had the highest log-likelihood (−2,918.565), although some nearby values were reached repeatedly, including −2,935.723 and −2,937.473 (each reached 7 times) and −2,940.043 (reached 5 times). Raw parameters vary across these models, but the estimated marginal effects are similar.
We considered models with 3-7 classes. The 3-class model converged for roughly 60% of starting values. The 5- and 6- class models converged less than 5% of the time, while the 7-class model rarely converged. Hence, 4 was the largest number of classes for which we could reasonably argue that at least one of our starting values reached a global maximum.
Estimation Results
Parameter estimates are shown in table 1. The log-likelihood value (−2,918.56), represents a dramatic improvement over the conditional logit model (−11,338.81), which can be thought of as a latent class model with only one class, and a significant improvement over a 4-class model that includes only alternative-specific constants (−3,064.04). Average estimated probabilities are roughly equal to the sample shares (table 2a); rangeland is overestimated by 2 percentage points, while the other three land uses are underestimated by one percentage point or less.
| Class 1 | Class 2 | Class 3 | Class 4 | |
|---|---|---|---|---|
| Alternative (0-1): Cropland | 0.872 | 3.888 | 6.127 | −2.817 |
| 3.08a | 7.66 | 5.16 | −9.32 | |
| Alternative (0-1): Hay/Pasture | 3.104 | −0.434 | 2.297 | −4.712 |
| 12.46 | −0.53 | 1.81 | −8.57 | |
| Alternative (0-1): Rangeland | −0.049 | 207.246 | −133.872 | −4.429 |
| −0.14 | 2.49 | −3.08 | −5.92 | |
| Net Revenue | 0.006 | −0.002 | 0.000 | 0.013 |
| 6.2 | −0.58 | 0.05 | 5.44 | |
| Irrigation (0−1) | 1.274 | 137.204 | 231.478 | 27.511 |
| 7.77 | 2.84 | 3.53 | 92.63 | |
| Land Productivity: Cropland | 4.103 | 2.668 | −5.806 | 0.480 |
| 4.03 | 2.14 | −0.96 | 0.51 | |
| Land Productivity: Hay/Pasture | 2.505 | 1.856 | −10.820 | 3.153 |
| 2.6 | 0.91 | −1.54 | 2.05 | |
| Land Productivity: Rangeland | 2.679 | −802.289 | 555.022 | −2.590 |
| 2.16 | −2.44 | 3.13 | −6.86 | |
| Class Shares | 0.167 | 0.549 | 0.189 | 0.095 |
- a a t-statistics are below parameters. Parameter values in bold are significant at the 5% level.
| Average Predicted Probabilities | ||||||
|---|---|---|---|---|---|---|
| Class 1 | Class 2 | Class 3 | Class 4 | Overall | Sample Proportion | |
| (a) Predicted Probabilities by Land Use and Class | ||||||
| Cultivated Crops | 0.027a | 0.297 | 0.098 | 0.013 | 0.435 | 0.439 |
| Hay and Pasture | 0.131 | 0.003 | 0.001 | 0.001 | 0.136 | 0.143 |
| Rangeland | 0.004 | 0.247 | 0.090 | 0.000 | 0.342 | 0.321 |
| Cons. Reserve | 0.004 | 0.002 | 0.000 | 0.081 | 0.087 | 0.097 |
| Class Shares | 0.167 | 0.549 | 0.189 | 0.095 | 1.000 | 1.000 |
| Class 1 | Class 2 | Class 3 | Class 4 | Overall | ||
| (b) Share of Predicted Land Use, by Class | ||||||
| Cultivated Crops | 0.063b | 0.683 | 0.225 | 0.029 | 1.000 | |
| Hay and Pasture | 0.964 | 0.019 | 0.008 | 0.009 | 1.000 | |
| Rangeland | 0.013 | 0.724 | 0.263 | 0.001 | 1.000 | |
| Cons. Reserve | 0.046 | 0.021 | 0.005 | 0.928 | 1.000 | |
- a a Average estimated probability of land use conditional on class-specific parameters.bShares of predicted land use in (b) are calculated from corresponding cells and row totals in (a), i.e., 0.027/0.435=0.063.
The model implies active land use margins between cropland and hay/pasture (class 1) and cropland and CRP (class 4). For class 1, marginal effects (table 3) indicate that cropland and hay/pasture probabilities are much more responsive to change in either crop or hay/pasture revenue than to change in rangeland or CRP revenue. Rangeland and CRP probabilities are relatively unresponsive to any revenue change. While we estimate (using hnc(β,s) for each parcel) that class 1 represents only 17% of all NRI sites in our dataset, it includes 96% of the estimated probability weight (across all classes) for hay/pasture, 6% for cropland, 5% for CRP and 1% for rangeland (table 2b). Likewise, class 4 marginal effects (table 3) indicate that cropland and CRP probabilities are much more responsive to changes in crop or CRP revenue than to revenue change in hay/pasture or rangeland. Hay/pasture and rangeland probabilities are relatively unresponsive to any revenue change. Class 4 includes an estimated 9.5% of the sites, including 92% of probability weight for CRP, 3% for cropland, and less than 1% for hay/pasture and range (table 2b).
| Estimated via EM Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Change in Revenue: | Change in Probability: | Class 1 | Class 2 | Class 3 | Class 4 | Overall | Cond. Logit |
| Crop | Cropland | 7.433 | −0.169 | 0.016 | 6.018 | 1.724 | 9.544 |
| Hay/Pasture | −7.013 | 0.085 | −0.009 | −0.111 | −1.137 | −2.843 | |
| Rangeland | −0.224 | 0.022 | −0.003 | −0.014 | −0.027 | −4.786 | |
| CRP | −0.196 | 0.061 | −0.004 | −5.894 | −0.559 | −1.914 | |
| Hay/Pasture | Cropland | −7.013 | 0.085 | −0.009 | −0.111 | −1.137 | −2.843 |
| Hay/Pasture | 9.385 | −0.086 | 0.009 | 1.686 | 1.683 | 5.763 | |
| Rangeland | −1.222 | 0.000 | 0.000 | −0.004 | −0.204 | −2.243 | |
| CRP | −1.150 | 0.001 | 0.000 | −1.571 | −0.341 | −0.677 | |
| Range | Cropland | −0.224 | 0.022 | −0.003 | −0.014 | −0.027 | −4.786 |
| Hay/Pasture | −1.222 | 0.000 | 0.000 | −0.004 | −0.204 | −2.243 | |
| Rangeland | 1.485 | −0.023 | 0.003 | 0.309 | 0.266 | 8.549 | |
| CRP | −0.039 | 0.000 | 0.000 | −0.291 | −0.034 | −1.520 | |
| CRP | Cropland | −0.196 | 0.061 | −0.004 | −5.894 | −0.559 | −1.914 |
| Hay/Pasture | −1.150 | 0.001 | 0.000 | −1.571 | −0.341 | −0.677 | |
| Rangeland | −0.039 | 0.000 | 0.000 | −0.291 | −0.034 | −1.520 | |
| CRP | 1.384 | −0.062 | 0.004 | 7.756 | 0.934 | 4.111 | |
- a a Estimated model includes net revenue (=gross revenue−cost). Therefore, the marginal effects of gross revenue and cost are equal in absolute value and reversed in sign.
The effect of land productivity is modest in classes 1 and 4. For class 1, the land productivity (NCCPI) coefficient for cultivated cropland is slightly larger than that of hay/pasture, indicating that cropland probability increases relative to hay/pasture probability as NCCPI increases (figure 1a). Irrigation also increases the probability of cropland relative to hay/pasture, although irrigated land is not always in cultivated crops (about 20% of irrigated sites in our dataset are in hay/pasture). In class 4, the cropland NCCPI coefficient is small and not significantly different from zero, implying that it is not significantly different from the CRP coefficient given that CRP is the normalized alternative (figure 1d).
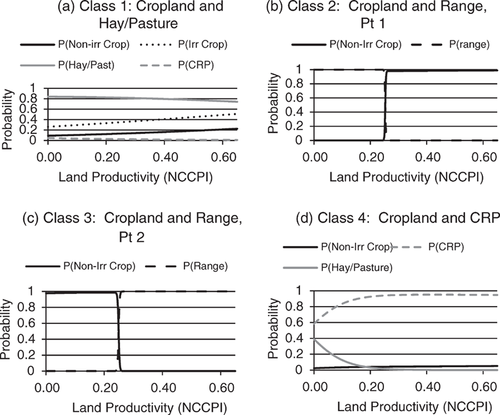
The effect of land quality on land use probability
Classes 2 and 3 appear to represent the large majorities of cropland (86% of sites) and rangeland (98% of sites) that did not change use during the study period. For both classes, the marginal effects of revenue change are quite small for every land use and revenue combination. These classes are estimated to represent 74% of the sites in our dataset (55% in class 2 and 19% in class 3), and are made up almost entirely of cropland and rangeland.
For classes 2 and 3, land use probabilities shift very quickly when NCCPI is roughly 0.25. Non-irrigated class 2 sites with NCCPI<0.25 are very likely to be rangeland, while higher productivity class 2 sites are very likely to be cropland (figure 1b). In contrast, non-irrigated class 3 sites with NCCPI<0.25 are very likely to be cropland, while higher productivity sites are very likely to be rangeland (figure 1c). While we generally expect the probability of crop production to increase as productivity rises, the class 3 result is consistent with the data. Class 3 cropland with NCCPI<0.25 is estimated to account for 10% of the sites, while class 3 rangeland with NCCPI≥0.25 accounts for an estimated 9% of the sites. In the data, roughly 11% of the sites are actually cropland with NCCPI<0.25, while 9% of the sites are rangeland with NCCPI≥0.25. In both classes 2 and 3, the almost instantaneous shift of probabilities emphasizes that that there is little or no land along the margin between cropland and range. Irrigated land in classes 2 and 3 is very likely to be cropland, regardless of NCCPI.
Discussion and Conclusions
Although our analysis is exploratory, it does indicate that the latent class model is a unique alternative for land use research. Results differ considerably from conditional logit, where the largest cross-marginal effect of crop revenue is on rangeland probability (table 3), which is a direct result of IIA. Our model indicates that rangeland probability is relatively unresponsive to changes in crop revenue. That is more consistent with the data, which shows that 50 sites moved between cropland and hay/pasture, and 43 moved between cropland and CRP, while only 6 sites moved between cropland and rangeland. Classes defined by the EM algorithm indicate that some of the cropland in our dataset is on the margin with hay/pasture (class 1) or CRP (class 4), while other cropland is unlikely to change use, even in response to fairly wide swings in revenue (class 2 or 3). Although each class-specific set of parameter estimates is from a conditional logit model, IIA does not hold because the classes represent different land use margins, allowing a more complex pattern of overall cross-effects.
Nested logit allows researchers to group the data into nests that include land uses that are similar relative to other alternatives. Unlike our latent class model, however, nested logit cannot identify subsets of land that are in the same use but respond differently to revenue change. In our model, endogenously formed classes represent different segments of the cropland base according to activity (or non-activity) along a specific land use margin, for example, cropland versus hay/pasture. Nonetheless, the nested logit model can be estimated for larger datasets with fewer convergence problems, suggesting that a more thorough comparison with nested logit may be helpful.
We see little advantage in a random parameters (mixed logit) model specified using parametric distributions. Even if optimization time was not an issue, the discrete distribution obtained via the EM algorithm may be more illuminating. Our results–that classes form around different types of land based on the propensity to change (or not change)–are intuitively plausible and may offer greater insight on land use and land use change than can be gleaned from models built around parametric distributions. Moreover, we did not constrain net revenue parameters to be positive as is often done through selection of distributions that are defined only for values greater than zero (e.g. lognormal). Even though the sign for the net revenue parameter in class 2 is reversed, the sign reversal did little damage because it was small and associated with a class where land use appears to be insensitive to revenue change.
Although our model has many attractive features, the underlying likelihood function is still very complex. Optimization often fails or converges to a local rather than global maximum, requiring the use of many starting values to be sure that a global maximum has been attained. While the number of estimated parameters can be large, it is not open ended. With 9 parameters per class, we found that 3 and 4 class models worked well. Five and six class models, however, containing 45 and 54 parameters, respectively, converged for only a modest portion of starting values, and seven class models rarely converged. It is not clear that our model could be applied to a nationwide dataset (as in Lubowski, Plantinga, and Stavins 2008 or Gardner, Hardie, and Parks 2010).




