Technological vs. Ecological Switch and the Environmental Kuznets Curve
Raouf Boucekkine is a Professor at Aix-Marseille School of Economics (AMSE), Aix-Marseille University, France, and Professor in UCLouvain, IRES and CORE, Belgium. Aude Pommeret ([email protected]) is a Professor in the Department of Economics, University of Savoie, France, and University of Lausanne, Switzerland. Fabien Prieur ([email protected]) holds a junior chair at INRA, the French Institute for Research in Agriculture, and University Montpellier I, France. We would like to thank Krishna Paudel for inviting us to participate in the AAEA session “Environmental Kuznets Curve: Theoretical and Methodological Perspectives”. We also thank Jeffrey Vincent for his constructive and stimulating comments.
This article was presented in an invited paper session at the 2012 ASSA annual meeting in Chicago, IL. The articles in these sessions are not subjected to the journal's standard refereeing process.
For some time, it has been claimed that the relationship between income and pollution is an inverted U-shape, yielding the so-called Environmental Kuznets Curve (EKC hereafter). This claim, based on several early empirical studies (see for example, Grossman and Krueger 1993), has been at the heart of a massive empirical and theoretical literature. Empirical research has mainly consisted in examining a wide variety of pollutants for evidence of the inverted U-shaped pattern, resulting in the conclusion that such a shape is valid for many local and flow pollutants. But it does not seem to be the rule for stock pollutants like CO2 which generate a monotonically increasing relation between wealth and pollution (see Brock and Taylor 2005, for a survey). In parallel, a large number of theoretical analyses have been devoted to identifying the conditions under which the EKC arises.
Growth models typically provide two arguments for the EKC: a regime switch to abatement activities and the adoption of new environmental-friendly technologies. In their equilibrium model, John and Pecchenino (1994) emphasize the role of abatement. Along the equilibrium trajectory, abatement begins only after a large amount of capital, and thus pollution, is accumulated, ultimately generating the decreasing part of the EKC. A similar scheme gives rise to the EKC in Dinda (2004)'s optimal growth model. Stokey (1998) on the other hand adapts the second argument. In the early development stages, the most productive, but also the dirtiest, technologies are used to create wealth. Once the economy becomes rich enough, greener technologies, which are typically costly to implement, start to be used and pollution eventually goes down. In all of these studies, the EKC emerges even for stock pollutants.
We shall take this approach in this paper. More precisely, we consider an optimal technology adoption AK model in line with Boucekkine, Krawczyk and Vallée (2011): an economy, caring about consumption and pollution as well, starts with a given technological regime and may decide to switch at any moment to a cleaner technology at a given permanent output cost. At the same time, we posit that there exists a pollution threshold above which the assimilation capacity of Nature goes down, involving a kind of irreversible ecological regime. It has been shown by Prieur (2009) that introducing such irreversibility in the John and Pecchenino model considerably weakens the case for an EKC. We study how the irreversibility mechanism interacts with the ingredients of the optimal technological switch problem outlined above, with special attention being paid to the outcomes regarding the capital-pollution relationship.
Our contribution is twofold. First of all, our contribution is technical. It is well known that including irreversibility in the above sense also induces an optimal switching time problem from the reversible to the irreversible ecological regime. Accordingly, our optimal AK growth model involves two optimal timing problems associated with technological and ecological switching times respectively. Original multi-stage optimal control techniques will be developed to solve the model, extending previous work of Tomiyama (1985) on technological switching and Tahvonen and Withagen (1996) on ecological switching. Second, and more importantly, the interaction between the ecological and technological mechanisms generates a large set of potential optimal solutions. These solutions lead to different relationships between capital and pollution. For our calibrated model, if a single technological switch is optimal, one recovers the EKC provided initial pollution is high enough. If exceeding the ecological threshold is optimal, then the latter configuration is far from being the rule.
The problem
We consider an optimal growth AK model with two stocks, physical capital (K) and pollution (P). Two production technologies are available from t=0. Each can be described by two parameters (Ai,qi), i={1,2}: Ai is marginal productivity of capital since the production function is Y =AiK, while qi measures the degree of dirtiness of technology i. Concretely, qi captures the marginal contribution of capital to the flow of pollution. The economy starts with technology i=1 and has to decide: (a) whether it switches to technology i=2, and (b) when. The economy cares about both the levels of consumption and pollution. So for the problem to be nontrivial, we assume that A1>A2 but q1>q2: technology 1 is more productive but dirtier. A1−A2 measures the cost of adopting a cleaner technology, we assume that it is permanent.
The problem is at this stage similar to the one tackled in Boucekkine, Krawczyk and Vallée (2011). There are however two major differences with respect to the latter contribution: first the existence of capital accumulation and second, pollution decay. We also introduce a key feature: that of irreversible pollution as in Prieur, Tidball and Withagen (2011). More precisely, the two state variables evolve according to the following laws of motion: 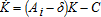 , for i={1,2}, C being consumption and δ the depreciation rate, and
, for i={1,2}, C being consumption and δ the depreciation rate, and 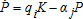 , with i={1,2}, j={1,2}. The j subscript refers to the ecological regime, here parameterized by the pollution natural decay rate αj. While the technological switch from regime i=1 to i=2 does not require a minimal level of physical capital to take place, an ecological switch from j=1 to j=2, where α1>α2≥0, entails the idea that Nature cannot regenerate in the same way for low and high levels of the stock of pollution. Typically, this is modeled through a threshold value for pollution, say
, with i={1,2}, j={1,2}. The j subscript refers to the ecological regime, here parameterized by the pollution natural decay rate αj. While the technological switch from regime i=1 to i=2 does not require a minimal level of physical capital to take place, an ecological switch from j=1 to j=2, where α1>α2≥0, entails the idea that Nature cannot regenerate in the same way for low and high levels of the stock of pollution. Typically, this is modeled through a threshold value for pollution, say 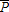 , above which the decay rate falls.1
, above which the decay rate falls.1
As explained in the introduction, bringing together technological and ecological switches considerably enriches the economic discussion. From the technical point of view, the problem sounds at first glance strongly asymmetric, the technological switch involving explicit timing decisions while ecological switches are essentially based on a posited threshold pollution level. It is however easy to see that this apparent asymmetry can be attenuated: in line with the pioneering contribution of Tahvonen and Withagen (1996), it is quite straightforward to reformulate the ecological switching problem also as an optimal timing problem: indeed, if such a switch occurs, there exists a date, say tP, where 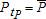 (assuming
(assuming 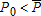 ). As we shall see, this does not mean that the laws of motion of the two state variables imply similar optimality conditions. However, the previous observation justifies the formulation of both switching problems as optimal timing problems.
). As we shall see, this does not mean that the laws of motion of the two state variables imply similar optimality conditions. However, the previous observation justifies the formulation of both switching problems as optimal timing problems.
Hereafter, tK with  will refer to the timing of technological switching while tP with
will refer to the timing of technological switching while tP with 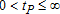 does the job on the ecological side.
does the job on the ecological side.
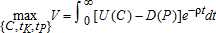
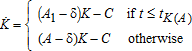
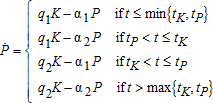
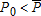 and K0 are given, and ρ>0 is the rate of pure time preference. The control set includes the two timing variables mentioned above, plus consumption. The social welfare function is the same as in Tahvonen and Withagen (1996). The following standard regularity conditions assure the concavity of the problems we will have to treat:
and K0 are given, and ρ>0 is the rate of pure time preference. The control set includes the two timing variables mentioned above, plus consumption. The social welfare function is the same as in Tahvonen and Withagen (1996). The following standard regularity conditions assure the concavity of the problems we will have to treat:Assumption 1
The utility function, U(C), satisfies: U(0)=0, 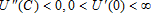 and
and 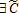 such that
such that 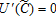 . The damage function, D(P), satisfies: D(0)=0, D′(P)>0, D′′(P)≥0 and D′(0)=0.
. The damage function, D(P), satisfies: D(0)=0, D′(P)>0, D′′(P)≥0 and D′(0)=0.
The optimal control problem stated above is novel in that the two timing problems are of a different nature. In particular, one involves a threshold level for the state variable while the other does not. Problems with multiple timing have already been addressed in the literature (see Saglam 2011) but the focus is on technological switching only. Here the two types of timing problem are treated in the same framework; needless to say, the interaction of both is very likely to give rise to a richer set of outcomes. A quick inspection of the set of admissible solutions in our enlarged problem is enough to illustrate this point. A priori, one can list the following optimality candidates: 1. Don't switch, 2. Technological switch only, 3. Ecological switch only, 4. Two switches: technological then ecological and 5. Two switches: ecological then technological.
It is not obvious at all which candidate will yield the optimum given initial conditions, preferences and available technological and ecological menus. Even worse, one can identify within the optimal outcomes with at least one switch, different classes of solutions: interior (that is tK>0 and/or tP>0) or corner (tK=0). Seven solutions are thus possible. Moreover, one might be interested in distinguishing the case when there is a simultaneous ecological and technological switch, which adds another possibly interesting sub-case.
The next section presents our approach to solving this problem.
The solution approach
We proceed as follows. First, for every possible candidate, we write the corresponding first-order necessary conditions, solve the problem and compute the resulting welfare function, V. Then, we pick the candidate which delivers the highest social welfare, that is we identify the global maximum for the problem. The challenge is first analytical because the general optimal control problem involved is nontrivial. It is also computational because comparing eight possible solutions is very demanding. We ultimately resort to numerical comparison because our underlying optimal control problem does not permit a closed-form solution in most regimes.
In the following, we provide the general control theory foundations in order to identify the solutions with two interior switches; this covers three cases: 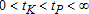 ,
, 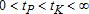 , and
, and 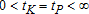 . The other cases can be immediately recovered from the literature with one possible technological switch (see Boucekkine, Saglam and Vallée 2004) or one possible ecological switch (Tahvonen and Withagen 1996), including corner regimes.2
. The other cases can be immediately recovered from the literature with one possible technological switch (see Boucekkine, Saglam and Vallée 2004) or one possible ecological switch (Tahvonen and Withagen 1996), including corner regimes.2
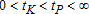 :
:
-
The third interval sub-problem: the problem in this regime is:
subject to,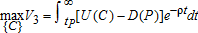 where tP and the initial conditions K(tP) and
where tP and the initial conditions K(tP) and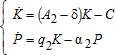
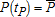 are fixed. The associated Hamiltonian is:
are fixed. The associated Hamiltonian is: 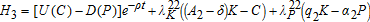 , where
, where 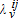 is the co-state variable associated with the state variable v={K,P} in technological menu i and ecological regime j. The resulting value-function is of the form
is the co-state variable associated with the state variable v={K,P} in technological menu i and ecological regime j. The resulting value-function is of the form 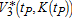 .
.
-
The second interval sub-problem: in the next interval, the maximization problem is:
subject to the corresponding dynamics, for regime i=2 and j=1, where tK, K(tK) and P(tK) are given, and tP and K(tP) are free. Denote by H2 and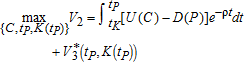
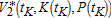 the corresponding Hamiltonian and value-function respectively.
the corresponding Hamiltonian and value-function respectively.
-
The first interval sub-problem: This sub-problem concerns the interval [0tK]:
subject to the dynamics of regimes i=1 and j=1, with K(0) and P(0) given, and with free tK, K(tK) and P(tK). We denote the Hamiltonian by H1 and it is obvious that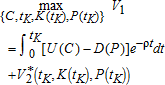
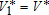 .3
.3
Notice that each optimal control sub-problem is well-behaved and we will not spend space writing the corresponding standard Pontryagin conditions. Instead, we focus on uncovering the much trickier optimality conditions with respect to the timing variables and the so-called matching conditions. This is solved by the following theorem.
Theorem 1
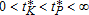 be the optimal timing decisions. Then:
be the optimal timing decisions. Then:
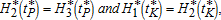 (1)
(1)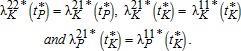 (2)
(2)The proof is online in the Supplementary Data. A few comments are in order here. First of all, the five optimality conditions above yield the continuity or matching conditions at the junction times. In this respect, conditions (1) impose the continuity of the Hamiltonian at the optimal junction times while conditions (2) ensure the continuity of co-state variables at these times. Interestingly enough, one can observe that while at the technological switching time, both co-state variables are optimally continuous, only the one associated with K is necessarily continuous at the ecological switching time. This underlines the major difference between the two switching types: in the latter, pollution is fixed at the switching time, and equal to the threshold value, while at the technological switching time, both state variables can be freely chosen. This generally implies discontinuity of the co-state variable associated with P at tP.
Second, one can interpret the matching conditions (1) as first-order optimal timing conditions for tP and tK respectively. Generally speaking, the matching condition for timing tv may be written as: 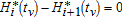 , for i={1,2} and v={K,P}. This condition is quite common in the literature on multi-stage technological switching (see Saglam 2011). We show here that it applies also to ecological switches. Keeping the discussion non-technical, one may interpret the difference
, for i={1,2} and v={K,P}. This condition is quite common in the literature on multi-stage technological switching (see Saglam 2011). We show here that it applies also to ecological switches. Keeping the discussion non-technical, one may interpret the difference 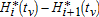 as the marginal gain from extending the regime inherent to one of the two first time intervals at the expense of the regime associated with the next interval. Because there are no direct switching costs, the marginal switching cost is nil. Therefore, the matching conditions on Hamiltonians do equalize the marginal benefits and costs of delaying switching times. Hence they do constitute first-order necessary conditions with respect to those critical dates.4
as the marginal gain from extending the regime inherent to one of the two first time intervals at the expense of the regime associated with the next interval. Because there are no direct switching costs, the marginal switching cost is nil. Therefore, the matching conditions on Hamiltonians do equalize the marginal benefits and costs of delaying switching times. Hence they do constitute first-order necessary conditions with respect to those critical dates.4
There are two remaining cases of interest with two interior switches, which derive quite trivially from the analysis of the benchmark case. If ecological switching precedes technological switching, that is if 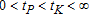 , Theorem 1 still applies integrally. It is in fact invariant to the sign of tK−tP as one can infer from the discussion following Theorem 1. The final case follows the same logic. The list of corresponding first-order timing and matching conditions is shorter because only two successive regimes are involved, rather than three: one before tK=tP=ts and one after. Denoting by Hi,
, Theorem 1 still applies integrally. It is in fact invariant to the sign of tK−tP as one can infer from the discussion following Theorem 1. The final case follows the same logic. The list of corresponding first-order timing and matching conditions is shorter because only two successive regimes are involved, rather than three: one before tK=tP=ts and one after. Denoting by Hi, 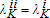 and
and 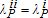 , i={1,2}, the Hamiltonians and co-state variables corresponding to the sub-problems on the intervals [0,ts] and
, i={1,2}, the Hamiltonians and co-state variables corresponding to the sub-problems on the intervals [0,ts] and 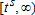 respectively, the optimality conditions reduce to
respectively, the optimality conditions reduce to 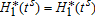 and
and 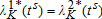 .
.
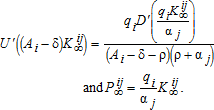
One does not know in general how 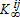 and
and 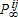 respond to changes in the technological menu (Ai,qi). In addition, if
respond to changes in the technological menu (Ai,qi). In addition, if 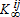 is decreasing in αj,
is decreasing in αj, 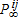 may not be monotonic in αj. The intuition runs as follows. Suppose the planner adopts, at some point in time, the new technological menu. The reduction in Ai generates the usual income and substitution effects that have an ambiguous effect on investment. Moreover, the associated decrease in the intensity of pollution qi, induced by the adoption of the new technology, lowers the social cost of capital accumulation and stimulates investment. Thus, there are different forces at play and it is not immediately obvious which effect will prevail in the long run. In the same vein, the impact of technology adoption on pollution is unclear. Of course, the decrease in qi is a means of slowing down pollution accumulation. But depending on whether technical change stimulates investment, there is an indirect effect that may go the other way. In the numerical exercise that follows, we find it reasonable to assume that the adoption of the new cleaner technology allows the economy to reach a steady state with less pollution.
may not be monotonic in αj. The intuition runs as follows. Suppose the planner adopts, at some point in time, the new technological menu. The reduction in Ai generates the usual income and substitution effects that have an ambiguous effect on investment. Moreover, the associated decrease in the intensity of pollution qi, induced by the adoption of the new technology, lowers the social cost of capital accumulation and stimulates investment. Thus, there are different forces at play and it is not immediately obvious which effect will prevail in the long run. In the same vein, the impact of technology adoption on pollution is unclear. Of course, the decrease in qi is a means of slowing down pollution accumulation. But depending on whether technical change stimulates investment, there is an indirect effect that may go the other way. In the numerical exercise that follows, we find it reasonable to assume that the adoption of the new cleaner technology allows the economy to reach a steady state with less pollution.
Regarding the impact of the ecological switch on steady state pollution, two effects are pushing in opposite directions. A decrease in αj makes it more difficult for Nature to regenerate itself. At the same time however, with everything else equal, it tends to reduce the incentive to invest in capital (through the higher social cost of pollution 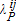 ). From now on, we consider the more realistic case where the ecological switch translates into higher pollution.
). From now on, we consider the more realistic case where the ecological switch translates into higher pollution.
It is now time to apply this theoretical analysis to the problem described in Section 2.
Numerical investigation
What is the solution to the optimal growth problem with ecological and technical switches? To what extent does this solution respond to changes in the fundamentals of the economy? What is the relationship between the two state variables, capital and pollution, along the optimal path? These are the questions we shall address in this numerical analysis.
Model calibration
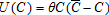 and D(P)=νP, with
and D(P)=νP, with 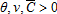 . The set of baseline parameters used is
. The set of baseline parameters used is
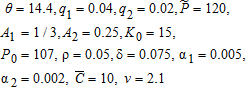 (3)
(3)The discount rate is close to what western governments use for most long term investments. A depreciation rate of 7.5% is between the reference values, 5% and 10%, that depend on the level of economic development. The technology parameter A1 is chosen to be consistent with the observed capital-output ratio: K11/Y11=3.
The environmental parameters α1, q1 and ν are set according to the estimates found in the literature on the economics of climate change (see Hoel and Karp 2002 and Nordhaus 2008). The literature suggests α1=0.005 for carbon dioxide. The emission-output ratio for the year 2010 is equal to 0.12. This implies q1=0.04. The social costs of carbon dioxide emissions cannot be less than 20$or 30$per ton but could probably not exceed 50$per ton. We use a value of 40$to represent the shadow price of pollution. From the following steady state relation 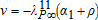 , one gets ν=2.1. At the steady state, one also finds
, one gets ν=2.1. At the steady state, one also finds 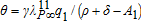 , where γ stands for relative risk aversion. Assuming that the latter is equal to 5 gives θ=14.4. The parameter
, where γ stands for relative risk aversion. Assuming that the latter is equal to 5 gives θ=14.4. The parameter 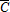 in the utility function has been arbitrarily chosen because it is a scale parameter that does not affect the results. In line with the discussion about the impact of ecological and technical switches on the steady state, parameters (A2,q2,α2) are set so that steady state pollution is lower (resp. larger) after the technical (resp. ecological) switch than before. For the values reported in (3), it appears that steady state capital is higher after the technical switch than before.5 So, while the adoption of the new technology is costly in terms of investment in the short run, it is ultimately beneficial to capital accumulation.
in the utility function has been arbitrarily chosen because it is a scale parameter that does not affect the results. In line with the discussion about the impact of ecological and technical switches on the steady state, parameters (A2,q2,α2) are set so that steady state pollution is lower (resp. larger) after the technical (resp. ecological) switch than before. For the values reported in (3), it appears that steady state capital is higher after the technical switch than before.5 So, while the adoption of the new technology is costly in terms of investment in the short run, it is ultimately beneficial to capital accumulation.
The final discussion is about the set of initial conditions. For the particular issue of climate change, irreversible switches are likely to occur if no dramatic action is undertaken soon. Indeed, there is now growing evidence that oceans (the most important carbon sink) display a buffering capacity that is approaching saturation. At the same time, the assimilation capacity of terrestrial ecosystems will likely peak by mid-century and then decline to become a net source of carbon by the end of this century. Finally, the potential collapse of the North Atlantic meridional overturning circulation is drawing much attention because it may happen for a 450 ppm CO2 concentration, and we have already reached 390 ppm (Yohe, Schlesinger and Andronova 2006).
These considerations lead us to perform the analysis with a level of initial pollution close enough to – but below – the ecological threshold. In addition, we have chosen a threshold that satisfies 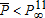 . This implies that a switch, either technical and/or ecological, will necessarily occur at some point in time. We further assume that a technological switch can be a means of avoiding the ecological switch because
. This implies that a switch, either technical and/or ecological, will necessarily occur at some point in time. We further assume that a technological switch can be a means of avoiding the ecological switch because 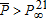 . Finally, the initial endowment in capital satisfies
. Finally, the initial endowment in capital satisfies 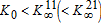 .
.
The benchmark scenario
Our calibrated AK model with pollution and switches has several optimality candidates. Solutions to the necessary optimality conditions exist for three of the eight possible candidates: 1. Technological switch alone, 2. Simultaneous technological and ecological switches and 3. Immediate technological switch alone.
Interestingly enough, as far as the nature of the relationship between K and P is concerned, these three candidates have very distinct features. Figure 1 illustrates the different relationships that may take place. Note that the shorter the distance between two marks, the slower the dynamic process.
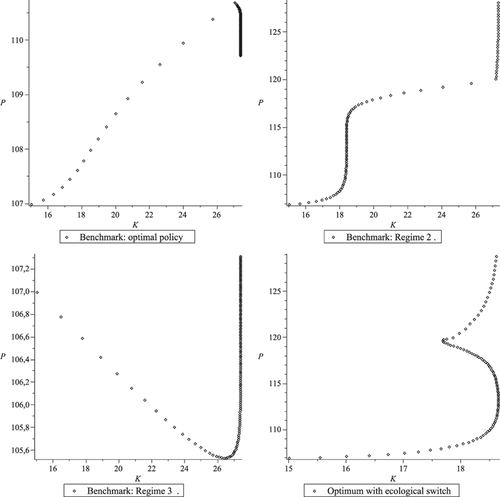
Relationship between capital and pollution in the K−P plan
Along the first regime, there is sustained capital accumulation during the period before the switch, investment being more efficient than after tK. Consequently, 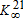 is nearly reached at the time of the switch and pollution rises during this phase (see figure 1, top left). At some point in time (tK=15.61), the accumulated pollution and the level of capital become so high that it is worthwhile to adopt the new greener technology. From that point on, pollution, starting at a high level, decreases because natural assimilation now prevails on the reduced emissions due to the new technology.
is nearly reached at the time of the switch and pollution rises during this phase (see figure 1, top left). At some point in time (tK=15.61), the accumulated pollution and the level of capital become so high that it is worthwhile to adopt the new greener technology. From that point on, pollution, starting at a high level, decreases because natural assimilation now prevails on the reduced emissions due to the new technology.
By contrast capital accumulation is delayed in the second regime, in order to reach 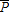 as late as possible (see figure 1, top right). Once the double switch has occurred, pollution grows at a high rate because the economy can no longer rely on a high regeneration rate. Finally, the economy may choose to immediately adopt the new technology. In this third regime, the relationship between K and P is U-shaped (see figure 1, bottom left): there is a first stage during which the economy is able, with the new technology, to accumulate capital while reducing the pollution stock.
as late as possible (see figure 1, top right). Once the double switch has occurred, pollution grows at a high rate because the economy can no longer rely on a high regeneration rate. Finally, the economy may choose to immediately adopt the new technology. In this third regime, the relationship between K and P is U-shaped (see figure 1, bottom left): there is a first stage during which the economy is able, with the new technology, to accumulate capital while reducing the pollution stock.
What is the optimal solution? It turns out that it is the regime with a technical switch alone (V1=2464.6>V2=2432.81>V3=1948.3). This result is very intuitive. Throughout regime 1, the planner can avoid the ecological threshold and is therefore better off than under regime 2. Regime 1 also dominates regime 3 because in the former, capital accumulation benefits from a higher investment efficiency. To conclude this analysis, it is worth mentioning that the optimal policy, with technical change alone, involves a capital-pollution relationship that has the form of the EKC. 6
Let us investigate whether these results are robust to modifications of critical parameters.
Sensitivity analysis
This section reviews all the possible variations of the baseline scenario. Table 1 summarizes our findings.
| Tech. switch | Eco. switch | t K <tP | t P <tK | |
|---|---|---|---|---|
| Bench. | t K =15.6, V =2464.6 | no | no | no |
| K 0=5 | t K =22, V =1257.9 | no | no | no |
| P 0=50 | t K =15.6, V =4641 | no | no | no |
| K 0=5, P0=50 | t K =22, V =3434.3 | no | no | no |
| q 2=0.01 | t K =10.2, V =2578.2 | no | no | no |
| q 2=0.03 | no | no | no | no |
| α 2=0.001 | t K =15.6, V =2464.6 | no | no | no |
| α 2=0.003 | t K =15.6, V =2464.6 | t P =96, V =2431.3 | no | (tP,tK)=(108.4,122.2), V =2431.5 |
| ν=1 | t K =19.7, V =4872.8 | t P =78.6, V =4857.4 | no | no |
| ρ=0.1 | no | t P =81.9, V =1206.5 | no | no |
| A 2=0.3 | t K =5.9, V =2568 | no | no | no |
| t K =0 | t K =tP=t | Opt. | Relation K, P | |
| Bench. | V =1948.3 | t=72.7, V =2428.4 | Tech. switch | EKC |
| K 0=5 | V =378.4 | no | Tech. switch | no EKC |
| P 0=50 | V =4124.7 | t=247.4, V =4610.2 | Tech. switch | no EKC |
| K 0=5, P0=50 | V =2563.8 | no | Tech. switch | no EKC |
| q 2=0.01 | V =2132 | t=72.5, V =2434.2 | Tech. switch | EKC |
| q 2=0.03 | V =1768 | t=72.9, V =2422.7 | Switch tK=tP | no EKC |
| α 2=0.001 | V =1948.3 | t=74, V =2426.1 | Tech. switch | EKC |
| α 2=0.003 | V =1948.3 | t=71.5, V =2430.8 | Tech. switch | EKC |
| ν=1 | V =4280.8 | t=64.8, V =4856.8 | Tech. switch | EKC |
| ρ=0.1 | V =714.58 | t=68.8, V =1206.4 | Eco. switch | no EKC |
| A 2=0.3 | V =2503.2 | t=84.8, V =2432.6 | Tech. switch | EKC |
Several interesting conclusions hold whatever the scenario considered. Firstly, the regime with immediate technical switch always exists and is always dominated by another solution. Secondly, there is no solution involving a technical switch followed by an ecological switch. Thirdly, each time a candidate with a technical switch alone exists, this yields the optimum. Last but not least, when the optimum is a technological switch alone, the relationship between capital and pollution entails a turning point. This relationship is inverted U-shaped when the initial level of capital and pollution are high enough.7
Finally, it is worth mentioning that in some scenarios, our conclusions markedly differ. In case where the intensity of pollution remains relatively high after adoption (q2=0.03), the technological switch is not attractive for the planner. It implies that the optimum is the regime with a simultaneous double switch. A not too damaging level of pollution (ν=1), a small ecological threat (α2=0.003), or more impatient agents (ρ=0.1), leads to less attention being paid to the ecological threshold and solutions to the regime with an ecological switch alone exist. Exceeding the threshold is optimal only when agents are relatively impatient. In such a case, the capital-pollution relationship is not at all like an EKC. It encompasses an intermediate stage where pollution increases as capital decreases (see figure 1, bottom right).
Concluding remarks
This paper investigates the income-pollution relationship within an optimal AK growth model with technological and ecological switches. We show that the EKC, that is usually seen as a description of the relationship between wealth and pollution along the different development stages of a country, can also emerge as a result of the implementation of an optimal policy in the current development stage of the economy.
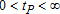 and tK=0, one has to solve for the ecological switch in the problem in question with tK=0 given and the implied law of motion for capital.
and tK=0, one has to solve for the ecological switch in the problem in question with tK=0 given and the implied law of motion for capital.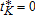 implies
implies 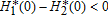 .
.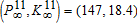 ,
, 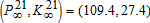 ,
, 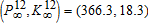 and
and 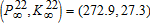 .
.



