An Evaluation of the Efficiency of Minnow Traps for Estimating the Abundance of Minnows in Desert Spring Systems
Abstract
Desert springs are sensitive aquatic ecosystems that pose unique challenges to natural resource managers and researchers. Among the most important of these is the need to accurately quantify population parameters for resident fish, particularly when the species are of special conservation concern. We evaluated the efficiency of baited minnow traps for estimating the abundance of two at-risk species, Foskett Speckled Dace Rhinichthys osculus ssp. and Borax Lake Chub Gila boraxobius, in desert spring systems in southeastern Oregon. We evaluated alternative sample designs using simulation and found that capture–recapture designs with four capture occasions would maximize the accuracy of estimates and minimize fish handling. We implemented the design and estimated capture and recapture probabilities using the Huggins closed-capture estimator. Trap capture probabilities averaged 23% and 26% for Foskett Speckled Dace and Borax Lake Chub, respectively, but differed substantially among sample locations, through time, and nonlinearly with fish body size. Recapture probabilities for Foskett Speckled Dace were, on average, 1.6 times greater than (first) capture probabilities, suggesting “trap-happy” behavior. Comparison of population estimates from the Huggins model with the commonly used Lincoln–Petersen estimator indicated that the latter underestimated Foskett Speckled Dace and Borax Lake Chub population size by 48% and by 20%, respectively. These biases were due to variability in capture and recapture probabilities. Simulation of fish monitoring that included the range of capture and recapture probabilities observed indicated that variability in capture and recapture probabilities in time negatively affected the ability to detect annual decreases by up to 20% in fish population size. Failure to account for variability in capture and recapture probabilities can lead to poor quality data and study inferences. Therefore, we recommend that fishery researchers and managers employ sample designs and estimators that can account for this variability.
Received September 29, 2014; accepted January 29, 2015
Desert spring systems, often termed cienegas (Hendrickson and Minckley 1985), are generally small, aquatic ecosystems that originate in low gradient areas where groundwater emerges at the surface. These spring systems do not drain into a stream but drain into wetlands where they evaporate and are therefore considered isolated. Cienegas often serve as paleorefugia for aquatic biota and many of these systems contain unique assemblages with high degrees of endemism (Unmack and Minckley 2008). Fish communities in cienegas are generally depauperate and often consist of a single fish species. The severe isolation of these systems combined with human modification naturally places desert fish species at greater risk of extinction. In fact, Helfman et al. (2009) estimate that approximately two-thirds of the endangered and threatened fishes in North America are desert fishes.
To prevent further declines in desert fishes, managers need reliable information on the current status of populations and their recent trends. Sampling fish in cienegas, however, can be particularly challenging. The surface water in these systems is often alkaline with high ion concentrations (Naiman 1981), which preclude the use of electrofishing methods. Most of these spring systems also contain large amounts of submergent and emergent vegetation that can prevent effective seining. Further, the relative sensitivity of these systems to physical disturbance combined with the need to minimize harm to at-risk fish species often limits sampling to passive techniques, such as minnow traps. Sample data collected with passive gear, however, are often highly variable and can be biased by factors that affect fish capture efficiency, such as fish size, gear selectivity, and the characteristics of sample area (Peterson and Paukert 2009). Failure to account for these biases can result in misleading estimates of population status and trends and erroneous decision making by management. The best means to determine the reliability of a sample method is to conduct a gear efficiency evaluation, preferably using an unbiased estimate of fish abundance (Peterson et al. 2004). Such an evaluation has never been conducted with any fish sample method in cienegas.
The difficulties associated with sampling at-risk fish species inhabiting cienegas are typified by two species in southeastern Oregon. The Foskett Speckled Dace Rhinichthys osculus ssp. is represented by a single naturally occurring population that inhabits Foskett Springs in Lake County. The Borax Lake Chub Gila boraxobius is a small minnow endemic to Borax Lake and adjacent wetlands in the Alvord Basin in Harney County. Both species were listed in the early 1980s, Borax Lake Chub as endangered and Foskett Speckled Dace as threatened, under the federal Endangered Species Act (USFWS 1982, 1985) and have been monitored using minnow traps for more than a decade (Scheerer 2011; Scheerer and Bangs 2011). These monitoring efforts estimated population size using two-sample capture–recapture estimators that assume constant probability of capture (i.e., Lincoln–Petersen estimator). That is, they assume that the probability of capture on the first occasion and second occasion are equal and that marked and unmarked fish have the same capture probability. However, assumptions of constant probability are seldom met for most fish sampling methods (Peterson and Paukert 2009), and violations of estimator assumptions can result in what has been defined as “highly precise wrong answers” (Anderson et al. 1985) that can lead to misguided management decisions. Thus, our objectives were to (1) identify the optimal sample design for evaluating the efficiency of minnow traps, (2) examine the influence of habitat characteristics, species, and fish size on trap capture efficiency for two at-risk minnow species, and (3) evaluate how variability in trap capture efficiency can affect population estimates and the ability to statistically detect population trends.
METHODS
Study area.
We evaluated fish trap capture efficiency at two cienegas on the east side of the Cascade Mountain Range. Foskett Springs is a small, natural spring located in the Warner Basin in south-central Oregon (Figure 1). The spring rises from a springhead pool, flows through a narrow spring brook into a series of shallow marshes, and then disappears into the soil of Coleman Lake, which is usually dry except for years with extremely high precipitation. The spring consists of four distinct habitat areas that vary in size and structure and were treated as strata in the sample design (Figure 1). The spring pool is a shallow marshy pool that extends 11 m and is dominated by emergent aquatic vegetation, including rushes Juncas sp., monkey flower Mimulus sp., and cattails Typha latifolia with little open water (Table 1). The spring pool flows into a shallow, narrow (0.4 m), topographically constrained spring brook that extends approximately 68 m. The spring brook spreads out and empties into an emergent tule marsh, dominated by hardstem bulrush Schoenoplectus acutus, that extends 102 m with only a few narrow, open-water channels. The tule marsh transitions into a similar marsh that is dominated by cattails. The cattail marsh is very shallow (average depth, 0.03 m), extends 103 m, and has essentially no open-water habitat. The U.S. Bureau of Land Management acquired and fenced Foskett Springs in 1987 to exclude cattle and minimize disturbance to the spring. Foskett Springs is inhabited by a single fish species, the Foskett Speckled Dace.
| Habitat | Average depth (m) | Wetted area (m2) | Open-water area (m2) | Number of traps |
|---|---|---|---|---|
| Foskett Springs | ||||
| Spring pool | 0.26 | 57 | 4 | 6 |
| Spring brook | 0.20 | 248 | 31 | 11 |
| Tule marsh | 0.12 | 3,153 | 86 | 11 |
| Cattail marsha | 0.04 | 1,438 | 0 | 0 |
| Borax Lake | ||||
| Main lake | 1.24 | 37,990 | 37,990 | 102 |
| Wetland | 0.83 | 905 | 905 | 12 |
| Outflow channel | 0.18 | 44 | 44 | 6 |
- a Not sampled due to a lack of open water and very shallow depths.
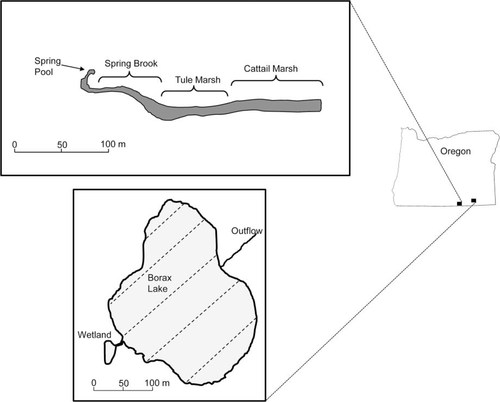
Locations of Foskett Springs (upper panel) and Borax Lake (lower panel) in Oregon showing habitat areas. Broken lines on Borax Lake represent transects where traps were placed.
The second study area, Borax Lake, is a 4.1-ha, geothermally heated, alkaline lake located in the Alvord Basin in southeastern Oregon (Figure 1). The lake is fed by several small springs and is generally shallow (<2 m) but reaches a maximum depth of 27 m at the thermal vent (Schneider and McFarland 1995). The lake bed is primarily composed of fine silt with patchy areas of bedrock and gravel. Aquatic vegetation in the lake is relatively sparse with stonewort Chara hornemannii covering approximately 61% of the lake bed. A small wetland (currently inactive, secondary spring vent) is attached to the western side of Borax Lake through a small channel and is surrounded by dense aquatic vegetation primarily composed of American three-square bulrush Schoenoplectus americanus and beaked spikerush Eleocharis rostellata. On the east side of the lake, water flows from the lake through an outflow channel for approximately 100 m where it disappears into the soil. Borax Lake also is inhabited by a single fish species, the Borax Lake Chub.
Sample design simulation.
Fish capture probabilities can be estimated through a variety of approaches including stocking known numbers of fish into sample sites, using dual-gear sampling methods, and by capturing, marking, and recapturing marked individuals (Peterson and Paukert 2009). We employed the latter approach because it was the only feasible method given the species and systems we studied. Multiple capture occasions (i.e., more than two) are needed to reliably model variability in capture and recapture probabilities with capture–recapture estimators (Williams et al. 2002). The accuracy of these estimates generally increases with additional capture occasions. However, we were concerned that excessive handling of these at-risk species could lead to mortality. Therefore, we evaluated the effectiveness of alternative sample designs via simulation with program MARK (White and Burnham 1999) using the Huggins closed-capture estimator (Huggins 1989, 1991). The Huggins estimator can be used to model the probability of capture (i.e., the capture of an unmarked fish) and recapture (i.e., the capture of a marked fish) as varying through time and as a function of covariates. We conducted 1,000 replicate simulations for all combinations of the number of capture occasions at three, four, five, and six; population sizes of 1,000, 3,000, 5,000, and 10,000; and all combinations of capture and recapture probabilities of 0.1, 0.2, and 0.3 (i.e., capture and recapture probabilities could differ). These values were based, in part, on estimated capture probabilities from previous surveys at Foskett Springs and Borax Lake that employed a Lincoln–Petersen population estimator (Scheerer 2011; Scheerer and Bangs 2011) and on our experiences evaluating gear efficiency. Using the simulation results, we estimated the bias in the population estimate as the difference between the estimated and known population size. We calculated error as the square root of the mean of squared differences between estimated and known population size, across replicates. These values were expressed as a percentage of the known population size. In addition, we estimated the percentage of fish in the simulated population that was handled at least once. The percent bias, error, and number of fish handled then were averaged for each number of sample occasions to identify the design that minimized bias, error, and the number of fish handled.
Fish sampling.
Based on results from the simulations described above, fish at Foskett Springs were collected on four consecutive days in late July 2012 at the spring pool, spring brook, and tule marsh using 3.2-mm-mesh Gee galvanized steel minnow traps with approximately 2.5-cm openings and baited with one-third slice of wheat bread. The cattail marsh was not sampled because we were unable to find open water with sufficient depth to submerge the traps. We attempted to use the same effort in each habitat by uniformly distributing the traps throughout each at a density of approximately one trap per 6 m2 (Table 1) and placing them in areas where the trap openings were completely submerged. Traps were placed in the morning, left in place for 3–4 h, and retrieved by field personnel. Captured fish were immediately placed in live wells with ambient spring water and aeration.
Borax Lake Chub were collected during three consecutive days in mid-September 2012 in the lake, wetland, and outflow channel using multiple minnow traps, as described above (Table 1). Thus, there were only three capture occasions. Traps were placed in the lake approximately 25 m apart along transects and along the shoreline and were uniformly distributed in the wetland and outflow channel (Figure 1). In addition, a small fyke net with 3.2-mm mesh was placed at the mouth of the wetland channel to capture fish and prevent movement between the lake and wetland. In contrast to Foskett Springs, traps were set in the evening and removed the following morning at Borax Lake. All captured fish also were placed in live wells with aerated ambient lake water.
Following capture, we marked fish with a partial fin clip that was unique to each sampling occasion, adding a partial upper caudal fin clip for all fish captured on the first sampling occasion, a partial dorsal fin clip on the second sampling occasion, and a partial anal fin clip on the third sampling occasion. Partial clips involved removal of the outer one-third to one-half of the fin, effectively squaring off the pointed area of the fin. Fish also were visually categorized into one of three length groups as small (<35 mm TL), medium (35–59 mm TL), and large (>60 mm TL) to minimize handling. Fish with lengths near the 35-mm and 60-mm cutoffs were typically measured with a graduated measuring board. The visual assessment was verified by measuring TL of a subsample of fish (154 dace and 265 chub). Marked fish were immediately returned to buckets and allowed to recover for a minimum of 15 min before being released. We made an attempt to disperse the fish throughout the habitat from which they were collected.
We measured and recorded physical habitat characteristics at each location in conjunction with fish sampling. Site dimensions of each habitat type were measured using a tape measure or a laser range finder (Bushnell Yardage ProSport 850) to the nearest 0.5 and 1.0 m, respectively, and from these measurements we calculated the open-water area and vegetated surface area. We also estimated wetted surface area by measuring channel length and channel widths, to the nearest 0.25 m, along regularly spaced transects (every 20 m). Areas were summed for each distinct habitat type. Water depth was measured using a graduated depth staff to the nearest 0.01 m.
Definitions and statistical analyses.
We estimated trap capture and recapture probabilities separately for each study area using the Huggins closed-capture model (Huggins 1989, 1991) as implemented in program MARK (White and Burnham 1999). Here the total catch from all traps set at a location (i.e., a habitat stratum) and date were combined for each body size-group and treated as a single capture occasion. This resulted in capture histories that corresponded to individual habitats and fish body size-group, which allowed us to evaluate the relation between habitat characteristics, other covariates, and trap capture and recapture probabilities. Our primary objective was to obtain the best approximating model for estimating trap capture probabilities. Therefore, we developed global models (i.e., one for each study area) that modeled capture and recapture probabilities as a function of: fish body size-class, with medium as the statistical baseline; the number of traps used; the amount of time the traps were fished; the habitat type sampled; and two-way interactions between body size and habitat type; habitat type, the number of traps used, and the amount of time the traps were fished; and the number of traps used and the amount of time the traps were fished. These models also contained binary-coded parameters (0, 1) associated with capture occasion that accounted for variation in capture and recapture probabilities in time that were not related to the predictors described above. We then fit all subsets of the global model and included candidate models where capture and recapture probabilities were equal and were constant through time. The relative fit of each candidate model was assessed by calculating Akaike's information criterion (AIC; Akaike 1973) with the small-sample bias adjustment (AICc; Hurvich and Tsai 1989) and Akaike weights (Burnham and Anderson 2002). We compared the relative fit of different models by calculating the ratio of Akaike weights.
All inferences about the effect of factors on trap capture probabilities were made using the best approximating model for each study area. Precision of the parameter estimates for the best models were expressed by calculating 95% CIs. Because we used a logit link to fit the capture probability models, we also calculated odds ratios (Hosmer and Lemeshow 2000) to facilitate interpretation of the model parameters.
We assessed the goodness of fit of the two global capture probability models (i.e., Foskett Springs and Borax Lake) using a bootstrap goodness-of-fit procedure with 1,000 iterations. Here capture–recapture data were simulated with R statistical software (R Development Core Team 2010) using the parameters estimated from the global model, and the simulated data were fit using program MARK. Goodness of fit then was evaluated by comparing the distribution of 1,000 randomly generated overdispersion parameters (ĉ) to the observed parameter (Williams et al. 2002). We assumed that the model fit was adequate if the observed overdispersion parameter was contained within the 90th percentiles of the bootstrapped values.

Finally, we wanted to evaluate how variability in capture and recapture probabilities, if ignored, influence the ability to statistically detect trends in population size. We conducted two sets of simulations: the first set evaluated the power to detect trends using (raw) single-sample catch data, and the second set used abundance estimates from the LP estimator. The simulations began with an initial population size of 2,500 and simulated constant decreases in population size of 5, 10, 15, and 20% per year over a 5-year period. The initial population size was based, in part, on our estimated population size of Foskett Speckled Dace. For each set of simulations, we first ran simulations where capture (and recapture) probabilities were equal and fixed (i.e., did not differ through time). To evaluate the effect of capture probability on statistical power, 1,000 replicate simulations were conducted for each combination of the constant decrease in population size and capture probabilities that ranged from 10% to 100%, in 10% increments. To evaluate the effects of annual variability in capture and recapture probabilities, we also ran simulations that randomly generated capture and recapture probabilities assuming two levels of variability, specifically SDs of 5% and 10% of the mean simulated probabilities. For all simulations, the virtual population was sampled using the capture efficiency estimate and the simulated fish abundance, assuming a binomial distribution. The simulated sampling data then were fit using linear regression with simulated catch data or LP estimates as the dependent variable and year as the independent variable. The proportion of the 1,000 replicates where P < 0.05 was calculated for each simulation set and used as an estimate of statistical power. All simulations were conducted using R statistical software (R Development Core Team 2010).
RESULTS
Simulation of alternative sample designs indicated that bias and error decreased with increasing number of capture occasions, whereas the proportion of the population that was captured and handled increased (Figure 2). The greatest decrease in bias and error occurred when the number of capture occasions increased from three to four, and the decrease was much less after four capture occasions. However, the proportion of fish handled increased steadily with the number of capture occasions. Therefore, we considered four capture occasions to be optimal.
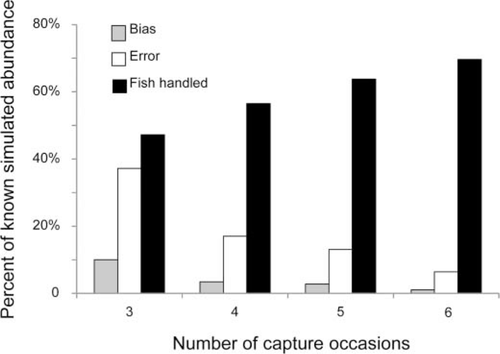
Mean estimated bias and error from simulated capture–recapture data fit with Huggins closed-capture estimator and simulated number of fish sampled expressed as a proportion of known simulated abundance. Bias in the population estimate was estimated as the difference between the estimated and known population size. Error was estimated as the square root of the mean of squared differences between estimated and known population size across replicates.
The overdispersion parameter of the global Foskett Springs and Borax Lake global capture probability models were 5.20 and 3.31, respectively. These were well within the 90th percentiles of the bootstrapped values for Foskett Springs (4.27–7.01) and Borax Lake (1.93–4.82). Therefore, we assumed that the subsets of the global models fit adequately.
The best approximating Foskett Speckled Dace capture probability model included fish body size, habitat type, recapture, two-way interactions between body size and spring pool habitat type, and time-varying parameters (Table 2). Based on Akaike weights, the model was only 1.02 times more likely than the next best approximating model that contained the same parameters with the exception of the interaction between small body size and spring pool habitat type. Parameter estimates from the best approximating model indicated that dace were more than three times more likely to be captured in spring pool and spring brook than in tule marsh (Table 3). Capture probabilities also were related to body size and were greatest for medium-sized fish (Figure 3a). The parameter estimates suggest that small and large fish were 7.1 and 1.5 times, respectively, less likely to be captured than medium fish in tule marsh (Table 3). Capture and recapture probabilities also varied with time and were greatest for marked fish during sample occasion 2 and lowest for first capture during occasions 3 and 4 (Figure 3b). Dace recapture probabilities also decreased with time.
| Candidate model | K | AICc | ΔAICc | w | Evidence ratio |
|---|---|---|---|---|---|
| Foskett Speckled Dace | |||||
| p(t1 = t2a, spring pool, spring brook, small, large, small × spring pool, large × spring pool, small × spring brook), c(t)b | 12 | 5,332.6 | 0.000 | 0.317 | 1.00 |
| p(t1 = t2, spring pool, spring brook, small, large, small × spring brook), c(t) | 10 | 5,332.7 | 0.042 | 0.310 | 1.02 |
| p(t1 = t2, spring pool, spring brook, small, large, recapture, large × spring pool), c(t) | 11 | 5,333.9 | 1.314 | 0.164 | 1.89 |
| p(t1 = t2, spring pool, spring brook, small, large, small × spring pool, large × spring pool, small × spring brook, large × spring brook), c(t) | 13 | 5,334.0 | 1.371 | 0.160 | 1.99 |
| p(t1 = t2, spring pool, spring brook, small, large, recapture, large × spring pool), c(t2 = t3, t4)c | 10 | 5,338.3 | 5.735 | 0.018 | 17.59 |
| Borax Lake Chub | |||||
| p = c(t2, small, large, wetland, outflow, t2 × wetland, t2 × outflow, small × wetland, large × wetland)d | 10 | 14,169.8 | 0.000 | 0.256 | 1.00 |
| p = c(t2, small, large, wetland, outflow, t2 × wetland, t2 × outflow, small × wetland) | 9 | 14,170.6 | 0.766 | 0.174 | 1.47 |
| p = c(t2, small, large, wetland, outflow, t2 × wetland, t2 × outflow, small × wetland, large × wetland, small × outflow, large × outflow) | 12 | 14,172.0 | 2.190 | 0.085 | 2.99 |
| p = c(t2, small, large, wetland, outflow, t2 × wetland, t2 × outflow, small × wetland, large × wetland, small × outflow) | 11 | 14,171.4 | 1.562 | 0.117 | 2.18 |
| p(t2, small, large, wetland, outflow, t2 × wetland, t2 × outflow, small × wetland, large × wetland, small × outflow, large × outflow), c(.)e | 13 | 14,172.4 | 2.607 | 0.069 | 3.68 |
- a Capture probabilities were equal for capture occasion 1 and 2.
- b Recapture probabilities differed for each capture occasion.
- c Recapture probabilities for capture occasion 2 and 3 were equal but differed from occasion 4.
- d Capture and recapture probabilities were equal.
- e Recapture probabilities were equal across capture occasions.
| Parameter | Estimate | SE | Lower CI | Upper CI | OR |
|---|---|---|---|---|---|
| Foskett Speckled Dace | |||||
| Intercept | −2.253 | 0.274 | −2.789 | −1.717 | 0.11 |
| Occasions 1, 2 | 0.897 | 0.123 | 0.656 | 1.138 | 2.45 |
| Spring pool | 1.292 | 0.159 | 0.981 | 1.603 | 3.64 |
| Spring brook | 1.325 | 0.148 | 1.035 | 1.616 | 3.76 |
| Small | −1.973 | 0.540 | −3.032 | −0.915 | 0.14 |
| Large | −0.443 | 0.171 | −0.778 | −0.108 | 0.64 |
| Small × spring pool | 0.757 | 0.558 | −0.336 | 1.851 | 2.13 |
| Large × spring pool | −1.213 | 0.325 | −1.850 | −0.576 | 0.30 |
| Small × spring brook | 0.988 | 0.565 | −0.119 | 2.094 | 2.68 |
| Recapture | 1.368 | 0.184 | 1.007 | 1.728 | 3.93 |
| Recapture × occasion 3 | −0.757 | 0.603 | −1.939 | 0.082 | 0.47 |
| Recapture × occasion 4 | −1.424 | 0.452 | −2.310 | −0.198 | 0.24 |
| Borax Lake Chub | |||||
| Intercept | −1.534 | 0.048 | −1.628 | −1.440 | 0.22 |
| Occasion 2 | 0.076 | 0.040 | −0.002 | 0.153 | 1.08 |
| Small | −1.050 | 0.126 | −1.296 | −0.803 | 0.35 |
| Large | −0.755 | 0.348 | −1.437 | −0.073 | 0.47 |
| Wetland | 1.407 | 0.083 | 1.244 | 1.571 | 4.08 |
| Outflow | 1.781 | 0.097 | 1.591 | 1.971 | 5.94 |
| Wetland × occasion 2 | −0.951 | 0.087 | −1.120 | −0.781 | 0.39 |
| Outflow × occasion 2 | −0.233 | 0.116 | −0.460 | −0.006 | 0.79 |
| Small × wetland | −0.915 | 0.316 | −1.534 | −0.296 | 0.40 |
| Large × wetland | 0.581 | 0.372 | −0.148 | 1.311 | 1.79 |
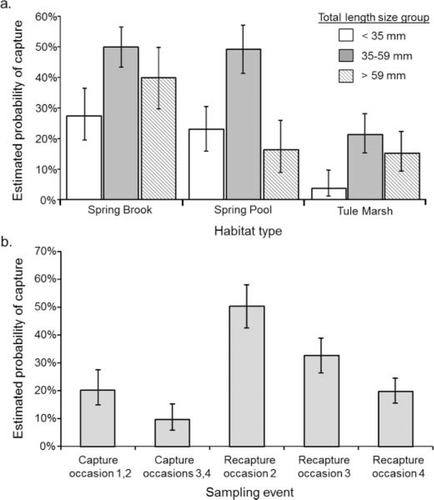
Estimated Foskett Speckled Dace capture probabilities, and 95% CIs (error bars) by (a) body size and habitat type for the first capture occasion and (b) capture event for medium-sized fish at tule marsh. Estimates are from the best approximating model. There is no recapture occasion 1, as there were no marked fish on the first sampling occasion.
The Borax Lake Chub best approximating capture–recapture model included body size, habitat, a two-way interaction between body size and wetland habitat, and time-varying parameters (Table 2). The model was 1.47 times more likely to be the best approximating model compared with the second-best model, which was similar but did not contain the large body size by wetland habitat interaction. There was some evidence that recapture probabilities differed from capture probabilities, but it was relatively weak with an evidence ratio of 3.68 between the best approximating model and the best model that had differing capture and recapture probabilities. Parameter estimates suggested that chub were 4.1 and 5.9 times more likely to be captured in the wetland and outflow habitats, respectively, than in the main body of the lake (Table 3). Similar to dace, chub capture probabilities were greatest for medium-sized and smallest for small-sized individuals and the differences varied with habitat (Figure 4). Interestingly, capture probabilities also were greater on occasion 2 than on occasions 1 and 3, and fish capture was 1.08 times more likely on occasion 2.

Estimated capture probabilities and 95% CIs (error bars) for Borax Lake Chub by body size and habitat type for the first capture occasion. Estimates are from the best approximating model.
As expected, we found that the LP estimator underestimated Foskett Speckled Dace abundance. The Huggins model-derived estimates were, on average, 2.1 times greater than the corresponding LP estimates (Table 4). The confidence intervals also were narrower for the LP estimates and were, on average, ±10% of the abundance estimate compared with the Huggins estimates (±27%). The Huggins-derived estimates for Borax Lake Chub were 1.3 times greater than the LP population estimates (Table 4). However, the relative width of the confidence intervals was similar between the two estimators.
| Huggins estimator | Lincoln–Petersen estimator | |||||
|---|---|---|---|---|---|---|
| Body size | Estimate | Lower CI | Upper CI | Estimate | Lower CI | Upper CI |
| Foskett Speckled Dace | ||||||
| Small | 746 | 577 | 1,007 | 266 | 218 | 328 |
| Medium | 873 | 740 | 1,278 | 601 | 534 | 682 |
| Large | 229 | 176 | 330 | 121 | 89 | 165 |
| All sizes | 1,848 | 1,489 | 2,503 | 988 | 898 | 1,098 |
| Borax Lake Chub | ||||||
| Small | 2,716 | 2,470 | 2,997 | 2,091 | 1,687 | 2,749 |
| Medium | 6,432 | 6,018 | 6,910 | 5,639 | 5,237 | 6,108 |
| Large | 553 | 507 | 609 | 452 | 351 | 594 |
| All sizes | 9,702 | 9,042 | 10,452 | 7,835 | 7,316 | 8,433 |
Evaluation of the effect of capture probability and variation in capture probabilities indicated that the ability to detect trends with raw catch data were greatest when capture probabilities were generally greater than 10% and were constant from year to year (Figure 5). When year-to-year variation was ±10%, it greatly reduced the power to detect trends using raw catch data, and power was less than the nominal 80% level for all average capture probabilities < 90% (Figure 5). The effect of capture probabilities and year-to-year variation was less pronounced for LP estimates compared with the raw catch data (Figure 6). Nonetheless, power was low for all but the greatest simulated decreases in population sizes when capture probabilities were <30%, values similar to those observed in Borax Lake and the tule marsh habitat at Foskett Springs.
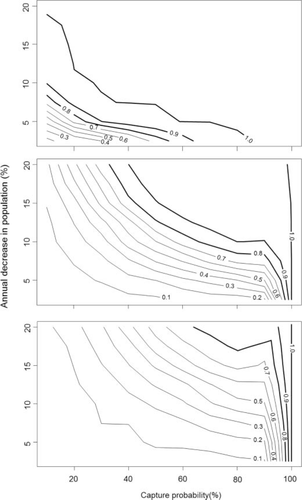
Estimated statistical power (with α = 0.05) to detect annual decreases in population size over 5 years using (raw) catch data versus capture probability assuming constant capture probability across years (top panel) and capture probability varying by 5% and 10% among years (middle and bottom panels, respectively). Labeled contour lines represent levels of power and bold lines indicate power of at least 0.8.
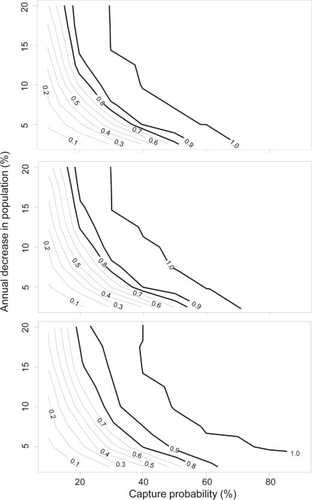
Estimated statistical power (with α = 0.05) to detect annual decreases in population size over 5 years using Lincoln–Petersen population estimates versus capture probability assuming constant capture probability across years (top panel) and capture probability varying by 5% and 10% among years (middle and bottom panels, respectively). Labeled contour lines represent levels of power and bold lines indicate power of at least 0.8.
DISCUSSION
To our knowledge, this is the first study that has evaluated the capture efficiency of minnow traps for sampling fish in cienegas. We found that capture probabilities were similar for Foskett Speckled Dace and Borax Lake Chub and varied with fish body size, the characteristics of the areas sampled, and for reasons that could not be explained by the predictor variables considered (e.g., time). In addition, we found that fish behavior changed in response to being captured and marked. Variability in capture and recapture probabilities also resulted in substantially biased estimates from a constant capture probability estimator and reduced our ability to detect simulated changes in population sizes. Therefore, it is crucial that biologists understand the sources of variability and, if possible, develop sample designs and use estimators that can account for them.
Trap capture efficiency was greatest for medium-sized fish and least for the smallest fish for both species. To capture a fish in a minnow trap, the fish must swim into the trap mouth and remain inside of the trap until it is retrieved. The lower capture efficiency of smaller fish was potentially due to three factors. First, small fish may move less frequently or for shorter distances than larger-bodied fish, reducing their chances of encountering the trap. Second, smaller-sized fish may have been able to escape the trap through the trap mesh. Lastly, small fish may not have perceived the trap mouth to be as great a barrier to escape through as did larger fish, and so, the trap mouth may have been less effective at retaining small fish that entered the trap. Of these, we believe it unlikely that a significant proportion of small-bodied fish were able to pass through the mesh because of its small size (3.2 mm). The relatively high density of our traps in Foskett Springs also suggests that fish did not have to swim great distances (generally <4 m) to encounter a trap. Furthermore, trap density was not related to trap capture probability. Rather, we hypothesize that the extent to which fish perceive a trap throat to be a barrier is relative to the body size of the fish. Under this hypothesis, small fish enter the trap and may not perceive the throat to be as great a barrier to escape as do larger fish, whereas larger fish may perceive the trap throat as a barrier to entering the trap. Thus, both small and large fish should have lower capture probabilities, which is consistent with our observations. Regardless of the mechanisms, the observed nonlinear relation between fish body size and trap capture probability has important implications for age-structure and demographic studies.
The model selection results indicated that there was little evidence that soak time, sample area, trap density, and water depth were individually related to trap capture probability. However, we did find strong evidence that trap capture probabilities varied with sample location. We believe that the differences in capture among locations were due to a combination of factors rather than any single factor. Capture probability was lowest in Foskett Springs tule marsh habitat and the main body of Borax Lake, and both of these habitats were the largest and had the lowest trap density of any other habitat. Tule marsh also had the least amount of open water and greatest amount of vegetation compared with the other habitats, which is consistent with the Dupuch et al. (2011) observation that trapping efficiency of Northern Redbelly Dace Chrosomus eos in vegetated mesocosms was less than half that in mesocosms without vegetation. Many of the predictors used in the model selection, such as trap density and soak time, also were constant or relatively constant at a location from one capture occasion to the next, so that predictor effects could not be separated from location effects. This suggests that future investigations of minnow trap efficiency should incorporate study designs that purposely vary these potential influences through time and among sample locations. This will provide the basis for identifying sample designs that optimize sampling effort.
We used simulation to identify the sample design that increased model accuracy and minimized the handling of individual fish. We used this optimal design to sample fish in Foskett Springs and detected and estimated the effects of multiple factors on fish capture and recapture probabilities. Unfortunately, personnel and resource limitations prevented us from using the optimal design at Borax Lake, and that may have affected our modeling results. We believe that simulation is a useful tool that should be employed in the planning stages of studies to optimize the expenditure of scarce management and research resources. Simulations of alternative sample designs can be based on published demographic and capture rates or best professional judgment and require little to no additional resources (e.g., an hour or two at the computer). It also can be used to evaluate tradeoffs in model accuracy or statistical power associated with varying levels of sampling effort (e.g., sample occasions) and number of marked fish. Simulations also provide fishery biologists with a means to evaluate whether proposed designs will meet study objectives quickly and efficiently. Further, it provides a more justifiable and ethical basis for the use of animals for research purposes. Indeed, recent guidelines on the use of fish recommend that studies should use the fewest number of fish needed for addressing research objectives (Use of Fish in Research Committee 2014). Given the availability of software for conducting simulations (e.g., MARK), we further believe that studies that attempt to estimate demographic parameters (e.g., population size, survival, occupancy) should evaluate alternative designs a priori and provide a justification for the design used.
There was strong evidence that the behavior of Foskett Speckled Dace changed after capture and marking. Surprisingly, the recapture probabilities increased after the first capture, presumably due to fish learning to enter the trap to access the bait. This “trap-happy” behavioral response resulted in biased low LP population estimates, because the recapture probability was greater than the initial capture probability. However, the “trap-happy” behavior decreased with time, which we believe may have been due to fish experiencing multiple captures and possibly avoiding the traps. The capture probability of Borax Lake Chub was greatest on the second occasion, but the evidence of a behavioral change was relatively weak. We believe that this weak evidence may have been a result of the sample design (i.e., three capture occasions rather than four) rather than the lack of a behavioral response. This highlights the importance of using the proper design and estimator to estimate capture probabilities and population size.
There is mounting evidence that variability in capture probabilities in space and time is the rule rather than the exception for active and passive fish sampling methods (Peterson and Paukert 2009 and references therein). Biologists may be tempted to ignore variability in capture probabilities in the mistaken belief that these estimates are conservative indices of population size. We have shown that failure to account for this variability can lead to systematic biases in population estimates of cienega-dwelling cyprinids by as much as 100%. This is similar to the 88% underestimated abundance that was attributed to heterogeneity in electrofishing capture probabilities of stream-dwelling salmonids (Peterson et al. 2004). It would be surprising if management decisions or research conclusions were unaffected by biases of this magnitude. The biased estimates of variance also would provide decision makers with a potentially risky, false sense of security that the biased estimates are precise. The population trend simulations also indicated that nonsystematic variability (i.e., random variation) can affect the ability to statistically detect important changes. For example, a relatively small amount of year-to-year variation in capture probabilities of 10% substantially affected the ability to detect even an annual 20% decrease in population over 5 years. This lack of power could lead to poor decision making and, potentially, catastrophic consequences for at-risk taxa. Therefore, we strongly recommend that fishery biologists and managers evaluate the performance of their sample methods and designs prior to adopting their use for research or management.
Overcoming the effects of variability in capture probability on assessments of the status and trends in fish populations requires the use of both the proper sample design and estimator. This does not imply that fishery managers must expend significantly more resources when sampling or monitoring populations. Sample designs, such as double sampling (Williams et al. 2002; Peterson and Paukert 2009), have been developed for use in situations where sampling resources are limited and unbiased or minimally biased estimates are needed. Double sampling requires sampling a small subset of sample sites using effort-intensive methods (e.g., capture–recapture) and a lower-effort method. The remaining sites are sampled with the lower-effort method. Using the data from the intensively sampled sites, the relationship between catch with the lower-effort method and the population size can be modeled and used to adjust data from the remaining sites. Alternatively, unbiased population estimates can be obtained from sampling data by dividing the number of fish captured by the capture probability (Thompson and Seber 1994). Fish capture probability also has been modeled for a number of fish sampling methods and protocols, and most of these models are available in published reports and journal articles. Peterson and Paukert (2009) included information from more than 20 such studies. All of these techniques also can be incorporated into a variety of sample designs, such as simple random sampling, rotating panels, and adaptive cluster sampling. For example, we developed a rotating panel design for monitoring at Foskett Springs where one habitat is sampled each year using three or four occasions and mark–recapture, and the remaining habitats are sampled on one or two occasions without marking fish. We then incorporate the new capture–recapture data with data collected in previous years into Bayesian hierarchical models for estimating capture probabilities and fish abundance at all habitats. The approach allows us to obtain unbiased estimates with minimal effort. The optimal sample design, however, depends on the objectives and resources available to the researcher or manager. Therefore, we suggest that interested biologists consult the literature cited or take advantage of workshops or continuing education courses to develop an understanding of these flexible approaches.
ACKNOWLEDGMENTS
Thanks are extended to J. Booth, J. D. Jones, J. Leal, and J. Saenz for assistance with the field work and B. Bangs for GIS assistance. This work was funded by the U.S. Fish and Wildlife Service, Cooperative Agreement F12AC01064. The manuscript was improved with suggestions from M. Colvin, S. Bonar, C. Shea, M. Falcy, D. Jepsen, and anonymous reviewers. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. The Oregon Cooperative Fish and Wildlife Research Unit is jointly sponsored by the U.S. Geological Survey, the U.S. Fish and Wildlife Service, the Oregon Department of Fish and Wildlife, Oregon State University, and the Wildlife Management Institute.




