Raciation and speciation in house mice from the Alps: the role of chromosomes
Abstract
There are at least 24 different karyotypic races of house mouse in the central Alps, each characterized by a different complement of ancestral acrocentric and derived metacentric chromosomes; altogether 55 different metacentric chromosomes have been described from the region. We argue that this chromosome variation largely arose in situ. If these races were to make contact, in most cases they would produce F1 hybrids with substantial infertility (sometimes complete sterility), due to nondisjunction and germ cell death associated with the formation of long-chain and/or ring configurations at meiosis. We present fertility estimates to confirm this for two particular hybrid types, one of which demonstrates male-limited sterility (in accordance with Haldane’s Rule). As well as a model for speciation in allopatry, the Alpine mouse populations are of interest with regards speciation in parapatry: we discuss a possible reinforcement event. Raciation of house mice appears to have happened on numerous occasions within the central Alps. To investigate one possible source of new karyotypic races, we use a two-dimensional stepping stone model to examine the generation of recombinant races within chromosomal hybrid zones. Using field-derived ecological data and laboratory-derived fertility estimates, we show that hybrid karyotypic races can be generated at a reasonable frequency in simulations. Our model complements others developed for flowering plants that also emphasize the potential of chromosomal hybrid zones in generating new stable karyotypic forms.
Introduction
The house mouse (Mus musculus domesticus) has a standard karyotype consisting of 40 acrocentric (one-armed) chromosomes. In 1969, Alfred Gropp and co-workers discovered a population of mice with 26 chromosomes in the Alpine valley of Poschiavo, and showed that this reduced diploid number had come about by Robertsonian (Rb) fusions, the joining together of pairs of acrocentrics at their centromeres to form metacentric (two-armed) chromosomes (Gropp et al. 1969). Subsequent work has demonstrated that Poschiavo, on the Swiss–Italian border, is within an area covering much of the central Alps and its environs (south Germany, east Switzerland, northeast Italy) which is characterized by numerous distinct karyotypic races of house mouse, each with a different set of metacentrics (Gropp et al. 1982b; Adolph & Klein 1983; Winking et al. 1988; Belkhir et al. 1991; Hübner 1992; Hauffe & Searle 1993; Garagna et al. 1997). This extensive chromosomal variation, coupled with demonstrations of sterility associated with chromosomal heterozygosity, prompted an interest in the system as a model of the thesis developed by White (1978) and King (1993) that chromosomal rearrangements are important in promoting speciation in mammals, insects and other organisms. Although the ideas of White and King are not in favour with many in the field (e.g. Coyne 1993), in this paper we hope to demonstrate that the system of karyotypic races of the house mouse in the Alps still has plenty to offer to our understanding of speciation. As well as a survey of our current state of knowledge of the system based on both published and new data, we will present new simulations relating to an early phase of the speciation process: race-formation. We believe that the Alpine mouse system can provide rich insights into this crucial aspect of the generation of species.
High rate of accumulation of chromosomal rearrangements
Over an area of more than 40 000 km2 extending from southern Germany to northern Italy, there are at least 24 distinct karyotypic races, each defined by a particular set of metacentrics in a homozygous state and usually occupying a continuous geographical area (R Hübner et al. unpublished data). Fifty-five different metacentrics are known from this region (Table 1), with various combinations of these chromosomes defining the different races. Although the 40-chromosome all-acrocentric karyotype is undoubtedly predominant in Mus musculus domesticus, metacentric races are found elsewhere, both on the islands and the mainland of western and southern Europe and northern Africa (Nachman & Searle 1995), but always as single races or small clusters of races over smaller (usually much smaller) areas than the system of karyotypic races in the central Alps.
| 1.3 | 2.4 | 3.4 | 4.6 | 5.6 | 6.7 | 7.8 | 8.9 | 9.10 | 10.11 | 11.13 | 13.14 | 14.17 | 16.17 |
| 1.5 | 2.5 | 3.6 | 4.10 | 5.7 | 6.10 | 7.15 | 8.10 | 9.13 | 10.12 | 11.16 | 13.16 | ||
| 1.6 | 2.8 | 3.8 | 4.12 | 5.10 | 6.11 | 7.18 | 8.11 | 9.14 | 10.13 | 11.18 | |||
| 1.10 | 2.12 | 3.17 | 5.13 | 6.15 | 8.12 | 9.16 | 10.14 | ||||||
| 1.18 | 2.14 | 5.14 | 6.17 | 8.15 | 10.15 | ||||||||
| 5.15 | 8.16 | 10.17 | |||||||||||
| 8.17 |
- Metacentrics in format x.y denoting the ancestral acrocentrics (among autosomes 1–18) that are combined together at their centromeres.
Archaeological data indicate that the central Alps were colonized by house mice within the last 5000 years (Capanna 1982; Auffray et al. 1990). It is possible that some of the metacentrics arrived with the mice colonizing the region, and recent molecular data suggest that metacentric 5.15 may have colonized northern Italy from central Italy (Riginos & Nachman 1999). However, on several grounds it can be argued that the large majority of metacentrics in the central Alps arose in situ.
First, many of the metacentrics in the central Alps have not been found elsewhere in the distribution of the house mouse. Where there is sharing of metacentrics with karyotypic races located in other regions, convergent evolution is often considerably more likely than common ancestry (e.g. 4.10 has been found in the central Alps and northern Scotland but nowhere in the large intervening distance) and has been demonstrated to be the case for the sharing of 5.15 between Spain and Italy (Riginos & Nachman 1999).
Second, the continuous region occupied by metacentric mice in the central Alps is surrounded on all sides by areas where the standard karyotype predominates (Gropp et al. 1982b; Klein et al. 1987; R. Hübner et al. unpublished data). There are no tracks of colonization by karyotypic races, as observed, for instance, in the common shrew (Searle 1984; Bulatova et al. 2000). Given that the house mouse is a commensal, some metacentrics may have arrived with long-distance stowaways (Baker 1994), but this surely cannot explain most of the metacentrics observed.
Third, it is very difficult to see how the complex variety of karyotypic races with different sets of metacentrics, as exemplified by those in northern Italy (Table 2), could have been imported. Such a varied set of races in a relatively small geographical area is indicative of much local fixation of new chromosomal rearrangements. There are some metacentrics that are shared between races, but these can readily be considered early formed rearrangements, or metacentrics involved in hybrid race formation (see below).
| Karyotypic race | Race code | 2n | Race-specific metacentrics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Poschiavo | POS | 26 | 1.3 | 4.6 | 5.15 | 8.12 | 9.14 | 11.13 | 16.17 | |||||
| Mid-Valtellina | M-V | 24 | 1.3 | 4.6 | 5.15 | 7.18 | 8.12 | 9.14 | 11.13 | 16.17 | ||||
| Upper Valtellina | U-V | 24 | 1.3 | 2.8 | 4.6 | 5.15 | 9.14 | 10.12 | 11.13 | 16.17 | ||||
| Lower Valtellina | L-V | 22 | 1.3 | 2.8 | 4.6 | 5.15 | 7.18 | 9.14 | 10.12 | 11.13 | 16.17 | |||
| Cremona | CRE | 22 | 1.6 | 2.8 | 3.4 | 5.15 | 7.18 | 9.14 | 10.12 | 11.13 | 16.17 | |||
| Binasco | BIN | 24 | 2.8 | 3.4 | 5.15 | 6.7 | 9.14 | 10.12 | 11.13 | 16.17 | ||||
| Seveso | SEV | 24 | 2.12 | 3.4 | 5.15 | 6.7 | 8.11 | 9.14 | 10.13 | 16.17 | ||||
| Gallarate | GAL | 24 | 2.4 | 3.6 | 5.15 | 7.8 | 9.14 | 10.12 | 11.13 | 16.17 | ||||
| Luino | LUI | 24 | 2.4 | 3.8 | 5.13 | 6.7 | 9.14 | 10.12 | 11.18 | 16.17 | ||||
| Chiavenna | CHI | 34 | 4.12 | 10.11 | 16.17 | |||||||||
- For each race, those autosomes not listed as present in metacentrics occur instead in the ancestral acrocentric state. Each of these races occupies a discrete area within the north Italian system of metacentric races (in particular, see the maps in Capanna et al. 1985 and Hauffe & Searle 1993). The ‘Gallarate’ and ‘Binasco’ races have also been referred to as the ‘Milano I’ and ‘Milano II’ races, respectively.
Finally, in northern Italy, standard race (40-chromosome) mice are genetically very similar to metacentric race mice (Nei’s D = 0.01 based on studies with 34 allozyme loci), consistent with the metacentric forms arizing in situ from local all-acrocentric mice (Britton-Davidian et al. 1989).
Therefore, a large number of metacentrics have accumulated in a short period of time in the central Alps. A high rate of chromosomal mutation is almost certainly part of the explanation for this. In laboratory mice, Rb fusions show a high mutation rate (10−2–10−3) in lineages that already have such fusions (Nachman & Searle 1995). Because of loss of most centromeric DNA and all proximal telomeric sequences in those chromosomes involved in Rb fusion (Garagna et al. 1995), back-mutations generating the acrocentric condition (Rb fissions) are unlikely in the house mouse. Hence, once the first Rb fusions become fixed, there may be an evolutionary ratchet leading to an ever increasing number of metacentrics within karyotypic races of house mouse, consistent with the low chromosome numbers of many races (Searle et al. 1990).
Although metacentrics are unlikely to evolve into acrocentrics, they may swap arms with other metacentrics or acrocentrics, generating new types of metacentrics, a mutation known as a whole-arm reciprocal translocation (WART; Searle et al. 1990; Hauffe & Piálek 1997). In this way, even a karyotypic race with 22 chromosomes (nine pairs of metacentrics) may continue to evolve its karyotype (other rearrangements such as ‘normal’ reciprocal translocations, inversions, etc., are not common in wild house mice). There are data from both the laboratory and field demonstrating the occurrence of WARTs in house mice (Crocker & Cattanach 1981; Winking 1986; Capanna & Redi 1995), although nothing is known about the rate of occurrence of these rearrangements. As an example, Hauffe & Piálek (1997) suggested that the metacentrics 2.4 and 3.8 of the Luino race may have been generated by a WART from metacentrics 2.8 and 3.4 of the Binasco race (see Table 2).
Newly arisen Rb fusions occur in the heterozygous state. Although heterozygotes for some types of chromosomal rearrangement may suffer severe meiotic aberrations and reduced fertility, which can hinder the fixation of the rearrangement, this is not the case for single Rb fusions in the house mouse (Britton-Davidian et al. 1990; Wallace et al. 1992). So stepwise fixation of Rb fusions (Capanna 1982) is not particularly difficult to envisage, especially given that genetic drift in small populations has been well-demonstrated in the house mouse (Berry & Peters 1977; Fraguedakis-Tsolis et al. 1997). Meiotic drive may also have a role in fixation of Rb fusions (see Wyttenbach et al. 1998).
There may be more difficulties associated with fixation of WARTs. While heterozygotes for single Rb fusions form a CIII configuration (a chain-of-three chromosomes) at meiosis I, heterozygotes for a WART may form either a CIV or a RIV (a ring-of-four chromosomes) at meiosis (depending on the type of WART mutation, Hauffe & Piálek 1997). Chain configurations longer than CIII are associated with substantial anaphase I nondisjunction (which leads to chromosomally unbalanced gametes and zygotes) and germ cell death (which even for CIV configurations may lead to male sterility) (Gropp et al. 1982a; Searle 1993). On the other hand, the fertility of heterozygotes with RIV configurations may not be much reduced relative to CIII heterozygotes, although this has not been measured in the house mouse (but see Narain & Fredga 1997).
Reduced fertility of chromosomal hybrids
Because the metacentric races of the house mouse accumulate different Rb fusions and WARTs, the hybrids they generate generally have even more elaborate meiotic configurations than those associated with single Rb fusions or WARTs. Those configurations expected on crosses between the karyotypic races of northern Italy are shown in Table 3.
| POS | M-V | U-V | L-V | CRE | BIN | SEV | GAL | LUI | |
|---|---|---|---|---|---|---|---|---|---|
| M-V | CIII | ||||||||
| U-V | CV | CV,CIII | |||||||
| L-V | CV,CIII | CV | CIII | ||||||
| CRE | CV,CIII,RIV | CV,RIV | CIII,RIV | RIV | |||||
| BIN | CVI,CV | CVII,CV | CVI | CVII | CV | ||||
| SEV | CVII,CVI | CVII,CVII | CVI,RVI | CVII,RVI | CV,RVI | RVI | |||
| GAL | CVI,CV | CVI,CVI | CVIII | CIX | CIX | RVI | RX | ||
| LUI | CVI,CVI,CV | CX,CVI | CVIII,CVI | CXIII | CIX,RIV | CVI,RIV | CXII | CVI,RIV | |
| CHI | CV,CIV | CV,CIV | CVII | CVII | CVII | CVII | CV,CV | CVII | CVII |
- CIII,RIV, chain-of-three and ring-of-four configuration expected; Races: POS, Poschiavo; M-V, Mid-Valtellina; U-V, Upper Valtellina; L-V, Lower Valtellina; CRE, Cremona; BIN, Binasco; SEV, Seveso; GAL, Gallarate; LUI, Luino; CHI, Chiavenna. At meiosis, homologous chromosome segments pair. Therefore, if the same ancestral acrocentric is in two different conformations in the hybridizing races (as an acrocentric in one and as part of a metacentric in another or as part of two different metacentrics in the two races), then a heterozygous configuration is expected in the meiosis of the F1 hybrid. For example: The Poschiavo race differs from the Mid-Valtellina race by presence of acrocentrics 7 and 18 in the former and metacentric 7.18 in the latter, so a CIII configuration (7, 7.18, 18) is produced in the meiosis of the F1 hybrid. The Poschiavo race has chromosomes 2, 8.12, 10 and the Upper Valtellina race has 2.8, 10.12, so the F1 hybrid produces a CV configuration (2, 2.8, 8.12, 12.10, 10). Finally, the Poschiavo race differs from the Lower Valtellina race by all these chromosomes, and so the F1 hybrid produces both a CV and a CIII configuration. (Note that the chromosomes are listed in such a way to emphasize their homology, in the example above.)
We have examined the fertility of two of the chromosomally most simple hybrids that can be generated by crossing northern Italian mice, i.e. individuals that are expected to produce a CV configuration at meiosis. We have quantified germ cell death in F1(BIN × CRE) and F1(U-V × POS) mice by the methods of Hauffe & Searle (1998), adding to previous information for these hybrids (Table 4). These combined data demonstrate well that CV heterozygotes suffer substantial infertility through enhanced germ cell death and nondisjunction. They also show clearly that the degree of infertility varies according to the races that are being crossed. Thus, male F1(BIN × CRE) hybrids are completely sterile due to massive germ cell death while although the germ cell numbers in male F1(U-V × POS) hybrids are reduced relative to homozygotes, this reduction may not be sufficient to impair fitness (Hauffe & Searle 1998). It is generally accepted that sperm counts need to be less than 10% of normal values to cause complete sterility (Searle & Beechey 1974).
| Karyotypic form | M/F | Germ cell death | Nondisjunction | References |
|---|---|---|---|---|
| Homozygotes | M | 24% (n = 12 mice) | 0% (n = 600 cells) | Hauffe & Searle (1998) |
| F | 0% (n = 2 mice) | — | Garagna et al. (1990) | |
| F | —a | 13% (n = 124 cells) | Hauffe & Searle (1998) | |
| F1(BIN × CRE) | M | 98% (n = 3 mice) | —b | Present study |
| M | ≈ 100% (n = 1 + mice)c | —b | Gropp et al. (1982a) | |
| F | 54% (n = 2 mice) | — | Garagna et al. (1990) | |
| F1(U-V × POS) | M | 70% (n = 2 mice) | — | Present study |
| M | 56% (n = 3 mice) | 19% (n = 108 cells) | Hauffe & Searle (1998) | |
| F | —a | 38% (n = 48 cells) | Hauffe & Searle (1998) |
- BIN, CRE, U-V and POS, respectively, refer to the Binasco, Cremona, Upper Valtellina and Poschiavo races of northern Italy. The homozygotes being compared with the F1 hybrids represent pure race individuals. The germ cell death estimates for males represent a comparison with the theoretical expectation of one spermatocyte : four spermatids (see Hauffe & Searle 1998). For females, the germ cell numbers in homozygotes aged 20 days (arbitrarily recorded as 0% germ cell death), were compared with those for the hybrids. For germ cell death a single germ cell estimate was obtained per mouse; for anaphase I nondisjunction, chromosome counts were made on individual cells and pooled from several mice. aAlthough oocyte numbers were not fully quantified, the numbers of growing follicles were recorded in 12 homozygotes and four F1(U-V × POS) hybrids, and did not differ significantly. There is clearly substantial germ cell survival in F1(U-V × POS) females, though whether of greater or lower magnitude than that seen in F1(BIN × CRE) females is unknown. bThese estimates would have been meaningless, given the insufficient number of sperm for fertilization. cGropp et al. (1982a) show a histological section of one of the testes of a sterile hybrid male with complete spermatogenic breakdown, but provide no further details.
In total, 38 out of 45 types of F1 hybrid that could be generated by crossing karyotypic races of house mouse in northern Italy produce a meiotic chain configuration of at least five elements (Table 3). Therefore, it is clear that substantial hybrid unfitness is the normal expectation if races in northern Italy come into contact. In those cases where there is a very long configuration expected at meiosis [e.g. F1(L-V × LUI): CXIII] or where there are several moderately long configurations [e.g. F1(M-V × SEV): CVII + CVII], complete sterility of both sexes may be expected. In general, the more meiotic configurations and the greater their length, the greater the infertility (Gropp et al. 1982a; Searle 1993). However, for the North Italian system there are few direct data on fertility of hybrids of metacentric races beyond those in Table 4.
Although hybrids with very long meiotic configurations are expected to be sterile in both sexes through enhanced germ cell death and nondisjunction, among hybrids with shorter configurations it is only males that are likely to be sterile. This is an example of Haldane’s Rule, that if inviability or sterility is limited to one sex, it will be the heterogametic sex (the male in the case of mammals) that will be affected (Haldane 1922; see Forejt 1996). In particular, it is heterozygotes with relatively short meiotic chain configurations (CIV or somewhat longer), rather than those with meiotic rings, that may demonstrate male-limited sterility due to massive germ cell death (Gropp et al. 1982a). The F1(BIN × CRE) hybrids are a good example (Table 4).
Chain configurations are associated with greater germ cell death than ring configurations in both males and females (Gropp et al. 1982a; Garagna et al. 1990; Searle 1993). However, spermatocytes appear to be more sensitive to the presence of a meiotic chain than oocytes. Forejt (1996) has suggested that this is because the meiotic chain has a tendency to interact with the XY bivalent at early stages of meiosis, disrupting the transcriptionally inactive state of that configuration, thereby perturbing cell physiology and promoting cell death. Thus, male-limited sterility of hybrids between karyotypic races of house mice appears to have a ‘chromosomal’ basis (Forsdyke 2000) rather than the more usual ‘genic’ explanations of Haldane’s Rule (e.g. Turelli & Orr 2000).
Speciation
There are instances where the metacentric races of house mice in the central Alps appear to have become reproductively isolated from each other. First, we will consider reproductive isolation in allopatry. Thus, among the northern Italian races, we have already described cases where two races have built up such distinctive sets of metacentrics that they would produce sterile hybrids if they were to come into contact (e.g. the Lower Valtellina and Luino races). This can be viewed as a stepwise accumulation of metacentrics by Rb fusions and WARTs in the two races, as envisaged in the speciation models of Capanna (1982) and Baker & Bickham (1986). However, it is important to emphasize that races that produce hybrids with CIV, RIV or longer configurations are not necessarily reproductively isolated, even though this is often implied in the literature. As is clear from the previous section, studies on both male and female hybrids are essential to demonstrate that races in allopatry have acquired complete reproductive isolation.
If metacentric races come into contact which produce infertile but not completely sterile hybrids, then there is the possibility that reproductive isolation may evolve in parapatry, by reinforcement (Dobzhansky 1970). We have suggested that reinforcement occurred after the Upper Valtellina and Poschiavo races came into contact in the village of Migiondo in the Italian Alps (Hauffe & Searle 1992). In the late 1970s and early 1980s it was shown that the Upper Valtellina and Poschiavo races were present without hybrids in Migiondo (90 Poschiavo mice: 60 Upper Valtellina mice scored), even though, as we showed later, the two races were present with hybrids in other villages in the same valley (Capanna & Corti 1982; Hauffe & Searle 1992, 1993). In captivity, the Upper Valtellina and Poschiavo races produce hybrids with a meiotic CV configuration and reduced fitness (Table 4). It is known that in these hybrids there is reduced crossing-over close to the centromere for at least one of the chromosomes involved in the CV configuration: chromosome 10 (R. G. Ward et al. unpublished data). If a gene located close to the centromere on chromosome 10 generates a product x that can be detected by other mice and can influence their mate choice, and if different alleles for that gene were present in the Upper Valtellina and Poschiavo mice that colonized Migiondo, this could have created the opportunity for assortative mating to develop. Under these circumstances a particular version of product x would almost always have been associated with the Upper Valtellina race and a different version associated with the Poschiavo race. Homozygotes that mated with other individuals with only the same version of product x would have had more grand-progeny than other individuals (because the latter would produce CV hybrids with reduced fecundity). Hence, there would have been a considerable selective advantage for homozygotes to mate assortatively, and any tendency to do so would have been favoured. It is known that house mice may mate assortatively in response to particular gene products, e.g. salivary androgen-binding protein (Laukaitis et al. 1997).
Reinforcement in this case could therefore have followed the ‘discrimination enhancement model’ of Kelly & Noor (1996), with selection favouring any modifier that increases the ability of mice to discriminate as mating partners those individuals generating the same version of product x. Kelly & Noor (1996) provide theoretical support for this model.
Migiondo is separated by very strong geographical barriers from other villages, and this may help to explain why assortative mating developed there but has not been detected in other villages where the Upper Valtellina and Poschiavo races occur together (we plan to test for partial assortative mating in those other villages). In effect, the Migiondo population was closed, allowing perfect circumstances for assortative mating to evolve without the problems of unselected alleles migrating in from elsewhere (Hauffe & Searle 1992). Unfortunately, a small closed population is also vulnerable to rapid demographic change; and during the 1980s one of the reproductively isolated forms in Migiondo (the Upper Valtellina race) became extinct (Hauffe & Searle 1992).
These examples of reproductive isolation illustrate the value of the metacentric races of house mice in the central Alps for the study of speciation. It should be emphasized that this is a model system for the study of the processes involved in allopatric and parapatric speciation, not a system where species, as defined by the Biological Species Concept (Mayr 1963), are actually generated. Although the metacentric races may, in some cases, be reproductively isolated from each other, there is no evidence that any of them are reproductively isolated from the standard 40-chromosome race (see Searle 1993). Therefore, there is still the potential for gene flow between all the metacentric races, via the standard race (Searle 1998).
Raciation
We have already discussed the fixation of new Rb fusions or WARTs within populations of the house mouse in the central Alps. As we have seen, these populations can be defined as karyotypic races (see Hausser et al. 1994) and they may be extremely localized (e.g. the Seveso race is known from only one village: Garagna et al. 1997) or be present over a substantial area (e.g. the Lower Valtellina race covers an area of more than 1000 km2: Capanna et al. 1985). Karyotypic races in the house mouse are dynamic, in that they may accumulate further chromosomal rearrangements (perhaps over only part of their range) thereby evolving into or generating new races, and they may expand, contract, or move their ranges (for example in response to changes in the distribution of human settlements). They may also come into contact with each other. We have discussed how this may, in certain circumstances, lead to the two races becoming reproductively isolated. In the remainder of the paper we will consider another possible outcome from the contact of races: the formation of new recombinant races that have a complement of metacentrics derived from both the parental races.
We have used the term ‘zonal raciation’ for the formation of new races in the region of hybridization (the ‘hybrid zone’) (Searle 1991, 1993; Hauffe & Piálek 1997). In the context of the metacentric races of the house mouse in the central Alps, a new hybrid karyotypic race can be generated if the two parental races making contact can produce at least some fertile F1 hybrids and if those hybrids have at least two heterozygous configurations at meiosis I. Under those circumstances a new homozygous form may be produced within the hybrid zone and, given opportunities to colonize new areas, it may expand its range like any other race.
Considering the F1 hybrids that would be produced on contact of each pairwise combination of karyotypic races in northern Italy (Table 3), 23 out of 45 hybrid types are characterized by at least two heterozygous meiotic configurations. Therefore, about half the possible interracial contacts in northern Italy have the possibility of zonal raciation. Zonal raciation could have occurred at various stages in the formation of the suite of races that are currently present in northern Italy. It is particularly interesting that, as in the case of WARTs, zonal raciation allows forms with many metacentric chromosomes and low diploid numbers to generate new races. In a phylogenetic analysis of the races in northern Italy and southern Switzerland, we found that both WARTs and zonal raciation were important in generating the shortest evolutionary trees (Hauffe & Piálek 1997). The Cremona race (2n = 22) and Poschiavo race (2n = 26) could have, for instance, generated the Lower Valtellina Race (2n = 22) by zonal raciation. The F1(Cremona × Poschiavo) hybrid has the following heterozygous configurations (with chromosomes listed in a way to illustrate their homologies, and Cremona chromosomes shown in bold): CV (2, 2.8, 8.12, 12.10, 10), CIII (7, 7.18, 18), RIV (1.3, 3.4, 4.6, 6.1). Because the different heterozygous configurations can segregate independently, a gamete could be produced which has the following Poschiavo chromosomes: 1.3, 4.6 and the following Cremona chromosomes: 2.8, 10.12, 7.18. On fertilization with another similar gamete, a Lower Valtellina individual would be generated.
Clearly, it is simple to see how new homozygous individuals could be formed on hybridization between karyotypic races, but it is important to determine the conditions under which the new homozygous form could increase in frequency and establish a new race. Obviously, some sort of global advantage of the new homozygous combination would allow it to increase, but as yet there have been no documented cases where one metacentric combination in the house mouse has been shown to have an advantage over another. Another possibility is that a hybrid homozygous form could increase in frequency by genetic drift. This is simplest to imagine in a situation where there are few individuals of the parental races, such as may occur when long distance migrants first penetrate an area (Nichols & Hewitt 1994). Finally, there may be selective advantage of the new homozygous form in the area of hybridization, relating to the types of heterozygotes it generates on crosses with other homozygous forms. Thus, while Poschiavo and Cremona individuals generate F1 hybrids with CV + CIII + RIV configurations, Lower Valtellina individuals produce CV + CIII heterozygotes if they mate with Poschiavo individuals and RIV heterozygotes if they mate with Cremona individuals, but they cannot produce the most highly heterozygous (and therefore most unfit) CV + CIII + RIV hybrids on crosses with the parental races. It is this reduced tendency to produce the most highly heterozygous (and unfit) types of hybrid, that we have emphasized in promoting the concept of zonal raciation in the contact between karyotypic races (Searle 1993; Hauffe & Piálek 1997).
In a karyotypic study of house mice in Upper Valtellina in the Italian Alps, we found three races, the Lower Valtellina (L-V), Poschiavo (POS) and Mid-Valtellina (M-V), the first two of which could have generated the third by zonal raciation (Hauffe & Searle 1993). We have chosen this system to model the process of zonal raciation, because we have a clear scenario as to how the hybrid race was formed (Hauffe & Searle 1993), information on the ecology of mice in the area concerned (Hauffe et al. 2000; H. C. Hauffe unpublished data) and data on the unfitnesses associated with chromosomal heterozygotes produced on hybridization of the different forms (Hauffe & Searle 1998).
Simulation studies of zonal raciation
We propose that the hybrid M-V race was formed by zonal raciation from the L-V and POS races. Specifically, the L-V and POS races are believed to have colonized the middle section of Upper Valtellina after its recovery from a flood in 1807, and it is following that colonization that we believe that the M-V race was generated (Hauffe & Searle 1993). Through simulations, we aimed to determine the conditions under which the recombinant race could have become established over the ≈200 years between the putative colonization event and our discovery of the M-V race in this area (Hauffe & Searle 1993).
The L-V and POS races differ by metacentrics 2.8 and 10.12 in the former and metacentric 8.12 and acrocentrics 2 and 10 in the latter (Table 2). In hybrids a CV meiotic configuration is produced (Table 3). The segregants from this CV complex are also 2.8 and 10.12 on the one hand, and 8.12, 2 and 10 on the other, and these two possible chromosome combinations are designated ‘alleles’ A and a, respectively, in the simulation model we developed. Hybrids between the L-V and POS races also produce a CIII meiotic configuration, because the L-V race is characterized by metacentric 7.18 which occurs as acrocentrics 7 and 18 in the POS race. These two chromosome types were designated alleles B and b in the model, respectively. Therefore, the L-V race can be considered an AABB homozygote, the POS race an aabb homozygote and the M-V race an aaBB homozygote.
The two-dimensional stepping-stone model on which we based our simulations shares the same philosophy as that of Piálek & Barton (1997) and derives from the hybrid zone theory developed by Nick Barton over many years (e.g. Barton & Hewitt 1985; Barton & Gale 1993). It differs in that there are two loci that can generate 10 different genotypes (AABB, AABb, AaBB, AaBb-cis, Aabb, AabB-trans, AAbb, aaBB, aaBb, aabb). A two dimensional array of 21 × 7 demes was divided into three equal parts of 7 × 7 demes. At the start of each simulation, the L-V and POS races were placed in the outer thirds and the inner third was treated as a patch available for colonization by the two races (hereafter, the ‘empty patch model’). The inner third was considered to have geographical barriers separating it from the outer thirds. Thus, the L-V, empty and POS populations can be considered as existing within a linear array of villages, each separated by a strong but not totally impermeable geographical barrier. For the purposes of the simulation, this array structure was a simple way to generate the colonization event and to allow further racial interactions by occasional migration from neighbouring villages. It reflects, in a general sense, the situation in Upper Valtellina, in that villages are distributed linearly along the valley and there is much more movement within villages than between villages (Hauffe & Searle 1993). However, the precise situation in Upper Valtellina may have been more complex in the formation and maintenance of the M-V race. The M-V race currently predominates in several villages rather than just one and in addition to the L-V, POS and M-V races there are two other races currently present in Upper Valtellina (the Upper Valtellina and standard races), which may have been present in the valley for a considerable time (Hauffe & Searle 1993).
The model required particular parameters for deme size (N = 8 with growth each generation to 12 before migration, following the logistic equation), migration out of demes (m = 0.25) and barrier strength (B = 15). These demographic parameters, together with the particular array structure, were based on mark–release–recapture studies of house mice in Upper Valtellina (Hauffe et al. 2000; H. C. Hauffe unpublished data). In the simulations, generations were considered discrete (a simplification for the house mouse: Pelikán 1981) and the individuals within a deme were generated randomly from the gametes produced by the previous generation. The number of migrants out of each deme each generation was taken randomly from the binomial distribution with parameters m and N. Each emigrant had the same probability (P = 0.25) of entering one of four adjacent demes unless there was a barrier in the direction of movement. In that case the probability of entering the neighbouring deme was decreased by the strength of the barrier. A random, frequency-dependent choice of parental genotypes followed migration. Reproduction of individuals was decided deterministically such that heterozygous individuals had their output reduced according to a fitness table (Table 5). There is an expectation that the presence of heterozygous configurations at meiosis leads to meiotic aberrations and reduced fertility (see above).
| BB | Bb | bb | |
|---|---|---|---|
| AA | 1 | 1 –s2 | 1 |
| Aa | 1 –s1 | 1 – (s1 + s2)* | 1 –s1 |
| aa | 1 | 1 –s2 | 1 |
- The ‘alleles’ of the Lower Valtellina race are 2.8, 10.12 (A) and 7.18 (B) and those of the Poschiavo race are 2, 8.12, 10 (a) and 7, 18 (b). s1 and s2 represent selection coefficients.
- * This is the equation for the additive model; for the epistatic model the term (s1 + s2) is square-rooted.
The system as described is subject to substantial random drift due to small array size and deme size. Hence, one may assume that, given sufficient time, it would reach a stable equilibrium characterized by fixation of a single genotype (when the system is dominated by random drift rather than selection) or two (or more) genotypes (depending on interactions between random drift, selection and the barrier). It should be mentioned at this point that we did not look for such stable equilibria by allowing indefinite run times until a stable state was reached. Instead, we tried to find out: (i) whether the time estimated since the flooding event was sufficient to allow a novel recombinant race to arise and establish itself; and (ii) the extent to which the establishment of the new race was affected by selection at the two loci. The simulations were terminated when one of the recombinant races AAbb or aaBB reached a frequency of 30% over the whole array, or after 400 generations, which roughly corresponds to the number of generations since the putative colonization event (based on unpublished data of H. C. Hauffe). For each set of conditions, the data that we present are a summary of 100 separate runs. The probability of establishment of a new race, P, was calculated as the number of runs where a new recombinant race was established divided by the total number of runs for the corresponding set of conditions.
To infer the effect of selection, we did not vary demographic parameters in the simulations but we did vary the magnitude of the selection coefficients s1 and s2 (see Table 5). These coefficients were associated with production of a CV configuration and a CIII configuration, respectively. For our first estimate of these coefficients, we averaged all available data on anaphase I nondisjunction of CV and CIII heterozygotes derived from Upper Valtellina (Hauffe & Searle 1998). We assumed that there was no reduced fertility associated with germ cell death. There is enhanced germ cell death associated with the CV heterozygotes, but this was not so large for the specific chromosomes in the chain-of-five that would be produced in F1(L-V × POS) hybrids [which are the same as in F1(U-V × POS) hybrids (Table 4)] as to decrease fitness much below the level caused by nondisjunction (see above). The nondisjunction estimates gave us s1 = 0.221 and s2 = 0.186.
Although nondisjunction estimates provide a useful indication of the relative infertility of different types of chromosomal heterozygote, they may overestimate the extent of unfitness, because mice standardly produce more embryos than are actually born and weaned (Pelikán 1981). Therefore, a moderately increased number of inviable embryos may only lead to a small reduction in final litter size (and therefore fitness) (see Searle 1993; Hauffe & Searle 1998). Consequently, we carried out simulations with selection coefficients a quarter and a tenth of the first values (i.e. s1 = 0.055, s2 = 0.046 and s1 = 0.022, s2 = 0.019, respectively).
We also carried out simulations with a greater differential between s1 and s2. The nondisjunction values that Hauffe & Searle (1998) obtained for CIII heterozygotes for individuals derived from Upper Valtellina were surprisingly high relative to previous studies (e.g. Wallace et al. 1992). So we carried out a series of six simulations with s2 either a quarter or a tenth of s1 (with s1 = 0.221, 0.055 or 0.022). It has even been suggested that CIII heterozygotes should be viewed as selectively neutral (e.g. Bauchau et al. 1990), so we did three further simulations with s1 = 0.221, 0.055 or 0.022 and s2 = 0. We also carried out a simulation with s1 = s2 = 0.
For all selective regimes, we ran simulations according to an additive model, i.e. CV + CIII heterozygotes have the sum of unfitnesses of CV heterozygotes and CIII heterozygotes. We also ran the same selective regimes with an epistatic model, i.e. where the CV + CIII heterozygotes have an unfitness greater than the additive expectation (see Table 5).
The results of these simulations are summarized in 1, 2. The general picture seen was that one race or other crossed the barrier first and expanded into the empty area before there could be substantial penetration by the other race. After a few generations, the race became established in the empty patch and then the individual result depended on the selection regime used in the particular run. We obtained four different types of result. Firstly, if both selection coefficients were small, both races tended to spread easily across the barriers and interbred widely with one another producing a large region with high introgression (Fig. 1a). Secondly, when there was a large difference in the magnitude of s1 (high value) and s2 (low value), generally there was a large area of occurrence of CIII heterozygotes, indicating high introgression between the races, but the area of occurrence of CV heterozygotes was limited to the immediate area around one of the barriers (Fig. 1b). Thirdly, when s1 and s2 were both large, contact between the races usually became stuck at one of the barriers, with few hybrids present at the end of the simulation run (Fig. 1c). Fourthly, with intermediate values for s1 and s2, a recombinant race (either aaBB or AAbb) could be formed in the central area (Fig. 1d). However, whatever the selection regime, only a very small proportion of simulations generated a recombinant race (Fig. 2a). The maximum probability of establishment of a new recombinant race was P = 0.03 for s1 = 0.055 and s2 = 0.046. Those simulation runs that did generate a recombinant race were more usually those involving the epistatic model. No recombinant races were generated with either the selection regime based directly on the nondisjunction data (s1 = 0.221, s2 = 0.186), nor that based on complete neutrality (s1 = s2 = 0). These results with the empty patch simulations suggest that it is unlikely that the M-V race was formed by occasional long-distance migrants of the L-V and POS races entering the empty middle section of Upper Valtellina by natural dispersal.
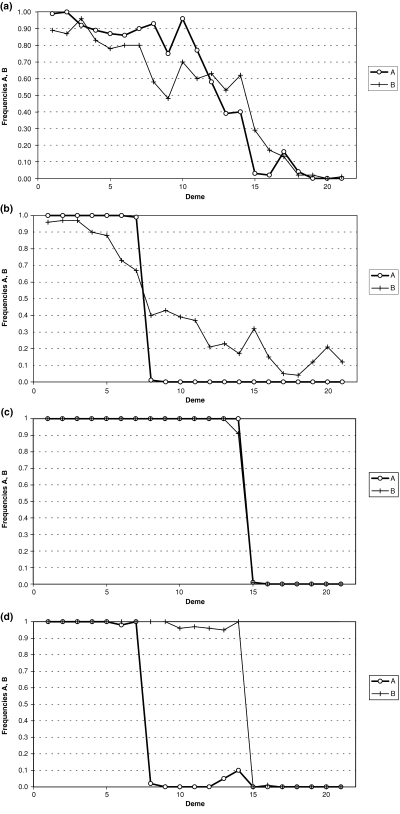
Examples of simulation results. See Table 5 for details of ‘alleles’ A and B (and the alternative alleles a and b). (a) and (b) show examples of simulations where a hybrid zone with substantial polymorphism is generated (c) shows a case where the two parental races come to lie on either side of one of the barriers, with very few hybrids produced (d) shows a case where a recombinant race with ‘genotype’ aaBB has come to occupy the central area between the two races AABB and aabb.
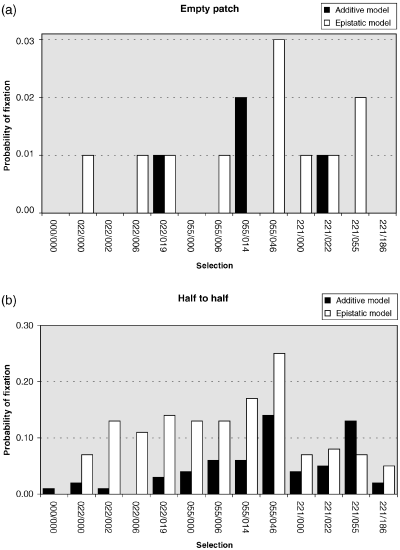
Probability of generation of a recombinant race with different deme arrays, (a) ‘empty patch’ and (b) ‘half-to-half’, under the various selection regimes (s1/s2) described in the text, following either the additive or epistatic model (Table 5). A recombinant race was considered fixed when its frequency exceeded 0.3 over all arrays (i.e. it essentially filled the central third of the total array of demes).
In the preceding simulations, the basic obstacle preventing formation of a new recombinant race was the difference in the time that the races crossed the barrier. To simulate an event when both races colonized the empty patch at the same time we modified the model. The new ‘half-to-half’ model differed from the empty patch model in that we introduced both races into the central third of the deme array, such that approximately 50% of the demes in that array had the L-V race and 50% had the POS race. The ‘half-to-half’ model simulates a simultaneous colonization of the middle section of Upper Valtellina by reasonable numbers of individuals of both races. This was precisely the situation envisaged by Hauffe & Searle (1993). With recovery of the middle section of Upper Valtellina following the flood in 1807, many materials and foodstuffs would have been brought in from nearby areas. It is reasonable to suggest that large numbers of house mice would be associated with such materials. If materials and mice came from both an area where the L-V race was found and an area where the POS race predominated, then a situation similar to our simulation may have been generated.
We had much more success in generating recombinant races under the ‘half-to-half’ model. In one case (s1 = 0.055, s2 = 0.046), 25% of simulation runs resulted in a recombinant race (Fig. 2b). As for the empty patch simulations, the epistatic model outperformed the additive model and recombinant races were very rarely formed when there was complete neutrality. Under the epistatic model, low to moderate unfitnesses were better for the generation of recombinant races than high unfitnesses. Under the additive model, moderate to high unfitnesses were more successful than low unfitnessess in generating recombinant races. It is encouraging that using ecological parameters estimated from current-day populations and selection regimes that are mid-way in the range that we considered, we managed to mimic the formation of a recombinant race in a high frequency of our simulation runs. These results suggest that the mode of formation of the M-V race hypothesized by Hauffe & Searle (1993) is a reasonable one.
It should be noted that although we were interested in modelling the formation of one particular recombinant race (the M-V race) in Upper Valtellina; in our simulations with the empty patch and half-to-half models, the alternatives aaBB and AAbb were equally likely to become established. This is of particular interest because while aaBB represents the M-V race present in Upper Valtellina, AAbb represents another race found in the valley: the Upper Valtellina (U-V) race (Hauffe & Searle 1993). Therefore, the U-V race could also have been formed by zonal raciation within Upper Valtellina (see Hauffe & Piálek 1997).
Therefore, we have shown that zonal raciation can satisfactorily explain the generation of recombinant races from the L-V and POS races, given our knowledge of the ecology of house mice in Upper Valtellina and likely selection against F1(L-V × POS) hybrids. Because zonal raciation may have occurred in this particular situation, it can be suggested that it has occurred in other situations, such as the postulated generation of the L-V race from the POS and Cremona races (see above) and may have made an important contribution to the diversity of karyotypic races of the house mouse in northern Italy. From our simulation results, it would appear that three conditions may be particularly important in generating recombinant races: mass simultaneous colonization of an area by both parental races, low to moderate unfitnesses associated with each meiotic configuration that occurs in the F1 hybrid and a greater than additive unfitness associated with having more than one of these configurations. Recent results with more general simulations support our findings of the importance of low to moderate selection in the modification of hybrid zones (J. Piálek & N. H. Barton unpublished data) and the potential importance of epistatic selection in such situations has long been realized (Barton & Bengtsson 1986; Searle 1993; Gavrilets 1997).
Wider relevance of the model for zonal raciation
‘Zonal raciation’ refers to the generation of a new race within a hybrid zone (Searle 1991). Here we have particularly concentrated on the origin of recombinant races within hybrid zones. It is also possible for new races to arise by mutation within the hybrid zone. The acrocentric forms that dominate certain chromosomal hybrid zones between metacentric races of common shrew may have arisen in this way (Searle 1986, 1993).
The idea of new recombinant homozygous karyotypes becoming fixed within chromosomal hybrid zones has long been recognized in flowering plants (Grant 1958; Rieseberg 1997). Indeed, it has been viewed as a possible mode of species-formation and is termed ‘hybrid speciation’, ‘recombinational speciation’ or ‘homoploid speciation’ (e.g. McCarthy et al. 1995; Rieseberg 1997; Buerkle et al. 2000). The sunflower Helianthus anomalus is a particularly convincing and well-studied example of a new plant species that has arisen in this fashion (Rieseberg et al. 1995; Ungerer et al. 1998).
The process of recombinational speciation in flowering plants has been modelled by McCarthy et al. (1995) and Buerkle et al. (2000). The model of Buerkle et al. (2000) has particular relevance because, as in our ‘empty patch’ model, the parental species were allowed to colonize and hybridize within an empty central area of a two-dimensional grid. It was found that, under a model of multiplicative selection against heterozygous karyotypes, new hybrid species originated at reasonable frequencies if, in the simulation, the central area was geographically isolated and of a habitat to which a hybrid species would be better adapted than either parental species. This ecological selection was added to the model because of the observation that hybrid plant species often do have different habitat characteristics from the parental types.
Clearly, we have identified other characteristics that are important to test in future models of recombinational speciation: mass invasion of the central area by the two parental species and epistatic selection. Our model together with those of McCarthy et al. (1995) and Buerkle et al. (2000) indicate that under selective regimes and ecological conditions that are realistic for both mice and flowering plants, recombinant homozygous karyotypes can arise and become fixed at reasonable frequency in chromosomal hybrid zones. This further emphasizes the growing realization that hybridization is an important process in generating organismal diversity (Arnold 1997).
Acknowledgements
We are grateful to Roland Hübner, Richard Ward and John Dallas for unpublished data and to Miloš Macholán, Loren Rieseberg and two anonymous referees for comments on the manuscript. Nick Barton is acknowledged for introducing the first author to the magic of simulations and Godfrey Hewitt is thanked by the last author for introduction to the marvels of hybrid zones. We thank the Department of Zoology, University of Oxford who provided facilities for some of this work. We acknowledge the support of the Royal Society of London, the European Union, the Natural Environment Research Council, the Grant Agency of the Academy of Sciences of the Czech Republic and the Ministry of Education, Youth and Sport of the Czech Republic.
References
Heidi Hauffe and Jeremy Searle have been studying raciation and speciation in Alpine house mice for the last dozen years, and Jaroslar Piálek and Kate Rodríguez-Clark have contributed to this work with modelling and fertility analysis, respectively.




