Drivetrain fatigue strength characteristics of model-predictive control for wind turbines
Abstract
Wind turbines play a crucial role in the revolution towards renewable resources. They need to be economically competitive to be sustainable. This still requires to lower the cost of energy (COE). To this end, nonlinear model predictive control (NMPC) is used within this paper. As known from literature, NMPC significantly improves the energy extracting performance as well as the mitigation of tower loads of wind turbines. As it is shown in this paper, the drivetrain fatigue strength drops disproportionally in parallel, which either increases the demands on the turbine design or decreases the lifetime of drivetrain components. Without additional boundary conditions to the underlying optimal control problems (OCPs), the application of energy-maximizing NMPC might so even raise the COE. Only penalizing axial torque oscillations by quadratic terms decreases energy-extracting performance below the level of classical wind turbine controllers. This makes more sophisticated conditions necessary. In this paper, the increase of the drivetrain damage by NMPC is analyzed, and appropriate boundary conditions are derived, to balance the two contradicting objectives of energy maximization and drivetrain load mitigation. An NMPC approach based on indirect methods is used, to obtain a solution of the OCPs very efficiently. It applies the Hamilton equations and Pontryagin's maximum principle. Its accuracy and efficiency to solve OCPs was presented over the last decades.
1 INTRODUCTION
In market systems, energy sources need to be economically competitive to be sustainable. For wind turbines, this still requires reducing the costs of manufacturing and operation.1, 2 The latter can be optimized by increasing the energy production or by lowering the costs of maintenance or by extending the life time. The damage of drivetrain components can be significantly reduced by advanced control strategies like state space controllers.3, 4 A point-wise linear model predictive control approach for wind turbines allows to reduce extreme loads.5 Nonlinear model-predictive control (NMPC) for wind turbines shows an excellent impact on increasing the energy production as well as on mitigating tower loads.6-9 Special interpolation of the nonlinear power coefficient allows to obtain a solution efficiently, if the turbine dynamics can be predicted exactly and no model deviations are taken into account.10, 11
NMPC describes a control strategy in which a consecutive sequence of optimal control problems (OCPs) is solved on large prediction horizons,12, 13 for example, 10 s. The solution of each of these OCPs is applied for the length of the control interval, for example, 100 ms. The resulting state of the system serves as input for the next OCP, whereby the prediction horizon needs to be significantly larger than the length of the control interval.12, 13
Within this paper, indirect methods are used to solve the OCPs. In addition to the state equations, a set of differential equations for the adjoint variables is derived from the Hamilton equations. The optimal control is determined from an algebraic expression, which depends on the state and adjoint state variables.14, 15 This algebraic expression is derived from Pontryagin's maximum principle. In total, this forms a boundary value problem (BVP), which involves transition conditions in the interior of the prediction horizon as well as terminal conditions. The interior and terminal conditions may vary with the structure of the solution. This structure describes the number and order of arcs, on which state-constraints are active or inactive.
In the presented example, the constraints on the minimum pitch angle and the maximum generator torque of the wind turbine get active and inactive very regular. To profit from the accuracy and efficiency of indirect methods in NMPC, an automated strategy to detect these changes and to determine a valid structure is used. To evaluate the quality of NMPC, the impact on the drivetrain fatigue strength is compared with the impact of a standard reference controller using objective criteria like the damage sum and damage equivalent load (DEL). They will be calculated from six representative full-field turbulent wind speeds at a mean of 11
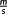 on a length of 600 s. The damage sum is a scalar to assess the fatigue strength of machine elements and requires detailed knowledge of loads, design, and the fatigue process. It is determined from the utilization factor, which is defined by the Forschungskuratorium Maschinenbau e.V. (FKM) guideline.16, 17 As controllers will only affect loads, the DEL is commonly used to compare their performance. From the control point of view, both the damage sum and the DEL can be reduced by lowering stress or load amplitudes. As NMPC is based on an optimization, the drivetrain fatigue strength can be directly considered within the determination of the optimal control. But the damage sum and DEL need to be determined on the full range of the load signal, which goes far beyond any time horizon, on which a feasible prediction of the wind turbine dynamics can be done. In the following, two terms are considered within the optimization to reduce the damage sum and DEL. The first one reduces the maximum amplitude of the generator torque within the signal passed in the last 300 s. The second one is chosen such that it reduces the amplitudes in the higher frequency range. Simultaneously, it regularizes the OCP. These two additional terms allow either to obtain a controller configuration, for which the damage sum and DEL are kept within the range of the original specification while the energy production is increased, or to obtain a controller, which has the energy production as originally specified with a significant decrease of both, the damage sum and DEL.
on a length of 600 s. The damage sum is a scalar to assess the fatigue strength of machine elements and requires detailed knowledge of loads, design, and the fatigue process. It is determined from the utilization factor, which is defined by the Forschungskuratorium Maschinenbau e.V. (FKM) guideline.16, 17 As controllers will only affect loads, the DEL is commonly used to compare their performance. From the control point of view, both the damage sum and the DEL can be reduced by lowering stress or load amplitudes. As NMPC is based on an optimization, the drivetrain fatigue strength can be directly considered within the determination of the optimal control. But the damage sum and DEL need to be determined on the full range of the load signal, which goes far beyond any time horizon, on which a feasible prediction of the wind turbine dynamics can be done. In the following, two terms are considered within the optimization to reduce the damage sum and DEL. The first one reduces the maximum amplitude of the generator torque within the signal passed in the last 300 s. The second one is chosen such that it reduces the amplitudes in the higher frequency range. Simultaneously, it regularizes the OCP. These two additional terms allow either to obtain a controller configuration, for which the damage sum and DEL are kept within the range of the original specification while the energy production is increased, or to obtain a controller, which has the energy production as originally specified with a significant decrease of both, the damage sum and DEL.
The second section covers both, the required principals of fatigue strength assessment of machine elements—in terms of a damage sum based on nominal torsional stress and in terms of a DEL—as well as the necessary conditions of optimal control based on Hamilton. This is followed by a section, which covers the concept of indirect NMPC in general. In Section 4, the application of indirect NMPC for wind turbines is described, and its impact on the maximization of energy extraction in parallel to the according fatigue strength of the drivetrain is discussed.
2 FATIGUE LIFE VERIFICATION AND OPTIMAL CONTROL
2.1 Relative assessment of fatigue strength
The relative assessment of the fatigue strength is based on two different concepts—the DEL and the damage sum D. The calculation of a DEL was originally derived, to compare damaging of differing load signals.18 It is independent of a specific component geometry, purely based on load signals and applies only general material properties. D is stress-based and correlated to the scalar utilization factor aBK, which is defined by the FKM guideline.16, 17 The FKM guideline describes, among others, industrially used methods for fatigue strength verification of variable amplitude nominal stress signals for rod-shaped components. D is strongly dependent on the cross-section of a component. But a relative comparison of two D resulting from two different load signals acting on the same component allows to eliminate this dependency. Within this paper, only torsional stresses and loads are considered to determine D and the DEL.
Definition 1. ((nominal torsional stress[19]).)Consider a circular cross section with radius r>0 of a rod-shaped machine element. Let
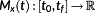 denote the torque signal on the cross section in axial direction. Let the x−axis be perpendicular to the cross section and positioned at its centroid. The torsional stress
denote the torque signal on the cross section in axial direction. Let the x−axis be perpendicular to the cross section and positioned at its centroid. The torsional stress
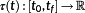 is given by
is given by
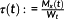 , where
, where
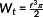 is the corresponding polar section modulus.
is the corresponding polar section modulus.
The calculation of D is based on S-N curves, which relates the allowable number of cycles to failure to an alternating, that is, mean-free, stress amplitude. Equivalently, a DEL is based on M-N curves,18, 20 which relates the allowable number of cycles to failure to an alternating load amplitude. A time domain analysis based on turbulent full-field wind speeds results in variable amplitude spectra with variable means stress and load. In order to map them to mean-free spectra, at first, a classification of both signals into stress and load amplitudes along with its corresponding number of cycles and mean stress and mean load values is done by the rainflow counting method. This results in two sets of 3-tupels
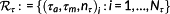 and
and
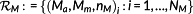 . Second, the amplitudes are mapped to damage-equivalent alternating stress and load amplitudes. To this end, each element of
. Second, the amplitudes are mapped to damage-equivalent alternating stress and load amplitudes. To this end, each element of
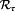 is scaled by a mean stress factor.
is scaled by a mean stress factor.
Definition 2. ((mean stress factor and damage-equivalent alternating stress amplitude[17]).)For some i ∈ {1,…,Nτ} consider a 3-tupel
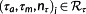 . The corresponding mean stress factor KAK is determined based on the amplitude τa and its corresponding mean value τm. For torsional stresses from variable amplitude and variable mean stress signals, it is given by
. The corresponding mean stress factor KAK is determined based on the amplitude τa and its corresponding mean value τm. For torsional stresses from variable amplitude and variable mean stress signals, it is given by
 (1)
(1)where R denotes the stress ratio
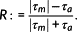 (2)
(2)Mτ is called the mean stress sensitivity and here given for stainless steel. Rm denotes the tensile strength and depends on the material. The damage-equivalent alternating stress amplitude
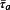 is given by
is given by
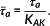 (3)
(3)This results in a damage-equivalent set of 3-tupels
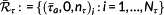 . Equivalently, a Goodman-correction is applied to map a variable amplitude and mean load classification into a set of damage-equivalent alternating load amplitudes.
. Equivalently, a Goodman-correction is applied to map a variable amplitude and mean load classification into a set of damage-equivalent alternating load amplitudes.
Definition 3. ((Goodman-correction[18]).)The Goodman-correction is determined based on the amplitude Ma and its corresponding mean value Mm. The corrected mean-free amplitude
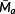 is given by
is given by
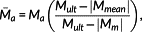 (4)
(4)This results in a damage-equivalent set of 3-tupels
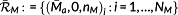 . The utilization factor aBK and its corresponding damage sum D are determined by the component variable amplitude fatigue strength.
. The utilization factor aBK and its corresponding damage sum D are determined by the component variable amplitude fatigue strength.
Definition 4. ((component variable amplitude fatigue strength[17]).)The component variable amplitude fatigue strength TBK is given by
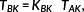 (5)
(5)where TAK=KAKTWK denotes the amplitude of component fatigue limit. The mean stress factor KAK is equal to 1.0 for signals without a mean stress.17 The component fatigue limit for completely reversed stress TWK is independent of the stress signal and will be eliminated in a relative comparison. For a variable amplitude stress spectrum, the variable amplitude fatigue strength factor KBK is calculated by the elementary version of Miner's rule.
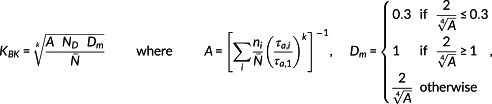 (6)
(6)where
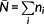 , ND=106 denotes the number of cycles at the knee point and k denotes the slope of the component amplitude S-N curve for shear stresses of non-welded stainless steel.
, ND=106 denotes the number of cycles at the knee point and k denotes the slope of the component amplitude S-N curve for shear stresses of non-welded stainless steel.
Definition 5. ((cyclic degree of utilization and damage sum[17]).)The cyclic degree of utilization of rod-shaped components aBK and its corresponding damage sum are defined by
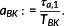 (7)
(7)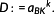 (8)
(8)
Remark 1..Please note that
 (9)
(9)In the later, only the relation of two damage sums DNMPC and DReference will be analyzed for the same rod-shape machine element. Both stress signals will be obtained from the same multibody simulation (MBS) model. As the component fatigue limit for completely reversed stress TWK is independent from the actual stress signal τ(t),17 it is not necessary to be determined.
To map the alternating amplitudes of
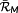 to a scalar value DEL, the hypothesis about linear accumulation of damage is consequently used.18
to a scalar value DEL, the hypothesis about linear accumulation of damage is consequently used.18
Definition 6. ((DEL[18]).)The DEL for a variable amplitude alternating load spectrum
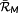 is given by
is given by
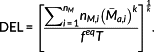 (10)
(10)feq denotes the DEL-frequency, for example. 1 Hz, and T=tf−t0 the time domain of the load signal Mx(t). k denotes the slope of the M-N curve.
2.2 Optimal control
NMPC describes an iterative strategy in which an OCP is solved in each step. An OCP of ordinary differential equations (ODEs) is defined as an optimization problem, where functions of one independent variable—for example, the time t – is determined such that they without loss of generality (w.l.o.g.) minimize a given target function. Optimal control theory provides first- and second-order necessary conditions for optimality. In this section, these necessary conditions are summarized up to that level, which is needed to formulate an NMPC scheme based on indirect methods.
In the following functions, whose derivative is not explicitly occurring in the problem formulation, are called control variables. They are queued up in the vector
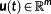 where
where
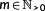 defines its number. The optimization includes conditions like ODEs. In contrast to a control variable, each function, whose derivative is defined by this ODE, is called a state variable. They are queued up in the vector
defines its number. The optimization includes conditions like ODEs. In contrast to a control variable, each function, whose derivative is defined by this ODE, is called a state variable. They are queued up in the vector
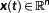 , where
, where
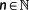 defines its number. OCPs may also involve inequality constraints and terminal conditions. The following defines the most general OCP used within this paper. W.l.o.g. is assumed to be autonomous.
defines its number. OCPs may also involve inequality constraints and terminal conditions. The following defines the most general OCP used within this paper. W.l.o.g. is assumed to be autonomous.
Problem 1..Let
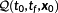 denote the following OCP.
denote the following OCP.
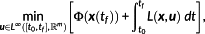 (11)
(11)subject to
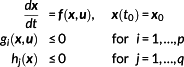 (12)
(12)with
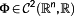 1
1
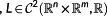 and
and
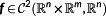 ,
,
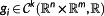 ∀i∈{1,…,p} and
∀i∈{1,…,p} and
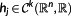 ∀j∈{1,…,q} with k ≥ 2 sufficiently high.
∀j∈{1,…,q} with k ≥ 2 sufficiently high.
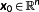 is called initial value, g(x,u) control constraints and h(x) state constraints.
is called initial value, g(x,u) control constraints and h(x) state constraints.
Definition 7..Let the following sets be defined:
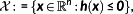 (13)
(13)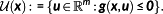 (14)
(14)
Definition 8. ((Hamiltonian and augmented Hamiltonian).)The Hamiltonian
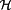 and the augmented Hamiltonian
and the augmented Hamiltonian
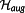 are defined by
are defined by
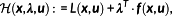 (15)
(15)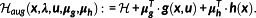 (16)
(16)
Definition 9. ((order of state constraint).)The order of a state constraint hj(x) is defined by the smallest number
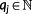 such that there exists at least one i ∈ {1,…,m} for which the following holds
such that there exists at least one i ∈ {1,…,m} for which the following holds
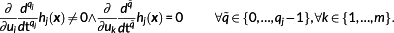 (17)
(17)
Definition 10. ((solution structure).)Let (x⋆, u⋆) be a solution of
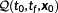 . The sets of the active control constraints, the almost active control constraints, and the active state constraints are defined by
. The sets of the active control constraints, the almost active control constraints, and the active state constraints are defined by
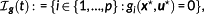 (18)
(18)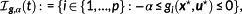 (19)
(19)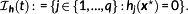 (20)
(20)Moreover, the sets
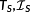 are defined by
are defined by
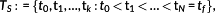 (21)
(21)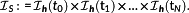 (22)
(22)If
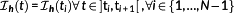 , then
, then
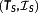 is called a solution structure.
is called a solution structure.
Definition 11. ((regular Hamiltonian).)Let (x⋆,u⋆) solve
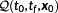 . Then,
. Then,
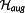 is called regular, if ∃ α>0 such that for almost all t∈[t0,tf]
is called regular, if ∃ α>0 such that for almost all t∈[t0,tf]
-
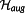 is uniformly strict convex:
is uniformly strict convex:
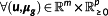
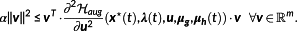 (23)
(23) - The constraint qualification is fulfilled: let
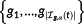 and
and
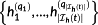 be the sets of active constraints at time t (after index renumbering); let the matrices Ag,Ah are defined by
be the sets of active constraints at time t (after index renumbering); let the matrices Ag,Ah are defined by
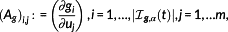 (24)Let
(24)Let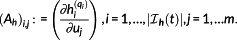 (25)
(25)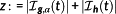 . Then, the following conditions hold
. Then, the following conditions hold
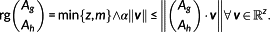 (26)
(26)
If
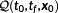 does not contain state constraints, then the necessary conditions of first order are given by the following theorem.
does not contain state constraints, then the necessary conditions of first order are given by the following theorem.
Theorem 1..Consider the OCP
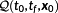 with no state constraints, that is, p=0. Assume the optimal solution (x⋆,u⋆) to exist. Let
with no state constraints, that is, p=0. Assume the optimal solution (x⋆,u⋆) to exist. Let
 be defined by Definition 8. Then, there exist
be defined by Definition 8. Then, there exist
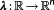 and
and
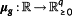 such that ∀t∈[t0,tf] the (x⋆,u⋆,λ,μg) solve the optimality condition
such that ∀t∈[t0,tf] the (x⋆,u⋆,λ,μg) solve the optimality condition
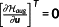 , the adjoint equations
, the adjoint equations
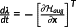 , and the transversality condition
, and the transversality condition
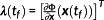 .
.
Proof..The proof is given, for example in Dmitruk.21
In case of general state constraints, a complete theory is not yet available. Necessary conditions in case of one scalar state constraint and no control constraints are provided in Jacobson et al.22 In case of multiple state constraints, necessary conditions are described in Maurer.23 A survey of the necessary conditions for state constrained problems is given in Hartl et al.15 For a problem with a regular Hamiltonian and first-order state constraints, the adjoint variables λ(t) and the Lagrangian multipliers associated to the control constraints μg(t) are continuous.24
Lemma 1..Let (x⋆,u⋆) solve
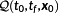 . Let λ(t) and μh(t) exist. If
. Let λ(t) and μh(t) exist. If
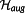 is regular and all state constraints are of first order, then u⋆, λ and μg are continuous.
is regular and all state constraints are of first order, then u⋆, λ and μg are continuous.
Proof..The proof is given in Bonnans et al.24
3 INDIRECT NONLINEAR MODEL PREDICTIVE CONTROL
NMPC covers a variety of different control strategies. They generally have in common, that the determination of the control relies on a mathematical model, which adequately predicts the dominant dynamic behavior of the system for a specific time period—the prediction horizon
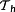 .
.
Definition 12. ((prediction horizon
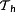 ).)The function
).)The function
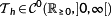 is called the prediction horizon. It needs not necessarily to be constant.
is called the prediction horizon. It needs not necessarily to be constant.
NMPC generally exhibits its strengths, if inequality constraints—especially on state variables—need to be fulfilled. The control, which is determined on the prediction horizon
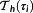 , is not applied to the system for the full length of
, is not applied to the system for the full length of
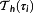 , but for a smaller period—the length of the control interval
, but for a smaller period—the length of the control interval
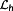 , which is the inverse of the controller sampling rate.
, which is the inverse of the controller sampling rate.
Definition 13. ((length of control interval
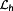 ).)Consider a uniform discretization of the time [0,∞[ by
).)Consider a uniform discretization of the time [0,∞[ by
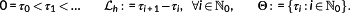 (27)
(27)
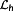 is called the length of the control interval. The τi are called sampling points and define the macro discretization Θ.
is called the length of the control interval. The τi are called sampling points and define the macro discretization Θ.
At each sampling point, τi a state measurement provides the corrected initial values x0(τi). They serve as input for the NMPC step.
Definition 14. ((corrected initial values x0(τi)).)The measured states x0(τi) are called the corrected initial values for the sampling point τi. For τ∉Θx0(t0u) is the piecewise linear interpolation of the measured states at the sampling points. Thus,
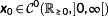 is continuous.
is continuous.
In one of the most important NMPC strategies, the control is the solution of a sequence of OCPs
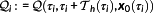 on finite prediction horizons
on finite prediction horizons
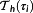 . It minimizes a given objective while meeting conditions on state and control variables. Then, the optimal control (
. It minimizes a given objective while meeting conditions on state and control variables. Then, the optimal control (
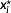 ,
,
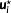 ) is applied to the system for t∈[τi,τi+1] in a permanently repeating process. To approximate the infinite horizon OCP
) is applied to the system for t∈[τi,τi+1] in a permanently repeating process. To approximate the infinite horizon OCP
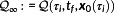 for tf→∞, the prediction horizon needs to be significantly larger than the control interval
for tf→∞, the prediction horizon needs to be significantly larger than the control interval
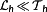 .12, 13
.12, 13
In the presented indirect NMPC approach, the solution of these OCPs
 is identified with the solution of the Hamilton equations. Each
is identified with the solution of the Hamilton equations. Each
 results in a multipoint BVP
results in a multipoint BVP
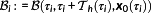 on the time horizon
on the time horizon
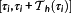 with the initial state x0(τi). As soon as the solution structure
with the initial state x0(τi). As soon as the solution structure
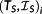 is known,
is known,
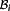 can efficiently be solved by the advanced multiple shooting method JANUS.25 The solution structure
can efficiently be solved by the advanced multiple shooting method JANUS.25 The solution structure
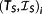 cannot assumed to be constant
cannot assumed to be constant
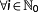 , but strongly depends on τi and x0(τi) and
, but strongly depends on τi and x0(τi) and
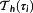 .
.
In the following, it is assumed that every change of
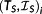 happens continuously: let the structure
happens continuously: let the structure
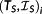 be valid for t0=τi. Based on
be valid for t0=τi. Based on
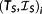 a solution of the BVP is determined for the next sampling point t0=τi+1. If it neither violates a state constraint nor it violates any first-order condition,
a solution of the BVP is determined for the next sampling point t0=τi+1. If it neither violates a state constraint nor it violates any first-order condition,
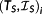 is accepted as a valid structure for
is accepted as a valid structure for
 , and
, and
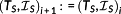 is set. On the contrary, if the solution for t0=τi+1 based on the structure
is set. On the contrary, if the solution for t0=τi+1 based on the structure
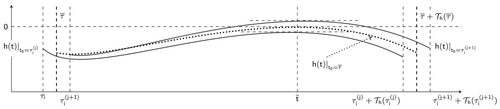
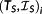 violates a state constraint—for instance h(t) ≤ 0 for a time
violates a state constraint—for instance h(t) ≤ 0 for a time
 (cf. Figure 1)—a change in the structure is detected. If this change is continuous, then there exists a
(cf. Figure 1)—a change in the structure is detected. If this change is continuous, then there exists a
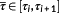 such that,
such that,
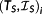 is also valid for
is also valid for
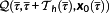 with the corresponding solution
with the corresponding solution
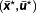 . This intermediate sampling point
. This intermediate sampling point
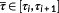 is characterized by a touch point
is characterized by a touch point
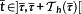 for the state constraint, that is,
for the state constraint, that is,
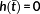 . This means, that for
. This means, that for
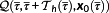 , there is a second valid solution structure
, there is a second valid solution structure
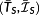 , which contains a boundary arc for h(t) ≤ 0 at
, which contains a boundary arc for h(t) ≤ 0 at
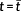 with zero length. This
with zero length. This
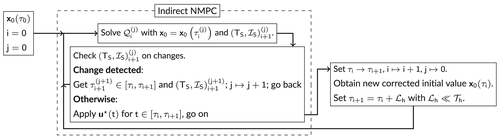
 is set as the new valid solution structure. The process to determine and resolve changes of the solution structure on [τi,τi+1] results in a second time discretization, which is called the micro discretization. The continuity of the solution structure for the sketched case—the violation of a state constraint appears in the interior of prediction horizon for a first order state constraint and scalar control—was already shown.26 The overall indirect NMPC process is sketched in Figure 2.
is set as the new valid solution structure. The process to determine and resolve changes of the solution structure on [τi,τi+1] results in a second time discretization, which is called the micro discretization. The continuity of the solution structure for the sketched case—the violation of a state constraint appears in the interior of prediction horizon for a first order state constraint and scalar control—was already shown.26 The overall indirect NMPC process is sketched in Figure 2.
Definition 15. ((macro and micro discretization Θ and θi).)The macro discretization Θ is defined by Definition 13. The micro discretization
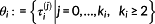 is synthesized by the ki−2 changes in solution structure from
is synthesized by the ki−2 changes in solution structure from
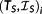 to
to
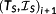 . By definition,
. By definition,
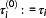 and
and
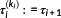 holds. At each
holds. At each
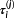 for j=1,…,ki−1, the solution structure changes.
for j=1,…,ki−1, the solution structure changes.
-
For the first OCP the macro discretization is extended by τ−1 with τ−1=τ0. For τ−1, the following conditions are set:
- •
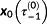 is chosen such that no state constraint is active.
is chosen such that no state constraint is active. - •
The prediction horizon
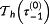 is set to a very small value (e.g.,
is set to a very small value (e.g.,
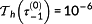 s).
s).
This provides a feasible starting condition for the multiple shooting method. It also provides an initial valid solution structure, in which no state constraint is active.
- •
-
The sketched scheme of continuously detecting and resolving changes in the structure results in a micro discretization
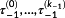 with
with
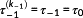 . The prediction horizon
. The prediction horizon
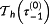 is continuously increased—for example, by linear interpolation—to finally meet the desired prediction horizon
is continuously increased—for example, by linear interpolation—to finally meet the desired prediction horizon
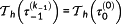 . Equivalently, x−1(τ0) is continuously driven to the actual initial states x0(τ0).
. Equivalently, x−1(τ0) is continuously driven to the actual initial states x0(τ0).
This results in a valid initial solution structure
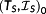 . In the six examples below, this initial structure was determined within 20 to 60 ms.
. In the six examples below, this initial structure was determined within 20 to 60 ms.
4 INDIRECT NMPC OF A WIND TURBINE
4.1 Mathematical model of the wind turbine
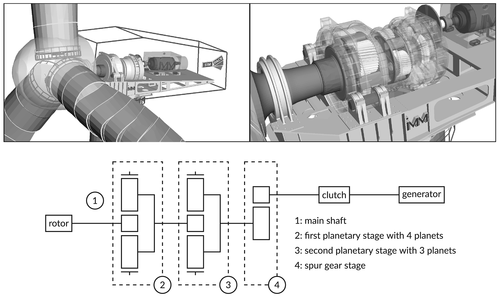
In this section, two models of the wind turbine with different levels of fidelity are used. The first one is an MBS model based on the definition of the NREL-5 MW reference wind turbine.28 It is also provided with the MBS software Simpack 2 and was extended by a standard appropriate planetary gear box by the IMM 3 of the Technische Universität Dresden. It consists of two planetary stages with four and three planets and the outer rings fixed to the gear box housing. A spur gear stage is located between the second planetary stage and the clutch (cf. Figure 3). To account for small torsional flexible deformations in the drivetrain, the main shaft, the two planetary carriers, the intermediate, and the high speed shaft are modeled flexible by standard modal linear model order reduction techniques for finite element models. This MBS model serves as the system to be controlled and analyzed. To predict the dominant dynamic characteristics within the NMPC approach, a nonlinear model of reduced order (NMOR-model) is derived from the MBS model.
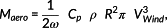 (28)
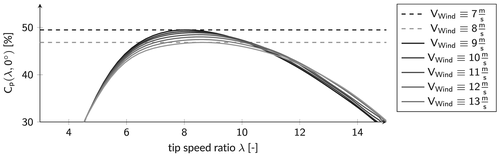
(28)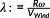 and pitch angles β. The array entries are determined by quasi-static equilibria of a wind turbine MBS model. The only MBS velocity states, which are not vanishing in terms of these equilibria, are all the rotor speed related states. The nominal rotor speed is given by λ, for which the Cp-table is created. As λ also depends on the wind speed, a nominal VWind needs to be specified to obtain Cp(λ,β) in terms of λ and β.
and pitch angles β. The array entries are determined by quasi-static equilibria of a wind turbine MBS model. The only MBS velocity states, which are not vanishing in terms of these equilibria, are all the rotor speed related states. The nominal rotor speed is given by λ, for which the Cp-table is created. As λ also depends on the wind speed, a nominal VWind needs to be specified to obtain Cp(λ,β) in terms of λ and β.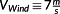 is round about 49.48%, and for
is round about 49.48%, and for
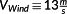 , it is round about 46.83%, which makes a difference of round about 2.6% in the estimated efficiency. When including conditions into the OCP to consider drivetrain fatigue strength, it turned out that a Cp dependent on λ and β only does not capture the dynamics sufficiently. Alternatively, Cp(ω,VWind(t),β) is considered to be dependent on the rotor speed ω, the rotor effective wind speed VWind(t), and the collective pitch angle β.
, it is round about 46.83%, which makes a difference of round about 2.6% in the estimated efficiency. When including conditions into the OCP to consider drivetrain fatigue strength, it turned out that a Cp dependent on λ and β only does not capture the dynamics sufficiently. Alternatively, Cp(ω,VWind(t),β) is considered to be dependent on the rotor speed ω, the rotor effective wind speed VWind(t), and the collective pitch angle β.
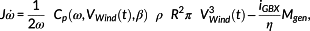 (29)
(29) (30)
(30)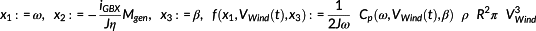 (31)
(31)
A tensor product of Chebyshev polynomials is used to interpolate the Cp-data.32, 33 The rotor speed related polynomials are of order 10, the wind speed related ones are of order 8, and the pitch related polynomials are of order 6. These orders were found by a sensitivity analysis. In Figure 5, the rotor speed of the NMOR model is plotted versus the rotor speed of the MBS model. As it can be seen, the NMOR model captures the dominant dynamics of the rotor speed sufficiently.

 (32)
(32)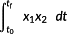 (33)
(33)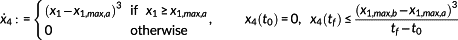 (34)
(34)In the later, x1,max,a=10.1 rpm and x1,max,b=12.1 rpm was chosen. This leads to small violations of the maximum rotor speed of 12.1 rpm, which are accepted by the reference controller in the same way. An equivalent term with the according conditions is added regarding the maximum generator power. Pmax,a=4 MW and Pmax,b=5 MW are the corresponding limits.
4.2 Regularization and fatigue strength consideration
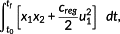 (35)
(35)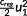 generally prevents an oscillation of the generator torque. To reduce the maximum stress amplitude, the coefficient creg in Equation (35) needs to be chosen that large, such that the energy extraction efficiency is also reduced in ranges, which have small influence on the fatigue strength. More sophisticated conditions are necessary to take the fatigue strength into account.
generally prevents an oscillation of the generator torque. To reduce the maximum stress amplitude, the coefficient creg in Equation (35) needs to be chosen that large, such that the energy extraction efficiency is also reduced in ranges, which have small influence on the fatigue strength. More sophisticated conditions are necessary to take the fatigue strength into account.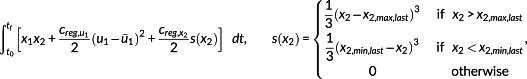 (36)
(36)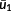 denotes the mean value of u1 from the preceding NMPC step and x2,max,last is the maximum and x2,min,last is the minimum generator torque applied to the system within the last 300 s.
denotes the mean value of u1 from the preceding NMPC step and x2,max,last is the maximum and x2,min,last is the minimum generator torque applied to the system within the last 300 s.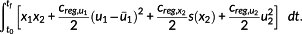 (37)
(37)4.3 Simulation results
The presented indirect NMPC scheme was applied to six sample load cases. Each of it is a standard A-classified full-field turbulent wind speed with a mean of 11
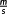 and was created with the NREL software TurbSim.35 Their configurations are given in Table 1. The following discussion is limited to this mean value, to allow a reasonable discussion of the results. The presented approach can easily be extended to a broad range of mean wind speeds, which is shown in Schwarz and Schulz.36
and was created with the NREL software TurbSim.35 Their configurations are given in Table 1. The following discussion is limited to this mean value, to allow a reasonable discussion of the results. The presented approach can easily be extended to a broad range of mean wind speeds, which is shown in Schwarz and Schulz.36
| RandSeed1: | 1,…,6 | RandSeed2: | RANLUX | WRBLFF: | True | AnalysisTime: | 660 s | TimeStep: | 250 ms |
|---|---|---|---|---|---|---|---|---|---|
| TurbModel: | IECKAI | IECStandard: | 1-Ed3 | IECTurbc: | A | IEC_WindType: | NTM | URef: | 11.0 |
- The total extracted energy including the net kinetic energy stored in the rotation of the rotor
- The D determined from the cutting torque between the main shaft and the first planetary carrier in axial direction.
- The DEL determined from the cutting torque between the main shaft and the first planetary carrier in axial direction.
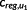 and
and
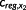 allow to further configure the indirect NMPC. Three different settings are determined.
allow to further configure the indirect NMPC. Three different settings are determined.
- Purely maximize the extracted amount of energy without explicitly constraining the damage of drivetrain components.
- Maximize the extracted amount of energy while keeping the damage sum at the level of the reference controller.
- Further reduce the damage sum while keeping the energy performance at the level of the reference controller.
Configuration 1: The energy extraction performance of these three settings is analyzed in relation to the reference controller and illustrated in the first plot of Figure 6. The largest increase of 0.6% to 1.32% can be obtained, when damaging is not explicitly considered. Its prediction capability allows NMPC to keep the rotor speed close to its optimal value, which strongly depends on the wind speed, cf. Figure 4. This requires the generator torque signal to oscillate around its optimal value,27 cf. fourth plot of Figure 6. It illustrates the maximum load amplitude, the mean load value (position of the box), and the standard deviations of the load signal (vertical size of the box). For all the six load cases, both the maximum torque amplitude and the standard deviation of the torque signal is increased (black vs. red bars). Thus, the amplitudes are increased significantly for low and high frequencies. At the same time, the D is raised by round about 147% to 269%, cf. second plot of Figure 6. A similar result can be observed for the DEL, which is increased by 8.9% and 19.3%, cf. third plot in Figure 6.
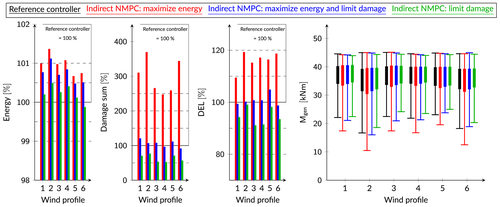
Configuration 2: Larger costs of construction and operation to run NMPC for a wind turbine may not be compensated by this increase of extracted energy, cf. configuration 1. The nature of NMPC allows to explicitly consider the damage, while still obtaining a control signal maximizing the energy. Thus,
 and
and
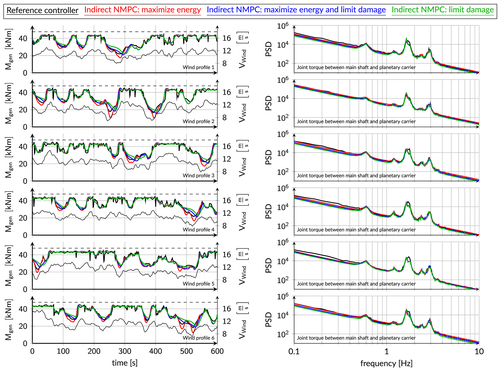
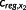 are chosen by a parameter variation such that D and DEL are kept at the level of the reference controller, cf. blue bars in Figure 6. The extracted energy can still be raised by 0.4% to 1.0%.
are chosen by a parameter variation such that D and DEL are kept at the level of the reference controller, cf. blue bars in Figure 6. The extracted energy can still be raised by 0.4% to 1.0%.
Configuration 3: The prediction capability of NMPC can also be used to focus on the reduction of D and DEL. The maximization of the energy extraction is still the objective of NMPC. But the damage is penalized such that the amount of extracted energy is kept at the level of the reference controller. This allows to reduce D by 23.8% to 48.3%. Equivalently, the DEL is decreased by 1% to 9%. The advantage of NMPC with this configuration will be the reduction of the maintenance rate as well as the extension of the life time.
In Figure 7, the generator torque is plotted in the time domain in the left column for all six load cases. The red curves of NMPC configuration 1 show large maximum load amplitudes, whereas the corresponding amplitudes of the blue and black curves are almost coincident. The green curves of NMPC configuration 3 illustrate significant smaller maximum load amplitudes. In the right column, the power spectral density (PSD) of the joint torque between the main shaft and the first planetary carrier is plotted on a double logarithmic scale. The amplitude peaks at 0.6, 1.2, 1.6, 2.4, and 2.9 Hz all can be identified with eigenmodes of the MBS system, which have strong torsional character. It can be seen that the amplitudes below the resonance at 0.6 Hz are reduced by all NMPC configurations. For frequencies above 0.6 Hz, NMPC configuration 1 shows the largest amplitudes, whereas the NMPC configuration 3 still have the smallest amplitudes beside of the resonance frequencies. These resonances are currently not taken into account of NMPC and show further potential, especially when combining the approach with a linear state space model of the drivetrain like it is done in Schulz.4
The optimal control in each NMPC step was determined within a mean time period of 5 ms and a maximum of 51 ms.
5 CONCLUSION
In accordance with recent publications, NMPC can significantly increase the overall performance of extracting electrical power by a wind turbine. The application of NMPC with the focus on purely maximizing the extracted energy shows a control characteristic with a large increase of the load amplitudes within the drivetrain, leading to a reduction of components lifetime. From the mechanical and economical point of view, this needs to be taken into account within the controller, to obtain a competitive control strategy. As the fatigue strength is a characteristic of the entire load signal, terms to limit the DEL and damage sum within the NMPC approach need to be determined.
They need to be chosen such that they prevent large load amplitudes, but also allow the NMPC to profit from its prediction capability and its control precision. NMPC provides the possibility to find such a balance between originally specified requirements on the mean amount of extracted energy or the total life time of the drivetrain and the need to continuously increase the overall performance of a wind turbine. The application of indirect methods allowed to determine the optimal control for the presented load cases significantly faster than 100 ms on a workstation CPU.
REFERENCES
- 1
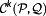 denotes the function space of k-times continuous differentiable functions from
denotes the function space of k-times continuous differentiable functions from
 to
to

- 2 https://www.simpack.com/
- 3 https://tu-dresden.de/ing/maschinenwesen/imm




