Quality and Reliability Engineering International

RESEARCH ARTICLE

Open Access

Novel Bayesian CUSUM and EWMA control charts via various loss functions for monitoring processes

Chelsea L. Jones

Department of Statistical Science and Operations Research, College of Humanities and Sciences, Virginia Commonwealth University, Richmond, Virginia, USA

Search for more papers by this author

Abdel-Salam G. Abdel-Salam,

Corresponding Author

Abdel-Salam G. Abdel-Salam

[email protected]

orcid.org/0000-0003-4905-6489

Department of Mathematics, Statistics and Physics, Statistics Program, College of Arts and Sciences, Qatar University, Doha, Qatar

Correspondence

Department of Mathematics, Statistics and Physics, CAS, Qatar University, Doha, Qatar.

Email: [email protected]

Search for more papers by this author

D'Arcy Mays,

D'Arcy Mays

Department of Statistical Science and Operations Research, College of Humanities and Sciences, Virginia Commonwealth University, Richmond, Virginia, USA

Search for more papers by this author

Chelsea L. Jones,

Chelsea L. Jones

Department of Statistical Science and Operations Research, College of Humanities and Sciences, Virginia Commonwealth University, Richmond, Virginia, USA

Search for more papers by this author

Abdel-Salam G. Abdel-Salam,

Corresponding Author

Abdel-Salam G. Abdel-Salam

[email protected]

orcid.org/0000-0003-4905-6489

Department of Mathematics, Statistics and Physics, Statistics Program, College of Arts and Sciences, Qatar University, Doha, Qatar

Correspondence

Department of Mathematics, Statistics and Physics, CAS, Qatar University, Doha, Qatar.

Email: [email protected]

Search for more papers by this author

D'Arcy Mays,

D'Arcy Mays

Department of Statistical Science and Operations Research, College of Humanities and Sciences, Virginia Commonwealth University, Richmond, Virginia, USA

Search for more papers by this author

First published: 17 November 2022

https://doi.org/10.1002/qre.3229

Citations: 2

Share a link

Email
Wechat
Bluesky

Abstract

In this work, both the cumulative sum (CUSUM) and exponentially weighted moving average (EWMA) control charts have been reconfigured to monitor processes using a Bayesian approach. Our construction of these charts are informed by posterior and posterior predictive distributions found using three loss functions: the squared error, precautionary, and linex. We use these control charts on count data, performing a simulation study to assess chart performance. Our simulations consist of sensitivity analysis of the out-of-control shift size and choice of hyper-parameters of the given distributions. Practical use of theses charts are evaluated on real data.

1 INTRODUCTION

In statistical process monitoring (SPM), control charts are a vital visual tool used to monitor a process and alert of any discrepancies. Many control charts have been developed to encompass the different processes to monitor, mainly falling into two categories: memory-less and memory-based. A memory-less chart does not take into consideration previous observations and are best used to detect large/sudden changes. Memory-based charts compute the current statistic using the previous' and are ideal for detecting small/gradual changes. The Shewhart control chart, first outlined in Shewhart¹, is a frequently used memory-less chart while the cumulative sum (CUSUM)² and exponentially weighted moving average (EWMA)³ charts are well-known memory-based charts. Review papers, Refs. 4 and 5 show the direction that statistical process control (SPC) has taken over the past decade, leaving room for Woodall and Faltin⁶ to address how we approach the current methods and rethink their uses going forward. In their practitioner's guide, Jones et al.⁷ provide detailed examples of the use and comparison of the most commonly used charts, allowing novice users to join the discussion. Recently, Ali⁸ constructed Bayesian control charts to monitor time-between events and⁹ modified the EWMA location chart with Bayesian methods assessing its performance on mechanical and sports applications.

In Riaz et al.¹⁰, the EWMA control chart is considered under a Bayesian approach. A comparison analysis is conducted on control limits found using the classical approach and the Bayesian approach under a symmetric loss function and two asymmetric loss functions: squared error loss function (SELF), precautionary loss function (PLF), and Linex loss function (LLF). A normal conjugate prior is used on data that is normally distributed throughout the paper. For each of the loss functions, a sensitivity analysis is done for the choice of hyper-parameter and its effect on the performance of the Bayesian EWMA chart. The measurement tools used for comparative purposes are the average run length (ARL) and standard deviation run length (SDRL). We conduct analysis of a Bayesian EWMA and a Bayesian CUSUM chart via ARL, SDRL, average time to signal (ATS), and standard deviation of time to signal (SDTS) using a Poisson likelihood and Gamma prior distribution under the same loss functions.

This research introduces new Bayesian EWMA and CUSUM charts for profile monitoring based on different common loos functions in the literature and application. We perform a comprehensive sensitivity analysis for the proposed Bayesian EWMA/CUSUM charts under the Poisson conjugate case, seeking to contribute a Bayesian substitute to the classical EWMA and CUSUM charts for count data without the need for a data transform. Given the current pandemic, it is vital to track and predict when devastating outbreaks will occur. This manuscript provides a monitoring tool used to understand patterns of respiratory disease-related hospitalizations and allows for accurate/immediate identification of a spike in counts.

We first conduct analysis of the Bayesian CUSUM chart under the Normal conjugate case and compare results to that obtained using the Bayesian EWMA. Then, we complete an analysis of the respective control charts under a Poisson likelihood and Gamma prior. Last, we conduct a real data analysis of count data to show application of our method. Our objective is to assess the choice of loss function in relation to distribution and deduce generality of the Bayesian EWMA and Bayesian CUSUM control charts.

In Section 2, we define and discuss the use of loss functions as a tool in Bayesian Inference. This chapter is to introduce readers to how these Bayesian techniques work and how we will implement them in our research.

2 BAYESIAN INFERENCE

Bayes theorem combines the likelihood function, which is determined by the data, with the expert-chosen prior distribution to determine what the posterior distribution will be (Equation 1).

\begin{equation} \begin{aligned} p(\theta | {\bf X}) = \frac{ p({\bf X}|\theta )p(\theta ) }{p({\bf X} )} \end{aligned} \end{equation}

(1)

where, θ is the parameter of interest, X is the data, P(θ) is the prior distribution, P(X) is the marginal distribution of the data, and P(X|θ) is the likelihood function. Once the posterior distribution is found, it is be combined with the likelihood of future y data and integrated with respect to θ to obtain the posterior predictive distribution (Equation 2).

\begin{equation} \def\eqcellsep{&}\begin{array}{rl}{p(y|\mathbf{X})}& \displaystyle{=\int p(\mathbf{y}|\theta )p(\theta |\mathbf{X})d\theta}\\ {\text{where,}\ p(\mathbf{y}|\theta )}& {\text{is the likelihood function for the future data}}\end{array} \end{equation}

(2)

2.1 Loss functions

In Bayesian statistics, a loss function can be used to obtain the best estimator for the parameter of interest. The idea is to minimize the expected loss presented using a specified loss function, with the general form seen in Equation (3).

\begin{equation} \def\eqcellsep{&}\begin{array}{rl}{{\hat{\theta}}^{\ast}}& {=\underset{\hat{\theta}}\min{E}_{\theta}[L(\hat{\theta},\theta )]}\\ {\text{where,}\ {\hat{\theta}}^{\ast}}& {\text{is the estimator, which minimizes the expected loss.}}\end{array} \end{equation}

(3)

We study the three loss functions that are shown in Table 1 for our method. The first is the SELF, which is a symmetric loss function known for its simplicity and easy application. Next we study the PLF, first outlined in Norstrom¹¹ to prevent parameter overestimation. Unlike the SELF, this loss function weights positive and negative errors differently and is known to produce better estimators for low failure rate problems. The LLF, our final choice, is similar to the PLF in that it is also asymmetric aiming to identify parameter overestimation. The constant, c, in the LLF is user-defined such that if c > 0, overestimation takes precedence, but if c → 0, the loss function becomes symmetric.

TABLE 1. Bayes estimators for loss functions

Loss function	$\bm {L(\theta , \hat{\theta }) =}$	$\bm {\hat{\theta ^{*}} =}$
Squared error	$(\theta - \hat{\theta })^{2}$	E[θ\|x]
Precautionary	$\displaystyle\frac{(\theta - \hat{\theta })^{2}}{\hat{\theta }}$	$\sqrt {E[\theta ^{2}\| x]}$
Linex	$(e^{c(\hat{\theta }-\theta )} - c(\hat{\theta }-\theta )-1)$	$-\displaystyle\frac{1}{c}lnE[e^{-c\theta }]$

3 BAYESIAN FRAMEWORK

3.1 Normal conjugate

Identifying that the sample data are normal with the mean of the population unknown and the population variance known, we are able to use the Normal conjugate. In Table 2, we provide the Bayes estimators for each of the loss functions. Within Tables 2 and 3, $\sigma^{2}_{0}$ represents the prior variance and σ² represents the known variance of the likelihood distribution. The calculation of the variances for the posterior, posterior predictive, and Bayes estimator of the posterior predictive distributions remains the same under each loss function as what is seen in Riaz et al.¹⁰. The Bayes estimator in this work is calculated by joining the loss function with the mean of the posterior distribution, it is not considered to be the mean of the posterior or posterior predictive distribution in particular. Rather it is used to find the best estimator for the parameter of interest, which here is the mean of the posterior distribution. The posterior predictive distribution is solely used to generate more data for us to compare against our Bayes estimator.

TABLE 2. Bayes estimators for loss functions

Loss function	Bayes estimator
Squared error	$\mu _{SELF, NN} = \displaystyle\frac{n\bar{x}\sigma^{2}_{0} + \sigma^{2}\mu _{0}}{\sigma^{2}+n\sigma^{2}_{0}}$
Precautionary	$\mu _{PLF, NN} = \sqrt {\displaystyle\frac{(\sigma^{4}+\sigma^{2} \sigma^{2}_{0}(n+1))(\sigma^{2} + n\sigma^{2}_{0}) + (n\bar{x}\sigma^{2}_{0} + \sigma^{2}\mu _{0})^{2} }{(\sigma^{2} + n\sigma^{2}_{0})^{2} } }$
Linex	$\mu _{LLF, NN} = \displaystyle\frac{n\bar{x}\sigma^{2}_{0} + \sigma^{2}\mu _{0}}{\sigma^{2}+n\sigma^{2}_{0}} -\displaystyle\frac{c}{2}\left(\sigma^{2} + \displaystyle\frac{\sigma^{2}\sigma^{2}_{0}}{\sigma^{2}+n\sigma^{2}_{0}}\right )$

TABLE 3. Variances based on distribution

Distribution	Variance
Posterior	$\sigma^{2}_{n} = \displaystyle\frac{\sigma^{2}\sigma^{2}_{0}}{\sigma^{2}+n\sigma^{2}_{0}}$
Posterior predictive	$\sigma^{2}_{ppd} = \sigma^{2} + \sigma^{2}_{n}$
Bayes estimator of posterior predictive	$\sigma^{2}_{\bar{Y}} = \displaystyle\frac{\sigma^{2}}{n} + \sigma^{2}_{n}$

where, n is the sample size, $\bar{x}$ is the sample mean, μ₀ is the prior mean, $\sigma^{2}_{0}$ is the prior variance, σ² is the known variance, and c is the LLF symmetry constant.

The hyper-parameters of interest in Table 4 are μ and σ², while n and $\bar{x}$ in the aforementioned tables are the parameters of the distributions.

TABLE 4. Distribution definitions

	Distribution
Likelihood	μ\|X ∼ N(μ₀, σ²)
Posterior	$\mu \|{\bf X} \sim N(\mu , \sigma^{2}_{n})$
Posterior predictive	${\bf Y}\|{\bf X} \sim N(\mu , \sigma^{2}_{ppd})$
Bayes estimator	${\bf \bar{Y}}\|{\bf X} \sim N(\mu _{LF}, \sigma^{2}_{\bar{Y}})$

3.2 Poisson conjugate

The Poisson distribution is best for modeling count data, and when used under Bayesian inference, its conjugate prior is the Gamma distribution. When combined under Equation (1), we obtain the following posterior distribution: $Gamma(n \bar{x}+\alpha , n+\beta )$ , with shape $= (n \bar{x}+\alpha )$ and inverse scale =(n + β). Once the posterior distribution is obtained, we are able to derive the posterior predictive distribution to be $NegBin(n \bar{x}+\alpha , n+\beta )$ under Equation (2). Derivations for the above posterior and posterior predictive distributions can be seen in Section A.1 of the appendix. The means for both the posterior and posterior predictive distributions are derived under each of the loss functions and are seen in Table 5. Since our method tracks the Bayes estimator of a profile, we need the variance of the Bayes estimator of the posterior predictive distribution, $\sigma^{2}_{\bar{Y}}$ (see Table 6). Note that because we track profile averages as our Bayes Estimator, our μ under each loss function will be different, but our variances will remain the same regardless of the loss function used.

TABLE 5. Bayes estimators for loss functions

Loss function	Bayes estimator
Squared error	$\mu _{SELF, PG} = \displaystyle\frac{n \bar{x}+\alpha }{n+\beta }$
Precautionary	$\mu _{PLF, PG} = \displaystyle\frac{ \sqrt {(n\bar{x} + \alpha )(n\bar{x} + \alpha )^{2}}}{n + \beta }$
Linex	$\mu _{LLF, PG} = -\displaystyle\frac{1}{c} ln \left[\displaystyle\frac{ \beta ^{\alpha }}{(c + \beta )^{\alpha }}\right]$

TABLE 6. Variances based on distribution

Distribution	Variance
Posterior	$\sigma^{2}_{PD} = \displaystyle\frac{n \bar{x} + \alpha }{(n + \beta )^{2}}$
Posterior predictive	$\sigma^{2}_{PPD} = \displaystyle\frac{n \bar{x} + \alpha }{(n + \beta )^{2}}(n + \beta + 1)$
Bayes estimator of posterior predictive	$\sigma^{2}_{\bar{Y}} = \displaystyle\frac{n \bar{x} + \alpha }{n(n + \beta )^{2}}(n + \beta + 1)$

Where, n is the sample size, $\bar{x}$ is the sample mean, α is the shape parameter, β is the inverse scale parameter, and c is the LLF symmetry constant.

The hyper-parameters of interest in Table 7 are α and β, while n and $\bar{x}$ are the parameters.

TABLE 7. Distribution definitions

	Distribution
Likelihood	x\|λ ∼ Poisson(λ)
Posterior	$\lambda \|{\bf X} \sim Gamma(n \bar{x}+\alpha , n+\beta )$
Posterior predictive	${\bf Y}\|{\bf X} \sim NegBin(n \bar{x}+\alpha , n+\beta )$
Bayes Estimator	${\bf \bar{Y}}\|{\bf X} \sim NegBin(n \bar{x}+\alpha , n+\beta )$

4 CONTROL CHART SCHEMATICS

The control limits for the Bayesian EWMA and Bayesian CUSUM control charts follow the same form as the standard EWMA and CUSUM charts, respectively. The mean and standard deviation used for the chart limits are based on the mean and standard deviation obtained using the Bayes estimator posterior predictive distribution under each loss function. Note that the plotting statistics in Equations (4) and (5) also follow the standard form for the EWMA and CUSUM control charts.

EWMA posterior predictive control limits:

\begin{equation} \begin{aligned} UCL/LCL &= \mu _{LF} \pm L\sigma _{\bar{Y}}\sqrt {\frac{\tau }{2 - \tau }} \\[-3pt] CL &= \mu _{LF}\\[-3pt] z_{i} = \tau (\bar{y}|x) &+ (1-\tau )z_{i-1} \end{aligned} \end{equation}

(4)

CUSUM posterior predictive control limits:

\begin{equation} \begin{aligned} UCL/LCL &= \pm h * \sigma _{\bar{Y}} \\[-3pt] CL &= \mu _{LF}\\[-3pt] c_{i} = \max [0, c_{i-1} &+ (\bar{y}|x) - k] \end{aligned} \end{equation}

(5)

where, μ_LF and

\sigma _{\bar{Y}}

are the mean and standard deviation from the Bayes estimator posterior predictive distribution respective to the loss function used,

(\bar{y}|x)

is the Bayes estimator for the set of predicted data, τ is a user-defined constant determining the amount of memory, h determines the control limits for the CUSUM chart, and k is user-defined constant. For the Poisson conjugate case, we only consider upper limits for our control charts. This is because we are concerned with an unusual rise in counts rather than a drop in counts.

5 SENSITIVITY ANALYSES

We conduct a sensitivity analysis for the hyper-parameters and the sample size for the Bayesian EWMA and CUSUM control charts under the Poisson conjugate and the Bayesian CUSUM control chart under the Normal conjugate to test their performance. For both analyses, our performance measurements are the ARL, standard deviation of the run length (SDRL), ATS, and the SDTS. We assess the performance by first obtaining the desired in-control ARL, then determine which method has the greatest decrease once the initial shift is imposed.

We impose 11 relatively small shift sizes denoted as δ = 0 to 2.5 by 0.25, where the shift size is defined as μ₁ = μ₀*(1 + δ). Note that δ = 0 indicates our desired in-control ARL of around 500 (ARL₀ = 500) for the Poisson case and 370 (ARL₀ = 370) for the Guassian case, using m = 10,000 iterations to calculate our results.

5.1 Normal conjugate

The Guassian conjugate-based CUSUM chart uses h = 6 and k = 0 to obtain the desired ARL₀ = 370. When generating the initial data, we use a standard normal (N(0, 1)), where the out-of-control mean is μ₁ = μ + δ and choices for the hyper-parameters are μ₀ = {5, 10, 15} and σ = {2, 4, 6}.

For the sample size analysis under both control charts, we choose n = {5, 10, 20, 30}. Simulations for the EWMA chart calculates these measurements under varying smoothing parameter values as well (τ = 0.15, 0.30, 0.70).

Table 8 shows simulation results from the Bayesian CUSUM control chart under a normal conjugate prior. Constant values of h = 6 and k = 0 were used to obtain in-control ARL results of around 370. The prior mean and variance were adjusted for sensitivity analysis of the hyper-parameters while applying shifts to the in-control mean (μ₀). For all of the loss functions, the initial shift in the mean returns a drastic drop in the ARL and SDRL. After the first shift, as the shifts increase the ARL and SDRL gradually decrease. This shows that a relatively small shift is detectable when using the Bayesian CUSUM control chart and detection is consistent over several loss functions. Results also show that as you adjust the input for the hyper-parameters, this control chart performs consistently. ATS and SDTS values, in seconds, are not significantly different within each loss function, but overall, the LLF has values that are noticeably smaller than the squared error and PLFs.

TABLE 8. Bayesian CUSUM chart hyper-parameter sensitivity analysis for normal conjugate

Shifts	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS
	μ₀ = 5, σ₀ = 2				μ₀ = 10, σ₀ = 4				μ₀ = 15, σ₀ = 6
	SELF
0	382.56	314.01	2.10E-07	1.85E-06	377.59	310.84	2.06E-07	1.84E-06	381.31	311.04	1.96E-07	1.80E-06
0.25	25.15	6.74	2.18E-07	1.89E-06	25.11	6.69	2.29E-07	1.98E-06	25.23	6.69	1.67E-07	1.66E-06
0.5	12.29	2.39	1.98E-07	1.80E-06	12.35	2.43	2.09E-07	1.85E-06	12.29	2.37	1.97E-07	1.80E-06
0.75	7.98	1.33	1.79E-07	1.71E-06	7.99	1.33	2.10E-07	1.85E-06	7.97	1.32	2.13E-07	1.87E-06
1	5.85	0.88	2.29E-07	1.94E-06	5.84	0.88	2.12E-07	1.86E-06	5.87	0.90	2.18E-07	1.89E-06
1.25	4.56	0.66	1.90E-07	1.76E-06	4.56	0.67	1.94E-07	1.78E-06	4.57	0.67	2.18E-07	1.89E-06
1.5	3.71	0.55	1.73E-07	1.68E-06	3.73	0.56	2.29E-07	3.63E-06	3.71	0.55	2.24E-07	1.92E-06
1.75	3.10	0.41	2.01E-07	1.81E-06	3.11	0.41	2.34E-07	1.96E-06	3.11	0.41	1.93E-07	1.78E-06
2	2.70	0.47	2.04E-07	1.83E-06	2.70	0.47	1.93E-07	1.78E-06	2.69	0.47	1.91E-07	1.77E-06
2.25	2.21	0.41	2.03E-07	1.82E-06	2.21	0.41	2.16E-07	1.97E-06	2.22	0.41	2.27E-07	1.93E-06
2.5	2.01	0.14	2.00E-07	1.81E-06	2.01	0.14	2.15E-07	1.87E-06	2.01	0.15	1.96E-07	1.79E-06
	PLF
0	386.09	317.27	1.73E-07	1.68E-06	383.81	308.29	2.36E-07	1.96E-06	382.06	309.74	2.19E-07	1.90E-06
0.25	25.08	6.83	1.90E-07	1.76E-06	25.26	6.76	2.30E-07	1.94E-06	25.36	6.90	2.06E-07	1.84E-06
0.5	12.29	2.44	2.17E-07	1.88E-06	12.29	2.40	1.98E-07	1.80E-06	12.30	2.41	1.66E-07	1.66E-06
0.75	7.98	1.33	1.65E-07	1.65E-06	7.99	1.34	2.06E-07	1.88E-06	7.98	1.31	1.93E-07	1.78E-06
1	5.85	0.90	1.98E-07	1.80E-06	5.83	0.90	1.96E-07	1.80E-06	5.86	0.88	1.83E-07	1.73E-06
1.25	4.56	0.67	2.03E-07	1.83E-06	4.57	0.67	2.23E-07	1.91E-06	4.58	0.67	1.65E-07	1.65E-06
1.5	3.72	0.55	2.23E-07	1.91E-06	3.7171	0.55	1.90E-07	1.77E-06	3.72	0.56	1.81E-07	1.73E-06
1.75	3.11	0.42	1.95E-07	1.79E-06	3.10	0.40	1.89E-07	1.76E-06	3.11	0.411	2.07E-07	1.84E-06
2	2.69	0.47	2.23E-07	1.91E-06	2.70	0.47	2.26E-07	1.92E-06	2.69	0.47	1.80E-07	1.72E-06
2.25	2.21	0.41	1.83E-07	1.73E-06	2.21	0.41	1.96E-07	1.79E-06	2.22	0.42	1.92E-07	1.77E-06
2.5	2.01	0.15	2.00E-07	1.81E-06	2.02	0.15	1.99E-07	1.81E-06	2.02	0.14	1.81E-07	1.72E-06
	LLF
0	382.63	310.76	2.16E-07	1.88E-06	379.76	312.01	1.98E-07	1.80E-06	381.62	311.29	2.05E-07	1.84E-06
0.25	25.28	6.81	1.90E-07	1.77E-06	25.19	6.71	1.55E-07	1.60E-06	25.22	6.70	1.66E-07	1.65E-06
0.5	12.30	2.43	2.14E-07	1.87E-06	12.26	2.40	1.81E-07	1.72E-06	12.26	2.36	1.86E-07	1.75E-06
0.75	7.96	1.31	2.00E-07	1.81E-06	7.98	1.32	1.82E-07	1.73E-06	7.99	1.32	2.06E-07	1.84E-06
1	5.83	0.89	1.88E-07	1.76E-06	5.83	0.89	1.83E-07	1.73E-06	5.85	0.89	2.02E-07	1.82E-06
1.25	4.56	0.67	2.14E-07	1.87E-06	4.58	0.66	1.46E-07	1.55E-06	4.57	0.67	1.85E-07	1.74E-06
1.5	3.72	0.56	2.04E-07	1.83E-06	3.73	0.55	1.74E-07	1.69E-06	3.73	0.55	1.88E-07	1.76E-06
1.75	3.10	0.40	2.15E-07	1.88E-06	3.11	0.41	1.96E-07	1.80E-06	3.10	0.41	1.81E-07	1.72E-06
2	2.69	0.47	2.07E-07	1.84E-06	2.69	0.47	1.81E-07	1.72E-06	2.69	0.47	2.34E-07	1.96E-06
2.25	2.21	0.41	2.04E-07	1.83E-06	2.20	0.40	1.41E-07	1.53E-06	2.22	0.41	1.86E-07	1.75E-06
2.5	2.02	0.14	2.43E-07	2.01E-06	2.01	0.14	1.64E-07	1.64E-06	2.02	0.14	2.08E-07	1.85E-06

Similar trends about the Bayesian CUSUM chart that were noticed in Table 8 can also be seen in Table 9. By decreasing the h value and holding k = 0 as the sample size increases, we obtain ARL₀ values around 370. This is intuitive since increasing sample size typically delays detection, thus shrinking the bounds for the control limits allows for timely detection. As before, we notice that there is an immediate drop in ARL when the initial mean shift is applied and a gradual decrease after for all loss functions. We notice that as we increase n while applying the mean shifts, the drop in the ARL is larger in the larger samples. This shows that detection ability grows with sample size. ATS and SDTS are also effected by increasing sample size; detection time decreases as sample size increases.

TABLE 9. Bayesian CUSUM chart sample size sensitivity analysis for normal conjugate

n	h	0	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25	2.5
	Shifts
SELF
5	8.4	375.4	37.16	18.26	11.95	8.82	6.93	5.68	4.78	4.14	3.61	3.18
		(308.23)	(11.95)	(4.22)	(2.34)	(1.55)	(1.11)	(0.87)	(0.72)	(0.60)	(0.55)	(0.45)
		2.07E-07	2.18E-07	1.76E-07	2.06E-07	2.01E-07	2.46E-07	1.69E-07	2.16E-07	2.11E-07	2.11E-07	1.80E-07
		(1.86E-06)	(1.89E-06)	(1.70E-06)	(1.84E-06)	(1.81E-06)	(2.01E-06)	(1.67E-06)	(1.88E-06)	(1.86E-06)	(1.87E-06)	(1.72E-06)
10	6	381.09	25.21	12.32	8.002	5.85	4.58	3.71	3.11	2.69	2.21	2.02
		(313.34)	(6.77)	(2.44)	(1.35)	(0.89)	(0.66)	(0.55)	(0.41)	(0.47)	(0.41)	(0.14)
		2.60E-07	1.67E-07	2.19E-07	1.97E-07	1.75E-07	1.89E-07	1.82E-07	1.97E-07	1.78E-07	1.78E-07	1.72E-07
		(2.06E-06)	(1.66E-06)	(1.89E-06)	(1.80E-06)	(1.69E-06)	(1.76E-06)	(1.73E-06)	(1.80E-06)	(1.71E-06)	(1.71E-06)	(1.68E-06)
20	4.18	369.38	16.97	8.18	5.27	3.81	2.97	2.30	2.00	1.81	1.25	1.01
		(299.40)	(3.83)	(1.40)	(0.79)	(0.56)	(0.38)	(0.46)	(0.13)	(0.39)	(0.43)	(0.11)
		1.90E-07	1.57E-07	2.11E-07	2.14E-07	1.92E-07	2.07E-07	1.93E-07	2.03E-07	1.50E-07	1.91E-07	2.09E-07
		(1.76E-06)	(1.60E-06)	(1.86E-06)	(1.88E-06)	(1.77E-06)	(1.84E-06)	(1.78E-06)	(1.83E-06)	(1.57E-06)	(1.77E-06)	(1.85E-06)
30	3.4	373.03	13.54	6.47	4.1425	2.99	2.19	1.96	1.43	1.02	1.00	1.00
		(304.37)	(2.84)	(1.03)	(0.60)	(0.39)	(0.39)	(0.19)	(0.50)	(0.15)	(0.00)	(0.00)
		2.33E-07	2.25E-07	2.08E-07	2.14E-07	2.09E-07	2.31E-07	2.59E-07	1.97E-07	2.14E-07	2.70E-07	2.24E-07
		(1.95E-06)	(1.92E-06)	(1.84E-06)	(1.87E-06)	(1.85E-06)	(1.95E-06)	(2.06E-06)	(1.79E-06)	(1.87E-06)	(2.10E-06)	(1.91E-06)
PLF
5	8.4	375.60	37.21	18.24	11.98	8.78	6.93	5.67	4.79	4.12	3.61	3.18
		(310.61)	(12.12)	(4.25)	(2.34)	(1.53)	(1.11)	(0.86)	(0.70)	(0.60)	(0.55)	(0.44)
		2.09E-07	1.94E-07	2.10E-07	2.01E-07	1.70E-07	1.64E-07	1.56E-07	1.96E-07	1.87E-07	1.83E-07	2.08E-07
		(1.85E-06)	(1.79E-06)	(1.85E-06)	(1.82E-06)	(1.67E-06)	(1.64E-06)	(1.60E-06)	(1.79E-06)	(1.75E-06)	(1.73E-06)	(1.85E-06)
10	6	377.37	25.17	12.27	7.98	5.85	4.57	3.73	3.11	2.70	2.21	2.01
		(303.99)	(6.63)	(2.42)	(1.34)	(0.89)	(0.66)	(0.56)	(0.41)	(0.47)	(0.41)	(0.14)
		1.88E-07	2.17E-07	2.01E-07	2.05E-07	1.87E-07	2.10E-07	1.84E-07	2.08E-07	1.65E-07	1.84E-07	1.93E-07
		(1.75E-06)	(1.90E-06)	(1.82E-06)	(1.83E-06)	(1.75E-06)	(1.85E-06)	(1.74E-06)	(1.85E-06)	(1.65E-06)	(1.74E-06)	(1.78E-06)
20	4.18	368.62	16.94	8.15	5.26	3.81	2.97	2.29	1.99	1.81	1.26	1.01
		(297.55)	(3.80)	(1.39)	(0.80)	(0.57)	(0.39)	(0.46)	(0.13)	(0.39)	(0.44)	(0.11)
		1.88E-07	1.96E-07	2.04E-07	1.98E-07	3.03E-07	1.76E-07	2.16E-07	2.10E-07	1.97E-07	2.08E-07	1.71E-07
		(1.76E-06)	(1.79E-06)	(1.83E-06)	(1.80E-06)	(2.22E-06)	(1.70E-06)	(1.88E-06)	(1.86E-06)	(1.80E-06)	(1.85E-06)	(1.68E-06)
30	3.41	367.25	13.59	6.52	4.14	3.00	2.19	1.96	1.45	1.02	1.00	1.00
		(295.35)	(2.83)	(1.03)	(0.60)	(0.39)	(0.39)	(0.19)	(0.50)	(0.14)	(0.01)	(0.00)
		1.80E-07	2.03E-07	1.80E-07	2.09E-07	2.17E-07	2.38E-07	1.98E-07	1.91E-07	2.22E-07	1.98E-07	1.88E-07
		(1.72E-06)	(1.82E-06)	(1.72E-06)	(1.85E-06)	(1.89E-06)	(1.97E-06)	(1.80E-06)	(1.77E-06)	(1.90E-06)	(1.80E-06)	(1.76E-06)
LLF
5	8.4	376.36	37.18	18.20	11.97	8.82	6.92	5.68	4.81	4.14	3.60	3.18
		(314.90)	(12.01)	(4.27)	(2.32)	(1.53)	(1.10)	(0.87)	(0.72)	(0.59)	(0.55)	(0.44)
		1.52E-07	1.56E-07	2.10E-07	2.15E-07	1.97E-07	1.75E-07	1.75E-07	1.93E-07	1.75E-07	1.71E-07	1.53E-07
		(1.58E-06)	(1.61E-06)	(1.86E-06)	(1.88E-06)	(1.80E-06)	(1.69E-06)	(1.69E-06)	(1.78E-06)	(1.69E-06)	(1.68E-06)	(1.59E-06)
10	6	378.46	25.35	12.26	7.96	5.85	4.57	3.72	3.10	2.70	2.20	2.01
		(312.25)	(6.71)	(2.38)	(1.34)	(0.88)	(0.67)	(0.55)	(0.41)	(0.47)	(0.40)	(0.13)
		1.76E-07	1.60E-07	2.19E-07	1.86E-07	1.81E-07	1.81E-07	1.89E-07	1.84E-07	2.19E-07	1.90E-07	1.75E-07
		(1.70E-06)	(1.62E-06)	(1.90E-06)	(1.75E-06)	(1.73E-06)	(1.72E-06)	(1.76E-06)	(1.74E-06)	(1.89E-06)	(1.77E-06)	(1.70E-06)
20	4.18	371.93	16.97	8.17	5.26	3.81	2.97	2.29	2.00	1.81	1.25	1.01
		(310.14)	(3.87)	(1.39)	(0.79)	(0.56)	(0.38)	(0.46)	(0.12)	(0.39)	(0.43)	(0.12)
		1.80E-07	2.58E-07	1.53E-07	1.83E-07	1.98E-07	1.94E-07	2.01E-07	1.69E-07	2.04E-07	1.85E-07	1.90E-07
		(1.72E-06)	(2.05E-06)	(1.58E-06)	(1.73E-06)	(1.80E-06)	(1.79E-06)	(1.82E-06)	(1.67E-06)	(1.83E-06)	(1.74E-06)	(1.76E-06)
30	3.41	368.33	13.59	6.51	4.16	3.01	2.19	1.97	1.46	1.02	1.00	1.00
		(304.74)	(2.85)	(1.02)	(0.60)	(0.38)	(0.39)	(0.18)	(0.50)	(0.15)	(0.01)	(0.01)
		1.88E-07	1.68E-07	2.27E-07	1.63E-07	1.71E-07	1.58E-07	1.92E-07	1.70E-07	1.65E-07	1.69E-07	2.31E-07
		(1.76E-06)	(1.67E-06)	(1.92E-06)	(1.64E-06)	(1.68E-06)	(1.61E-06)	(1.77E-06)	(1.67E-06)	(1.65E-06)	(1.67E-06)	(1.95E-06)

5.2 Poisson conjugate

Here we ran simulations for the Bayesian control charts under the Poisson–Gamma case. We designed both a Bayesian EWMA and Bayesian CUSUM chart to obtain an in-control ARL of 500 and assess their performances with imposed shifts defined as μ₁ = μ₀*(1 + δ). We use values μ₀ = [10, 15, 20] and σ₀ = [4, 6, 8] to solve for our values of α₀ and β₀ to obtain our prior information. These values are α = [16, 36, 64] and $\beta = [\frac{5}{8}, \frac{5}{12}, \frac{5}{16} ]$ as calculated in Section A.1.2. Our initial data are generated from a Poisson distribution with parameter λ = 25.

Our hypter-parameter sensitivity analysis results are found in Table 10. The sample size analysis uses the same values for n as in Section 5.1 and the values for τ and h are determined based on our desired ARL₀ = 500 and are seen in Table 11.

TABLE 10. Bayesian CUSUM chart hyper-parameter sensitivity analysis for poisson conjugate

Shifts	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS
	α₀ = 16, $\beta _{0}=\frac{5}{8}$				α₀ = 36, $\beta _{0}=\frac{5}{12}$				α₀ = 64, $\beta _{0}=\frac{5}{16}$
SELF
0	520.04	520.77	2.28E-07	5.00E-06	523.70	523.31	2.26E-07	6.75E-06	502.16	500.22	2.40E-07	1.98E-06
0.25	26.18	25.88	2.17E-07	7.46E-06	28.88	28.59	2.31E-07	6.72E-06	28.77	28.50	2.06E-07	1.84E-06
0.5	6.33	5.91	1.66E-07	6.53E-06	5.68	5.47	2.17E-07	6.93E-06	6.17	5.91	2.16E-07	1.88E-06
0.75	2.65	2.49	1.86E-07	6.94E-06	2.57	2.47	2.47E-07	5.60E-06	2.59	2.52	2.07E-07	1.85E-06
1	1.47	1.48	2.01E-07	7.18E-06	1.38	1.45	2.28E-07	6.51E-06	1.42	1.48	2.11E-07	1.86E-06
1.25	0.86	1.02	2.01E-07	7.22E-06	0.85	1.02	2.18E-07	4.05E-06	0.83	1.02	1.99E-07	1.80E-06
1.5	0.59	0.80	2.00E-07	7.18E-06	0.57	0.78	2.23E-07	6.93E-06	0.57	0.79	1.94E-07	1.78E-06
1.75	0.41	0.64	2.07E-07	7.27E-06	0.42	0.64	2.17E-07	5.96E-06	0.38	0.63	2.19E-07	1.89E-06
2	0.29	0.54	1.96E-07	7.13E-06	0.29	0.53	1.83E-07	6.60E-06	0.27	0.52	2.12E-07	1.86E-06
2.25	0.20	0.44	2.09E-07	7.36E-06	0.21	0.45	1.79E-07	6.79E-06	0.19	0.44	2.02E-07	1.82E-06
2.5	0.16	0.39	2.07E-07	7.27E-06	0.14	0.37	2.19E-07	5.75E-06	0.15	0.38	2.36E-07	1.98E-06
PLF
0	497.945	498.277	2.49E-07	7.98E-06	498.043	497.059	2.40E-07	7.85E-06	503.656	504.027	2.28E-07	5.35E-06
0.25	28.1911	27.7613	2.00E-07	7.18E-06	25.8255	25.549	2.20E-07	7.54E-06	28.5426	28.2013	2.20E-07	5.39E-06
0.5	6.13445	5.87661	2.58E-07	8.15E-06	5.76852	5.52295	2.10E-07	7.36E-06	6.40804	6.22733	2.28E-07	5.39E-06
0.75	2.63193	2.5283	2.10E-07	7.36E-06	2.54016	2.46418	1.98E-07	7.13E-06	2.49894	2.50251	2.07E-07	5.15E-06
1	1.3573	1.45241	2.39E-07	7.81E-06	1.48763	1.50498	2.19E-07	7.50E-06	1.43639	1.51323	2.22E-07	5.31E-06
1.25	0.89725	1.04922	2.19E-07	7.54E-06	0.87801	1.03212	2.15E-07	7.45E-06	0.87516	1.05679	2.16E-07	5.92E-06
1.5	0.58849	0.79213	2.34E-07	7.73E-06	0.57087	0.780319	2.56E-07	8.11E-06	0.57353	0.796626	2.13E-07	5.16E-06
1.75	0.40317	0.640347	2.24E-07	7.63E-06	0.40193	0.638187	1.86E-07	6.94E-06	0.41875	0.655758	2.09E-07	5.19E-06
2	0.29456	0.536968	2.31E-07	7.72E-06	0.27371	0.522564	2.39E-07	7.78E-06	0.27141	0.522959	2.10E-07	5.16E-06
2.25	0.2008	0.444071	2.37E-07	7.77E-06	0.19407	0.43537	2.49E-07	7.99E-06	0.1925	0.435435	2.25E-07	5.32E-06
2.5	0.15608	0.38838	2.61E-07	8.19E-06	0.16315	0.398788	1.95E-07	7.13E-06	0.14069	0.373117	2.24E-07	5.33E-06
LLF
0	511.163	514.059	1.94E-07	6.27E-06	511.677	511.93	1.77E-07	6.28E-06	506.904	507.725	2.19E-07	7.14E-06
0.25	29.4728	29.1113	1.96E-07	6.17E-06	30.1145	29.7191	1.92E-07	6.57E-06	23.7271	22.7815	2.22E-07	7.44E-06
0.5	6.84833	6.502	1.35E-07	4.94E-06	6.72874	6.34084	2.05E-07	6.78E-06	5.18563	4.67402	2.21E-07	7.41E-06
0.75	2.76337	2.63444	2.14E-07	6.45E-06	2.78938	2.62285	2.24E-07	6.98E-06	2.45799	2.18901	2.37E-07	7.74E-06
1	1.53064	1.54693	1.83E-07	4.69E-06	1.54514	1.54216	2.08E-07	6.97E-06	1.40388	1.3565	2.34E-07	7.64E-06
1.25	0.90341	1.05374	2.09E-07	6.44E-06	0.98446	1.09237	2.47E-07	7.56E-06	0.90978	0.977599	2.03E-07	7.19E-06
1.5	0.6385	0.829095	1.84E-07	5.68E-06	0.62572	0.815889	2.20E-07	7.08E-06	0.66242	0.798536	2.36E-07	7.69E-06
1.75	0.39512	0.634461	2.02E-07	5.92E-06	0.41974	0.655102	2.67E-07	7.80E-06	0.4376	0.642407	2.09E-07	7.24E-06
2	0.29178	0.536455	1.80E-07	6.84E-06	0.28497	0.531509	2.54E-07	7.45E-06	0.33495	0.555732	2.06E-07	7.23E-06
2.25	0.19793	0.441717	2.09E-07	7.32E-06	0.21774	0.46001	2.05E-07	7.02E-06	0.21106	0.447318	2.07E-07	7.21E-06
2.5	0.15885	0.393162	1.94E-07	5.52E-06	0.1721	0.406548	2.23E-07	7.16E-06	0.16768	0.39563	2.61E-07	7.37E-06

TABLE 11. Bayesian CUSUM chart sample size sensitivity analysis for Poisson conjugate

	Shifts
n	h	0	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25	2.5
SELF
5	15	496.298	32.2171	15.6029	9.9113	7.5339	5.6834	4.8584	4.0162	3.5874	3.2056	2.5967	ARL
		(456.631)	(14.6619)	(5.95053)	(3.7745)	(2.80757)	(2.2271)	(1.92649)	(1.63295)	(1.53856)	(1.38807)	(1.24388)	SDRL
		1.71E-07	2.00E-07	1.32E-07	2.30E-07	2.14E-07	2.37E-07	2.87E-07	2.46E-07	2.67E-07	1.56E-07	2.49E-07	ATS
		(6.02E-06)	(6.91E-06)	(5.83E-06)	(7.44E-06)	(7.38E-06)	(7.35E-06)	(8.37E-06)	(7.84E-06)	(8.25E-06)	(5.89E-06)	(7.83E-06)	SDTS
10	5.6	473.362	26.3559	5.38841	2.46537	1.3864	0.85102	0.56017	0.42677	0.29204	0.2053	0.14904	ARL
		(474.171)	(25.6893)	(5.00599)	(2.27279)	(1.38406)	(0.985893)	(0.763662)	(0.638543)	(0.526149)	(0.443703)	(0.376891)	SDRL
		4.34E-07	5.14E-07	5.86E-07	5.65E-07	5.50E-07	5.90E-07	5.92E-07	5.90E-07	5.39E-07	5.13E-07	6.04E-07	ATS
		(8.21E-06)	(7.60E-06)	(8.87E-06)	(9.01E-06)	(1.13E-05)	(8.10E-06)	(9.35E-06)	(9.19E-06)	(1.01E-05)	(1.13E-05)	(8.50E-06)	SDTS
20	25.6	507.147	8.1758	3.1675	1.9069	1.176	0.8272	0.581	0.4307	0.2965	0.1923	0.1012	ARL
		(490.265)	(4.43099)	(1.54947)	(0.97736)	(0.715279)	(0.603937)	(0.556272)	(0.515167)	(0.462588)	(0.395627)	(0.302256)	SDRL
		2.69E-07	2.34E-07	2.47E-07	2.49E-07	2.44E-07	3.04E-07	2.45E-07	3.22E-07	3.00E-07	3.20E-07	2.89E-07	ATS
		(2.09E-06)	(1.95E-06)	(2.01E-06)	(2.02E-06)	(2.00E-06)	(2.22E-06)	(2.00E-06)	(2.27E-06)	(2.20E-06)	(2.26E-06)	(2.16E-06)	SDTS
30	20.05	507.798	5.60247	1.52877	0.68668	0.30691	0.12068	0.04604	0.01606	0.0062	0.002	0.00075	ARL
		(504.214)	(4.3489)	(1.1703)	(0.688368)	(0.49185)	(0.329175)	(0.210096)	(0.125706)	(0.0784956)	(0.0446766)	(0.0273759)	SDRL
		2.61E-07	2.50E-07	2.62E-07	2.70E-07	2.77E-07	2.92E-07	2.71E-07	2.77E-07	2.59E-07	2.55E-07	2.55E-07	ATS
		(2.06E-06)	(2.02E-06)	(2.06E-06)	(2.09E-06)	(2.12E-06)	(2.17E-06)	(2.10E-06)	(2.12E-06)	(2.06E-06)	(2.04E-06)	(2.04E-06)	SDTS
PLF
5	15	485.852	32.0134	15.7883	10.1827	7.62142	5.87656	4.9891	4.03255	3.38085	3.10012	2.78037	ARL
		(441.163)	(14.464)	(6.05076)	(3.77094)	(2.82046)	(2.25137)	(1.92472)	(1.64968)	(1.46048)	(1.37412)	(1.24799)	SDRL
		3.65E-07	4.62E-07	7.03E-07	4.33E-07	3.43E-07	3.41E-07	3.98E-07	3.43E-07	3.37E-07	3.31E-07	3.51E-07	ATS
		(4.35E-06)	(4.46E-06)	(6.62E-06)	(4.91E-06)	(3.89E-06)	(4.01E-06)	(4.34E-06)	(4.62E-06)	(4.34E-06)	(4.44E-06)	(4.45E-06)	SDTS
10	5.65	503.703	25.2912	5.77501	2.57142	1.34871	0.90072	0.60849	0.4113	0.3099	0.228	0.16009	ARL
		(505.085)	(24.6767)	(5.24267)	(2.32112)	(1.36733)	(1.00502)	(0.780647)	(0.630248)	(0.541297)	(0.465571)	(0.392481)	SDRL
		1.94E-07	2.15E-07	2.55E-07	2.35E-07	2.19E-07	2.63E-07	2.06E-07	2.47E-07	2.29E-07	2.22E-07	2.15E-07	ATS
		(7.02E-06)	(7.25E-06)	(7.89E-06)	(7.62E-06)	(7.36E-06)	(8.01E-06)	(7.02E-06)	(7.80E-06)	(7.55E-06)	(7.36E-06)	(7.24E-06)	SDTS
20	26	525.639	8.40693	3.34964	1.88663	1.30903	0.89353	0.58188	0.43516	0.28612	0.18427	0.10412	ARL
		(516.751)	(4.54815)	(1.59026)	(0.963669)	(0.724341)	(0.606856)	(0.55519)	(0.517664)	(0.458143)	(0.389351)	(0.305743)	SDRL
		2.46E-07	2.42E-07	2.27E-07	2.11E-07	2.23E-07	2.00E-07	2.19E-07	2.25E-07	2.18E-07	1.93E-07	2.11E-07	ATS
		(7.94E-06)	(7.90E-06)	(7.68E-06)	(7.41E-06)	(7.59E-06)	(7.18E-06)	(7.50E-06)	(7.63E-06)	(7.46E-06)	(7.03E-06)	(7.41E-06)	SDTS
30	19.68	525.041	5.96356	1.55198	0.66585	0.2828	0.11563	0.04548	0.01557	0.00519	0.0021	0.00067	ARL
		(523.562)	(4.71551)	(1.19914)	(0.693104)	(0.477958)	(0.323481)	(0.208882)	(0.123885)	(0.0718545)	(0.0457776)	(0.0258757)	SDRL
		2.41E-07	2.62E-07	2.70E-07	2.56E-07	2.44E-07	2.55E-07	2.35E-07	2.41E-07	2.45E-07	2.47E-07	2.46E-07	ATS
		(7.73E-06)	(8.23E-06)	(8.36E-06)	(8.07E-06)	(7.94E-06)	(8.07E-06)	(7.81E-06)	(7.90E-06)	(7.98E-06)	(7.94E-06)	(7.98E-06)	SDTS
LLF
5	12	538.844	28.2244	13.2126	8.57527	6.00356	4.79641	4.21672	3.16248	2.7339	2.39553	1.98138	ARL
		(506.553)	(14.7659)	(5.7545)	(3.5996)	(2.56895)	(2.0908)	(1.80989)	(1.50578)	(1.35128)	(1.23558)	(1.1248)	SDRL
		1.95E-07	2.15E-07	2.18E-07	2.24E-07	2.21E-07	1.82E-07	2.08E-07	2.09E-07	1.78E-07	2.03E-07	2.14E-07	ATS
		(6.85E-06)	(7.26E-06)	(7.31E-06)	(7.16E-06)	(7.25E-06)	(6.65E-06)	(7.11E-06)	(7.11E-06)	(6.52E-06)	(7.01E-06)	(7.14E-06)	SDTS
10	5.33	519.013	30.9964	6.4453	2.71976	1.50492	0.92406	0.62997	0.43218	0.29822	0.21673	0.14393	ARL
		(518.483)	(30.6673)	(6.08091)	(2.53317)	(1.49928	(1.04987)	(0.811891)	(0.65547)	(0.541041)	(0.458146)	(0.375199)	SDRL
		2.09E-07	2.87E-07	2.24E-07	1.94E-07	1.82E-07	1.80E-07	1.82E-07	2.13E-07	1.91E-07	2.19E-07	2.26E-07	ATS
		(5.37E-06)	(7.58E-06)	(6.27E-06)	(6.86E-06)	(5.67E-06)	(5.44E-06)	(4.83E-06)	(5.43E-06)	(7.00E-06)	(5.61E-06)	(7.08E-06)	SDTS
20	20.1	509.815	8.08598	2.77656	1.4704	0.99445	0.60287	0.37462	0.25715	0.13602	0.0824	0.0489	ARL
		(506.393)	(5.18941)	(1.59694)	(0.931431)	(0.712263)	(0.594927)	(0.510881)	(0.446211)	(0.345136)	(0.275482)	(0.215983)	SDRL
		2.40E-07	2.55E-07	2.26E-07	2.49E-07	2.37E-07	2.57E-07	2.32E-07	2.25E-07	2.19E-07	2.20E-07	2.21E-07	ATS
		(6.95E-06)	(7.53E-06)	(6.75E-06)	(7.69E-06)	(7.56E-06)	(7.20E-06)	(6.90E-06)	(7.63E-06)	(7.54E-06)	(3.62E-06)	(7.55E-06)	SDTS
30	20	476.63	5.55564	1.49389	0.64454	0.31084	0.12206	0.04281	0.01663	0.00516	0.00173	0.0008	ARL
		(474.056)	(4.30695)	(1.15642)	(0.675831)	(0.493314)	(0.331544)	(0.202873)	(0.128037)	(0.0716476)	(0.0415573)	(0.028273)	SDRL
		4.41E-07	3.27E-07	2.78E-07	2.84E-07	3.01E-07	2.99E-07	3.96E-07	2.82E-07	2.82E-07	3.00E-07	2.58E-07	ATS
		(5.30E-06)	(4.61E-06)	(4.08E-06)	(4.22E-06)	(4.26E-06)	(4.73E-06)	(5.21E-06)	(4.24E-06)	(4.04E-06)	(4.81E-06)	(5.11E-06)	SDTS

Loss function specific results for the hyper-parameter sensitivity analysis are given in Table 12. Results for the squared error method showed a steep decrease in the ARL after the initial shift change of 0.25 was introduced and as we increased the hyper-parameter, this decrease became larger. We also noticed that as we increased the hyper-parameter, the SDRL increases and quicker detection also happens based on the ATS. These findings also translate to the precautionary case, except as the hyper-parameter increases under the PLF, the ATS increases. For the linex case, getting results for the third condition under the analysis with n = 20 and τ = 0.15 was difficult. This is similar to the classical EWMA under each of the hyper-parameters. Results were received, but the number of simulation runs were significantly more than when using the SELF or PLF methods.

TABLE 12. Bayesian EWMA chart hyper-parameter sensitivity analysis for Poisson conjugate

Shifts	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS	ARL	SDRL	ATS	SDTS
	α₀ = 16, $\beta _{0}=\frac{5}{8}$				α₀ = 36, $\beta _{0}=\frac{5}{12}$				α₀ = 64, $\beta _{0}=\frac{5}{16}$
	SELF
0	457.812	584.427	2.83E-07	5.90E-06	503.518	987.898	1.93E-07	1.78E-06	536.307	2725.14	2.64E-07	2.40E-06
0.25	3.1181	5.08246	2.39E-07	5.51E-06	0.4183	1.57915	2.18E-07	1.86E-06	0.0245	0.430697	2.33E-07	1.95E-06
0.5	0.375	0.809058	2.36E-07	5.31E-06	0.0363	0.244504	2.07E-07	1.84E-06	0.0022	0.0616049	1.96E-07	1.79E-06
0.75	0.2198	0.554877	2.75E-07	5.97E-06	0.0469	0.278029	2.19E-07	1.90E-06	0.0006	0.0282779	2.71E-07	2.10E-06
1	0.0389	0.202452	3.54E-07	6.60E-06	0.0065	0.081595	2.01E-07	1.82E-06	0.0004	0.019996	2.36E-07	2.01E-06
1.25	0.0238	0.156312	2.23E-07	5.35E-06	0.0006	0.0244875	2.17E-07	1.89E-06	0.0001	0.0099995	2.19E-07	1.90E-06
1.5	0.0077	0.0874112	1.96E-07	4.97E-06	0.0007	0.0264483	2.06E-07	1.84E-06	0	0	1.96E-07	1.80E-06
1.75	0.0031	0.0555913	2.31E-07	5.38E-06	0.0001	0.0099995	2.71E-07	2.10E-06	0	0	2.04E-07	1.83E-06
2	0.0007	0.0264483	2.35E-07	5.51E-06	0.0001	0.0099995	2.13E-07	1.87E-06	0	0	2.33E-07	1.95E-06
2.25	0.0006	0.0244875	1.69E-07	4.63E-06	0	0	1.97E-07	1.80E-06	0	0	2.38E-07	1.97E-06
2.5	0.0002	0.0141407	2.78E-07	5.98E-06	0	0	1.98E-07	1.80E-06	0	0	2.45E-07	2.00E-06
	PLF
0	458.006	721.484	2.25E-07	1.92E-06	564.132	1231.69	2.68E-07	5.45E-06	520.414	3476.57	8.96E-07	6.42E-06
0.25	0.9618	2.42271	2.47E-07	2.01E-06	0.6846	2.78538	2.44E-07	2.00E-06	0.0187	0.337861	8.65E-07	6.29E-06
0.5	0.2256	0.73014	2.29E-07	1.94E-06	0.0895	0.476329	2.06E-07	1.84E-06	0.0019	0.0607979	8.90E-07	7.16E-06
0.75	0.0299	0.190804	2.35E-07	1.96E-06	0.0087	0.111464	2.21E-07	1.90E-06	0.0003	0.0173179	9.73E-07	6.47E-06
1	0.0122	0.114242	2.31E-07	1.95E-06	0.0017	0.041196	2.21E-07	5.39E-06	0	0	8.61E-07	6.31E-06
1.25	0.0112	0.109884	2.19E-07	1.90E-06	0.0003	0.0173179	1.82E-07	6.88E-06	0	0	7.87E-07	5.85E-06
1.5	0.0006	0.0244875	2.32E-07	1.96E-06	0.0001	0.0099995	2.60E-07	8.23E-06	0	0	8.58E-07	6.13E-06
1.75	0.0001	0.0099995	2.26E-07	1.93E-06	0	0	2.08E-07	7.36E-06	0	0	7.49E-07	5.54E-06
2	0.0001	0.0099995	2.15E-07	1.88E-06	0.0001	0.0099995	2.52E-07	4.10E-06	0	0	8.54E-07	5.61E-06
2.25	0.0001	0.0099995	2.39E-07	1.98E-06	0	0	2.19E-07	1.90E-06	0	0	6.09E-07	5.55E-06
2.5	0	0	2.46E-07	2.00E-06	0	0	2.01E-07	1.81E-06	0	0	3.75E-07	4.36E-06
	LLF
0	495.076	473.145	4.16E-07	4.90E-06	522.696	527.33	3.24E-07	2.42E-06	0	0	2.60E-07	8.23E-06
0.25	15.2008	5.3951	3.24E-07	2.30E-06	6.6035	4.99663	3.14E-07	2.26E-06	0	0	1.82E-07	6.89E-06
0.5	6.7224	1.65636	4.47E-07	3.65E-06	2.163	1.50307	3.48E-07	2.39E-06	0	0	1.57E-07	6.37E-06
0.75	4.9824	1.16829	4.05E-07	2.58E-06	1.123	0.878562	3.10E-07	2.25E-06	0	0	2.23E-07	6.94E-06
1	3.813	0.912705	3.38E-07	2.35E-06	0.6609	0.660539	3.32E-07	2.32E-06	0	0	2.31E-07	6.98E-06
1.25	3.0444	0.770343	2.83E-07	2.15E-06	0.3802	0.529385	3.43E-07	2.36E-06	0	0	2.22E-07	5.93E-06
1.5	2.4436	0.671133	3.48E-07	2.38E-06	0.2101	0.419473	2.97E-07	2.20E-06	0	0	2.12E-07	7.37E-06
1.75	2.0438	0.600568	3.35E-07	2.34E-06	0.1009	0.302191	3.93E-07	2.54E-06	0	0	1.61E-07	6.38E-06
2	1.7136	0.570942	3.12E-07	2.25E-06	0.0654	0.248038	3.19E-07	2.29E-06	0	0	3.39E-07	9.38E-06
2.25	1.5086	0.546558	3.40E-07	2.38E-06	0.0335	0.179938	2.92E-07	2.18E-06	0	0	2.08E-07	7.36E-06
2.5	1.3524	0.503998	3.35E-07	2.33E-06	0.0158	0.1255	3.09E-07	2.25E-06	0	0	2.86E-07	8.63E-06
	Classical
0	469.116	574.412	2.93E-07	2.18E-06	445.19	547.614	4.40E-07	3.84E-06	447.05	542.769	2.41E-07	1.99E-06
0.25	3.3321	5.24559	3.44E-07	2.37E-06	6.8104	9.65327	3.47E-07	2.38E-06	4.282	6.43761	2.41E-07	1.99E-06
0.5	0.6292	1.59019	3.63E-07	2.43E-06	0.4254	1.22883	3.36E-07	2.39E-06	0.6291	1.56567	2.61E-07	2.07E-06
0.75	0.0837	0.435998	3.05E-07	2.23E-06	0.3659	1.08463	3.61E-07	2.42E-06	0.128	0.566053	2.73E-07	2.11E-06
1	0.034	0.25699	2.88E-07	2.17E-06	0.0771	0.407376	3.63E-07	2.44E-06	0.0518	0.322671	2.51E-07	2.03E-06
1.25	0.0138	0.14356	2.79E-07	2.14E-06	0.0091	0.114966	3.22E-07	2.29E-06	0.0138	0.144947	2.54E-07	2.04E-06
1.5	0.0034	0.0691986	2.83E-07	2.16E-06	0.0032	0.0692081	3.19E-07	2.28E-06	0.0025	0.0607762	2.47E-07	2.01E-06
1.75	0.002	0.050951	2.59E-07	2.06E-06	0.0022	0.0528693	2.88E-07	2.17E-06	0.0014	0.0446994	2.56E-07	2.05E-06
2	0.0003	0.0173179	2.66E-07	2.09E-06	0.0007	0.0299918	3.26E-07	2.30E-06	0.0018	0.0468696	2.21E-07	1.90E-06
2.25	0	0	3.16E-07	2.27E-06	0	0	2.97E-07	2.20E-06	0.0002	0.0141407	2.18E-07	1.89E-06
2.5	0.0001	0.0099995	2.78E-07	2.13E-06	0	0	3.35E-07	2.33E-06	0	0	2.25E-07	1.92E-06

Besides the classical method, we conclude that the LLF method performed the worst under the hyper-parameter analysis. The ARL results suggest that the PLF was the best performer, but based on all four performance measurements, the SELF was the top performer.

We see from Table 13 that for the SELF, PLF, and LLF methods, as the sample size increased, the L tuning parameter had to be increased to reach the desirable ARL. Also, we note that there was not a significant change in ATS, but we did take note that it does take slightly less time for detection with the sample size increase. The most interesting result for all of the loss functions was as we increase the sample size, implementing the initial mean shift, the distance between the ARL₀ and out-of-control ARL grew smaller. That is, the larger the sample size, the chances of the chart signaling decreases.

TABLE 13. Bayesian EWMA chart sample size sensitivity analysis for Poisson conjugate

	Shifts
	n	L	0	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25	2.5
SELF
20	−3.7	495.851	0.8169	0.0132	0.0032	0.0006	0.0006	0.0001	0.0001	0.0001	0	0	ARL
		(534.0910)	(1.9407)	(0.9694)	(0.7192)	(0.5475)	(0.5286)	(0.5093)	(0.2843)	(0.2984)	(0.3869)	(0.4422)	(SDRL)
		3.83E-07	3.37E-07	3.45E-07	3.04E-07	3.69E-07	3.81E-07	3.73E-07	3.69E-07	2.52E-07	3.74E-07	4.92E-07	ATS
		(6.70E-06)	(5.75E-06)	(5.33E-06)	(4.99E-06)	(5.07E-06)	(6.01E-06)	(5.29E-06)	(5.23E-06)	(5.01E-06)	(5.07E-06)	(5.23E-06)	(SDTS)
30	78	551.883	7.4582	4.1796	2.9312	2.1155	1.6517	1.4455	1.0171	0.9431	0.826	0.7363	ARL
		(313.336)	(6.77449)	(2.4378)	(1.34781)	(0.885223)	(0.662202)	(0.547244)	(0.410889)	(0.47444)	(0.410161)	(0.140624)	(SDRL)
		2.60E-07	1.67E-07	2.19E-07	1.97E-07	1.75E-07	1.89E-07	1.82E-07	1.97E-07	1.78E-07	1.78E-07	1.72E-07	ATS
		(7.14E-06)	(6.51E-06)	(8.30E-06)	(6.37E-06)	(5.10E-06)	(4.31E-06)	(8.79E-06)	(9.19E-06)	(7.40E-06)	(7.43E-06)	(1.00E-05)	(SDTS)
40	91	571.68	10.735	5.8342	3.8241	2.3965	2.0413	1.5571	1.1684	1.0935	0.9508	0.8813	ARL
		(551.8080)	(3.0739)	(1.3374)	(0.8558)	(0.5859)	(0.5093)	(0.5201)	(0.3858)	(0.3202)	(0.2675)	(0.3377)	(SDRL)
		3.70E-07	2.91E-07	2.74E-07	2.74E-07	2.79E-07	3.96E-07	3.18E-07	2.97E-07	3.12E-07	2.81E-07	2.91E-07	ATS
		(2.45E-06)	(2.18E-06)	(2.12E-06)	(2.12E-06)	(2.14E-06)	(2.53E-06)	(2.29E-06)	(2.20E-06)	(2.25E-06)	(2.14E-06)	(2.18E-06)	(SDTS)
50	150.5	519.9830	10.1315	5.8238	3.6264	2.8496	2.2708	1.8720	1.4312	1.1828	1.0606	0.9870	ARL
		(507.6630)	(2.2237)	(1.0494)	(0.6668)	(0.5562)	(0.4817)	(0.4150)	(0.4965)	(0.3873)	(0.2501)	(0.1779)	(SDRL)
		3.79E-07	2.97E-07	3.65E-07	4.22E-07	2.37E-07	2.68E-07	2.96E-07	2.37E-07	2.21E-07	2.70E-07	2.26E-07	ATS
		(5.69E-06)	(4.19E-06)	(4.94E-06)	(7.88E-06)	(5.97E-06)	(2.09E-06)	(6.55E-06)	(7.39E-06)	(6.93E-06)	(4.15E-06)	(7.38E-06)	(SDTS)
PLF
20	−1.3	533.02	0.9092	0.23	0.0582	0.0191	0.0115	0.0005	0.0012	0.0002	0.0002	0	ARL
		(843.3900)	(2.3949)	(0.7468)	(0.2814)	(0.1495)	(0.1121)	(0.0224)	(0.0374)	(0.0141)	(0)	(0)	(SDRL)
		3.43E-07	1.90E-07	2.86E-07	2.94E-07	2.12E-07	2.58E-07	2.35E-07	2.36E-07	2.60E-07	3.12E-07	2.60E-07	ATS
		(8.68E-06)	(6.90E-06)	(8.63E-06)	(8.64E-06)	(7.37E-06)	(3.25E-06)	(1.96E-06)	(7.81E-06)	(8.23E-06)	(9.02E-06)	(8.23E-06)	(SDTS)
30	35	571.1220	9.3364	3.8706	2.5543	1.5837	1.1444	0.8933	0.6677	0.4379	0.3461	0.1830	ARL
		(560.1300)	(4.0645)	(1.3741)	(0.9362)	(0.6414)	(0.5039)	(0.4511)	(0.4957)	(0.4999)	(0.4772)	(0.3867)	(SDRL)
		7.47E-07	9.50E-07	1.14E-06	8.62E-07	9.14E-07	9.58E-07	6.96E-07	8.69E-07	9.00E-07	1.14E-06	9.97E-07	ATS
		(5.19E-06)	(5.49E-06)	(1.02E-05)	(6.24E-06)	(7.47E-06)	(5.55E-06)	(4.68E-06)	(5.20E-06)	(5.61E-06)	(7.61E-06)	(6.87E-06)	(SDTS)
40	86	453.1480	10.3685	4.5154	2.8399	2.3914	1.7211	1.3709	1.1544	1.0223	0.9054	0.7773	ARL
		(435.9740)	(3.0808)	(1.0119)	(0.6610)	(0.5891)	(0.5139)	(0.4908)	(0.3794)	(0.2720)	(0.3182)	(0.4175)	(SDRL)
		6.89E-07	9.27E-07	8.86E-07	9.99E-07	9.41E-07	9.89E-07	9.55E-07	8.66E-07	9.93E-07	9.63E-07	9.23E-07	ATS
		(3.23E-06)	(3.72E-06)	(3.62E-06)	(4.46E-06)	(3.78E-06)	(4.64E-06)	(3.85E-06)	(3.61E-06)	(6.19E-06)	(3.80E-06)	(3.68E-06)	(SDTS)
50	157	499.929	10.4253	6.3638	4.0256	2.9648	2.3144	1.9576	1.5789	1.2491	1.0912	0.9895	ARL
		(478.347)	(2.28837)	(1.13236)	(0.703523)	(0.564235)	(0.493105)	(0.390643)	(0.498773)	(0.433416)	(0.294419)	(0.166102)	(SDRL)
		5.58E-07	4.17E-07	4.60E-07	3.51E-07	3.62E-07	5.35E-07	2.73E-07	3.43E-07	1.93E-07	3.33E-07	4.24E-07	ATS
		(6.25E-06)	(6.07E-06)	(5.73E-06)	(5.08E-06)	(4.97E-06)	(5.50E-06)	(7.00E-06)	(9.04E-06)	(6.79E-06)	(8.96E-06)	(3.63E-06)	(SDTS)
LLF
20	9	569.539	6.9163	2.1641	1.1105	0.6095	0.371	0.2089	0.11	0.056	0.0334	0.0194	ARL
		(564.402)	(5.01854)	(1.49183)	(0.881073)	(0.64731)	(0.522072)	(0.420786)	(0.315119)	(0.23079)	(0.179679)	(0.137926)	(SDRL)
		3.15E-07	7.62E-07	7.25E-07	6.69E-07	5.58E-07	5.42E-07	9.25E-07	5.88E-07	5.54E-07	5.68E-07	5.29E-07	ATS
		(2.34E-06)	(7.55E-06)	(3.41E-06)	(3.60E-06)	(3.03E-06)	(2.99E-06)	(9.43E-06)	(3.10E-06)	(2.99E-06)	(3.03E-06)	(2.94E-06)	(SDTS)
30	51	490.549	9.766	4.7005	3.0601	2.1493	1.6644	1.309	1.0308	0.9438	0.8303	0.6172	ARL
		(472.874)	(3.371)	(1.301)	(0.861677)	(0.644678)	(0.57059)	(0.493071)	(0.372091)	(0.3642)	(0.406327)	(0.490371)	(SDRL)
		3.44E-07	3.28E-07	3.27E-07	3.40E-07	3.53E-07	3.36E-07	5.33E-07	4.09E-07	4.01E-07	3.78E-07	3.57E-07	ATS
		(2.37E-06)	(2.31E-06)	(2.31E-06)	(2.35E-06)	(2.39E-06)	(2.34E-06)	(7.28E-06)	(2.57E-06)	(2.56E-06)	(2.48E-06)	(2.44E-06)	(SDTS)
40	104.8	550.602	10.1719	5.6892	3.5607	2.7699	2.1549	1.6974	1.3898	1.1228	1.0275	0.9842	ARL
		(542.454)	(2.58313)	(1.13649)	(0.717715)	(0.599962)	(0.48673)	(0.499633)	(0.491992)	(0.341057)	(0.249286)	(0.230544)	(SDRL)
		3.07E-07	3.84E-07	6.50E-07	3.58E-07	3.71E-07	3.67E-07	5.29E-07	5.07E-07	3.58E-07	4.29E-07	3.62E-07	ATS
		(2.24E-06)	(2.50E-06)	(1.16E-05)	(2.42E-06)	(2.45E-06)	(2.44E-06)	(4.22E-06)	(2.92E-06)	(2.41E-06)	(2.79E-06)	(2.43E-06)	(SDTS)
50	169.5	454.27	9.9823	5.8387	4.0167	2.9774	2.4399	2.0352	1.7157	1.3985	1.1213	1.0251	ARL
		(432.075)	(2.00589)	(0.960564)	(0.680603)	(0.53767)	(0.515546)	(0.3717)	(0.464407)	(0.489998)	(0.329221)	(0.182948)	(SDRL)
		3.24E-07	2.97E-07	3.41E-07	3.50E-07	3.28E-07	2.86E-07	4.39E-07	3.03E-07	3.26E-07	3.31E-07	3.08E-07	ATS
		(2.30E-06)	(2.21E-06)	(2.36E-06)	(2.39E-06)	(2.31E-06)	(2.16E-06)	(6.30E-06)	(2.22E-06)	(2.30E-06)	(2.32E-06)	(2.24E-06)	(SDTS)

Observation of the individual performance of the each loss function showed that for the PLF, the SDRL values decreased as we increased the sample size and the LLF performed sub-par compared to the other loss functions based on ARL values.

5.3 Results plots

We plot the ARL values against mean shifts for each hyper-parameter scenario to visualize the data given in the previous tables. For each plot in both Figures 1 and 2, we zoom in on the first three mean shift values to observe the initial drop in ARLs. Beyond the initial drop in ARLs, the curve flattens for each chart. Figure 1 represents data given in Table 10, and we see that compared to the Bayesian charts, the classical CUSUM chart requires a larger shift to signal out-of-control. All three variations of the Bayesian CUSUM chart are near zero after the smallest shift is introduced.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

CUSUM PG ARL comparisons

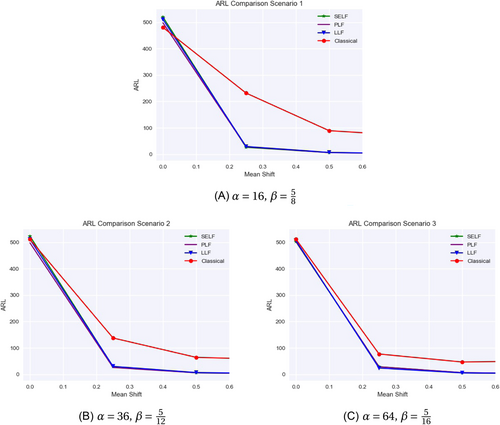
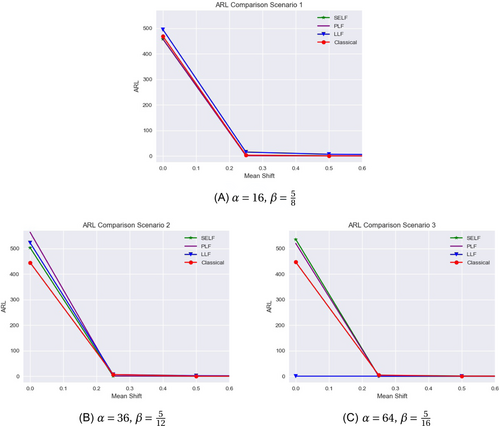
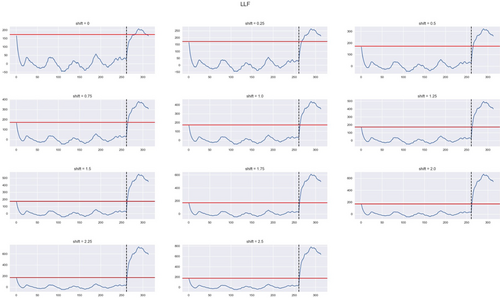
Table 12 data are represented in Figure 2 showing that the Bayesian charts, along with the classical chart, achieve a low ARL once the first/smallest shift happens. The curve for the LLF in the 3rd scenario is flat across as we saw in Section 5.2, likely due to the choice of the constant, c.

6 REAL DATA ANALYSIS

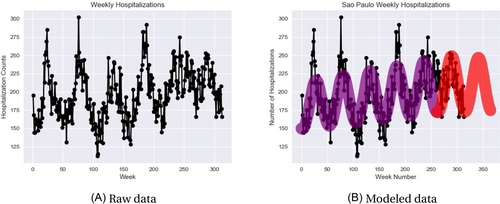
We consider our method on a dataset found at https://www2.datasus.gov.br seen in Alencar et al.¹² and Urbieta et al.¹³. The data are count series of respiratory disease-related hospitalizations for people over 65 years old in São Paulo, Brazil. Originally, data were collected to represent daily counts from January 2006 to December 2011, but we chose to look at the weekly average of hospitalizations, totaling 313 weeks. In Figure 3 we show the week plotted against the average weekly count, observing that the weekly average has a positive linear trend and a seasonal pattern over time. That is, there are a greater number of hospitalizations in the São Paulo winter months (June–August) than in their summer months (December–February).

Since we have count data with dispersion present, we consider the negative binomial distribution with our generalized linear model. We account for the seasonal pattern using the sine and cosine functions. Population is used as an offset variable along with the log link function to properly model hospitalization rate per 100,000 inhabitants. We assume that counts for January 2006 to December 2010 are nonepidemic and use this to construct the model. We validate our model using the weekly data for 2011 and predict weekly counts for 2012.

\begin{equation} \begin{aligned} ln{\left[ 100,000 * \frac{\mu _{0,t}}{P_{t}}\right]} = \beta _{0} + \beta _{1} \sin {\left(\frac{ 2\pi t }{52} \right)} + \beta _{2} \cos {\left(\frac{ 2\pi t }{52} \right)} \end{aligned} \end{equation}

(6)

where, μ_{0, t} is the nonepidemic average number of hospitalizations and P_t is the population size for week t, and 52 represents the seasonal period. This model follows the same make up as what is seen in Urbieta et al.¹³, however, since we do not consider daily counts, we do not use day-of-week dummy variables.

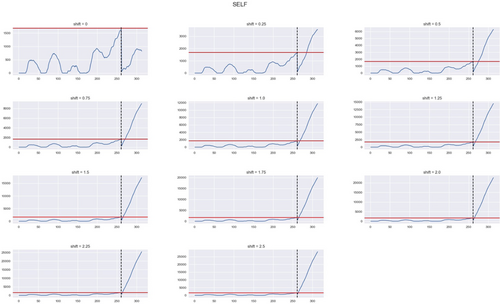
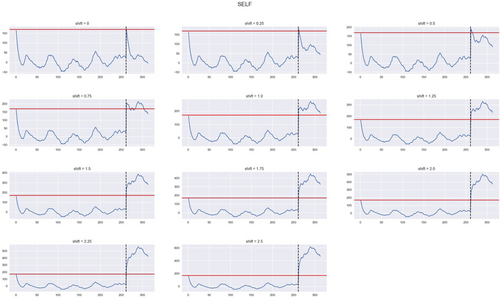
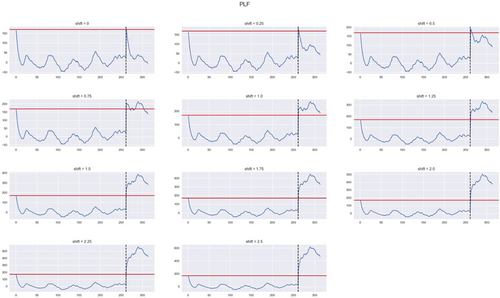
Figures 4-6 track the weekly number of hospitalizations for January 2006 to December 2011. Without an induced shift, the weekly data for 2011 fall below the upper control limit under the SELF and PLF chart, but once a shift occurs both charts signal out-of-control. However, under the LLF chart, a breach of the control limit occurs regardless if a shift was imposed, and this is likely a result of the chosen value for c. For each variation of the chart, as we increase the shift size, the out-of-control detection of the charts occurs earlier. We observe a delay in detection at the beginning of 2011 because of the seasonal affects. Although we increase the counts via our shifts, in application, it is not alarming that hospitalizations would increase by 25\% or 50\% per 100,000 inhabitants.

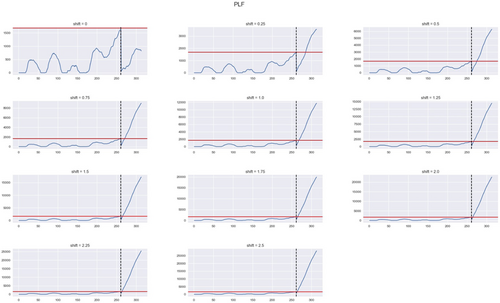
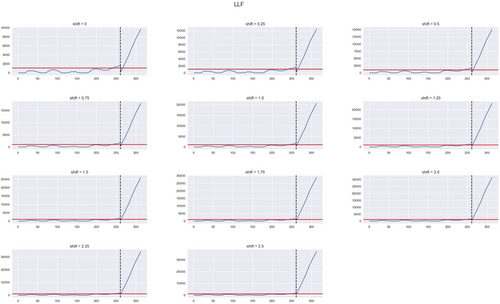
Below in Figures 7-9 are the results for the hospitalization data under each of the loss functions using the EWMA control chart with shift increments added. Under the SELF and PLF cases, we notice that both charts detect an epidemic after the initial shift of 0.25 is implemented. For the LLF chart, it detects an epidemic without any shift, which indicates that the user-defined c parameter for the LLF may need to be adjusted.

7 DISCUSSION

In our work, we examined the detection capabilities of the EWMA and CUSUM charts under different loss functions for the Normal–Normal and Poisson–Gamma conjugate cases. We conducted simulations, implementing shifts on the in-control mean, while adjusting the hyper-parameter values and the sample size. The performance measurements used were the ARL, SDRL, ATS, and the SDTS, which were recorded for the in-control case and each of the out-of-control shifts. After simulation results were analyzed, we tested the charts' ability to detect epidemic-like instances on respiratory-disease-related hospitalizations for seniors in São Paulo, Brazil.

7.1 EWMA charts

From the simulation study and real data analysis, the squared error and PLFs performed similarly, with the PLF having better ARL results and the SELF out-performing overall. The LLF had suboptimal results in both simulation studies and the real data analysis compared to the other options. In the hyper-parameter study, calculations for the ARL and SDRL for $\alpha _{0} = 64, \beta _{0} = \frac{5}{16}$ resulted in either zeros or unending simulations. Compared to the classical EWMA chart, the SELF and PLF are ideal substitutes when considering count series data, while the LLF performed roughly the same. It is also important to note that simulations for the classical EWMA required significantly more runs than the Bayesian charts. We recommend the use of the SELF Bayesian control chart as it performed the best in most of the measurement criteria. The PLF would be the best option for use of an asymmetric loss function, and we only recommend the LLF when a valid study is done to attain the c value.

7.2 CUSUM charts

We constructed Bayesian CUSUM control charts with the use of the self-error, precautionary, and LLFs. Our objective was to assess the detection capabilities of the charts under the Gaussian conjugate and Poisson conjugate cases. The performance measurements for our study were the ARL, SDRL, ATS, and SDTS. Based on these measurements, we recommend the use of any of the three CUSUM control charts. Each performed well in obtaining the desired ARL₀ and detecting a shift in the mean, while maintaining a relatively low ATS. We applied the charts to a count series dataset and analyzed their real-world capabilities. All the charts quickly detected the out-of-control occurrences, and the squared error and PLFs performed similarly in tracking in-control and out-of-control occurrences. The LLF signaled early in the in-control and out-of-control scenarios. This is because it is exponential in nature due to the chosen value of its constant, c and signifies overestimation over underestimation. Overall, we recommend the use of any of the control charts under different distributions and regardless of the sample size and hyper-parameters.

8 FUTURE DIRECTION

The EWMA and CUSUM control charts are made for tracking univariate data and have modified alternatives that can be used for tracking data with more than a single variable. Future directions of this work includes using these modified charts, mCUSUM and mEWMA, under similar Bayesian methods used in this paper to create a multivariate Bayesian control chart. While recent works by Noor et al.¹⁴ and Noor-ul Amin and Noor¹⁵ have created Bayesian EWMA charts, there is a piece of the literature missing on creating multivariate versions. We also recognize a lack in Bayesian mEWMA and mCUSUM charts for monitoring nonparametric and semi-parametric models.

APPENDIX A

A.1 Poisson–Gamma derivations

Poisson likelihood:

\begin{align} x|\lambda \sim \textit{Pois}\textit{son}(\lambda )\nonumber\\ \displaystyle f(x|\lambda )=\frac{{e}^{-n\lambda}{\lambda}^{{\sum}_{i=1}^{n}{x}_{i}}}{\displaystyle\prod _{i=1}^{n}{x}_{i}!} \end{align}

(A1)

Gamma prior:

\begin{equation} \begin{aligned} \lambda \sim Gamma(\alpha , \beta )\\ f(\lambda ) = \frac{\beta ^{\alpha }}{\Gamma (\alpha )} \lambda ^{\alpha - 1} e^{-\beta \lambda } \end{aligned} \end{equation}

(A2)

Gamma posterior:

\begin{equation} \begin{aligned} \lambda |x \sim Gamma(n \bar{x} + \alpha , n+ \beta )\\ f(\lambda |x) = \frac{\beta ^{\alpha }}{\Gamma (\alpha )} \lambda ^{(n \bar{x} + \alpha ) - 1} e^{-(n + \beta ) \lambda } \end{aligned} \end{equation}

(A3)

Posterior predictive for Poisson conjugate:

\begin{equation} \begin{aligned} y|x \sim Poisson(\lambda )\\ f(y|x) = \frac{e^{-\lambda } \ \ \lambda ^{y}}{y!}\\ \end{aligned} \end{equation}

(A4)

\begin{equation} \begin{aligned} f(y|x) &= \int f(\lambda |x)f(y|\lambda ) d\lambda \\ &= \int \frac{(\beta + n)^{n \bar{x} + \alpha }}{\Gamma (n \bar{x} + \alpha )} e^{-(n + \beta )\lambda } \lambda ^{(n \bar{x} + \alpha ) - 1} \frac{e^{-\lambda } \ \ \lambda ^{y}}{y!} d\lambda \\ &= \frac{(\beta + n)^{n \bar{x} + \alpha }}{\Gamma (n \bar{x} + \alpha )y!} \int e^{-(n + \beta )} e^{-\lambda } \lambda ^{(n \bar{x} + \alpha ) - 1} \lambda ^{y} d\lambda \\ &\text{let c = } \frac{(\beta + n)^{n \bar{x} + \alpha }}{\Gamma (n \bar{x} + \alpha )y!}, \ \ c \int e^{-(n + \beta ) \lambda - \lambda } \lambda ^{(n \bar{x} + \alpha ) - 1 + y} d\lambda \\ &= c \int e^{-(n + \beta + 1) \lambda } \lambda ^{(n \bar{x} + y + \alpha ) - 1} d\lambda \\ &= \frac{(\beta + n)^{n \bar{x} + \alpha }}{\Gamma (n \bar{x} + \alpha )y!} \cdot \frac{\Gamma (n \bar{x} + \alpha ) + y}{(\beta + n + 1)^{n \bar{x} + \alpha + y}}\\ &= \frac{\Gamma (n \bar{x} + \alpha + y)}{\Gamma (n \bar{x} + \alpha )y!} \cdot \frac{(\beta + n)^{n \bar{x} + \alpha }}{(\beta + n + 1)^{n \bar{x} + \alpha + y}}\\ &= \frac{(n \bar{x} + \alpha + y)!}{(n \bar{x} + \alpha )!y!} \cdot {\left(\frac{\beta + n}{\beta + n + 1}\right)}^{n \bar{x} + \alpha } {\left(\frac{1}{\beta + n + 1}\right)}^{y}\\ &\binom{n \bar{x} + \alpha + y - 1}{y - 1} \cdot {\left(1- \frac{1}{\beta + n + 1} \right)}^{n \bar{x} + \alpha } {\left(\frac{1}{\beta + n + 1}\right)}^{y} \end{aligned} \end{equation}

(A5)

\begin{equation} \begin{aligned} f(y|x) = \binom{n \bar{x} + \alpha + y - 1}{y-1}&{\left(1 - \frac{1}{\beta + n + 1}\right)}^{n \bar{x} + \alpha } {\left(\frac{1}{\beta + n + 1}\right)}^{y}\\ y|x &\sim NegBin(n \bar{x} + \alpha , n+ \beta ) \end{aligned} \end{equation}

(A6)

A.1.1 Loss functions best estimators

SELF:

\begin{equation} \begin{aligned} \hat{\lambda }^{*} = E[\lambda |x] = \frac{n \bar{x} + \alpha }{n + \beta },\\ {\left[ \mu _{SELF, PG} = \hat{\lambda }^{*} = \frac{n \bar{x} + \alpha }{n + \beta } \right]} \end{aligned} \end{equation}

(A7)

PLF:

\begin{equation} \begin{aligned} \hat{\lambda }^{*} &= \sqrt {E[\lambda ^{2}|x]}\\ VAR[\lambda |x] &= E[\lambda ^{2}|x] - E[\lambda |x]^{2}\\ \frac{n \bar{x} + \alpha }{(n + \beta )^{2}} &= E[\lambda ^{2}|x] - {\left(\frac{n \bar{x} + \alpha }{n + \beta } \right)}^{2}\\ \frac{n \bar{x} + \alpha }{(n + \beta )^{2}} &= E[\lambda ^{2}|x] - \frac{(n \bar{x} + \alpha )^{2}}{(n + \beta )^{2}}\\ E[\lambda ^{2}|x] &= \frac{(n \bar{x} + \alpha ) + (n \bar{x} + \alpha )^{2}}{(n + \beta )^{2}}\\ \sqrt { E[\lambda ^{2}|x] }& = \sqrt { \frac{(n \bar{x} + \alpha ) + (n \bar{x} + \alpha )^{2}}{(n + \beta )^{2}} }\\ &{\left[ \mu _{PLF, PG} = \hat{\lambda }^{*} = \frac{\sqrt { (n \bar{x} + \alpha ) + (n \bar{x} + \alpha )^{2}} }{(n + \beta )} \right]} \end{aligned} \end{equation}

(A8)

LLF:

\begin{equation} \begin{aligned} \hat{\lambda }^{*} &= -\frac{1}{c}ln {\left[ E[e^{-c\lambda }] \right]}\\ E[e^{-c\lambda }] &= \int e^{-c \lambda } \cdot \frac{\beta ^{\alpha }}{\Gamma (\alpha )} \lambda ^{\alpha - 1} e^{-\beta \lambda } d\lambda \\ &= \frac{\beta ^{\alpha }}{\Gamma (\alpha )} \int e^{-c \lambda } \lambda ^{\alpha - 1} e^{-\beta \lambda } d\lambda \\ &= \frac{\beta ^{\alpha }}{\Gamma (\alpha )} \int e^{-(c + \beta ) \lambda } \lambda ^{\alpha - 1} d\lambda \\ &= \frac{\beta ^{\alpha }}{{ \Gamma (\alpha )} } \cdot \frac{{\Gamma (\alpha )}}{(c+ \beta )^{\alpha }}\\ &{\left[ \mu _{LLF, PG} = \hat{\lambda }^{*} = -\frac{1}{c}ln {\left[\frac{\beta ^{\alpha }}{(c + \beta )^{\alpha }} \right]} \right]} \end{aligned} \end{equation}

(A9)

A.1.2 Solving for α and β

Given μ₀ = [10, 15, 20] and $\sigma^{2}_{0}= [16, 36, 64]$ :

\mu _{0} = 10, \ \sigma^{2}_{0} = 16

\begin{equation} \begin{aligned} 10 &= \frac{\alpha }{\beta } \Rightarrow \alpha = 10\beta \\ 16 &= \frac{\alpha }{\beta ^{2}} \Rightarrow 16 = \frac{10 \beta }{\beta ^{2}} \Rightarrow {\left[ \beta = \frac{5}{8} \right]} \\ 10 &= \frac{\alpha }{5/8} \Rightarrow {\left[ \alpha = 16 \right]} \end{aligned} \end{equation}

(A10)

\mu _{0} = 15, \ \sigma^{2}_{0} = 36

\begin{equation} \begin{aligned} 15 &= \frac{\alpha }{\beta } \Rightarrow \alpha = 15\beta \\ 36 &= \frac{\alpha }{\beta ^{2}} \Rightarrow 36 = \frac{15 \beta }{\beta ^{2}} \Rightarrow {\left[ \beta = \frac{5}{12} \right]} \\ 15 &= \frac{\alpha }{5/12} \Rightarrow {\left[ \alpha = 36 \right]} \end{aligned} \end{equation}

(A11)

\mu _{0} = 20, \ \sigma^{2}_{0} = 64

\begin{equation} \begin{aligned} 20 &= \frac{\alpha }{\beta } \Rightarrow \alpha = 20\beta \\ 64 &= \frac{\alpha }{\beta ^{2}} \Rightarrow 64 = \frac{15 \beta }{\beta ^{2}} \Rightarrow {\left[ \beta = \frac{5}{16} \right]} \\ 20 &= \frac{\alpha }{5/16} \Rightarrow {\left[ \alpha = 64 \right]} \end{aligned} \end{equation}

(A12)

Biographies

Chelsea Jones, Ph.D., is a recent graduate from the Systems Modeling and Analysis program at Virginia Commonwealth University (2021). She holds a BS (2016) in Actuarial Science with a minor in Computer Science from Virginia State University. Her research interests include statistical process control, profile monitoring, nonparametric statistics, semiparametric statistics, and Bayesian statistics. Currently, she is serving on a Fulbright Grant at the University of the Philippines Diliman (UPD) in Manila, Philippines.
Abdel-Salam G. Abdel-Salam, Ph.D., is an Associate Professor of Statistics and, Head of the student data management section, Student Experience Department, VP for Student Affairs at Qatar University. He holds BS and MS (2004) degrees in Statistics from Cairo University and MS (2006) and Ph.D. (2009) degrees in Statistics from Virginia Tech. Dr Abdel-Salam is a member of the American Society for Quality and the American Statistical Association. His research interests include all aspects of industrial statistics, including statistical process control, multivariate analysis, mixed models, profile monitoring and Health-related monitoring, and prospective public health surveillance.
D'Arcy Mays, Ph.D., is a Professor of statistics in the Department of Statistical Sciences and Operations Research. He is the founding chair of the department and served as chair from 2001 to 2021. His research areas include regression analysis, design and analysis of experiments, and response surface methodology, and he is focused on two-stage experimental designs in the presence of nonstandard conditions to include heterogeneous variance. He also has numerous publications with students in many disciplines and provides statistical expertise to the projects.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

Supporting Information

REFERENCES

1Shewhart WA. Quality control charts. Bell Syst Tech J. 1926; 5(4): 593-603.
10.1002/j.1538-7305.1926.tb00125.x
Google Scholar
2Page ES. Continuous inspection schemes. Biometrika. 1954; 41(1/2): 100-115.
10.2307/2333009
Web of Science® Google Scholar
3Roberts S. Control chart tests based on geometric moving averages. Technometrics. 1959; 1(3): 239-250.
10.1080/00401706.1959.10489860
Google Scholar
4Woodall WH. Current research on profile monitoring. Producao. 2007; 17(3): 420-425.
10.1590/S0103-65132007000300002
Google Scholar
5Woodall WH, Montgomery DC. Some current directions in the theory and application of statistical process monitoring. J Qual Technol. 2014; 46(1): 78-94.
10.1080/00224065.2014.11917955
Web of Science® Google Scholar
6Woodall WH. Faltin FW. Rethinking control chart design and evaluation. Qual Eng. 2019; 31(4): 596-605.
10.1080/08982112.2019.1582779
Web of Science® Google Scholar
7Jones CL, Abdel-Salam A-SG, Mays D. Practitioners guide on parametric, nonparametric, and semiparametric profile monitoring. Qual Reliab Eng Int. 2021; 37(3): 857-881.
10.1002/qre.2770
Web of Science® Google Scholar
8Ali S. A predictive Bayesian approach to EWMA and CUSUM charts for time-between-events monitoring. J Stat Comput Simul. 2020; 90(16): 3025-3050.
10.1080/00949655.2020.1793987
Web of Science® Google Scholar
9Aslam M, Anwar SM. An improved Bayesian modified-EWMA location chart and its applications in mechanical and sport industry. PloS One. 2020; 15(2):e0229422.
10.1371/journal.pone.0229422
CAS PubMed Web of Science® Google Scholar
10Riaz S, Riaz M, Hussain Z, Abbas T. Monitoring the performance of Bayesian EWMA control chart using loss functions. Comput Ind Eng. 2017; 112: 426-436.
10.1016/j.cie.2017.08.023
Web of Science® Google Scholar
11Norstrom JG. The use of precautionary loss functions in risk analysis. IEEE Trans Reliab. 1996; 45(3): 400-403.
10.1109/24.536992
Web of Science® Google Scholar
12Alencar AP, Lee Ho L, Albarracin OYE. Cusum control charts to monitor series of negative binomial count data. Stat Methods Med Res. 2017; 26(4): 1925-1935.
10.1177/0962280215592427
PubMed Web of Science® Google Scholar
13Urbieta P, Lee HO L, Alencar A. CUSUM and EWMA control charts for negative binomial distribution. Qual Reliab Eng Int. 2017; 33(4): 793-801.
10.1002/qre.2057
Web of Science® Google Scholar
14Noor S, Noor-ul Amin M, Abbasi SA. Bayesian EWMA control charts based on exponential and transformed exponential distributions. Qual Reliab Eng Int. 2021; 37(4): 1678-1698.
10.1002/qre.2820
Web of Science® Google Scholar
15Noor-ul Amin M, Noor S. Bayesian EWMA control chart with measurement error under different loss functions. Qual Reliab Eng Int. 2021; 37(8): 3362-3380.
10.1002/qre.2922
Web of Science® Google Scholar

Citing Literature

Volume39, Issue1

February 2023

Pages 164-189

Novel Bayesian CUSUM and EWMA control charts via various loss functions for monitoring processes

Abstract

1 INTRODUCTION